 Open Access Article
Open Access ArticleA microscopic view on the large scale chain dynamics in nanocomposites with attractive interactions
Thomas Glomanna,
Adrian Hamma,
Jürgen Allgaiera,
Eike G. Hübnerd,
Aurel Radulescub,
Bela Faragoc and
Gerald J. Schneider*b
aJülich Centre for Neutron Science (JCNS-1) & Institute for Complex Systems (ICS-1), Forschungszentrum Jülich, Jülich, Germany
bJülich Centre for Neutron Science (JCNS) at Heinz Maier-Leibnitz Zentrum, Lichtenbergstraße 1, 85747 Garching, Germany. E-mail: g.j.schneider@fz-juelich.de
cInstitut Laue-Langevin (ILL), 6 rue Jules Horowitz, 38000 Grenoble, France
dTechnische Universität Clausthal, Institut für Organische Chemie, Leibnizstraße 6, 38678 Clausthal-Zellerfeld, Germany
First published on 13th August 2013
Abstract
We use neutron spin-echo spectroscopy to investigate the large scale chain dynamics in unentangled polymer nanocomposites where stable polymer layers around nanoparticles are dynamically formed due to attractive segment–surface interactions. The work here focuses on the detailed microscopic characterization of the dynamics within these layers of bound poly(ethylene glycol) (PEO) and poly(butylene oxide) (PBO) chains at a fixed silica nanoparticle fraction of 15%. The substitution of hydroxy by methoxy terminated chains thereby clearly evidences the importance of the chain end chemistry in these systems as the layer structure and dynamics therein significantly depend on the specific interaction mechanism. The experimental data reveal a densely packed thick shell of end-attached chains in the case of hydroxy ends contrasted by a thin shell of laterally adsorbed chains with multiple attachments in the methoxy case. In all cases a consistent quantitative modeling is presented that evidences unchanged segmental dynamics within the bound layers. The obtained picture is further validated on an independent model system based on PBO polymers which shows surprisingly similar chain dynamics as for PEG in the nanocomposite pointing to a very generic dynamic scenario.
Introduction
Polymer nanocomposites (PNCs) promise substantially improved material properties such as increased tensile strength, abrasion resistance, conductivity and gas barrier properties by adding small fractions of nano-sized particles.1 In contrast to microcomposites with particle sizes or aggregates on the micron scale, surface interactions between the particles and polymer segments are non-negligible due to the large surface-to-volume ratios and close inter-particle distances comparable to the dimensions of the embedding polymer chains.In poly(ethylene oxide)–silica nanocomposites it is well known that the strong attractive interactions cause polymer chains to adsorb onto the particle surface which can enhance the colloidal stability against coagulation by steric repulsion between adsorbed polymer layers but it can also lead to destabilization by bridging flocculation when the surface separation distance is on the order of the chain end-to-end distance.2–9
Although extensive research in the field of PNCs has led to substantial progress toward the physical understanding of the interrelation of polymer–filler affinity, the filler structure and rheological properties of filled polymer melts, the microscopic dynamics of the underlying polymer phase and the interaction mechanisms remain poorly understood. For instance the polymer reference interaction site model (PRISM) is able to predict equilibrium properties of the composite microstructure with near-quantitative precision for low-molecular weight PEG liquids.10 However, non-equilibrium chain adsorption was found to occur if the molecular weight increases as reported recently by Zukoski.11 The non-equilibrium adsorption leads to a net attraction between particles that promotes particle gelation as the polymer segment–particle surface energy εpc effectively decreases.11
Network formation and gelation by polymer bridges above a certain particle fraction was also reported by Kim et al.12 using NMR investigations on entangled PEO–silica nanocomposites. They correlate the onset of polymer network formation with the changes in the viscoelastic properties as reported by Anderson and Zukoski13 that is found to coincide with ductile to brittle transition.12
While there seems to be general agreement on the identification of polymer–particle networks as the microscopic origin of the macroscopic reinforcement effect12,14–20 a full molecular understanding of the structural and in particular dynamical properties within the adsorbed polymer layers is yet to be achieved as often apparently contradictory results are presented. Fully atomistic molecular dynamics simulation by Barbier et al. highlights the particular role of chain end groups in the interaction mechanism by showing that hydrogen bonding interactions may be the strongest for hydroxy terminated ends.21 Recent NMR investigations of PEO–silica nanocomposites ascribed “glassy” (immobilized) dynamics to a nanometer thick strongly adsorbed layer around the particles that is independent of molecular weight and chain end groups.12 Experimental investigations of the polymer conformation using scattering techniques revealed a layer of bound polymer with an altered segment density in agreement with PRISM theory calculations.22–24 Computer simulations found no change of the average Gaussian chain structure but show effectively slowed Rouse dynamics and enhanced entanglement density in the vicinity of the particles.25–27
In order to resolve these issues experimental techniques with spatial and temporal resolution on the length and time scale of the polymer chain relaxation are necessary. For instance, the neutron spin-echo technique has been proven to yield detailed insight into the dynamics of the polymer phase in nanocomposites as was shown earlier for a model system with essentially repulsive polymer–particle interactions.28–30 Recently, high resolution neutron spectroscopic investigations of attractively interacting PEG–silica nanocomposites revealed a very rich dynamical picture.31 The polymer dynamics was interpreted by a two-phase model assuming a free bulk phase with suppressed translational diffusion and a layer of the adsorbed polymer that, however, remains internally highly mobile on the segmental scale.31 The large scale chain dynamics was found to depend strongly on the chain end termination and thus the interaction mechanisms.31
Here, we elaborate on the large scale chain dynamics of these unentangled poly(ethylene glycol) (PEG) nanocomposites31 and present a comprehensive model analysis in terms of the above mentioned two-phase model.31 The high space and time resolution of neutron spin-echo (NSE) spectroscopy is used to resolve and distinguish the chain center-of-mass diffusion as well as the internal polymer chain relaxation dynamics. The interaction mechanisms between the polymer segments and the particle surface are scrutinized by varying the chain termination from hydroxy (OH) to methoxy (CH3) groups, leading to substantial differences in the dynamics of the nanocomposites. For both cases, a detailed model picture of the structure and dynamics within the adsorbed layers is deduced and discussed in detail.
In addition, we compare the results to dynamic data on a further model nanocomposite based on poly(butylene oxide) (PBO) that is expected to have comparable segment–surface interaction strengths as the chemically similar PEG. It has the unique advantage to allow future complementary rheology and dielectric spectroscopy experiments which make PBO–silica an ideal model system to bridge the gap between the investigations on the microscopic and the macroscopic scale.
Theoretical background
Neutron scattering
Neutron scattering techniques reveal the spatially averaged microscopic structure and dynamics of soft matter materials with a spatial and temporal resolution determined by the momentum transfer![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i −
i − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s and energy transfer E = ħω between the incident and scattered neutrons with wavelength λ = 2π/|
s and energy transfer E = ħω between the incident and scattered neutrons with wavelength λ = 2π/|![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |. The direction of the wave vector
|. The direction of the wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) points along the flight path of the neutrons which scatter from the atomic nuclei in the sample into the solid angle dΩ. The double differential cross-section d2σ/dΩdE (scattering probability) can be expressed in terms of the dynamic structure factor S(Q, ω):
points along the flight path of the neutrons which scatter from the atomic nuclei in the sample into the solid angle dΩ. The double differential cross-section d2σ/dΩdE (scattering probability) can be expressed in terms of the dynamic structure factor S(Q, ω):
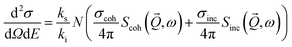 | (1) |
The coherent and incoherent dynamic structure factors
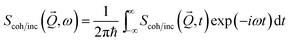 | (2) |
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , t), which express the response functions as thermal averages of the time-dependent pair- and self-correlation function of the position operators
, t), which express the response functions as thermal averages of the time-dependent pair- and self-correlation function of the position operators ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) of the N scattering centers (monomers)
i(t) of the N scattering centers (monomers)
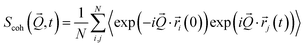 | (3) |
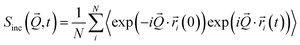 | (4) |
In that sense the double differential cross-section can be seen as the linear response of the sample to the spectrum of spontaneous microscopic fluctuations as stated by the fluctuation–dissipation theorem.
The intermediate scattering function S(Q, t) is directly recorded by the neutron spin-echo technique which exploits the precession of the neutron spin in a magnetic field to achieve the highest energy resolution. As the incoherent scattering process flips the spin with a probability of 2/3 the measured normalized S(Q, t)/S(Q) function is given by
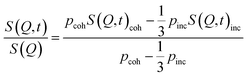 | (5) |
Single particle form factor P(Q)
For elastic scattering (no energy transfer) the momentum transfer Q = 4π/λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Θ/2) is related to the scattering angle Θ and the wavelength λ. The single particle form factor P(Q) for homogeneous isotropic spheres with radius R is given by:
sin(Θ/2) is related to the scattering angle Θ and the wavelength λ. The single particle form factor P(Q) for homogeneous isotropic spheres with radius R is given by:
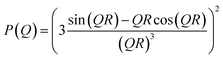 | (6) |
The finite size polydispersity of actual nanoparticles can be described by integrating the monodisperse form factor P(Q) over the log-normal distribution density function D(r, R, σ) with the median R and the width parameter σ:
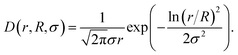 | (7) |
The arithmetic mean or expected value 〈R〉 and the N-th moment 〈RN〉 of the distribution are given by
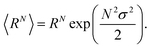 | (8) |
For a dilute suspension of polydisperse particles in a solvent the absolute scattering intensity I(Q) depends on the particle concentration ϕp, particle volume Vp and the scattering contrast Δρ = ρp − ρs between the scattering length densities of the particles ρp and the solvent ρs:
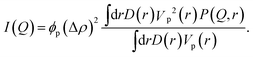 | (9) |
Gaussian conformation – structure factor S(Q)
The conformation of polymer chains in the melt obeys Gaussian statistics with the polymer radius of gyration being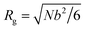 . The structure factor Sc(Q) for the finite-length Gaussian chain is given by32
. The structure factor Sc(Q) for the finite-length Gaussian chain is given by32
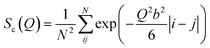 | (10) |
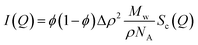 | (11) |
Rouse model – intermediate scattering function S(Q, t)
The idealized Rouse model describes the dynamics of a Gaussian chain in a heat bath with temperature T representing the surrounding melt chains. The chain is coarse-grained into N Gaussian sub-segments of mean statistical segment size b with temperature-dependent friction coefficient ζ. Entropic forces originating from conformational fluctuations and stochastic frictional forces from the heat bath drive the dynamics. The model's solutions are given by N internal chain relaxation (Rouse) modes p with relaxation times τp = τR/p2 = (ζN2b2)/(3π2kBTp2) and by the translational chain center-of-mass diffusion with diffusion coefficient DR. The Rouse time τR denotes the longest relaxation time (p = 1) after which all internal modes of the chain have fully relaxed.The Rouse dynamics in terms of the coherent intermediate scattering function S(Q, t) is given by:33
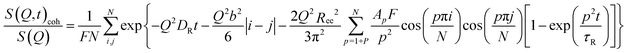 | (12) |
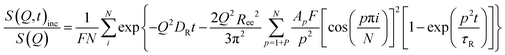 | (13) |
Experimental
Materials and preparation
The experiments were performed on model nanocomposites comprising monodisperse poly(ethylene glycol) (PEG) and poly(butylene oxide) (PBO) polymers and colloidal silica nanoparticles. Hydrogenous (h) and deuterated (d) polymers were synthesized in our lab by anionic polymerization and characterized by size exclusion chromatography. h-PEG–OH was purchased from Merck. The polymers are below the entanglement molecular weight with an average number n = 45 ± 4 monomers corresponding to MPEGw = 2 kg mol−1 and MPBOw = 3 kg mol−1. The PEG chain contains either two hydroxy groups (PEG–OH) or two methoxy groups (PEG–CH3). The PBO chains contain at one end a hydroxy group and at the other chain end a tert-butoxy group (OC4H9).The detailed characterization of the polymers is summarized in Table 1.
Charge stabilized silica nanoparticles in solution of either water (SNOWTEX® ST-40 for PEGs) or isopropanol (ORGANOSILICASOL™ Ipa-ST for PBOs) were obtained from Nissan Chemical. The particle diameters and polydispersity were determined by fitting neutron small-angle scattering data of diluted particle solution (0.05%) in respective deuterated solvents with the single particle form factor given by eqn (6) as shown in Fig. 1(a). The average diameter for both species yields 〈D〉 = 12.9 ± 0.1 nm corresponding to a specific surface area of about 200 m2 g−1. The width of the log-normal size distribution (eqn (9)) is σ = 0.30 ± 0.01. The neutron scattering length densities ρST-40 = 3.69 × 1010 cm−2 and ρIpa-ST = 3.48 × 1010 cm−2 were obtained from the evaluation of the minimum ΦH,0 in the intensity of the respective contrast variation series in solution as shown in Fig. 1(b).
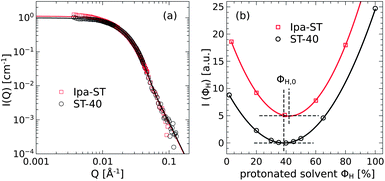 | ||
| Fig. 1 (a) The superposition of the SANS data of the Ipa-ST and ST-40 particles directly shows identical particles. The lines are fits with the spherical particle form factor P(Q) with polydispersity. (b) The coherent scattering intensities of both particle species were measured for various hydrogenous/deuterated water (ST-40) and isopropanol (Ipa-ST) ratios. The minima of the parabolas (lines) denote the zero average contrast condition in solution. | ||
The matrices and nanocomposites with about 15 vol% silica fraction were prepared under the silica contrast matching conditions by first blending hydrogeneous and deuterated polymers in solution and then adding the silica nanoparticle solution. Immediate rapid shaking after addition of the silica yielded a homogenous transparent solution which was then stirred for another 12–24 h. The solvent was removed by either freeze-drying (PEG samples) or by rapid solvent removal by blowing off isopropanol with an argon gas stream and subsequent drying in a vacuum oven at 60 °C (PBO samples). The nanocomposites were then further dried under vacuum (<10−4 mbar) until a constant sample weight was obtained. The preparation of the PEG–OH sample was conducted under dilute conditions with a solvent-to-PEG ratio of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 while the PEG–CH3 and PBO samples were mixed in the semi-dilute regime with a 4
1 while the PEG–CH3 and PBO samples were mixed in the semi-dilute regime with a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The details of the sample composition are summarized in Table 2.
1 ratio. The details of the sample composition are summarized in Table 2.
Neutron spin-echo spectroscopy (NSE)
The large scale dynamics of the polymers was measured using the IN15 spectrometer at the Institute Laue-Langevin in Grenoble, France. For the NSE experiments the samples were filled into top-loading niobium containers with a sample thickness of 1 mm ensured by glass spacers. In order to prevent sample degradation at the high temperatures of the measurement the preparation was done in a glove box under an argon atmosphere and the cells were tightly sealed by Teflon strips. While the amorphous liquid-like PBO samples required no special treatment the crystalline PEG nanocomposites were premoulded to the desired shape at about 80–100 °C in order to fill the containers homogeneously.The accessible time range from 0.1 to 220 ns was obtained by measuring at two wavelengths λ = 8 and 16 Å. Momentum transfers Q in the range from 0.05 to 0.2 Å−1 were measured at a temperature of 413 K by installing the samples in an electrically controlled and evacuated furnace with an equilibration time of about 45–60 min to ensure a stable sample temperature (±1 K). For the background corrections deuterated PEG and PBO matrices, respectively were measured at the same temperature and configuration as the samples. The resolution of the instrument was measured by a thin block of graphite at room temperature. The fraction of (in/)coherent scattering was obtained by the polarization analysis of the scattered intensity under the measurement conditions and are summarized in Table 3.
| Sample | Q [Å−1] | |||
|---|---|---|---|---|
| 0.05 | 0.096 | 0.15 | 0.20 | |
| PEG–OH-15 | 0.92 | 0.88 | 0.80 | 0.74 |
| PEG–CH3-15 | 0.90 | 0.83 | 0.75 | 0.63 |
| PBO/PBO-15 | 0.94 | 0.90 | 0.82 | 0.72 |
Small-angle neutron scattering (SANS)
Prior to the dynamics experiments a structural characterization of the polymer matrices and nanocomposites by SANS was performed at JCNS instruments KWS-1 and KWS-2 at the Heinz Maier-Leibnitz Zentrum (MLZ) in Garching, Germany.34 The PEG samples were moulded between two quartz discs sealed by a Viton o-ring yielding an average sample thickness of 0.6 ± 0.1 mm. The glass discs were fixed in brass containers. The liquid-like PBO samples were readily filled into Hellma glass cuvettes of 1 mm thickness.The samples were measured at the 2 and 8 m detector distance at a wavelength of 4.5 or 7 Å and heated to the same temperature as in the NSE experiment. The measured scattering intensities were corrected for detector efficiency, normalized to absolute units by a plexiglass standard, corrected for incoherent background scattering and normalized to the polymer volume fraction.
Results
Structural characterization
In Fig. 2 the SANS data of the PEG (a) and PBO (b) nanocomposites (filled symbols) are compared to the respective pure matrices (unfilled symbols). For a direct comparison of the PEG–OH-15 sample the intensity was additionally scaled by a factor F = 1.2 to yield good overlap in the asymptotic high-Q regime (Q > 0.1 Å−1). The matrix data conform well to the structure factor S(Q) (eqn (10)) for short Gaussian chains as evidenced by the green lines. The fitted value for the statistical segment lengths is identical for all three polymers with b = 5.7 ± 0.1 Å. Note that the Q−1.7 power law at high-Q is slightly lower than the typical limiting power law for long chains (Debye-limit I ∝ Q−2) which is also reflected in a lower characteristic ratio CN = 5.0 ± 0.1 as compared to C∞ = 5.5 for PEG and PBO.35 The radius of gyration for the chains is 15.4 ± 0.4 Å. The good agreement of nanocomposite data at larger Q > 0.1 Å−1 with respect to the neat matrices indicates not only a good contrast matching of the silica particles but also unperturbed Gaussian chain statistics on the more local scale. On the large length scales at Q = 0.03 Å−1 an increase in the scattering appears that is associated with heterogeneities and/or long-range density fluctuations.36 Since this regime is far outside of the neutron spin-echo window as indicated by the gray area (0.05 Å−1 < Q < 0.20 Å−1), it will not be discussed further here. However, in the PEG–OH-15 sample a further scattering intensity appears in the intermediate Q range that overlaps with the lowest Q value of the NSE measurement (Q = 0.05 Å−1). The inset in Fig. 2(a) shows the relative contribution of the excess scattering with respect to the neat melt which drops off at large Q by a Q−4 power law. It should be noted that the excess intensity peaks at Q ≈ 0.04 Å−1 correspond to the length scale of the particle diameter (≈2π/Q). It may be interpreted in terms of polymer density fluctuations induced by the silica particle due to bound chains in qualitative agreements with experimental results reported by Sen et al.23 There, liquid state theory calculations confirmed unperturbed Gaussian chains, but more importantly identified the correlation peak in the intermediate region as a signature of an enhanced density close to the nanoparticle. It is assumed that this correlation peak gives rise to a superimposed elastic signal in the intermediate scattering function of the NSE experiment that has to be subtracted from the data.31 Therefore, we extracted the Q-dependent elastic fractions s from the coherent SANS intensities (as indicated in the inset) and re-normalized the coherent model function by a fixed elastic contribution s:| S(Q, t)modelcoh = (1 − s)S(Q, t)coh + s | (14) |
 | ||
| Fig. 2 Scattering intensities of the PEG (a) and PBO (b) matrices (open symbols) and nanocomposites (filled symbols). The inset displays the relative excess intensity of the PEG–OH-15 sample between Q = 0.05 and 0.096 Å−1. The gray area marks the Q-range of the NSE experiment. | ||
The elastic fractions s were evaluated as the relative ratio of the SANS intensities of the PEG–OH-15 sample with respect to the pure matrix. The extracted Q-dependent values are summarized in Table 4. It should be noted that the contribution is only significant for the lowest Q-value of the PEG–OH-15 sample and is absent for all other samples.
| Sample | Q [Å−1] | ||
|---|---|---|---|
| 0.05 | 0.096 | 0.2 | |
| PEG–OH-15 | 0.15 ± 0.01 | 0.017 ± 0.0003 | 0 |
| PEG–CH3-15 | 0 | 0 | 0 |
| PBO-15 | 0 | 0 | 0 |
Dynamics of the PEG/PBO matrices
At first the dynamics of the pure matrices are analyzed in terms of the Rouse model to provide the reference for the dynamics in the nanocomposites. Fig. 3 displays the measured intermediate scattering function S(Q, t)/S(Q) of the PEG–OH matrix (a) for times up to 25 ns and (b) of the PBO matrix for longer times. The solid lines represent the full Rouse model description of the datasets while the dashed lines single out the contribution of the internal chain relaxation modes (S(Q, t)modes). The dynamic parameters of the Rouse model fits are summarized in Table 5 for both matrices. We mention that the Rouse dynamics in the pure PEG melt is independent of the choice of end groups. | ||
| Fig. 3 Measured intermediate scattering functions of the PEG (a) and PBO (b) matrices together with the Rouse model description (lines). The dashed lines in (a) show the internal relaxation modes alone. The inset in (b) displays the mean-square displacement of the PBO chains ((a) adapted from ref. 31). | ||
| Sample | Wb4 [nm4 ns−1] | DR [Å2 ns−1] | τR [ns] | ζ0 [kg ns−1] |
|---|---|---|---|---|
| PEG–OH | 1.9 ± 0.1 | 4.7 | 9.7 | 2.9 × 10−21 |
| PBOs | 1.4 ± 0.1 | 3.2 | 15.6 | 4.1 × 10−21 |
For the sake of readability, the displayed Q values for the PEG–OH sample have been limited to three selected certain values to demonstrate how the NSE technique is able to discriminate between different dynamic regimes: at the lowest Q = 0.05 Å−1 (largest length scale) no internal chain dynamics are resolved (S(Q, t)modes = 1) and the decay of the scattering function is solely given by the translational diffusion of the chain. In contrast, the experiment is primarily sensitive to the internal chain relaxation at the highest Q = 0.2 Å−1 (smallest length scale) where the Rouse modes provide a significant contribution to t < τR as evidenced by the dashed red line. Note that without the diffusion term the correlation function assumes a finite plateau for t > τR.
The obtained Rouse diffusion coefficient DR and the Rouse rate W for the PEG melt are about 20% lower than previous values reported by Niedzwiedz et al.37 The discrepancy results from the well-known sub-diffusive behavior with power-law t0.8±0.04 as discussed by Brás et al.38 It results from a contribution of interchain interactions, not covered by the diffusive Brownian motion underlying the Rouse model.
A more rigorous inspection of the sublinear diffusion could be obtained in the case of the PBO melt due to the availability of dynamic data on one order of magnitude longer times. The inset in Fig. 3(b) displays the center-of-mass mean-square displacement of the PBO chains obtained from the Q = 0.05 Å−1 value by the general relationship derived from Fick's law 〈rcm2〉 = −6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[S(Q, t)/S(Q)]/Q2. At shorter times the dynamic data clearly evidence sublinear diffusion with a power-law behavior t0.8 as indicated by the dotted line. For times longer than the so-called decorrelation time τdecorr = Rg2/D = 77 ns a transition to normal diffusion occurs where 〈rcm2〉 = 6DRt holds as predicted by the Rouse model. Therefore, we used the region t > 100 ns to obtain the Rouse related diffusion leading to a noticeable but expected discrepancy of the Rouse model (solid lines) at shorter times. We note, a further discussion of the melt dynamics of PBO polymers will be subject to future work.
ln[S(Q, t)/S(Q)]/Q2. At shorter times the dynamic data clearly evidence sublinear diffusion with a power-law behavior t0.8 as indicated by the dotted line. For times longer than the so-called decorrelation time τdecorr = Rg2/D = 77 ns a transition to normal diffusion occurs where 〈rcm2〉 = 6DRt holds as predicted by the Rouse model. Therefore, we used the region t > 100 ns to obtain the Rouse related diffusion leading to a noticeable but expected discrepancy of the Rouse model (solid lines) at shorter times. We note, a further discussion of the melt dynamics of PBO polymers will be subject to future work.
Dynamics of the PEG nanocomposites
The results of the measurements of the PEG nanocomposites are shown in Fig. 4 for the PEG–OH-15 (a, circles) and the PEG–CH3-15 (b, squares) samples. The solid lines are the best model fits that will be discussed below and the dotted line represents the pure PEG–OH melt in terms of the Rouse model calculations. The chain dynamics of the nanocomposites is largely affected by the nanoparticles. In comparison to the neat polymer, the decay of the correlation function is generally retarded and levels off to finite plateaus S0(Q) at long times. Note that the plateaus are distinctly different in the PEG–OH and PEG–CH3 nanocomposites with respect to the plateau level and the Q-dependence, which unequivocally evidences that the chain end groups are of particular importance in these attractively interacting systems.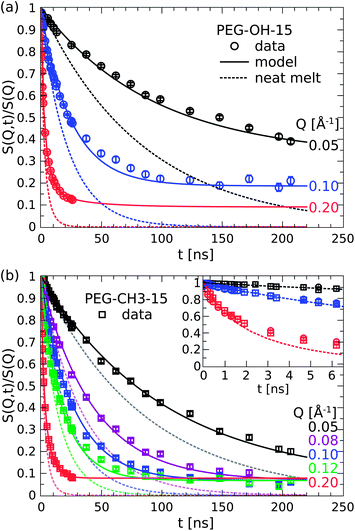 | ||
| Fig. 4 Comparison of the dynamics of the PEG–OH (a) and PEG–CH3 (b) nanocomposites (symbols) to the pure melt. The inset compares the dynamics of the pure melt (dots) and both PEG samples at short times below the Rouse time (figure adapted from ref. 31). | ||
These results are remarkable in the sense that one can already infer a rich picture of the dynamics in these systems. The appearance of a plateau in S(Q, t) is ultimately related to the existence of an elastic component and thus provides a strong indication for confined motion on the time and length scale of observation. As the translational diffusion is the only motion for times longer than τR the emergence of an elastic plateau directly evidences the fraction of chains that is fixed on the silica particles and thus not participating in the diffusion. In a similar fashion, the distinct Q-dependence of the plateaus can be interpreted on a qualitative basis. In the PEG–OH case, the clearly higher plateau at the highest Q immediately tells that the apparently confined chains on the intermediate length scale exhibit large-scale internal dynamics. The motions on a smaller length scale, where the long wave-length Rouse modes are observed (see Fig. 3(a)), account for the further decay at higher Q.
The picture however changes completely by substituting the hydroxy ends by methoxy groups which do significantly less interact with the hydroxy groups on the silica surface. In the PEG–CH3 case, the plateaus now assume a single level independent of Q. So unlike in the previous case, the confined fraction of chains appears to be immobile on all length scales of observation. Besides the Q-independent nature it is also the plateau level itself that changes by the substitution of the chain ends. As the emergence of a plateau has been already correlated with chain binding one can conclude that this fraction is about three times lower in the case of the methoxy terminated chains (SOH0 = 0.2, 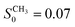 for Q = 0.1 Å−1).
for Q = 0.1 Å−1).
In all cases, however, it must be noted that the underlying relaxation rate W of the chain remains unaffected by the addition of the interacting silica nanoparticles as evidenced in the inset in Fig. 4(b). At very short times the initial decay of the intermediate scattering function, which is most sensitive to the Rouse rate W, is identical for both nanocomposites and the pure melt. The finding of unchanged local segmental dynamics was also corroborated by neutron time-of-flight experiments on the same PEG–silica nanocomposites.31 Therefore, it is concluded that the adsorbed PEG–CH3 chains remain highly flexible but their dynamics is limited to at most small scale motions less than 1 nm as estimated in analogy to the reptation confinement (S0(Q) = 1 − exp(−Q2d2/36)) with d being the dynamic confinement length.31
Dynamics of the PBO nanocomposite
The dynamics of the PBO-15 nanocomposite sample is displayed in Fig. 5 (diamonds) and compared to the pure reference melt (dotted line). The solid lines represent again the model calculation as will be discussed below. The experimental results in the PBO case here qualitatively agree with the findings for the hydroxy terminated PEG nanocomposite, however, the magnitude of the effects is much weaker.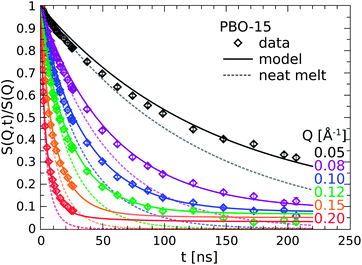 | ||
| Fig. 5 Comparison of the PBO nanocomposite dynamics (symbols) to the pure melt reference (dotted lined). The solid lines are model calculations (see text). | ||
The decay of the correlation function is again retarded as observed in all previous cases and levels off to a constant plateau for long times. Although the plateau is just about to be established in the time frame of observation an explicit Q-dependence is more than evident and well resolved up to Q = 0.115 Å−1. The levels of the plateaus have decreased to about half the value as for PEG–OH-15 (S0(Q = 0.1 Å−1) = 0.1). From this observation we conclude that only about half the fraction of PBO polymers bind on the silica particles in comparison to the PEG–OH case.
Modeling
The qualitative observations can be quantified by introducing a simple two-phase model comprising a pinned chain fraction α and a bulk-like fraction (1 − α) of free chains. The dynamics of both fractions are governed by the bulk Rouse rate W of the unfilled melt. While the translational diffusion is taken to be suppressed for the bound chains (DadsR = 0) we allow for a possible reduction r of the diffusion constant for the bulk fraction (DbulkR = rDR) as found earlier.29,39 As the adsorption density appears to be much higher for the OH terminated chains we conclude that hydroxy ends provide a strong mechanism so that chains bind primarily at their end yielding a brush or micelle-like structure similar to end-grafted chains. For these chains the internal dynamics are subject to the different boundary conditions as reflected by the parameters F and P. For the methoxy terminated chains, no observable internal chain dynamics is ascribed to the fraction of tethered chains (S(Q, t)ads = 1) by fixing Ap = 0. The model function for the nanocomposites S(Q, t)NC is then composed of weighted fractions| S(Q, t)NC = αS(Q, t)ads + (1 − α)S(Q, t)free | (15) |
The solid lines in Fig. 4 show the best model fits to eqn (15) while the lines in Fig. 5 result from pure model calculations using the same parameters obtained from the PEG–OH-15 sample except for the smaller α. All the model parameters are summarized in Table 6. The values in italics were kept fixed for the fitting/calculation.
| Sample | α | Ap | r |
|---|---|---|---|
| PEG–OH-15 | 0.23 ± 0.01 | 0.34 ± 0.01 | 0.9 |
| PEG–CH3-15 | 0.06 ± 0.01 | 0 | 0.85 ± 0.01 |
| PBO-15 | 0.10 | 0.35 | 0.9 |
For both the PEG and the PBO nanocomposites the simple two-phase model yields a very good description of the nanocomposite dynamics over the full time and Q range. As expected from the qualitative observation the bound fraction for the hydroxy terminated PEG chains is about 4 times as large as for the methoxy ones and twice as large as for the PBO chains. The chain diffusion for the freely relaxing (non-bound) chains is found to be reduced by 10–15%. This result is in good quantitative agreement with the recent findings reported for the case of non-interacting nanocomposites with comparable silica nanoparticles.29 There, NSE experiments in combination with simulations revealed a systematic reduction of the center of mass diffusion with increasing particle fraction due to obstacles that slow down the chain diffusion. The cited work evidences that the diffusion of non-interacting chains assumed in the Rouse model is not affected. However, because the simulation can include interchain interactions, a reduction of the center of mass diffusion can be explained.
Furthermore, the modeling clearly evidences that the internal chain relaxation dynamics fundamentally depends on the interaction mechanism between the silica surface and the polymer chains. If the hypothesized chain end attraction mechanism is disabled by changing to methoxy groups the large scale internal dynamics appears to be suppressed while in the opposite case the chains remain fully relaxing albeit with on average reduced motional amplitudes (Ap < 1).
This intriguing result is also fully mirrored even by changing to another polymer species. The dynamics of the PBO nanocomposite shows exactly the same behavior as in the PEG–OH case as evidenced by the model calculations in Fig. 5. Having the same backbone chemistry as PEG, it is assumed that the “bulkiness” of the alkyl side-chain of the PBO creates some steric hindrance that lowers the adsorption density with respect to the PEG–OH case. We want to note that such a lower adsorption energy could also be related to the dispersion as revealed by Hall et al. in the case of a different polymer.40 In the case of PBO we do not find any experimental evidence of aggregation. However, the interplay between the available surface and adsorption strength deserves further attention in future work.
Finally, it should be noted that the re-normalization due to the elastic fraction s (eqn (14)) does not create some arbitrariness in the data modeling as it affects merely the lowest Q value and thus the reduced chain diffusion. The essential information concerning the different behavior in the large scale internal dynamics as seen at higher Q values remains untouched. This is shown in Table 4, where the zero values show that there is no correction.
Interpretation and discussion
Structure and interaction mechanisms
Now let us arrive at a physical interpretation of these results. First of all, the adsorption density and a “dynamic” layer thickness can be estimated from the obtained fractions α of bound chains which can then be translated to a structural picture of the bound polymer layers. The estimation assumes a constant polymer density equal to the bulk value and a perfectly homogeneous dispersion of the particles. As all volume fractions are known the total number of chains can be related to the available particle surface to yield an average “grafting” density γ of chains per nm2 silica surface area. Likewise an average layer thickness t is estimated by equating the bound volume fractions with the volume of spherical shells of thickness t around the particles. The effect of the particle size distribution was included in the calculations but yielded only minor corrections with respect to the monodisperse case. A considered volume of 1 cm3 contains about 3 × 1020 chains and 1.9 × 1017 particles with a total surface of 7.2 × 1019 nm2. The results of the estimation are summarized in Table 7.| Sample | α | γ [chains per nm2] | t [nm] |
|---|---|---|---|
| PEG–OH-15 | 0.23 | 0.96 | 2.0 |
| PEG–CH3-15 | 0.06 | 0.28 | 0.7 |
| PBO-15 | 0.10 | 0.20 | 1.1 |
The high adsorption fraction found for the PEG–OH nanocomposite translates to a very high grafting density of 1 chain per nm2. Such a high grafting density can only be rationalized if the chain is adsorbed/grafted at its end. At this point, it is interesting to mention that the SANS diagram of the composite in Fig. 2 is unchanged at the Q values of the NSE experiment compared with the pure polymer melt. This clearly indicates unperturbed Gaussian chain statistics on the length-scale where the NSE experiment is taken. However, this SANS result implies a chain end-to-end distance 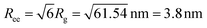 . In other words the polymer coil needs almost a factor of 4 more space than suggested by the grafting density of 1 chain per nm2. At this point, the reason cannot be revealed. We speculate, it may be related to the curvature of the particle or mutually interpenetration of neighboring chains. The last argument would imply a reduction of the mode amplitude compared with the single chain, as further discussed below.
. In other words the polymer coil needs almost a factor of 4 more space than suggested by the grafting density of 1 chain per nm2. At this point, the reason cannot be revealed. We speculate, it may be related to the curvature of the particle or mutually interpenetration of neighboring chains. The last argument would imply a reduction of the mode amplitude compared with the single chain, as further discussed below.
A visualization of the imagined model picture is presented on the left half of the middle image of Fig. 6 showing the self-assembly into micelle- or brush-like structures of densely pinned chains around the spherical silica. The zoomed region on the very left shows three exemplary chains in different colors to highlight that the hydroxy chain-end is attached to the silica surface. In the other case of the methoxy terminated chains, the layer thickness yields a much smaller average size of 0.7 nm. It is noteworthy that this thickness coincides well with dynamic confinement size d estimated above, for which an upper bound of d = 0.77 nm is deduced from the plateau level of the highest Q = 0.2 Å−1. As the polymer has all the same chain statistics as the OH case that low number can only be understood if the chains adopt a more stretched conformation in a parallel direction that in turn covers more of the silica surface. The assumed lateral adsorption along the chain backbone would be realized by multiple attachments per chain as sketched on the right of Fig. 6. A crude estimate in terms of Rg reveals that on average only three anchoring points would be necessary to yield a laterally attached chain comprising four virtual sub-chains as visualized in the zoomed region on the very right of Fig. 6. The Rg = 0.7 nm of such a (Gaussian) sub-chain with 10 segments equals just the estimated layer thickness.
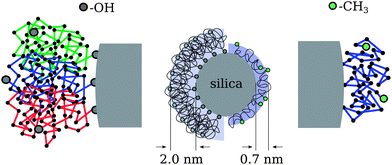 | ||
| Fig. 6 Model picture of the nanocomposite systems with different chain end groups. | ||
Here it should be noted that the detailed structural picture was not deduced from the SANS data of the nanocomposites. The structural characterization presented above indicated unperturbed chain statistics on the local scale. We conclude that the polymer chains retain their internal Gaussian nature consistent with unchanged segmental mobility.
These findings on the layer structure for the CH3 polymers are consistent with the recent NMR investigations on comparable PEG–silica nanocomposites by Kim et al.,12 if their results are extrapolated to 15% particle contents and the difference in particle size (D = 44 nm) is taken into account. Using a similar estimation they arrive at a molecular weight independent thickness of 0.8–1.0 nm from which they deduce that the chains attach laterally as in the case here for the methoxy terminated chains.12 However, they conclude that the chain termination and in particular hydroxy ends do not play a role in the bound layer structure.12
In contrast, fully atomistic equilibrium MD simulations of oligomeric PEG–silica nanocomposites by Barbier et al.21 clearly pointed out that the chain end-functionalization has a drastic effect on the interfacial structure and dynamics of the adsorbed chains. The attractive interactions lead to densely packed polymer shells around the particles where the alignment of the PEG molecules was found to depend strongly on the end groups in full agreement with our results.21 Chains with two hydroxy ends tended to position themselves rather perpendicularly with respect to the silica surface while the one with methoxy ends showed rather parallel preference.21 Furthermore, the cited work highlights the major role of hydroxy ends in the PEG–silica interfacial attraction where the hydroxy oxygens and the silanol hydrogens form very strong hydrogen-bonding interactions leading to a much higher affinity of OH end groups for the silica than the backbone oxygens.21
The role of the chain termination in unentangled PEG–silica nanocomposites was furthermore corroborated by Anderson and Zukoski7 using rheology and small-angle X-ray scattering experiments. They attribute the effective increase in the hydrodynamic radius of the particles by adsorbed polymer layers with a thickness that scales with Rg for the PEG–OH chains but is invariant to the molecular weight in the PEG–CH3 case.6,7,13 Likewise, the particle microstructure shows similar molecular weight independence for the latter chains in contrast to the hydroxy case, where the polymer layers contribute to effective hard-sphere particle interactions leading to a system similar to a colloidal glass at high particle concentrations.6,7
The polymer reference site interaction model (PRISM) of Schweizer and co-workers is able to describe the microstructure of the nanocomposites for low molecular weight polymers24 but does not provide the molecular weight dependence of the layer thickness and composite structure.7,11 The discrepancy for longer chains is ascribed to non-equilibrium adsorption configurations associated with increased residence time of polymer segments at the particle surface.7 Here, the stable plateau in S(Q, t) as seen in the NSE experiments evidences a minimum lifetime τads much longer than 200 ns. The strength of the monomer–particle interactions can thereby be estimated by a Boltzmann factor that describes the adsorption strength as an activation energy Eads for the desorption process:
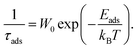 | (16) |
If the desorption rate W0 (attempt frequency) is taken as the inverse Rouse rate of the monomer τ0 = τR/402 the adsorption energy must be at least 10 kBT or 35 kJ mol−1. This high interaction energy thus supports our interpretation that hydroxy end-groups provide a very strong mechanism for adsorption which promotes preferential adsorption at the chain ends. In the case of the PRISM theory a value of about 0.5 kBT (ref. 24) per segment is calculated. When we multiply this value with the number of PEG monomers, the total energy obtained by the PRISM model is the same as in our experiments. However, we would like to note that this is most likely a coincidence. The analysis of the experimental data shows that the PEG is preferentially adsorbed at the OH chain and, and thus the energy is located in a single molecule. We note, it is not possible to describe the experimental PEG–OH NSE data by a model assuming laterally attached chains.
To estimate the influence of hydrogen bonding from the silica surface toward PEG, density functional theory (DFT) calculations (basis set: LACVP*, DFT-functional: BP86) on model compounds were performed. (MeO)3Si–OH was chosen as a model for the silica surface and dimethoxyethane and methoxyethanol as models for the methoxy-terminated PEG and hydroxy-terminated PEG, respectively.41 To estimate the hydrogen bond strength, the reaction energy dE as well as the wavenumber of the corresponding SiO–H vibrational stretching mode have been considered. A stronger shift of the IR vibration to lower wave-numbers corresponds with a weakening of the SiO–H bond and as a consequence indicates a stronger hydrogen bond formed via the examined hydrogen atom. For dimethoxyethane, an energy release of about 36 kJ mol−1 was calculated, neglecting entropic effects for the small model compound. The vibrational mode of the SiO–H bond has been shifted by 430 cm−1 upon formation of the hydrogen bond from (MeO)3Si–OH to one of the oxygen atoms of dimethoxyethane (Fig. 7). This is in well accordance with experimental results known in the literature reporting a shift of the SiO–H stretching vibration of silica in contact with diethylether, which is in possession of a comparable oxygen atom, of about 450 cm−1.42 The energy release upon hydrogen bonding of the terminal hydroxy group in methoxyethanol was calculated to be 55 kJ mol−1. This result must be discussed with caution, since two hydrogen bonds are formed in this case: one from the silica surface toward the terminal hydroxy group and the other formed from the alcoholic hydrogen PEG–OH back to the silica surface (Fig. 7).
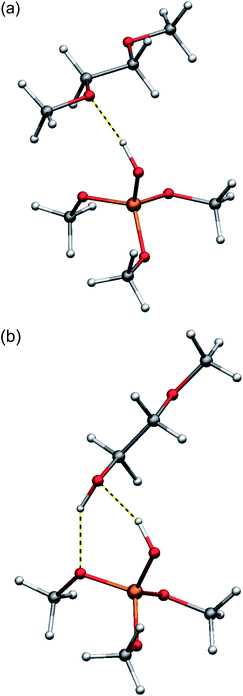 | ||
| Fig. 7 Calculated structures (DFT: LACVP*/BP86) of the hydrogen bonding between (MeO)3Si–OH as a model for a silica surface and dimethoxyethane (a) as a model for PEG–CH3 and methoxyethanol (b) as a model for PEG–OH. | ||
As expected, the shift of the PEG–O–H vibrational mode of the hydroxy-endgroup of methoxyethanol, which is less acidic than a SiO–H hydrogen atom, upon formation of the hydrogen bond toward the silica surface is calculated lower to 260 cm−1. The shift of the IR vibration of the SiO–H bond by 490 cm−1 upon hydrogen bonding toward the terminal hydroxy-group indicates a stronger hydrogen bond from SiO–H toward methoxyethanol compared to dimethoxyethane. Still, the strength of the hydrogen bonding is not expected to differ too much in the case of the two comparable hydrogen-bond acceptors, in both cases an oxygen atom for PEG–OH and PEG–CH3. Therefore, a second process should be considered and may explain an immobilization of hydroxy-terminated PEG on the silica surface. It is well known for the terminal hydroxy-groups of PEG–OH to perform a condensation with Si–OH via elimination of water and formation of a covalent SiO–R bond at higher temperatures (Fig. 8).43
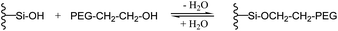 | ||
| Fig. 8 Reversible condensation reaction of terminal hydroxy-groups of PEG–OH with silanol residues on a silica surface. | ||
Although the grafting process must be accepted to be reversible in the presence of water, it may lead to covalently attached and totally immobilized PEG–OH chains on the silica surface on the timescale of the NSE experiments. From the experiments reported here, it is not possible to finally distinguish which of these processes lead to the adherence of the chain-ends of PEG–OH on the silica surface. This, is an interesting subject for future work.
Confined dynamics of PEG–OH
The chain relaxation dynamics within the adsorbed layers shall now be inspected in greater detail and checked for consistency with the presented model picture involving the specific adsorption mechanisms.At first, the strong end adsorption behavior of the hydroxy ends is discussed with respect to the introduced mode amplitude weighting factor Ap and how the specific boundary conditions are reflected in the unaltered Rouse relaxation rate W. Although the translational center-of-mass diffusion is suppressed for an end-fixed chain it can still freely rotate around the anchoring point and thus explore all the surrounding space by configurational reorientation of e.g. the end-to-end vector. This motion naturally involves the longest wavelength Rouse mode p = 1 corresponding to the relaxation of the whole chain. As depicted in the inset in Fig. 9(b), about half of the surrounding space is however inaccessible due to the impenetrable silica core. Consequently, the (dominant) first Rouse mode has to be restricted in some way.
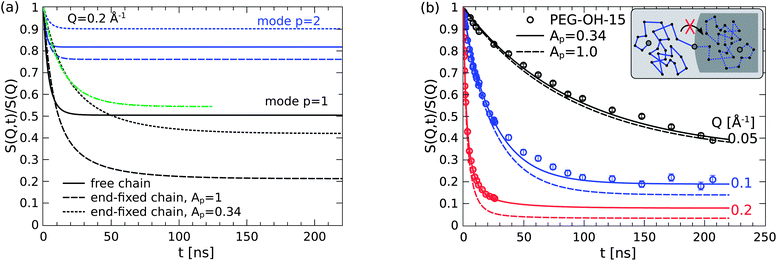 | ||
| Fig. 9 (a) The primary relaxation mode of the end-fixed chain (dashes) has greater freedom than the free chain (lines). The initial decay with reduced mode amplitude Ap (dots) mocks a slowed Rouse rate (green line). (b) The model overestimates the motional freedom of the adsorbed chains if the relaxation modes contribute with their full weight (dashes). | ||
In order to elucidate this point it is very instructive to look at the mode contribution of the relaxation spectrum for the free and the end-fixed (Rouse) chain. Such comparison of the internal relaxation modes (DR = 0) is presented in Fig. 9 for Q = 0.2 Å−1. The direct comparison of the first mode p = 1 (black color) clearly reveals that the end-fixed chain (dashed line) has apparently more “freedom” than the free Rouse chain (solid line). The obtained mode amplitude from the fitting brings up the plateau in S(Q, t) much closer to the level of the free chain. For the second mode p = 2 the situation is similar but the reduction appears to overcompensate the mode amplitude. One might therefore assign a mode dependent reduction but without any specific theory we keep the most simple approximation by a common factor.
From a theoretical point of view the relaxation mode amplitudes should be reduced by a factor of 2 (Ap = 0.5) to account for the excluded half-space. However, as shown in Fig. 9(b) a good fitting of the data can only be yielded if the amplitudes are additionally restricted resulting in the total factor of 0.34. Considering the high grafting density of 1 chain per nm2 the experimental finding of an additional factor of 2/3 is attributed to the dense “crowding” on the silica surface that we assume to provide another source for restricted mobility. It should be added that the fitting of Ap is most sensitive at the highest Q and thus rather independent from the other model parameters.31
Here, an important comment on the importance of the different boundary conditions for the adsorbed chains has to be made. Without showing we mention that we were able to obtain equivalently good fits of the experimental PEG–OH-15 data by assuming a slightly different model, where the special boundary condition is dropped but an independent Rouse rate Wads for the adsorbed chains is introduced instead. Fixing the diffusion reduction to the previous value (r = 0.9) yields essentially the same adsorbed fraction α = 0.20 ± 0.01 but the freely varied rate Wads = 4.5 ± 0.5 ns−1 is found to be considerably lower than the bulk value by a factor of 4.
Interestingly, a similar slowed-down Rouse dynamics was also found by Dionne et al.25 using on-lattice Monte-Carlo simulations for attractive interactions between fillers and polymers. The reported slowing down thereby affects all subsections of the chain independent of how small they are. In a mean-field sense this is interpreted as an increased average monomer friction.
Their findings thus agree very well with the “simple” model of a reduced Rouse rate within the adsorbed layer. The obvious contradiction to our findings can be explained by a comparison of the first mode contributions of the chain with Wads = 1/4W but normal mode counting and the end-fixed chain with modified mode counting but reduced amplitude. Note that in Fig. 9(a) the rescaled mode by 0.34 (dotted black line) yields an effectively slower decay of the correlation function which perfectly superimposes with the first mode of the Rouse chain with a reduced Rouse rate (green line) as suggested by the second model.
If we ignore that the equal initial decay of the intermediate scattering functions of neat PEG and the composite suggests an unchanged Rouse rate, obviously one can construct two contradicting models of equal quality with respect to the description of the experimental data. However, our NSE experiments show the same initial decay of neat PEG and the composite. Furthermore, complementary neutron time-of-flight experiments31 seem to support this. In theoretical work it was also shown that a chain end-adsorbed on surfaces has a different spectrum,44 although the Rouse rate is not changed.44 We therefore conclude from our experiments that the reported slowed dynamics originate from the misinterpretation of the Rouse dynamics of the end-adsorbed chains for which a different mode spectrum needs to be considered.
All in all, the dense packing and the restricted space of the end-tethered chains is fully consistent with our model picture of the description of the layer dynamics in terms of a modified Rouse spectrum with unchanged bulk-like segment mobility.
Confined dynamics of PEG–CH3
For the chains with the methoxy ends we found an apparently immobilized layer due to assumed lateral adsorption of the chains along their backbone. Like before, we checked the consistency of the adsorption behavior by taking the effect of multiple adsorption sites on the internal dynamics into account. If monomers are fixed along the chain, one can certainly assume that the long wavelength relaxation modes are suppressed.45 The longest/first Rouse mode p = 1 involves the motions of all monomers of the chain from one end to the other. In total there are N modes so the number of monomers involved in the p-th mode with wavelength λp is
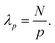 | (17) |
If multiple attachments occur then only Rouse modes with index p ≥ pmin will be active thus excluding all lower modes. The model can easily be checked by replacing the previous fixed relation S(Q, t)ads = 1 with a regular Rouse function where Ap = 0 for p < pmin for the adsorbed chain fraction in addition to the suppressed diffusion. These model calculations are presented in Fig. 10. The measured Q-independent plateau is naturally reproduced just by excluding the long wavelength modes. Already at pmin = 3 the shorter wavelength dynamics can no longer be resolved at that Q. As expected, the lower Q values are even less sensitive to the small scale motions. Already at Q = 0.096 Å−1 there is no more distinction between the longest and shorter wavelength motion of the internal relaxation dynamics.
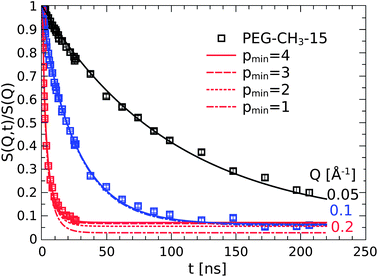 | ||
| Fig. 10 The Q-independent plateau at long times results from the suppression of wavelength Rouse motions with p ≤ 4. | ||
One has to recall here that of course only the resolvable modes are contributing to the decay of S(Q, t). As the long(est) modes are excluded, the apparent Q-independent plateau for Q = 0.2 Å−1 is merely a consequence from the inability to resolve these small scale motions.
The successful modeling of the confined dynamics for the PEG–CH3 polymers is again fully consistent with the assumed interaction mechanism depending on the chain termination. The chains obviously attach and multiply with on average at least 2–3 grafting points per chain. A similar observation of internally highly mobile chain segments within the adsorbed/confined layer was also found by Krutyeva et al. for PDMS chains confined in anodized aluminum oxide nanopores.46 These results match well with the theoretical work of Migliorini et al. who demonstrated the freezing of modes by adsorption.45
Conclusion
In conclusion, we investigated the structure and in particular large scale dynamics of the polymer phase in unentangled model nanocomposites with attractive polymer–particle interactions based on PEG and PBO chains. We thereby varied the chemistry of the chain termination to investigate the role of chain ends on the interaction mechanisms in these systems. While the static characterization by neutron small-angle scattering did not find any apparent changes to the overall polymer structure, the dynamic neutron spin-echo investigations on the large scale dynamics of the chains revealed a detailed picture of the structure and dynamics of adsorbed chains in the nanocomposite. One key result is that hydroxy chain-ends provide a very strong mechanism for chain adsorption that can be considered as irreversible on the time scale of observation.Polymer chains with the hydroxy ends assemble into a micelle-like corona extending away from the surface of the particles. Although the motional amplitudes are somewhat restricted due to the very dense packing of the adsorbed chains the overall mobility remains as high as in the bulk.31 The modeling clearly showed that there is no reduction of the basic Rouse relaxation rate in the adsorbed layers, which implies to apply the right boundary conditions for end-attached chains. The interaction energy for the strong hydroxy bonded chain end interactions was estimated to be higher than 10 kBT and thus much higher than the interaction energies predicted by the PRISM mean-field theory.
If the strong mechanism of the chain-ends is deactivated by changing to methoxy groups the mechanism of adsorption changes completely. The chains adopt a presumably more flat conformation in the vicinity of the particles due to multiple adsorptions per chain. In turn, the fraction of bound polymer chains decreases considerably. As the segmental motions can no longer be resolved by the NSE technique the polymer dynamics appears to be immobile on the length scale of the entire chain. However, earlier results on the local dynamics evidenced that the molecular motion is essentially unperturbed and as mobile as in the bulk.
The obtained model picture of the adsorption mechanism, structure and dynamics was further successfully validated by the modeling of the PBO nanocomposite. The chains with a single hydroxy end showed the same dynamic behavior as the corresponding PEG with two hydroxy ends. It was only the amount of adsorbed chains that was found to be lower by a factor of two which may be explained by the rather bulky structure due to the alkyl side-chain.
Acknowledgements
We would like to express our gratitude to Prof. Dieter Richter for his stimulating discussions and support, without which this work would have not been possible.References
- J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser and S. S. Sternstein, Polymer, 2010, 51, 3321–3343 CrossRef CAS.
- J. C. Dijt, M. A. Cohen Stuart and G. J. Fleer, Macromolecules, 1994, 27, 3219–3228 CrossRef CAS.
- Z. Fu and M. Santore, Macromolecules, 1999, 32, 1939–1948 CrossRef CAS.
- B. Wind and E. Killmann, Colloid Polym. Sci., 1998, 276, 903–912 CAS.
- A. A. Zaman, Colloid Polym. Sci., 2000, 278, 1187–1197 CAS.
- B. J. Anderson and C. F. Zukoski, Macromolecules, 2008, 41, 9326–9334 CrossRef CAS.
- B. J. Anderson and C. F. Zukoski, Langmuir, 2010, 26, 8709–8720 CrossRef CAS.
- S. Liu, V. Legrand, M. Gourmand, F. Lafuma and R. Audebert, Colloids Surf., 1996, 111, 139–145 CrossRef CAS.
- E. W. Kaler and M. L. Lynch, Langmuir, 2010, 26, 13823–13830 CrossRef.
- S. Y. Kim, K. S. Schweizer and C. F. Zukoski, Phys. Rev. Lett., 2011, 107, 225504 CrossRef.
- T. Jiang and C. F. Zukoski, Macromolecules, 2012, 45, 9791–9803 CrossRef CAS.
- S. Y. Kim, H. W. Meyer, K. Saalwächter and C. F. Zukoski, Macromolecules, 2012, 45, 4225–4237 CrossRef CAS.
- B. J. Anderson and C. F. Zukoski, Macromolecules, 2009, 42, 8370–8384 CrossRef CAS.
- A. S. Sarvestani and C. R. Picu, Polymer, 2004, 45, 7779–7790 CrossRef CAS.
- A. S. Sarvestani and E. Jabbari, Macromol. Theory Simul., 2007, 16, 378–385 CrossRef CAS.
- A. S. Sarvestani, Eur. Polym. J., 2008, 44, 263–269 CrossRef CAS.
- K. K. Kabanemi and J.-F. Hétu, J. Non-Newtonian Fluid Mech., 2010, 165, 866–878 CrossRef CAS.
- Q. Zhang and A. Archer, Langmuir, 2002, 18, 10435–10442 CrossRef CAS.
- M. Surve, V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2006, 125, 064903 CrossRef.
- G. Filippone and M. Salzano de Luna, Macromolecules, 2012, 45, 8853–8860 CrossRef CAS.
- D. Barbier, D. Brown, A.-C. Grillet and S. Neyertz, Macromolecules, 2004, 37, 4695–4710 CrossRef CAS.
- J. B. Hooper and K. S. Schweizer, Macromolecules, 2005, 38, 8858–8869 CrossRef CAS.
- S. Sen, Y. Xie and S. K. Kumar, Phys. Rev. Lett., 2007, 98, 128302 CrossRef.
- S. Y. Kim, K. S. Schweizer and C. F. Zukoski, Phys. Rev. Lett., 2011, 107, 225504 CrossRef.
- P. J. Dionne, R. Ozisik and C. R. Picu, Macromolecules, 2005, 38, 9351–9358 CrossRef CAS.
- M. S. Ozmusul, C. R. Picu, S. S. Sternstein and S. K. Kumar, Macromolecules, 2010, 38, 4495–4500 CrossRef.
- Y. Li, M. Kröger and W. K. Liu, Macromolecules, 2012, 45, 2099–2112 CrossRef CAS.
- G. J. Schneider, K. Nusser, L. Willner, P. Falus and D. Richter, Macromolecules, 2011, 44, 5857–5860 CrossRef CAS.
- G. J. Schneider, K. Nusser, S. Neueder, M. Brodeck, L. Willner, B. Farago, O. Holderer, W. J. Briels and D. Richter, Soft Matter, 2012, 9, 4336–4348 RSC.
- K. Nusser, S. Neueder, G. J. Schneider, M. Meyer, W. Pyckhout-Hintzen, L. Willner, A. Radulescu and D. Richter, Macromolecules, 2010, 43, 9837–9847 CrossRef CAS.
- T. Glomann, G. J. Schneider, J. Allgaier, A. Radulescu, W. Lohstroh, B. Farago and D. Richter, Phys. Rev. Lett., 2013, 110, 178001 CrossRef CAS.
- A. Wischnewski and D. Richter, Polymer Dynamics in Melts, in Soft Matter, ed. G. Gompper and M. Schick, Wiley-VCH Verlag GmbH & Co. KGaA, vol. 1: Polymer Melts and Mixtures, 2005 Search PubMed.
- L. Willner, R. Lund, M. Monkenbusch, O. Holderer, J. Colmenero and D. Richter, Soft Matter, 2010, 6, 1559–1570 RSC.
- A. Radulescu, V. Pipich, H. Frielinghaus and M. S. Appavou, J. Phys.: Conf. Ser., 2012, 351, 012026 CrossRef.
- C. Gerstl, G. J. Schneider, W. Pyckhout-Hintzen, J. Allgaier, S. Willbold, D. Hofmann, U. Disko, H. Frielinghaus and D. Richter, Macromolecules, 2011, 44, 6077–6084 CrossRef CAS.
- D. Schwahn, V. Pipich and D. Richter, Macromolecules, 2012, 45, 2035–2049 CrossRef CAS.
- K. Niedzwiedz, A. Wischnewski, W. Pyckhout-Hintzen, J. Allgaier, D. Richter and A. Faraone, Macromolecules, 2008, 41, 4866–4872 CrossRef CAS.
- A. R. Brás, R. Pasquino, T. Koukoulas, G. Tsolou, O. Holderer, A. Radulescu, J. Allgaier, V. G. Mavrantzas, W. Pyckhout-Hintzen, A. Wischnewski, D. Vlassopoulos and D. Richter, Soft Matter, 2011, 7, 11169–11176 RSC.
- S. Gam, J. S. Meth, S. G. Zane, C. Chi, B. A. Wood, K. I. Winey, N. Clarge and R. J. Composto, Soft Matter, 2012, 8, 6512–6520 RSC.
- L. M. Hall, B. J. Anderson, C. F. Zukoski and K. S. Schweizer, Macromolecules, 2009, 42, 8435–8442 CrossRef CAS.
- Jaguar, version 7.7, Schrodinger, LLC, New York, NY, 2010 Search PubMed.
- H. L. Hair, Infrared Spectroscopy in Surface Chemistry, Marcel Dekker, New York, 1967 Search PubMed.
- H. B. Ouada, H. Hommel, A. P. Legrand, H. Balard and E. Papirer, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 3865–3876 RSC.
- M. Koch, J.-U. Sommer and A. Blumen, J. Phys. A: Math. Gen., 1997, 30, 5007–5022 CrossRef CAS.
- G. Migliorini, V. Rostiashvili and T. A. Vilgis, Eur. Phys. J. B, 2003, 33, 61–73 CrossRef CAS.
- M. Krutyeva, A. Wischnewski, M. Monkenbusch, L. Willner, J. Maiz, C. Mijangos, A. Arbe, J. Colmenero, A. Radulescu, O. Holderer, M. Ohl and D. Richter, Phys. Rev. Lett., 2013, 110, 108303 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
