Open Access Article
Open Access ArticleThe interplay of sedimentation and crystallization in hard-sphere suspensions
John
Russo
*a,
Anthony C.
Maggs
*b,
Daniel
Bonn
*c and
Hajime
Tanaka
*a
aInstitute of Industrial Science, University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan. E-mail: russoj@iis.u-tokyo.ac.jp; tanaka@iis.u-tokyo.ac.jp
bPCT, ESPCI, 10 Rue Vauquelin, 75005 Paris, France. E-mail: anthony.maggs@espci.fr
cInstitute of Physics, University of Amsterdam, Science Park 904, 1098XH Amsterdam, The Netherlands. E-mail: D.Bonn@uva.nl
First published on 11th June 2013
Abstract
We study crystal nucleation under the influence of sedimentation in a model of colloidal hard spheres via Brownian dynamics simulations. We introduce two external fields acting on the colloidal fluid: a uniform gravitational field (body force), and a surface field imposed by pinning a layer of equilibrium particles (rough wall). We show that crystal nucleation is suppressed in proximity of the wall due to the slowing down of the dynamics, and that the spatial range of this effect is governed by the static length scale of bond orientational order. For distances from the wall larger than this length scale, the nucleation rate is greatly enhanced by the process of sedimentation, since it leads to a higher volume fraction, or a higher degree of supercooling, near the bottom. The nucleation stage is similar to the homogeneous case, with nuclei being on average spherical and having crystalline planes randomly oriented in space. The growth stage is instead greatly affected by the symmetry breaking introduced by the gravitation field, with a slowing down of the attachment rate due to density gradients, which in turn cause nuclei to grow faster laterally. Our findings suggest that the increase of crystal nucleation in higher density regions might be the cause of the large discrepancy in the crystal nucleation rate of hard spheres between experiments and simulations, on noting that the gravitational effects in previous experiments are not negligible.
1 Introduction
Crystal nucleation is a fundamental physical process whose understanding has far-reaching consequences in many technological and industrial products, like pharmaceuticals, enzymes and foods.1–7 The simplest crystallization process is the homogeneous nucleation case, in which solid clusters spontaneously form from the melt throughout the system. The opposite case is instead the heterogeneous nucleation process, where nuclei of the solid phase form preferentially around external surfaces, like containers walls or impurities present in the melt.8,9 But the crystallization processes in practical systems are often very far from these idealized cases, for example when multiple fields concurrently affect the crystallization behaviour, making it difficult to match theoretical expectations with experimental outcomes. Quoting the famous words of Oxtoby,10 “nucleation theory is one of the few areas of science in which agreement of predicted and measured rates to within several orders of magnitude is considered a major success”. The most idiomatic example comes from the simplest crystallization process, the homogeneous crystallization of hard spheres, where the discrepancy between predicted nucleation rates and experimental measurements stretches as far as 10 orders of magnitude. In particular, numerical simulations using a variety of techniques (Brownian dynamics, biased Monte Carlo, and rare-events methods) found that the nucleation rate increases dramatically with the colloid volume fraction ϕ, growing by more than 15 orders of magnitude from ϕ = 0.52 to ϕ = 0.56, where it has a maximum.11–18 On the other side, experiments found the nucleation rate to be much less sensitive on the volume fraction.19–23 This is probably the second worst prediction in physics, the first being the 100 orders of magnitude difference between the cosmological constant predicted from the energy of the vacuum and that measured from astronomical data.24In the present work we address a very important factor affecting the crystallization process, which often occurs in real experiments of colloidal suspensions but has been ignored in most simulations: how the crystallization process is affected by the sedimentation of particles. We perform Brownian dynamics simulations of a model of colloidal hard spheres, and induce sedimentation by introducing both a gravitational force G and rough walls which confine the system along the direction of gravity. The effects of rough walls on both the static and dynamic properties of the colloidal fluid are analyzed in detail. In particular we will show that there is strong slowing down of the dynamics close to the walls, and that this effect has a static origin. Correspondingly, the crystallization process is strongly suppressed in proximity of the walls, which allow us to study the nucleation process under gravity without interference from the walls. We will show in fact that both the nucleation rates, crystal shape and the orientation of crystalline planes are similar to what observed at bulk conditions. On the other hand, the gravitation field strongly affects the growth stage, and we will show that nuclei grow more slowly across a density gradient, and thus prefer to grow laterally. This indicates that not only local density but also its gradient affect the crystallization behavior.
We also provide new insights on the debated origin of the discrepancy between theoretical predictions and experimental measurements of nucleation rates in hard spheres. We first note that the experiments measuring the nucleation rates in hard spheres are usually characterized by rather short gravitational lengths (and quite marked sedimentation effects have indeed been reported19,25). We will then present some arguments to show that sedimentation should have a rather big effect in these experiments, especially at lower volume fractions, where the discrepancy is much more significant.
The paper is organized as follows. In Section 2 we describe the methods employed in our study and the choice of the state points considered. Section 3 presents the results of the study, logically divided in five parts. Section 3.1 examines the effects of gravity on the nucleation rates measured by simulation. Section 3.2 deals with the effects of gravity on the static properties of the suspension. Section 3.3 investigates the effects of the walls, both on the dynamics and the statics. Section 3.4 considers instead the growth of the nuclei as affected by gravity. Section 3.5 compares our results with previous experimental investigation of the crystallization in hard-sphere colloidal systems. We conclude in Section 4.
2 Methods
We perform Brownian Dynamics (BD) simulations of spherical particles interacting through the Weeks–Andersen–Chandler (WCA) potential26where σ is the length scale, ε is the energy scale and β = 1/kBT (kBT: the thermal energy). In the following we set the energy scale to ε = 1. The WCA potential is a purely repulsive short-range potential. The value of β fixes the hardness of the interaction, and we choose β = 40 for which a mapping to the hard-sphere phase diagram is known. In particular in ref. 16 the freezing density was located at ρF = 0.712, which can be compared to the volume fraction of hard spheres at the freezing transition (ϕF = 0.492) to define an effective hard-sphere volume (veff) for WCA particles, ρFveff = ϕF. The mapping of the WCA system onto the HS phase diagram is then simply given by the relation
| ρWCAveff = ϕHS. | (1) |
The effective hard-sphere diameter d of our particles is then given by  .
.
In BD the equation of motion of particle i is
The systematic force acting on particle i has two terms
| fi = −∇iU + fB |
| fB = veff(ρf − ρP)ẑ ≡ −Gẑ, |
The gravitational force, breaking the translational symmetry in the z direction, produces a z-dependent density profile, also called barometric law ρ(z).28 This density profile can be calculated from the pressure difference between two altitudes zi and zj as
 | (2) |
where ϕ = ρveff is the volume fraction. Eqn (2) can then be rewritten as an integral equation whose solution is given in an implicit form by the roots of the following equation
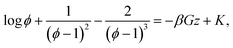 | (3) |
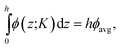 | (4) |
Before applying the external force we need to bound the system with walls in the direction perpendicular to the external field. Choosing flat walls would induce heterogeneous nucleation, whereas we want to study the homogeneous process which happens in the bulk in the presence of the external field. We then choose to confine our systems with rough walls, obtained by freezing the positions of particles in equilibrated fluid configurations. We will show in Section 3.3, that rough walls indeed disfavour nucleation in their proximity and are thus the appropriate choice for our investigation. It is also well known that rough walls do not induce layering effects, as the fluid's density remains unperturbed in their proximity.29,30 Ideally we wish thus to prepare the walls at the same state point of the layer of fluid in contact with the wall. Since the external field will induce a density gradient in the system we thus need to predict the density of the fluid at z = 0 and z = h (h being the height of the box, see Fig. 1).
 | ||
| Fig. 1 Simulation box configuration. The fluid is confined between z = 0 and z = h by two rough walls of height hW each. The external force (with body force of G) acts in the negative ẑ direction. Wall particles are depicted by dark (gray) spheres, while fluid particles are depicted by light (blue) spheres. We choose hW = 3σ and the box length along x (and y) equal to h. | ||
A representation of the simulation box is depicted in Fig. 1. The protocol for the simulations is as follows.
Profile prediction: given G, h and ϕavg we solve eqn (3) and (4) to obtain the density profile ρ(z).
Wall preparation: two independent BD simulations are run respectively at ρ(0) and ρ(h) in the absence of the external field. Since the predicted ρ(0) is often very high, nucleation could occur at this stage, so we add a biasing potential Ubias which prevents the systems from nucleating. The biasing potential has the form of Ubias = kn2, where k is an harmonic constant and n is the size of the largest crystal in the box at each time step.
Box setup: a slab of height hW is cut from each of the two previous configurations. The slab at density ρ(0) is placed at −hW < z < 0 of the new simulation box, whereas the slab at density ρ(h) is placed between h < z < h + hW. N fluid particles are placed randomly between 0 < z < h at the volume fraction ϕavg, and then equilibrated with the external field switched off. A typical simulation box is depicted in Fig. 1.
Simulation run: at t = 0 the field G is switched on and simulations are run until the size of the largest nucleus reaches nmax = 500. The position of wall particles is kept fixed.
We set N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fluid particles (not including wall particles), with the height h equal to the box dimensions in both the x and y directions, for which periodic boundary conditions are imposed.
000 fluid particles (not including wall particles), with the height h equal to the box dimensions in both the x and y directions, for which periodic boundary conditions are imposed.
2.1 Identification of crystal particles
To identify crystal particles we use the local bond-order analysis introduced by Steinhardt et al.,31 first applied to study crystal nucleation by Frenkel and Auer.32 A (2l + 1) dimensional complex vector (ql) is defined for each particle i as , where l is a free integer parameter, and m is an integer that runs from m = −l to m = l. The functions Ylm are the spherical harmonics and
, where l is a free integer parameter, and m is an integer that runs from m = −l to m = l. The functions Ylm are the spherical harmonics and ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij is the vector from particle i to particle j. The sum goes over all neighbouring particles Nb(i) of particle i. Usually Nb(i) is defined by all particles within a cutoff distance, but in an inhomogeneous system the cutoff distance would have to change according to the local density. Instead we fix Nb(i) = 12 which is the number of nearest neighbours in close packed crystals (like hcp and fcc) which are known to be the only relevant structures for hard spheres. If the scalar product (q6(i)/|q6(i)|)·(q6(j)/|q6(j)|) between two neighbours exceeds 0.7 then the two particles are deemed connected. We then identify particle i as crystalline if it is connected with at least 7 neighbours. A useful order parameter which is built from the previous bond-order analysis is
ij is the vector from particle i to particle j. The sum goes over all neighbouring particles Nb(i) of particle i. Usually Nb(i) is defined by all particles within a cutoff distance, but in an inhomogeneous system the cutoff distance would have to change according to the local density. Instead we fix Nb(i) = 12 which is the number of nearest neighbours in close packed crystals (like hcp and fcc) which are known to be the only relevant structures for hard spheres. If the scalar product (q6(i)/|q6(i)|)·(q6(j)/|q6(j)|) between two neighbours exceeds 0.7 then the two particles are deemed connected. We then identify particle i as crystalline if it is connected with at least 7 neighbours. A useful order parameter which is built from the previous bond-order analysis is | (5) |
It measures the coarse-grained bond orientational order of particle i, which is a very effective order parameter to measure the coherence of crystal-like bond orientational order. Hereafter we call this “crystallinity”.33 However, we note that it is not a direct indicator for the presence of crystals, but rather a measure for a tendency to promote crystallization.
2.2 Gravitational length and time scales
The gravitational field breaks the translational symmetry of the system and introduces a characteristic length scale called the gravitational length, lG. The gravitational length describes the typical length scale over which the density profile decreases in the z direction. For a dilute gas the density profile is given by the barometric law ϕ(z) ∼ e−Gz/kBT, and thus | (6) |
In addition to the length scale, the gravitational field defines also a time scale, the sedimentation time τS, which is the time it takes for a particle to move over the distance d due to the gravitational pull. The velocity attained by a sphere pulled by the gravity inside a fluid is simply given by vdrag = G/ζ, where ζ is the drag coefficient (which can be computed from the viscosity of the solvent by using the Stokes law). The sedimentation time is then given by τS = dζ/G. The Péclet number, Pe, is given by the ratio of the diffusion time to the sedimentation time. The Brownian time is simply τB = d2/D = d2ζ/kBT, and so
 | (7) |
In our simulations lG > d and so we are working in the regime of small Péclet numbers, which is the relevant regime for colloidal dispersions used in estimating the nucleation rate (see Table 2). All results reported in the following sections are taken after waiting for at least 3τS before acquiring data.
2.3 Choice of state points
The state points simulated in the present work are reported in Table 1 (the volume comprised by the walls along z and the periodic boundaries along x and y directions is cubic, and the height h can be readily obtained from ϕavg). The points are divided into the following four groups.| Group | l G/d | ϕ avg | kd 5/D | 〈z〉/d |
|---|---|---|---|---|
| I | 2.07 | 0.530 | 9.5 × 10−6 | 5.6 |
| 1.90 | 0.525 | 6.5 × 10−6 | 5.2 | |
| 1.75 | 0.520 | 5.7 × 10−6 | 4.9 | |
| II | 1.75 | 0.540 | 1.7 × 10−5 | 7.2 |
| 1.75 | 0.520 | 5.7 × 10−6 | 4.9 | |
| 1.75 | 0.510 | 2.9 × 10−6 | 4.0 | |
| III | 7.59 | 0.530 | ||
| 5.70 | 0.525 | |||
| 4.56 | 0.520 | |||
| IV | 3.10 | 0.520 | 7.4 × 10−7 | 3.8 |
| 3.10 | 0.525 | 1.0 × 10−6 | 4.2 | |
| 3.10 | 0.530 | 1.9 × 10−6 | 4.6 | |
| 3.10 | 0.540 | 4.4 × 10−6 | 6.7 | |
| 3.10 | 0.550 | 6.1 × 10−6 | 8.8 | |
| 3.10 | 0.560 | 7.5 × 10−6 | 11.1 |
(I) Once the profile is settled, these simulations have the same average density at z = 0 but differ for their gravitational lengths lG. With these simulations we investigate the effect of the strength of the density gradient produced by the gravitational field on the crystallization process.
(II) These simulations all have the same gravitational length lG but differ for their average densities. With these simulations we can investigate the effect of the walls on the nucleation process.
(III) All simulations have a density low enough to avoid the crystallization of the system, and are thus suited to study the effect of the gravitational field and of the walls on the dynamics of the melt (or, supercooled liquid) prior to crystallization. With these simulations we can investigate the effect of the walls on the nucleation process.
(IV) These simulations have a gravitational length lG comparable with that of several experiments in index matched but not density matched solvents.19,21 This group is used to study the effects of gravity on the nucleation rates.
We show the theoretical profiles calculated from eqn (3) and (4) for the state points in group I–III in Fig. 2. State points with the same gravitational length are characterized by the same density gradient across the box. Decreasing the gravitational length increases the density gradient.
 | ||
| Fig. 2 Theoretical volume fraction profiles calculated from eqn (3) and (4) for the state points of groups I, II and III, in Table 1. Group I state points are depicted with continuous lines: they are characterized by ϕ(z = 0) ∼ 0.570 and different density gradients. Group II simulations are depicted with open symbols: they all have the same gravitational length and accordingly the density profiles are parallel. Group III simulations are depicted with dashed lines: their volume fraction ϕ < 0.54 and thus nucleation events are never observed during our observation time. | ||
3 Results
3.1 Nucleation rates
We directly measure nucleation rates in our simulations by running 50 independent simulations for each state point in groups I, II and IV (see Table 1). In the absence of a gravitation field, the nucleation rate as calculated by simulations has a very strong dependence on the density, growing by 15 orders of magnitude by just going from ϕ = 0.52 to ϕ = 0.54 (ref. 34) (see Fig. 14). The direct simulation of nucleation events becomes unfeasible for ϕ < 0.53 and one has to resort to rare-events sampling techniques in order to extract the nucleation rate.13,34 This is not the case in the presence of a gravitational field: most of our simulation state points are within ϕavg < 0.53 but still we are able to observe directly nucleation events, for all state points of groups I, II and IV. For the calculation of the nucleation rate k we resort to the direct formula | (8) |
3.2 Static properties
Previous studies have addressed the crystallization of hard spheres in gravity by confining the system with flat walls.35–40 In this case the high nucleation rates were due to heterogeneous nucleation on the walls. In order to prevent heterogeneous nucleation, we confine our system with rough walls, i.e. walls that are obtained by freezing a zone of colloidal particles, occupying positions that are characteristic of the bulk liquid. It is well known that such frozen walls do not induce the density layering typical of flat smooth walls.29,41 This is due to the fact that the roughness leads to the lack of the phase coherence of the density waves.As a first step to prove that walls are not enhancing our nucleation rate, we run simulations of the WCA fluid confined by rough walls prepared at volume fraction of ϕw = 0.5657 in the absence of gravity. The fluid within the walls was prepared at different volume fractions, from ϕ = 0.54 to ϕ = 0.57, and nucleation events were seen to occur randomly in the simulation box, without any apparent enhancement in the proximity of the walls.
When a gravitational field is turned on, a density profile is induced in the simulation box. We first start by visually locating the nucleation events, as shown in Fig. 3. From these direct observations we can already infer that the location of the nucleation events depends sensibly on the local density. For ϕavg = 0.510 (top row) nucleation occurs very close (but not in contact) with the wall, while for ϕavg = 0.540 (bottom row) it is located too far away to be due to wall effects. While always distinct, many nucleation events can occur in the simulation box, a consequence of the high nucleation rate, and in principle interactions between the different nuclei will occur.
 | ||
| Fig. 3 Nucleation snapshots for simulations of group II, at ϕavg = 0.510 (top row) and ϕavg = 0.540 (bottom row). Wall particles are coloured in grey, whereas only crystalline particles are shown and coloured according to the cluster they belong to. An algorithm is used to identify particles belonging to the same cluster in time, so that the colouring of the clusters should remain consistent across the time frames. For ϕavg = 0.510 snapshots are taken at a time interval of Δt = 3τB after waiting for t0 = 3τS to ensure the settling of the profile. For ϕavg = 0.510 snapshots are taken at a time interval of Δt = 1.5τB after waiting for t0 = τS. The snapshots span clusters from pre-critical to post-critical sizes. | ||
To study these events in detail we determine the average location of the nucleation events, 〈z〉, which is summarized also in Table 1. To calculate 〈z〉 we first detect all individual nuclei via a cluster algorithm, and then calculate the average height of the centers of mass as a function of the size of the nucleus n. The results are reported in Fig. 4. For each state point, the average height of the centers of mass has a characteristic dependence on the size of the nucleus. For very small nuclei (n ≲ 10) the height of the center of mass decreases with n: this is due to the fact that small nuclei randomly form in a large portion of the simulation box, so that their average height is high, while growing nuclei form preferentially at the bottom of the simulation box. With increasing n, 〈z〉 reaches a plateau which encompasses the critical nucleus size and can thus be considered as the average height at which nucleation events occur. The average nucleation height is clearly correlated with the density profile of each state point, as we will see shortly. Interestingly, for n ≳ 60 the average height increases again, which means that the growth of nuclei occurs on average more in the positive z direction, thus opposite to the direction of gravity.
 | ||
| Fig. 4 Average height of the centers of mass of nuclei as a function of their size, for all state points of group I (closed symbols) and group II (open symbols). Averages are done separately for each nucleus size, and then sizes within the same histogram bin (in logarithmic scale) are averaged together. The average height displays a clear plateau at intermediate sizes, which corresponds to the average height 〈z〉 of nucleation events and is reported in Table 1. | ||
Fig. 5 plots the volume fraction profile ϕ(z) for group I ((a) top panel) and group II ((b) bottom panel) state points. The measured profile (symbols) is obtained by averaging over configurations where the biggest nucleus is of size between 50 and 60 particles, thus capturing the profile just before the growth stage. The measured profile (symbols) can be compared with the expected equilibrium profiles, calculated from eqn (3) and (4), and plotted in Fig. 5 as dashed lines. For all state points we note that the actual profile at the time of nucleation is in very good agreement with the equilibrium one for distances not too close to the wall (z = 0). Next to the walls, instead the density saturates to a constant value. Density profiles are practically unchanged also at later times, when nuclei have started filling the system. In Fig. 5 we also report as dotted vertical lines the average height of nucleation events, as determined in Fig. 4. By intersecting these lines with the corresponding density profiles we note that all nucleation events (irrespective of ϕavg and gravitational length) occur in regions where 0.55 ≲ ϕ(z) ≲ 0.56. This interval is exactly the volume fraction where the nucleation rate in bulk has a maximum. It is thus clear that the origin of the high nucleation rates, and the localization of the nucleation events, corresponds to homogeneous nucleation occurring in regions characterized by a local volume fraction of 0.55 ≲ ϕ(z) ≲ 0.56. In the next section we will provide an explanation for the saturation of the density profile close to the walls, but in the meanwhile we emphasize that nucleation events occur in regions of the simulation box where density has relaxed.
 | ||
| Fig. 5 Volume fraction profiles ϕ(z) for group I (a) and group II (b) simulations, obtained by means of Voronoi diagrams. The simulated profiles are represented by symbols, while dashed lines are theoretical predictions based on eqn (3) and (4). The vertical dotted lines show the average height of nucleation as determined from the plateaus in Fig. 4. The coloured horizontal band in both figures represents the ϕ region where average nucleation events occur, as determined by the intersection of the density profiles with the vertical dotted lines. Simulation profiles are calculated by averaging configurations with the biggest nucleus having size between 50 and 60 particles, and by dividing the z dimension into bins of size Δz = σ. | ||
By looking at the density profiles it is difficult to detect the presence of the growing nuclei, since the density change between the small nuclei and the fluid phase is very small. Moreover, growing nuclei are known to have a density closer to the melt than to the bulk crystal up to sizes many times larger than the critical nucleus size.33 Growing crystals are more easily detected by bond orientational order parameters, such as the one introduced in eqn (5) which we refer to as crystallinity order parameter.33,42 A plot of the profile for this order parameter is shown in Fig. 6 for the state point of group I with lG = 1.9. The different curves show the average profile for configurations with embedded nuclei of different size n (we take n as the size of the largest nucleus in each configuration). As the size of the nucleus n grows, the crystallinity rapidly increases. The average mean position of the crystalline peak is in good agreement with the one extracted from Fig. 4. Also we note that the average peak position shifts to higher values of z as the size of the nuclei grow, as was also observed in Fig. 4. We thus once again confirm that, along the z direction, the growth of the nuclei occurs preferentially opposite to the gravitational force.
 | ||
| Fig. 6 Average crystallinity order parameter, as defined by eqn (5), for the state point of group I and lG = 1.9. The different curves are averages of the crystallinity for configurations with nuclei of size n ± 5, for the following values of n = 25, 55, 105, 155, 205, 355, and 405 (the order is specified by the arrow). The crystallinity profile increases rapidly with the size of the growing nuclei. | ||
We conclude this section by raising two questions. The first one is why the density does not relax to its equilibrium value close to the walls, even long after nucleation has started. A second question, possibly related to the first one, is why nucleation never occurs close to the wall. As for this last question, let us take as an example the state point of group II and ϕavg = 0.510. As can be seen from Fig. 5(b) the nucleation starts on average at a distances around 4σ from the wall, despite the fact that the density approaches ϕ = 0.56 going closer to the wall, where the nucleation rate should have its maximum. To answer these questions, in the next section we study the effects of rough walls on the static and dynamical properties of the fluid.
3.3 Wall effects
The effects of walls on the static and dynamical properties of fluids is of great interest, and many studies have been devoted to this problem.29,30,41,43 To study the combined effects of gravity and rough walls we use state points of group III in Table 1, where nucleation events do not occur within the simulated time.We start by looking at the dynamics. In Fig. 7(a) we plot the lateral mean square displacement for trajectories belonging to parallel slabs at distance z from the wall. We compute the lateral mean square displacement according to the following formula44
 | ||
| Fig. 7 Lateral mean square displacement ((a) top panel) and intermediate scattering function ((b) bottom panel) as a function of the distance z from the wall, for the state point of group III and ϕavg = 0.53. We divide the systems into slabs of Δz = σ and calculate the mean square displacement (a) and the intermediate scattering function (b) for those trajectories which do not leave the slab. The different lines correspond to the following values z/σ = 1, 2, 3, 4, 5, 7, 9, 11, 13, and 15 and the order is given by the arrow. The inset in panel (a) shows the lateral mean square displacement (〈Δr‖2〉/2 – continuous lines) and the perpendicular mean square displacement (〈Δrz2〉 – dashed lines) for those trajectories starting at z = 0 (black lines) and z = 4σ (red lines). Unlike the main panel (a), these trajectories are allowed to leave the slab. | ||
In Fig. 7(b) we plot the intermediate scattering function for density fluctuations in the (x, y) plane with a wave number q = |q| corresponding to the first peak in the structure factor, calculated according to the following formula:
The different curves correspond to slabs at different heights. Again, for z ≲ 3σ we can see that the self scattering function has still not decayed to zero, meaning that density fluctuations are not able to relax in the observed time window. Near the walls the dynamics slows considerably, and this is at the origin of the non-equilibrium profile observed in the previous section (Fig. 5) for slabs close to the wall.
We can investigate the range of the wall effects by comparing the dynamics between simulations with different gravitational lengths. In Fig. 8 we plot the dynamics of slabs located at different distances from the wall but with the same local volume fraction. The main panel shows the volume fraction profiles ϕ(z) for the group III state points. For each of the state points, the dynamics of slabs having the average density of ϕ = 0.54 (left inset) and ϕ = 0.537 are then compared. In the right inset all slabs are at distance z ≥ 4σ and they display the same dynamics. Thus the dynamics is bulk-like for z ≳ 4σ, and independent of the local density gradient. For ϕ = 0.54 (left inset), the dynamics of the slabs located at z = 1σ is much slower than the dynamics at z = 3σ. We can again conclude that for z ≲ 3σ there are strong wall effects.
 | ||
| Fig. 8 Volume fraction profile ϕ (z) for state points of group III, and comparison of the lateral mean square displacement for slabs at ϕ = 0.54 (left inset) and at ϕ = 0.537 (right inset). Choices of colours and symbols are consistent between the volume fraction profiles in the main panel and the lateral mean square displacements in the two insets. | ||
We now proceed to study the effects of the walls on the static properties of the fluid. We consider positional order (as expressed by the local density) and bond orientational order (expressed by the crystallinity order parameter defined in eqn (5)), both depicted in Fig. 9. Both translational and bond orientational order grow as z decreases, but their behavior in the proximity of wall is very different. While density is almost unperturbed on approaching the wall, crystallinity is instead strongly suppressed. The range of this suppression coincides well with the region where deviations from bulk dynamics were observed. A link between static and dynamic properties under confinement was recently proposed in ref. 41, and it is compatible with our findings. Moreover it was recently argued that crystallization is driven by bond orientational order and not by positional order,33 and this is clearly shown in our results: while density is rather unperturbed on approaching the wall, bond orientational order is strongly suppressed and in fact we do not find any nucleation events happening in close proximity to the walls. As a first approximation, density can be used as a measure of positional order, but more rigorous definitions are also possible.33,45 The range of the perturbation induced by the rough wall is governed by the correlation length of bond orientational order in the bulk phase. It is well known that such structural correlation lengths increase as the density is increased, but its absolute value is always very small (no static correlation length has been found that exceeds a few particles diameters43,45–48), thus the value of the crossover is rather insensitive of the state point considered. We can thus conclude that the perturbation induced by the walls in our system extends roughly only for distances up to z ≲ 3σ, and what we observe are genuine homogeneous nucleation events.
 | ||
| Fig. 9 Crystallinity (solid lines, left axis scale) and volume fraction (dashed lines, right axis scale) profiles for state points of group III. Results are averaged by taking slabs with Δz = σ. | ||
3.4 Gravity effects on crystal growth
In this section we address the question of how nuclei grow in the presence of a gravitational field. We already observed in previous sections that the average position of the centers of mass of nuclei shifts to higher z as the nuclei grow. We also argued that this is due to the differences in the dynamics of the fluid particles on the two sides of the growing nuclei. The side with higher z is characterized by a faster dynamics and consequently a faster crystal growth.Fig. 10 plots the mean first passage time for simulations of group I. The mean first passage time 〈tfp(n)〉 is defined as the average time elapsed until the appearance of a nucleus of size n in the system. For homogeneous systems it was shown that the following expression applies49
 | (9) |
 . Here ΔF′′(nc) is the second derivative of the nucleation barrier ΔF(n) at its maximum and thus c characterizes the curvature at the top of the nucleation barrier profile. A direct fit is attempted for n < 120 and represented as continuous lines in Fig. 10. We limit the fit to small nuclei, since as the nucleus grows it likely feels the effects of the density gradient, which eqn (9) does not take into account. Moreover the growth of the nucleus is also affected by the presence of surrounding smaller nuclei, as described in ref. 18. The fit gives us nucleation times in good agreement with the one reported in Table 1 and a critical nucleus size of approximately 50 particles for all state points. The coincidence of the critical nucleus size is not surprising, as we have shown that nucleation occurs for all state points in regions with similar volume fractions. Note the relation between the mean first passage time and the gravitational length: longer gravitational lengths correspond to shorter mean first passage times, i.e. faster growth. This relationship is much deeper: in the right inset of Fig. 10 we show that it is possible to collapse all mean first passage times by just rescaling the time unit with a scaling factor α. This rescaling can be explained in the context of mean first passage theory of activated processes, as developed in ref. 49 (we follow here its notation). One first introduces the auxiliary function
. Here ΔF′′(nc) is the second derivative of the nucleation barrier ΔF(n) at its maximum and thus c characterizes the curvature at the top of the nucleation barrier profile. A direct fit is attempted for n < 120 and represented as continuous lines in Fig. 10. We limit the fit to small nuclei, since as the nucleus grows it likely feels the effects of the density gradient, which eqn (9) does not take into account. Moreover the growth of the nucleus is also affected by the presence of surrounding smaller nuclei, as described in ref. 18. The fit gives us nucleation times in good agreement with the one reported in Table 1 and a critical nucleus size of approximately 50 particles for all state points. The coincidence of the critical nucleus size is not surprising, as we have shown that nucleation occurs for all state points in regions with similar volume fractions. Note the relation between the mean first passage time and the gravitational length: longer gravitational lengths correspond to shorter mean first passage times, i.e. faster growth. This relationship is much deeper: in the right inset of Fig. 10 we show that it is possible to collapse all mean first passage times by just rescaling the time unit with a scaling factor α. This rescaling can be explained in the context of mean first passage theory of activated processes, as developed in ref. 49 (we follow here its notation). One first introduces the auxiliary functionwhere Pst(n) is the stationary time-independent probability of finding a nucleus of size n and b is the size at which simulations are stopped (b = 480 in our case). First we note that Pst(n) is the same for all state points reported in Fig. 10 (group I), since Pst(n) depends on the density accessible to the system, and not on the density gradient. This is seen in the right inset of Fig. 10 which shows that even the full crystal size distribution P(n), which includes both stationary and non-stationary states with clusters bigger than the critical size, is unchanged for all state points. The decay of P(n) is slow, and for the limited sizes available to our study, it resembles a power law with Fisher exponent τ ≃ 1.9. As we will see soon, the growth of the nucleus occurs faster laterally, and this exponent can suggest a similarity with a two-dimensional percolation process (where τ = 187/91), in which the largest nucleus grows by merging with smaller nuclei. A consequence of the observed scaling of 〈tfp(n)〉 is that all state points of group I are characterized by the same function B(n). Once the function B(n) is known, one can reconstruct the free energy landscape from the expression49
 | ||
| Fig. 10 Mean first passage time as a function of the nucleus size n for state points of group I. Symbols are measured mean first passage times, whereas continuous lines are fits to eqn (9) up to n = 120. The left inset shows that by scaling the times all curve at different field strengths collapse on the same curve. The right inset shows the average distribution of crystal sizes P(n) for all configurations in which the biggest cluster has size smaller than 400 particles. The dashed line represents a power-law crystal size distribution with Fisher exponent, τ = 1.9. | ||
This means that the simulations with different gradients share the same free energy landscape, as already noted with the equivalence of the critical nucleus sizes. B(n) enters also into the definition of the generalized diffusion coefficient D(n), which expresses the rate of attachment of particles to a nucleus of size n:49
The above theory provides a basis for understanding the effects of density gradient on the initial processes of crystallization shown in Fig. 10. Since we have established that B(n) is the same for all simulations of group I, we conclude that the growth of the nuclei, as expressed by the mean first passage time, is simply inversely proportional to the generalized diffusion D(n). We observed in Fig. 10 that shorter gravitational lengths are accompanied by slower growth, which is a consequence of smaller D(n). Physically this corresponds to a more difficult growth of interfaces when the density gradient is stronger. On noting that D(n) is the rate of attachment of particles to a nucleus of size n, we speculate there are two origins behind the gradient-induced slowing down of crystal growth: a dynamical and a thermodynamic origin. First we consider the dynamical origin. The diffusion constant is a very strong decreasing function of ϕ near ϕg. Thus the density gradient has a nonlinearly amplified strong perturbation on the dynamics. This should lead to a significant slowing down of particle diffusion on the high density side of a nucleus. On the other hand, the thermodynamic origin may play an important role in the slowing down of the growth on the opposite side (the low density side). The thermodynamic driving force decreases dramatically when the liquid density decreases toward the melting volume fraction, where the crystal and the liquid have the same free energy. Thus, we expect that the lower density of the liquid surrounding a crystal leads to the weaker driving force for crystal growth and thus to the slower growth.
We conclude this section by looking at the effects of the gravitational field on the shape and the orientation of the growing nuclei. The shape can be determined by calculating the inertia tensor of nuclei
 | (10) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i is the vector from particle i to the center of mass of a nucleus, l and m are its vector components, and δ is the Kronecker delta. The eigenvalues of the inertia tensor represent the inertia moments along the principal axis of inertia, given by the corresponding eigenvectors. The ratio between the maximum eigenvalue and the minimum eigenvalue describes the asphericity of the crystalline nucleus. In Fig. 11 we report the values of this ratio as a function of the size of the nuclei for two different types of averages. The first one is simply the average of the ratio λmax/λmin for individual nuclei, and is reported in the square (red) symbols. It clearly shows that individual nuclei are always very aspherical. This comes not as a surprise, since the volume fraction at which the nuclei are forming is always rather high, and deviations from the spherical shape have already been reported at these volume fractions.18,50 We observe that despite the aspherical shape, nuclei are always clearly distinct from each other: we are still far from a spinodal type of nucleation. The second type of average is reported with the round (black) circles in Fig. 11, and it is the ratio λmax/λmin for the average inertia tensor. Averaging the inertia tensor of different nuclei corresponds to looking at the convolution of their shapes. If nuclei are aspherical but randomly oriented, their convoluted shape will still be spherical. This is exactly what we observe for small nuclei in Fig. 11, where the ratio λmax/λmin ∼ 1 for small n. As the nuclei grow the ratio increases steadily, and this is due to an asymmetric growth induced by gravity. In the inset of Fig. 11 we report the components of the principal axis of inertia (corresponding to the maximum eigenvalue) of the convoluted shape. Clearly this inertia axis is oriented along the z direction, i.e., along the gravity field. This means that the nuclei grow as ellipsoids with the two major axes laying in the (x, y) plane. A process which contributes to this result is probably also the merging of different nuclei in the x, y directions, as we have already shown that many nuclei form in a rather narrow z strip.
i is the vector from particle i to the center of mass of a nucleus, l and m are its vector components, and δ is the Kronecker delta. The eigenvalues of the inertia tensor represent the inertia moments along the principal axis of inertia, given by the corresponding eigenvectors. The ratio between the maximum eigenvalue and the minimum eigenvalue describes the asphericity of the crystalline nucleus. In Fig. 11 we report the values of this ratio as a function of the size of the nuclei for two different types of averages. The first one is simply the average of the ratio λmax/λmin for individual nuclei, and is reported in the square (red) symbols. It clearly shows that individual nuclei are always very aspherical. This comes not as a surprise, since the volume fraction at which the nuclei are forming is always rather high, and deviations from the spherical shape have already been reported at these volume fractions.18,50 We observe that despite the aspherical shape, nuclei are always clearly distinct from each other: we are still far from a spinodal type of nucleation. The second type of average is reported with the round (black) circles in Fig. 11, and it is the ratio λmax/λmin for the average inertia tensor. Averaging the inertia tensor of different nuclei corresponds to looking at the convolution of their shapes. If nuclei are aspherical but randomly oriented, their convoluted shape will still be spherical. This is exactly what we observe for small nuclei in Fig. 11, where the ratio λmax/λmin ∼ 1 for small n. As the nuclei grow the ratio increases steadily, and this is due to an asymmetric growth induced by gravity. In the inset of Fig. 11 we report the components of the principal axis of inertia (corresponding to the maximum eigenvalue) of the convoluted shape. Clearly this inertia axis is oriented along the z direction, i.e., along the gravity field. This means that the nuclei grow as ellipsoids with the two major axes laying in the (x, y) plane. A process which contributes to this result is probably also the merging of different nuclei in the x, y directions, as we have already shown that many nuclei form in a rather narrow z strip.
 | ||
| Fig. 11 Shape of nuclei as a function of size n for the state point of group II and ϕavg = 0.520. The shape is expressed as the ratio between the maximum and minimum eigenvalue of the inertia tensor matrix. Two different types of averages are considered. The first one is just the simple average over the eigenvalues of individual nuclei, and is represented by the square (red) symbols. With the round (black) symbols we represent instead the ratio between the maximum and minimum eigenvalue of the averaged inertia tensor. The inset shows the x (black), y (red) and z (green) components of the eigenvector corresponding to the maximum eigenvalue of the averaged inertia tensor. | ||
In Fig. 12 we consider the orientation of crystal planes for the state point with lG = 1.75 and ϕavg = 0.520. It is well known that for hard potentials the relevant crystal polymorphs are either fcc or hcp (and rhcp which is given by randomly stacking fcc and hcp planes).33 Both polymorphs are characterized by hexagonal planes. For fcc the hexagonal plane is written as (1,1,1) in Miller indices (due to the C4 symmetry of cubic crystals, there are actually 4 planes differing for a π/2 rotation along any of the unit cell vectors). For hcp the hexagonal plane is written as (0,0,0,1) in Miller–Bravais indices. For each crystalline particle in a nucleus we detect the direction of the hexagonal plane (the vector perpendicular to the plane) and plot its probability distribution in spherical coordinates, according to the usual transformations:  , θ = cos−1(z/r) and ψ = tan−1(y/x) (z is the direction of gravity). The probability to find a crystalline particle with hexagonal planes pointing in the (θ + dθ, ψ + dψ) direction is then given by P(θ, ψ)sin θdθdψ. We have approximately 50 independent trajectories, and for each we analyse the orientation of crystal particles belonging only to the largest cluster in the system, and only if the cluster has size bigger than 20 particles (to avoid the contribution from metastable nuclei). In Fig. 12 the peaks corresponding to the orientation of the individual crystals are still visible, but it is already clear that P(θ, ψ) has no sensible ψ dependence.
, θ = cos−1(z/r) and ψ = tan−1(y/x) (z is the direction of gravity). The probability to find a crystalline particle with hexagonal planes pointing in the (θ + dθ, ψ + dψ) direction is then given by P(θ, ψ)sin θdθdψ. We have approximately 50 independent trajectories, and for each we analyse the orientation of crystal particles belonging only to the largest cluster in the system, and only if the cluster has size bigger than 20 particles (to avoid the contribution from metastable nuclei). In Fig. 12 the peaks corresponding to the orientation of the individual crystals are still visible, but it is already clear that P(θ, ψ) has no sensible ψ dependence.
 | ||
| Fig. 12 Probability distribution, in spherical coordinates (θ, ψ), for the orientation of the hexagonal plane of crystals formed at the state point with lG = 1.75 and ϕavg = 0.520. θ is the angle between the vector perpendicular to the plane and the z-axis (along which gravity is directed). ψ is the angle between the projection on the (x, y) plane of the vector perpendicular to the plane and the x axis. Note that we consider weighted averages, where each nucleus enters in the definition of P(θ, ψ) with a weight equal to its size (similar results are obtained with unweighted averages). | ||
To examine the θ dependence, in Fig. 13 we plot the reduced probability distribution P(θ) = ∫P(θ, ψ)dψ. This plot shows that, for all state points in groups I and II, there is no noticeable θ dependence for the orientation of the crystalline planes. This means that the nucleation stage occurs homogeneously, with nuclei having no preferred orientation. Since the rotational diffusion of nuclei is much slower than the growth process, the nuclei retain their random orientation even when the average shape of the nuclei becomes asymmetric (Fig. 11). One example of crystal orientation and of its inclination θ is shown in the inset of Fig. 13 (the same value of θ is indicated in the main panel as a dashed-dotted line). In Fig. 13 we note that for the state point where the average nucleation event is closest to the wall (lG = 1.75 and ϕavg = 0.510), there is a small probability excess close to  . This orientation corresponds to a cubic crystal oriented with its lattice vectors along the (x, y, z) directions, as shown in the dashed curve for a thermal fcc crystal. We can speculate that, for nucleation events occurring very close to the wall (low values of ϕavg and high G values) the orientation of crystals could become anisotropic, but a confirmation of this effect needs more statistical significance.
. This orientation corresponds to a cubic crystal oriented with its lattice vectors along the (x, y, z) directions, as shown in the dashed curve for a thermal fcc crystal. We can speculate that, for nucleation events occurring very close to the wall (low values of ϕavg and high G values) the orientation of crystals could become anisotropic, but a confirmation of this effect needs more statistical significance.
 | ||
| Fig. 13 Probability distribution function P(θ) for all state points of group I and II (continuous lines with symbols), scaled so that P(θ) = 1 represents a uniform distribution. The dashed line shows the probability distribution for a bulk fcc crystal with lattice vectors oriented along the (x, y, z) directions and at volume fraction ϕ = 0.535 (the distribution function is scaled to improve readability). The inset shows a snapshot from a nucleation event at lG = 1.75 and ϕavg = 0.520: the continuous lines are traced along the hexagonal planes while the dashed line gives the plane orientation. The θ angle of the nucleus in the inset is shown as the dashed-dotted line in the main panel. | ||
3.5 Comparison with experiments
We now address the question whether a gravitational field can enhance the crystallization rate in a colloidal suspension of hard spheres. We first report in Table 2 some experimental parameters relevant to our study. The experiments can be clearly distinguished according to their gravitational lengths lG. Experiments in ref. 19 and 21 involve colloidal particles suspended in an index-matched solvent but not in a density matched one, resulting in very short gravitational lengths. Experiments in ref. 20, 22 and 23 instead improve considerably the density matching by either employing small particles, or by using swelling microgels whose density is very close to the density of the solvent. In Fig. 14 we compare the adimensional nucleation rates as a function of volume fraction calculated in these experiments (all experimental results are plotted with black symbols). Experiments with shorter gravitational lengths (plus symbols21 and stars19) are characterized by higher nucleation rates when compared to experiments with longer gravitational lengths (crosses20 and diamonds22). This shows that a reduction of the gravitational effects goes indeed in the right direction of explaining the discrepancy between experiments and simulations.| Experiment | Colloids | d | Solvent | l G/d |
|---|---|---|---|---|
| Schätzel et al.19 | PMMA | 1 μm | Decalin/tetralin | 2.9 |
| ρ P = 1.19 g cm−3 | ρ f = 0.92 g cm−3 | |||
| Harland and van Megen20 | PMMA | 0.40 μm | Decalin/CS2 | 138 |
| ρ P = 1.19 g cm−3 | ρ f = 0.97 g cm−3 | |||
| Sinn et al.21 | PMMA | 0.89 μm | Decalin/tetralin | 4.1 |
| ρ P = 1.19 g cm−3 | ρ f = 0.92 g cm−3 | |||
| Iacopini et al.22 | Polystyrene microgel | 0.86 μm | 2-Ethyl-naphthalene | 80 |
| Franke et al.23 | ρ P = 1.01 g cm−3 | ρ f = 0.992 g cm−3 |
 | ||
| Fig. 14 Adimensional crystal nucleation rates estimated from simulations (dashed red lines) and from experiments (black symbols). The legends have the following correspondence: Filion et al. (1) is ref. 13, Filion et al. (2) is ref. 16, Kawasaki et al. is ref. 14, Schätzel and Ackerson is ref. 19 (lG = 2.9d), Harland and Van Megen is ref. 20 (lG = 138d), Sinn et al. is ref. 21 (lG = 4.1 d) and Iacopini et al. is ref. 22 (lG = 80d). Nucleation rates for the simulations of group IV and the two-state model fit are reported as continuous green lines. This figure is drawn starting from Fig. 6 of ref. 16 and Fig. 12 of ref. 20. | ||
To assess the importance of gravitational effects in the crystallization of hard spheres we define the following quantity: Q(l) = τs/τx, where τs is the average time for a colloid to move the distance l due to the gravity field, and τx is the average time for a nucleation event to occur in the volume l3. Q(l) is thus an adimensional number which quantifies the relative importance of the sedimentation timescale with respect to the crystallization timescale, at any particular length scale l. For Q(l) ≫ 1 we expect gravitational effects to be negligible, and the observed nucleation rate in experiments to be the same as in gravity-free simulations. On the other hand, for Q(l) ≪ 1 gravitational effects cannot be ignored as they become significant on timescales much shorter than the average nucleation time. The most relevant length scale l in this problem is the size of the critical nucleus Rc, since below that size, l < Rc, nuclei can convert back into the metastable melt. We will thus focus on Q(Rc) at ordinary experimental conditions. Table 2 reports some experimental parameters relevant to the determination of Q(Rc), namely, the diameter of the colloids d, the density of the solvent ρf, and the gravitational length lG, and the density of a colloidal particle ρP. The details of the calculations are given in the Appendix. We find that the condition Q(Rc) ∼ 1 is realized in a small windows of |Δμ| (the chemical potential difference between the solid and fluid phase), β|Δμ| ∼ 0.38, and ϕ ∼ 0.525, for the experiments in ref. 19 and 21. These values are slightly less (as expected) for the experiments with a longer gravitational length, ref. 20 and 22, i.e. β|Δμ| ∼ 0.36 and ϕ ∼ 0.522. Thus, for ϕ ≳ 0.525, we find Q(Rc) ≫ 1 and gravitational effects can be ignored. But for ϕ ≲ 0.525 the converse is true, and gravitational effects become increasingly important. Thus, for ϕ significantly larger than 0.525 we expect that experiments without density matching (ref. 19 and 21) and gravity-free simulations will measure similar nucleation rates, whereas a big discrepancy, due to gravitational effects, should emerge at ϕ ≲ 0.525. This can be confirmed by looking at the nucleation rates in Fig. 14 where experiments are plotted with (black) symbols, while simulations without gravity as (red) lines and symbols, confirming that the value obtained from our simple dimensional analysis, ϕ ∼ 0.525, is indeed between these two regimes.
The same behaviour is seen within our simulations. In Fig. 15 we plot the z profiles of both volume fraction, ϕ, and crystallinity, S, for the state points in group IV. The profiles are taken by averaging all configurations in which the largest nucleus has a size comprised between 20 and 30 particles, in order to have a picture of the nucleation process in its early stage. The figure reveals that, at the beginning of the nucleation events, a z-dependent profile has developed both for ϕ and S. While ϕ has a smooth monotonic behavior, apparently unaffected by the ongoing crystallization process, the crystallinity order parameter S reveals that the location of the nucleation events is in the density enhanced regions. The extent of these regions depends on the average volume fraction, ϕavg. This is shown by the dashed-dotted line in Fig. 15 which clearly separates two regimes: for ϕ ≲ 0.525 the ϕ and S profiles display the same z dependence, while ϕ ≳ 0.525 marks the beginning of the nucleation events. We recall from our previous adimensional analysis that Q(ϕ = 0.525) ∼ 1, again confirming that for ϕ ≳ 0.525 nucleation events are bulk-like and the same as in a gravity-free environment, whereas for ϕ ≲ 0.525 sedimentation can occur on shorter time-scales than nucleation, and significant deviations are to be expected with respect to the zero gravity case. The nucleation process under gravity is inevitably out of equilibrium and even hydrodynamics should play an important role eventually. However, we argue that within the incubation time (at most ∼ 102 Brownian times) there may be no macroscopic processes involved and gravity-induced density fluctuations via diffusion may be a major process. This is indirectly shown by the experiments in ref. 19 which report that the first indication of crystallization could be observed on timescale of 103 s with a solvent viscosity of 2.37 × 10−3 Pa s. This corresponds to incubation times of the order of 102 Brownian times, which is the same range measured in our simulations. Despite having similar incubation times, experiments in non-density matched solvents and simulations differ for their nucleation rates, as can be seen in Fig. 14, where the nucleation rates of simulations in group IV are reported as (green) squares. But this difference is trivially due to the different volumes accessible in simulations and experiments (the nucleation rate is obtained by dividing the average incubation time by the total volume of the system). Simulations measure nucleation events in strips of height z, while experiments measure nucleation events in regions of height ∼104z (the section of the laser beam), so that the difference in nucleation rates between experiments and simulations at the lowest volume fraction is expected to be of the order of 104, provided that the experiments are sensitive enough to detect the formation of only a few nuclei. This estimation well matches with the ratio in the nucleation rate between the experiment and our simulation observed at ϕ = 0.52, as shown in Fig. 14. The physical picture which emerges is thus that, at low volume fraction, the nucleation rate is controlled by small density inhomogeneities induced by gravity. On small scales these inhomogeneities should resemble the ones obtained in simulations.
 | ||
| Fig. 15 Volume fraction profiles ϕ(z) (full lines) and crystallinity profiles S(z) (dashed lines) for state points in group IV. The ϕ scale and the S scale are reported respectively on the left and right axis. The nearly horizontal dashed-dotted line marks the value ϕ = 0.525, separating the region of crystal formation from the metastable region. Profiles are obtained by averaging all configurations in which the biggest nucleus size is between 20 and 30 particles, and by dividing the z dimension into bins of size Δz = σ. | ||
Given the previous physical picture, we can easily build a model to connect the results at high ϕ (where bulk crystallization dominates) and low ϕ (where sedimentation dominates). We adopt a simple two-state model, with high-density regions (ϕ > ϕ* and with nucleation rates similar to the ones extracted from our simulations) coexisting with low-density regions (ϕ < ϕ*, and with nucleation rates similar to the bulk behavior in absence of gravity). Due to the steep increase in nucleation rates we can take the value ϕ* as the density of the nucleation rate maximum, ϕ* ∼ 0.56. The nucleation rate in the sample can thus be written as k = kSx + kH(1 − x), where kS is the rate extracted from our simulations, kH is the rate obtained without gravity, and x is the fraction of the volume in the sample with ϕ > ϕ* due to gravity (and not thermal fluctuations). We model the ϕ dependence of x by a Fermi function to account for the constraint on x from the conservation of the total volume fraction ϕ: x(ϕ) = 1/(1 + exp{κ(ϕ − ϕ*)/G}), so that at G = 0 density inhomogeneities are null, while for G > 0 the extent of the fluctuations is proportional to exp(ϕ − ϕ*). κ ∼ 1.5 is fixed from the equivalence of nucleation rates at ϕ = 0.52, as previously discussed. The results of the model are depicted in Fig. 14 as a dashed line for the experiments in ref. 19 and 21. As expected, for ϕ > 0.525 the nucleation rate gradually recovers its gravity free value with an increase in ϕ. The good agreement shows that, at least in principle, nucleation enhanced by gravity-induced density fluctuations is a viable mechanism to explain the discrepancy between experimental and theoretical results.
4 Conclusion
In the previous sections we have considered the interplay between sedimentation and crystallization in a model of colloidal hard spheres. Gravity is a very important factor that determines the crystallization behaviour in many experimental situations:52 as we have shown, even density-matched suspensions are characterized by rather small gravitational lengths (see Table 2).The first noticeable effect of gravity is the strong enhancement of nucleation rates, which is due to the increase of the local density in proximity of the walls. Nucleation events occur preferentially in regions where, due to sedimentation, the volume fraction is approximately 55–56%, in correspondence of the nucleation rate maximum in bulk hard spheres. In this respect, the nucleation process is similar to a homogeneous nucleation event, with similar nucleation rates, and with pre-critical nuclei which are on average spherical and have crystal planes randomly oriented with respect to the direction of gravity. The symmetry breaking induced by the gravitational field is seen in the growth stage, where a steeper density profile (shorter gravitational length) slows down the dynamics of the growth process, as seen by the reduction of the generalized diffusion coefficient D(n). The bottom side of the nucleus is in contact with a slowly relaxing fluid, while on the opposite side the dynamics is much faster, leading to an increase of the average height of the center of mass position as the nuclei grow. But the faster dynamics on the top side of the nucleus is eventually compensated by a smaller thermodynamic driving force to crystallization, due to the decrease of density along the z direction. On average thus the nuclei will grow faster laterally, as shown by the study of the average inertia tensor. As the nuclei grow, they become on average more asymmetric, with their principal axis of inertia located along the z axis, which again signals a faster growth on the x, y plane. An important contribution to crystal growth is also the merging of different nuclei along the x, y plane, as revealed by the distribution of crystal sizes. The orientation of crystalline planes remains isotropic also in the growth stage, as the rotational diffusion of nuclei is a slower process compared to their growth.
We devoted special attention to the study of the effects of rough walls. By predicting the density profile from the equation of state, we were able to prepare walls at thermodynamic conditions close to the nearby fluid, thus minimizing the disturbance introduced by the walls on the liquid structure. First we determined that the effects of the walls on the dynamic properties of the fluid vanish on a length scale comparable to the static correlation length in the bulk fluid. Close to the walls the dynamics is greatly slowed down, and a decoupling of lateral and perpendicular diffusion occurs. These dynamic anomalies are accompanied by a suppression of bond orientational order. This is the structural origin of the suppression of crystallization close to the walls, and confirms previous simulations where it was shown that nucleation is mainly controlled by the development of bond orientational order.33 Positional order, i.e. density, is instead almost unaffected by the presence of the walls, providing a clean example where slowness is linked to many-body correlators (like bond-orientational order) and not to two-body quantities (like density).45
Finally we looked at the experimental results on the crystallization of hard sphere suspensions in the light of the gravitational effects, which we believe do play a major role in non-density matched samples. We first identified the regime where sedimentation is possibly controlling the crystallization behaviour, and showed that density inhomogeneities induced by the gravitational field are indeed capable of enhancing the nucleation rate up to the values reported in the literature. However, there are other non-ideal features in experiments, such as the presence of effects of shear flow or other hydrodynamic effects, which our simulations do not take into account. In order to single out unambiguously the mechanism responsible for the discrepancy between simulations and experiments, experiments with improved density matching should be carried out, possibly showing a significant decrease in the nucleation rates. Already the results of some experiments20,22,23,53 suggest that this might be a promising mechanism, and we hope that the present work will stimulate more efforts towards this direction.
Appendix: calculation of Q(l)
For hard spheres Q(l) can be immediately calculated as follows. τs is given by the Richardson–Zaki expression54 for hindered settling at low Reynolds numbers: τs = lΞ/G(1 − ϕ)4.65, where Ξ is the Stokes drag coefficient and G is the gravitational pull on the colloids. To obtain τx we need an estimate of the nucleation rate k in hard-spheres. This can be calculated within the framework of Classical Nucleation Theory (CNT), where the nucleation rate k is simply the product of a kinetic term K and a thermodynamic term U, the former expressing the mobility of the fluid–solid interface, and the latter accounting for the free energy barrier of formation of a crystal nucleus. For the kinetic term we use the expression K = ρfZf+c, where ρf is the density of the suspending fluid, is the Zeldovich factor, and f+c is the attachment rate of particles to the critical cluster containing nc particles, usually written as f+c = 24Dnc2/3/λ. In the previous expressions |Δμ| is the chemical potential difference between the solid and fluid phase, D is the short-time diffusion coefficient, λ is the typical distance over which diffusing particles attach to the interface (which we set as a fraction of the particle's diameter λ = 0.4d as was determined in ref. 55), and β = 1/kBT. The thermodynamic term of the nucleation rate is simply given by the free energy barrier of formation of the critical nucleus, U = exp(−βΔGc). We model the free energy with the CNT expression, corrected with a radius (R) dependent interfacial free energy γ(R), namely ΔG = 4πR2
is the Zeldovich factor, and f+c is the attachment rate of particles to the critical cluster containing nc particles, usually written as f+c = 24Dnc2/3/λ. In the previous expressions |Δμ| is the chemical potential difference between the solid and fluid phase, D is the short-time diffusion coefficient, λ is the typical distance over which diffusing particles attach to the interface (which we set as a fraction of the particle's diameter λ = 0.4d as was determined in ref. 55), and β = 1/kBT. The thermodynamic term of the nucleation rate is simply given by the free energy barrier of formation of the critical nucleus, U = exp(−βΔGc). We model the free energy with the CNT expression, corrected with a radius (R) dependent interfacial free energy γ(R), namely ΔG = 4πR2![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) (1 −
(1 − ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) /R2) − 4πR3ρs|Δμ|/3, where
/R2) − 4πR3ρs|Δμ|/3, where ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) and
and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) are model-dependent constants, and ρs is the density of the solid phase. In ref. 56, the values β
are model-dependent constants, and ρs is the density of the solid phase. In ref. 56, the values β![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) d2 = 0.741 and
d2 = 0.741 and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) /d2 = −0.279 were shown to describe very accurately the hard-spheres case. Combining the above expressions for τs and τx we obtain Q(l) as a function of ϕ and |Δμ|, which can be further simplified by using an equation of state |Δμ|(ϕ), which we derived by a fit to simulation results13 in the ϕ-range of interest.
/d2 = −0.279 were shown to describe very accurately the hard-spheres case. Combining the above expressions for τs and τx we obtain Q(l) as a function of ϕ and |Δμ|, which can be further simplified by using an equation of state |Δμ|(ϕ), which we derived by a fit to simulation results13 in the ϕ-range of interest.
Acknowledgements
This work was partially supported by Grant-in-Aid for Scientific Research (S) and Specially Promoted Research from JSPS, Aihara Project, the FIRST program from JSPS, initiated by CSTP, and a JSPS Postdoctoral Fellowship.References
- K. Kelton and A. L. Greer, Nucleation in Condensed Matter: Applications in Materials and Biology, Pergamon, 2010 Search PubMed.
- T. Palberg, Curr. Opin. Colloid Interface Sci., 1997, 2, 607–614 CrossRef CAS.
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815 CrossRef CAS.
- S. Auer and D. Frenkel, Adv. Polym. Sci., 2005, 173, 149–207 CrossRef CAS.
- R. Sear, J. Phys.: Condens. Matter, 2007, 19, 033101 CrossRef.
- U. Gasser, J. Phys.: Condens. Matter, 2009, 21, 203101 CrossRef CAS.
- N. C. Karayiannis, K. Foteinopoulou and M. Laso, Int. J. Mol. Sci., 2012, 14, 332–358 CrossRef.
- A. Cacciuto, S. Auer and D. Frenkel, Nature, 2004, 428, 404–406 CrossRef CAS.
- D. Winter, P. Virnau and K. Binder, Phys. Rev. Lett., 2009, 103, 225703 CrossRef.
- D. W. Oxtoby, Acc. Chem. Res., 1998, 31, 91–97 CrossRef CAS.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS.
- E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704 CrossRef CAS.
- L. Filion, M. Hermes, R. Ni and M. Dijkstra, J. Chem. Phys., 2010, 133, 244115 CrossRef CAS.
- T. Kawasaki and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14036 CrossRef CAS.
- P. N. Pusey, E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon and M. E. Cates, Philos. Trans. R. Soc., AA, 2009, 367, 4993–5011 CrossRef CAS.
- L. Filion, R. Ni, D. Frenkel and M. Dijkstra, J. Chem. Phys., 2011, 134, 134901 CrossRef CAS.
- T. Schilling, S. Dorosz, H. J. Schöpe and G. Opletal, J. Phys.: Condens. Matter, 2011, 23, 194120 CrossRef CAS.
- C. Valeriani, E. Sanz, P. N. Pusey, W. C. K. Poon, M. E. Cates and E. Zaccarelli, Soft Matter, 2012, 8, 4960 RSC.
- K. Schätzel and B. J. Ackerson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3766 CrossRef.
- J. L. Harland and W. Van Megen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3054 CrossRef CAS.
- C. Sinn, A. Heymann, A. Stipp and T. Palberg, Prog. Colloid Polym. Sci., 2001, 266–275 CrossRef CAS.
- S. Iacopini, T. Palberg and H. J. Schöpe, J. Chem. Phys., 2009, 130, 084502 CrossRef.
- M. Franke, A. Lederer and H. J. Schöpe, Soft Matter, 2011, 7, 11267–11274 RSC.
- M. P. Hobson, G. P. Efstathiou and A. N. Lasenby, General relativity: an introduction for physicists, Cambridge University Press, 2006 Search PubMed.
- S. M. Underwood, J. R. Taylor and W. Van Megen, Langmuir, 1994, 10, 3550–3554 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- M. Allen and D. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989, vol. 18 Search PubMed.
- R. Piazza, T. Bellini and V. Degiorgio, Phys. Rev. Lett., 1993, 71, 4267–4270 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, EPL, 2002, 59, 701 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, J. Phys. Chem. B, 2004, 108, 6673–6686 CrossRef CAS.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805 CrossRef CAS.
- S. Auer and D. Frenkel, J. Chem. Phys., 2004, 120, 3015–3029 CrossRef CAS.
- J. Russo and H. Tanaka, Sci. Rep., 2012, 2, 505 CrossRef.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS.
- I. Volkov, M. Cieplak, J. Koplik and J. R. Banavar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061401 CrossRef.
- J. P. Hoogenboom, P. Vergeer and A. van Blaaderen, J. Chem. Phys., 2003, 119, 3371 CrossRef CAS.
- A. Mori, S. Yanagiya, Y. Suzuki, T. Sawada and K. Ito, Sci. Technol. Adv. Mater., 2006, 7, 296–302 CrossRef CAS.
- M. Marechal and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061404 CrossRef.
- I. B. Ramsteiner, K. E. Jensen, D. A. Weitz and F. Spaepen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011403 CrossRef CAS.
- E. Allahyarov and H. Löwen, EPL, 2011, 95, 38004 CrossRef.
- K. Watanabe, T. Kawasaki and H. Tanaka, Nat. Mater., 2011, 10, 512–520 CrossRef CAS.
- J. Russo and H. Tanaka, Soft Matter, 2012, 8, 4206–4215 RSC.
- W. Kob, S. Roldán-Vargas and L. Berthier, Nat. Phys., 2012, 8, 164–167 CrossRef CAS.
- P. Liu, E. Harder and B. J. Berne, J. Phys. Chem. B, 2004, 108, 6595–6602 CrossRef CAS.
- M. Leocmach, J. Russo and H. Tanaka, J. Chem. Phys., 2013, 138, 12A536 CrossRef.
- H. Tanaka, T. Kawasaki, H. Shintani and K. Watanabe, Nat. Mater., 2010, 9, 324–331 CrossRef CAS.
- H. Tanaka, Eur. Phys. J. E, 2012, 35, 113 CrossRef CAS.
- M. Leocmach and H. Tanaka, Nat. Commun., 2012, 3, 974, DOI:10.1038/ncomms1974.
- J. Wedekind and D. Reguera, J. Phys. Chem. B, 2008, 112, 11060–11063 CrossRef CAS.
- E. Sanz, C. Valeriani, E. Zaccarelli, W. C. K. Poon, P. N. Pusey and M. E. Cates, Phys. Rev. Lett., 2011, 106, 215701 CrossRef.
- C. P. Royall, W. C. Poon and E. R. Weeks, Soft Matter, 2013, 9, 17–27 RSC.
- J. Zhu, M. Li, R. Rogers, W. Meyer, R. Ottewill, W. Russel and P. Chaikin, et al. , Nature, 1997, 387, 883–885 CrossRef CAS.
- J. Taffs, S. R. Williams, H. Tanaka and C. P. Royall, Soft Matter, 2013, 9, 297–305 RSC.
- J. F. Richardson and W. N. Zaki, Trans. Inst. Chem. Eng., 1954, 32, 35–53 CAS.
- S. Auer and D. Frenkel, Annu. Rev. Phys. Chem., 2004, 55, 333–361 CrossRef CAS.
- S. Prestipino, A. Laio and E. Tosatti, Phys. Rev. Lett., 2012, 108, 225701 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |