 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermophoretically induced flow field around a colloidal particle
Mingcheng
Yang
* and
Marisol
Ripoll
Theoretical Soft-Matter and Biophysics, Institute of Complex Systems, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: m.yang@fz-juelich.de; m.ripoll@fz-juelich.de
First published on 25th March 2013
Abstract
A colloidal particle suspended in a fluid solvent with a non-homogeneous temperature undergoes a thermophoretic force. This force may translate into a directed drift of the particle and a source-dipole-like flow field around it. Alternatively, if the colloid is fixed in space, the accompanying flow is long-ranged. In this work, we provide a first simulation study of the thermophoretic force-induced flow fields by a particle-based mesoscopic method. The simulation results are quantitatively consistent with theoretical predictions obtained by solving hydrodynamic equations. Based on these results, we propose a single-particle microfluidic pump without movable parts, in which the flow direction can be reversed. Furthermore, we quantify the long-range hydrodynamic attraction between two suspended particles near the boundary wall induced by the thermophoretic flow field.
I Introduction
In the presence of a temperature gradient, a colloidal particle experiences a directional motion. This phenomenon is known as thermophoresis, thermal diffusion, or Soret effect.1–3 Practical applications of thermophoresis are numerous, for example, in separation of macromolecules in solution4,5 or biological processes.6,7 Another interesting and less known effect of colloidal thermophoresis is the induced fluid flow. The thermophoretic force exerted on the colloid is not an external driving force but results from the interactions of the colloid with the solvent which is inhomogeneous due to the temperature gradient. The reaction force of the thermophoretic force induces in turn a motion of the surrounding fluid. Currently, small scale hydrodynamic flows are receiving rapidly increasing attention, especially in microfluidic and biophysical applications. The thermophoretically induced flow is therefore a promising alternative mechanism to originate small scale hydrodynamic flows.Although the thermo-osmotic flow in porous media was investigated a long time ago,8,9 its existence in colloidal suspensions has only been experimentally proved very recently.10,11 The experiments showed that in temperature gradients colloidal spheres can form a two-dimensional crystal on a boundary wall, which is similar to the electric field-induced colloidal crystal on electrode surfaces.12,13 The formation of thermophoretic crystals clearly indicates the existence of the thermophoretic flow field around a fixed colloidal particle in non-isothermal suspensions. However, a precise observation of this flow by means of experiments or computer simulations is still lacking. A detailed investigation will not only justify the analytical predictions, but also help to understand more deeply the thermophoretic effect in liquids, whose microscopic basis is still under debate.2,3,14–16 Furthermore, this study will provide insight into how to design high-performance temperature gradient driven nanomachines.17,18
Here, we employ computer simulations to investigate the thermophoretic flow field induced by a colloidal sphere immersed in a non-isothermal solvent. Both the colloidal spheres and solvent are modeled at the particle level by a hybrid mesoscopic-molecular dynamics scheme.19,20 The induced flow field around a colloidal sphere is analyzed in the case that the colloid is externally fixed and in the case that the colloid is drifting freely, showing a fundamentally different behavior. The obtained results are quantitatively consistent with the theoretical calculations. Further, the effect of boundary walls is studied by fixing the particle near one wall, in which a significant lateral flow is observed. This provides a direct simulation evidence for the appearance of a long-ranged inter-colloidal hydrodynamic attraction due to the thermophoretic flow field. Finally, we suggest a single-particle microfluidic pump based on the thermophoretic effect, in which no movable parts are required and in which the flow direction can be reversed. The feasibility of this pump is demonstrated by simulations.
II Simulation method
The typical sizes of a colloidal particle and the surrounding solvent particles are separated by two to four orders of magnitude, which translates into even larger differences in the typical time scales of both components. This intrinsic difficulty has motivated the development of various mesoscopic simulation methods. Here, we employ a hybrid scheme that describes the solvent by a particle-based simulation technique known as multi-particle collision dynamics (MPC),19–22 while the interactions of the colloidal particle with the solvent are simulated by standard molecular dynamics (MD). This hybrid scheme is especially appropriate for our purposes due to three main reasons. Firstly, hydrodynamic interactions and thermal fluctuations are correctly captured on a large length scale.23,24 Secondly, the precise local conservation of energy enables the sustainability of temperature inhomogeneities and heat transport.25 Thirdly, the particle–solvent interactions can be naturally included and tuned, which will have a relevant influence on the simulated colloidal thermophoretic properties.26The MPC method consists of alternating streaming and collision steps. In the streaming step, the solvent particles of mass m move ballistically for a certain time h. In the collision step, particles are sorted into the cells of a cubic lattice of size a, and their velocities relative to the center-of-mass velocity of each cell are rotated around a random axis by an angle α, ensuring mass, momentum and energy local conservation. The solvent transport properties are determined by the MPC parameters,27,28 for which we employ standard values α = 130°, h = 0.1, and the mean number of solvent particles per cell ρ = 10. Other parameters determine the simulation reference units for which we take m = 1, a = 1 and kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1, where kB is the Boltzmann constant and
= 1, where kB is the Boltzmann constant and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) is the average system temperature. Note that by construction, the solvent dynamics in MPC is coarse grained by the collisions within each collision cell. Hydrodynamic interactions can then be reproduced for lengths larger than a.35
is the average system temperature. Note that by construction, the solvent dynamics in MPC is coarse grained by the collisions within each collision cell. Hydrodynamic interactions can then be reproduced for lengths larger than a.35
In order to impose the presence of a constant gradient of temperature, methods developed for non-equilibrium molecular dynamics can be employed with the MPC solvent as extensively discussed in ref. 25. In the present work we employ two different system configurations. In the first configuration the fluid is confined between parallel walls, with periodic boundary conditions (PBCs) in the other two directions. The walls are implemented with the bounce back rule, which approximately results in stick boundary conditions.29,30 In this case a temperature difference on a thin layer close to each wall is imposed by the velocity exchange algorithm,25,31,32 which consists of interchanging the velocity of the warmest particle in the cold layer with the coldest particle of the hot layer. The second configuration considers PBCs in the three directions. The way of obtaining the required periodicity in the temperature gradient direction consists of dividing the box into two halves with a cold layer imposed in one extreme of the box and a warm layer in the middle. In this case we obtain a temperature gradient by thermalizing at different temperatures the warm and the cold layers.25 In both configurations linear temperature profiles are nicely obtained. It should be emphasized that, although MPC has shown liquid-like dynamical properties,33 the equation of state corresponds to the one of an ideal gas, due to the lack of potential inter-particle interactions. The temperature gradient translates therefore into a non-constant distribution of the solvent density, which could eventually yield to some compressibility or thermal expansion effects. The influence of compressibility in our simulations will be carefully discussed later.
Solvent and colloidal particles have a potential interaction. Although different potentials can in principle be selected, in this work we employ a truncated and shifted Lennard-Jones potential,34
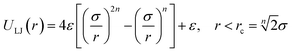 | (1) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and σ = 3a. High values of σ/a reproduce more accurately the flow field, and also increase significantly the computational cost. Padding and Louis36 showed that for σ/a = 2 the flow field around a sedimenting colloid can be simulated with a small relative error. The chosen σ/a = 3 in the simulations presented here is therefore a good compromise to obtain an accurate description of the flow field. A central potential like that in eqn (1) is known to result in slip boundary conditions. Between two MPC collision steps, Nm MD steps are implemented for the solvent particles that are in the interaction range of the colloid. The equations of motion are integrated by the velocity-Verlet algorithm with a time step Δt = h/Nm, where we use Nm = 50.
and σ = 3a. High values of σ/a reproduce more accurately the flow field, and also increase significantly the computational cost. Padding and Louis36 showed that for σ/a = 2 the flow field around a sedimenting colloid can be simulated with a small relative error. The chosen σ/a = 3 in the simulations presented here is therefore a good compromise to obtain an accurate description of the flow field. A central potential like that in eqn (1) is known to result in slip boundary conditions. Between two MPC collision steps, Nm MD steps are implemented for the solvent particles that are in the interaction range of the colloid. The equations of motion are integrated by the velocity-Verlet algorithm with a time step Δt = h/Nm, where we use Nm = 50.
III Thermophoretic force and flow field
In the presence of a temperature gradient, the inhomogeneities of the solvent interactions result in a net thermophoretic force fT on the colloid, which is, in general, directly proportional to the temperature gradient. The direction and intensity of this force completely depend on the nature of the solvent colloid interactions. In simulations, different potentials have shown to translate in important differences in the thermophoretic colloid behavior. The thermophoretic force can be not only weaker or stronger, but also change from thermophobic to thermophilic, this is changing the direction of the drift motion from cold to warm regions.26 The soft repulsive potential in eqn (1) induces a relatively strong thermophilic force. The coefficient that characterizes the most relevant system thermophoretic properties is the so-called Soret coefficient ST, or its dimensionless equivalent αT =![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ST, the thermal diffusion factor.2,3 This factor indicates the separation ratio between components in a binary mixture, and although in the most general case it depends on the thermophoretic force exerted in both components,37 for the case of large particles the following approximation is accepted,
ST, the thermal diffusion factor.2,3 This factor indicates the separation ratio between components in a binary mixture, and although in the most general case it depends on the thermophoretic force exerted in both components,37 for the case of large particles the following approximation is accepted,| fT = −αTkB∇T, | (2) |
According to Newton's third law the surrounding solvent experiences a reaction force −fT, which translates into a fluid flow. The analytical expression of the velocity field around a spherical particle in the low Reynolds number regime is standardly calculated by solving the Stokes equation.38 We implicitly assume that the boundary layer approximation is valid (short-range particle–solvent interactions), and the case of an incompressible liquid. We first consider the case of a fixed particle in the presence of a temperature gradient, which implies the presence of a thermophoretic force, and the following boundary conditions: (i) vanishing velocity field at infinity, (ii) vanishing normal component of the flow field at the particle surface, and (iii) the integral of stress tensor over the particle surface corresponding to fT. The resulting stationary flow field11,39 is,
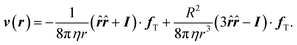 | (3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) = r/|r| and I the unit tensor. The flow is the superposition of a Stokelet and a source-dipole. Eqn (3) indicates that the flow velocity around a fixed particle in a temperature gradient has an opposite direction to the thermophoretic force, and that it is of long range since it decays linearly with the inverse distance from the particle center.
= r/|r| and I the unit tensor. The flow is the superposition of a Stokelet and a source-dipole. Eqn (3) indicates that the flow velocity around a fixed particle in a temperature gradient has an opposite direction to the thermophoretic force, and that it is of long range since it decays linearly with the inverse distance from the particle center.
A different configuration is when the particle is not fixed, but freely moving. In this case, the thermophoretic force results in an averaged drift velocity, the thermophoretic velocity uT. These quantities can be directly related by fT = γuT, with γ the friction coefficient. Note that for this analytical calculation the friction is approximated to be spatially constant.40 As a consequence of the drifted motion, not only the thermophoretic force but also a balancing viscous drag is exerted on the particle. The boundary conditions to solve the Stokes equation are now: (i) vanishing velocity field at infinity, similar as before, (ii) the normal component of the flow field is vanishing only in the particle reference frame, and (iii) the balancing forces on the particle result in a vanishing integral of stress tensor over the particle surface. The obtained velocity flow field38,41 reads,
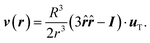 | (4) |
The flow velocity across the colloidal center and along the temperature gradient has now the same direction as the thermophoretic force, and decays with the inverse of the distance cubed; this is much faster than in the case of a fixed particle. Note that the friction coefficient is related to the particle radius with γ = AηR, where the numerical factor is A = 6π for stick boundary and A = 4π for slip boundary conditions. This also distinguishes the flows of the fixed and moving colloids, since in the case of a fixed colloid the relation between the flow field and the thermophoretic force does not vary if the colloid has stick or slip boundary conditions.
To conclude this section, it is instructive to compare the two previous solutions of the Stokes equations, with the solution of a sedimenting colloidal particle. The boundary conditions (i) are similar in the three systems, while the conditions (ii) are similar to the drifting thermophoretic particle. For the sedimenting particle, the gravitational force g is directly applied on the particle, and not the result of the interactions with the surrounding solvent. The integral of the stress tensor over the particle surface corresponds then to −g, similar to conditions (iii) of the fixed particle. The result is the Rotne–Prager–Yamakawa (RPY) tensor,42,43 which can also be understood as an extension of the Oseen tensor. The RPY tensor has a similar structure to the one in eqn (3), differing only in the numerical prefactor of both contributions. The main difference is though that the signs are opposite in both cases. That is, the flow induced by a sedimenting particle has the same direction as the gravitational force, while the flow induced by a temperature gradient of a fixed particle has the opposite sign to the corresponding thermophoretic force.
IV Simulation results
A Flow field of a colloid fixed between parallel walls
We first study the flow field induced by a colloid fixed equidistant to two parallel walls which are thermalized at different temperatures (Fig. 1). In simulations the colloid is fixed just by freezing its motion. In experiments this can correspond to the existence of a balancing external force, like in the case of laser tweezers. The considered size of the simulation box in the temperature gradient direction is Lz = 50a, and L⊥ = 40a in the two perpendicular ones. After reaching the stationary state, both the thermophoretic force and the velocity field can be computed. Within this configuration, fT can be measured by directly summing the colloid–solvent interactions.26 In these simulations ∇T ≃ 0.0125![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /a, and the thermal diffusion factor in eqn (2) is estimated to be αT ≃ −200. By convention, the negative αT is related to a resulting force towards the warm area. The magnitude of αT in our simulation model is about 50-fold smaller than that of a 1μ colloidal sphere in previous experiments regarding the thermophoretic flow.10,11 The flow field around the colloidal particle is obtained by time-averaging the fluid particle velocities in small cubic bins that we choose to be of the same size as the collision cells. The thermophoretic flow field is subjected to thermal fluctuations and it is proportional to αT, such that with our parameters a long running time is necessary to obtain a clear flow pattern. For the example in Fig. 1, a total time of t = 105 in simulation units, and an average over 50 independent runs has been employed. In principle, smoother flow lines could be obtained by using a different mesoscopic method which would neglect hydrodynamic fluctuations, like the standard lattice Boltzmann method.44–46 Nevertheless when using this method, other technical problems, like the potential colloid implementation, would then need to be taken into account, apart from evaluating the effect of neglecting fluctuations.
/a, and the thermal diffusion factor in eqn (2) is estimated to be αT ≃ −200. By convention, the negative αT is related to a resulting force towards the warm area. The magnitude of αT in our simulation model is about 50-fold smaller than that of a 1μ colloidal sphere in previous experiments regarding the thermophoretic flow.10,11 The flow field around the colloidal particle is obtained by time-averaging the fluid particle velocities in small cubic bins that we choose to be of the same size as the collision cells. The thermophoretic flow field is subjected to thermal fluctuations and it is proportional to αT, such that with our parameters a long running time is necessary to obtain a clear flow pattern. For the example in Fig. 1, a total time of t = 105 in simulation units, and an average over 50 independent runs has been employed. In principle, smoother flow lines could be obtained by using a different mesoscopic method which would neglect hydrodynamic fluctuations, like the standard lattice Boltzmann method.44–46 Nevertheless when using this method, other technical problems, like the potential colloid implementation, would then need to be taken into account, apart from evaluating the effect of neglecting fluctuations.
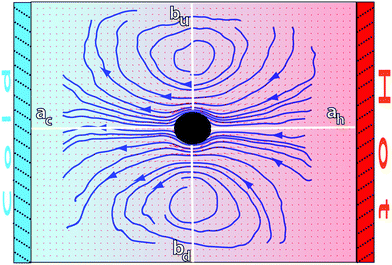 | ||
| Fig. 1 Cross-section of the flow field induced by a thermophilic colloid fixed between parallel cold and hot walls. Small red arrows indicate the flow velocity direction and intensity, while the thick blue lines correspond to the flow stream lines. The axes where the flow velocities are quantified in Fig. 2 are displayed here in white. | ||
The stream lines in the colloid neighborhood in Fig. 1 show that the flow goes from hot to cold, consistent with the thermophilic behavior of the implemented colloid and eqn (3). In a system bounded by walls, the steady-state net flow through any section is zero. This means that the thermophoretically induced flow field must be balanced by a wall-induced backflow (flow in the opposite direction to the main flow), which originates the vortex ring in Fig. 1. In the theoretical calculation in eqn (3), an infinite system is considered, such that the backflow is negligible. This contrasts to the finite-size simulation boxes presented here, where the backflow effect and the consequent vortex structure are significant.
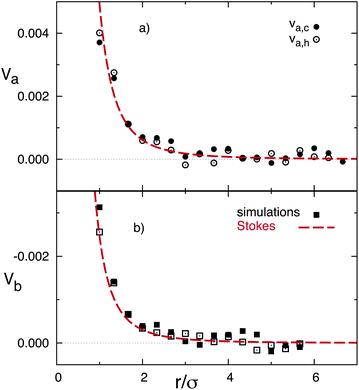
The quantitative values of the simulated velocity fields are displayed in Fig. 2 where we also compare with the analytical predictions. The component along the temperature gradient of the flow velocity is displayed in two axes that cross the colloidal center, showing in both cases a decrease of the magnitude with distance from the particle consistent with eqn (3). One axis is perpendicular to the walls and along the temperature gradient, and one parallel to the walls. These axes are indicated as a and b in Fig. 1. The open and closed symbols in Fig. 2b denote the velocity values computed in both directions of axis-b, which we could call ‘up’ and ‘down’. These two directions have no intrinsic difference such that the differences between these symbols just give an indication of the statistical error. Similarly, the open and closed symbols in Fig. 2a refer to velocity values computed in the cold and warm directions of axis-a, where compressibility effects could be of importance, given the ideal gas equation of state of the MPC solvent. Nevertheless, it can be observed that the differences are only slightly significant in the close neighborhood of the colloid, where the velocity in the cold side of the colloid is about 15% larger than in the warm side. Therefore, compressibility effects will not be of great importance when applying the MPC solvent to study the hydrodynamic interactions in non-isothermal suspensions with small temperature gradients.
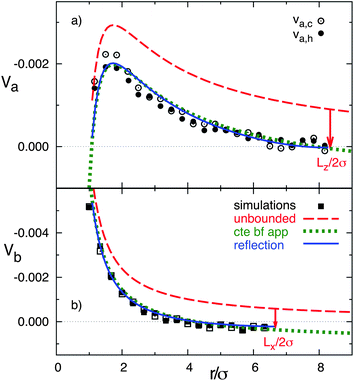 | ||
| Fig. 2 Flow velocity as a function of distance from the colloidal center. Symbols correspond to simulation results, dashed lines to the theoretical calculation in eqn (3), dotted lines to the constant backflow approximation, and solid lines to theoretical calculation with the reflection method. Arrows indicate the position of the system boundaries. (a) Velocity in axis a. (b) Velocity in axis b. | ||
In order to perform a quantitative comparison with the theoretical prediction in eqn (3), the shear viscosity is calculated from MPC kinetic theory28 as 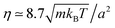 , and its temperature dependence is disregarded. The soft potential in eqn (1) employed in our simulations does not clearly determine a particle radius. We employ the standard choice of considering it equal to the interaction length parameter, this is R = σ. The solution of the Stokes equation in eqn (3) (dashed lines in Fig. 2) displays similar functional dependence as the simulation data except from an upward shift. The shift arises from the wall-induced backflow not included in eqn (3) which effectively considers the presence of walls placed at an infinite distance. A down constant displacement of eqn (3), enforcing zero velocity at the walls, corresponds to the approximation of uniform backflow. This simple approximation (dotted lines in Fig. 2) matches very well the simulation data. A more fundamental approximation that corrects eqn (3) without considering uniform backflow can be analytically calculated by using the reflection method.47–49 The fact that the system is bound by two walls instead of by one indicates that multiple reflections are necessary to obtain a satisfactory convergent result (see calculation details in the Appendix). Interestingly, the analytical corrections with the reflection method of eqn (3) (solid lines in Fig. 2) almost perfectly coincide with the uniform backflow approximation in very good agreement with the simulation data. If the backflow is understood as an additional constant flow in the direction of the thermophoretic force, it is to be expected that an additional friction force is exerted on the colloid which enhances the magnitude of the computed fT. The intensity of the backflow decreases linearly with system size and is exerted in the fT direction. This nicely explains the strong finite-size effects observed in our recent work,26 which have then a significant different nature than other finite-size effects. As a standard example, the diffusion of the center-of-mass diffusion of a polymer in equilibrium increases with box size, as a consequence of the spectra truncation.23,50,51 Meanwhile, the thermal diffusion factor αT in confined systems decreases with system size, as a consequence of the decreasing backflow.26
, and its temperature dependence is disregarded. The soft potential in eqn (1) employed in our simulations does not clearly determine a particle radius. We employ the standard choice of considering it equal to the interaction length parameter, this is R = σ. The solution of the Stokes equation in eqn (3) (dashed lines in Fig. 2) displays similar functional dependence as the simulation data except from an upward shift. The shift arises from the wall-induced backflow not included in eqn (3) which effectively considers the presence of walls placed at an infinite distance. A down constant displacement of eqn (3), enforcing zero velocity at the walls, corresponds to the approximation of uniform backflow. This simple approximation (dotted lines in Fig. 2) matches very well the simulation data. A more fundamental approximation that corrects eqn (3) without considering uniform backflow can be analytically calculated by using the reflection method.47–49 The fact that the system is bound by two walls instead of by one indicates that multiple reflections are necessary to obtain a satisfactory convergent result (see calculation details in the Appendix). Interestingly, the analytical corrections with the reflection method of eqn (3) (solid lines in Fig. 2) almost perfectly coincide with the uniform backflow approximation in very good agreement with the simulation data. If the backflow is understood as an additional constant flow in the direction of the thermophoretic force, it is to be expected that an additional friction force is exerted on the colloid which enhances the magnitude of the computed fT. The intensity of the backflow decreases linearly with system size and is exerted in the fT direction. This nicely explains the strong finite-size effects observed in our recent work,26 which have then a significant different nature than other finite-size effects. As a standard example, the diffusion of the center-of-mass diffusion of a polymer in equilibrium increases with box size, as a consequence of the spectra truncation.23,50,51 Meanwhile, the thermal diffusion factor αT in confined systems decreases with system size, as a consequence of the decreasing backflow.26
B Flow field by two colloidal particles in a periodic gradient
In order to minimize the effects of confinement in simulations the usual procedure is to employ PBCs. As introduced in Section II, in the presence of a temperature gradient PBCs are obtained by dividing the simulation box in two halves with temperature gradients of opposite signs.25,52,53 Given the system symmetry it is standard to average the properties in both system halves by only regarding about the sign difference. Here we study the flow velocity induced by two colloids fixed in the center of the two simulation half boxes (Fig. 3). The size of the simulation box in the temperature gradient direction is 2Lz with Lz = 50a, and L⊥ = 40a in the two perpendicular ones. This geometry is similar to the existing simulation studies of colloids in a temperature gradient.26,54 The repulsive solvent colloid interactions in eqn (1) result in a colloid with thermophilic properties and in a solvent that goes to the cold regions in the axis crossing the colloidal center along the temperature gradient. This means that solvent flows with opposite directions converge in the cold and hot layers, what enforces a vanishing flow velocity at the boundary layers in the direction of the temperature gradient. The resulting flow profile for each fixed colloidal particle is therefore very similar to the flow for a fixed particle between walls, as can be seen in Fig. 3, with a noticeable presence of backflow. It should be though noted that it is more accurate to state that the flow is equivalent to the one originated by walls with slip boundary conditions since the velocity in the directions perpendicular to the temperature gradient does not necessarily vanish. Therefore, the use of PBCs with the presence of periodic temperature gradient does not help to minimize the effects of confinement.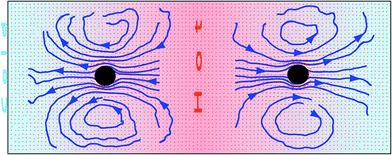 | ||
| Fig. 3 Cross-section of the flow field induced by two thermophilic colloids symmetrically fixed in neighbouring temperature gradients with opposite signs, and PBCs in the three dimensions. | ||
C Flow field by one drifting thermophoretic particle
It is a considerably more difficult task to directly obtain the flow field around a drifting thermophoretic particle than the case of a fixed particle due mainly to two facts. Since PBCs are accompanied by a periodic gradient, it should be completely ensured that the colloidal particle does not reach the system boundaries. On the other hand, the motion of the particle will explore areas with different temperatures which correspond to areas with varying density, viscosity and eventually thermophoretic properties. This makes the precise comparison with the analytical approaches that consider properties without temperature dependence difficult. In order to circumvent these difficulties, we investigate the behaviour of a different system and we show how to precisely map it to the freely moving particle.The system we investigate in the first place consists of a periodic gradient with PBCs in three dimensions. The box size is 2Lz with Lz = 40a in the direction along the temperature gradient, and L⊥ = 36a in the two perpendicular directions. The employed temperature gradient is ∇T = 0.0082![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /a. Here one of the half boxes includes the presence of a fixed colloid in the center, while there is no colloid in the other half box with opposite temperature gradient, as depicted in Fig. 4. When the temperature gradient is switched on, the originally quiescent fluid is initially accelerated by the thermophoretic force. In contrast with the examples previously discussed, the boundary conditions do not enforce a vanishing velocity at the cold and hot layer boundaries. This, together with the mass conservation conditions, results in a continuous net flow across the whole system, as can be clearly observed in Fig. 4. At the same time, the net flux of the fluid on the colloidal surface exerts a friction force in the flow direction, which gradually weakens the fluid acceleration until a constant velocity is reached. In the stationary state, the thermophoretic force fT is exactly balanced by the friction force fγ, such that the integral of the stress tensor over the particle surface vanishes.
/a. Here one of the half boxes includes the presence of a fixed colloid in the center, while there is no colloid in the other half box with opposite temperature gradient, as depicted in Fig. 4. When the temperature gradient is switched on, the originally quiescent fluid is initially accelerated by the thermophoretic force. In contrast with the examples previously discussed, the boundary conditions do not enforce a vanishing velocity at the cold and hot layer boundaries. This, together with the mass conservation conditions, results in a continuous net flow across the whole system, as can be clearly observed in Fig. 4. At the same time, the net flux of the fluid on the colloidal surface exerts a friction force in the flow direction, which gradually weakens the fluid acceleration until a constant velocity is reached. In the stationary state, the thermophoretic force fT is exactly balanced by the friction force fγ, such that the integral of the stress tensor over the particle surface vanishes.
 | ||
| Fig. 4 Cross-section of the flow field induced by one thermophilic colloid fixed in one of the two neighboring temperature gradients with opposite signs, and PBCs in the three dimensions. | ||
In systems where the Galilean invariance is fulfilled, the problem of a colloid moving with velocity U in a quiescent solvent is exactly equivalent to that of a flow past fixed colloid, with velocity − U at an infinitely distant position. The velocity distribution of the solvent around the moving colloid can be obtained from the solvent velocity around the fixed colloid by simply subtracting the velocity; the fluid is then at rest at infinity. MPC satisfies Galilean invariance,55 and in our situation, the equivalence can be understood by further verifying the validity of the boundary conditions to solve the Stokes equations in the case of a freely moving particle, as specified to obtain eqn (4). It can be checked that this is the case, since, for example, in both systems a vanishing force is exerted on the colloidal surface. The flow velocity around one fixed colloid in a periodic gradient v(r) can therefore be understood as the superposition of two independent flow fields, v(r) = u(r) + v(r). Here, v(r) corresponds to the flow field around a moving particle, and u(r) to the velocity of the fluid infinitely separated from the colloid with a constant net flux. In an incompressible fluid, a constant net flux implies a constant velocity field, but since MPC has an ideal equation of state, the solvent density depends together with the temperature on the spatial coordinate along the temperature gradient, z, such that the superimposed flow velocity field u(r) = u(z) with u(z)ρ(z) = J. This implies that the velocity u(z) will have the same functional dependence as the temperature, namely it grows linearly from the cold to the warm side. The contribution u(z) can be obtained directly in the simulations by computing the average velocity in an axis along the temperature gradient that is as distant as possible to the colloidal particle, where v(r) is approximately vanishing. The values obtained in such axis result indeed in a linear velocity profile and in a constant flux J except from fluctuations smaller than 1%.
Consequently, the flow field of a moving particle can be determined simply by subtracting the two velocities directly computed in the simulations as v(r) = v(r) − u(z). Fig. 5 shows the flow field of a freely drifting thermophilic colloidal sphere mapped from the flow field of one fixed particle in a periodic gradient. The flow field has the direction of the colloidal thermophoretic force along the temperature gradient in the axis that crosses the colloidal center, as predicted by eqn (4), and there is no backflow.41 Precisely, the absence of backflow facilitates the analytical calculation of the flow field in this case, which is shown in the inset of Fig. 5 and as can be seen it agrees very well with the simulated one.
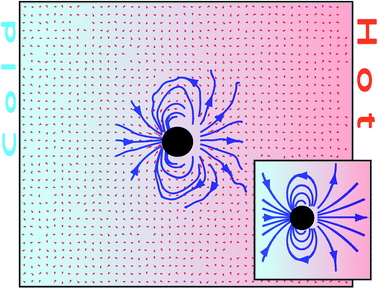 | ||
| Fig. 5 Cross-section of the velocity field around a freely drifting thermophilic colloidal sphere in a temperature gradient. The velocity field is obtained from the simulation shown in Fig. 4. The inset shows the theoretical result from eqn (4). | ||
In order to quantify the colloidal thermophoretic velocity uT, the mapping procedure has to be inversely considered, and it can be obtained from the subtracted velocity of the fluid. As explained the subtracted velocity is position dependent, and in order to quantify uT, the velocity should be considered at the colloidal position, 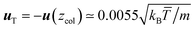 . With this velocity, a quantitative comparison with the velocity field predicted from the Stokes equation in eqn (4) can be performed. The comparison is displayed in Fig. 6, and it is carried out in two axes that cross the colloidal center. One axis is in the direction of the temperature gradient and one perpendicular to it (similar to Fig. 1). The analytical prediction in eqn (4) does not contain any adjustable parameter, and given the fast decay of the velocity, no further corrections need to be performed due to the finite size of the simulation box. The results in Fig. 6 show a very good agreement between simulations and the solution of the Stokes equation in both analyzed axes. Moreover, in Fig. 6a the simulation results va,c and va,h have no larger differences than those produced due to statistical errors, which further confirms that the effect of the compressibility can be neglected in our non-isothermal simulations.
. With this velocity, a quantitative comparison with the velocity field predicted from the Stokes equation in eqn (4) can be performed. The comparison is displayed in Fig. 6, and it is carried out in two axes that cross the colloidal center. One axis is in the direction of the temperature gradient and one perpendicular to it (similar to Fig. 1). The analytical prediction in eqn (4) does not contain any adjustable parameter, and given the fast decay of the velocity, no further corrections need to be performed due to the finite size of the simulation box. The results in Fig. 6 show a very good agreement between simulations and the solution of the Stokes equation in both analyzed axes. Moreover, in Fig. 6a the simulation results va,c and va,h have no larger differences than those produced due to statistical errors, which further confirms that the effect of the compressibility can be neglected in our non-isothermal simulations.
 | ||
| Fig. 6 Velocity field around a drifting thermophoretic particle as a function of distance from the particle, with the positive direction toward the hot side. Symbols refer to the simulation results, lines to the theoretical calculation from eqn (4). (a) Velocity field Va, solid and open symbols correspond to Va,c and Va,h, respectively. (b) Velocity field Vb. | ||
In the case of one colloidal particle fixed between parallel walls, or equivalently of two colloids in a periodic temperature gradient, the thermophoretic force could be obtained by directly measuring the colloid solvent interactions. This is not the case now since the direct interactions provide a net vanishing force on the colloidal particle. The thermophoretic force can be alternatively estimated by its relation with the thermophoretic velocity fT = γuT, where the friction coefficient γ needs to be determined. In principle, this coefficient can be determined from the colloid self-diffusion coefficient, or approximated as γ = 4πηR, which considers slip boundary conditions. This relationship together with eqn (2) allows us to calculate the thermal diffusion factor as αT ≃ −220, which is 10% higher than the one computed in Section IV-A. The lack of backflow in this setup would make us to expect an effective smaller value of αT, such that other factors should contribute to explain this deviation. Although we do not have a quantitative estimation of these factors, it can be expected that besides the intrinsic statistical error of the simulations, the overestimation of the hydrodynamic radius of the colloidal sphere36 might have a noticeable influence.
Another important consideration is the fluid temperature. When the moving colloid is considered in a quiescent fluid (Fig. 5), the fluid is completely thermalized. Meanwhile, when one fixed colloid is considered in a moving fluid (Fig. 4), the fluid moves over a region with different temperatures, such that it is in principle partially thermalized. These partial thermalizations can be neglected if the heat conduction is much faster than the fluid motion. Otherwise the real fluid temperature could be different than the one assumed by the existing temperature gradient, such that a correction factor would be required to map these two systems as exactly equivalent. The characteristic times of the heat conduction and the fluid translation can be expressed as τχ ∼ σ2/χ with χ the thermal diffusivity of the solvent, and τu ∼ σ/u with u the typical velocity of the moving fluid, respectively. Using the estimated χ from kinetic theory28 and uT obtained in the simulations, we have τχ/τu ∼ 10−1. Although the time scale separation is only of one order of magnitude, the trend indicates that the assumption used in our mapping strategy is justified. On the other hand, this could also be the origin of the deviation of the estimated value of αT.
V Applications
The existence of a thermophoretically induced fluid flow has interest not only from the fundamental point of view, but can also find numerous practical applications. In the following we present and discuss two of these applications. The first one is the existence of inter-colloidal hydrodynamic attraction induced by the thermophoretic flow, which has already been shown to be able to form thermophoretic crystals. And the second one is the possibility of designing a single particle thermophoretic pump.A Thermophoretically induced colloidal attraction
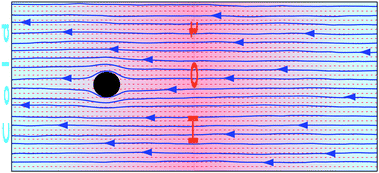
In the cases where fixed particles have so far been investigated, the colloids have been considered equidistant from the walls or the boundary layers, which intends to better reproduce the properties in bulk. However, when the colloidal particles are not considered to be fixed, they will naturally drift towards one of the walls as a consequence of their directional thermophoretic force. The colloids may then stay at an averaged fixed distance of the confining wall performing a two-dimensional Brownian motion.10,11 It is then to be expected that the thermophoretically induced flow field will significantly vary from the symmetric case in Fig. 1.In order to study the wall effect in the thermophoretic flow field, we perform simulations of a thermophilic colloidal particle confined between walls at different temperatures, where the colloidal position is fixed at a distance hw = 5.5a from the hot wall. Note that the particle wall separation hw is large enough to consider more than one MPC collision box between the colloidal surface and the wall, such that the hydrodynamic behavior can be properly resolved. The distance between the walls is Lz = 30, while PBCs are employed in the other two directions with box size L⊥ = 40a. The steady flow field is depicted in Fig. 7 where the significant asymmetry of the streamlines is easily observed. This flow pattern is the same as the analytical prediction.11,39
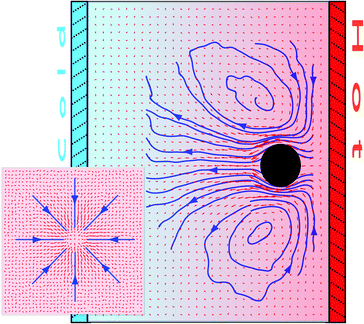 | ||
| Fig. 7 Cross-section of the flow field around a thermophilic particle fixed in a near-wall environment. The inset shows the velocity field in a plane parallel to the walls and between the colloid and the hot wall. | ||
In contrast to the symmetric system in Fig. 1, the thermophoretically induced flow field has now a strong lateral component toward the colloidal sphere and parallel to the wall, which necessarily affects the motion of ambient particles. If a second particle is in the neighbourhood of the colloid, it will suffer hydrodynamic drag toward the first particle. When the lateral flow is strong enough (high |αT|), the attraction force can be larger than other repulsive contributions or than the thermal fluctuation, originating stable colloidal aggregation. Such 2D colloidal crystals induced by the presence of thermophoretic flow fields have indeed been experimentally observed.10,11 Experiments are performed with thermophobic colloids such that the colloidal accumulation takes place in the cold wall in contrast to our case. Note that if the colloid would be fixed by an external force to the opposite wall of their thermophoretic affinity (e.g. thermophobic colloid fixed at the hot wall) the contribution of the thermophoretic flow would induce a repulsive interaction.
By computing the typical lateral flow velocity as 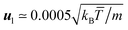 , the first quantitative estimation of the hydrodynamic force can be performed as fH ≃ 4πησul ≃ 0.15kBT/a. In order to evaluate more precisely the hydrodynamic attraction induced by the lateral flow, we perform simulations of two thermophilic colloidal particles fixed at a distance hw = 5.5a from the hot wall. The distance between the walls is now Lz = 30, and the box size in the other two perpendicular directions is L⊥ = 50a. The attraction force can be directly obtained in our simulations by evaluating the solvent–colloid interactions that now will have a non-vanishing component not only in the direction of the temperature gradient but also perpendicular to it, in the direction of the second colloid. Independent simulations with colloids placed at different positions allow us to obtain the attraction force as a function of inter-particle separation as shown in Fig. 8. Similar to the particle wall separation, the smallest separation between colloids is large enough to properly capture hydrodynamic interactions. The computed magnitude of fH in Fig. 8 is consistent with our first rough evaluation. The attraction force decreases monotonously with the separation, which qualitatively agrees with the experimental results.10,11 From the force curve, an effective potential between particles can be obtained with a potential well depth of ∼1.5kBT. Thermal fluctuations will then contribute to eventually overcome the attractive potential between colloids with non-fixed positions, such that no stable aggregation occurs in our system. Stable configurations can be achieved by, for example, increasing the size of the colloid,10 which increases the thermal diffusion factor αT of the colloids.
, the first quantitative estimation of the hydrodynamic force can be performed as fH ≃ 4πησul ≃ 0.15kBT/a. In order to evaluate more precisely the hydrodynamic attraction induced by the lateral flow, we perform simulations of two thermophilic colloidal particles fixed at a distance hw = 5.5a from the hot wall. The distance between the walls is now Lz = 30, and the box size in the other two perpendicular directions is L⊥ = 50a. The attraction force can be directly obtained in our simulations by evaluating the solvent–colloid interactions that now will have a non-vanishing component not only in the direction of the temperature gradient but also perpendicular to it, in the direction of the second colloid. Independent simulations with colloids placed at different positions allow us to obtain the attraction force as a function of inter-particle separation as shown in Fig. 8. Similar to the particle wall separation, the smallest separation between colloids is large enough to properly capture hydrodynamic interactions. The computed magnitude of fH in Fig. 8 is consistent with our first rough evaluation. The attraction force decreases monotonously with the separation, which qualitatively agrees with the experimental results.10,11 From the force curve, an effective potential between particles can be obtained with a potential well depth of ∼1.5kBT. Thermal fluctuations will then contribute to eventually overcome the attractive potential between colloids with non-fixed positions, such that no stable aggregation occurs in our system. Stable configurations can be achieved by, for example, increasing the size of the colloid,10 which increases the thermal diffusion factor αT of the colloids.
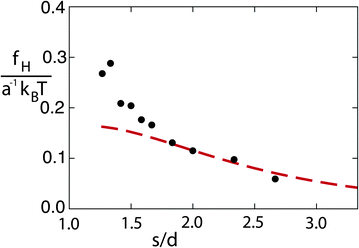 | ||
| Fig. 8 Hydrodynamic attraction force as a function of the inter-particle separation. Symbols correspond to simulation data and the dashed line to the analytical prediction in eqn (5). | ||
Analytically, the attraction induced by the thermophoretic flow field has been calculated using the reflection method. To the first reflection, the attraction force fH is expressed as11,39
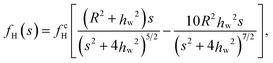 | (5) |
B Single-particle microfluidic pump
In Section IV-C we have investigated the flow field around one particle fixed in a periodic temperature gradient. As shown in Fig. 4, this configuration results in a net solvent flow which can be exploited to fabricate a single-particle microfluidic pump. In order to validate this idea we perform simulations of one thermophilic spherical colloid fixed in a periodic gradient confined between parallel walls. Walls are implemented with stick boundary conditions by using the bounce-back of the MPC particles at the wall. The chosen wall separation is L⊥ = 12a. PBCs are used in the other two directions. The box size in the direction of the periodic temperature gradient is 2Lz with Lz = 22a, and the third and neutral direction is L⊥ = 12a. The employed temperature gradient is ∇T = 0.0135![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /a. As depicted in Fig. 9, the colloidal sphere is fixed equidistant from the walls and from the cold and the hot layer, while no colloidal particle is considered in the neighbouring half-box where the temperature gradient has an opposite sign. In this configuration the colloid has the hot layer on its right, which originates a flow from right to left. The direction of the flow could be reverted by placing the hot layer on the left of the thermophilic colloid, or by employing instead a colloid with thermophobic properties.
/a. As depicted in Fig. 9, the colloidal sphere is fixed equidistant from the walls and from the cold and the hot layer, while no colloidal particle is considered in the neighbouring half-box where the temperature gradient has an opposite sign. In this configuration the colloid has the hot layer on its right, which originates a flow from right to left. The direction of the flow could be reverted by placing the hot layer on the left of the thermophilic colloid, or by employing instead a colloid with thermophobic properties.
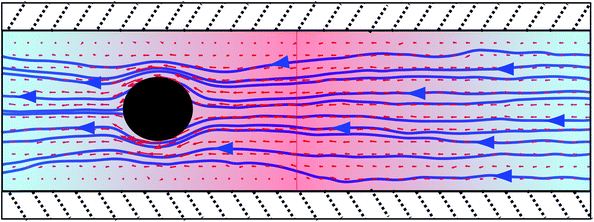 | ||
| Fig. 9 Single-particle thermophoretic pump. Thermophilic colloidal particle confined between parallel walls, with both extremes of the tube connected by PBCs, and larger temperatures in the tube center. Given that the colloid is thermophilic and has the hot layer on its right, the solvent continuously flows from right to left. | ||
The so-called Knudsen pumps59,60 are also pumps operated without any moving parts and with a temperature gradient along the walls of a micro-channel. The driving mechanism is though completely different from the one presented in our work. The Knudsen pumps are driven thermal creep gas flows,61,62 while here we present a pump driven by liquid thermophoretic forces. Thermal creep flow occurs when the molecules of a rarefied gas interact with walls that have a position dependent temperature. The molecules in a high temperature region can transfer more momentum to the wall than those in a low temperature region, such that the gas exerts a net force on the wall against the temperature gradient.62 This in turn translates into an effective flow velocity that goes always from cold to warm areas. In the present thermophoretic pumps, flow can occur in both directions. A different family of microfluidic manipulation that has been widely used63,64 is based on the existence of a surface tension gradient in the direction of a temperature gradient. For example, liquid droplets or films on a surface can be transported along or against a temperature gradient.65,66 A very recent simulation work shows that liquids can also be pumped by a symmetric temperature gradient through a composite nanochannel,67 in which one half of the channel wall has a low fluid–wall surface energy while the other half has a high one. Essentially, the physical mechanism is the same as the pump we present here, since the single particle can be regarded as a curved surface or as a building-block of planar walls. The variant proposed here is based on the properties of a single particle which provides an important additional degree of flexibility in the design of microfluidic devices.
We analyze the averaged velocity profile across the tube in the simulated single particle pump. Two bins 5a wide are chosen at both sides of the cold layer. These are completely at the left and at the right of the tube as displayed in Fig. 9. The results in Fig. 10 show the expected parabolic profile, although the two bins are significantly different. This difference originates from the thermal creep flow, since in our simulations the mean free path cannot be taken to be arbitrarily small due to computational costs. For the left half of the channel in Fig. 9, the thermal creep flow is against the thermophoretic flow field such that it effectively reduces the slip on the wall. However, the thermal creep flow in the right half of the channel has the same direction as the thermophoretic flow field which noticeably enhances the slip. This difference can also be directly seen in Fig. 9 where the left half of the wall seems stickier than the right half. The inset of Fig. 10 shows the parabolic profile of the flow in a similar configuration but with a thermophobic colloid. Here, the flow is in the opposite direction.
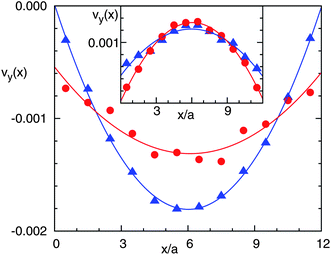 | ||
| Fig. 10 Velocity parallel to the walls and between them for the flow in Fig. 9. Triangles correspond to the average profile in a bin 5a wide just on the right of the cold layer. Circles relate to a bin 5a wide just on the left of the cold layer. Lines refer to a parabolic fit. The inset corresponds to the velocity profile in the same layers but for a thermophobic colloid. | ||
A final point that distinguishes the flow of this pump and the flow displayed in Fig. 4 is the existence of wall friction, besides the friction of the colloidal surface. This means that the integral of stress tensor over the particle surface for the case of the pump is not zero. It can be therefore expected that the magnitude of the solvent flow decreases with increasing tube length.
VI Discussion and conclusions
A colloidal particle in solution in the presence of a temperature gradient does not only suffer a thermophoretic directed force, but also induces a thermophoretic flow field. This flow is here extensively studied by means of mesoscopic simulations. The obtained results quantitatively agree with the analytical predictions, which support both the assumptions made in the theory and the validity of the MPC simulation technique to investigate the dynamics of non-isothermal solutions. The flow field in the case that the colloidal particle is fixed is first analyzed. The force exerted on the colloid is in this case the thermophoretic force, and the induced flow field is Stokeslet-like and therefore long ranged. This is in some aspects similar to a sedimenting particle, although the lack of motion and the fact that the driving force is not external make them clearly different. We also investigate the flow field around a freely moving particle. The thermophoretic force balances with the friction force due to the colloidal motion, such that the total force on the colloid vanishes. The induced flow field is then source-dipole-like and therefore very short ranged. The fluid motion in these two examples does not violate the second principle of thermodynamics since these are non-equilibrium systems to which external energy has to be constantly supplied in order to maintain the temperature gradient. During the fluid motion, thermal energy is continuously transformed into translational kinetic energy of the fluid, which is simultaneously dissipated by viscous friction. In the stationary state, the two processes balance each other.The importance of hydrodynamic interactions in the thermophoretic phenomena has long been a subject of debate.3,68 The most important example is the explanation of the size independence of thermal diffusion coefficient of a dilute high-weight polymer solution.14,41,69,70 From the study presented in this manuscript, it is straightforward to argue that the thermophoretically induced flow field around a fixed colloidal particle accounts for the effect of the thermophoretic force, while the flow around a moving colloid accounts for the combination of the thermophoretic and friction forces. In a recent work37 we show how the long ranged hydrodynamic contribution of the flow field can explain the size independence of thermal diffusion coefficient of a dilute high-weight polymer solution. In our reasoning this occurs just as a cancelling effect of the dependence of the thermophoretic force and the self-diffusion coefficient.
As a practical application, we show that long-ranged attraction between colloids can be induced as a consequence of the hydrodynamic thermophoretic flow field near a boundary wall. This is consistent with the theoretical calculations and the recent experimental observations.10,11 Our simulations offer a complementary verification of this effect. An enhancement of the attraction at short distance with respect to the analytical prediction is observed in our simulation results. Finally we present a prototype of a single-particle thermophoretic pump which has not yet been experimentally verified. In this pump the flow field can be generated given the presence of a thermophoretic particle and a temperature field with an alternating gradient. The implementation of this pump does not require the presence of any movable part. The direction of the flow is determined by the orientation of the alternating temperature gradients and the thermophoretic properties of the employed particle. One very important advantage of this pump in comparison with other existing pumps59,60,63,64,67 is that the flow can be controlled at a single particle level which will allow the development of promising microfluidic applications.
VII Appendix A: reflection method to calculate wall-induced backflow
The Stokes equation for the flow field is solved in eqn (3) considering vanishing velocity field at infinity. In general, the effect of one near wall can be analytically described by using the reflection method. In order to cancel the fluid velocity on the wall (stick boundary conditions), the flow field can be evaluated by considering an image particle with respect to the wall.47,48 The flow field at a point r = (rx, ry, rz) due to the image placed at r′ = (r′x, r′y, r′z) is found to be47,48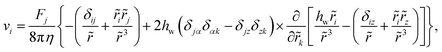 | (A1) |
![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) denotes the relative position
denotes the relative position ![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) = r′ − r and its modulus is
= r′ − r and its modulus is ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) . Here z is the direction perpendicular to the wall, the indices i, j, and k ∈ (x, y, z), α ∈ (x, y), and the Einstein's summation convention is employed. Fj is the force exerted on the solvent by the image, and hw is the image–wall distance. Note that eqn (A1) only includes the Stokeslet part of the flow produced by the image particle, and higher-order source doublet contributions are neglected.
. Here z is the direction perpendicular to the wall, the indices i, j, and k ∈ (x, y, z), α ∈ (x, y), and the Einstein's summation convention is employed. Fj is the force exerted on the solvent by the image, and hw is the image–wall distance. Note that eqn (A1) only includes the Stokeslet part of the flow produced by the image particle, and higher-order source doublet contributions are neglected.
For the case of the thermophoretic flows va and vb considered in Fig. 1 the flow and force are both perpendicular to the wall and eqn (A1) is simplified as
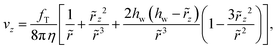 | (A2) |
 | ||
| Fig. 11 Schematic diagram of the reflection method used in our calculations. With solid lines, the actual walls and the central colloid; with dashed lines the corresponding images. | ||
Acknowledgements
We are very much indebted to Daniel Lüsebrink, Gerhard Gompper, Chien-Cheng Huang and Ulf D. Schiller for useful discussions.References
- S. Wiegand, J. Phys.: Condens. Matter, 2004, 16, R357 CrossRef CAS.
- R. Piazza and A. Parola, J. Phys.: Condens. Matter, 2008, 20, 153102 CrossRef.
- A. Würger, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- J. Giddings, Science, 1993, 260, 1456 CrossRef CAS.
- C. B. Mast and D. Braun, Phys. Rev. Lett., 2010, 104, 188102 CrossRef.
- P. Baaske, F. M. Weinert, S. Duhr, K. H. Lemke, M. J. Russell and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9346 CrossRef CAS.
- I. Budin, R. J. Bruckner and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 9628 CrossRef CAS.
- B. V. Derjaguin and G. P. Sidorenkov, Dokl. Akad. Nauk SSSR, 1941, 32, 622.
- B. V. Derjaguin, N. V. Churaev and V. M. Muller, Surface Forces, Consultants Bureau, New York, 1987 Search PubMed.
- F. M. Weinert and D. Braun, Phys. Rev. Lett., 2008, 101, 168301 CrossRef.
- R. Di Leonardo, F. Ianni and G. Ruocco, Langmuir, 2009, 25, 4247 CrossRef.
- M. Trau, D. A. Saville and A. Aksay, Science, 1996, 272, 706 CrossRef CAS.
- S. R. Yel, M. Seul and B. I. Shraiman, Nature, 1997, 386, 57 CrossRef CAS.
- J. Rauch and W. Köhler, Macromolecules, 2005, 38, 3571 CrossRef CAS.
- J. K. G. Dhont and W. J. Briels, Eur. Phys. J. E, 2008, 25, 61 Search PubMed.
- D. Stadelmaier and W. Köhler, Macromolecules, 2008, 41, 6205 CrossRef CAS.
- H. R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 Search PubMed.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 2000, 112, 7260 CrossRef CAS.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1 CAS.
- K. Mussawisade, M. Ripoll, R. G. Winkler and G. Gompper, J. Chem. Phys., 2005, 123, 144905 CrossRef CAS.
- M. Ripoll, R. G. Winkler and G. Gompper, Eur. Phys. J. E, 2007, 23, 249 Search PubMed.
- D. Lüsebrink and M. Ripoll, J. Chem. Phys., 2012, 136, 084106 Search PubMed.
- D. Lüsebrink, M. Yang and M. Ripoll, J. Phys.: Condens. Matter, 2012, 24, 284132 Search PubMed.
- E. Tüzel, M. Strauss, T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036701 CrossRef CAS.
- E. Tüzel, T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 056702 CrossRef CAS.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, Europhys. Lett., 2001, 56, 319 CrossRef CAS.
- C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. Winkler, J. Comp. Physiol., 2010, 229, 168 Search PubMed.
- B. Hafskjold, T. Ikeshoji and S. K. Ratkje, Mol. Phys., 1993, 80, 1389 CAS.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082 CrossRef.
- M. Ripoll, K. Mussawisade, R. G. Winkler and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 016701 CrossRef CAS.
- G. A. Vliegenthart, J. F. M. Lodge and H. N. W. Lekkerkerker, Phys. A, 1999, 263, 378 CrossRef CAS.
- C. Huang, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056711 Search PubMed.
- J. T. Padding and A. A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 93, 031402 Search PubMed.
- M. Yang and M. Ripoll, J. Phys.: Condens. Matter, 2012, 24, 195101 Search PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61 CrossRef.
- J. Morthomas and A. Würger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051405 Search PubMed.
- M. Yang and M. Ripoll, J. Chem. Phys., 2012, 136, 204508 Search PubMed.
- A. Würger, Phys. Rev. Lett., 2007, 98, 138301 CrossRef.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831 CrossRef CAS.
- H. Yamakawa, J. Chem. Phys., 1970, 53, 436 CrossRef CAS.
- B. Dünweg and A. J. C. Ladd, Adv. Polym. Sci., 2009, 221, 89.
- Y. Peng, C. Shu, Y. T. Chew and T. Inamuro, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 016703 Search PubMed.
- M. Fyta, S. Melchionna, S. Succi and E. Kaxiras, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036704 CrossRef.
- J. R. Blake, Proc. Cambridge Philos. Soc., 1971, 70, 303 Search PubMed.
- J. R. Blake and A. T. Chwang, J. Eng. Math., 1974, 8, 23 CrossRef.
- T. M. Squires, J. Fluid Mech., 2001, 443, 403 Search PubMed.
- B. Dünweg and K. Kremer, J. Chem. Phys., 1993, 99, 6983 CrossRef.
- M. Ripoll and M. H. Ernst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011101 Search PubMed.
- M. Zhang and F. Müller-Plathe, J. Chem. Phys., 2006, 125, 124903 CrossRef.
- P. A. Artola and B. Rousseau, Phys. Rev. Lett., 2007, 98, 125901 CrossRef.
- G. Galliéro and S. Volz, J. Chem. Phys., 2008, 128, 064505 Search PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201(R).
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics, Kluwer Academic Publishers Group, Dordrecht, The Netherlands, 1983 Search PubMed.
- M. D. Carbajal-Tinoco, R. Lopez-Fernandez and J. Arauz-Lara, Phys. Rev. Lett., 2007, 99, 138303 Search PubMed.
- M. Braibanti, D. Vigolo and R. Piazza, Phys. Rev. Lett., 2008, 100, 108303 CrossRef.
- M. Knudsen, Ann. Phys., 1909, 336, 205 Search PubMed.
- S. McNamara and Y. B. Gianchandani, J. Microelectromech. Syst., 2005, 14, 4 Search PubMed.
- J. C. Maxwell, Philos. Trans. R. Soc. London, 1879, 170, 231 CrossRef.
- Y. Sone, Annu. Rev. Fluid Mech., 2000, 32, 779 Search PubMed.
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381 CrossRef.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977 CrossRef CAS.
- A. M. Cazabat, F. Heslot, S. M. Troian and P. Carles, Nature, 1990, 346, 824 CrossRef CAS.
- J. B. Brzoska, F. Brochard-Wyart and F. Rondelez, Langmuir, 1993, 9, 2220 CrossRef CAS.
- C. Liu and Z. Li, Phys. Rev. Lett., 2010, 105, 174501 CrossRef.
- J. K. G. Dhont, S. Wiegand, S. Duhr and D. Braun, Langmuir, 2007, 23, 1674 CrossRef CAS.
- F. Brochard and P. G. de Gennes, C. R. Acad. Sci. Paris II, 1981, 293, 1025 Search PubMed.
- E. Bringuier, Phys. A, 2010, 389, 4545 Search PubMed.
| This journal is © The Royal Society of Chemistry 2013 |
