 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the collapse transition of a polymer brush: the case of lateral mobility
F. A. M.
Leermakers
a and
S. A.
Egorov
b
aLaboratory of Physical Chemistry and Colloid Science, Wageningen University, Dreijenplein 6, 6703 HB Wageningen, The Netherlands
bDepartment of Chemistry, University of Virginia, Charlottesville, Virginia 22901, USA
First published on 11th February 2013
Abstract
We consider a polymer brush composed of end-grafted polymer chains. Classical theory advocates that a worsening of the solvent quality results in a smooth decrease of the brush height from a swollen to a dense brush. We report that a homogeneous brush under poor solvent conditions can have a negative surface pressure, indicating an instability in favour of lateral segregation. Also by using a two-gradient version of the self-consistent field (SCF) theory we show that, in contradiction to the classical result, but in line with the negative pressure, the collapse transition for laterally mobile chains has a first-order character, exemplified by the presence of a compact brush that coexists with a dilute gas of end-grafted chains. The dense brush assumes a pancake shape wherein the chains balance the stretching entropy against surface energies. The height of the pancake scales sub-linearly with the chain length because the local grafting density decreases with increasing chain length. In analogy with wetting studies we discuss how the spreading parameter has an influence on the pancake structure. Accordingly, the height increases with worsening of the solvent quality and decreases with increased affinity for the substrate. The two-phase state is expected in many practical situations.
I Introduction
A collection of linear chains grafted onto a substrate or anchored onto an interface, such that the chains are strongly interacting, is known as a polymer brush. Polymer brushes are popular structures not only from an experimental and application point of view, but also from a theoretical perspective.1–7 There are many unique results known for the polymer brush. For example, when the number of chains per unit area, that is the grafting density σ, exceeds the overlap threshold σ > 1/N, with N being the number of segments per polymer chain, we know that the height H of this layer is invariably proportional to the chain length:8| H ∝ Nσ1/3ν1/3 (good solvent ν = 1 − 2χ > 0) | (1) |
| H ∝ Nσ1/2ω1/2 (theta solvent χ = 0.5) | (2) |
| H ∝ Nσ (poor solvent χ > 0.5) | (3) |
Note that these predictions are generated using the classical SCF theory and are elaborated by a scaling analysis which requires as a prerequisite that the brush remains laterally homogeneous. The lateral homogeneity is undisputed unless the solvent quality is poor. In this paper we will focus on the poor solvent case and test the validity of this result.
It is well known that the classical theory predicts that the brush height decreases smoothly, that is not jump-like, upon worsening the solvent quality.9 In other words it predicts that the collapse transition is not a first-order transition. To illustrate this point we present the prediction of the numerical SCF theory (for details see below) for the height H of the brush as a function of the Flory–Huggins interaction parameter in Fig. 1. In this result the height of the brush is defined by the first moment of the end-point distribution (cf.eqn (11)). The results shown in Fig. 1 are for brushes with chain lengths N = 100,…,5000. Inspired by the linear chain length dependence (cf.eqn (1–3)), the height is normalised to the degree of polymerisation. As is seen, the collapse of the neutral brush has a universal dependence on the FH interaction parameter. The grafting density was fixed to σ = 0.02 which is just a factor two larger than the overlap threshold for N = 100. This explains the relatively large deviations from the universal χ dependence for the shortest chains. The universal dependence for the larger chain lengths strongly supports the idea that even in the limit of N → ∞ the transition remains smooth. Close inspection of the ‘universal’ curve shows that for a sufficiently large N the curvature ∂2H/∂χ2 = 0 changes sign at χ = 0.5.
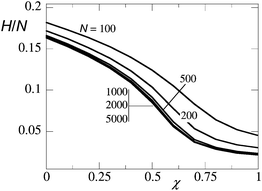 | ||
| Fig. 1 The height of the brush H, scaled by the chain length N, as a function of the Flory–Huggins parameter χ as found by the classical SCF theory. The grafting density is given by σ = 0.02, and the chain lengths N = 100, 200, 500, 1000, 2000 and 5000 from top to bottom lines (for the longer chain lengths, the curves overlap). | ||
The prediction for the collapse transition of the brush is remarkable. To elaborate on this we first consider a system of polymer chains in a monomeric solvent whose chains are not grafted to any surface. Upon worsening of the solvent quality in this system, it is well known that above a critical value of the interaction parameter χ, the system features a solubility gap. In this case there is a concentrated polymer solution in equilibrium with a (monomeric) solvent phase with a very low polymer concentration. Within the Flory–Huggins theory10 the critical point of this system is
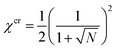 | (4) |
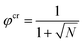 | (5) |
It is known11 that the interfacial tension γPS and the density difference of polymer Δϕ between the polymer-rich and solvent-rich phase, that is Δϕ = φpolymer rich phaseP − φsolvent rich phaseP, obey (in the mean field) to the power-law dependences
| γPS ∝ (χ − χcr)3/2 = Δχ3/2 | (6) |
| Δϕ = ∝Δχ1/2 | (7) |
Now let us consider the scenario of a polymer–solvent system in the case that χ > χcr, and discuss how the polymer phase (minority phase) interacts with a substrate. The possible scenarios are well known in the field of wetting.12 Basically there are three cases. (i) The substrate (W) is wet by the polymer. In this case the polymer covers the substrate completely; the film thickness is homogeneous and the thickness is given by the amount of polymer available per unit area of the substrate. In this case there are just two interfaces, namely substrate–polymer (that is the polymer-rich phase) and polymer–solvent (that is, phases rich in polymer (P) and solvent (S), respectively). (ii) The substrate is wet by the solvent. In this case the solvent is preferentially at the substrate and the polymer-rich phase is formed somewhere in the bulk and exists as a spherical drop. Again there are just two interfaces, namely substrate–solvent and polymer–solvent. (iii) The surface is partially wet by the polymer. In this case there are three interfaces in the system, namely the polymer–solvent (PS), the substrate–polymer (WP) and substrate–solvent (WS) interfaces.
The three interfaces have an interfacial free energy per unit area (interfacial tension) γPS, γWP and γWS. Let us assume that the polymer is the minority phase and consider that the polymer drop is on the surface. At the edge of the drop there is a three-phase contact line; that is where the polymer-rich phase, the solvent-rich phase and the substrate come together. At this three-phase contact line there exists a contact angle α. Balancing the interfacial tensions leads to Young's law:
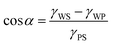 | (8) |
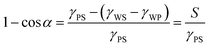 | (9) |
In the absence of gravity the curvature of the sessile drop is homogeneous and thus the shape is a sphere cap. Importantly, for large drops the PS interface becomes sufficiently far separated from the WP interface so that the corresponding interfacial energies are well defined.
One way to look at this result is that laterally along the surface we see the coexistence of a polymer-rich phase (at the location of the drop) and a solvent-rich phase (outside the drop), which may be seen as a ‘gas’ of polymers. This coexistence of the two phases is of course possible due to the choice of the interaction parameters with the substrate (partial wetting), but is primarily the signature of a first-order phase transition of the polymer–solvent system, that is, χ exceeds the critical value.
Let us now see how the case of a sessile drop of polymers in two-phase coexistence differs from the polymer brush under poor solvent conditions. One immediately notices that a chain in the polymer-rich phase is completely mobile, whereas the chains are pinned to the substrate/interface in the case of a brush. This pinning constraint has, as we will see, a few major consequences. Importantly we notice that for a brush it is not always true that the lateral mobility is necessarily absent. Indeed there are cases wherefore the polymer chains are tethered (by way of some anchoring group) onto a mobile interface (e.g. a liquid–vapour interface). Then the lateral mobility of the chains will allow them to organise themselves laterally along the surface. In such a case the difference between the polymer-rich phase in the drop and the polymer brush comes down to the restriction of the end-point in a 3D volume versus a 2D plane. Below we will focus on the case that the grafted chains are laterally mobile.
In our view a brush in poor solvent, that is χ > χcr, is not so much different from a collection of chains in a polymer-rich phase. Of course, in the case of a collapsed brush the ‘drop’ shape will typically deviate strongly from the sphere cap. Another important difference is that the interfacial free energies of the free polymer–solvent (PS) and the polymer–surface (PW) cannot be determined independently from each other. Indeed the two interfaces are necessarily in close proximity due to the chains that bridge elastically between the two interfaces. Below we take a pragmatic standpoint and still consider the PW and PS interfaces separately and assign phenomenologically interfacial free energies to the individual PS and PW interfaces. Here we will write ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) to remind ourselves that strictly these quantities are only pragmatically defined.
to remind ourselves that strictly these quantities are only pragmatically defined.
It must be stressed that there are already a number of reports in the literature that a brush can undergo a jump-like phase transition when the solvent quality becomes poor.8,15 Also the lateral aggregation of surfactants, lipids or polymers in Langmuir troughs is well documented.16 Our report adds to the evidence that a transition should be expected. We will elaborate on this below, both in one-gradient and in two-gradient SCF computations. We will complement our results by scaling arguments.
II Numerical self-consistent field model
The SCF theory for polymer brushes is well documented.17,18 Here we will elaborate on the Scheutjens–Fleer variant wherein a lattice is used as a means to discretise space. The polymer chains are assumed to be composed of segments that fit the size of a lattice site. Within this SF-SCF approach it is possible to elaborate on models wherein the polymer density can vary normal to the grafting surface (one-gradient model) but also wherein the polymer density gradients can develop in two directions (two-gradient models).19 The latter can be used to study directly the phase coexistence of laterally mobile chains. We refer to the literature for details and mention the prerequisites of the numerical SCF theory while introducing the model(s).Let us consider linear polymer chains composed of segments (P), that is spherical units of size b, numbered s = 1,…,N. The first segment is constrained to a coordinate z = 1, just above a surface W position at z ≤ 0. The target is to predict the distribution of polymer segments in the space above the surface, that is in lattice layers z = 1,…,M. The use of a lattice facilitates the counting of the conformations. The cells in the lattice have a dimension b so that a segment fits on the lattice site. All linear lengths used below are normalised by the segment length b.
Apart from the polymer chains we have a monomeric solvent S, which takes up all space besides the polymer. Polymer conformations are generated using a freely jointed chain model and the single chain partition function is evaluated using a discretised version of the Edwards diffusion equation.20 Here we do not go into details, but we mention that the conformations are weighted using the segment potentials. In these potentials the solvent quality is specified by the FH parameter χ and short-range surface contacts are given by χW. The number of contacts is estimated using the Bragg–Williams approximation. Here we implement the insight that only the difference of WP and WS contact is needed: χW ≡ χPW − χPS.17 On top of this, the self-consistent field potential has a Lagrange field contribution, which is coupled to the incompressibility constraint φP(r) + φS(r) = 1 implemented for all coordinates r.21
In the one-gradient model we focus on the volume fraction profile perpendicular to the surface, that is we have r = z and apply the mean-field approximation in the x–y plane. Most of the results discussed below are generated using a two-gradient model r = (x, z) wherein we apply the mean-field approximation in the y direction only. Again the z direction is perpendicular to the surface and the x = 1,…,Mx direction runs parallel to the surface. When we consider a pancake of polymer chains in equilibrium with a very dilute phase of grafted chains, we have a straight line separating the two phases.
As we will see, it is possible to find the two-phase state when the solvent quality is poor. The concentrated phase is positioned at small values of x and the ‘gas’ phase at large values of x. Reflecting boundary conditions apply both between coordinates x = 0 and x = 1 and x = Mx and x = Mx + 1. It is of interest to measure the effective grafting density at coordinate x, that is σ(x):
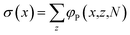 | (10) |
It is also of interest to give a measure of the local height H(x). One option is that we use the distribution of the free ends of the polymer chains for this and evaluate the first moment according to
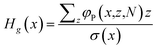 | (11) |
Alternatively, we can use all polymer segments for this
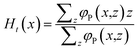 | (12) |
The local average segment density in the pancake may be estimated from ϕ(x) = σ(x)N/H. As the collapsed brush has more or less a homogeneous density we can also use the product θ(x) = σ(x)N, which is the amount of polymer segments in the brush at coordinate x (per unit length in the y direction) as a measure of the height of the pancake.
The pancake is in mechanical equilibrium with the (extremely) dilute phase of grafted chains. Unless the system is near the critical point, the lateral pressure is to a good approximation zero, simply because the chains outside the pancake are separated sufficiently far from each other so that the (ideal gas) pressure vanishes. Hence the grand potential Ω in the system, which is easily computed from the SCF result,21 can directly be identified as the line tension τ. Upon the approach of the critical point, however, the lateral pressure π becomes finite, and the line tension is given by τ = Ω + Mxπ. Below, all energies are normalised by the thermal energy kBT. Hence the line tension is normalised by kBT/b. Similarly interfacial tensions are normalised by kBT/b2.
III Numerical SCF results and a scaling analysis
One-gradient analysis
The reference results for the collapse transition of a polymer brush in a one-gradient SCF model are already shown in Fig. 1. One may think that the one-gradient analysis is not informative about the instability of the brush under poor solvent conditions. This is of course not the case. One characteristic for phase coexistence is that both phases should have the same pressure. To elaborate on this we have computed the grand potential, Ω = F − σμ (the chemical potential of the solvent is zero). This quantity may be interpreted as minus the surface pressure π in the brush. For stability we should expect that the surface pressure is an increasing function with grafting density. Thus the surface pressure cannot be negative. Deviations from these trends indicate the possibility of phase coexistence. Then, for coexisting phases the pressure should be the same in both phases.As an example we show the grand potential as a function of the grafting density for the case where chains are N = 200 segments long and the substrate has equal affinity for the polymer segments and the solvent monomers χW = 0 in Fig. 2. Similar loops in the pressure profile have been reported before.13,14 Here we focused deliberately on a solvent quality which is close to the critical value χ = 0.6 > χcr. Indeed the grand potential is not a monotonically decreasing function, and thus the surface pressure does not continuously increase with the grafting density. Also, it is easily seen that one can have two systems that differ in the grafting density that have the same lateral pressure. From classical thermodynamics we know that the open system will tend to go to the lowest possible grand potential in the system. Indeed from the perspective of the brush that is allowed to choose its own grafting density, the systems are open with respect to the grafting density. The two phases that coexist are connected to each other by a dotted horizontal line. The two coexisting grafting densities are the grafting density of the dilute phase (below we refer to this as the ‘gas’) and the grafting density in the ‘pancake’.
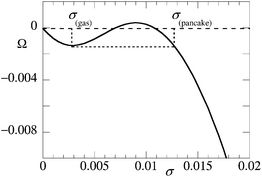 | ||
| Fig. 2 Grand potential Ω = −π of the brush as a function of the grafting density. N = 200, χ = 0.6 (only slightly above the critical value), χW = 0, surface interactions are ‘neutral’, that is polymer segments have equal affinity for the substrate compared to solvent monomers. σgas is the grafting density for the dilute phase; σpancake is the grafting density in the pancake. | ||
Upon decreasing the solvent quality, we will show below that very quickly the grafting density for the gas-phase goes towards zero. Hence the coexisting pressures will evolve towards zero. We can therefore routinely search for the grafting density of the ‘pancake’ phase by searching for the grafting conditions for which the grand potential vanishes. Below we have used this Ansatz frequently to complement two-gradient analysis. Although much of the analysis can be done in a one-gradient model, we proceed to present the remainder of the result in the two-gradient setting. The advantage of the latter is that we get information about the line tension as well.
Two-gradient analysis
Let us proceed to consider the brush composed of laterally mobile chains under poor solvent conditions using an SCF model within a two-gradient (x, z) coordinate system. As an example we focus on a case where N = 200 in a poor solvent χ = 1 for a neutral surface χW = 0 (polymer segments and solvent molecules have equal affinity for the substrate). Fig. 3 gives a two-gradient equal density contour plot for the polymer chains for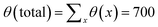 . As anticipated we notice that there is a pancake with a homogeneous height, in this case running from x = 1,…,50, and the edge of the pancake has a near 90° contact angle. This high contact angle is anticipated because χW = 0. Note that the mirror-like boundary condition applies at the boundaries in the x direction: Fig. 1 thus only shows the cross-section through half the pancake. Upon close inspection one notices that the density profile of polymers just near the surface is a bit lower than in the remainder of the pancake. One of the origins of this depression of the polymer density is the entropy loss the polymer chains experience near the impenetrable surface. Only when there is sufficient adsorption energy χW < −1 this depression vanishes.
. As anticipated we notice that there is a pancake with a homogeneous height, in this case running from x = 1,…,50, and the edge of the pancake has a near 90° contact angle. This high contact angle is anticipated because χW = 0. Note that the mirror-like boundary condition applies at the boundaries in the x direction: Fig. 1 thus only shows the cross-section through half the pancake. Upon close inspection one notices that the density profile of polymers just near the surface is a bit lower than in the remainder of the pancake. One of the origins of this depression of the polymer density is the entropy loss the polymer chains experience near the impenetrable surface. Only when there is sufficient adsorption energy χW < −1 this depression vanishes.
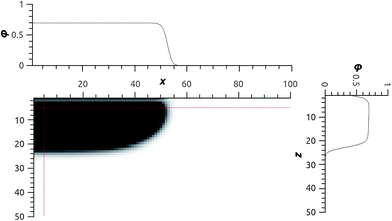 | ||
| Fig. 3 Equal volume fraction contour plot in the x–z plane for N = 200, θ (total) = 700, χ = 1 and χW = 0. The two satellite graphs give a cross-section profile (top) φ(x, 5) and (right) φ(5, z). In the x-direction reflecting (mirror-like) boundaries are implemented (hence the cross-section of only half of the drop is shown). The substrate is placed at z = 0 and the chains are pinned with their ends in the layer z = 1 and are allowed to move in the x–y plane. | ||
It is of interest to point to a few characteristics of the pancake. Inside the pancake the polymer density is homogeneous as can be concluded also from the satellite cross-section profiles φ(x, 5) and φ(5, z) in Fig. 3. We expect that this density of segments in the pancake, ϕ, is a function of Δχ and not so much a function of σ or N.
The brush height results from a balance of stretching energy and interfacial free energies. For each chain the interfacial free energy is inversely proportional to the grafting density. As in a collapsed brush σN/H = ϕ we find that the interfacial energy is given by ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) /σ =
/σ = ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) N/(ϕH). The proportionality with a spreading parameter
N/(ϕH). The proportionality with a spreading parameter ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is motivated by the observation that each chain in the pancake forms PS and PW interfaces at the cost of a corresponding piece of the SW interface. The bar notation is used to recall that its value is not identical to S introduced in eqn (9), but has ‘corresponding’ phenomenological contributions. Again, we expect that
is motivated by the observation that each chain in the pancake forms PS and PW interfaces at the cost of a corresponding piece of the SW interface. The bar notation is used to recall that its value is not identical to S introduced in eqn (9), but has ‘corresponding’ phenomenological contributions. Again, we expect that ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (Δχ). Combining the interfacial energy with the Gaussian stretching energy of the brush chains gives a free energy (per chain) of the form
(Δχ). Combining the interfacial energy with the Gaussian stretching energy of the brush chains gives a free energy (per chain) of the form
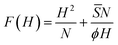 | (13) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) :
:H ∝ N2/3![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 1/3ϕ−1/3 1/3ϕ−1/3 | (14) |
σ ∝ N−1/3![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 1/3ϕ2/3 1/3ϕ2/3 | (15) |
As is seen, the height of the pancake grows sub-linearly with the chain length. This is because the grafting density of the chains inside the pancake is not fixed: the grafting density decreases with increasing chain length.
To test these chain length dependences, we fixed χ = 1, so both ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) as well as ϕ are expected to be constants. In Fig. 4 we show the height (a) and grafting density (b) dependences as a function of the chain length in double logarithmic coordinates. It is easily seen that the pancake obeys to a good approximation the laws given by eqn (14) and (15).
as well as ϕ are expected to be constants. In Fig. 4 we show the height (a) and grafting density (b) dependences as a function of the chain length in double logarithmic coordinates. It is easily seen that the pancake obeys to a good approximation the laws given by eqn (14) and (15).
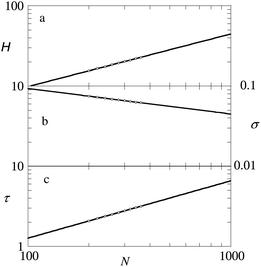 | ||
| Fig. 4 (a) The height, given by eqn (12), (slope is close to 2/3) (b) the grafting density σ (slope is close to −1/3) and (c) the line tension of the pancake (slope is close to 2/3) as a function of the chain length in double logarithmic coordinates. Parameters: χ = 1, and χW = 0. All quantities are made dimensionless as explained in the modelling section. | ||
The line tension is for obvious reasons expected to scale with the height of the brush and also this dependence is observed (cf.Fig. 4c). One may further expect that the line tension is proportional to the interfacial tension between a polymer-rich and solvent-rich phase (cf.eqn (6)). Using the numerical result for the interfacial tension as given by eqn (6), γPS ≈ 0.125 for χ = 1. The Ansatz τ = HγPS gives a value of τ = 2.5 when H = 20. From Fig. 4 we extract a line tension τ ≈ 2.7 for H = 20, which is very close to the estimate τ = HγPS. Recall that in this example the influence of the substrate on the line tension is expected to be small because χW = 0.
From eqn (14) and (15) we notice that we should expect a decrease of the height of the pancake when ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) increases. Recalling that χW ≡ χPW − χSW, we realise that when χW < 0 the polymer segments have a higher affinity for the substrate than the solvent molecules. With decreasing (more negative) χW we expect
increases. Recalling that χW ≡ χPW − χSW, we realise that when χW < 0 the polymer segments have a higher affinity for the substrate than the solvent molecules. With decreasing (more negative) χW we expect ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) PW −
PW − ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) SW to decrease as well. The corresponding decrease of
SW to decrease as well. The corresponding decrease of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) leads to a decrease of the height of the pancake. Further, when
leads to a decrease of the height of the pancake. Further, when ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 0 we should expect that H ∝ N1/2 because in this case the chains can freely adopt their Gaussian dimension R ∝ N1/2. For
= 0 we should expect that H ∝ N1/2 because in this case the chains can freely adopt their Gaussian dimension R ∝ N1/2. For ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 0 we also should find σ ∝ N−1/2.
= 0 we also should find σ ∝ N−1/2.
When the polymer chains are strongly attracted to the surface, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) < 0, the brush height becomes less than the unperturbed radius of gyration. To squeeze the pancake to small heights, H < R leads to an entropy loss. This entropic penalty is expected to scale with N (extensive property). Moreover, we expect that the entropy should scale proportional to R/H, and thus the entropy change is given by N/H2. Combining this with the interfacial term gives
< 0, the brush height becomes less than the unperturbed radius of gyration. To squeeze the pancake to small heights, H < R leads to an entropy loss. This entropic penalty is expected to scale with N (extensive property). Moreover, we expect that the entropy should scale proportional to R/H, and thus the entropy change is given by N/H2. Combining this with the interfacial term gives
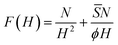 | (16) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) < 0. By optimising this free energy to H gives H ∝ |
< 0. By optimising this free energy to H gives H ∝ |![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) |−1. The thinning of the brush with increasing affinity for the surface continues until all segments are in contact with the substrate. Such a continuous decrease of the pancake with decreasing values of
|−1. The thinning of the brush with increasing affinity for the surface continues until all segments are in contact with the substrate. Such a continuous decrease of the pancake with decreasing values of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is obviously only possible when the average grafting density of chains is sufficiently small, that is when the original system of grafted chains is below the overlap threshold. Unfortunately it is not trivial to estimate for which χW the spreading parameter
is obviously only possible when the average grafting density of chains is sufficiently small, that is when the original system of grafted chains is below the overlap threshold. Unfortunately it is not trivial to estimate for which χW the spreading parameter ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) changes sign.
changes sign.
Fig. 5 presents the amount of polymer segments θ(x) = σ(x)N in the pancake as a function of x (brush contour plot), for a fixed overall amount of polymer chains θ (total) = 700 and a given solvent quality χ = 1 and chain length N = 200. Several results are collected for a range of surface interactions χW as indicated. Here we limited ourselves to the regime of modest surface attraction so that the brush is not completely attracted to the surface yet. In line with the arguments given above, we see a decrease of the brush height upon an increase of the affinity of the polymer for the surface. Note that θ(x) is a measure of the brush height because the density in the brush ϕ is not a function of χW. With decreasing χW we notice also a modest change at the edge of the pancake. Gradually the contact angle becomes less than 90°.
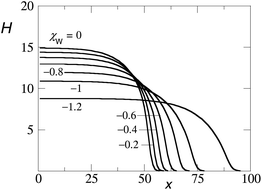 | ||
| Fig. 5 The height of the brush H(x) where the height is given by θ(x) = σ(x)N, for θ (total) = 700, χ = 1, N = 200, for different values of χW as indicated. | ||
A more detailed analysis of the pancake height as a function of the affinity of the surface is presented in Fig. 6 for somewhat larger chains. Here the amount of polymer (in the homogeneous part of the pancake, i.e. near x = 1) is plotted as a function of χW. We see that with increasing affinity (more negative χW) the brush height decreases consistently with Fig. 5. Below θ = 10 (indicated by the horizontal dotted line) the drop of the brush appears very fast. We tried to analyse these predictions using a guess for the spreading parameter. We assume that ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is linearly related to χW. More explicitly,
is linearly related to χW. More explicitly, ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) WP −
WP − ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) SW is expected to be closely related to χW. As we do not know how large
SW is expected to be closely related to χW. As we do not know how large ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) PS is, we used the Ansatz that
PS is, we used the Ansatz that ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 0 when χW ≈ −1.5. For this reason we used
= 0 when χW ≈ −1.5. For this reason we used ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 1.5 + χW. In the insets of Fig. 6 we present the prediction of the height of the pancake as a function of
= 1.5 + χW. In the insets of Fig. 6 we present the prediction of the height of the pancake as a function of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (top inset) or −S (bottom inset) in double logarithmic coordinates. The open circles give θ values and the open squares are the first moment over the overall profile Ht. As long as the height is larger than the Gaussian size of the coils we find that the height scales as
(top inset) or −S (bottom inset) in double logarithmic coordinates. The open circles give θ values and the open squares are the first moment over the overall profile Ht. As long as the height is larger than the Gaussian size of the coils we find that the height scales as ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 1/3 to a good approximation. This scaling is not so much dependent on the choice of the exact definition of
1/3 to a good approximation. This scaling is not so much dependent on the choice of the exact definition of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) . When the layer is compressed with respect to the Gaussian size, the inverse dependence with −S is found with some imagination. However, it must be noted that in this case the exact value of the scaling exponent does depend on the way
. When the layer is compressed with respect to the Gaussian size, the inverse dependence with −S is found with some imagination. However, it must be noted that in this case the exact value of the scaling exponent does depend on the way ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is computed.
is computed.
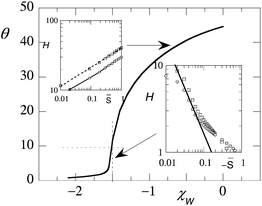 | ||
Fig. 6 The amount of polymer per unit area in the pancake θ = σ(x)N as a function of the affinity for the surface χW. Parameters χ = 1, N = 1000. In the insets two measures of the height θ (open squares) and Ht (open circles) are plotted as a function of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (top left inset) or – (top left inset) or –![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (bottom right inset) in double logarithmic coordinates. The (bottom right inset) in double logarithmic coordinates. The ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is defined in the text. The horizontal and vertical dotted lines bracket the regimes of compression and expansion of the brush. is defined in the text. The horizontal and vertical dotted lines bracket the regimes of compression and expansion of the brush. | ||
Let us return to the χW = 0 case and focus on the dependence of the pancake on the variable solvent quality χ. In this case we expect that ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ≈
≈ ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) PS and is a decreasing function of Δχ. In addition, the polymer density in the pancake ϕ decreases with Δχ. A polymer phase under poor solvent conditions is found to be composed of blobs with size ξ that contain g segments. Locally the chain remains Gaussian and thus ξ2 ∝ g. The polymer density ϕ ∝ g/ξ3 ∝ ξ−1. The interfacial energy of the polymer–solvent interface has an excess energy which may be approximated by
PS and is a decreasing function of Δχ. In addition, the polymer density in the pancake ϕ decreases with Δχ. A polymer phase under poor solvent conditions is found to be composed of blobs with size ξ that contain g segments. Locally the chain remains Gaussian and thus ξ2 ∝ g. The polymer density ϕ ∝ g/ξ3 ∝ ξ−1. The interfacial energy of the polymer–solvent interface has an excess energy which may be approximated by ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) PS ≈ ξ−2 (one kBT per blob at the surface). Hence, we expect
PS ≈ ξ−2 (one kBT per blob at the surface). Hence, we expect ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) /ϕ ∝ ξ−1. Again we should anticipate that the blob size itself is a (decreasing) function of Δχ, and thus
/ϕ ∝ ξ−1. Again we should anticipate that the blob size itself is a (decreasing) function of Δχ, and thus ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) /ϕ should be an increasing function of Δχ. Inspired by eqn (7) we can expect
/ϕ should be an increasing function of Δχ. Inspired by eqn (7) we can expect ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) /ϕ ∝ (Δχ)1/2. Inspection of eqn (14) leads us to the prediction that H increases with decreasing solvent quality.
/ϕ ∝ (Δχ)1/2. Inspection of eqn (14) leads us to the prediction that H increases with decreasing solvent quality.
In Fig. 7 we have collected data for the condensed pancake (labelled by ‘thick’) in coexistence with the dilute ‘gas’ (labelled by ‘thin’) of grafted chains in dependence of the solvent quality. A pancake can only form when the solvent quality is sufficiently poor. Here we find a critical value of χcr (brush) ≈ 0.58 (vertical dotted line in Fig. 7a). The critical solvency by eqn (4) (bulk chains) gives for chains with a degree of polymerisation N = 200 a value χcr ≈ 0.573, which is slightly lower than that found for the brush. The exact reason for the small discrepancy is not fully clear, but we can anticipate that a truly two-dimensional pancake for which all segments lay on the surface, the critical value is 6/4 times that for the chains in the 3D bulk, simply because the polymer in 2D has fewer contacts Z = 4 with other polymers than in the bulk Z = 6, and the χ parameter is normalised using the Z = 6 value.
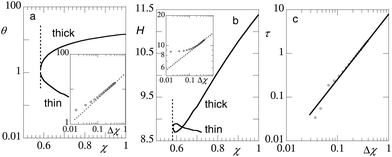 | ||
| Fig. 7 (a) The amount of polymers per unit area θ = σN as a function of the solvent quality χ in log-lin coordinates. The inset shows θ(Δχ) of the thick film in double logarithmic coordinates. The dotted line has a slope of 2/3. (b) The height of the brush H ≡ Ht as a function of the solvent quality χ. The inset shows H(Δχ) for the thick film in double logarithmic coordinates. The dotted line has a slope of 1/6. (c) The line tension as a function Δχ = χ − χcr in double logarithmic coordinates. Parameters: N = 200, and χW = 0. The vertical dotted lines in panels (a) and (b) are at χ = χcr ≈ 0.58; the value for the pancake is labelled ‘thick’ and the value outside the pancake is labelled ‘thin’. | ||
The number of chain segments per unit area θ = σN as a function of χ is given in Fig. 7a for both coexisting phases. The critical θ ≈ 1. This value is close to the overlap threshold and brushes in such a low grafting density should evolve to a Gaussian size 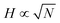 . At the critical point, the polymer density is thus φcr ∝ N1/2. This density is consistent with the well-known binodal volume fraction given by eqn (5). With increasing values of χ the brush height of the pancake increases as expected. In the inset we have plotted the amount of polymer as a function of Δχ and found a scaling of 2/3 to a good approximation.
. At the critical point, the polymer density is thus φcr ∝ N1/2. This density is consistent with the well-known binodal volume fraction given by eqn (5). With increasing values of χ the brush height of the pancake increases as expected. In the inset we have plotted the amount of polymer as a function of Δχ and found a scaling of 2/3 to a good approximation.
In Fig. 7b we present the height of the condensed brush (‘thick’) as well as the height of the chain layer in the gas phase (‘thin’). Again at χ = χcr we should expect that both heights should converge to the same value. From the figure we can see that the approach to the critical H ≈ 8.81 is rather odd: the pancake comes from below and the ‘gas’ phase comes from above this common value. The far field profiles, that is, the φ(x′, z) profile far enough from the contact line, both in the pancake (x′ = 1) as well as in the ‘gas’ phase (x′ = Mx) are given by the one-gradient profile provided that the local σ(1) and σ(Mx) are used. We do not give these profiles here, but inspection of these profiles proves that the profile for the ‘gas’ phase is a Gaussian-like profile which extends slightly further in solution than the (also Gaussian-like) profile of the phase with a somewhat higher grafting density. This is consistent with the unusual H-dependence near the critical point.
The values for the two heights also cross around χ ≈ 0.63. This crossing is necessary because the pancake should become thicker with decreasing solvent quality and eventually will be higher than the dilute brush (which height remains near H ≈ R). In passing we note that the isolated chains in the gas phase do not collapse in the SCF model. The averaged density is too low for this to happen. Arguably when intra-molecular excluded volume effects are properly accounted for one may expect a slightly different behaviour. These effects may be seen in computer simulation studies or in single chain mean field modelling.15
In the inset we show H(Δχ) in double logarithmic coordinates and find a slope of approximately 1/6. Combining the results of the insets of panels (a) and (b) leads to the observation that θ/H ∼ ϕ ∝ (Δχ)1/2, consistent with the van der Waals result (cf.eqn (7)). Hence, we find that the blob size ξ ∝ (Δχ)−1/2. Using these scaling results we reconcile the solvency dependences for H (cf.eqn (14)) and σ (cf.eqn (15)) with the results given in the insets of panels (a) and (b), proving the internal consistency. These results indicate that the free energy per unit area associated with the polymer–solvent interface ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) PS scales linearly with Δχ. This should be contrasted with the van der Waals result given by eqn (6). It is noticed that for the polymer–solvent interface of a brush in the pancake shape, the interfacial width of the PS interface is proportional to ξ < H2. Clearly, this width cannot diverge upon the approach of the critical point. Hence the interfacial tension is dominated by the enthalpic contribution, and thus cannot be super-linear with Δχ.
PS scales linearly with Δχ. This should be contrasted with the van der Waals result given by eqn (6). It is noticed that for the polymer–solvent interface of a brush in the pancake shape, the interfacial width of the PS interface is proportional to ξ < H2. Clearly, this width cannot diverge upon the approach of the critical point. Hence the interfacial tension is dominated by the enthalpic contribution, and thus cannot be super-linear with Δχ.
The numerical prediction for the line tension is shown in Fig. 7c. In this figure it is seen that the line tension drops to zero when χ → χcr as expected. The scaling behaviour is consistent with the idea that the line tension scales with the interfacial tension HγPS as given in eqn (6). We find a scaling dependence slightly higher than 3/2 but less than 5/3. Clearly the super-linear dependence is consistent with the observation that the width of the edge of the pancake diverges upon the approach to the critical point.
IV Discussion
Above we have shown that a collection of grafted chains can undergo a first-order phase transition when the solvent quality deteriorates from marginal to poor. Unless χ = χcr the grafting density in the pancake is much higher than that in the ‘gas’ phase. Obviously the chains in the pancake assume a grafting density so that the chains interact and overlap. Invariably the chains in the ‘gas’ phase have a too low grafting density to call this phase a brush. As we did not yet impose that the overall grafting density is high so that overall the chains are strongly overlapping, we cannot yet claim that the classical brush theory is wrong in the poor solvent case.Let us therefore consider a brush with the given grafting density ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) which is sufficiently large so that the brush chains strongly overlap, that is, N
which is sufficiently large so that the brush chains strongly overlap, that is, N![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) > 1. The classical theory predicts a height in the poor solvent case which is given by H = N
> 1. The classical theory predicts a height in the poor solvent case which is given by H = N![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) /(Δχ)1/2. When it is allowed to have lateral inhomogeneities we found H ∝ N2/3(Δχ)1/6 for the pancake. Of course the inhomogeneous situation can only exist when the pancake height is larger than that of the homogeneous brush, and thus
/(Δχ)1/2. When it is allowed to have lateral inhomogeneities we found H ∝ N2/3(Δχ)1/6 for the pancake. Of course the inhomogeneous situation can only exist when the pancake height is larger than that of the homogeneous brush, and thus
Δχ > N1/2![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 3/2 3/2 | (17) |
Here we have assumed that the average density of the collapsed brush in the classical theory is of the same order as in the pancake. Taking a typical value of σ = 0.02 and a chain length N = 1000, it is easily checked that the chains strongly overlap and thus are in the brush regime. In this case the brush becomes laterally inhomogeneous when Δχ > 0.09, that is, when χ > 0.62. This condition is easily met of course. Moreover, in typical cases when the number of polymer segments on the surface is fixed, that is 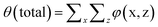 is fixed, we see that the condition specified by eqn (17) is naturally obeyed at elevated chain lengths. So we conclude that the classical theory fails to describe the brush under poor solvent conditions. The same conclusion could have been drawn by noting that the amount of polymer per unit area in the pancake θ typically exceeds by far the value of unity (cf.Fig. 7a). Any brush with an average θ that is below the pancake value is subject to a first-order collapse transition. In practice, such a first-order transition should thus be expected in many and perhaps most situations.
is fixed, we see that the condition specified by eqn (17) is naturally obeyed at elevated chain lengths. So we conclude that the classical theory fails to describe the brush under poor solvent conditions. The same conclusion could have been drawn by noting that the amount of polymer per unit area in the pancake θ typically exceeds by far the value of unity (cf.Fig. 7a). Any brush with an average θ that is below the pancake value is subject to a first-order collapse transition. In practice, such a first-order transition should thus be expected in many and perhaps most situations.
However, one can take another standpoint, namely that for any solvent quality and grafting density there exists a threshold chain length N above which the brush remains laterally homogeneous. The reason for this is the sub-linear scaling of the pancake height with N. More specifically, when
N > (Δχ)2![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) −3 −3 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Such a brush has θ = 600 equivalent monolayers polymer material at the surface. Admittedly, one can claim that the classical brush theory survives asymptotically, but this appears mostly of academic interest.
000. Such a brush has θ = 600 equivalent monolayers polymer material at the surface. Admittedly, one can claim that the classical brush theory survives asymptotically, but this appears mostly of academic interest.
Finally, we may speculate on how a (homogeneous) pinning of the chains to specified locations will alter the picture. Of course the collection of all chains into a single pancake is no longer possible, and the inhomogeneities, if these form can develop only locally. There are a few papers in the literature that consider the formation of so-called pinned micelles in sparsely grafted layers, but how these structures can develop in a polymer brush with a high overall grafting density is less clear.22,23 Also in simulations25 inhomogeneous layers with ‘clusters’ and ‘dimples’ have been seen. Indeed, the negative pressure of a brush under poor solvent conditions signals that the homogeneity of the brush is not guaranteed. We think that it is possible to study this more systematically using three-gradient SCF analysis.24
V Conclusion
Using a two-gradient model of the self-consistent field theory we showed that end-tethered chains which are laterally mobile can undergo a first-order gas–liquid phase transition upon worsening the solvent quality from marginal to poor. Such a first order transition was not anticipated from the classical SCF theory. It has largely been overlooked that under poor solvent conditions a brush has a lateral pressure that does not increase monotonically with an increase of the grafting density. The point is that the classical theory assumes that the chains remain homogeneously distributed, that is the grafting density is homogeneous and fixed. When this constraint is lifted, we find that under sufficiently poor solvent conditions a collection of mobile end-grafted chains organise themselves spontaneously in a dense pancake, which becomes in equilibrium with a dilute gas of grafted chains. We have shown that the height of the pancake scales sub-linearly with the chain length because the grafting density decreases with the chain length. We found a continuous decrease of the height of the pancake with increasing substrate affinity, which stops only when all segments are in contact with the substrate. On the other hand, the height of the pancake increases with decreasing solvent quality. The line tension, which is the excess free energy of the contact line between the pancake and the gas, scales with the height of the pancake and is proportional to the interfacial free energy of a polymer-rich phase in equilibrium with a solvent-rich phase (as can be found from the corresponding bulk phase behaviour).References
- S. Alexander, J. Phys., 1977, 38, 983 CAS.
- P. G. de Gennes, Macromolecules, 1980, 13, 1069 CrossRef CAS.
- M. Muthukumar and J.-S. Ho, Macromolecules, 1989, 22, 965 CrossRef CAS.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1988, 21, 2610 CrossRef CAS.
- S. T. Milner, Science, 1991, 251, 905 CAS.
- M. Murat and G. S. Grest, Phys. Rev. Lett., 1989, 63, 1074 CrossRef CAS.
- R. Toral, A. Chakrabarti and A. Dickman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 343 CrossRef CAS.
- A. Halperin, J. Phys., 1988, 49, 547–550 Search PubMed.
- E. B. Zhulina, O. V. Borisov, V. A. Priamitsyn and T. M. Birshtein, Macromolecules, 1991, 24, 140–149 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell Univ. Press, Ithaca NY, 1953 Search PubMed.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell Univ. Press, Ithaca and London, 1979 Search PubMed.
- P.-G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- M. A. Carignano and I. Szleifer, J. Chem. Phys., 1994, 100, 3210 CrossRef CAS.
- M. A. Carignano and I. Szleifer, Adv. Chem. Phys., 1996, 94, 165 CrossRef.
- H. Tang, M. A. Carignano and I. Szleifer, J. Chem. Phys., 1995, 102, 3404 CrossRef CAS.
- C. Bernardini, S. D.Stoyanov, M. A. Cohen Stuart, L. N. Arnaudov and F. A. M. Leermakers, Langmuir, 2010, 26, 11850–11861 CrossRef CAS.
- G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Chapman & Hall, London, 1993 Search PubMed.
- T. Cosgrove, T. Heath, B. van Lent, F. Leermakers and J. Scheutjens, Macromolecules, 1987, 20, 1692–1696 CrossRef CAS.
- F. A. M. Leermakers, M. Ballauff and O. V. Borisov, Langmuir, 2007, 23, 3937–3946 CrossRef CAS.
- S. F. Edwards, Proc. Phys. Soc., 1965, 85, 613 CrossRef CAS.
- O. A. Evers, J. M. H. M. Scheutjens and G. J. Fleer, Macromolecules, 1990, 23, 5221–5232 CrossRef CAS.
- E. M. Sevick and D. R. M. Williams, Phys. Rev. Lett., 1999, 82, 2701–2704 CrossRef CAS.
- E. B. Zhulina, C. Singh and A. C. Balazs, Macromolecules, 1996, 29, 8254–8259 CrossRef CAS.
- S. K. Pattanayek, T. T. Pham and G. G. Pereira, J. Chem. Phys., 2005, 122, 214908 CrossRef.
- G. S. Grest and M. Murat, Macromolecules, 1993, 26, 3108–3117 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
