 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding diluted dispersions of superparamagnetic particles under strong magnetic fields: a review of concepts, theory and simulations
Jordi
Faraudo
*a,
Jordi S.
Andreu
ab and
Juan
Camacho
b
aInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus UAB, E-08193 Bellaterra, Spain. E-mail: jfaraudo@icmab.es
bDept. de Física, Universitat Autònoma de Barcelona, Campus UAB, E-08193 Bellaterra, Spain
First published on 22nd March 2013
Abstract
In recent years, there has been a great progress in the development of superparamagnetic particles targeted to a wide range of applications, including fields as diverse as biotechnology or waste removal. However, the physics behind their behaviour under usual conditions (diluted dispersions and high magnetic fields) has many, fundamental, open questions. In this review, we revisit the advances in the basic physical concepts and predictive analytical and simulation tools. We focus on recent developments in the understanding and prediction of phenomena induced by magnetic fields both in uniform fields (for example, chain formation) and in magnetic gradients (cooperative magnetophoresis).
 Jordi Faraudo | Jordi Faraudo received his PhD in Physics from Universitat Autònoma de Barcelona (UAB), Spain, in 1999. In 2007 he joined the Institut de Ciència de Materials de Barcelona (ICMAB-CSIC) as a tenured scientist. His research interests are in the field of theory and simulation of soft matter, with particular emphasis on self-assembly and on problems involving colloidal interactions beyond the classical DLVO theory. |
 Jordi S. Andreu | Jordi Andreu received his degree in Physics from the Universitat Autònoma de Barcelona (UAB), Spain, in 2005. He has obtained his PhD in Materials Science also from UAB in 2013 under the supervision of Drs Faraudo and Camacho with a thesis devoted to the theory and simulation of superparamagnetic colloidal dispersions under magnetic fields. |
 Juan Camacho | Juan Camacho has been an Associate Professor in the Physics Department at the Universitat Autònoma de Barcelona from 1995. His current research interests are in the fields of complexity and statistical physics. In particular, he is interested in biological systems, and statistical physics of magnetic dispersions, including foundations and applications. |
1 Introduction
Superparamagnetic colloids are a successful example of a development from a new behavior arising at the nanoscale which has reached the marketplace (see for example ref. 1 for a review of commercially available particles designed for biotechnological applications). The peculiar magnetic behavior known as superparamagnetism is exhibited only by nanometer sized grains of magnetic materials such as iron oxides.2 At zero applied field, the magnetization of superparamagnetic particles is zero. In the presence of an external field, the particles acquire a magnetic dipole. At high fields, large saturation values of the magnetization can be obtained, hence the term superparamagnetism. The magnetic colloids employed in typical applications are composite materials made of superparamagnetic nanoparticles inserted in a matrix of nonmagnetic material such as polystyrene or silica (see for example ref. 3 and 4). In this way, one obtains composite particles with sizes of the order of 102 nm or larger which are still superparamagnetic (for a discussion on the relationship between the magnetic response of the composite and their individual components see ref. 5). The high magnetic response of these composites makes them appropriate for applications such as T2 contrast agents in magnetic resonance.6 Also, many other biomedical applications are possible (see ref. 1 and 7 for reviews).In many applications, the superparamagnetic colloids are functionalized with appropriate chemical groups in order to bind to or capture specific targets.8,9 Once the particles have bound to their target or captured the desired molecule, they can be removed using magnetic gradients. It has to be noted here that uniform magnetic fields are unable to induce a drift velocity in magnetic particles so that a magnetic gradient is required. The motion of magnetic particles in a magnetic gradient is called magnetophoresis.10 There are many recent examples which involve the use of functionalized superparamagnetic particles and their recovery using magnetophoresis. For example, biotechnological applications include protein isolation, cell separation, drug delivery, and biocatalysis.11 Other interesting applications involve the capture and extraction of pollutants12,13 and the processing of bacteria for biofuel applications.14 In the marketplace, companies are offering superparamagnetic microspheres to use in combination with magnetophoretic systems as alternatives to conventional chromatography resins in automated high throughput protocols replacing centrifugation, organic solvents and filtration.
It is convenient to compare the magnetic dispersions of interest here with more classical and well established applications of dispersions of magnetic particles such as ferrofluids or magnetorheological (MR) fluids.15 MR fluids are typically highly concentrated dispersions of magnetic particles in which the objective is to tailor the mechanical response of a global entity (the MR fluid) employing the appropriate ingredients in its formulation. For a recent review of MR fluids, the reader is referred to ref. 16. In contrast, in the systems of interest here, the focus is on the individual particle and its functional behavior. Although they are mostly employed in diluted dispersions (typical concentrations are of the order of 1 g l−1), they show rich and interesting physics due to their strong magnetic response. As an example, we show in Fig. 1 images of the magnetophoresis of a diluted dispersion (1 g l−1) of commercial Estapor® M1-30/40 particles (d = 410 nm) under a bar magnet17 (videos of these experiments are freely available online18,19). Similar images can be found in other experiments, see for example ref. 20 and 21. The large induced magnetic dipoles drive the particles to organize in anisotropic structures aligned in the direction of the external field. Since the applied magnetic field is inhomogeneous, the structures move in the direction of the gradient of the magnetic field intensity, indicated with arrows in the figure. An interesting observation is that, in these experiments the observed structures dissolve after suppression of the magnetic field, recovering the initial state of dispersion, without chains of particles (see the free video18 and also the experiments in ref. 20). This is of course due to the lack of magnetic moment of the particles in the absence of the magnetic field (and also due to a good colloidal stabilization of the particles). The fact that the structures arising in dispersions of superparamagnetic colloids can be completely controlled by an external field is a property of great interest for many applications. This is also an essential difference between dispersions of superparamagnetic and ferromagnetic particles: in the case of particles with a permanent magnetic dipole (ferromagnetic particles) aggregates are still observed in the absence of the magnetic field due to the remanent dipole–dipole interaction.
 | ||
| Fig. 1 Optical micrograph of a solution of concentration 1 g l−1 of Estapor® M1-030/40 particles under a bar magnet at times (a) 0 s, (b) 120 s, (c) 240 s and (d) 360 s after placing the magnet. The scale bar in (a) is valid from (a) to (d). Linear aggregates form in the direction of the local field (vertical) and move in the direction of the magnetic field gradient (towards the left), as indicated by white arrows. As time goes, aggregates collide laterally and thicker aggregates are formed (figure reproduced from ref. 17). See also the videos of these experiments in YouTube.18,19 | ||
It is important to recall that the formation of structures as those seen in Fig. 1 plays a major role in many applications. For example, we have shown17,22 that this field-induced reversible aggregation dramatically enhances magnetophoresis. In contrast, in therapeutic applications, aggregation is often an undesired effect which affects biocompatibility. Another interesting example involves particles designed for imaging applications. It has been shown that the T2 response of water molecules in magnetic resonance experiments is strongly modified if the superparamagnetic particles used as contrast agents form chains under the strong fields (>1 T) employed in these applications.23 Some of the superparamagnetic particles designed for these applications (which are designed to have a large saturation magnetization)4 are not observed to form chains24 but others tend to form chains under these strong fields.23,25
Therefore, it is clear that the possibility of predicting the behavior of colloidal dispersions of superparamagnetic particles under a magnetic field has an enormous practical importance, in addition to its fundamental physico-chemical interest. This includes predictions about the conditions necessary for the formation of aggregates or chains under strong fields, their size and shape and their kinetics, and quantitative predictions of their influence on the various processes of interest (magnetophoretic velocity, for example). Our objective in this review is to highlight recent advances obtained in this direction.
2 Superparamagnetic dispersions under magnetic fields: interactions between particles
2.1 The dipole–dipole interaction
In practical applications, colloidal dispersions of superparamagnetic particles are under the action of an external magnetic field, which can be intense (fields in the range of 0.1–1 T are typical). In this case, the superparamagnetic particles acquire large induced magnetic dipoles and strong dipole–dipole interactions arise. The interaction energy between two superparamagnetic particles with dipole m (induced by an external magnetic field), separated by a distance r is given by: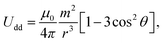 | (1) |
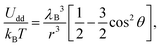 | (2) |
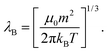 | (3) |
Physically, λB can be interpreted as the characteristic length scale at which magnetic interactions are significant as compared with thermal effects. The Bjerrum length concept is a key element in the classical theory of (electrostatic) pairing between electrolytes in solution and this magnetic analog was introduced in ref. 17 and 22. The interaction energy given by eqn (2) is represented in Fig. 2 for a typical value of λB. As seen in this figure, the dipole–dipole interaction is highly anisotropic, with strongly attractive or strongly repulsive regions due to the θ dependence in eqn (1). Hence, the anisotropy of the particle–particle interaction justifies the tendency of the particles to form anisotropic structures or assemblies in solution, as those illustrated in Fig. 1. The dipole–dipole interaction (eqn (1)) is attractive for angles θ smaller than θ0 = 54.7° and repulsive for θ > θ0. The minimum energy configuration corresponds to θ = 0 and interparticle distance of r = d (where d is the diameter of the particles) and has an energy Umaxdd/kBT = −λB3/d3. Hence, it is reasonable to characterize the strength of the magnetic interaction by a magnetic coupling parameter Γ defined as26
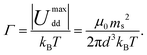 | (4) |
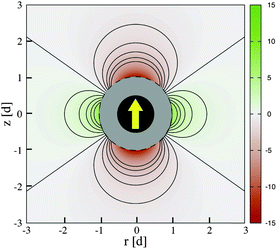 | ||
| Fig. 2 Magnetic dipole–dipole interaction energy (eqn (2)) experienced by an imaginary test particle due to the interaction with the (identical) superparamagnetic particle shown in black. The calculation corresponds to the case Γ = 15 (λB ≃ 2.47d). The yellow arrow indicates the dipole of the particle, directed in the direction of the field. The interaction energy shown as the color scale is given in units of kBT and the distance (in cylindrical coordinates) is measured in units of the diameters of the particle d. The red color corresponds to attractive regions and the green color corresponds to repulsive regions. | ||
In eqn (4), we consider that the particles are at saturation magnetization with dipoles ms (i.e. they have the maximum dipole which can be obtained under a strong field). Hence, the parameter Γ compares the maximum possible strength of the attractive particle–particle magnetic interaction (i.e. that obtained under strong fields) with the thermal energy.26 Physically, Γ ≫ 1 corresponds to a situation dominated by magnetic interactions, whereas in the opposite limit of Γ ≪ 1, thermal agitation dominates.
What are the typical values of Γ accessible in the laboratory? In the case of superparamagnetic nanoparticles, one has typical values in the range of 0.5–5. For example, for the 12 nm maghemite (γ-Fe2O3) nanocrystals employed in ref. 24, we have Γ = 2.5. This means that at saturation magnetization, the magnetic interaction between these nanoparticles is significant (as compared with thermal energy) up to distances of ∼1.4 times the size of the particle (since λB ≃ 1.4d). In this case, chain formation was not observed experimentally.
For composite colloids one has a wide range of values of Γ, depending on the kind and number of NPs embedded inside the composite particle. As an example, we mention here two different particles designed as contrast agents for magnetic resonance imaging (MRI). In one case,4 composite particles with 160 nm diameter with about 40 iron oxide nanoparticles were obtained. These composites have24Γ = 3.5 and they do not form chains under strong fields. In ref. 23, the authors had composite particles of diameter about 88 nm, Γ = 247 and chain formation was observed in this case. Even larger values of Γ can be obtained. Commercial Estapor® M1-30/40 particles (d = 410 nm) employed in the experiments illustrated in Fig. 1 correspond to an extreme situation with Γ ∼ 103.
In all these examples, Γ is larger than 1, so dipole–dipole interactions are expected to dominate. However, formation of structures (chains) is not observed in some of these examples, as mentioned before. This is a very important point to note, because based on previous works in ferrofluids (see for example ref. 15), researchers usually assume that when the magnetic energy is larger than thermal energy (Γ > 1) chain formation will take place. However, the experimental evidence mentioned above shows that reality is more complex than that. A criterion which is able to correctly predict the observed onset of chain formation was derived recently26 and it will be discussed in the next section. Before that, we need to discuss a few more results concerning particle–particle interaction.
2.2 Colloidal stability and the secondary minimum
In colloidal science, it is well known that particles in dispersions have a strong tendency to aggregate due to van der Waals forces.27,28 For this reason, the dispersions require stabilization by adding a suitable repulsive interaction between the particles in order to prevent an irreversible flocculation of the dispersion. Of course, this is also the case with superparamagnetic particles in dispersion, so we need to discuss also this issue here before proceeding to more specific topics. There are two general strategies to stabilize a colloidal dispersion and avoid its flocculation, namely electrostatic stabilization and steric stabilization. Electrostatic stabilization is based on the repulsive force arising between electrical charges with equal sign. In general, the stability of the particles is achieved by covering the particle's surface with charged groups (such as sulfate or carboxyl groups), conferring a net surface charge to the particle and creating a repulsive force between them, able to overcome the van der Waals forces. Another option is steric stabilization, which consists of covering the particles with sufficiently long chain molecules (typically polymers) preventing the particles to get close in the range of attractive forces.The classical theory which describes colloidal stability is the so-called DLVO theory (named after Derjaguin, Landau, Verwey and Overbeek), which provides explicit formulae to compute attractive van der Waals forces and repulsive electrostatic forces.28 In our case, this theory can be easily generalized by adding the magnetic interaction given by eqn (2). Here we will describe the predictions of the theory qualitatively, whereas explicit calculations for particles of interest can be found for example in ref. 22 and 30. The typical shape of the interaction energy between two electrostatically stabilized superparamagnetic particles in a magnetic field is shown in Fig. 3. At very short separations, there is a deep primary minimum due to van der Waals attraction. In this example, particles are prevented from approaching this primary minimum through an energy barrier created by electrostatic repulsion (electrostatic stabilization). Before the energy barrier, there is a secondary minimum (with a depth depending on the value of Γ), which is responsible for the reversible aggregation of particles in the presence of a magnetic field. If the energy barrier is large enough, a particle captured in the secondary minimum will remain there without falling into the primary minimum. Once the magnetic field is removed, the secondary minimum disappears, and particles captured in this secondary minimum redisperse again without the necessity of sonication or addition of energy to the system (redispersion of particles located in the primary minimum requires large inputs of energy in the form of sonication, for example).
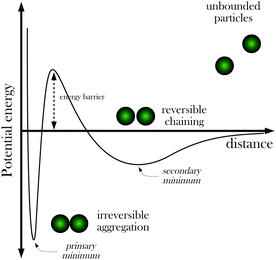 | ||
| Fig. 3 Scheme showing the free energy profile of interaction between two superparamagnetic particles in a strong magnetic field according to a generalized DLVO theory including magnetic interactions (adapted from ref. 22 and 29). It is assumed that the particles are stabilized electrostatically. | ||
The validity of the predictions of the theory and in particular the validity of the concepts illustrated in Fig. 3 have been tested experimentally in different works. For example, in ref. 31 the authors measure force versus distance curves for superparamagnetic particles under magnetic fields with a ∼0.2 nm resolution in distance and sub pN force resolution. In the case of electrostatically stabilized colloids, they found an excellent agreement with the predictions of the DLVO theory. The possibility of transitions between the primary and the secondary minimum was investigated experimentally by Martinez-Pedrero et al. in ref. 29. Adding electrolytes at different concentrations, they tuned the height of the electrostatic barrier which separates the primary and the secondary minimum (see Fig. 3). For monovalent electrolyte concentrations lower than 0.50 mM, aggregated particles were located in the secondary minimum and all aggregates dissolve after suppression of the magnetic field. As the electrolyte concentration is increased, the height of the barrier decreases (due to screening of electrostatic repulsion by the electrolyte) and transitions from the secondary to the primary minimum were observed. After suppression of the magnetic field, some aggregates still remained in the solution, which correspond to particles trapped in the primary minimum. For monovalent electrolyte concentrations of 50 mM or larger, the energy barrier was unable to prevent the transition of particles from the secondary to the primary minimum, and the aggregates still remained after suppression of the magnetic field.
In the case of steric stabilization of particles, the DLVO theory has to be replaced by a theory describing the steric interactions between the particles, in addition to the attractive van der Waals force. In the case of particles covered with long chains of polymers, the steric repulsion is well described by the mean field theory of Milner et al.32 (based on the scaling arguments of Alexander and de Gennes33). In this case, the theory predicts the suppression of the primary minimum, so in principle flocculation is always inhibited. In the absence of a magnetic field, the interaction between particles is always repulsive, and decays strongly with their separation. The addition of the magnetic interaction induces the appearance of a small free energy minimum very similar to the secondary minimum shown in Fig. 3. The theory has been tested experimentally by Li et al.31 for the case of superparamagnetic particles covered by oligomers of different lengths. In the case of particles covered by 75-base and 50-base oligomers, the agreement between theory and experiment was excellent. However, in the case of 15-base and 35-base oligomers, the steric repulsion between the superparamagnetic particles is substantially weaker than predicted by theory.
3 Predicting chain formation under uniform fields
As we said, the possibility of predicting the conditions (magnetization of particles, concentration of the dispersion,…) at which field-induced aggregation appears is of great interest. In order to establish the conditions for the formation of chains, and obtain further insight into the chain formation phenomena, we studied26 the simplest possible model for a dispersion of superparamagnetic colloidal particles. In this simple model, we have a given number of magnetic spheres of diameter d inside a viscous fluid and we assume that the magnetization of colloids has reached saturation. This means that each sphere has a dipole ms corresponding to saturation magnetization pointing in the direction of the magnetic field (this is a reasonable hypothesis for fields larger than 0.1 T, typical of many experimental situations). The model is characterized by two dimensionless parameters: the magnetic coupling parameter Γ and the volume fraction of particles ϕ0. It has to be emphasized here that the mechanism of stabilization of the particles (electrostatic or steric) and their consequences on chain formation are ignored in this simple model. This simplified model assumes that in the absence of the magnetic field the dispersion is colloidally stable and also that in the presence of the magnetic field a secondary minimum (reversible aggregation) is obtained.The model was studied by computer simulations (Langevin dynamics) and analytically by employing a mean-field approximation. In order to illustrate typical results from the simulations, we show here (Fig. 4) the results for four different values of Γ and a fixed value ϕ0 = 5.23 × 10−4 of the volume fraction (which corresponds to 0.5 g l−1 if the particles have a density of 1 g cm−3). Results for other (dilute) concentrations are also presented in the original work.26 In all cases, Γ > 1, so the dipole–dipole interaction between two particles in close proximity is stronger than thermal agitation. We found three different possibilities for the behavior of the system: (a) no aggregation, (b) an equilibrium state with a constant value for the average size of the chains and (c) a non-equilibrium state with a continuous growth of chains with time. In Fig. 4, we can see an example of case (a) for Γ = 3. In this case, we did not find chain formation, in contradiction with the classical criterion for chain formation (Γ > 1). We also recall here that this finding is consistent with the experiments in ref. 24, mentioned in the previous section. In Fig. 4, we also show two examples of case (b), corresponding to Γ = 10 and Γ = 11. In this case, we obtain an equilibrium state with an average chain length which strongly depends on Γ. It should be emphasized that this equilibrium state is dynamical, in the sense that, during the simulations, we observe both creation and destruction of chains which proceed at the same rate. For large enough Γ, we obtain regime (c) in which chains are very stable and the destruction of chains becomes a rare event. In this case, the average length of the chains increases with time, as illustrated in Fig. 4 for Γ = 40.
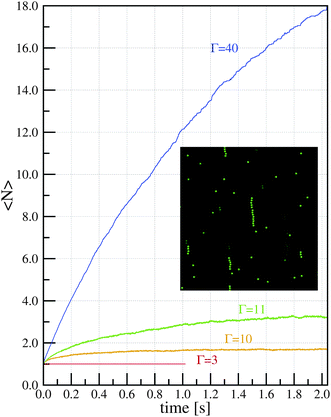 | ||
| Fig. 4 Time evolution of the average chain size 〈N〉 (data from ref. 26) as obtained from simulations with different values of Γ and volume fraction ϕ0 = 5.23 × 10−4 (concentration 0.5 g l−1). Inset: snapshot of the simulation with Γ = 10 illustrating the chains formed in the equilibrium state (only a small portion of the system is shown). | ||
A mean-field thermodynamical analysis of this simple model, also presented in ref. 26, allows one to understand in more depth the results of the simulations. The main result of the analysis is that the behavior of the system is controlled by the aggregation parameter N*, defined as:
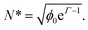 | (5) |
In the case of N* ≤ 1, the system does not form chains. For N* > 1, the equilibrium state of the system consists of chains of different sizes, with a distribution given by:
| ns ∝ ϕs/s ≃ (1 − 1/N*)s ≈ e−s/N*, | (6) |
| 〈N〉 = N*, | (7) |
Now, we can understand why, in certain situations with Γ > 1, no chain formation is observed. For example, in the simulations of Fig. 4 with Γ = 3 and ϕ0 = 5.23 × 10−4, eqn (5) gives N* = 0.06. Therefore, our theory correctly predicts that chains should not be observed in this system. We can also understand the absence of chain formation in the experiments of ref. 24 mentioned in Section 2.1. In the case of a dispersion of 10 g l−1 of maghemite 12 nm NPs with Γ = 2.5, we obtain N* = 0.1. For a 1 g l−1 dispersion of 160 nm core–shell particles with Γ = 3.5, we obtain N* = 0.2.
In Fig. 5, we compare the predictions of our mean-field theory (eqn (5) and (7)) with the average number of particles in a chain 〈N〉 in the equilibrium state obtained from simulations with different values of Γ and different concentrations.26 It is quite remarkable that using these very simple equations, one can correctly predict simulation results which require lengthy calculations (months of CPU). At this point, it should be emphasized that an early ferrofluid model of Pincus and de Gennes15,34 also predicted the existence of an equilibrium state, with an explicit prediction of an equilibrium value of 〈N〉 which depends on Γ and ϕ. However, their model was unable to capture the behavior observed in our simulations, particularly the behavior observed in Fig. 5 and the role of the aggregation parameter N* (in fact, for some of our simulated values of ϕ and Γ it predicts nonphysical – negative – values of the mean number of colloids in a chain). Unfortunately, a clear experimental observation of this equilibrium state is still lacking. An experimental study reporting observations of the equilibrium state (regime (b)) by optical microscopy was reported in ref. 35 but for the case of a bidimensional system, so direct comparison with our predictions is not possible. More recently, Barrett et al.36 observed an equilibrium state for concentrated superparamagnetic dispersions, employing neutron scattering techniques. In this case, their conditions (high volume fraction) are typical of ferrofluids and make analytical predictions very difficult (in particular, our eqn (5) and (7) cannot be applied).
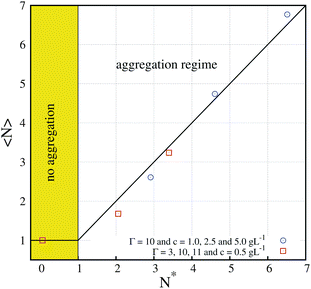 | ||
| Fig. 5 Average number of particles in a chain 〈N〉 in the equilibrium state of superparamagnetic colloids under a strong field as obtained from simulations at different values of the aggregation parameter N* defined by eqn (5). The simulations correspond to different values of the magnetic coupling parameter Γ and the volume fraction ϕ0. The predicted no aggregation (N* ≤ 1) and aggregation (N* > 1) regimes are indicated. The solid line corresponds to the prediction of eqn (7) for the equilibrium size of chains in the aggregation regime (results adapted from ref. 26). | ||
Another interesting feature of our model is the strong (exponential) dependence of the aggregation parameter N* with Γ (see eqn (5)). As long as one considers relatively large values of Γ, very large values of N* are obtained. For example, for the case of the largest magnetic strength considered in Fig. 4 (Γ = 40 and ϕ0 = 5.23 × 10−4), we obtain 〈N〉 = N* ∼ 6.7 × 106. Of course, we cannot obtain chains of this size either in simulations or in the laboratory (also, from a fit of the kinetics, we expect that the time needed to reach this equilibrium state is about 10 years). Therefore, in the case of large values of N* the equilibrium state is unreachable and the system will always be observed in a nonequilibrium state, in which the average chain size grows continuously with time. In this case, the chain growth follows a power law 〈N〉 ∼ tz asymptotically. In our simulations, we obtain a dynamical exponent z ≈ 0.64, as illustrated in the log–log plot of the simulation data for the case Γ = 40 and ϕ0 = 5.23 × 10−4 shown in Fig. 6.
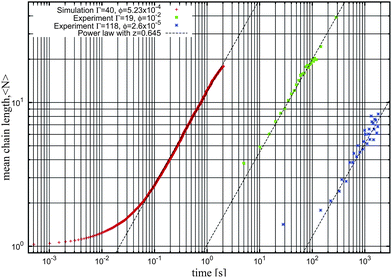 | ||
| Fig. 6 Log–log plot of the kinetics for the irreversible growth of chains as obtained in simulations and experiments. Crosses correspond to Langevin dynamics simulations26 with Γ = 40 and ϕ0 = 5.23 × 10−4 (as in Fig. 4), squares correspond to experiments from Promislow et al.37 with Γ = 19 and ϕ = 10−2 and stars correspond to experiments from Martínez-Pedrero et al.38,39 with Γ = 118 and ϕ = 2.6 × 10−5. The three dashed lines correspond to a power law asymptotic kinetics 〈N〉 ∼ tz with exponent z = 0.645. | ||
The existence of a power-law behavior and the value found for the exponent z are consistent with those observed in several experimental studies.37–42 This is also illustrated in Fig. 6, in which we plot experimental data from ref. 38 and 39 corresponding to a highly diluted dispersion of strongly magnetized colloids and data from ref. 37 corresponding to a more concentrated dispersion of particles with a smaller magnetic strength parameter Γ. In general, experimental results on very diluted systems provide values of z between 0.6 and 0.7 (as illustrated in Fig. 6) although more concentrated dispersions give values37z ≈ 0.4–0.5. The value of Γ also has been claimed37 to have an influence on z. At this point, it has to be emphasized that several theoretical studies42,43 claim that this asymptotic law is only a useful approximation, and more precise calculations reveal logarithmic corrections to this law.
In this situation of irreversible chain growth (very large aggregation parameter N*), one is typically interested in predicting the average number of particles in a chain as a function of time taking into account the effect of variables such as concentration, size of particles and magnetic response of the particles. At the present time, we are not aware of analytical solutions describing the full kinetics of the process. Hence, we have to resort to simulations. Due to the scales involved in the simulations (objects with sizes in the nm range with aggregation kinetics with time scales of seconds), the most appropriate category of simulation techniques is mesoscale simulations. Langevin dynamics simulations,26 as those reported in Fig. 6, are a reasonable option. Also, less demanding Brownian dynamics simulations such as those performed in ref. 44 and 45 are also quite appropriate. In addition to these two standard simulation methodologies, another interesting option could be to employ new, more accurate simulation techniques. One promising candidate is lattice Boltzmann simulation, a technique specially designed to cope with difficult hydrodynamic problems. This methodology has been applied with success to the case of a dispersion of ferromagnetic particles,46 but applications to superparamagnetic particles are lacking in the literature.
In certain cases, experimental time scales pose a difficult problem to simulation techniques. A paradigmatic example is given by the experiments by Chen et al.23 In these experiments, the kinetics of aggregation was followed until time scales of the order of 103 s in order to determine the effect of chain formation in the T2 response of colloidal dispersions designed as contrast agents in magnetic resonance. The simulation of this system using Langevin dynamics simulations required about 866 hours of CPU to obtain 6 s of simulation time.47 Therefore, the question is how to reach the relevant (macroscopic) time scales in the simulations while retaining sufficient detail at the nanoscale. Our option in this case was to introduce a new simulation strategy based on an on-the-fly coarse graining methodology.47 The basic concept is that the resolution of the simulation is not fixed a priori, but adjusted during the simulation. In the initial stages of the simulation, the system is described with the same detail as in ordinary Brownian dynamics simulations. As the simulation advances, chains of particles are formed. These chains are no longer described with all their structural details (including the relative positions and motions of the component particles) but described as coarse-grained (CG) objects. The diffusion and interactions of the coarse-grained objects follow appropriate rules designed to mimic the behavior of real aggregates. In this way, the computational requirements are dramatically reduced without losing essential physics. Our tests show that the new algorithm reproduces with good accuracy the results obtained from more demanding Langevin dynamics simulations. Time scales of 103 s were reached47 at a cost of only 24 h of CPU time, so prediction of experimental kinetics was possible (and indeed with good agreement between experiments and calculations). A simulation program with the new algorithm is freely available for academics from our webpage.48
Finally, we recall here that in all our previous examples, the aggregates had the simple geometry of chains. This is the typical geometry of aggregates found for very diluted systems. In concentrated solutions, the presence of more complex structures such as bundles, columns and fibers is also typical.16 In diluted solutions, these structures are also possible (see for example the images in Fig. 1 or the images in ref. 35) in the case of N* ≫ 1 provided that one waits for sufficiently long times. Fermigier and Gast35 suggested a kinetic argument for the appearance of these structures. Chains are formed due to addition of a new particle at the end of one chain or by the tip-to-tip aggregation of smaller chains. As time passes, individual isolated particles become scarce and chains become longer and longer, so this growth mechanism becomes extremely slow and inefficient. At this stage, lateral collisions between aggregates become more frequent than tip-to-tip aggregation resulting in the formation of thicker aggregates (with interdigitated dipoles). Experiments involving the direct interaction between two aggregates also confirm the existence of a lateral attraction between long aggregates.49 Nuclear magnetic resonance measurements50 show the existence of two different time scales in aggregation of magnetic dispersions, one which is associated with tip-to-tip aggregation and another associated with the formation of bundles of zippered chains. Also, the videos19 corresponding to the experiments17 shown in Fig. 1 are consistent with this view. Energy calculations22 also show the existence of a transition between tip-to-tip aggregation and lateral aggregation. The calculations show the existence of a critical size, Nc = 14. In the case of chains with N < Nc, tip-to-tip aggregation is energetically favorable, while for N > Nc it is lateral aggregation which is the energetically favored strategy.
4 Inhomogeneous fields: cooperative magnetophoresis
In the previous section, we have discussed the case of a superparamagnetic dispersion in a uniform magnetic field. As we have discussed in the Introduction, in many applications which involve recovery or control of the motion of the superparamagnetic particles, magnetophoresis10 is an essential step and magnetic gradients are employed. In spite of its technological interest, our understanding of magnetophoresis is still incomplete. In fact, a recent opinion piece51 has emphasized the notorious difficulty in understanding which particles will be suitable for magnetophoresis and why.Magnetophoretic velocities of individual particles have been measured experimentally52 and they can be predicted by theory, either analytically24 or by simulations,53 depending on the complexity of the profile of the magnetic field. Typical magnetophoretic velocities of individual particles are very small, of the order of μm s−1 or less for typical particles and 10–30 T m−1 magnetic gradients.17 Therefore, two strategies are possible. One option is to employ highly inhomogeneous magnetic fields, with high local magnetic gradients, which can be generated by appropriate devices.54 This method is known as High Gradient Magnetic Separation (HGMS) and it is discussed in detail elsewhere.10,12,54–57 Another strategy is to employ homogeneous magnetophoretic conditions (a uniform gradient)17,24,53,58,59 generated by a suitable arrangement of permanent magnets, which gives gradients of the order of 10–30 T m−1. In this case, an enhancement of the magnetophoretic velocity has to come from an appropriate choice of the dispersion. The magnetophoresis process can be dramatically enhanced if the aggregation parameter is large24 (N* ≫ 1). In this case, measured magnetophoretic velocities are orders of magnitude higher than expected from the predicted ones for a single particle, a phenomenon that we called cooperative magnetophoresis.17,22 The cooperative magnetophoresis process has been monitored by optical microscopy,17 and in fact the images presented in Fig. 1 correspond to this process (see also the videos freely available online18,19,60). The process proceeds as follows. Initially, the magnetophoretic velocity of the particles is very slow, but large chain-like aggregates are rapidly formed (since N* ≫ 1). These aggregates move rapidly and collisions between these aggregates produce even larger aggregates which move at a faster velocity.
Obviously, this cooperative process depends strongly on the concentration of particles. This strong dependence of magnetophoresis on concentration was demonstrated by measuring the separation times of different dispersions inside a magnetophoretic separator.17 Essentially, the experimental setup consists of a cylindrical vessel of radius 1.5 cm with a radial magnetic gradient of 30 T m−1 in which the solution was placed. Data from ref. 17 for the measured separation times for different kinds of particles (Estapor® M1-030/40 particles and Estapor® M1-020/50 particles) and different concentrations are plotted in Fig. 7. In this figure, the concentration is normalized in order to collapse the results for different particles into a single curve. The normalized concentration plotted in the abscissa is c/c* where c* is a characteristic concentration (with units of mass per unit volume) defined as:
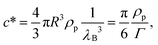 | (8) |
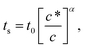 | (9) |
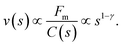 | (10) |
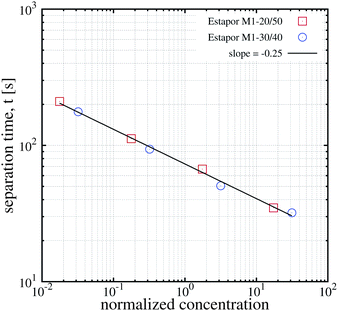 | ||
| Fig. 7 Experimental results for the magnetophoretic separation time of dispersions of two different commercial superparamagnetic particles as a function of concentration. For each kind of particle four different concentrations were considered (10 g l−1, 1 g l−1, 0.1 g l−1 and 0.01 g l−1). The solid line is a linear fit to the data (figure created with data from ref. 17). | ||
Now, we assume for the growth of aggregates with time a power law relation s ∝ (ϕ0t)z ∝ (ct)z as in the uniform field case shown in Fig. 6. Thus, we obtain for the equation of motion of a typical aggregate:
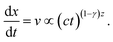 | (11) |
Integrating eqn (11) from an initial position x = 0 at t = 0 and a final time ts corresponding to position x = L (the size of the magnetophoretic setup), we obtain:
| ts ∝ L(1−α)c−α, | (12) |
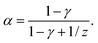 | (13) |
Eqn (13) connects the power law exponent in the concentration scaling of the magnetophoretic separation time with the dynamical exponent z describing the growth of the aggregates and exponent γ describing the dependence of the friction with the size of the aggregates. Although there is some uncertainty in the values of exponents z and γ, we can use some typical values to evaluate eqn (13). For example, the value α = 1/4 is consistent with z = 1/2 (as proposed in ref. 35 and 43) and γ = 1/3 (appropriate for an elongated object growing in a self-similar way).
Finally, it has to be remarked that recent experiments show a substantial influence of the stabilization of the particles (electrostatic or steric) on the aggregation behavior25 and on the magnetophoretic velocity.61,62 Clearly, the way in which particles are stabilized affects the secondary minimum described in Section 2.2 and hence the possibility of reversible aggregation and cooperative magnetophoresis. In any case, the interesting experiments reported in these works call for further theoretical work, in order to be able to predict the most suitable design for particles intended for use in magnetophoresis.
5 Concluding remarks and future challenges
It is clear that, in this field, theoretical concepts and methods are progressing at a slow pace as compared with the impressive development of new superparamagnetic particles and new protocols or devices which make use of these particles in applications. The theoretical and simulation methods revisited here provide useful tools for the design and interpretation of experiments, but we still face many challenges.As discussed in Section 2, it seems clear that the appropriate generalizations of DLVO and classical colloidal stability theories to include magnetic interactions give a useful description of the particle–particle interaction. For example, they correctly predict the reversible nature of the aggregation induced by a magnetic field and the influence of added salt.
With the methods discussed in Section 3, it is possible to predict fundamental aspects of the behavior of diluted superparamagnetic dispersions in strong magnetic fields. For example, it is possible to predict whether the system will form chain like aggregates or not, or the existence of an equilibrium state with a certain average value of the chain size. Also, we can predict, using appropriate simulation tools (Langevin or Brownian dynamics or more advanced methodologies), the kinetics of chain formation in a wide range of time scales, from fractions of seconds to long scales of the order of 103 s. However, these theoretical models and simulation techniques do not consider DLVO or other colloidal forces (they simply assume that the colloidal dispersion is, in some way, correctly stabilized). Experimental results show that in many cases the stabilization method plays an important role in the aggregation phenomena. Further work is required to include these forces in the models to quantitatively predict the joint effect of stabilization and magnetic interaction in field induced aggregation phenomena.
Another future challenge for theory and modeling corresponds to the case of new types of particles, such as those prepared in ref. 63. Usually, ferromagnetic particles form aggregates in the absence of applied magnetic fields due to their remanent magnetic moments (the strong dipole–dipole interaction overcomes typical steric or electrostatic stabilization). But the methodology recently developed in ref. 63 allows for the preparation of dispersions of ferromagnetic particles which do not form aggregates in the absence of a magnetic field. It will be interesting to characterize the effect of an applied external field in this case, and the methods described in this review to study superparamagnetic dispersions could be also relevant in this case.
A more complex, but also more interesting case corresponds to the formation of chains and structures in the presence of inhomogeneous fields, discussed in Section 3. This phenomenon gives rise to the cooperative magnetophoresis effect, which is both conceptually interesting from a fundamental point of view but also useful for practical applications of superparamagnetic particles. Although it seems that we understand the basic concepts behind this effect (the conditions needed for its appearance and its main underlying mechanisms or its dependence with critical variables such as concentration) we still have many open questions. In particular, we lack a full understanding of the observed scaling law for the separation time versus concentration, and we do not know basic things such as the dependence of the magnetophoretic velocity with the magnetic gradient, salt concentration or with the stabilization method of the particles.
There are many other interesting open questions. For example, an interesting application of magnetophoresis could be the separation of magnetic particles by size.58,64 Understanding chain formation in mixtures of particles with different sizes and/or different magnetic properties will allow the use of cooperative magnetophoresis to fast separation of magnetic mixtures.
Another interesting issue is the possibility of magnetophoresis of nonmagnetic particles immersed in a fluid containing magnetic nanoparticles. In this case, nonmagnetic particles behave as magnetic holes and experience negative magnetophoresis,53,65–67 a surprising effect with potential interesting applications. Current experiments and theory focus on the case in which there are no cooperative effects. It could be interesting to develop “inverse” cooperative magnetophoresis for non-magnetic particles, which could be more interesting (and useful) than non-cooperative magnetophoresis.
Acknowledgements
We acknowledge financial support from the Spanish Government grants no. FIS2009-13370-C02-02 and CONSOLIDER-NANOSELECT-CSD2007-00041 and the Catalan government grant 2009SGR164. We thank discussions from Ll. M. Martínez (SEPMAG, Spain), M. Benelmekki (OIST, Japan), A. Roig and A. Goñi (ICMAB, Spain) and M. Tirado-Miranda (Univ. Granada, Spain).References
- J. L. Corchero and A. Villaverde, Trends Biotechnol., 2009, 27, 468–476 CrossRef CAS.
- C. P. Bean and J. D. Livingston, J. Appl. Phys., 1959, 30, S120–S129 CrossRef.
- V. Salgueiriño-Maceira, M. A. Correa-Duarte, M. Spasova, L. M. Liz-Marzán and M. Farle, Adv. Funct. Mater., 2006, 16, 509–514 CrossRef.
- E. Taboada, R. Solanas, E. Rodríguez, R. Weissleder and A. Roig, Adv. Funct. Mater., 2009, 19, 2319–2324 CrossRef CAS.
- D. X. Chen, A. Sánchez, E. Taboada, A. Roig, N. Sun and H. C. Gu, J. Appl. Phys., 2009, 105, 083924 CrossRef.
- D. X. Chen, E. Taboada and A. Roig, J. Magn. Magn. Mater., 2011, 323, 2487–2492 CrossRef CAS.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181 CrossRef CAS.
- C. C. Berry and A. S. G. Curtis, J. Phys. D: Appl. Phys., 2003, 36, R198–R206 CrossRef CAS.
- M. Benelmekki, E. Xuriguera, C. Caparros, E. Rodríguez-Carmona, R. Mendoza, J. L. Corchero, S. Lanceros-Mendez and L. M. Martínez, J. Colloid Interface Sci., 2012, 365, 156–162 CrossRef CAS.
- G. Friedman and B. Yellen, Curr. Opin. Colloid Interface Sci., 2005, 10, 158–166 CrossRef CAS.
- C. T. Yavuz, A. Prakash, J. T. Mayo and V. L. Colvin, Chem. Eng. Sci., 2009, 64, 2510–2521 CrossRef CAS.
- G. D. Moeser, K. A. Roach, W. H. Green, T. Alan Hatton and P. E. Laibinis, AIChE J., 2004, 50, 2835–2848 CrossRef CAS.
- C. T. Yavuz, J. T. Mayo, W. W. Yu, A. Prakash, J. C. Falkner, S. Yean, L. Cong, H. J. Shipley, A. Kan, M. Tomson, D. Natelson and V. L. Colvin, Science, 2006, 314, 964–967 CrossRef.
- J. K. Lim, D. C. J. Chieh, S. A. Jalak, P. Y. Toh, N. H. M. Yasin, B. W. Ng and A. L. Ahmad, Small, 2012, 8, 1683–1692 CrossRef CAS.
- R. E. Rosensweig, Ferrohydrodynamics, Cambridge University Press, New York, 1st edn, 1985 Search PubMed.
- J. De Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- G. De Las Cuevas, J. Faraudo and J. Camacho, J. Phys. Chem. C, 2008, 112, 945–950 CAS.
- http://www.youtube.com/watch?NR=1/&v=QgjGjbESuKY .
- http://www.youtube.com/watch?v=MyTXF0SPWTU .
- G. P. Gajula, M. T. Neves-Petersen and S. B. Petersen, Appl. Phys. Lett., 2010, 97, 103103 CrossRef.
- R. J. Wilson, W. Hu, C. W. P. Fu, A. L. Koh, R. S. Gaster, C. M. Earhart, A. Fu, S. C. Heilshorn, R. Sinclair and S. X. Wang, J. Magn. Magn. Mater., 2009, 321, 1452–1458 CrossRef CAS.
- J. Faraudo and J. Camacho, Colloid Polym. Sci., 2010, 288, 207–215 CAS.
- D. X. Chen, G. Via, F. J. Xu, C. Navau, A. Sanchez, H. C. Gu, J. S. Andreu, C. Calero, J. Camacho and J. Faraudo, J. Appl. Phys., 2011, 110, 073917 CrossRef.
- J. S. Andreu, J. Camacho, J. Faraudo, M. Benelmekki, C. Rebollo and L. M. Martínez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021402 CrossRef CAS.
- S. Saville, R. Woodward, M. House, A. Tokarev, J. Hammers, B. Qi, J. Shaw, M. Saunders, R. Versani, T. St Pierre and O. Mefford, Nanoscale, 2013, 5, 2152–2163 RSC.
- J. S. Andreu, J. Camacho and J. Faraudo, Soft Matter, 2011, 7, 2336–2339 RSC.
- D. H. Everett, Basic Principles of Colloid Science, The Royal Society of Chemistry, London, 1st edn, 1988 Search PubMed.
- D. F. Evans and H. Wennerström, The Colloidal Domain, Wiley-VCH, New York, 2nd edn, 1999 Search PubMed.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Langmuir, 2009, 25, 6658–6664 CrossRef.
- S. Yiacoumi, D. A. Rountree and C. Tsouris, J. Colloid Interface Sci., 1996, 184, 477–488 CrossRef CAS.
- D. Li, C. N. Lam and S. L. Biswal, Soft Matter, 2010, 6, 239–242 RSC.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1988, 21, 2610–2619 CrossRef CAS.
- P. G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1st edn, 1979 Search PubMed.
- P. G. De Gennes and P. A. Pincus, Phys. Kondens. Mater., 1970, 11, 189–198 CrossRef CAS.
- M. Fermigier and A. P. Gast, J. Colloid Interface Sci., 1992, 154, 522–539 CrossRef CAS.
- M. Barrett, A. Deschner, J. P. Embs and M. C. Rheinstadter, Soft Matter, 2011, 7, 6678–6683 RSC.
- J. H. E. Promislow, A. P. Gast and M. Fermigier, J. Chem. Phys., 1995, 102, 5492–5498 CrossRef CAS.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011405 CrossRef.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, J. Colloid Interface Sci., 2008, 318, 23–28 CrossRef.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Colloids Surf., A, 2005, 270–271, 317–322 CrossRef.
- F. Martínez-Pedrero, A. El-Harrak, J. C. Fernández-Toledano, M. Tirado-Miranda, J. Baudry, A. Schmitt, J. Bibette and J. Callejas-Fernández, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011403 CrossRef.
- P. Domínguez-García, S. Melle, J. M. Pastor and M. A. Rubio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051403 CrossRef.
- M. Carmen-Miguel and R. Pastor-Satorras, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 826–834 CrossRef.
- P. Domínguez-García, S. Melle and M. A. Rubio, J. Colloid Interface Sci., 2009, 333, 221–229 CrossRef.
- V. Schaller, U. Kraling, C. Rusu, K. Petersson, J. Wipenmyr, A. Krozer, G. Wahnstrom, A. Sanz-Velasco, P. Enoksson and C. Johansson, J. Appl. Phys., 2008, 104, 093918 CrossRef.
- E. Kim, K. Stratford, P. J. Camp and M. E. Cates, J. Phys. Chem. B, 2008, 113, 3681–3693 CrossRef.
- J. S. Andreu, C. Calero, J. Camacho and J. Faraudo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 036709 CrossRef.
- MagChain Simulation Software, http://www.icmab.es/softmattertheory, 2012.
- E. M. Furst and A. P. Gast, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 6916–6925 CrossRef CAS.
- D. Heinrich, A. R. Goñi, A. Smessaert, S. H. L. Klapp, L. M. C. Cerioni, T. M. Osán, D. J. Pusiol and C. Thomsen, Phys. Rev. Lett., 2011, 106, 208301 CrossRef CAS.
- K. Mandel and F. Hutter, Nano Today, 2012, 7, 485–487 CrossRef CAS.
- J. Lim, C. Lanni, E. R. Evarts, F. Lanni, R. D. Tilton and S. A. Majetich, ACS Nano, 2010, 5, 217–226 CrossRef.
- J. S. Andreu, P. Barbero, J. Camacho and J. Faraudo, J. Nanomater., 2012, 2012, 678581 CrossRef.
- G. P. Hatch and R. E. Stelter, J. Magn. Magn. Mater., 2001, 225, 262–276 CrossRef CAS.
- M. R. Parker, Phys. Technol., 1981, 12, 263–268 CrossRef CAS.
- T. Y. Ying, S. Yiacoumi and C. Tsouris, Chem. Eng. Sci., 2000, 55, 1101–1113 CrossRef CAS.
- J. R. Stephens, J. S. Beveridge and M. E. Williams, Phys. Chem. Chem. Phys., 2012, 14, 3280–3289 RSC.
- M. Benelmekki, C. Caparrós, A. Montràs, R. Gonçalves, S. Lanceros-Méndez and L. M. Martínez, J. Nanopart. Res., 2011, 13, 3199–3206 CrossRef CAS.
- M. Benelmekki, A. Montràs, A. J. Martins, P. J. G. Coutinho and L. M. Martínez, J. Magn. Magn. Mater., 2011, 323, 1945–1949 CrossRef CAS.
- http://www.youtube.com/watch?v=BVipEdKoMh8 .
- S. P. Yeap, P. Y. Toh, A. L. Ahmad, S. C. Low, S. A. Majetich and J. K. Lim, J. Phys. Chem. C, 2012, 116, 22561–22569 CAS.
- S. P. Yeap, A. L. Ahmad, B. S. Ooi and J. K. Lim, Langmuir, 2012, 28, 14878–14891 CrossRef CAS.
- M. Zeltner, R. N. Grass, A. Schaetz, S. B. Bubenhofer, N. A. Luechinger and W. J. Stark, J. Mater. Chem., 2012, 22, 12064–12071 RSC.
- J. T. Mayo, S. S. Lee, C. T. Yavuz, W. W. Yu, A. Prakash, J. C. Falkner and V. L. Colvin, Nanoscale, 2011, 3, 4560–4563 RSC.
- B. B. Yellen, O. Hovorka and G. Friedman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8860–8864 CrossRef CAS.
- R. M. Erb, D. S. Sebba, A. A. Lazarides and B. B. Yellen, J. Appl. Phys., 2008, 103, 063916 CrossRef.
- M. Benelmekki, L. M. Martínez, J. S. Andreu, J. Camacho and J. Faraudo, Soft Matter, 2012, 8, 6039–6047 RSC.
| This journal is © The Royal Society of Chemistry 2013 |
