 Open Access Article
Open Access Article
DOI:
10.1039/C3SM00073G
(Paper)
Soft Matter, 2013,
9, 4767-4779
Diffusion of complex objects embedded in free and supported lipid bilayer membranes: role of shape anisotropy and leaflet structure
Received
8th January 2013
, Accepted 1st March 2013
First published on 20th March 2013
Abstract
We present a versatile numerical scheme to predict diffusion coefficients for arbitrarily shaped objects embedded in lipid bilayer membranes. Diffusion coefficients for micron-scale diamond-shaped solid domains are calculated for direct comparison to recent experiments. In supported membranes, identical objects in the distal and proximal leaflets may diffuse differently from one another; quantitative predictions for this asymmetry are provided, both for experimental systems and coarse-grained molecular simulations. We show that though recent experiments comparing the diffusion of monomeric, dimeric and trimeric protein assemblies moving over the surface of supported bilayers are inconsistent with the simplest Saffman–Delbrück model, they may be explained by a hydrodynamic model appropriate for supported membranes.
1 Introduction
Lateral diffusion of lipids, proteins, lipid domains and other supermolecular assemblies is a fundamental aspect of biological membrane dynamics required for proper physiological functioning in cellular biology.1–5 Diffusion coefficients for membrane-embedded objects may be predicted with the hydrodynamic Saffman–Delbrück–Hughes–Pailthorpe–White (SDHPW) theory,6,7 which describes the membrane as a two-dimensional structureless fluid sheet surrounded by an infinite bulk fluid and describes the diffusing object as a solid cylinder spanning the membrane and coupled to its surroundings via no-slip boundary conditions. This description has been remarkably successful for circular micron-scale domains in model membranes8,9 and thin liquid crystal films.10,11 Historically, SDHPW has also been widely accepted for the behavior of integral membrane proteins,12,13 though this has become controversial. Some recent measurements confirm SDHPW whereas others refute it.3,14–17 Despite this controversy, SDHPW remains essential for interpreting experiments, as deviations from the traditional hydrodynamic predictions indicate apparent failures of the “zeroth order” model and the need to consider more elaborate theoretical descriptions.18–20
Despite its successes, SDHPW has significant limitations even within the scope of purely hydrodynamic models. Its results apply only to isolated cylindrical inclusions completely spanning a bilayer in an infinite homogeneous bulk. This is appropriate for some experiments, but measurements involving supported membranes,21–24 monotopic (single-leaflet) proteins,25–27 and/or non-circular domains or proteins (or protein aggregates)14,28 can only be qualitatively compared to the predictions of SDHPW. Moreover, SDHPW is irrelevant to more biologically interesting situations involving immobile obstructions within the bilayer29,30 and/or asymmetric leaflet compositions.2,31 Directly extending the analytical boundary-value calculations employed by SDHPW to include such complications does not seem feasible. Even with the high symmetry of the SDHPW model geometry, the general predictions can be expressed only in terms of the solution to complicated integral equations (though simple empirical approximations to these solutions are now available9,28) and the required derivation is formidable.7
This paper introduces a numerical scheme capable of handling the various complications and generalizations to SDHPW discussed in the previous paragraph. We generalize the method of “regularized Stokeslets” (RS)32,33 to various hydrodynamic environments pertinent to membrane biophysics. For membranes modeled as a single sheet hosting simple cylindrical inclusions, our method reproduces both SDHPW results and the related results of Evans and Sackmann34 for membranes suspended above a solid support. Quantitative predictions for solid diamond-shaped lipid domains, as recently studied experimentally by Petrov, Petrosyan, and Schwille (PPS),28 are also obtained within the single sheet model and suggest that the experiments may be more sensitive to subtle hydrodynamic effects than was previously realized. Models that explicitly capture the dual-leaflet nature of the bilayer can also be studied in the framework of RS, allowing us to study diffusing objects associated with only one leaflet of a membrane, e.g. integral monotopic proteins25–27 and membrane-bound proteins.35 We present a number of results that emphasize the complex interplay between leaflet coupling, hydrodynamic environment surrounding the bilayer and diffusion of embedded proteins and discuss how signatures of this complex hydrodynamics might be observed in experiments and simulations. In particular, we analyze the experimental results of Knight et al.35 on membrane-bound protein assemblies diffusing over supported lipid bilayers and conclude that the results are consistent with a hydrodynamic description; however, it is essential that this hydrodynamic description include the effect of the proximal solid support as opposed to a direct application of the SDHPW theory.
The proposed RS method is versatile and straightforward to implement, involving only numerical evaluation of integrals and basic linear algebra operations that are available within high level numerical packages (e.g. MATLAB). This makes it practical to generate quantitative predictions for direct comparison to experiment, molecular simulations or approximate analytical theories with minimal effort and should prove very useful in the interpretation of dynamics at the surface of lipid bilayers.
2 Methodology
We calculate diffusion coefficients via numerical prediction of the mobility matrix,36 which is connected to diffusion by the Einstein relation.37 In this paper, we explicitly consider solid bodies moving in the 2D membrane plane with two mirror lines of symmetry. The three independent mobilities for such an object (i.e. the eigenvalues of the mobility matrix) are for translational motions parallel to the two orthogonal mirror lines and rotational motions about the object center, where the two mirror lines intersect. This means μ‖,⊥ = V‖,⊥/F‖,⊥ for translational mobilities parallel and perpendicular to the object's long axis, and μrot = Ω/τ for rotational mobility. The velocity V and angular velocity Ω are driven by the corresponding force F or torque (τ) with no cross-influence in this basis. Diffusion coefficients follow from the Einstein relation as D‖,⊥,rot = μ‖,⊥,rotkBT and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = (D‖ + D⊥)/2 is the long-time translational diffusion coefficient of the object as it thermally moves while rotating.38,39 (Treating objects of lesser symmetry requires simple calculations to identify the center of mobility and the diagonal basis for the object's mobility matrix, which are not generally obvious by simple inspection.36,39)
= (D‖ + D⊥)/2 is the long-time translational diffusion coefficient of the object as it thermally moves while rotating.38,39 (Treating objects of lesser symmetry requires simple calculations to identify the center of mobility and the diagonal basis for the object's mobility matrix, which are not generally obvious by simple inspection.36,39)
Determining the mobility matrix for a membrane-bound object requires the solution of a complicated boundary-value problem in three dimensions, which is a non-trivial analytical calculation.6,7,40 In contrast, it is fairly simple to analytically determine the Green's function tensor relating laterally directed forces to lateral lipid flow in a homogeneous membrane sheet devoid of any solid inclusions.41–43 Further, the analogous Green's function tensor may be written down for even significantly more complicated membrane models including leaflet structure and various other complications (see Appendix A). The approach we advocate below builds a numerical solution to membrane boundary-value problems directly from the appropriate membrane Green's functions. Our approach is similar in spirit, but different in approach and more general than the calculations introduced by Levine, Liverpool, and Mackintosh44,45 to study the diffusion of membrane-embedded rods.
In traditional three-dimensional (3D) hydrodynamics problems, the method of regularized Stokeslets (RS)32,33 provides a numerical route to determine mobility matrices for arbitrarily shaped solid bodies directly from Green's functions. The physical basis of the RS approach is quite simple and is similar in spirit to many other approaches found in the literature including the “shell method”,46,47 the Kirkwood approximation,37,44,45,48 and many others;49,50 see ref. 50 and references within. In all these approaches, the solid body is discretized into a dense assembly of small, rigidly connected and spherically symmetric sites embedded within the fluid. These sites are prescribed to interact with the embedding fluid by mirroring the local motion of the fluid and by locally transmitting force from the sites to the fluid (and vice versa). The approaches differ in implementation details of the velocity matching and force transmission requirements of the sites, but share the intuitively appealing feature of representing the continuous solid object by a collection of discrete points constrained to obey rigid-body motions. We have opted for the RS approach in this work as the approach is known to reproduce both the correct velocity fields and mobilities for a translating sphere in three dimensions33 and extension from the 3D case to membrane geometries is straightforward and requires no additional hydrodynamics calculations beyond determination of the relevant Green's functions. By contrast, the Kirkwood approximation is known to produce inexact and even unphysical results in certain situations51 and the shell method calculations that resolve these issues require use of the Rotne–Prager tensor,52 for which no membrane analog has yet been derived. The proposed RS scheme is the only method for determining diffusion coefficients of complex membrane-embedded objects that has been shown to quantitatively reproduce either the exact Saffman–Delbrück result6 for free membranes or the Evans–Sackmann result for supported membranes.34
We first consider the Saffman–Delbrück description of a membrane as a single thin flat viscous sheet of surface viscosity ηm surrounded by an infinite three-dimensional fluid of viscosity ηf. The Green's function tensor, TSD (also called an “Oseen tensor” or “Stokeslet”), can be used to calculate the lipid velocity field for a given applied force density f(r),
| | | vi(r) = ∫d2r′TSDij(r − r′)fj(r′) | (1) |
where
v is the
lipid velocity,
i,
j run over the
x and
y dimensions spanning the membrane surface, and the Einstein summation convention is assumed. The Fourier transform of
TSDij(
r) is
41–43| | 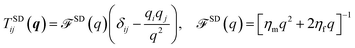 | (2) |
with the convention
f(
q) = ∫d
2re
−iq·rf(
r),
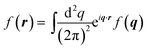
.
To implement the RS approach, we introduce a regularized Green's function TSDij(r;ε) in terms of a “blob function” ϕε(r). ϕε(r) is centered on the origin, integrates to one, and approaches a delta function as ε → 0; we choose a Gaussian blob function, 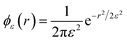 ↔
↔ ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε(q) = e−q2ε2/2 in this work.53 The regularized Green's function is
ε(q) = e−q2ε2/2 in this work.53 The regularized Green's function is
| | | TSDij(r;ε) = ∫d2r′TSDij(r − r′)ϕε(r′) | (3) |
so that a force density distributed over the blob envelope
f(
r) =
gϕε(
r) effects a velocity response
vi(
r) =
Tij(
r;
ε)
gjviaeqn (1).
We find 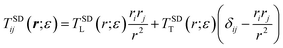 , (see Appendix A), with
, (see Appendix A), with
| | 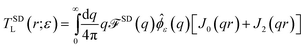 | (4) |
| | 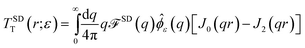 | (5) |
where
Jn(
u) are Bessel functions.
TSDij(
r;
ε) cannot be evaluated exactly in general, but reduces to
TSDij(
r) in the limit
r ≫
ε. For use in the numerical procedure discussed below, we evaluate the above integrals numerically using MATLAB's Gauss–Kronrod quadrature algorithm, quadgk (see Appendix A for details).
Membrane-embedded objects are discretized into N blobs centered at positions Rn (see Fig. 1). The force on blob n is written g[Rn] and the fluid response to all such forces (eqn (1)) predicts the velocity at Rm as
| | 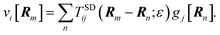 | (6) |
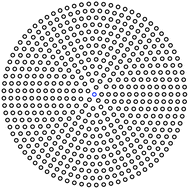 |
| | Fig. 1 In the RS approach, a circular object is represented by a collection of discrete blobs packed in concentric rings; the blobs have radial separation s, and points are separated on the circle by an arc length of s. For this illustration, s = 0.08R and the total number of points is N = 534. | |
Eqn (6) is a 2N × 2N matrix equation for the blob velocities in terms of applied forces.
Without any loss of generality, we assume the object is centered at the origin with its long axis aligned in the x direction. We enforce solid body motion by imposing v[Rm] = V + Ω × Rm for all m, and solve eqn (6) for the resulting forces g[Rn] using the generalized minimal residual method algorithm (GMRES).54 These blob forces combine to yield the total force and torque on the object: F = ∑mg[Rm] and τ = ∑mRm × g[Rm]. The mobilities and diffusion coefficients follow immediately as discussed above (e.g. D⊥ = μ⊥kBT = (Vy/Fy)kBT).
We stress an important difference between our application to membrane geometries and the traditional RS approach32,33 (and shell method approach46–48) in pure fluids. In traditional 3D or 2D problems it is only necessary to introduce a shell of blobs that cover the perimeter of the solid body, whereas our quasi-2D membrane problems require blobs tiling the entire 2D shape of the diffusing body. The Stokes equations in 2D and 3D naturally lead to rigid-body motion throughout the body when the perimeter behaves as a solid body;36 explicitly enforcing rigid body motion within the body is an unnecessary computational expense in 2D and 3D. In contrast, the equations of quasi-2D hydrodynamics (as summarized by eqn (1) and (2) in this work) do not share this property. For example, a rigid circular ring translating at velocity v in the membrane leads to a velocity vc < v at the center of the ring due to the traction imposed within the ring by the bulk fluid to either side of the membrane. To actually enforce solid body motion for a disc in a membrane, the entire disc must be prescribed to move in rigid fashion (see Fig. 1). In this context, it is worth re-emphasizing that our quasi-2D calculations reflect 3D physics. In particular, the behavior of the bulk fluids above and beneath the membrane are captured implicitly within eqn (2) and it is necessary to impose the rigid body constraint over all surfaces in contact with a fluid. These surfaces include the outer perimeter of the diffusing body, which is in contact with the membrane, and the top and bottom surfaces of the body, which are in contact with the bulk fluids. Within our quasi-2D model, the top and bottom surfaces are represented as the interior of the diffusing body.
3 Validation
To verify the membrane RS methodology, we have tested it on the two models where exact results are available, SDHPW and the closely related Evans–Sackmann problem for a membrane suspended above a solid support.34 Readers willing to accept our assertion that the RS approach provides quantitatively accurate numerical predictions for solid body mobilities in membranes can skip this section and proceed immediately to Section 4.
To generate numerical predictions for the SDHPW problem, we adopt the Green's function of eqn (2) and represent cylindrical objects of radius R embedded in the membrane by a collection of blobs packed in concentric circles (Fig. 1). We choose inter-blob spacings, s, within the range 0.03–0.07R, and choose ε to be half the spacing, as in ref. 32 and 33. At each value of s an RS calculation is performed and we find (see Fig. 2) that the mobilities change linearly in s. This allows us to extrapolate to the infinite-resolution limit s = 0, as in Bloomfield et al.48 and it is these extrapolated results that we report throughout this paper. We expect that the error of the method should vanish in the limit s → 0, and that the approach to zero error should be smooth; if this is true, we would generically expect from Taylor expansion that the error decreases linearly as s → 0. We see this to be true in Fig. 2; this extrapolation is also supported by its success in the shell method, reproducing known exact results in three-dimensional fluids.48,50 Quadratic extrapolation has also been used to extrapolate from larger values of s in shell methods.55 This process was repeated over a wide range of physical parameters and the resulting mobilities (translational and rotational) are displayed in Fig. 3. The “Saffman–Delbrück length”, LSD = ηm/2ηf, represents the wavelength for crossover from 2D-like hydrodynamics to 3D-like hydrodynamics in the SDHPW problem;41–43 our results include cylinders with radii that span both regimes. The agreement with SDHPW is excellent. The maximum error for the translational mobility is 0.2% and the maximum error for the rotational mobility is 0.4% over all cases studied. (Note that the “SDHPW theory” curves presented in Fig. 3 were generated using the interpolation formulas introduced by Petrov and co-workers.9,28 These formulas have a maximum error of less than 0.1% from the exact result, and are sufficient for our purposes.)
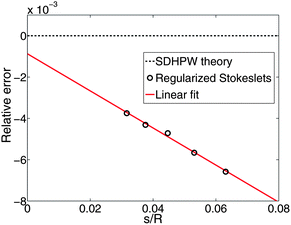 |
| | Fig. 2 We show the relative error on the translational mobility as a function of the discretization spacing s for R/LSD = 207; the mobility is a linear function of the spacing, and approaches the theoretical value as s → 0 (with a final relative error of 0.08%). Similar results are obtained for the rotational mobility. | |
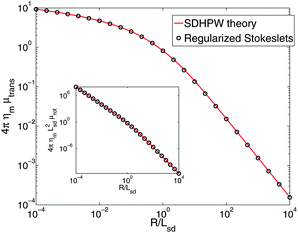 |
| | Fig. 3 RS calculations for the translational mobility of a cylindrical inclusion in a homogeneous free membrane. We observe good agreement with the results of ref. 7 with no free fitting parameters. The maximum deviation from the result of ref. 7 and 9 is 0.2% over the range 10−4 ≤ R/LSD ≤ 104. Inset: the rotational mobility is also in good agreement with ref. 7 and 28, with a maximum error of 0.4%. | |
Comparison to the Evans–Sackmann results proceed similarly to the SDHPW case (see Fig. 4), the primary difference being substitution of
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ES(q) = [ηmq2 + bsubstrate]−1 ES(q) = [ηmq2 + bsubstrate]−1 | (7) |
for
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) SD
SD(
q) in
eqn (2). The Evans–Sackmann model neglects all viscous losses in the bulk fluid surrounding the membrane, but does include a phenomenological friction on the membrane
via the coupling constant
bsubstrate. (In our general model of Appendix A, this corresponds to the limit
b →
∞,
K+(
q) = 0,
K−(
q) = −
bsubstrate, and
η+ =
η− =
ηm/2.) The analytic forms of the rotational and translational mobility for a cylinder of radius
R in an Evans–Sackmann membrane are known,
34| | 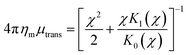 | (8) |
| | 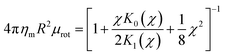 | (9) |
where
χ =
R/
LH and
LH = (
ηm/
bsubstrate)
1/2 is the hydrodynamic length scale for a supported membrane. These forms assume that the phenomenological drag between the substrate and the
protein is identical to that between the substrate and the membrane, which is compatible with the RS calculations.
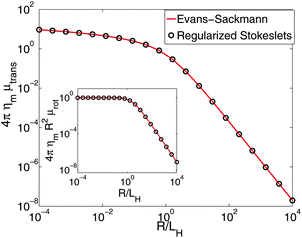 |
| | Fig. 4 RS calculations for the translational mobility of a cylindrical inclusion in a membrane above a solid support corresponding to the Evans–Sackmann limit.34 We observe good agreement with the result of ref. 34 with no free fitting parameters, with a maximum deviation of 2.4% over the range 10−4 ≤ R/LH ≤ 104. Inset: the rotational mobility is also in good agreement, with a maximum error of 1.0%. | |
4 Diamond-shaped domains in a membrane
PPS28 recently studied solid domains giant unilamellar vesicles of an equimolar mixture of the two phospholipids DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) and DPhPC (1,2-diphytanoyl-sn-glycero-3-phosphocholine). They observed that diamond-shaped solid domains (with a constant aspect ratio of 1.42, but variable overall size) diffuse within a fluid phase. PPS tracked the motion of these individual domains, and measured rotational and translational domain diffusion coefficients. We re-analyze the data presented by PPS using our RS calculations for solid diamonds embedded in a SD membrane, and directly compare our theory to experiment (Fig. 5). In our RS theory, the diffusion coefficient of a solid diamond will depend on its shape, the temperature, the bulk fluid viscosity ηf, and the membrane viscosity ηm. Since the surface viscosity of DPhPC–DPPC bilayers is not precisely known, ηm was treated as a fit parameter. The remaining physical parameters are known: ηf = 0.0115 poise (from an independent experiment) and T = 298.5 K.28 Fitting to reported translational diffusion coefficients (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ), we find ηm = (1.76 ± 0.13) × 10−6 poise cm; for rotational diffusion, we find ηm = (1.28 ± 0.09) × 10−6 poise cm. See Appendix C for more details on the fitting.
), we find ηm = (1.76 ± 0.13) × 10−6 poise cm; for rotational diffusion, we find ηm = (1.28 ± 0.09) × 10−6 poise cm. See Appendix C for more details on the fitting.
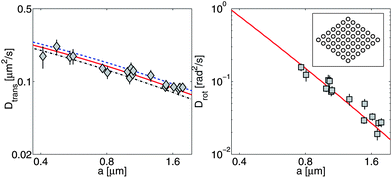 |
| | Fig. 5 PPS28 data for translational diffusion (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) , diamonds, left panel) and rotational diffusion (Drot, squares, right panel) of diamond-shaped domains compared to RS calculations (lines). Translational diffusion parallel to the long axis (D‖, dashed line) is faster than the diffusion perpendicular to it (D⊥, dash-dot line); , diamonds, left panel) and rotational diffusion (Drot, squares, right panel) of diamond-shaped domains compared to RS calculations (lines). Translational diffusion parallel to the long axis (D‖, dashed line) is faster than the diffusion perpendicular to it (D⊥, dash-dot line); ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) is the solid line. D⊥/D‖ ranges from 0.83 to 0.87 over the range of values shown, with the largest anisotropy for a ≫ LSD, as we would expect from ref. 44 and 45. Translational and rotational data are fit independently from one another and yield different values for ηm (see text). is the solid line. D⊥/D‖ ranges from 0.83 to 0.87 over the range of values shown, with the largest anisotropy for a ≫ LSD, as we would expect from ref. 44 and 45. Translational and rotational data are fit independently from one another and yield different values for ηm (see text). 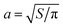 is the effective radius of the diamond, where S is the area of the domain. Inset: discretization of a diamond-shaped solid domain as a collection of blobs. A coarse discretization is shown; plotted results reflect the outcome of calculations involving thousands of blobs, extrapolated to infinite resolution. is the effective radius of the diamond, where S is the area of the domain. Inset: discretization of a diamond-shaped solid domain as a collection of blobs. A coarse discretization is shown; plotted results reflect the outcome of calculations involving thousands of blobs, extrapolated to infinite resolution. | |
The original analysis of this data by PPS approximated the domains by circles of equal area, i.e. they assumed the diffusion coefficients were given by the SDHPW model with an effective radius of 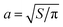 , where S is the area of the domain. With this assumption, they calculated ηm = (2.1 ± 0.1) × 10−6 poise cm and ηm = (2.3 ± 0.1) × 10−6 poise cm for translational and rotational measurements, respectively. These values are systematically higher than those found by the RS calculations. They also indicate a good correspondence between translation and rotation, whereas the RS results have a clear discrepancy. To the extent that the experiments correspond to a solid diamond in a SD membrane, the RS calculations are expected to be exact. The circular geometry assumed by PPS seems a reasonable, but somewhat uncontrolled approximation. Why then, should the more-correct RS calculation lead to inconsistent measurements of the viscosity from the translational and rotational diffusion coefficients? We suspect that the answer lies in the incompleteness of the model assumed for the membrane: there will be systematic deviations from the diffusion coefficients we predict, and they will affect rotation and translation differently. Both our RS calculations and SDHPW describe a perfectly flat membrane surrounded by a bulk fluid of infinite extent, while PPS observe a spherical vesicle pinned to a substrate. The substrate, vesicle geometry, and pinning will all change the diamond mobility.56–58 Translational mobility should be reduced more by these effects than rotational mobility, as the fluid flow around a translating object is longer-ranged than around a rotating one (see, e.g.ref. 59 in three dimensions). Also, if the diamond is distorted below the optical resolution (e.g. the tips of the solid domain have broken off) and thus has a smaller size or a different shape than that measured in ref. 28 and assumed here, we expect that the rotational mobility will increase more than the translational one. We have also performed RS calculations of diamonds with broken-off tips (data not shown); in these cases, the rotational diffusion coefficient increases more strongly than the translational one. It is common for rotational diffusion to depend more strongly on shape and size, e.g. a sphere with radius R in an infinite homogeneous 3D fluid has Dtrans ∼ 1/R but the rotational diffusion coefficient has a much stronger dependence on R: Drot ∼ 1/R3.36 This same pattern is evident in Fig. 5, where the rotational diffusion coefficient changes over two orders of magnitude while the translational one does not even change by a factor of 5. Both explanations are consistent with finding a larger effective viscosity for translational motion; more experiments are needed to distinguish between these two (or other) possibilities. The apparent inconsistency in ηm revealed by the RS calculations highlights the importance of this quantitative technique in the analysis of experimental data. Only with detailed calculations incorporating the proper domain shape was this apparent inconsistency discovered.
, where S is the area of the domain. With this assumption, they calculated ηm = (2.1 ± 0.1) × 10−6 poise cm and ηm = (2.3 ± 0.1) × 10−6 poise cm for translational and rotational measurements, respectively. These values are systematically higher than those found by the RS calculations. They also indicate a good correspondence between translation and rotation, whereas the RS results have a clear discrepancy. To the extent that the experiments correspond to a solid diamond in a SD membrane, the RS calculations are expected to be exact. The circular geometry assumed by PPS seems a reasonable, but somewhat uncontrolled approximation. Why then, should the more-correct RS calculation lead to inconsistent measurements of the viscosity from the translational and rotational diffusion coefficients? We suspect that the answer lies in the incompleteness of the model assumed for the membrane: there will be systematic deviations from the diffusion coefficients we predict, and they will affect rotation and translation differently. Both our RS calculations and SDHPW describe a perfectly flat membrane surrounded by a bulk fluid of infinite extent, while PPS observe a spherical vesicle pinned to a substrate. The substrate, vesicle geometry, and pinning will all change the diamond mobility.56–58 Translational mobility should be reduced more by these effects than rotational mobility, as the fluid flow around a translating object is longer-ranged than around a rotating one (see, e.g.ref. 59 in three dimensions). Also, if the diamond is distorted below the optical resolution (e.g. the tips of the solid domain have broken off) and thus has a smaller size or a different shape than that measured in ref. 28 and assumed here, we expect that the rotational mobility will increase more than the translational one. We have also performed RS calculations of diamonds with broken-off tips (data not shown); in these cases, the rotational diffusion coefficient increases more strongly than the translational one. It is common for rotational diffusion to depend more strongly on shape and size, e.g. a sphere with radius R in an infinite homogeneous 3D fluid has Dtrans ∼ 1/R but the rotational diffusion coefficient has a much stronger dependence on R: Drot ∼ 1/R3.36 This same pattern is evident in Fig. 5, where the rotational diffusion coefficient changes over two orders of magnitude while the translational one does not even change by a factor of 5. Both explanations are consistent with finding a larger effective viscosity for translational motion; more experiments are needed to distinguish between these two (or other) possibilities. The apparent inconsistency in ηm revealed by the RS calculations highlights the importance of this quantitative technique in the analysis of experimental data. Only with detailed calculations incorporating the proper domain shape was this apparent inconsistency discovered.
5 Membranes near walls and with leaflet structure
Many experimental studies involve “supported bilayers” (see Fig. 6), with membranes near flat solid supporting surfaces.60 Depending upon the surface, its proximity and mechanism of adhesion, these systems can show close correspondence with freely suspended membranes, or can show significant lowering of diffusion coefficients and even significant disparities in ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) between the two leaflets.21–24,61,62 Extensions of SDHPW to include a solid wall exist,34,56 but treat the membrane as a single sheet. To quantitatively compare to supported experiments, it is essential to explicitly account for the two-layered structure of the membrane. A supporting surface breaks the mirror symmetry through the bilayer midplane. Though a single sheet description is equivalent to a bilayer description for freely suspended membranes with objects symmetrically spanning two identical monolayers (as in SDHPW), there is no clear justification for the single sheet approach in a supported geometry.
between the two leaflets.21–24,61,62 Extensions of SDHPW to include a solid wall exist,34,56 but treat the membrane as a single sheet. To quantitatively compare to supported experiments, it is essential to explicitly account for the two-layered structure of the membrane. A supporting surface breaks the mirror symmetry through the bilayer midplane. Though a single sheet description is equivalent to a bilayer description for freely suspended membranes with objects symmetrically spanning two identical monolayers (as in SDHPW), there is no clear justification for the single sheet approach in a supported geometry.
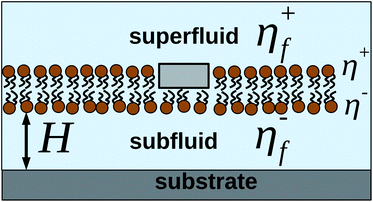 |
| | Fig. 6 Illustration of a common experimental situation, with a protein embedded in one leaflet of the membrane, which is suspended above a solid support. For the geometry shown here, K+(q) = −η+fq and K−(q) = −η−fqcoth(qH). | |
To model a two-leaflet membrane, we adopt the Seifert–Langer (SL)63 model of two coupled monolayers with a phenomenological drag between the upper (+) and lower (−) leaflets (though we assume the monolayers are incompressible, unlike SL). This approach and related theories64 have been successfully applied to the analysis of varied experiments and molecular simulations,64–67 though not to lateral diffusion (to our knowledge). While we do not expect this hydrodynamic model, nor any continuum model, to be completely accurate at lipid scale, we believe it may prove a useful qualitative guide to understand experimental results on lipid diffusion, while more quantitatively describing cases where hydrodynamic theories can be applied, e.g. larger monotopic membrane proteins.25–27
Eqn (1)–(6) are easily extended to other hydrodynamic environments and models that resolve the two-leaflet structure of the membrane. The generalized Green's function that relates the applied forces on both leaflets, f±, and velocities of the leaflets, v± is defined by
| | | vαi(r) = ∫d2r′Tαβij(r − r′)fβj(r′), | (10) |
where the Latin indices
i,
j are summed over (
x,
y) and Greek indices
α,
β are summed over the leaflets (+, −). An explicit expression for
Tαβij(
r) (in Fourier space), valid for many hydrodynamic environments surrounding the bilayer, is derived in Appendix A:
| | 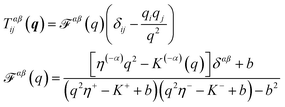 | (11) |
where (−
α) indicates the leaflet opposite to
α,
b is the SL interleaflet drag, and
η± is the surface viscosity of the upper (lower) monolayer. Here,
K±(
q) describes the influence of the bounding fluids on the leaflets they contact;
t±(
r) =
K± v±
v± = ∫d
2r′
K±(
r −
r′)
v±(
r′) is the traction from the fluid above (below) on the leaflet; see
ref. 41 and 68. If a leaflet is adjacent to an infinite column of fluid with viscosity
ηf, then
K(
q) = −
ηfq as in the free-membrane case; for a leaflet separated from a solid support by a distance
H,
K(
q) = −
ηfqcoth(
qH).
41 One may also include the presence of fixed obstacles through the presence of a “Brinkman equation”-like term,
K(
q) = −
k.
29,30 We also note that for a supported membrane in the limit of small
H and large subfluid viscosity
ηf, the result
K(
q) = −
ηfqcoth(
qH) approaches
K(
q) = −
ηf/
H,
i.e. the drag force from the presence of a substrate is simply
t = −
bsubstratev, which would be a natural phenomenological guess for a membrane on a rough surface. We shall primarily focus on a supported membrane as illustrated in
Fig. 6.
The behavior of eqn (11) depends crucially on the coupling between the leaflets. If the leaflets are uncoupled (b = 0), ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) αβ reduces to [q2ηα − Kα(q)]−1δαβ, i.e. force on one leaflet does not affect the other. In the limit of b → ∞,
αβ reduces to [q2ηα − Kα(q)]−1δαβ, i.e. force on one leaflet does not affect the other. In the limit of b → ∞, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) αβ becomes [q2(η− + η+) − (K− + K+)]−1, i.e. the bilayer acts as a single sheet with effective viscosity η− + η+ affected by the fluid both above and below it. The Green's function for a SD membrane is recovered from eqn (11) if we let η± = ηm/2, K±(q) = −ηfq, and let b → ∞. Extension of the RS method to the Green's function of eqn (11) is straightforward; details are presented in Appendix A. This technique allows us to calculate mobilities of complex objects embedded in either bilayer leaflet, transmembrane proteins embedded in both, or more complex assemblies. We only address single-leaflet objects in this section.
αβ becomes [q2(η− + η+) − (K− + K+)]−1, i.e. the bilayer acts as a single sheet with effective viscosity η− + η+ affected by the fluid both above and below it. The Green's function for a SD membrane is recovered from eqn (11) if we let η± = ηm/2, K±(q) = −ηfq, and let b → ∞. Extension of the RS method to the Green's function of eqn (11) is straightforward; details are presented in Appendix A. This technique allows us to calculate mobilities of complex objects embedded in either bilayer leaflet, transmembrane proteins embedded in both, or more complex assemblies. We only address single-leaflet objects in this section.
We have used the RS approach to calculate mobilities of cylindrical objects embedded in the top (+) or bottom (−) leaflets of membranes in the geometry of Fig. 6 and plot ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ± and Drot,± (Fig. 7). For sufficiently large interleaflet drag, b, the two leaflets become fully correlated, with no measurable discrepancy between “+” and “−”. For a freely suspended membrane (H → ∞), the ratio in diffusion coefficients between b = 0 and b → ∞ is exactly a factor of 2, as expected by symmetry considerations (twice SDHPW for b = 0 and exactly SDHPW for b → ∞). As the surface approaches the membrane, this ratio grows for the distal leaflet, but shrinks for the proximal leaflet.
± and Drot,± (Fig. 7). For sufficiently large interleaflet drag, b, the two leaflets become fully correlated, with no measurable discrepancy between “+” and “−”. For a freely suspended membrane (H → ∞), the ratio in diffusion coefficients between b = 0 and b → ∞ is exactly a factor of 2, as expected by symmetry considerations (twice SDHPW for b = 0 and exactly SDHPW for b → ∞). As the surface approaches the membrane, this ratio grows for the distal leaflet, but shrinks for the proximal leaflet.
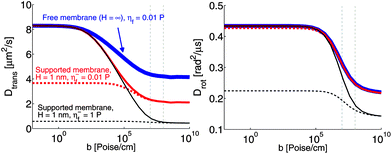 |
| | Fig. 7 Diffusion coefficients in the top (solid lines) and bottom (dashed lines) leaflets of a supported membrane (see Fig. 6) as a function of the interleaflet coupling parameter, b. R = 2 nm, H = 1 nm, η+f = 0.01 poise and η± = 2 × 10−7 poise cm, corresponding to a generic protein–lipid system and a closely supported geometry. T = 319 K (above the melting transition for DPPC). Vertical dashed lines indicate the window of known b values for experimental lipid systems. | |
The contrast in behavior between translational and rotational diffusion is significant and worth noting. Assuming the standard viscosity of water between the membrane and support, η−f = 0.01 poise, a supporting surface 1 nm from the membrane can yield (at small b) a sizable asymmetry between the leaflets for translational diffusion, but not for rotational diffusion. For more physical values of b (b ∼ 107 to 108 poise cm−1 (ref. 66 and 67)), there is no asymmetry, as suggested by simple estimates (see ref. 69 and Appendix B). However, various studies suggest that the thin layer of water confined between membrane and support does not behave as bulk water. In particular, it has been suggested that the confined water can become significantly ordered leading to a marked increase in viscosity.70–73 It should be acknowledged that this point is controversial74 and the behavior of the confined water layer almost certainly depends on the details of the membrane, supporting surface and separation between them in ways that are not fully understood. In particular, the viscosity η−f could become a function of H; we do not assume any particular form, but show results for different values of η−f and H, varied independently. If we increase the effective viscosity of η−f to 1 poise,75 as may be appropriate for confined water,70–73 rotational motion is asymmetric at H = 1 but translation is not (assuming experimentally relevant b). These seemingly incongruous results are actually sensible since fluid flow around a rotating object is more localized than around a translating one.59 For this reason, translation is more strongly affected by the presence of the support than is rotation. However, a larger b is required to synchronize leaflets for rotation, since the flow fields are more closely localized around the protein, and hence interleaflet friction is less effective. These results emphasize the complex interplay between b, η±f and geometry (H) as they affect both translational and rotational motion in supported systems. It is potentially misleading to draw broad conclusions about the similarity between freely suspended and supported systems without performing multiple different measurements.
As is apparent from Fig. 7, we would not expect large differences between diffusion coefficients in the top and bottom leaflets for physical values of the interleaflet coupling b unless there is significant ordering of the fluid (increasing viscosity by a factor of 100). However, for some coarse-grained simulations, some dynamical physical parameters are significantly different from those measured experimentally,76e.g. b is much lower. For such membranes, the asymmetry between the two leaflets can be significantly stronger than in physical experiments. Many of the relevant parameters have been measured for the MARTINI model of DPPC.77 MARTINI is a widely used and well-studied coarse-grained force-field for lipid bilayers and proteins; it represents several atoms (typically four) as a single interaction center. MARTINI also has explicit water. For this model, the membrane viscosity is ηm = 1.2 × 10−8 poise cm, the bulk water viscosity is ηwater = 7 × 10−3 poise, and the interleaflet coupling term is b = 2.4 × 105 poise cm−1.76 In particular, the interleaflet coupling is roughly two orders of magnitude lower than the experimental range of b ∼ 10−7 to 10−6 poise cm−1, and the membrane viscosity ηm is also lower than those typically observed in micron-scale experiments, which are of the order of 107 to 108 poise cm.28,78 Unfortunately, though ref. 71 simulated a MARTINI membrane above a solid substrate, and observed that the confined water under the membrane becomes significantly ordered, we are not aware of an explicit measurement of the confined fluid viscosity η−f in MARTINI. We therefore calculate diffusion coefficients for proteins in a supported MARTINI membrane as a function of the subfluid viscosity, with the superfluid viscosity fixed to η+f = ηwater, and a support height of H = 10−7 cm (Fig. 8). Our results suggest that the difference in diffusion coefficients between the top and bottom leaflets observed in MARTINI simulations (e.g.ref. 71) may be larger than that seen in experiments, because of the weaker interleaflet coupling of the MARTINI model.
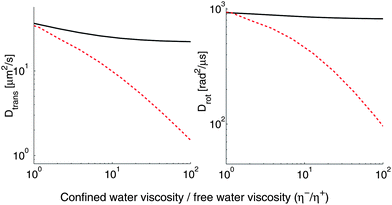 |
| | Fig. 8 With the anomalously low membrane viscosity and interleaflet coupling of the MARTINI model, a relatively low subfluid viscosity is required to create an asymmetry between top and bottom leaflets. This figure shows the diffusion coefficient of a protein-scale object in a supported membrane as a function of the subfluid viscosity; R = 2 nm, H = 1 nm. The solid line is for objects in the top (distal) leaflet, and the dashed line for the bottom (proximal) leaflet. These results have not been rescaled to match the physical timescale, as is sometimes done in reporting MARTINI numbers. | |
6 Membrane-bound protein assemblies
Knight et al.35 have recently observed monomers, dimers and trimers of membrane-bound proteins. These membrane-bound proteins are the PH domain of the general receptor for phosphoinositides, isoform 1 (GRP1 PH domains), and they bind to PIP3 (phosphatidylinositol-3,4,5-trisphosphate). Knight et al. study these proteins in supported lipid bilayers of DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) with a small fraction of PIP3 for the PH domains to bind to. They observe that a dimer of membrane-bound proteins has a diffusion coefficient half that of a monomer, and a trimer a third that of a monomer. Qualitatively similar results have also been reported for multimeric assemblies of protein pore complexes in the supported geometry.62 This would be the natural result if the assemblies are not hydrodynamically correlated, i.e. that they are in the “free draining” limit where a force on one monomer does not lead to a motion on the other monomer (e.g. Rouse dynamics in polymers37). Knight et al. suggest that the lipids attached to these proteins, which are 4–6 nm apart, are freely draining, and note that the Saffman–Delbrück theory for freestanding bilayers cannot explain these experimental results. We emphasize that the Saffman–Delbrück theory is not appropriate for supported bilayers. While we agree with the assessment that the SDHPW theory can not explain these experiments, we show below that there is not necessarily any inconsistency between hydrodynamic theory and experiment. There is, however, a potentially serious inconsistency in applying the simplest SDHPW theory to the supported membrane geometry.
Using the RS scheme, we can compute the diffusion coefficient of rigid dimers of membrane-embedded particles and determine their diffusion coefficients relative to the single-particle diffusion coefficient. In this case, almost all of the complications we have described above arise. The protein-bound lipids are only embedded in a single leaflet, the dimer has a complex, anisotropic shape, and (in the case of the experiments) the membrane is very close to a solid support.
We model the protein-bound lipids as solid cylinders with a fixed separation; we ignore the added drag from the protein associated with the lipid, and focus only on the lipids associated with the protein. We choose R = 0.45 nm for the lipid size (as assumed in Knight et al.35), and look at separations ranging from 0.9 nm to 9 nm. As a control, we first study a freestanding membrane with the protein-bound lipid dimer embedded in one leaflet (η± = ηm/2, η±f = ηf), and choose the membrane viscosity to be consistent with micron-scale fluorescence experiments, (though on the low end), ηm = 4 × 10−7 poise cm8,9,28,78 and ηf = 0.01 poise to be the viscosity of water. We choose b = 107 poise cm−1, consistent with experimental measurements.64,66,67 With these numbers and the freestanding geometry, the two monomers are highly correlated. Even at a separation of 9 nm, the rotationally averaged mobility of the dimer is still 72% of the monomer's mobility (Fig. 9) as compared to 50% for the free draining limit. This should not be surprising, as these values correspond to a Saffman–Delbrück length of LSD = 0.5 microns, and we would expect that two objects closer than the Saffman–Delbrück length are highly correlated; we will see this more explicitly through use of the Kirkwood approximation below.
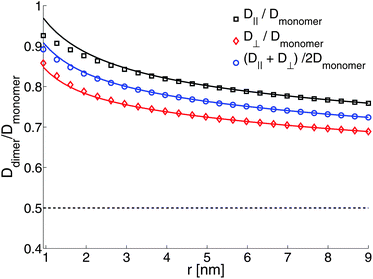 |
| | Fig. 9 Ratio of diffusion coefficients of a protein-bound lipid dimer compared to a protein-bound lipid monomer in a free membrane. The solid lines are the Kirkwood approximation (eqn (12)), which is a good approximation for well-separated objects. The dashed line is Ddimer/Dmonomer = 1/2, the free-draining limit. b = 107 poise cm−1, η± = 2 × 10−7 poise cm, η±f = 0.01 poise (i.e. water), R = 0.45. | |
The results of Fig. 9 describe the dynamics of membrane-bound proteins in a freestanding bilayer. We now treat the case of a supported bilayer, as studied experimentally by Knight et al.35 We choose parameters as above, but set the thin water layer to have viscosity η−f = 0.75 poise; the distance between membrane and substrate is chosen to be H = 1 nm. Though our choice for η−f is not based on a direct independent measurement, we note that this choice does seem consistent with the limited experimental data available. In particular, we find that at 20 °C, this predicts a monomer diffusion coefficient of 2.5 × 10−8 cm2 s−1 in the top leaflet and 1.9 × 10−8 cm2 in the bottom leaflet, compared to the value of 2.7 × 10−8 cm2 s−1 measured in ref. 35 (presumably for the top leaflet, but not specified). Our calculations also show that the diffusion coefficient for a monomer in a freestanding membrane with the same viscosity would be 5.9 × 10−8 cm2 s−1, consistent with ref. 61, who find that, for a different lipid system, the substrate reduces the lipid diffusion coefficient relative to the freely suspended case by a factor of about 2.5. We plot lipid flows around the dimer (Fig. 10) and the ratio of diffusion coefficients of the dimer compared to the monomer (Fig. 11). In ref. 35 it was suggested that the ratio of dimer to monomer diffusion coefficients should be similar for freestanding and supported lipid bilayers. Comparison of Fig. 9 and 11 suggest that this assertion is incorrect for the model discussed here. As we saw in Section 5, the presence of a solid support can significantly alter membrane dynamics relative to the freely suspended case; this conclusion extends to the ratio of diffusivities between monomers and dimers.
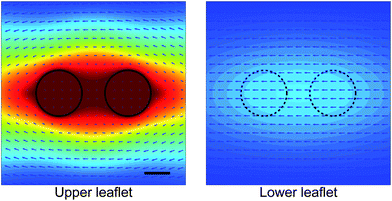 |
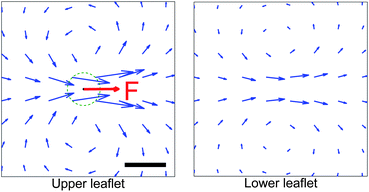
| | Fig. 10 Calculated lipid flows around a two-cylinder composite object modeling a membrane-associated protein dimer in a supported lipid membrane. The dimer is embedded in the upper leaflet and pushed along the axis connecting the monomers. The presence of the dimer in the upper leaflet also affects the flow in the lower leaflet. The velocity field is drawn in the rest frame of the dimer, and the color map indicates the magnitude of the velocity measured relative to the dimer's velocity. Parameters chosen as in Fig. 11. Scale bar is 0.5 nm. | |
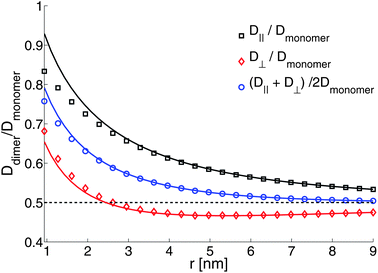 |
| | Fig. 11 Ratio of diffusion coefficients of a protein-bound lipid dimer compared to a protein-bound lipid monomer. The solid lines are the Kirkwood approximation (eqn (12)), which is a good approximation for well-separated objects. The dashed line is Ddimer/Dmonomer = 1/2, the free-draining limit. b = 107 poise cm−1, η± = 2 × 10−7 poise cm, η+f = 0.01 poise (i.e. water), η−f = 0.75 poise; H = 1 nm and R = 0.45. | |
As seen in Fig. 11, the mean diffusion coefficient of the dimer ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) decreases to the free-draining limit Dmonomer/2 once the dimer reaches a separation of roughly 6 nm. This is consistent with the data of Knight et al., but we note that focus on
decreases to the free-draining limit Dmonomer/2 once the dimer reaches a separation of roughly 6 nm. This is consistent with the data of Knight et al., but we note that focus on ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) alone is somewhat misleading. Considered separately, the individual components of diffusion, D⊥ and D‖, clearly do display hydrodynamic correlations and it is a cancellation of effects between the two that leads to the apparent free-draining result for
alone is somewhat misleading. Considered separately, the individual components of diffusion, D⊥ and D‖, clearly do display hydrodynamic correlations and it is a cancellation of effects between the two that leads to the apparent free-draining result for ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) . Further, D⊥ actually decreases below the free-draining limit (Ddimer/Dmonomer = 1/2), and then increases to approach this limit at larger separations; for motions directed perpendicular to the dimer axis the assembly can diffuse more slowly than in the absence of hydrodynamic interactions. This is solely a consequence of the presence of the substrate, and we can gain some additional understanding of this by using the Kirkwood approximation37,44 to calculate the dimer mobility. This approach describes the effect of one monomer on the other by treating the protein-bound lipids as point forces and has been used to interpret molecular dynamics simulations (M. G. Lerner, personal communication and ref. 35). Within this approximation, the parallel and perpendicular mobilities of a dimer with two protein-bound lipids in the top leaflet separated by a fixed distance r are given by
. Further, D⊥ actually decreases below the free-draining limit (Ddimer/Dmonomer = 1/2), and then increases to approach this limit at larger separations; for motions directed perpendicular to the dimer axis the assembly can diffuse more slowly than in the absence of hydrodynamic interactions. This is solely a consequence of the presence of the substrate, and we can gain some additional understanding of this by using the Kirkwood approximation37,44 to calculate the dimer mobility. This approach describes the effect of one monomer on the other by treating the protein-bound lipids as point forces and has been used to interpret molecular dynamics simulations (M. G. Lerner, personal communication and ref. 35). Within this approximation, the parallel and perpendicular mobilities of a dimer with two protein-bound lipids in the top leaflet separated by a fixed distance r are given by
| | 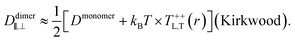 | (12) |
The Kirkwood approximation provides a good approximation, except for the points of closest approach (Fig. 9 and 11). As noted by Oppenheimer and Diamant,69 the perpendicular response function for a supported membrane in the “adsorbed” limit, where H ≪ LSD, is actually negative at large separations, which explains (through eqn (12)), the anomalous behavior of D⊥. T++T(r) becoming negative at some distances indicates that the response to a point force has a circulating flow. We explicitly show this, plotting the velocity response to a point force applied to the upper leaflet in Fig. 12.
 |
| | Fig. 12 The velocity response to a force applied on the upper leaflet of a supported membrane has circulation, as noted in the text. The force is regularized over a size ε = 2 nm (dashed line). Scale bar is 5 nm. Membrane parameters are as in Fig. 11. | |
While we do not attempt to study the parameter space here as extensively as we did in Section 5, we note that the primary cause of the quick decay in Fig. 11 is the increased viscosity of the subfluid. We have repeated the calculation of Fig. 11 but with η−f = 0.01 poise; the dimer–monomer ratio ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) dimer/Dmonomer decreases significantly slower with dimer separation, only reaching 0.6 at a separation of 9 nm. This shows the importance of the increased viscosity of the water beneath the membrane, which we expect will depend on the details of the SLB preparation. This suggests that the measurements of Knight et al.35 may be sensitive to substrate and preparation, as noted for lipid diffusion in Scomparin et al.23
dimer/Dmonomer decreases significantly slower with dimer separation, only reaching 0.6 at a separation of 9 nm. This shows the importance of the increased viscosity of the water beneath the membrane, which we expect will depend on the details of the SLB preparation. This suggests that the measurements of Knight et al.35 may be sensitive to substrate and preparation, as noted for lipid diffusion in Scomparin et al.23
It should be emphasized that this theoretical study cannot prove that the hydrodynamic model employed above is the correct physical picture to explain experiments on supported membranes. Without precise measurements of the effective viscosity of confined water, the surface viscosity of lipid monolayers and the interleaflet drag for specific systems, it is very difficult to quantitatively compare theory to experiment and vice versa. However, we do believe that the numbers introduced above are reasonable and they appear consistent with the experimental data that is available. To the extent that these numbers can be believed, our calculations suggest that hydrodynamics is consistent with the experiments of Knight et al. and that the underlying physical mechanism responsible for the unexpected “free-draining” results is the drag introduced by the supporting surface. Other explanations may be possible as well. In particular, if membrane viscosity is lower than previously believed, as recently suggested in ref. 57, this would significantly reduce the hydrodynamic coupling between monomers. Also, if the continuum approximation breaks down or there are additional non-hydrodynamic sources of drag present18,19 this could account for the experimental findings.
7 Discussion
We have applied our numerical RS approach to calculate translational and rotational diffusion coefficients for three increasingly complex and experimentally relevant membrane-embedded objects: diamond-shaped solid domains, monotopic proteins, and dimers of membrane-associated proteins. Our analysis of the diffusion of diamond-shaped domains on a vesicle suggests that it may be possible to experimentally observe deviations from the simplest Saffman–Delbrück model of the membrane due to the curvature of the vesicle and/or the presence of the substrate. We also note that, as in our analysis of the monomer vs. dimer vs. trimer diffusion studies of Knight et al., the presence of an underlying solid support can have potentially serious consequences for protein diffusion – even for proteins confined to the leaflet distal to the support. However, these effects will strongly depend on the extent to which the fluid below the membrane becomes more ordered, which may depend on the substrate preparation.71 Many aspects of lipid dynamics in supported systems can also depend on preparation,23 and the importance of the leaflet dynamics and supported hydrodynamics may depend on these details.
Since the work of Urbach and co-workers,14 several groups have observed membrane diffusion coefficients in simulation and experiment, and claimed a conflict with SDHPW.20,35,62 While we do not question that these works observe clear deviations from the SDHPW results, it is important to emphasize that many of these studies involve systems that are not necessarily described by SDHPW. The SDHPW theory only applies to cylindrical membrane-spanning solid bodies residing in an infinite flat membrane freely suspended within an infinite homogeneous bulk. The experiments in ref. 35 and 62 were carried out in the supported geometry, which we have shown above is potentially both quantitatively and qualitatively different from the free geometry. The appropriate theory for analyzing these experiments is not SDHPW, but the generalized theory we develop in Section 5, or (when the leaflet structure can be neglected), that presented in ref. 34, 56 and 69. Similarly, coarse-grained molecular dynamics simulations as in ref. 20 and 35 will not necessarily correspond to SDHPW because the “infinite bulk” requirement is violated; these studies are usually carried out in small periodic simulation boxes, in which the z distance between the membrane and its nearest periodic copy is on the order of the membrane thickness. While we make no attempt to explicitly analyze the periodic case in this work, we expect significant deviations between the periodic geometry and the infinite case, similar to those observed in 3D.79 Indeed, since membranes have even longer-ranged hydrodynamic correlations than bulk fluids, we would expect that the system-size dependence of the diffusion coefficients in periodic lipid membranes will have an even slower convergence than the (box length)−1 observed in 3D.
The RS approach for membranes is versatile and easily applied to cases beyond those explicitly considered here. The method can incorporate other generalizations of the SD Green's function without difficulty, including dynamics of membrane stacks,80 viscoelastic membranes and surroundings,42,81,82 and inertial effects.81,83 Calculation of relative diffusion coefficients between mobile bodies42,43 is straightforward49 and may be useful for the analysis of microrheological experiments on membranes and interfaces.84–87 RS can also include complications present in biomembranes, such as immobilized proteins29,30 and asymmetric leaflet compositions and viscosities,2,31 and should prove useful in calculating hydrodynamic membrane-protein mobilities in biological systems.
A Derivation of regularized Stokeslets for the two-leaflet model
We describe the hydrodynamics of a membrane in terms of a variant of the Seifert–Langer (SL)63 picture of the membrane as two coupled monolayers, with a phenomenological drag between the upper (+) and lower (−) leaflets. The Stokes equations should include (1) the viscous drag from each monolayer, which have surface viscosities of η±, (2) the surface pressure p±, (3) the drag from the fluid above the top leaflet, and below the bottom leaflet, K± v±, (4) the drag force between leaflets ∓b(v+ − v−), and (5) an applied force per unit area f±. We also require, unlike the original SL model, that the monolayers are incompressible, though this constraint can be relaxed.42,63
v±, (4) the drag force between leaflets ∓b(v+ − v−), and (5) an applied force per unit area f±. We also require, unlike the original SL model, that the monolayers are incompressible, though this constraint can be relaxed.42,63| | η±∇2v± − ∇p± + K± v± ∓ b(v+ − v−) = −f± v± ∓ b(v+ − v−) = −f± | (13) |
The convolution term t±(r) = K±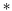 v± = ∫d2r′K±(r − r′)v±(r′) is the drag from the fluid surrounding the monolayer, and is usually described in terms of its Fourier transform, t±(q) = K±(q)v±(q). Our convention is K(q) = ∫d2re−iq·rK(r),
v± = ∫d2r′K±(r − r′)v±(r′) is the drag from the fluid surrounding the monolayer, and is usually described in terms of its Fourier transform, t±(q) = K±(q)v±(q). Our convention is K(q) = ∫d2re−iq·rK(r), 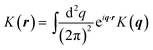 . The form of K±(q) will depend on the hydrodynamic environment of the leaflet; if a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 A common example is given in Fig. 6.
. The form of K±(q) will depend on the hydrodynamic environment of the leaflet; if a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 A common example is given in Fig. 6.
We can solve the coupled Stokes equations eqn (13) and (14) to determine a Green's function tensor (see, e.g.ref. 37); the Green's function indicates the relationship between the applied forces on both leaflets, f±, and the velocity of the leaflets, v±:
| | | vαi(r) = ∫d2r′Tαβij(r − r′)fβj(r′) | (15) |
where we assume the Einstein summation convention, and Latin indices
i,
j are summed over (
x,
y) and Greek indices
α,
β are summed over the leaflets (+, −). This convolution is obviously simpler in Fourier space, where
vαi(
q) =
Tαβij(
q)
fβj(
q). We determine the Green's function from
eqn (13) by Fourier transform; the Fourier transform of
eqn (13) is
| | | −q2η±v±(q) − iqp±(q) + K±(q)v±(q) ∓ b(v+(q) − v−(q)) = −f±(q) | (16) |
We can eliminate the pressure by using incompressibility, which requires that q·v±(q) = 0. We apply the projection operator ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) ij(q) ≡ δij − qiqj/q2 to eqn (16), which allows us to write a matrix equation for v±(q) as a function of f±(q),
ij(q) ≡ δij − qiqj/q2 to eqn (16), which allows us to write a matrix equation for v±(q) as a function of f±(q),
| | 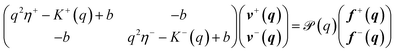 | (17) |
This matrix equation can be inverted to find
| | | vαi(q) = Tαβij(q)fβj(q) | (18) |
where
| | 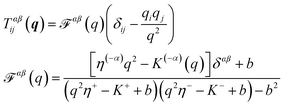 | (19) |
where (−
α) indicates the leaflet opposite to
α.
If we define
| | | Tαβij(r;ε) = ∫d2r′Tαβij(r − r′)ϕε(r′) | (20) |
then we can determine
Tαβij(
r;
ε) from
eqn (19) by Fourier transform, as
Tαβij(
q;
ε) =
Tαβij(
q)
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε
ε(
q), by applying the convolution theorem to
eqn (20). Because
ϕε(
r) is circularly symmetric, the tensor
Tαβij(
r;
ε) can only be constructed out of
r as
| | 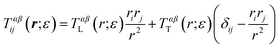 | (21) |
where
TαβL is the longitudinal response and
TαβT the transverse. To make this calculation simple, we assume (without loss of generality) that the vector
r is in the
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif)
direction; then
TαβL =
Tαβxx and
TαβT =
Tαβyy. It is then easy to find
| | 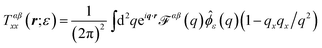 | (22) |
| | 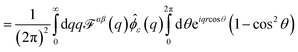 | (23) |
| | 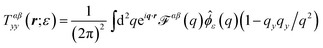 | (24) |
| | 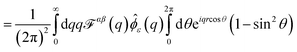 | (25) |
Evaluating the angular integrals, we find:
| | 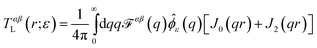 | (26) |
| | 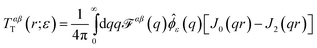 | (27) |
where
Jn(
u) is the usual Bessel function and, for clarity, we have indicated the Fourier transform of
ϕε explicitly by
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε
ε.
The evaluation of these integrals is potentially costly; in practice, when we need to evaluate TαβL(r;ε) and TαβT(r;ε) a large number of times, we create a table of precomputed values and use piecewise cubic interpolation; we use 1000–2000 points.
The generalization of eqn (6) relating the forces applied at the blobs to the velocities of the blobs is then
| | 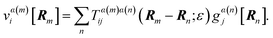 | (28) |
where
α(
n) indicates the leaflet that blob
n is present in (
i.e. α(
n) = +, −).
Eqn (28) is a 2
N × 2
N matrix equation for the blob velocities in terms of applied forces, where
N is the number of blobs. We note that there may be blobs in one leaflet and not in another, as in the case when a
protein is embedded in only one leaflet; there is no implied sum over all states
α, only those where there are blobs. For transmembrane
proteins, there will be blobs in both leaflets.
B Rough estimate of translational diffusion coefficient
If we are primarily interested in the scaling behavior of the translational diffusion coefficient of an isotropic object, we can apply an ad hoc approximation, representing our object as a single blob, taking the regularization size to be the particle radius R. This is similar to many previously established approximation schemes.81,88–90 This result is, for a particle in the α leaflet,| | 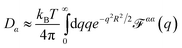 | (29) |
where no sum over α is implied. Because of the Gaussian term, wavenumbers with q ≫ 1/R do not contribute to the diffusion coefficient; qmax ∼ 1/R is the largest relevant wavenumber. Looking at eqn (19), we can find the relevant scale for b such that the two leaflets are correlated. Assuming that −K±(q) is a non-decreasing function of q (as it is for all cases studied here), we will need b ≫ η±qmax2 − K±(qmax) for the two leaflets to be perfectly correlated over all relevant wavenumbers. This produces that a sufficient, but not necessary value for b for the two leaflets to be correlated is b ≫ η±/R2 − K±(q = 1/R). For a supported membrane in the “adsorbed” region, K−(q) = −ηfqcothqH ≈ −ηf/H.69 In this case, for R = 2 nm and H = 1 nm, and η± = 2 × 10−7 poise cm, we find that b ≫ 5 × 106 poise cm−1 suffices to correlate the two leaflets, in agreement with the main body of the paper. We note that ref. 69 presents a slightly different estimate, requiring only b ≫ ηf/H; our results suggest this is not sufficient if R2 ≪ η−H/ηf.
C Details of fitting procedure
To more conveniently determine the viscosity of the membrane from the translational and rotational diffusion coefficients of diamond-shaped domains, we pre-calculate the theoretical diffusion coefficients as a function of membrane viscosity. A particularly convenient way to do this is to note that, for a fixed aspect ratio, Drot/D0,r ≡ hrot(a/LSD) with D0,r = kBT/4πηmLSD2 and D‖/D0 ≡ h‖(a/LSD), D⊥/D0 ≡ h⊥(a/LSD), with D0 = kBT/4πηm. We can then compute hrot,‖,⊥(x) numerically for a large number of points x, and use linear interpolation to determine h…(x) for any x. The experimental data from ref. 28 consists of measurements of Drot and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) as a function of a, the effective size, with uncertainties δD. We perform weighted nonlinear least squares fitting with MATLAB's nlinfit to determine LSD and hence ηm. To determine the error in ηm, we perform a simple Monte Carlo estimation. We vary each measurement D by a normally distributed random variable with mean zero and standard deviation equal to its uncertainty δD, and determine the distribution of ηm; the values reported above are the mean value of ηm from this procedure, and the uncertainty is the standard deviation of the distribution of fit ηm.
as a function of a, the effective size, with uncertainties δD. We perform weighted nonlinear least squares fitting with MATLAB's nlinfit to determine LSD and hence ηm. To determine the error in ηm, we perform a simple Monte Carlo estimation. We vary each measurement D by a normally distributed random variable with mean zero and standard deviation equal to its uncertainty δD, and determine the distribution of ηm; the values reported above are the mean value of ηm from this procedure, and the uncertainty is the standard deviation of the distribution of fit ηm.
Acknowledgements
We thank Paul Atzberger, Haim Diamant, Michael Lerner, Richard Pastor, Eugene Petrov, and Todd Squires for helpful conversations. We also thank the authors of ref. 28 for sharing their data and an early preprint of their work. This work was supported in part by the NSF (CHE-0848809, CHE-1153096, CNS-0960316). B. A. C. acknowledges the support of the Fannie and John Hertz Foundation. F. B. acknowledges support from the Camille and Henry Dreyfus Foundation.
References
- H. C. Berg and E. M. Purcell, Biophys. J., 1977, 20, 193–219 CrossRef CAS.
-
R. B. Gennis, Biomembranes: Molecular Structure and Function, Springer-Verlag, Berlin, 1989 Search PubMed.
- S. Ramadurai,
et al.
, J. Am. Chem. Soc., 2009, 131, 12650 CrossRef CAS.
- C. Eggeling, C. Ringemann, R. Medda, G. Schwarzmann, K. Sandhoff, S. Polyakova, V. N. Belov, B. Hein, C. von Middendorff, A. Schonle and S. W. Hell, Nature, 2009, 457, 1159 CrossRef.
- D. Lingwood and K. Simons, Science, 2010, 327, 46 CrossRef CAS.
- P. G. Saffman and M. Delbrück, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111 CrossRef CAS.
- B. D. Hughes, B. A. Pailthorpe and L. R. White, J. Fluid Mech., 1981, 110, 349 CrossRef CAS.
- P. Cicuta, S. L. Keller and S. L. Veatch, J. Phys. Chem. B, 2007, 111, 3328 CrossRef CAS.
- E. P. Petrov and P. Schwille, Biophys. J., 2008, 94, L41 CrossRef CAS.
- Z. H. Nguyen, M. Atkinson, C. S. Park, J. Maclennan, M. Glaser and N. Clark, Phys. Rev. Lett., 2010, 105, 268304 CrossRef.
- A. Eremin, S. Baumgarten, K. Harth, R. Stannarius, Z. Nguyen, A. Goldfain, C. Park, J. Maclennan, M. Glaser and N. Clark, Phys. Rev. Lett., 2011, 107, 268301 CrossRef CAS.
- R. Peters and R. J. Cherry, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 4317–4321 Search PubMed.
- W. L. C. Vaz, M. Criado, V. M. C. Madeira, G. Schoellmann and T. M. Jovin, Biochemistry, 1982, 21, 5608–5612 Search PubMed.
- Y. Gambin, R. Lopez-Esparza, M. Reffay, E. Sierecki, N. S. Gov, M. Genest, R. S. Hodes and W. Urbach, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 2098 CrossRef CAS.
- J. Kriegsmann, I. Gregor, I. Von Der Hocht, J. Klare, M. Engelhard, J. Enderlein and J. Fitter, ChemBioChem, 2009, 10, 1823 CrossRef CAS.
- S. Ramadurai, A. Holt, L. V. Schäfer, V. V. Krasnikov, D. T. S. Rijkers, S. J. Marrink, J. A. Killian and B. Poolman, Biophys. J., 2010, 99, 1447 Search PubMed.
- Y. Gambin, M. Reffay, E. Sierecki, F. Homblé, R. S. Hodges, N. S. Gov, N. Taulier and W. Urbach, J. Phys. Chem. B, 2010, 114, 3559 Search PubMed.
- A. Naji, A. J. Levine and P. Pincus, Biophys. J., 2007, 93, L49 Search PubMed.
- B. A. Camley and F. L. H. Brown, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061921 Search PubMed.
- G. Guigas and M. Weiss, Biophys. J., 2006, 91, 2393–2398 CrossRef CAS.
- M. Przybylo, J. Sýkora, J. Humpolíčková, A. Benda, A. Zan and M. Hof, Biochim. Biophys. Acta, 2010, 1798, 1377 CAS.
- L. Zhang and S. Granick, J. Chem. Phys., 2005, 123, 211104 CrossRef.
- C. Scomparin, S. Lecuyer, M. Ferreira, T. Charitat and B. Tinland, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 211 Search PubMed.
- S. Shenoy, R. Moldovan, J. Fitzpatrick, D. J. Vanderah, M. Deserno and M. Lösche, Soft Matter, 2010, 6, 1263 RSC.
- G. Blobel, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 1496 Search PubMed.
- P. W. Fowler, K. Balali-Mood, S. Deol, P. V. Coveney and M. S. P. Sansom, Biochemistry, 2007, 46, 3108 Search PubMed.
- D. Morozova, G. Guigas and M. Weiss, PLoS Comput. Biol., 2011, 7, e1002067 Search PubMed.
- E. P. Petrov, R. Petrosyan and P. Schwille, Soft Matter, 2012, 8, 7552 RSC.
- N. Oppenheimer and H. Diamant, Phys. Rev. Lett., 2011, 107, 258102 Search PubMed.
- S. J. Bussell, D. L. Koch and D. A. Hammer, Biophys. J., 1995, 68, 1836 Search PubMed.
-
H. Lodish, D. Baltimore, A. Berk, S. L. Zipursky, P. Matsudaira and J. Darnell, Molecular Cell Biology, Scientific American Books, New York, 3rd edn, 1995 Search PubMed.
- R. Cortez, SIAM J. Sci. Comput., 2001, 23, 1204 Search PubMed.
- R. Cortez, L. Fauci and A. Medovikov, Phys. Fluids, 2005, 17, 031504 Search PubMed.
- E. Evans and E. Sackmann, J. Fluid Mech., 1988, 194, 553 CrossRef.
- J. Knight, M. Lerner, J. Marcano-Velázquez, R. Pastor and J. Falke, Biophys. J., 2010, 99, 2879 CrossRef CAS.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover, 2005 Search PubMed.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1999 Search PubMed.
- Y. Han, A. Alsayed, M. Nobili, J. Zhang, T. Lubensky and A. Yodh, Science, 2006, 314, 626 CrossRef CAS.
- M. Makino and M. Doi, J. Phys. Soc. Jpn., 2004, 73, 2739–2745 Search PubMed.
- P. Saffman, J. Fluid Mech., 1976, 73, 593 CrossRef.
- D. K. Lubensky and R. E. Goldstein, Phys. Fluids, 1996, 8, 843 Search PubMed.
- A. J. Levine and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061606 CrossRef.
- N. Oppenheimer and H. Diamant, Biophys. J., 2009, 96, 3041 CrossRef CAS.
- A. J. Levine, T. B. Liverpool and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021503 CrossRef.
- A. J. Levine, T. B. Liverpool and F. C. MacKintosh, Phys. Rev. Lett., 2004, 93, 038102 CrossRef.
- J. McCammon and J. Deutch, Biopolymers, 1976, 15, 1397–1408 Search PubMed.
- E. Swanson, C. Teller and C. de Haën, J. Chem. Phys., 1978, 68, 5097–5102 Search PubMed.
- V. Bloomfield, W. Dalton and K. Van Holde, Biopolymers, 1967, 5, 135 CAS.
- P. Atzberger, J. Comput. Phys., 2011, 230, 2821 Search PubMed.
- J. G. de la Torre, G. del Rio Echenique and A. Ortega, J. Phys. Chem. B, 2007, 111, 955–961 CAS.
- R. Zwanzig, J. Kiefer and G. H. Weiss, Proc. Natl. Acad. Sci. U. S. A., 1968, 60, 381–386 Search PubMed.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- We found that using the power-law form originally suggested by Cortez led to systematic errors when comparing to the Evans–Sackmann results at large bsubstrate.
- Y. Saad and M. Schultz, SIAM J. Sci. Stat. Comput., 1986, 7, 856.
- B. Carrasco and J. García de la Torre, Biophys. J., 1999, 76, 3044 CrossRef CAS.
- H. A. Stone and A. Ajdari, J. Fluid Mech., 1998, 369, 151 Search PubMed.
- S. Aliaskarisohi, P. Tierno, P. Dhar, Z. Khattari, M. Blaszczynski and T. Fischer, J. Fluid Mech., 2010, 654, 417 Search PubMed.
- M. Henle and A. Levine, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011905 CrossRef.
- J. Leach, H. Mushfique, S. Keen, R. Di Leonardo, G. Ruocco, J. Cooper and M. Padgett, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 026301 CrossRef CAS.
- R. Macháň and M. Hof, Biochim. Biophys. Acta, 2010, 1798, 1377 CAS.
- M. Przybylo, J. Sỳkora, J. Humpolíčková, A. Benda, A. Zan and M. Hof, Langmuir, 2006, 22, 9096 CrossRef CAS.
- F. Harb, J. Sarkis, N. Ferte and B. Tinland, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 118 Search PubMed.
- U. Seifert and S. Langer, Europhys. Lett., 1993, 23, 71 CrossRef.
- E. Evans and A. Yeung, Chem. Phys. Lipids, 1994, 73, 39 CrossRef CAS.
- M. C. Watson and F. L. Brown, Biophys. J., 2010, 98, L9 CrossRef CAS.
- A.-F. Bitbol, J.-B. Fournier, M. I. Angelova and N. Puff, J. Phys.: Condens. Matter, 2011, 23, 284102 CrossRef.
- J. Fournier, N. Khalifat, N. Puff and M. Angelova, Phys. Rev. Lett., 2009, 102, 018102 CrossRef.
- F. L. Brown, Q. Rev. Biophys., 2011, 44, 391 Search PubMed.
- N. Oppenheimer and H. Diamant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041912 CrossRef.
- S. H. Khan, G. Matei, S. Patil and P. M. Hoffmann, Phys. Rev. Lett., 2010, 105, 106101 CrossRef.
- C. Xing and R. Faller, J. Phys. Chem. B, 2008, 112, 7086 CrossRef CAS.
- Y. Zhu and S. Granick, Phys. Rev. Lett., 2001, 87, 096104 CrossRef CAS.
- R. H. Coridan, N. W. Schmidt, G. H. Lai, P. Abbamonte and G. C. L. Wong, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031501 Search PubMed.
- U. Raviv, P. Laurat and J. Klein, Nature, 2001, 413, 51–54 CrossRef CAS.
- We note that at the nanometer length scales considered here, it is not obvious that the description of the sublayer as a fluid is even appropriate. However, in the limit of thin sublayers, the drag term K−(q) = −ηfqcoth(qH) is equivalent to a simple drag term appropriate to motion on a solid, K−(q) → −bsubstrate with bsubstrate = ηf/H.34.
- W. den Otter and S. Shkulipa, Biophys. J., 2007, 93, 423 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812 CrossRef CAS.
- B. A. Camley, C. Esposito, T. Baumgart and F. L. H. Brown, Biophys. J., 2010, 99, L44 CrossRef CAS.
- I. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873 CrossRef CAS.
- S. Ramachandran and S. Komura, J. Phys.: Condens. Matter, 2011, 23, 072205 Search PubMed.
- B. A. Camley and F. L. H. Brown, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021904 Search PubMed.
- S. Komura, S. Ramachandran and K. Seki, Europhys. Lett., 2012, 97, 68007 Search PubMed.
- T. Han and M. Haataja, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051903 Search PubMed.
- J. Ding, H. E. Warriner, J. A. Zasadzinski and D. K. Schwartz, Langmuir, 2002, 18, 2800 CrossRef CAS.
- P. Dhar, Y. Cao, T. M. Fischer and J. A. Zasadzinski, Phys. Rev. Lett., 2010, 104, 016001 CrossRef.
- M. H. Lee, D. H. Reich, K. J. Stebe and R. L. Leheny, Langmuir, 2010, 26, 2650 CrossRef CAS.
- K. Kim, S. Choi, J. Zasadzinski and T. Squires, Soft Matter, 2011, 7, 7782–7789 RSC.
- C. Peskin, Acta Numerica, 2002, 11, 1–39 Search PubMed.
- P. J. Atzberger, P. R. Kramer and C. S. Peskin, J. Comput. Phys., 2007, 224, 1255 CrossRef.
- A. J. Levine and T. C. Lubensky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041510 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = (D‖ + D⊥)/2 is the long-time translational diffusion coefficient of the object as it thermally moves while rotating.38,39 (Treating objects of lesser symmetry requires simple calculations to identify the center of mobility and the diagonal basis for the object's mobility matrix, which are not generally obvious by simple inspection.36,39)
= (D‖ + D⊥)/2 is the long-time translational diffusion coefficient of the object as it thermally moves while rotating.38,39 (Treating objects of lesser symmetry requires simple calculations to identify the center of mobility and the diagonal basis for the object's mobility matrix, which are not generally obvious by simple inspection.36,39)
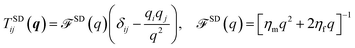
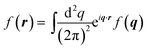 .
.
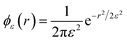 ↔
↔ ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε(q) = e−q2ε2/2 in this work.53 The regularized Green's function is
ε(q) = e−q2ε2/2 in this work.53 The regularized Green's function is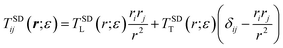 , (see Appendix A), with
, (see Appendix A), with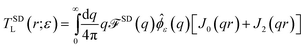
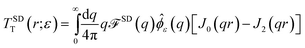
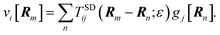



![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ES(q) = [ηmq2 + bsubstrate]−1
ES(q) = [ηmq2 + bsubstrate]−1![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) SD(q) in eqn (2). The Evans–Sackmann model neglects all viscous losses in the bulk fluid surrounding the membrane, but does include a phenomenological friction on the membrane via the coupling constant bsubstrate. (In our general model of Appendix A, this corresponds to the limit b → ∞, K+(q) = 0, K−(q) = −bsubstrate, and η+ = η− = ηm/2.) The analytic forms of the rotational and translational mobility for a cylinder of radius R in an Evans–Sackmann membrane are known,34
SD(q) in eqn (2). The Evans–Sackmann model neglects all viscous losses in the bulk fluid surrounding the membrane, but does include a phenomenological friction on the membrane via the coupling constant bsubstrate. (In our general model of Appendix A, this corresponds to the limit b → ∞, K+(q) = 0, K−(q) = −bsubstrate, and η+ = η− = ηm/2.) The analytic forms of the rotational and translational mobility for a cylinder of radius R in an Evans–Sackmann membrane are known,34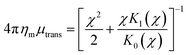
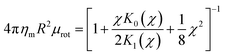

![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ), we find ηm = (1.76 ± 0.13) × 10−6 poise cm; for rotational diffusion, we find ηm = (1.28 ± 0.09) × 10−6 poise cm. See Appendix C for more details on the fitting.
), we find ηm = (1.76 ± 0.13) × 10−6 poise cm; for rotational diffusion, we find ηm = (1.28 ± 0.09) × 10−6 poise cm. See Appendix C for more details on the fitting.

![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) , diamonds, left panel) and rotational diffusion (Drot, squares, right panel) of diamond-shaped domains compared to RS calculations (lines). Translational diffusion parallel to the long axis (D‖, dashed line) is faster than the diffusion perpendicular to it (D⊥, dash-dot line);
, diamonds, left panel) and rotational diffusion (Drot, squares, right panel) of diamond-shaped domains compared to RS calculations (lines). Translational diffusion parallel to the long axis (D‖, dashed line) is faster than the diffusion perpendicular to it (D⊥, dash-dot line); ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) is the solid line. D⊥/D‖ ranges from 0.83 to 0.87 over the range of values shown, with the largest anisotropy for a ≫ LSD, as we would expect from ref. 44 and 45. Translational and rotational data are fit independently from one another and yield different values for ηm (see text).
is the solid line. D⊥/D‖ ranges from 0.83 to 0.87 over the range of values shown, with the largest anisotropy for a ≫ LSD, as we would expect from ref. 44 and 45. Translational and rotational data are fit independently from one another and yield different values for ηm (see text). 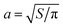 is the effective radius of the diamond, where S is the area of the domain. Inset: discretization of a diamond-shaped solid domain as a collection of blobs. A coarse discretization is shown; plotted results reflect the outcome of calculations involving thousands of blobs, extrapolated to infinite resolution.
is the effective radius of the diamond, where S is the area of the domain. Inset: discretization of a diamond-shaped solid domain as a collection of blobs. A coarse discretization is shown; plotted results reflect the outcome of calculations involving thousands of blobs, extrapolated to infinite resolution.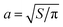 , where S is the area of the domain. With this assumption, they calculated ηm = (2.1 ± 0.1) × 10−6 poise cm and ηm = (2.3 ± 0.1) × 10−6 poise cm for translational and rotational measurements, respectively. These values are systematically higher than those found by the RS calculations. They also indicate a good correspondence between translation and rotation, whereas the RS results have a clear discrepancy. To the extent that the experiments correspond to a solid diamond in a SD membrane, the RS calculations are expected to be exact. The circular geometry assumed by PPS seems a reasonable, but somewhat uncontrolled approximation. Why then, should the more-correct RS calculation lead to inconsistent measurements of the viscosity from the translational and rotational diffusion coefficients? We suspect that the answer lies in the incompleteness of the model assumed for the membrane: there will be systematic deviations from the diffusion coefficients we predict, and they will affect rotation and translation differently. Both our RS calculations and SDHPW describe a perfectly flat membrane surrounded by a bulk fluid of infinite extent, while PPS observe a spherical vesicle pinned to a substrate. The substrate, vesicle geometry, and pinning will all change the diamond mobility.56–58 Translational mobility should be reduced more by these effects than rotational mobility, as the fluid flow around a translating object is longer-ranged than around a rotating one (see, e.g.ref. 59 in three dimensions). Also, if the diamond is distorted below the optical resolution (e.g. the tips of the solid domain have broken off) and thus has a smaller size or a different shape than that measured in ref. 28 and assumed here, we expect that the rotational mobility will increase more than the translational one. We have also performed RS calculations of diamonds with broken-off tips (data not shown); in these cases, the rotational diffusion coefficient increases more strongly than the translational one. It is common for rotational diffusion to depend more strongly on shape and size, e.g. a sphere with radius R in an infinite homogeneous 3D fluid has Dtrans ∼ 1/R but the rotational diffusion coefficient has a much stronger dependence on R: Drot ∼ 1/R3.36 This same pattern is evident in Fig. 5, where the rotational diffusion coefficient changes over two orders of magnitude while the translational one does not even change by a factor of 5. Both explanations are consistent with finding a larger effective viscosity for translational motion; more experiments are needed to distinguish between these two (or other) possibilities. The apparent inconsistency in ηm revealed by the RS calculations highlights the importance of this quantitative technique in the analysis of experimental data. Only with detailed calculations incorporating the proper domain shape was this apparent inconsistency discovered.
, where S is the area of the domain. With this assumption, they calculated ηm = (2.1 ± 0.1) × 10−6 poise cm and ηm = (2.3 ± 0.1) × 10−6 poise cm for translational and rotational measurements, respectively. These values are systematically higher than those found by the RS calculations. They also indicate a good correspondence between translation and rotation, whereas the RS results have a clear discrepancy. To the extent that the experiments correspond to a solid diamond in a SD membrane, the RS calculations are expected to be exact. The circular geometry assumed by PPS seems a reasonable, but somewhat uncontrolled approximation. Why then, should the more-correct RS calculation lead to inconsistent measurements of the viscosity from the translational and rotational diffusion coefficients? We suspect that the answer lies in the incompleteness of the model assumed for the membrane: there will be systematic deviations from the diffusion coefficients we predict, and they will affect rotation and translation differently. Both our RS calculations and SDHPW describe a perfectly flat membrane surrounded by a bulk fluid of infinite extent, while PPS observe a spherical vesicle pinned to a substrate. The substrate, vesicle geometry, and pinning will all change the diamond mobility.56–58 Translational mobility should be reduced more by these effects than rotational mobility, as the fluid flow around a translating object is longer-ranged than around a rotating one (see, e.g.ref. 59 in three dimensions). Also, if the diamond is distorted below the optical resolution (e.g. the tips of the solid domain have broken off) and thus has a smaller size or a different shape than that measured in ref. 28 and assumed here, we expect that the rotational mobility will increase more than the translational one. We have also performed RS calculations of diamonds with broken-off tips (data not shown); in these cases, the rotational diffusion coefficient increases more strongly than the translational one. It is common for rotational diffusion to depend more strongly on shape and size, e.g. a sphere with radius R in an infinite homogeneous 3D fluid has Dtrans ∼ 1/R but the rotational diffusion coefficient has a much stronger dependence on R: Drot ∼ 1/R3.36 This same pattern is evident in Fig. 5, where the rotational diffusion coefficient changes over two orders of magnitude while the translational one does not even change by a factor of 5. Both explanations are consistent with finding a larger effective viscosity for translational motion; more experiments are needed to distinguish between these two (or other) possibilities. The apparent inconsistency in ηm revealed by the RS calculations highlights the importance of this quantitative technique in the analysis of experimental data. Only with detailed calculations incorporating the proper domain shape was this apparent inconsistency discovered.![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) between the two leaflets.21–24,61,62 Extensions of SDHPW to include a solid wall exist,34,56 but treat the membrane as a single sheet. To quantitatively compare to supported experiments, it is essential to explicitly account for the two-layered structure of the membrane. A supporting surface breaks the mirror symmetry through the bilayer midplane. Though a single sheet description is equivalent to a bilayer description for freely suspended membranes with objects symmetrically spanning two identical monolayers (as in SDHPW), there is no clear justification for the single sheet approach in a supported geometry.
between the two leaflets.21–24,61,62 Extensions of SDHPW to include a solid wall exist,34,56 but treat the membrane as a single sheet. To quantitatively compare to supported experiments, it is essential to explicitly account for the two-layered structure of the membrane. A supporting surface breaks the mirror symmetry through the bilayer midplane. Though a single sheet description is equivalent to a bilayer description for freely suspended membranes with objects symmetrically spanning two identical monolayers (as in SDHPW), there is no clear justification for the single sheet approach in a supported geometry.

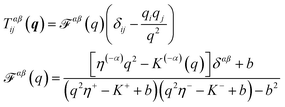
 v± = ∫d2r′K±(r − r′)v±(r′) is the traction from the fluid above (below) on the leaflet; see ref. 41 and 68. If a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq as in the free-membrane case; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 One may also include the presence of fixed obstacles through the presence of a “Brinkman equation”-like term, K(q) = −k.29,30 We also note that for a supported membrane in the limit of small H and large subfluid viscosity ηf, the result K(q) = −ηfqcoth(qH) approaches K(q) = −ηf/H, i.e. the drag force from the presence of a substrate is simply t = −bsubstratev, which would be a natural phenomenological guess for a membrane on a rough surface. We shall primarily focus on a supported membrane as illustrated in Fig. 6.
v± = ∫d2r′K±(r − r′)v±(r′) is the traction from the fluid above (below) on the leaflet; see ref. 41 and 68. If a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq as in the free-membrane case; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 One may also include the presence of fixed obstacles through the presence of a “Brinkman equation”-like term, K(q) = −k.29,30 We also note that for a supported membrane in the limit of small H and large subfluid viscosity ηf, the result K(q) = −ηfqcoth(qH) approaches K(q) = −ηf/H, i.e. the drag force from the presence of a substrate is simply t = −bsubstratev, which would be a natural phenomenological guess for a membrane on a rough surface. We shall primarily focus on a supported membrane as illustrated in Fig. 6.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) αβ reduces to [q2ηα − Kα(q)]−1δαβ, i.e. force on one leaflet does not affect the other. In the limit of b → ∞,
αβ reduces to [q2ηα − Kα(q)]−1δαβ, i.e. force on one leaflet does not affect the other. In the limit of b → ∞, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) αβ becomes [q2(η− + η+) − (K− + K+)]−1, i.e. the bilayer acts as a single sheet with effective viscosity η− + η+ affected by the fluid both above and below it. The Green's function for a SD membrane is recovered from eqn (11) if we let η± = ηm/2, K±(q) = −ηfq, and let b → ∞. Extension of the RS method to the Green's function of eqn (11) is straightforward; details are presented in Appendix A. This technique allows us to calculate mobilities of complex objects embedded in either bilayer leaflet, transmembrane proteins embedded in both, or more complex assemblies. We only address single-leaflet objects in this section.
αβ becomes [q2(η− + η+) − (K− + K+)]−1, i.e. the bilayer acts as a single sheet with effective viscosity η− + η+ affected by the fluid both above and below it. The Green's function for a SD membrane is recovered from eqn (11) if we let η± = ηm/2, K±(q) = −ηfq, and let b → ∞. Extension of the RS method to the Green's function of eqn (11) is straightforward; details are presented in Appendix A. This technique allows us to calculate mobilities of complex objects embedded in either bilayer leaflet, transmembrane proteins embedded in both, or more complex assemblies. We only address single-leaflet objects in this section.![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ± and Drot,± (Fig. 7). For sufficiently large interleaflet drag, b, the two leaflets become fully correlated, with no measurable discrepancy between “+” and “−”. For a freely suspended membrane (H → ∞), the ratio in diffusion coefficients between b = 0 and b → ∞ is exactly a factor of 2, as expected by symmetry considerations (twice SDHPW for b = 0 and exactly SDHPW for b → ∞). As the surface approaches the membrane, this ratio grows for the distal leaflet, but shrinks for the proximal leaflet.
± and Drot,± (Fig. 7). For sufficiently large interleaflet drag, b, the two leaflets become fully correlated, with no measurable discrepancy between “+” and “−”. For a freely suspended membrane (H → ∞), the ratio in diffusion coefficients between b = 0 and b → ∞ is exactly a factor of 2, as expected by symmetry considerations (twice SDHPW for b = 0 and exactly SDHPW for b → ∞). As the surface approaches the membrane, this ratio grows for the distal leaflet, but shrinks for the proximal leaflet.




![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) decreases to the free-draining limit Dmonomer/2 once the dimer reaches a separation of roughly 6 nm. This is consistent with the data of Knight et al., but we note that focus on
decreases to the free-draining limit Dmonomer/2 once the dimer reaches a separation of roughly 6 nm. This is consistent with the data of Knight et al., but we note that focus on ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) alone is somewhat misleading. Considered separately, the individual components of diffusion, D⊥ and D‖, clearly do display hydrodynamic correlations and it is a cancellation of effects between the two that leads to the apparent free-draining result for
alone is somewhat misleading. Considered separately, the individual components of diffusion, D⊥ and D‖, clearly do display hydrodynamic correlations and it is a cancellation of effects between the two that leads to the apparent free-draining result for ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) . Further, D⊥ actually decreases below the free-draining limit (Ddimer/Dmonomer = 1/2), and then increases to approach this limit at larger separations; for motions directed perpendicular to the dimer axis the assembly can diffuse more slowly than in the absence of hydrodynamic interactions. This is solely a consequence of the presence of the substrate, and we can gain some additional understanding of this by using the Kirkwood approximation37,44 to calculate the dimer mobility. This approach describes the effect of one monomer on the other by treating the protein-bound lipids as point forces and has been used to interpret molecular dynamics simulations (M. G. Lerner, personal communication and ref. 35). Within this approximation, the parallel and perpendicular mobilities of a dimer with two protein-bound lipids in the top leaflet separated by a fixed distance r are given by
. Further, D⊥ actually decreases below the free-draining limit (Ddimer/Dmonomer = 1/2), and then increases to approach this limit at larger separations; for motions directed perpendicular to the dimer axis the assembly can diffuse more slowly than in the absence of hydrodynamic interactions. This is solely a consequence of the presence of the substrate, and we can gain some additional understanding of this by using the Kirkwood approximation37,44 to calculate the dimer mobility. This approach describes the effect of one monomer on the other by treating the protein-bound lipids as point forces and has been used to interpret molecular dynamics simulations (M. G. Lerner, personal communication and ref. 35). Within this approximation, the parallel and perpendicular mobilities of a dimer with two protein-bound lipids in the top leaflet separated by a fixed distance r are given by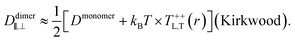

![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) dimer/Dmonomer decreases significantly slower with dimer separation, only reaching 0.6 at a separation of 9 nm. This shows the importance of the increased viscosity of the water beneath the membrane, which we expect will depend on the details of the SLB preparation. This suggests that the measurements of Knight et al.35 may be sensitive to substrate and preparation, as noted for lipid diffusion in Scomparin et al.23
dimer/Dmonomer decreases significantly slower with dimer separation, only reaching 0.6 at a separation of 9 nm. This shows the importance of the increased viscosity of the water beneath the membrane, which we expect will depend on the details of the SLB preparation. This suggests that the measurements of Knight et al.35 may be sensitive to substrate and preparation, as noted for lipid diffusion in Scomparin et al.23 v±, (4) the drag force between leaflets ∓b(v+ − v−), and (5) an applied force per unit area f±. We also require, unlike the original SL model, that the monolayers are incompressible, though this constraint can be relaxed.42,63
v±, (4) the drag force between leaflets ∓b(v+ − v−), and (5) an applied force per unit area f±. We also require, unlike the original SL model, that the monolayers are incompressible, though this constraint can be relaxed.42,63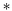 v± ∓ b(v+ − v−) = −f±
v± ∓ b(v+ − v−) = −f±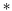 v± = ∫d2r′K±(r − r′)v±(r′) is the drag from the fluid surrounding the monolayer, and is usually described in terms of its Fourier transform, t±(q) = K±(q)v±(q). Our convention is K(q) = ∫d2re−iq·rK(r),
v± = ∫d2r′K±(r − r′)v±(r′) is the drag from the fluid surrounding the monolayer, and is usually described in terms of its Fourier transform, t±(q) = K±(q)v±(q). Our convention is K(q) = ∫d2re−iq·rK(r), 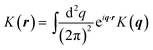 . The form of K±(q) will depend on the hydrodynamic environment of the leaflet; if a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 A common example is given in Fig. 6.
. The form of K±(q) will depend on the hydrodynamic environment of the leaflet; if a leaflet is adjacent to an infinite column of fluid with viscosity ηf, then K(q) = −ηfq; for a leaflet separated from a solid support by a distance H, K(q) = −ηfqcoth(qH).41 A common example is given in Fig. 6.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) ij(q) ≡ δij − qiqj/q2 to eqn (16), which allows us to write a matrix equation for v±(q) as a function of f±(q),
ij(q) ≡ δij − qiqj/q2 to eqn (16), which allows us to write a matrix equation for v±(q) as a function of f±(q),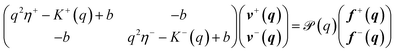
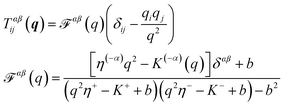
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε(q), by applying the convolution theorem to eqn (20). Because ϕε(r) is circularly symmetric, the tensor Tαβij(r;ε) can only be constructed out of r as
ε(q), by applying the convolution theorem to eqn (20). Because ϕε(r) is circularly symmetric, the tensor Tαβij(r;ε) can only be constructed out of r as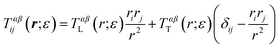
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) direction; then TαβL = Tαβxx and TαβT = Tαβyy. It is then easy to find
direction; then TαβL = Tαβxx and TαβT = Tαβyy. It is then easy to find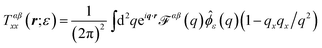
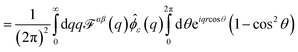
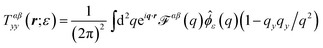
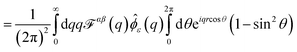
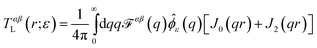
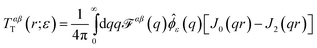
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ε.
ε.
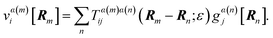
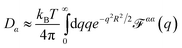
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) as a function of a, the effective size, with uncertainties δD. We perform weighted nonlinear least squares fitting with MATLAB's nlinfit to determine LSD and hence ηm. To determine the error in ηm, we perform a simple Monte Carlo estimation. We vary each measurement D by a normally distributed random variable with mean zero and standard deviation equal to its uncertainty δD, and determine the distribution of ηm; the values reported above are the mean value of ηm from this procedure, and the uncertainty is the standard deviation of the distribution of fit ηm.
as a function of a, the effective size, with uncertainties δD. We perform weighted nonlinear least squares fitting with MATLAB's nlinfit to determine LSD and hence ηm. To determine the error in ηm, we perform a simple Monte Carlo estimation. We vary each measurement D by a normally distributed random variable with mean zero and standard deviation equal to its uncertainty δD, and determine the distribution of ηm; the values reported above are the mean value of ηm from this procedure, and the uncertainty is the standard deviation of the distribution of fit ηm.
