 Open Access Article
Open Access ArticleMonitoring degradation of matrix metalloproteinases-cleavable PEG hydrogels via multiple particle tracking microrheology
Kelly M. Schultz and Kristi S. Anseth*
Department of Chemical and Biological Engineering, the BioFrontiers Institute and the Howard Hughes Medical Institute, University of Colorado at Boulder, Boulder, Colorado, USA. E-mail: Kristi.Anseth@colorado.edu; Tel: +1 303 4923147
First published on 7th December 2012
Abstract
The design of hydrogel matrices for cell encapsulation and tissue regeneration has become increasingly complex. Oftentimes, researchers seek to recapitulate specific biophysical and biochemical cues critical for the resident cell population and an in depth understanding of changes in the local microstructure and rheological properties of the synthetic matrix during enzymatic degradation would be extremely beneficial. Multiple particle tracking microrheology (MPT) enables simultaneous characterization of rheological properties and visualization of the microstructure in an evolving hydrogel scaffold. MPT measures the Brownian motion of fluorescently labeled probe particles embedded in the material, which is directly related to rheological properties using the Generalized Stokes–Einstein Relation (GSER). Here, we study a hydrogel scaffold consisting of a four-arm poly(ethylene glycol) (PEG) end functionalized with norbornene that is cross-linked with both a nondegradable PEG–dithiol and a matrix metalloproteinase (MMP) degradable peptide sequence (KCGPQG↓IWGQCK) using thiol–ene chemistry. The material degradation is measured as a function of time and extent of degradability, focusing on measuring the gel–sol transition. Using time–cure superposition, we determine the critical degradation time and critical extent of degradability for this specific gel formulation as tc = 1.85 h and pc = 0.589, respectively, and the critical relaxation exponent, n = 0.16. Finally, spatial information gained by MPT measurements quantifies the heterogeneity within the scaffold showing that these hydrogels degrade homogeneously when collagenase is introduced in solution at a concentration of 0.1–0.3 mg mL−1. Understanding the microstructural and rheological properties of a material near the gel–sol transition enables researchers to improve their insight as to how cells remodel their microenvironment when encapsulated in gels, and more precisely design and manipulate this parameter to improve three-dimensional culture systems.
Introduction
The development and engineering of synthetic hydrogel scaffolds have become more complex as researchers use both chemical and physical cues to recapitulate the native extracellular matrix.1–10 Using these scaffolds, cells are often encapsulated in three dimensions and basic cellular processes, such as migration and differentiation, are studied. Although it is generally appreciated that cells dynamically remodel and degrade the region directly around them, the pericellular region, measurements of dynamic rheological properties, even in the absence of cells, have proven to be difficult.10–12 Previous studies have focused on characterizing initial bulk material properties and qualitatively correlating this with cellular behavior.10,13–22 Similarly, degradation experiments have relied on measurements of mass loss and bulk rheological properties to understand the dissolution of the hydrogel scaffold.4,23–26,30–32To better understand the degradation and remodeling of a scaffold in the pericellular region, hydrogel scaffolds degraded in a controlled environment in the absence of cells can be informative. Previous bulk studies have accurately captured the initial degradation of the material, but cannot accurately measure the gel–sol transition.4,23–29 This transition is expected to be critical in understanding the degradation and remodeling of hydrogel networks by cell-secreted proteases, as cell motility and deposition of matrix molecules often coincide with this critical point.
The hydrogel system used in these investigations was formed using a radical mediated thiol–ene polymerization reaction.10,18,33,34 The scaffold consists of a four-arm poly(ethylene glycol) (PEG) molecule end functionalized with norbornene, which chemically cross-links with a nondegradable PEG–dithiol and matrix metalloproteinase (MMP) degradable peptide cross-linker. These step growth networks allow tailoring of the matrix connectivity and composition (e.g., peptide linker, extent of degradability) through the initial monomer composition, and both the time of degradation and overall degradability can be monitored as a function of exposure to appropriate enzymes.
In this work, we use multiple particle tracking microrheology (MPT) to measure enzymatic degradation of a PEG–norbornene hydrogel scaffold as a function of time and as the extent of degradability is varied (e.g., fraction of degradable cross-links). This technique enables the systematic characterization of material rheological properties and simultaneous visualization of the hydrogel microenvironment. In MPT, one micrometer fluorescently labeled probe particles were embedded into precursor solutions, and the Brownian motion of the particles was tracked. The Generalized Stokes–Einstein Relation (GSER) was used to directly relate movement of the probe particles to local hydrogel rheological properties.35–38 Due to the sensitivity of MPT in a low moduli, 10−3 to 4 Pa, and frequency range, 10−2 to 101 Hz, the critical transition from a gel to a sol can be precisely measured.35–40 This approach enables measurement of rheological properties during the critical gel–sol transition, defined as the degradation of the last sample spanning gel network, as a function of time and extent of degradability. These measurements were also used to characterize spatial heterogeneity within the material. Collectively, this work should expand the knowledge of properties of enzymatically degradable hydrogels and further improve strategies to characterize cell-mediated degradation within synthetic scaffolds.
Experimental methods
Hydrogel material synthesis and sample preparation
Hydrogels were synthesized using a thiol–ene photopolymerization to create covalently cross-linked and degradable PEG networks. Four-arm star PEG (Mn 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, JenKem, Inc.) macromolecules were end functionalized with norbornene (f = 4). The functionalization of the PEG molecule has been described previously.10,18,33,34 These molecules were reacted with a MMP degradable peptide (KCGPQG↓IWGQCK, Mn 1305 g mol−1, f = 2) or nondegradable, linear PEG dithiol (Mn 1500 g mol−1, f = 2, Sigma-Aldrich Co. LLC). The use of both of these molecules enabled the degree of degradation to be tailored within the network. The PEG–dithiol molecular weight was chosen due to its similarity in molecular weight compared to the MMP degradable peptide, enabling the structure and mesh size of the hydrogel to remain regular. The MMP degradable peptide sequence has a high degradability and is cleavable by both collagenase and MMPs secreted from cells, and has been widely used to encapsulate and culture cells in three-dimensions.10,41,42 An adhesion ligand, CGRGDS (Mn 594 g mol−1, f = 2), was also included in the hydrogel formulation as this promotes cell adhesion and motility for future investigations. The RGD (arginine-glycine-aspartic acid) sequence is chosen because it is known to bind to integrin receptors, promote adhesion to the extracellular matrix and is found in several adhesion proteins, including fibronectin.33 Finally, the monomer systems require a photoinitiator and initiating light source to induce photopolymerization. The initiator chosen was a highly water soluble initiator, lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP).43 To enable the measurement of material properties using passive microrheology, fluorescently labeled, carboxylated polystyrene probe particles (2a = 1.02 ± 0.03 μm, Polysciences, Inc.) were embedded into the macromolecular solution prior to gelation.
000 g mol−1, JenKem, Inc.) macromolecules were end functionalized with norbornene (f = 4). The functionalization of the PEG molecule has been described previously.10,18,33,34 These molecules were reacted with a MMP degradable peptide (KCGPQG↓IWGQCK, Mn 1305 g mol−1, f = 2) or nondegradable, linear PEG dithiol (Mn 1500 g mol−1, f = 2, Sigma-Aldrich Co. LLC). The use of both of these molecules enabled the degree of degradation to be tailored within the network. The PEG–dithiol molecular weight was chosen due to its similarity in molecular weight compared to the MMP degradable peptide, enabling the structure and mesh size of the hydrogel to remain regular. The MMP degradable peptide sequence has a high degradability and is cleavable by both collagenase and MMPs secreted from cells, and has been widely used to encapsulate and culture cells in three-dimensions.10,41,42 An adhesion ligand, CGRGDS (Mn 594 g mol−1, f = 2), was also included in the hydrogel formulation as this promotes cell adhesion and motility for future investigations. The RGD (arginine-glycine-aspartic acid) sequence is chosen because it is known to bind to integrin receptors, promote adhesion to the extracellular matrix and is found in several adhesion proteins, including fibronectin.33 Finally, the monomer systems require a photoinitiator and initiating light source to induce photopolymerization. The initiator chosen was a highly water soluble initiator, lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP).43 To enable the measurement of material properties using passive microrheology, fluorescently labeled, carboxylated polystyrene probe particles (2a = 1.02 ± 0.03 μm, Polysciences, Inc.) were embedded into the macromolecular solution prior to gelation.All hydrogel samples were polymerized at a PEG–norbornene concentration of 3 mM or 3.6 × 1017 -ene functional groups. The matrix connectivity is varied by changing the number of reacting thiol functional groups while keeping the concentration of -ene functional groups constant. Experiments were performed varying the thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) -ene at ratios of 0.55
-ene at ratios of 0.55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.85
1, 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. We define the variable R as the ratio of thiol
1. We define the variable R as the ratio of thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) -ene functional groups. The adhesion ligand, CGRGDS, and LAP concentration were kept constant at 1.5 mM and 1.7 mM, respectively. CGRGDS is covalently tethered to the hydrogel network but at this low concentration does not greatly affect the network connectivity or degradation. The final probe particle concentration in each hydrogel was approximately 0.04% solids per volume. All components of the hydrogel were dissolved in 1× Dulbecco's phosphate buffered saline (1× PBS, Life Technologies) prior to polymerization. Upon irradiation with visible and ultraviolet light (365–405 nm, 18 mW cm−2, 3 minutes), the alkene norbornene reacts with the thiol functionality at the end of the peptide or linear PEG molecules by a radical-mediated step-growth mechanism forming a chemically cross-linked network.10,18,33,34
-ene functional groups. The adhesion ligand, CGRGDS, and LAP concentration were kept constant at 1.5 mM and 1.7 mM, respectively. CGRGDS is covalently tethered to the hydrogel network but at this low concentration does not greatly affect the network connectivity or degradation. The final probe particle concentration in each hydrogel was approximately 0.04% solids per volume. All components of the hydrogel were dissolved in 1× Dulbecco's phosphate buffered saline (1× PBS, Life Technologies) prior to polymerization. Upon irradiation with visible and ultraviolet light (365–405 nm, 18 mW cm−2, 3 minutes), the alkene norbornene reacts with the thiol functionality at the end of the peptide or linear PEG molecules by a radical-mediated step-growth mechanism forming a chemically cross-linked network.10,18,33,34
Enzymatic degradation of hydrogels was carried out using a collagenase solution (Collagenase from Clostridium histolyticum, Sigma-Aldrich Co. LLC). Collagenase is a mixture of enzymes, mostly proteases, secreted from Clostridium histolyticum that degrade specific peptide sequences found at varying concentrations in collagen.44 Solid collagenase was dissolved in 1× PBS at concentrations of 0.1, 0.2 and 0.3 mg mL−1.
Device fabrication
Hydrogels were prepared in a glass-bottomed Petri dish (d = 35 mm, no. 1.5 glass coverslip, MatTek Corp.). A polydimethylsiloxane (PDMS, Dow Corning) chamber was created to immobilize the hydrogel as the extent of degradability was varied. This approach was necessary to ensure that the hydrogel did not move when the collagenase solution was added to the Petri dish. If the hydrogel was subjected to translation, MPT measurements of Brownian probe particle movement would be difficult. PDMS was cast in a Petri dish and cured using the manufacturer's instructions. The chamber that hydrogels were cured in were formed by cutting the PDMS sheet with two biopsy punches (Acuderm Inc.) creating a tube shape (O.D. 10 mm and I.D. 6 mm) (Fig. 1). | ||
| Fig. 1 Schematic of the sample chamber where hydrogels are degraded and MPT measurements are taken. | ||
Both the hydrogel and PDMS chamber were attached to a glass coverslip, previously functionalized with thiol using 3-mercaptopropyl triethoxysilane (Sigma-Aldrich Co. LLC), in the bottom of a Petri dish. The cured PDMS tube was chemically attached to the slide using a thin layer of uncured PDMS. The dish was then heated to 60 °C to increase the curing speed. After the PDMS was completely reacted, hydrogels were prepared in this device and attached to the thiol containing glass through reaction with free norbornene molecules at the bottom surface of the gel. The attachment of hydrogels to glass does not affect the extent of reaction of the hydrogel where MPT measurements are recorded, approximately 200 μm from the glass coverslip. Kinetically evolving hydrogels were not fabricated in the sample chamber but simply attached to the glass coverslip using the same chemistry. This was done to ensure that the material would be more homogeneously exposed to the enzyme, collagenase, and degrade homogeneously over a short time period.
Hydrogels were degraded in a concentrated collagenase solution as described above. The material properties of kinetically degrading samples were measured throughout the degradation reaction at 37 °C starting immediately after collagenase was introduced into the chamber. Data was collected for 30 s every 2.5 min throughout enzymatic degradation. For samples with the extent of degradability varied, each hydrogel was incubated in collagenase solutions for 12–24 h at 37 °C. The samples were removed from the incubator to collect data. All data was taken inside an environmental chamber held at 37 °C, which minimized the effect of temperature fluctuations on MPT measurements.
Multiple particle tracking microrheology
Multiple particle tracking microrheology was used to measure the properties of hydrogels near their gel–sol degradation transition. Multiple particle tracking microrheology is a passive microrheological techniques that measures the Brownian motion of probe particles within a material. Data were collected using an inverted microscope (Nikon TE2000E, Nikon Instruments Inc.). Probe particles were magnified 60× with a low numerical aperture objective (oil immersion objective, N. A. 1.4, 1× optovar, Nikon Instruments Inc.). Video microscopy was used to capture the movement of the probes particles and collected at 30 frames per s and an exposure time of 1000 μs (CMOS high-speed camera, Hi-Spec 3, 1024 × 1280 pixels, Fastec Imaging Corp.). These parameters were chosen to minimize static and dynamic particle tracking errors.38 Data were taken for gels with varying degradability at three different positions in each sample, and three separate samples were measured for each composition. This experimental design enables a quantitative comparison of the spatial heterogeneity in the material, such as differences in properties near the PDMS walls and in the center of the sample, and the consistency of rheological properties between gels.Particles were tracked using classic particle tracking algorithms.35,45 These algorithms identify the brightness-weighted centroid of each particle in each frame of the movie. These positions are then linked together into particle trajectories using a probability distribution function that accounts for the Brownian movement of a single particle.35
The ensemble-averaged mean-squared displacement (MSD), 〈Δr2(τ)〉, was calculated from particle trajectories. The MSD is calculated as a function of a lag time, τ, which is the separation time between images. The MSD can be directly related to rheological properties, such as the creep compliance J(t), by the GSER
 | (1) |
 , also indicates the state of the material, i.e. gel or sol. Brownian diffusion of probe particles in a viscous liquid is indicated by α = 1. A decrease in the slope indicates that the material being measured is a viscoelastic fluid. The state of a material is determined by whether the slope is greater than or less than n, the critical relaxation exponent.46–49 The critical scaling behavior near the critical sol–gel transition was first identified by Winter and Chambon.47,50–52 At the gel point the viscoelastic moduli of the gel exhibits power-law scaling with frequency, G′ ∼ G′′ ∼ ωn.47,50–52 The critical relaxation exponent also gives insight into the network connectivity of the gel. A high value of n (i.e., 0.5 < n < 1) indicates an open, loosely cross-linked gel network, while a low value of n (i.e., 0.1 < n < 0.5) is indicative of a densely cross-linked gel.47,52,53 When α < n the material is a viscoelastic solid, conversely, when α > n the sample is a viscoelastic fluid. As the measurement limit of MPT is approached, 4 Pa, α → 0 indicating that the material is a gel.40
, also indicates the state of the material, i.e. gel or sol. Brownian diffusion of probe particles in a viscous liquid is indicated by α = 1. A decrease in the slope indicates that the material being measured is a viscoelastic fluid. The state of a material is determined by whether the slope is greater than or less than n, the critical relaxation exponent.46–49 The critical scaling behavior near the critical sol–gel transition was first identified by Winter and Chambon.47,50–52 At the gel point the viscoelastic moduli of the gel exhibits power-law scaling with frequency, G′ ∼ G′′ ∼ ωn.47,50–52 The critical relaxation exponent also gives insight into the network connectivity of the gel. A high value of n (i.e., 0.5 < n < 1) indicates an open, loosely cross-linked gel network, while a low value of n (i.e., 0.1 < n < 0.5) is indicative of a densely cross-linked gel.47,52,53 When α < n the material is a viscoelastic solid, conversely, when α > n the sample is a viscoelastic fluid. As the measurement limit of MPT is approached, 4 Pa, α → 0 indicating that the material is a gel.40Bulk rheology
Gels were swollen in 1× PBS for several hours and then loaded onto a bulk rheometer (TA Instruments, Ares G2). 20 mm parallel plates were used to measure the initial swollen gel modulus at 37 °C using a frequency sweep between 0.1 and 10 Hz at an oscillatory stress of 0.2 Pa and a gap size between 200 and 300 μm. Measurements were taken in the linear viscoelastic response regime.Results and discussion
Hydrogel samples were polymerized at a constant ratio of thiol groups on the degradable peptide sequence or linear PEG to -ene functional groups on the four-arm PEG molecule. Three ratios were selected for these studies, R = 0.55, 0.85 and 1. The gels with the lowest cross-linking density, R = 0.55, were measured during enzymatic degradation as a function of time. This gel formulation is completely degradable (i.e., all multi-arm PEG molecules are cross-linked with MMP degradable peptides), and this formulation was chosen because it degrades over a relatively short period of time, 2.5 hours, at the collagenase concentrations employed, 0.2 mg mL−1.The remaining two hydrogel compositions, R = 0.85 and 1, were chosen to investigate the rheological differences between degradation of a more ideal, fully cross-linked network compared to a loosely cross-linked network that contains unreacted -enes as dangling ends. Due to the versatility of the thiol–ene chemistry, more than one type of cross-linker can be used in each gel sample, which enables the extent of degradability to be tailored by varying the concentration of MMP degradable peptide relative to non-degradable PEG dithiol cross-linkers. To quantify the critical transition of the degrading hydrogel system, the theoretical critical amount of cross-links needed to form a gel, pc, or the amount of non-degradable cross-links in the system was calculated from Flory–Stockmayer theory using the following equation
 | (2) |
 where n refers to the moles of the macromolecules.54–57 Flory–Stockmayer theory predicts gelation on a Bethe lattice and uses statistical methods to predict the critical gel–sol transition. The gel network is illustrated schematically in Fig. 2. The values that Flory–Stockmayer theory predicts for pc are 0.41, 0.53 and 0.57 for R = 0.55, 0.85 and 1, respectively. Experiments were designed such that the amount of nondegradable cross-links was varied near these values to better characterize the critical transition between the gel and sol.
where n refers to the moles of the macromolecules.54–57 Flory–Stockmayer theory predicts gelation on a Bethe lattice and uses statistical methods to predict the critical gel–sol transition. The gel network is illustrated schematically in Fig. 2. The values that Flory–Stockmayer theory predicts for pc are 0.41, 0.53 and 0.57 for R = 0.55, 0.85 and 1, respectively. Experiments were designed such that the amount of nondegradable cross-links was varied near these values to better characterize the critical transition between the gel and sol. | ||
Fig. 2 Hydrogel schematic of a thiol–ene hydrogel scaffold before and after it has been degraded. A four arm star PEG–norbornene molecule (Mn = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, n = 454) was irradiated with 365–405 nm light and cross-linked with PEG–dithiol (Mn = 1500 g mol−1, n = 34) and/or a MMP degradable peptide sequence (Mn = 1305 g mol−1, KCGPQG↓IWGQCK). The values of the required amount of cross-links to form a gel, pc, can be calculated from mean-field and Flory–Stockmayer theory. Values of pc calculated from Flory–Stockmayer theory for thiol 000 g mol−1, n = 454) was irradiated with 365–405 nm light and cross-linked with PEG–dithiol (Mn = 1500 g mol−1, n = 34) and/or a MMP degradable peptide sequence (Mn = 1305 g mol−1, KCGPQG↓IWGQCK). The values of the required amount of cross-links to form a gel, pc, can be calculated from mean-field and Flory–Stockmayer theory. Values of pc calculated from Flory–Stockmayer theory for thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) -ene, R, ratios used in experiments are reported. -ene, R, ratios used in experiments are reported. | ||
Hydrogels were degraded using three different concentrations of collagenase (0.1, 0.2 and 0.3 mg mL−1) in samples where the degree of degradability was controlled by the amount of MMP degradable peptide relative to nondegradable PEG dithiol. All measurements were collected after complete cleavage of the peptide, determined by no observable change in scaffold properties after several measurements were taken up to 48 hours. As expected, the extent of degradation in each sample was not affected by the concentration of collagenase, but the time to reach complete degradation depends significantly on this concentration.
Microrheological measurements were collected, as mentioned previously, in three different regions for each sample while the extent of gel degradation was varied. This approach quantifies spatial heterogeneity within the material. Since measurements were taken within a sample chamber, adequate time must be allowed for the collagenase to diffuse into the entire hydrogel and degrade the material. For example, using a collagenase concentration of 0.1 mg mL−1 causes complete cleavage of degradable cross-links in ∼48 hours, while using 0.3 mg mL−1 degrades the peptide cross-links in ∼24 hours. The kinetics of the degradation reaction are not diffusion limited in the hydrogel system. The approximate diffusivity, calculated using the Stokes–Einstein equation, for collagenase with a hydrodynamic radius of 4.4 nm is D = 7.4 × 10−7 cm2 s−1.58,59 This leads to a protein diffusion time, tD, of approximately 1.5 h using the equation  , where L is the thickness of the hydrogel sample.59 These results indicate that the degradation times required to fully degrade each hydrogel are much longer than the time scale required for enzymes to diffuse into the network, indicating that diffusion into the network is not limiting enzymatic degradation.
, where L is the thickness of the hydrogel sample.59 These results indicate that the degradation times required to fully degrade each hydrogel are much longer than the time scale required for enzymes to diffuse into the network, indicating that diffusion into the network is not limiting enzymatic degradation.
The logarithmic slope of the mean-squared displacement enables the state of the material to be identified as the time after the initiation of degradation and the extent of degradability is varied. In Fig. 3a, degradation of a loosely cross-linked hydrogel (R = 0.55) was monitored through time. Initially, the probe particles were completely arrested within the material. The probe particles then exhibit directed motion, due to equilibrium swelling of the hydrogel network. Once the hydrogel was equilibrated, there was no measurable movement of the probe particles until ∼1.75 h. At this point, a steady increase in the movement of the particles was measured. This particle movement correlates to a decrease in the network cross-linking density and elasticity of the gel and, finally, the transition to a sol. This plot represents typical data that was collected as a function of enzymatic degradation of the various gel formulations.
 | ||
Fig. 3 Logarithmic slope,  , of mean-squared displacement for degradable PEG–norbornene hydrogels. (a) Degradation of a completely degradable hydrogel with a composition of R = 0.55 using 0.2 mg mL−1 of collagenase through time. (b) Degradation of hydrogels with varying extents of degradation before (open symbols) and after degradation of the peptide cross-links (closed symbols) for R = 0.85 (diamonds) and R = 1 (circles) with 0.1 and 0.3 mg mL−1 collagenase. Dashed vertical lines represent the Flory–Stockmayer theory predictions for the gel–sol transition. Solid curves have been added to guide the eye. , of mean-squared displacement for degradable PEG–norbornene hydrogels. (a) Degradation of a completely degradable hydrogel with a composition of R = 0.55 using 0.2 mg mL−1 of collagenase through time. (b) Degradation of hydrogels with varying extents of degradation before (open symbols) and after degradation of the peptide cross-links (closed symbols) for R = 0.85 (diamonds) and R = 1 (circles) with 0.1 and 0.3 mg mL−1 collagenase. Dashed vertical lines represent the Flory–Stockmayer theory predictions for the gel–sol transition. Solid curves have been added to guide the eye. | ||
The second experiment, shown in Fig. 3b, measures the mean-squared displacement of particles in hydrogels while varying the extent of degradation. In these experiments, hydrogels were prepared with R = 0.85 and 1, varying the amount of nondegradable cross-links, p, and were degraded with 0.1 and 0.3 mg mL−1 of collagenase. The material properties were measured using MPT before and after complete degradation of the peptide cross-links, (1 − p). As the fraction of nondegradable cross-links, p, was increased in the material, p = 0.49–0.69 for R = 0.85 and p = 0.52–0.72 for R = 1, a corresponding decrease in the logarithmic slope, α, of the MSD was measured indicating an increase in the structure of the hydrogel. Scatter is observed in this data due to the inherent drift in the samples that is decreased by the device that hydrogels were degraded in and corrected for during analyses. Also, a contributor to this scatter is the inherent error in sample preparation as slight variation in the stoichiometry of the functional group concentrations in the initial gel formulations influences the accuracy of p.
The dashed vertical lines in Fig. 3b represent the prediction of pc from Flory–Stockmayer theory for the two gel formulations studied, R = 0.85 and 1. The logarithmic slope of the MSD starts to decrease as the ratio of degradable to nondegradable cross-links in the gel approaches the value of pc. This observation indicates that more of a network structure remains in these samples after enzymatic degradation and shows good agreement with theory. By changing the structure of the starting hydrogel material, by R or the maximum cross-link density, we measure a decrease in degradation at a lower value of p when hydrogels have an overall lower cross-link density (R = 0.85). The curves measured for the material degradation shows a nonlinear dependence on the fraction of nondegradable cross-links and the value of α, which is the slope of the mean-squared displacement. It is expected that as the degradability of the material is increased there will be a larger decrease in the elastic properties of the hydrogel, and this prediction is reflected in the values of α measured using MPT. This observation is illustrated in Fig. 3b by the solid curves added to guide the eye. Flory–Stockmayer theory predicts that the value of pc is proportional to  , which is also in agreement with the microrheological measurements.
, which is also in agreement with the microrheological measurements.
Heterogeneity within the material during degradation was also of great interest, especially when using these materials as scaffolds for cell encapsulation (e.g., to study motility).10,11 The variation in the network microstructure that cells experience can change the motility or migration direction or even influence deformation under load.10,28 In depth knowledge of these effects may enable a priori engineering of microenvironments to direct critical cellular functions. The microrheological measurements of this material use optical techniques to capture the Brownian motion of the probe particles. Such optical techniques afford the benefit of capturing spatial heterogeneity within the microenvironment by creating visual images of the movement of embedded probe particles.
By tracking the movement of probe particles, we can visualize the microstructure of the gel network with trajectory maps. These maps trace the movement of probe particles throughout a 30 s movie in the x–y plane. Using statistical tests, specifically an F-test, the displacement of each particle is compared and determined if it is statistically different using a 95% confidence interval.60 These particle tracks were clustered into two groups and color coded to visually indicate the degree of spatial heterogeneity that occurs during degradation within the material microenvironments. Fig. 4 show the results for R = 1 samples as the amount of nondegradable cross-links is increased beyond the predicted value of pc = 0.57. The colors on these trajectory maps are not indicative of the magnitude of the displacement between each sample, but the color indicates whether the displacement is statistically different from the first particle tracked, which is arbitrarily assigned by tracking algorithms. In these four distinct microenvironments, there is very minimal spatial heterogeneity, <20% of particle displacement is statistically significant from the first tracked particle indicating that they are experiencing a different microenvironment. The largest amount of heterogeneity is observed in p = 0.58, when 16% of the particles are experiencing a significantly different microenvironment, a sample that Flory–Stockmayer predicts is a loosely cross-linked network very close to the reverse gel point.
Similarly, heterogeneity can be quantified by calculating an ensemble-averaged van Hove correlation function at a given lag time, τ.60,61 Ensemble-averaged van Hove correlation functions, calculated at τ = 0.1 s, are fit with Gaussian distributions. The agreement with this distribution is a strong indication of the homogeneity of a material. If probe particles are diffusing isotropically and experiencing the same microenvironment, then each probe particle movement will display Gaussian dynamics. Therefore, if the ensemble-averaged displacement also displays Gaussian behavior, this is a strong indication that the material is homogeneous.60,61 Gaussian fits to data describe the movement of probe particles in one dimension by a random walk.60,61
 | (3) |
 can be determined from the width of the distribution.
can be determined from the width of the distribution.Ensemble-averaged van Hove correlation functions were calculated for these degrading hydrogel materials at the initial state and after enzymatic degradation, Fig. 5. Fig. 5a shows the distributions prior to degradation. By changing the fraction of non-degradable cross-links, from p = 0.52 to 0.59, no change in the displacement is observed supporting the conclusion that the initial networks are very similar in structure. All functions have a small width, an indication that there is very little movement of the probe particles in the hydrogel matrix, implying that this is a tightly cross-linked network structure. Fig. 5b is a graph of the van Hove correlation functions after degradation. The width of the distributions increases up to a value of p = 0.59, slightly higher than the Flory–Stockmayer prediction of pc = 0.57. Above the value of p = 0.59, all van Hove correlation functions show little to no particle movement, indicating that these samples remain gels. As the amount of nondegradable cross-links was increased in the hydrogel samples, we observed a narrowing of the distribution functions until the gel–sol transition was reached. After the predicted gel–sol transition, at p = 0.58, the distribution widened indicating that the probe particle movement has increased. At this value of p, the material is predicted to have its last sample spanning hydrogel cluster and the porosity of the material has reached a maximum. The increase in the particle movement may be due to unique flows within the sample due to the porosity of the hydrogel material and the diffusivity and solubilization of large polymer clusters. This is a reproducible effect that was observed in all experiments when the PEG–norbornene hydrogel was degraded at a composition near the gel–sol transition. All ensemble-averaged van Hove correlation functions fit well with Gaussian distributions. Both the statistical cluster of the particle displacements and the agreement of van Hove correlation functions with Gaussian distributions support the conclusion that this hydrogel scaffold degrades homogeneously in the presence of collagenase.
 | ||
| Fig. 4 Trajectories maps of probe particle movement in hydrogels with R = 1 as the extent of nondegradable polymers is increased from p = 0.52–0.63. Probe particles are colored coded into two clusters using an F test that determines whether their displacement is statistically significant using a 95% confidence interval. | ||
The measured MSD of material degradation, both through time and extent of degradation, was further analyzed using time–cure superposition to extract the critical degradation time, tc, and critical fraction of nondegradable cross-linker, pc, at the gel point. Time–cure superposition is the superposition of viscoelastic functions at different extents of reaction.12,40,46,47,49,62,63 This superposition is similar to time–temperature superposition, except this technique describes changes in connectivity instead of friction.49 At the critical transition, the correlation length of connectivity diverges and leads to dynamic behavior that has no analogue in critical thermodynamic transitions, such as the previously well described second-order phase transition. This superposition technique describes the dynamics of both the sol, gel and the entire relaxation modulus and is valid in the critical gel–sol regime.49 The self-similar shape of the MSD curves at the shortest lag time, Fig. 6a, enables the empirical shifting into pre- and postgel master curves, Fig. 6b. The references used for the master curves were the most degraded, liquid-like MSD measured to shift all the pre-gel curves and the MSD in the initial gel to shift all of the post-gel curves. Where the pre- and postgel master curves intersect is the critical extent and time of reaction, pc and tc, respectively, and the slope at this intersection is the critical relaxation exponent, n.12,40,46,47,49,62,63
 | ||
| Fig. 5 Ensemble-averaged van Hove correlation functions for PEG–norbornene hydrogels made with R = 1 and varying the amount of nondegradable cross-links, p, relative to the peptide cross-linker (a) prior to degradation and (b) after the material has been degraded with 0.3 mg mL−1 collagenase for 24 h. | ||
This analysis is only possible when the measured MSD display curvature at the shortest lag times, indicating that the measurements have captured the longest relaxation time of the polymers and networks in the sol and gel.40,49,51 MSD curves were shifted using a time shift factor, a, and MSD shift factor, b. These shift factors represent the critical scaling of the extent of degradation, p. The time shift factor relates the longest relaxation time of the polymer to the distance away from the critical extent of degradation, ε, by the scaling exponent, y, a ∼ εy, where ε is defined as ε = ∣p − pc∣/pc. Similarly, the MSD shift, b, factor relates the distance away from the critical extent of degradation to the equilibrium compliance by the scaling exponent z, b ∼ εz.12,40,46,47,49,62,63 The shift factors rapidly decrease at the critical extent of degradation, due to the divergence of the longest relaxation time and equilibrium compliance at the gel–sol transition.12
To demonstrate this analysis, the degradation of a loosely cross-linked PEG–norbornene hydrogel, R = 0.55, was tracked through time. The material degrades over a period of 2.5 h at a collagenase concentration of 0.2 mg mL−1 and a temperature of 37 °C. Initially, the hydrogel material swells showing drift of the probe particles. Once the material equilibrates, in approximately 0.43 h, the degradation reaction is captured, this is shown in Fig. 3a. For this analysis, time is assumed to be directly proportional to the extent of degradation. MPT measurements were collected for 30 s every 2.5 min throughout enzymatic degradation of the hydrogel, Fig. 6a. This time period is small compared to the overall time of degradation, 2.5 h; therefore, each measurement was assumed to be at a quasi-steady state of the material. After MSD curves were shifted on the time and MSD axes, gel and sol master curves were created, Fig. 6b. The critical degradation time, when the last sample spanning cluster degrades, occurs at tc = 1.85 h. As shown in Fig. 6c, the shift factors for the sol and gel diverge at this value of tc, which correlates to the divergence in the viscosity for the sol and equilibrium moduli for the gel. Fitting the shift factors enables the determination of the critical relaxation exponent, n = 0.16 ± 0.03, Fig. 6d. The error in the value of n is calculated by propagating errors in the fitting of the critical scaling exponents, y and z. This value is well below the value that describes a percolation type reaction, n = 0.5.64,65 A low value of n, like that measured here, indicates a densely cross-lined network.50,51,53,64
Similarly, time–cure superposition is used to analyze the properties of this hydrogel scaffold as the extent of degradability is varied by changing the amount of degradable cross-links in the network. The critical relaxation exponent is n = 0.25 ± 0.16 which is within the range of reported values of n = 0.1–0.9 and agrees with the value of n determined from degradation measurements as a function of time.49,64,66 The critical fraction of nondegradable cross-linkers needed to form a gel is calculated to be pc = 0.589. This agrees well with the value predicted from Flory–Stockmayer theory, pc = 0.57.54–56 The critical relaxation exponent is a material property and should be constant for this hydrogel network, which is measured.46
As a general approach, the entire degradation reaction, from the initial material properties to the gel–sol transition, was modeled using Michaelis–Menton enzymatic kinetics.67–69 As mentioned previously, this reaction is dominated by enzymatic degradation of the peptide bonds and is not limited by the diffusion of the enzymes into the hydrogel scaffold. The reaction equations used to describe the enzymatic degradation of this hydrogel system include the enzymatic cleavage of the MMP degradable peptide and the deactivation equation for collagenase.67 The deactivation of the collagenase was assumed to be a first-order decay described by
 | (4) |
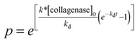 | (5) |
 .42,67 To relate the kinetics of degradation to rheological properties, the relation from time–cure superposition is used
.42,67 To relate the kinetics of degradation to rheological properties, the relation from time–cure superposition is used | (6) |
In the postgel regime,  where Ge is the equilibrium modulus of the material.40,49 The final model equation used to fit the data is
where Ge is the equilibrium modulus of the material.40,49 The final model equation used to fit the data is
 | (7) |
The fit of this model to measurements of gels where degradability is varied is shown in Fig. 7, the value of k* was found to be 2100 ± 70 M−1 s−1. This value falls within the range of previously measured data for degradation of this peptide sequence (GPQG↓IWGQ) with pure MMPs, 50–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 s−1.42 Collagenase is a mixture of enzymes, including proteases, secreted from Clostridium histolyticum,44 and we expect that the value of k* to be within the reported range. This model was also fit to the degradation of PEG–norbornene measured through time (data not shown). In this case, the value of k* fit from the model was 500 ± 22 M−1 s−1, also well within the previously measured range for this constant.42 The model describes the entire degradation reaction from the initial conditions, measured from bulk rheology, to the gel–sol transition, measured using microrheology. We have shown that kinetic constants can be predicted from mechanical measurements leading to the possibility of generalization to link other important properties in cross-linked networks.
000 M−1 s−1.42 Collagenase is a mixture of enzymes, including proteases, secreted from Clostridium histolyticum,44 and we expect that the value of k* to be within the reported range. This model was also fit to the degradation of PEG–norbornene measured through time (data not shown). In this case, the value of k* fit from the model was 500 ± 22 M−1 s−1, also well within the previously measured range for this constant.42 The model describes the entire degradation reaction from the initial conditions, measured from bulk rheology, to the gel–sol transition, measured using microrheology. We have shown that kinetic constants can be predicted from mechanical measurements leading to the possibility of generalization to link other important properties in cross-linked networks.
 | ||
| Fig. 6 Time–cure superposition of the degradation reaction of a hydrogel scaffold with R = 0.55 degraded with 0.2 mg mL−1 collagenase at 37 °C throughout time. (a) Initial measured mean-squared displacements that were (b) shifted into sol and gel master curves using time–cure superposition. (c) The shift factors diverged at the critical degradation time, tc and (d) were fit to calculate the critical scaling exponents, y and z, and critical relaxation exponent, n. | ||
Conclusions
A four-arm photopolymerizable PEG–norbornene hydrogel scaffold was characterized using MPT to capture the microstructure and material properties during enzymatic degradation, specifically at the critical gel–sol transition. The stiffness of the hydrogel and connectivity were varied by changing the ratio of thiol to -ene groups, R, and the amount of degradable cross-links in the hydrogel scaffold. Enzymatic degradation of this hydrogel matrix was characterized under conditions that did not limit diffusion of enzymes; therefore, all measurements reflect the cleavage of the degradable peptide sequences by enzymes. Time dependent measurements of the most loosely cross-linked hydrogel matrix, R = 0.55, showed complete enzymatic degradation over 2.5 h. Varying the degradability around the predicted fraction of nondegradable cross-links from Flory–Stockmayer theory also showed a decrease in degradation near the predicted values.Visualization of the microstructure using the trajectories of probe particles within each movie showed spatial homogeneity around the critical transition. This was confirmed by clustering the displacement of the particles into two groups using an F-test and 95% confidence interval. By use of an ensemble-averaged van Hove correlation function, the hydrogel average probe particle displacement displayed Gaussian dynamics, indicating quantitatively that the particles were experiencing the same microenvironment.
The critical scaling exponents, critical relaxation exponent and critical degradation time and degradability were determined from time–cure superposition. The critical relaxation exponent for a PEG–norbornene hydrogel with a cross-linker of 1500 g mol−1 is 0.16, measured from both degradation throughout time and as the extent of degradability was controlled. The critical degradation time and extent of degradation were calculated to be, tc = 1.85 h and pc = 0.589, respectively. A model was developed for enzymatic degradation using Michaelis–Menton kinetics, fitting for one parameter k* = kcat/KM. Using this model and fitting to rheological data changing the amount of degradable cross-links and monitoring degradation through time gave values within the range reported for this peptide.
 | ||
| Fig. 7 Measurement and theoretical modeling for enzymatic degradation of PEG–norbonene hydrogels, R = 1, at 37 °C with 0.2 mg mL−1 of collagenase as the degradability of the hydrogels is varied. | ||
Finally, measuring enzymatic hydrogel degradation will enable a better understanding of more complex degrading microenvironments, such as cell-laden hydrogels. In these microenvironments, the degradation will not be homogeneous since enzymes will be released from a point source, a cell, within the matrix. This study will allow us to better characterize the state of the material, i.e. sol or gel, immediately around a migrating cell, enabling more sophisticated studies of motility of cells encapsulated within a 3D scaffold and more precise engineering of material microenvironments that can be used to promote and direct cell migration.
Acknowledgements
Funding for this work was provided by Howard Hughes Medical Institute and the National Science Foundation (CTS 1236662). The authors would like to acknowledge Prof. Matthew Liberatore at the Department of Chemical and Biological Engineering at the Colorado School of Mines for assistance in rheology experiments and use of equipment.References
- A. J. Engler, S. Sen, H. Lee Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS.
- D. E. Discher, P. Jamney and Y.-l. Wang, Science, 2005, 310, 1139–1143 CrossRef CAS.
- M. L. Gardel, M. T. Valentine and D. A. Weitz, Microscale Diagnostic Techniques, Springer, 2005 Search PubMed.
- A. M. Kloxin, C. J. Kloxin, C. N. Bowman and K. S. Anseth, Adv. Mater., 2010, 22, 3484–3494 CrossRef CAS.
- T. Nie, A. Baldwin, N. Yamaguchi and K. L. Kiick, J. Controlled Release, 2007, 122, 287–296 CrossRef CAS.
- B. L. Seal and A. Panitch, Macromolecules, 2006, 39, 2268–2274 CrossRef CAS.
- T. Nie, R. E. Akins Jr and K. L. Kiick, Acta Biomater., 2009, 5, 865–875 CrossRef CAS.
- K. L. Kiick, Soft Matter, 2008, 4, 29–37 RSC.
- S. E. Sakiyama-Elbert and J. A. Hubbell, J. Controlled Release, 2000, 65, 389–402 CrossRef CAS.
- M. P. Schwartz, B. D. Fairbanks, R. E. Rogers, R. Rangarajan, M. H. Zaman and K. S. Anseth, Integr. Biol., 2010, 2, 32–40 RSC.
- R. J. Bloom, J. P. George, A. Celedon, S. X. Sun and D. Wirtz, Biophys. J., 2008, 95, 4077–4088 CrossRef CAS.
- K. M. Schultz and E. M. Furst, Soft Matter, 2012, 8, 6198–6205 RSC.
- D. T. Tambe, C. C. Hardin, T. E. Angelini, K. Rajendran, C. Y. Park, X. Serra-Picamal, E. H. Zhou, M. H. Zaman, J. P. Butler, D. A. Weitz, J. J. Fredberg and X. Trepat, Nat. Mater., 2011, 10, 469–475 CrossRef CAS.
- P. A. Janmey and D. A. Weitz, Trends Biochem. Sci., 2004, 29, 364–370 CrossRef CAS.
- Z. Liu, J. L. Tan, D. M. Cohen, M. T. Yang, N. J. Sniadecki, S. A. Ruiz, C. M. Nelson and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9944–9949 CrossRef CAS.
- J. L. West and J. A. Hubbell, Macromolecules, 1999, 32, 241–244 CrossRef CAS.
- M. P. Lutolf, J. L. Lauer-Fields, H. G. Schoekel, A. T. Metters, F. E. Weber, G. B. Fields and J. A. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5413–5418 CrossRef CAS.
- B. D. Fairbanks, M. P. Schwartz, A. E. Halevi, C. R. Nuttelman, C. N. Bowman and K. S. Anseth, Adv. Mater., 2009, 10, 3114–3121 Search PubMed.
- G. P. Raeber, M. P. Lutolf and J. A. Hubbell, Acta Biomater., 2007, 3, 615–629 CrossRef CAS.
- G. P. Raeber, M. P. Lutolf and J. A. Hubbell, Biophys. J., 2005, 89, 1374–1388 CrossRef CAS.
- M. P. Lutolf, F. E. Weber, H. G. Schmoekel, J. C. Schense, T. Kohler, R. Muller and J. A. Hubbell, Nat. Biotechnol., 2003, 21, 513–518 CrossRef CAS.
- J. A. Benton, B. D. Fairbanks and K. S. Anseth, Biomaterials, 2009, 30, 6593–6603 CrossRef CAS.
- A. T. Metters, C. N. Bowman and K. S. Anseth, J. Phys. Chem. B, 2000, 104, 7043–7049 CrossRef CAS.
- M. A. Rice and K. S. Anseth, J. Biomed. Mater. Res., Part A, 2004, 70, 560–568 Search PubMed.
- A. T. Metters, K. S. Anseth and C. N. Bowman, J. Phys. Chem. B, 2001, 105, 8069–08076 CrossRef CAS.
- P. Martens, A. T. Metters, K. S. Anseth and C. N. Bowman, J. Phys. Chem. B, 2001, 105, 5131–5138 CrossRef CAS.
- D. S. W. Benoit, A. R. Durney and K. S. Anseth, Tissue Eng., 2006, 12, 1663–1673 CrossRef CAS.
- S. J. Bryant and K. S. Anseth, J. Biomed. Mater. Res., 2002, 59, 63–72 CrossRef CAS.
- S. J. Bryant and K. S. Anseth, J. Biomed. Mater. Res., Part A, 2003, 64, 70–79 Search PubMed.
- A. T. Metter, K. S. Anseth and C. N. Bowman, Polymer, 2000, 41, 3993–4004 CrossRef.
- S. H. Lee, J. J. Moon, J. S. Miller and J. L. West, Biomaterials, 2007, 28, 3163–3170 CrossRef CAS.
- H. J. Kong, C. J. Kim, N. Huebsch, D. A. Weitz and D. J. Mooney, J. Am. Chem. Soc., 2007, 129, 4518–4519 CrossRef CAS.
- C. R. Nuttelman, M. C. Tripodi and K. S. Anseth, Matrix Biol., 2005, 24, 208–218 CrossRef CAS.
- A. A. Aimetti, A. J. Machen and K. S. Anseth, Biomaterials, 2009, 30, 6048–6054 CrossRef CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285 CrossRef CAS.
- T. G. Mason, Rheol. Acta, 2000, 39, 371–378 CrossRef CAS.
- T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623–638 CrossRef CAS.
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685–742 CrossRef.
- K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, ACS Macro Lett., 2012, 1, 706–708 CrossRef CAS.
- A. S. Gobin and J. L. West, FASEB J, 2002, 16, 751–753 CAS.
- J. Patterson and J. A. Hubbell, Biomaterials, 2010, 31, 7836–7845 CrossRef CAS.
- B. D. Fairbanks, M. P. Schwartz, C. N. Bowman and K. S. Anseth, Biomaterials, 2009, 30, 6702–6707 CrossRef CAS.
- Sigma-Aldrich, Product information for Collagenase from Clostrdium histolyticum, Sigma-aldrich technical report, 2012 Search PubMed.
- J. C. Crocker and E. R. Weeks, http://www.physics.emory.edu/%E2%88%BCweeks/idl/index.html, 2011.
- K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, Macromolecules, 2009, 42, 5310–5316 CrossRef CAS.
- T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001 CrossRef.
- H. H. Winter, Polym. Eng. Sci., 1987, 27, 1698–1702 CAS.
- D. Adolf and J. E. Martin, Macromolecules, 1990, 23, 3700–3704 CrossRef CAS.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697 CrossRef CAS.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- T. H. Larsen, Ph.D. thesis, University of Delaware, 2008.
- J. C. Scanlan and H. H. Winter, Macromolecules, 1991, 24, 47–54 CrossRef CAS.
- P. J. Flory, J. Am. Chem. Soc., 1941, 63, 3083–3090 CrossRef CAS.
- P. J. Flory, J. Phys. Chem., 1942, 46, 132–140 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45–55 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 1st edn, 2003 Search PubMed.
- N. Ohbayashi, N. Yamagata, G. Masafumi, K. Watanabe, Y. Yamagata and K. Murayama, Appl. Environ. Microbiol., 2012 DOI:10.1128/AEM.00808-12.
- L. M. Weber, C. G. Lopez and K. S. Anseth, J. Biomed. Mater. Res., Part A, 2009, 90, 720–729 CrossRef.
- M. T. Valentine, P. D. Kaplan, J. C. Crocker, T. Gisler, R. K. Prud'homme, M. Beck and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061506 CrossRef CAS.
- J. P. Rich, G. McKinley and P. S. Doyle, J. Rheol., 2011, 55, 273–299 CrossRef CAS.
- A. M. Corrigan and A. M. Donald, Langmuir, 2009, 25, 8599–8605 CrossRef CAS.
- A. M. Corrigan and A. M. Donald, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 457–462 CrossRef CAS.
- D. Stauffer, A. Coniglio and M. Adam, Adv. Polym. Sci., 1982, 44, 103–158 CrossRef CAS.
- M. Daoud, Le Journal de Physiques, 1979, 40, 201–205 CrossRef CAS.
- J. E. Martin, D. Adolf and J. P. Wilcoxon, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 1325–1332 CrossRef CAS.
- M. A. Rice, J. Sanchez-Adams and K. S. Anseth, Biomacromolecules, 2006, 7, 1968–1975 CrossRef CAS.
- Y. Cheng and R. K. Prud'homme, Biomacromolecules, 2000, 1, 782–788 CrossRef CAS.
- K. Suga, G. van Dedem and M. Moo-Young, Biotechnol. Bioeng., 1975, 17, 185–201 CrossRef CAS.
- I. Mandl, J. D. MacLennan, E. L. Howes, R. H. DeBellis and A. Sohler, J. Clin. Invest., 1953, 32, 1323–1329 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
