 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rotationally inelastic scattering of CD3 and CH3 with He: comparison of velocity map-imaging data with quantum scattering calculations†
Ondřej Tkáča,
Alan G. Sagea,
Stuart J. Greavesb,
Andrew J. Orr-Ewing*a,
Paul J. Dagdigian*c,
Qianli Mac and
Millard H. Alexanderd
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK. E-mail: a.orr-ewing@bris.ac.uk
bSchool of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS UK. E-mail: s.j.greaves@hw.ac.uk
cDepartment of Chemistry, The Johns Hopkins University, Baltimore, Maryland 21218-2685, USA. E-mail: pjdagdigian@jhu.edu
dDepartment of Chemistry and Biochemistry, Institute for Physical Science and Technology, University of Maryland, College Park, Maryland 20742-2021, USA. E-mail: mha@umd.edu
First published on 15th August 2013
Abstract
Rotationally inelastic scattering of methyl radicals (CD3 and CH3) in collisions with helium is examined by a combination of velocity map imaging experiments and quantum scattering calculations. In the experiments a beam of methyl radicals seeded in Ar intersects a beam of He atoms at 90° at a collision energy of 440 ± 35 cm−1 (CD3 + He) or 425 ± 35 cm−1 (CH3 + He). The methyl radicals are prepared photolytically in a gas expansion that cools them to 15 K, giving a distribution over a small number of initial (low) rotational angular momentum states. By resonance-enhanced multi-photon ionization detection, we obtain velocity map images which are specific to a single rotational angular momentum quantum number n′ of the methyl radicals, but averaged over a small subset of the projection quantum number k′. We extract resolved angular scattering distributions for n′ = 2–9 (for CD3). We compare these to predictions of scattering calculations performed based on a recent potential energy surface [P. J. Dagdigian and M. H. Alexander, J. Chem. Phys. 2011, 135, 064306] in which the methyl radical was fixed at its equilibrium geometry. The fully (n, k) → (n′, k′) resolved differential cross sections obtained from the calculations, when combined in weighted sums over initial (n, k) levels corresponding to the 15 K experimental radical temperature, and final k′ levels that are not resolved in the spectroscopic detection scheme, show excellent agreement with the experimental measurements for all final states probed. This agreement gives confidence in the calculated dependence of the scattering on changes in both the n and k quantum numbers.
Introduction
The methyl radical plays an important role in the combustion of hydrocarbons,1,2 chemical vapour deposition (CVD) of diamond films,3 and in the chemistry of the atmospheres of the outer planets in the solar system.4 In addition, CH3 has been detected in the interstellar medium via its infra-red emission bands.5 Observation of methyl radicals in the upper atmospheres of Saturn6 and Neptune7 indicates it is a reactive intermediate in the hydrocarbon photochemistry of these planets: methyl radicals are created by vacuum ultraviolet photodissociation of methane, and the self-recombination reaction is believed to be the only photochemical source of ethane. The atmospheres of giant planets such as Saturn and Neptune are composed mainly of molecular hydrogen and helium, with trace amounts of other substances. Therefore, photochemically generated methyl radicals will undergo elastic and inelastic collisions with He and H2 before reactive loss, with reaction cross sections that can depend on the internal energy of the radicals.The inelastic scattering of labile free radicals using molecular beams and laser spectroscopic techniques was reviewed in the mid 1990s.8–10 However, considerable advances have been made since then using methods such as ion imaging11 and velocity map imaging (VMI)12 with laser spectroscopic detection of the final levels. Most of these experimental studies have concentrated on scattering dynamics of diatomic radicals, with spectroscopic probes used to measure state-resolved integral cross sections (ICSs), and more recently differential cross sections (DCSs). The most extensively studied free radicals have been NO13–24 and OH,25–33 the latter because of its important role in atmospheric chemistry, astrochemistry and combustion. Sarma et al.34 used VMI to obtain fully quantum-state-specified product angular distributions for OH scattered by He and Ar, and VMI methods were also used to study collision induced alignment35 and orientation36 in NO – Ar scattering. Radical – radical scattering studies are rarer, but Kirste et al.37 recently reported state-to-state ICSs for collisions of Stark decelerated OH with NO.
Nevertheless, measurements of DCSs for inelastic scattering of free radicals other than NO are rare, and to the best of our knowledge have not been reported for reactive radicals larger than diatomics. Macdonald and Liu,38,39 and Lai et al.40 examined the inelastic scattering of the linear NCO radical with He and Ar, respectively, but concentrated on ICSs for spin–orbit conserving and spin–orbit changing collisions. ICSs have also been reported for rotationally inelastic collisions of NH2 with He.41 Greater attention has been paid to the inelastic scattering of closed-shell triatomic and polyatomic molecules, as illustrated by determinations of DCSs for scattering of ammonia42–44 and deuterated ammonia45 with rare gases and molecular hydrogen, and for water with helium46 and hydrogen.47
Along with advances in experimental techniques, there have been many quantum scattering calculations of ICSs, and also DCSs, employing high-quality potential energy surfaces (PESs). These have mostly concerned collisions of diatomic and stable polyatomic molecules.14,18,21,25–28,30–33,42,46–48 Dagdigian49 recently reviewed work on quantum scattering calculations of collisional rotational and vibrational energy transfer in small hydrocarbon intermediates and highlighted studies involving methylene (CH2)50,51 and methyl.52,53 The pathways for energy transfer in collisions of a polyatomic are more complicated than for collisions of a diatomic molecule. There is only one type of anisotropy in an atom–diatom interaction, namely the difference in interaction energy for end-on vs. side-on approach. By contrast, for collisions of a nonlinear polyatomic molecule there are two types of anisotropies, corresponding to approach of the collision partner in or perpendicular to the molecular plane.
Dagdigian and Alexander54 recently investigated rotational energy transfer of methyl in collisions with a helium atom through quantum scattering calculations on a computed PES. This PES was calculated with a coupled-cluster method that includes all single and double excitations, as well as perturbative contributions of connected triple excitations [RCCSD(T)]. Because of the anisotropy of the PES due to the repulsion of the He atom by the three H atoms on methyl, a strong propensity was found for Δk = ±3 transitions, where k is the body-frame projection of the rotational angular momentum n.
Ma et al.53 extended this work to the study of the vibrational relaxation of the ν2 mode of methyl by a He atom. Vibrational relaxation was found to be nearly two orders of magnitude less efficient than pure rotational relaxation. The vibrational relaxation rate also depends strongly upon the rotational quantum numbers n and k. Although methyl has an unpaired electron, these calculations53,54 ignored the electron spin. The dependence of the cross sections on the spin can be determined in a straightforward manner by assuming that it is a spectator during the collision.49
In the present work DCSs for collisions of CH3 and CD3 with helium are determined experimentally through the use of crossed molecular beam (CMB) and VMI methods. The measured DCSs are compared with quantum scattering calculations that use the computed PESs mentioned above.53,54 Comparison between experiment and theory at the level of state-resolved DCSs provides a critical test of the influence of both short-range repulsive and long-range attractive intermolecular interactions. Anticipating this comparison, we find excellent agreement between the measured and computed state-to-state DCSs. This confirms the accuracy of the computed PES.
This paper is organized as follows: Method Sections A and B describe the details of the experimental determination of the angular distributions. Method Sections C and D present, respectively, a brief description of the rotational levels of CH3 and CD3, specifically the different nuclear spin modifications, and the spectroscopic intricacies of the detection scheme. Section E describes the quantum scattering calculations. Results Sections A and B present and compare the measured and theoretical cross sections for collision of CD3 and CH3 with He, respectively. Discussion and Conclusions sections then follow.
Method
A. Experimental apparatus
Experimental measurements were carried out using a newly constructed, compact crossed molecular beam machine with velocity map imaging detection, based on the design of Strecker and Chandler.55 Pulsed molecular beams of jet-cooled methyl radicals (either CD3 or CH3) and helium crossed at 90° in a high vacuum chamber, and the velocities of the scattered methyl radicals were imaged following resonance enhanced multi-photon ionization (REMPI) with rotational level resolution. The resultant images were corrected by density to flux conversion prior to analysis of angular dependences to derive quantum-state-resolved differential cross sections. A schematic diagram of the top and side view of the instrument is depicted in Fig. 1, and the component parts are described in greater detail below.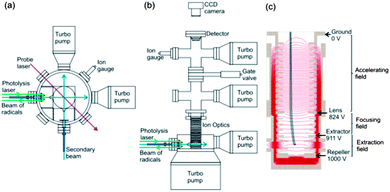 | ||
| Fig. 1 Schematic (a) top and (b) side views of the experimental miniature crossed molecular beam machine. (c) The design of the ion optics for DC slice imaging. The red lines represent the electric field lines of force created by the electrodes with applied voltages corresponding to experimental operation. The dimensions of key elements in the scattering region are given in the main text. | ||
Molecular beams were formed by supersonic expansion of gas samples through a pair of pulsed valves (General Valve Series 9), and the expansions were collimated by skimmers. The pulsed valves operated at 10 Hz repetition rate, the nozzle diameters were 0.8 mm, and the skimmer orifices were 1 mm diameter. The nozzle-skimmer distances could be adjusted in the range 0.2 cm to 4.3 cm, and for the current experiments were selected to be 3.2 cm. The distance from each skimmer to the scattering centre was 3.7 cm. The source chambers were evacuated by a turbomolecular pump (Edwards nEXT300D). The two skimmed beams propagated horizontally and crossed at a 90° intersection angle. The gas flows in both beams passed through the scattering region and were directed straight into two additional turbomolecular pumps (Pfeiffer HiPace 80). A typical base pressure for the scattering chamber was <10−8 Torr with the pulsed valves turned off, and this rose to ∼10−7 Torr when the valves were operating. Additional turbomolecular pumps were mounted just above the ion optics, and in the detector chamber.
The primary molecular beam was formed by expansion of a mixture of 3% CH3I or CD3I in Ar at a stagnation pressure of 4 bar. The secondary beam was formed by expansion of 3 bar of pure helium. Methyl radicals were generated by 266 nm photolysis of the CH3I or CD3I precursor, using 40 mJ per pulse of the fourth harmonic of a Nd:YAG laser (Surelite SLII-10). Both photolytic and electric discharge sources of methyl radicals were tested, but the discharge source was found to produce radicals with a rotational temperature of 120 K, that was too high for inelastic scattering experiments.
The front face of the valve used to generate the primary molecular beam was modified to accommodate prisms above and below the nozzle orifice, such that a UV laser beam could be passed across the gas expansion. Hence, methyl iodide molecules seeded in the argon expansion were photolysed in close proximity to the nozzle, where the high number density ensured the resultant methyl radicals underwent numerous collisions with atoms of the carrier gas. As is shown in ESI,† the methyl radicals cooled to a rotational temperature of ∼15 K with this method of preparation. Residual methyl iodide in the molecular beam was observed, but did not affect the velocity map images for methyl radical scattering because any photolysis of the methyl iodide by the probe laser generated methyl radicals with velocities substantially higher than those from the inelastic scattering of interest here.
The intersection region of the two molecular beams was located within a vertically mounted stack of electrodes forming an ion optics assembly (Fig. 1c) for VMI. Scattered methyl radicals were ionized by a probe laser focused at the intersection of the beams, and the electric field created by the ion optics accelerated the ions upwards towards a position-sensitive detector. A 51 cm long field-free drift region was located between the end of the stack of ion optics and the detector. The ion detector (Photek) consisted of a pair of microchannel plates (MCPs) (10 μm pore on 12 μm pitch), a phosphor screen (P46 phosphor) and CCD camera (BASLER A310f, 782 × 582 pixels). The voltages on the front and rear MCPs were maintained at 830 and 1300 V, respectively. An additional 500 V was applied to the rear MCP (making a total of 1800 V) for 20 ns to time-gate the detector (Photek GM-MCP-2) so as to detect only the narrowest possible, central portion of the scattered methyl radical Newton sphere. The voltage applied to the phosphor screen was 6300 V. Precise velocity calibration of the ion optics and imaging detector assembly was carried out using O2 multi-photon excitation and dissociation at a wavelength of 224.999 nm,56,57 which is a standard method to establish pixel radius to speed conversion factors in VMI.12,58,59
UV radiation in the wavelength range 285–288 nm required for REMPI detection of the methyl radicals was generated by frequency doubling the output of a tuneable pulsed dye laser (Sirah), operating with Pyromethane 597 dye, using a KDP doubling crystal. The dye laser was pumped by 532 nm light from an Nd:YAG laser (Surelite SLI-20). The energy, repetition rate and duration time of this probe laser beam were 4.5 mJ per pulse, 10 Hz and 4–6 ns, respectively, the laser linewidth was 0.0027 nm (0.32 cm−1) and the laser polarization was parallel to the scattering plane. The (2 + 1) REMPI scheme was used both to optimize the production of cold methyl radicals in the primary molecular beam, and to observe the inelastic scattering of these radicals in collisions with the He in the secondary beam. The maximum Doppler shift of inelastically scattered CD3 radicals is 0.1 cm−1, which is smaller than the laser linewidth. The laser was therefore fixed at a wavelength corresponding to the centre of the chosen REMPI line, as determined from the PGOPHER simulation described in Section D. Nozzle and skimmer alignments were set using two diode lasers, and the probe laser was then aligned and focused to the crossing point of the two molecular beams, with minor adjustment to optimize signal levels. The probe laser position remained the same for all image determinations.
The ion optics assembly for VMI, shown in Fig. 1c, consisted of 20 electrodes and was designed for direct current (DC) slice imaging.60 The ion optics were adapted from the design proposed by Lin et al.59 Careful consideration was given to the number of electrodes, their spacing and applied voltages, while limiting their diameters so that the assembly fitted within the confines of the miniature CMB machine. All these parameters were optimised using SIMION simulations, while ensuring precise velocity map imaging across the intersection volumes of the molecular beams and probe laser.12 Voltages on the electrodes in the bottom section of the ion optics stack formed the extraction and focusing fields, and these voltages could be adjusted separately, with 1 kV applied to the repeller electrode. The electrodes forming the accelerating field were connected by resistors that ensured a gradually decreasing field to the final ground electrode.
The electrodes forming the homogeneous acceleration field stretched the methyl ion packet along the flight axis according to the initial velocities of the neutral methyl radicals. The aforementioned short voltage pulse at the MCPs then allowed only a thin centre slice of the ion packet to be recorded, corresponding to methyl radicals scattered within, or close to the plane of the crossed molecular beams. Direct analysis of this slice image gave the three dimensional velocity distribution of the inelastically scattered methyl radicals without need for image reconstruction techniques, although some correction of the raw images was necessary to derive product fluxes, as is discussed further in Section B. The nozzle producing the secondary beam of pure He was operated in a repeating mode of 50 shots on and 50 shots off, thereby separately recording total ion signal and any background contributions from the interaction of the probe laser with the primary beam. The desired scattering signal was then obtained by subtraction of the background image from the total signal image.
B. Density-to-flux transformation
A Newton diagram for inelastic scattering of CD3 with He is shown in Fig. 2 and illustrates the laboratory frame velocities of CD3 [vCD3 = 550 ± 30 m s−1], and helium [vHe = 1710 ± 80 m s−1], and the pre- and post-collision centre-of-mass (CM) frame velocities of the methyl radical uCD3 and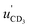 , respectively. The CM-frame scattering angle θ is defined as the angle between the CM-frame velocities of CD3 before and after a collision. Analysis of experimental images requires a density-to-flux transformation because the detection efficiency of the scattered products depends on their laboratory frame velocity. This detection bias leads to an asymmetry in the measured images with respect to the relative velocity vector (dashed line in Fig. 2).
, respectively. The CM-frame scattering angle θ is defined as the angle between the CM-frame velocities of CD3 before and after a collision. Analysis of experimental images requires a density-to-flux transformation because the detection efficiency of the scattered products depends on their laboratory frame velocity. This detection bias leads to an asymmetry in the measured images with respect to the relative velocity vector (dashed line in Fig. 2).
 | ||
| Fig. 2 Newton diagram for inelastic scattering of CD3 with helium. The displayed Newton sphere corresponds to the nk = 11 → n′k′ = 55 transition, for which ΔE = 91.3 cm−1. | ||
To correct the images for this detection bias, we employ the method of Monte Carlo simulation of the experiment, using a modification of the computer program of Eyles and Brouard.61 This code simulates an instrument function that determines a relative detection efficiency of scattered molecules that depends on their final laboratory frame velocity. The changes made to the Monte Carlo program include simulation of slicing of the central part of the Newton sphere. For reliable use of the simulation program, values for various parameters characterizing the experimental apparatus were carefully determined. These parameters included the speed and angular divergence distributions, temporal profiles, and spatial widths of the two molecular beams, as well as the temporal profile, Rayleigh range and beam waist of the focused probe laser. By sampling ∼2 × 108 sets of initial conditions from the distributions of molecular beam and laser beam properties, the Monte Carlo program was used to simulate the instrument function. As will be discussed in Section D, the k projection number is not resolved in the REMPI spectra of methyl radicals. A set of instrument functions was therefore simulated for individual k projection numbers and each was weighted according to the 2-photon line strength factors for the given detection line. The effect of varying k projection number is found to be negligible for low n, where the difference in energy between individual k-states is small, while it is more pronounced for higher n. A final, corrected image was then obtained by dividing the raw experimental image by this sum of instrument functions over k projection quantum numbers. As part of this analysis, the angular resolution of the experiment was calculated and is reported in Fig. S1 and S2 of the ESI.†
C. Rotational levels of CH3 and CD3
In this subsection, we briefly describe the rotational levels of the CH3 and CD3 radicals, and their nuclear spin symmetries. The rotational energies for the lower levels of CH3 and CD3 are plotted in Fig. 3. The methyl radical is an oblate symmetric top. We use n and k to designate, respectively, the rotational quantum number and its body-frame projection. Because the three H (D) atoms are equivalent, the ground vibronic state of CH3 has two nuclear spin modifications, labelled ortho and para.54,62 The ortho levels have nuclear spin symmetry A1 and include rotational levels for which k is a multiple of 3 (k = 0, 3, 6, …). In particular, the rotational levels with k = 0 and odd n do not exist for the ground vibronic state. The para levels have nuclear spin symmetry E and include all rotational levels for which k is not a multiple of 3 (k = 1, 2, 4, 5, …).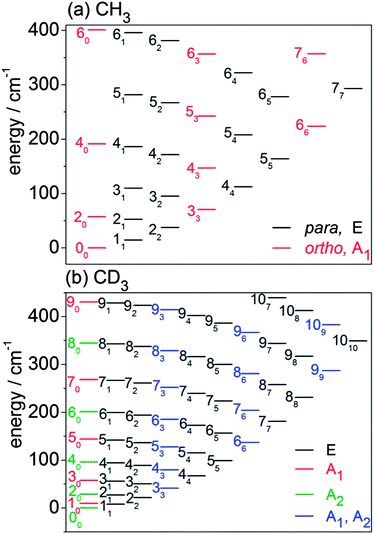 | ||
Fig. 3 Rotational energy level diagrams for the ground vibrational level of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) electronic state of (a) CH3 and (b) CD3. Levels are labelled by n and (subscript) k. The colour coding identifies the different nuclear spin modifications. electronic state of (a) CH3 and (b) CD3. Levels are labelled by n and (subscript) k. The colour coding identifies the different nuclear spin modifications. | ||
The CD3 radical has three nuclear spin modifications. The A1 nuclear spin functions are those with rotational levels with k = 0 and odd n and with levels for which k is a multiple of 3. The A2 nuclear spin functions correspond to rotational levels with even n and k = 0, and also with levels for which k is a multiple of 3. Thus, rotational levels with k = 3, 6, … have two components (A1 and A2). Finally, the E nuclear spin functions include all levels for which k is not a multiple of 3.
D. REMPI detection and state distribution in incident beams
The distribution of rotational levels in the supersonic incident CH3 and CD3 beams and the inelastically scattered final levels were detected using (2 + 1) REMPI spectroscopy through the 000 band of the 4p2A′′2 ←![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′′2 transition.63,64 Lines in the Q branch are by far the strongest and were employed to optimize the experimental conditions but were of no value in determining state-to-state DCSs because of spectral overlap.
2A′′2 transition.63,64 Lines in the Q branch are by far the strongest and were employed to optimize the experimental conditions but were of no value in determining state-to-state DCSs because of spectral overlap.
The level distributions in the incident radical beams were determined by comparison of experimental spectra with spectra simulated using the PGOPHER program.65 The simulation incorporated the effects of nuclear spin statistics of the three equivalent H or D atoms. The procedures used are described in the ESI,† which also contains an example spectrum (Fig. S3†). The derived relative populations are listed in Table 1 and correspond to a rotational temperature of 15 K. As expected from the smaller rotational constants of CD3, more rotational levels have significant populations than in the CH3 isotopologue.
It should be noted that the lines in the REMPI spectrum of methyl are resolved in the n rotational quantum number, but not in the k projection quantum number. Depending upon the spectroscopic branch, and hence Δn (≠0) of the line used to detect the final level, the k projection levels of a given n contribute differently. The levels associated with the DCSs reported below are denoted by nk1k2… to indicate that the unresolved nk1, nk2, … levels have been detected on the given transition. The relative contributions of the different k projection levels to the measured REMPI intensity were determined by calculating 2-photon line strength factors using the PGOPHER program.
The levels of the excited 4p2A′′2 electronic state are predissociated, and the linewidths for the CH3 isotopologue are larger than for CD3. Hence, the efficiency of detection of CH3 rotational levels is lower, and it was possible to determine DCSs for fewer final levels than for CD3. In addition, the computed integral cross sections for formation of higher CH3 rotational levels were found to be smaller than for CD3 levels of comparable rotational angular momentum.
E. Quantum scattering calculations
We used the HIBRIDON suite of programs66 to carry out fully quantum, close-coupled, state-resolved differential cross section calculations for collisions of CH3 and CD3 with He. The bulk of the calculations employed our previously computed54 PES for the interaction of CH3, fixed at its equilibrium geometry, with helium. Since the centre of mass of methyl is located at the carbon atom, this PES could be used without modification for the CD3 isotopologue. Some additional calculations on CD3–He were carried out with a PES for which the CD3 geometry was averaged over the probability distribution for the ν2 umbrella coordinate, using our previously determined53 4-dimensional PES involving this degree of freedom.Rotational energies were computed with a rigid rotor symmetric top Hamiltonian using spectroscopic studies by Yamada et al.67 for CH3 and Sears et al.68 for CD3. The methyl radical is an open-shell species, with doublet spin multiplicity, so that each rotational level, with rotational angular momentum n, is split into spin doublets, with total angular momentum j = n ± 1/2. We have ignored spin in our scattering calculations since the spin-rotation splitting and hyperfine splittings are small69 and not resolved in the REMPI spectra. Separate calculations were carried out for each of the three nuclear spin modifications since they are not interconverted in collisions with closed-shell species without nuclear spin.
We checked convergence of the differential cross sections with respect to the size of the rotational basis and the number of partial waves in the calculation. Rotational levels whose energies were less than 1100 cm−1 were included in the channel basis, and the calculations included total angular momenta J ≤ 130ħ.
Since the CH3 and CD3 incident beams each contained several rotational levels, DCSs for formation of a specific final rotational level nk were determined by weighting the computed state-to-state DCSs at the experimental collision energy by the experimentally determined rotational level populations in the incident beam, which are listed in Table 1. Since the k projection number of the scattered radicals is not resolved in the REMPI spectra, theoretical DCSs for comparison with the experimental measurements were weighted according to the 2-photon line strength factors for the given detection line. More details can be found in ESI.†
We observed previously that CH3 + He integral cross sections computed with the rigid-molecule PES were virtually identical (within 1%) to those computed using a PES in which the umbrella motion was averaged over the ν2 = 0 probability distribution.53 We find a similar excellent agreement of CD3 + He DCSs computed with rigid-molecule and umbrella-averaged PESs. The only exception was a slight increase (∼5%) of the forward (θ < 10°) scattering for low-Δn, Δk = +3 transitions, e.g. 10 → 33 as shown in Fig. S6 of the ESI.† Consequently, for comparison with experiment we used the DCSs calculated with the rigid-molecule PES.
Results
A. DCSs for CD3 + He collisions
From the measured beam speed distributions (see ESI†), the mean CD3 + He collision energy was calculated to be 440 cm−1 with an expected spread of ±35 cm−1. Fig. 4 presents the raw images recorded for detection of CD3 final rotational levels for n′ = 2–9. These images were each typically accumulated for 8 to 10 hours. The scattered products cannot be observed in the portions of the images corresponding to the forward direction because of imperfect subtraction of background signals arising from unscattered CD3 radicals present in the parent molecular beam. The incomplete cooling of the methyl radicals to the lowest rotational level of a given nuclear spin modification during the supersonic expansion is the origin of this masking of the scattering signals and is more significant when lower rotational levels are probed. Nevertheless, from examination of the images, we see that the scattering is confined relatively close to the incident beam direction for detection of low n′ final levels. This suggests that the scattering is largely in the forward direction for these levels. By contrast, significant intensity extends to a much larger range of scattering angles for high n′ final levels.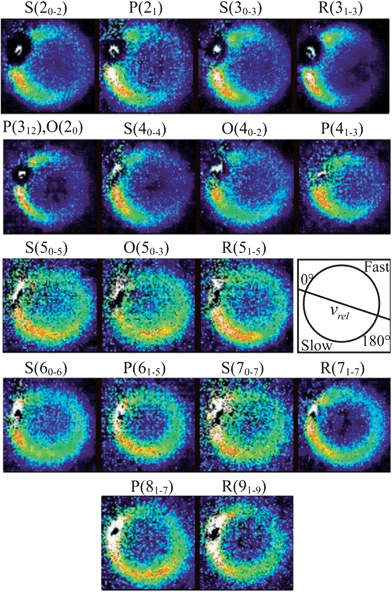 | ||
Fig. 4 Raw images for inelastic scattering of CD3 radicals by He at a collision energy of 440 ± 35 cm−1. The images are denoted by the symbol 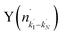 for final rotational levels from n′ = 2–9, with unresolved final k′ projection levels as discussed in the text. Y denotes the spectroscopic branch. The rotational angular momentum of the incident CD3 beam was predominantly n = 1 (see Table 1 for the complete incident level distribution). The orientation of the relative velocity vector vrel is indicated in one panel. for final rotational levels from n′ = 2–9, with unresolved final k′ projection levels as discussed in the text. Y denotes the spectroscopic branch. The rotational angular momentum of the incident CD3 beam was predominantly n = 1 (see Table 1 for the complete incident level distribution). The orientation of the relative velocity vector vrel is indicated in one panel. | ||
The recorded images were analysed following the procedures described in Method Section B to correct for the density-to-flux transformation in order to derive the DCSs. Fig. 5 displays the determined DCSs for final levels n′ = 2–4, while Fig. 6 presents the DCSs for n′ = 5–9. In both figures, the unresolved k′ projections are specified for each n′ – resolved DCS. Also shown in Fig. 5 and 6 are theoretical DCSs. The experimental DCSs are not shown for θ < 30° for final levels with n′ = 2 and 3 and for θ < 20° for final levels with higher n′ because of contributions to these angles from unscattered radicals in the parent beam, as discussed above. The calculated DCSs show pronounced diffraction oscillations in this strongly forward scattered region. Unfortunately, even with greater initial state purity the angular resolution of the experiments, imposed by the velocity and angular spreads of the two molecular beams, would be insufficient to resolve these structures clearly. For the current experiments on the CD3 + He system, this angular resolution ranges varies from 3 to 16° depending on the scattering angle (see ESI† for further details).
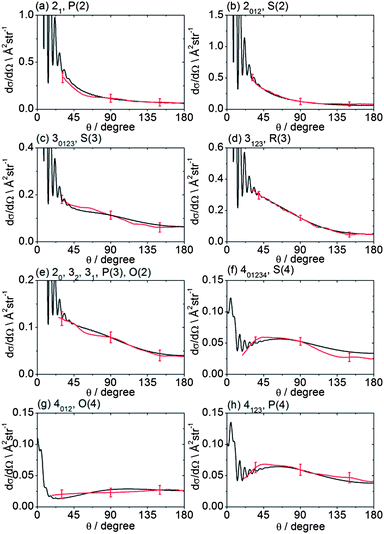 | ||
| Fig. 5 DCSs for inelastic scattering of CD3 radicals by He at a collision energy of 440 ± 35 cm−1 into final rotational levels n′ = 2–4. The REMPI line employed for detection is indicated, along with the range of k′ projection levels contributing to the scattering. Red curves: DCSs determined from the measured images displayed in Fig. 4; black curves: theoretical DCSs computed as described in Method Section E. The method of normalization of the experimental DCSs is described in the main text. | ||
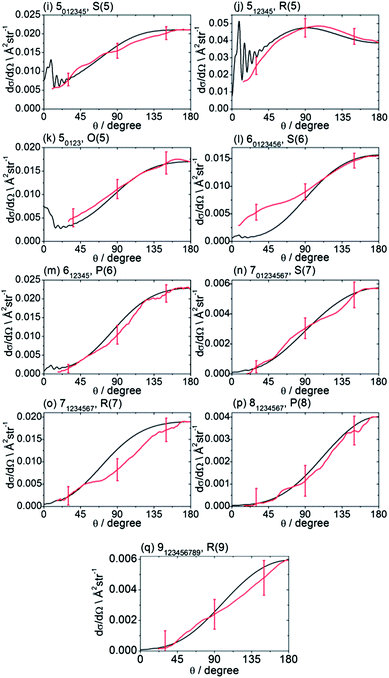 | ||
| Fig. 6 DCSs for inelastic scattering of CD3 radicals by He at a collision energy of 440 ± 35 cm−1 into final rotational levels n′ = 5–9. The REMPI line employed for detection is indicated, along with the range of k′ projection levels contributing to the scattering. Red curves: DCSs determined from the measured images displayed in Fig. 4; black curves: theoretical DCSs computed as described in Method Section E. The normalization of the experimental DCSs is described in the main text. | ||
For quantitative comparison with the theoretical calculations, the experimental angular distributions are normalized by scaling the experimental value to match the theoretical value at either 90° for levels with n′ ≤ 4, or at 180° for higher n′ states. These choices were made to ensure that the comparison was done at angles where the experimental signal levels were strongest. The error bars associated with the experimental DCSs were determined by combining the standard deviation determined from comparison of several (typically 3) measured images for a single final state with the uncertainty introduced by application of the density-to-flux transformation. The latter factor was quantified by comparing DCSs extracted from the two halves of the image separated by the relative velocity vector (which should be symmetric after perfect transformation). The theoretical DCSs reproduce satisfactorily all the features of the measured DCSs to within the experimental uncertainty. The n′-dependent DCSs are a sensitive probe of both attractive and repulsive parts of the potential. The near quantitative agreement for all final n′ levels confirms the high quality of the calculated ab initio PES54 and the accuracy of the close-coupling treatment of the scattering dynamics.
In most cases, different spectroscopic branches can be used to detect a given methyl rotational level n′. The unresolved k′ projections of the given n′, weighted according to the 2-photon line strength factors (see Method Section D) will give rise to slightly different predicted DCSs. As an illustration of this subtle effect, we see in Fig. 5 and 6 that the experimental and theoretical DCSs for a given n′ are slightly different for detection of this level on REMPI lines of different Δn′. This is most dramatically illustrated in Fig. 5 in the comparison of detection of n′ = 4 on the O(4), P(4), and S(4) lines. The differing measured DCSs reflect the fact that the k′ projection levels of final rotational level n′ = 4 have different DCSs. This point will be taken up again in the Discussion.
B. DCSs for CH3 + He collisions
The collision energy of 425 ± 35 cm−1 for inelastic scattering of CH3 radicals (seeded in excess Ar) with He is slightly smaller than for the scattering of CD3 by He, because of the smaller reduced mass. The spectroscopic lines for CH3 are also not resolved in the k projection quantum number, although the spacings between the lines detecting different k levels of the same n are larger than for CD3. In addition, the CH3 REMPI transitions are more broadened by predissociation of the intermediate Rydberg state, which lowers the detection efficiency. Consequently, velocity map images for CH3 scattering were recorded only for the three strongest spectroscopic lines.Fig. 7 presents representative examples of these images. The DCSs derived from the density-to-flux transformation (Method Section B) and normalized to the theoretical DCSs are presented in Fig. 8. In two of the panels in Fig. 8, experimental DCSs derived from images accumulated on different days are compared. We see that these DCSs lie almost entirely on top of each other, which demonstrates excellent reproducibility. Fig. 8 also compares these experimental DCSs with theoretical calculations. There is agreement for the n′k′ = 3123 and 21 final levels, except for small angle scattering. However, the experimental DCS for scattering into n′k′ = 2012 does not agree with the comparable theoretical DCS for θ ≤ 90°, computed under the assumption that the probe laser excites all three k′ projection levels. Re-measurement of the images confirms the reproducibility of the experimentally determined DCSs (red and blue lines in Fig. 8b). However, careful examination of the 2-photon transition wavenumbers reveals that lines originating from these k′ levels are separated by more than their widths. If we assume that the k′ = 2 level was preferentially excited, then we obtain good agreement of the computed DCS [green curve in Fig. 8b] with the experimental DCS.
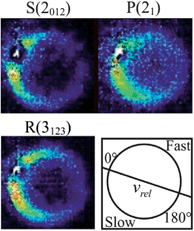 | ||
Fig. 7 Raw images for inelastic scattering of CH3 radicals by He at a collision energy of 425 ± 35 cm−1. The images are denoted by the symbol 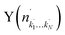 for final rotational levels with n′ = 2 and 3 and unresolved final k′ projection levels as discussed in the text and shown with each image. Y denotes the spectroscopic branch. The rotational angular momentum of the incident CH3 beam was predominantly n = 0 and 1 (see Table 1 for the complete incident level distribution). The orientation of the relative velocity vector vrel is indicated in one panel. for final rotational levels with n′ = 2 and 3 and unresolved final k′ projection levels as discussed in the text and shown with each image. Y denotes the spectroscopic branch. The rotational angular momentum of the incident CH3 beam was predominantly n = 0 and 1 (see Table 1 for the complete incident level distribution). The orientation of the relative velocity vector vrel is indicated in one panel. | ||
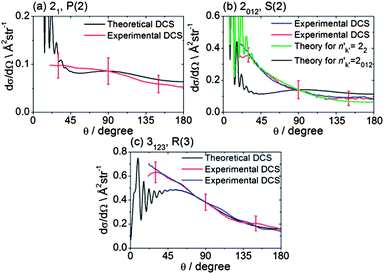 | ||
| Fig. 8 DCSs for inelastic scattering of CH3 radicals by He at a collision energy of 425 ± 35 cm−1 into final rotational levels n′ = 2 and 3. The REMPI line employed for detection is indicated, along with the range of k′ projection levels contributing to the scattering. Panels (b) and (c) also compare experimental DCSs for repeat measurements made on different days to demonstrate the reproducibility of the experimental determinations. | ||
Discussion
The agreement between the measured and calculated DCSs for scattering of both CH3 and CD3 radicals with He at respective collision energies of 425 and 440 cm−1 lends considerable confidence to the quality of the theoretical treatment outlined in Method Section E. We can therefore derive insights into the scattering dynamics not only from comparison with experiment (as we have done in the case of Fig. 5, 6 and 8), but also by analysis of the calculated, fully state resolved DCSs.The raw experimental images immediately reveal a trend that is borne out by the derived DCSs and by the scattering calculations: for both CD3 or CH3 the angular distributions for transitions into n′ = 2–4 (averaged over k′), where the degree of translational to rotational energy transfer is small, peak in the forward hemisphere, whereas those with n′ ≥ 5 (i.e. intermediate to large energy transfer) are predominantly sideways and backwards scattered. The degree of backward scattering increases steadily with increasing n′, and hence with Δn, because the initial levels of CD3 populated have mostly n = 1 (Table 1).
Similar behaviour is observed in the inelastic scattering of atoms such as He with diatomic molecules,19,22,23 and reveals that low impact parameter collisions (with, presumably, larger angles of deflection) are necessary for large changes in the rotational angular momentum. Classically, the rotational angular momentum of the molecule is induced by a torque that acts on the molecule for the duration of the collision.70 The magnitude of the torque is proportional to the gradient of the intermolecular potential, which is largest at short range.
Beyond the Δn dependence of the DCSs, we can also explore the efficiency of changes in the projection quantum number k. The experimental DCSs determined using CD3 REMPI lines originating from the same n′ level but corresponding to different spectroscopic branches probe different groups of k′ projection quantum numbers. Thus, as highlighted earlier, Fig. 5 illustrates the DCSs for transition into n′ = 4 obtained by O(4), P(4) and S(4) transitions, which probe, respectively, k′ projections 0–2, 1–3, and 0–4. The varying DCSs obtained indicate clearly that there is a significant variation with k′. The calculations reveal the fully k′-resolved dependence: compare, for example, the 11 → 41, 42 and 44 DCSs displayed in Fig. 9 for scattering of both CH3 and CD3.
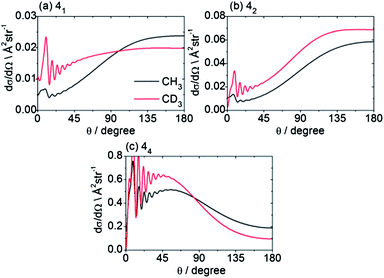 | ||
| Fig. 9 Theoretical state-to state CH3/CD3 + He inelastic DCSs out of the level nk = 11 into levels with n′ = 4, at a collision energy of 425/440 cm−1. | ||
In the previous theoretical study,54 the 3-fold corrugation of the PES resulting from repulsion of the helium atom by the three H atoms on the methyl radical gave rise to a strong propensity for Δk = ±3 in the integral CH3 + He inelastic cross sections. To illustrate this corrugation, Fig. 10 presents the atom–molecule separation R at which the interaction energy is equal to 440 cm−1 (the collision energy) as a function of the angles (θHe, ϕHe) that define the orientation of the He atom (see Fig. 1 of ref. 54). The heavy line in Fig. 10 shows the 3-fold corrugation of the PES for approach of the He atom in the molecular plane.
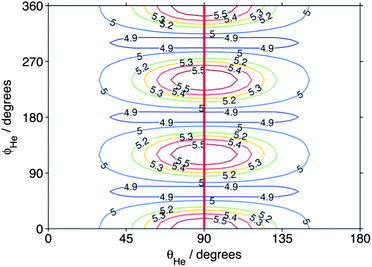 | ||
| Fig. 10 Atom–molecule separation (in bohr) at which the CD3–He interaction energy equals the (440 cm−1) collision energy. The angular coordinates are defined in Fig. 1 of ref. 54. The heavy line indicates the direction of approach of the atom within the molecular plane. | ||
It is also interesting to ask how the periodic corrugation of the PES might be manifested in the angular dependence of the state-to-state scattering. Fig. 11 presents computed state-to-state DCSs for scattering of the lowest rotational levels of each nuclear spin modification of CH3 and CD3 into the n′ = 2 and 3 final rotational levels. The sums of such DCSs weighted by the distribution of populations over initial CD3 or CH3 levels given in Table 1, but resolved by final n′ and k′ level, are plotted in the ESI† section. The DCSs plotted in Fig. 11 for the same initial rotational level of the two isotopologues are similar. Consequently, we henceforth concentrate on the CD3 isotopologue.
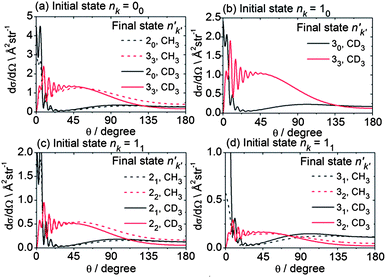 | ||
| Fig. 11 Theoretical state-to state DCSs for inelastic scattering of CH3 and CD3 with He out of the lowest rotational levels of each nuclear spin modification, at respective collision energies of 425 and 440 cm−1. | ||
The DCSs for all Δk = 0 transitions have a similar shape, namely a reasonably sharp forward peak and a broad, lower intensity peak in the backward hemisphere. These transitions in all the nuclear spin modifications are induced primarily by the v20 term in the expansion of the PES.54 By contrast, the |Δk| ≠ 0 transitions all display a broad DCS, starting from zero intensity at θ = 0° and extending over the entire angular range, with oscillations at small angles (θ ≤ 45°). In the case of the levels of A1 and A2 nuclear spin symmetry, these transitions involve Δk = 3 and are enabled by the strong v33 term in the angular expansion of the PES, as discussed previously in some detail.54 For the levels of E symmetry, many Δk = 1 transitions, e.g. 11 → 22, can be described as a Δk = ±3 transition from the k = ±1 component of the initial level to the k′ = ∓2 component of the final level.54 Again, this transition is enabled by the v33 term. Hence, for the low Δn, Δk ≠ 0 transitions, the shapes of the DCSs are closely connected with the change in the k projection quantum number in the collision.
To gain further insight into the origin of the differences in the DCSs for Δk = 0 vs. ±3 transitions, we can consider the dependence of the scattering upon the impact parameter. Since the initial and final rotational quantum numbers n and n′ are small compared to the orbital angular momentum L, the orbital angular momentum is approximately equal to the total angular momentum J. The partial cross sections (the contribution to the ICS from each value of J) give information about which range of impact parameters contributes to a particular transition. Fig. 12 presents a plot of the partial cross sections from the 10 level to the 30 and 33 levels, and to the higher 50 and 66 levels. The scattering into both n′ = 3 final levels is dominated by the same range of J (i.e., classically, by the same range of impact parameters), but the partial cross sections for the 30 level exhibit a bimodal distribution peaking at J = 16 and 33. The high-J and low-J peaks are related to the strong forward and backward peaks seen in the DCS for this transition. In contrast, the partial cross sections for the 33 level display a single peak at J = 22. Similarly, for this transition, only a single broad peak appears in the DCS. Also, we observe that the scattering into the higher rotational levels, exemplified here by the 50 and 66 levels, occurs at smaller values of J (i.e. impact parameters). The torque required for a large Δn transition requires a hard collision at small impact parameters.
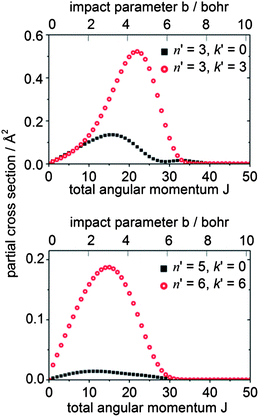 | ||
| Fig. 12 Partial cross sections for CD3 + He collisions at 440 cm−1 for scattering from the nk = 10 initial level. | ||
Since the contribution to the integral cross sections into the 30 and 33 levels occurs over the same range of impact parameters, it is not possible to use the partial cross sections to explain fully the difference in the DCSs for these two levels. Possibly, the orientation of the CD3 molecule plays a significant role. The rotational angular momentum of the CD3 molecule in the 33 level is oriented along the C3 symmetry axis, so that the molecule is rotating perpendicular to this axis. Excitation of this rotational motion will be most readily induced by a collision in which the He atom approaches in the plane of the three D (or three H) atoms (i.e. θHe ≈ 90° in Fig. 10). In contrast, in the 30 level the CD3 molecule rotates about an axis perpendicular to the C3 symmetry axis. Excitation of this motion will require a collision with a He atom approaching out of the hydrogenic plane (i.e. θHe away from 90° in Fig. 10).
For all final levels measured, the experimental DCSs for inelastic scattering of CD3 are somewhat more forward peaking than those for CH3 (see Fig. S7 of ESI† for direct comparisons). As mentioned above and shown in Fig. 9, the state-to-state DCSs of the two isotopologues are, however, very similar. The differences in the measured DCSs may be explained by considering the initial level population in the primary molecular beam. For the CH3 radical the 10 level is missing, and the 00 level is the most populated, whereas for CD3 the most populated levels have n = 1. Accessing a particular final n′ level therefore involves a smaller Δn′ for CD3 than in the case of CH3.
Fig. 13 shows theoretical DCSs for inelastic scattering of CD3 out of the various k = 1 and 2 rotational levels with n = 1–3 into levels with n′k′ = 44 and 55. Different behaviour is seen, as a function of the initial rotational angular momentum k of the CD3 molecule. For the 44 final level, the DCSs for k = 1 initial levels peak in the forward hemisphere, while those for k = 2 peak in the backward hemisphere. The former and latter involve Δk = 3 and 6 transitions (the latter probably involving two virtual Δk = 3 transitions), respectively. The situation for the 55 final level is reversed; in this case, transitions out of the k = 1 and 2 initial levels involve Δk = 6 and 3 transitions, respectively.
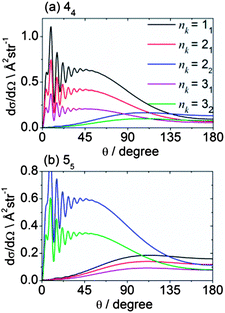 | ||
| Fig. 13 Theoretical state-to state DCSs for inelastic scattering of CD3 with He out of several initial rotational levels into the n′k′ = 44 and 55 final levels, at a collision energy of 440 cm−1. | ||
Fig. 14 displays theoretical state-to-state DCSs for inelastic scattering of CD3 out of the nk = 11 rotational level into k′ = 1 rotational levels with n′ = 2–7. These Δk = 0 collisions induce additional rotation about an axis perpendicular to the C3 symmetry axis but do not change the projection k of the rotational angular momentum along the symmetry axis. The corresponding DCSs provide insight into which collisions lead to a change in the magnitude of n while preserving its component along the C3 axis. We observe that as n′ (and hence Δn) increases, the bimodal distribution present for the 21 and 31 final levels develops into a single peaked backward distribution.
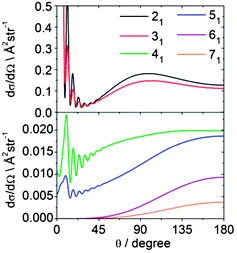 | ||
| Fig. 14 Theoretical state-to state DCSs for inelastic scattering of CD3 with He out of the nk = 11 level into rotational levels with k′ = 1, but with varying n′ at a collision energy of 440 cm−1. | ||
We can also explore the dependence of scattering on the initial angular momentum by comparison of the dependence on n of state-to-state DCSs for a fixed increase in n. Fig. 15 shows theoretical state-to-state DCSs for inelastic scattering of CD3 by He for Δk = 0 transitions involving different k = 1 initial levels and Δn = 1. When normalized to the maximum value, the DCSs appear remarkably similar. There is very little sensitivity to the initial level, even though the energy transfer associated with these transitions is larger for higher initial n, as can be seen in Table 2.
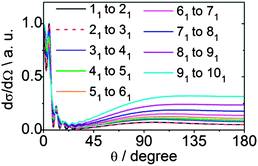 | ||
| Fig. 15 Theoretical state-to-state DCSs for inelastic scattering of CD3 with He for transitions involving a change in the rotational angular momentum quantum number Δn = 1 but with conservation of the k quantum number at a collision energy of 440 cm−1. | ||
| Transition nk → n′k′ | ΔE/cm−1 |
|---|---|
| 11 → 21 | 19.2 |
| 21 → 31 | 28.8 |
| 31 → 41 | 38.4 |
| 41 → 51 | 47.9 |
| 51 → 61 | 57.4 |
| 61 → 71 | 67.0 |
| 71 → 81 | 76.4 |
| 81 → 91 | 85.9 |
The comparisons made in Fig. 9 and 11–15 are far from exhaustive, but provide examples of insights that can be drawn from the state-to-state DCSs. They illustrate the consequence of the angular periodicity in the PES, and the additional complexity that arises when the collision partner is nonlinear.
Conclusions
We have presented an in-depth comparison of differential cross sections for rotationally inelastic scattering of methyl radicals (both CH3 and CD3) with He. The measurements made use of a newly constructed crossed molecular beam and velocity map imaging instrument. The results presented here represent (to our knowledge) the first reported determinations of DCSs for inelastic scattering of a polyatomic free radical. The agreement is excellent with the predictions of close-coupling scattering calculations on a recently reported ab initio potential energy surface. CD3 radical scattering was examined for final n′ levels up to n′ = 9 in the vibrational ground state, whereas experiments for CH3 radicals were limited to n′ = 2 and 3. Because of limitations in the REMPI detection scheme, the CM-frame experimental angular distributions represent sums over an unresolved group of k′ projection levels.The accuracy of the calculated, fully state-resolved state-to-state DCSs out of initial states with nk = 00 and 11 is confirmed by comparison with the less highly resolved experimental data. The theoretical calculations also allow an instructive study of how the features of the underlying PES influence the relative magnitude of the differential scattering into various n′ and k′ final states.
The excellent agreement between theory and experiment is very satisfying, but limited (so far) to the single collision energy used here, and to the use of He as a single collision partner. We are initiating comparable experimental and theoretical studies of the scattering of methyl radicals with Ar, H2 and D2 to ascertain whether we can achieve a comparable level of agreement and understanding for collisions of CD3 (CH3) with heavier or more structurally complicated collision partners.
Acknowledgements
The Bristol group acknowledges financial support from the EPSRC Programme Grant EP/G00224X and from the EU Marie Curie Initial Training Network ICONIC (for an Early Career Researcher position for OT). We thank Dr Kevin E. Strecker and Dr David W. Chandler (Sandia National Laboratory, Livermore) for inspiring the construction of the crossed molecular beam and velocity map imaging instrument, and for valuable discussions about its design. We are grateful to Dr C. M. Western (University of Bristol) for assistance with the PGOPHER simulation of methyl radical REMPI spectra. SJG thanks EPSRC for award of a Career Acceleration Fellowship EP/J002534/2. The theoretical portion of this work was supported by the Chemical, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy, under Grant no. DESC0002323.Notes and references
- J. A. Miller, R. J. Kee and C. K. Westbrook, Annu. Rev. Phys. Chem., 1990, 41, 345–387 CrossRef CAS.
- Gas-Phase Combustion Chemistry, ed. W. C. Gardiner Jr, Springer, New York, 2000 Search PubMed.
- P. W. May, N. L. Allan, M. N. R. Ashfold, J. C. Richley and Y. A. Mankelevich, J. Phys.: Condens. Matter, 2009, 21, 364203 CrossRef.
- J. I. Moses, B. Bezard, E. Lellouch, G. R. Gladstone, H. Feuchtgruber and M. Allen, Icarus, 2000, 143, 244–298 CrossRef CAS.
- H. Feuchtgruber, F. P. Helmich, E. F. van Dishoeck and C. M. Wright, Astrophys. J., 2000, 535, L111–L114 CrossRef CAS.
- B. Bezard, H. Feuchtgruber, J. I. Moses and T. Encrenaz, Astron. Astrophys., 1998, 334, L41–L44 CAS.
- B. Bezard, P. N. Romani, H. Feuchtgruber and T. Encrenaz, Astrophys. J., 1999, 515, 868–872 CrossRef CAS.
- P. J. Dagdigian, in The Chemical Dynamics and Kinetics of Small Radicals, Part I, ed. K. Liu and A. F. Wagner, World Scientific, Singapore, 1995, p. 315 Search PubMed.
- J. C. Whitehead, Rep. Prog. Phys., 1996, 59, 993–1040 CrossRef CAS.
- A. Schiffman and D. W. Chandler, Int. Rev. Phys. Chem., 1995, 14, 371–420 CrossRef CAS.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- F. J. Aoiz, J. E. Verdasco, M. Brouard, J. Kłos, S. Marinakis and S. Stolte, J. Phys. Chem. A, 2009, 113, 14636–14649 CrossRef CAS.
- M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina, S. Stolte and M. P. de Miranda, J. Chem. Phys., 2013, 138, 104309 CrossRef CAS.
- M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina and S. Stolte, J. Chem. Phys., 2013, 138, 104310 CrossRef CAS.
- C. J. Eyles, M. Brouard, H. Chadwick, F. J. Aoiz, J. Kłos, A. Gijsbertsen, X. Zhang and S. Stolte, Phys. Chem. Chem. Phys., 2012, 14, 5420–5439 RSC.
- C. J. Eyles, M. Brouard, H. Chadwick, B. Hornung, B. Nichols, C. H. Yang, J. Kłos, F. J. Aoiz, A. Gijsbertsen, A. E. Wiskerke and S. Stolte, Phys. Chem. Chem. Phys., 2012, 14, 5403–5419 RSC.
- C. J. Eyles, M. Brouard, C. H. Yang, J. Kłos, F. J. Aoiz, A. Gijsbertsen, A. E. Wiskerke and S. Stolte, Nat. Chem., 2011, 3, 597–602 CrossRef CAS.
- J. J. Kay, J. D. Steill, J. Kłos, G. Paterson, M. L. Costen, K. E. Strecker, K. G. McKendrick, M. H. Alexander and D. W. Chandler, Mol. Phys., 2012, 110, 1693–1703 CrossRef CAS.
- J. Kłos, F. J. Aoiz, J. E. Verdasco, M. Brouard, S. Marinakis and S. Stolte, J. Chem. Phys., 2007, 127, 031102 CrossRef.
- H. Kohguchi, T. Suzuki and M. H. Alexander, Science, 2001, 294, 832–834 CrossRef CAS.
- A. Gijsbertsen, H. Linnartz, G. Rus, A. E. Wiskerke, S. Stolte, D. W. Chandler and J. Kłos, J. Chem. Phys., 2005, 123, 224305 CrossRef CAS.
- M. S. Westley, K. T. Lorenz, D. W. Chandler and P. L. Houston, J. Chem. Phys., 2001, 114, 2669–2680 CrossRef CAS.
- L. S. Bontuyan, A. G. Suits, P. L. Houston and B. J. Whitaker, J. Phys. Chem., 1993, 97, 6342–6350 CrossRef CAS.
- M. Kirste, L. Scharfenberg, J. Kłos, F. Lique, M. H. Alexander, G. Meijer and S. Y. T. van de Meerakker, Phys. Rev. A, 2010, 82, 042717 CrossRef.
- S. Marinakis, G. Paterson, J. Kłos, M. L. Costen and K. G. McKendrick, Phys. Chem. Chem. Phys., 2007, 9, 4414–4424 RSC.
- G. Paterson, S. Marinakis, M. L. Costen, K. G. McKendrick, J. Kłos and R. Tobola, J. Chem. Phys., 2008, 129, 074304 CrossRef.
- Z. Pavlovic, T. V. Tscherbul, H. R. Sadeghpour, G. C. Groenenboom and A. Dalgarno, J. Phys. Chem. A, 2009, 113, 14670–14680 CrossRef CAS.
- K. Schreel, J. Schleipen, A. Eppink and J. J. ter Meulen, J. Chem. Phys., 1993, 99, 8713–8722 CrossRef CAS.
- M. Brouard, A. Bryant, Y. P. Chang, R. Cireasa, C. J. Eyles, A. M. Green, S. Marinakis, F. J. Aoiz and J. Klos, J. Chem. Phys., 2009, 130, 044306 CrossRef CAS.
- M. Brouard, H. Chadwick, Y. P. Chang, C. J. Eyles, F. J. Aoiz and J. Kłos, J. Chem. Phys., 2011, 135, 084306 CrossRef CAS.
- L. Scharfenberg, K. B. Gubbels, M. Kirste, G. C. Groenenboom, A. van der Avoird, G. Meijer and S. Y. T. van de Meerakker, Eur. Phys. J. D, 2011, 65, 189–198 CrossRef CAS.
- M. C. van Beek, J. J. ter Meulen and M. H. Alexander, J. Chem. Phys., 2000, 113, 628–636 CrossRef CAS.
- G. Sarma, S. Marinakis, J. J. ter Meulen, D. H. Parker and K. G. McKendrick, Nat. Chem., 2012, 4, 985–989 CrossRef CAS.
- J. I. Cline, K. T. Lorenz, E. A. Wade, J. W. Barr and D. W. Chandler, J. Chem. Phys., 2001, 115, 6277–6280 CrossRef CAS.
- K. T. Lorenz, D. W. Chandler, J. W. Barr, W. W. Chen, G. L. Barnes and J. I. Cline, Science, 2001, 293, 2063–2066 CrossRef CAS.
- M. Kirste, X. Wang, H. C. Schewe, G. Meijer, K. Liu, A. van der Avoird, L. M. C. Janssen, K. B. Gubbels, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2012, 338, 1060–1063 CrossRef CAS.
- R. G. Macdonald and K. P. Liu, J. Chem. Phys., 1992, 97, 978–990 CrossRef CAS.
- R. G. Macdonald and K. P. Liu, J. Chem. Phys., 1993, 98, 3716–3725 CrossRef CAS.
- L. H. Lai, Y. H. Chiu and K. P. Liu, J. Chem. Phys., 1995, 103, 8492–8500 CrossRef CAS.
- P. J. Dagdigian, J. Chem. Phys., 1989, 90, 2617–2625 CrossRef CAS.
- G. Ebel, R. Krohne, H. Meyer, U. Buck, R. Schinke, T. Seelemann, P. Andresen, J. Schleipen, J. J. ter Meulen and G. H. F. Diercksen, J. Chem. Phys., 1990, 93, 6419–6432 CrossRef CAS.
- H. Meyer, J. Chem. Phys., 1994, 101, 6686–6696 CrossRef.
- H. Meyer, J. Phys. Chem. A, 1995, 99, 1101–1114 CrossRef CAS.
- J. J. Kay, S. Y. T. van de Meerakker, E. A. Wade, K. E. Strecker and D. W. Chandler, J. Phys. Chem. A, 2009, 113, 14800–14806 CrossRef.
- C. H. Yang, G. Sarma, J. J. ter Meulen, D. H. Parker, U. Buck and L. Wiesenfeld, J. Phys. Chem. A, 2010, 114, 9886–9892 CrossRef CAS.
- C. H. Yang, G. Sarma, D. H. Parker, J. J. ter Meulen and L. Wiesenfeld, J. Chem. Phys., 2011, 134, 204308 CrossRef.
- G. Paterson, A. Relf, M. L. Costen, K. G. McKendrick, M. H. Alexander and P. J. Dagdigian, J. Chem. Phys., 2011, 135, 234304 CrossRef CAS.
- P. J. Dagdigian, Int. Rev. Phys. Chem., 2013, 32, 229–265 CrossRef CAS.
- L. Ma, M. H. Alexander and P. J. Dagdigian, J. Chem. Phys., 2011, 134, 154307 CrossRef.
- L. Ma, P. J. Dagdigian and M. H. Alexander, J. Chem. Phys., 2012, 136, 224306 CrossRef.
- P. J. Dagdigian and M. H. Alexander, J. Chem. Phys., 2011, 135 Search PubMed.
- Q. Ma, P. J. Dagdigian and M. H. Alexander, J. Chem. Phys., 2013, 138, 104317 CrossRef.
- P. J. Dagdigian and M. H. Alexander, J. Chem. Phys., 2011, 135, 064306 CrossRef.
- P. Jansen, D. W. Chandler and K. E. Strecker, Rev. Sci. Instrum., 2009, 80, 083105 CrossRef.
- B. Buijsse, W. J. van der Zande, A. Eppink, D. H. Parker, B. R. Lewis and S. T. Gibson, J. Chem. Phys., 1998, 108, 7229–7243 CrossRef CAS.
- D. H. Parker and A. Eppink, J. Chem. Phys., 1997, 107, 2357–2362 CrossRef CAS.
- G. Wu, W. Zhang, H. Pan, Q. Shuai, B. Jiang, D. Dai and X. Yang, Rev. Sci. Instrum., 2008, 79, 094104 CrossRef.
- J. J. Lin, J. G. Zhou, W. C. Shiu and K. P. Liu, Rev. Sci. Instrum., 2003, 74, 2495–2500 CrossRef CAS.
- D. Townsend, M. P. Minitti and A. G. Suits, Rev. Sci. Instrum., 2003, 74, 2530–2539 CrossRef CAS.
- C. J. Eyles, D. Phil. Thesis, University of Oxford, 2010.
- M. Zahedi, J. A. Harrison and J. W. Nibler, J. Chem. Phys., 1994, 100, 4043 CrossRef CAS.
- I. Powis and J. F. Black, J. Phys. Chem., 1989, 93, 2461–2470 CrossRef CAS.
- J. F. Black and I. Powis, J. Chem. Phys., 1988, 89, 3986–3992 CrossRef CAS.
- C. M. Western, PGOPHER, a Program for Simulating Rotational Structure, University of Bristol, 2010 Search PubMed.
- M. H. Alexander, D. E. Manolopoulos, H.-J. Werner, B. Follmeg, P. J. Dagdigian and Q. Ma, HIBRIDON, a package of programs for the time-independent quantum treatment of inelastic collisions and photodissociation. More information and/or a copy of the code can be obtained from the website http://www2.chem.umd.edu/groups/physical/hibridon/hib43.
- C. Yamada, E. Hirota and K. Kawaguchi, J. Chem. Phys., 1981, 75, 5256 CrossRef CAS.
- T. J. Sears, J. M. Frye, V. Spirko and W. P. Kraemer, J. Chem. Phys., 1989, 90, 2125 CrossRef CAS.
- S. Davis, D. T. Anderson, G. Duxbury and D. J. Nesbitt, J. Chem. Phys., 1997, 107, 5661 CrossRef CAS.
- J. T. Yardley, Introduction to Molecular Energy Transfer, Academic, New York, 1980 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI contains further details of the experiments and additional plots of computed DCSs in support of the main text. See DOI: 10.1039/c3sc52002a |
| This journal is © The Royal Society of Chemistry 2013 |
