Water in the Earth's mantle: a solid-state NMR study of hydrous wadsleyite

Abstract

Wadsleyite, β-(Mg,Fe)₂SiO₄, is the main component of the transition zone in the Earth's mantle, at depths of 410–530 km below the surface. This mineral has received considerable interest as a potential reservoir for the vast amount of hydrogen, as hydroxyl, referred to as water, that is thought to be contained within the mantle. However, the exact way in which water is incorporated into the structure of wadsleyite is not fully understood and has been the subject of considerable debate. In this work, ¹⁷O, ²⁵Mg, ²⁹Si, ¹H and ²H solid-state NMR spectra were obtained from isotopically enriched samples of anhydrous and hydrous β-Mg₂SiO₄. First-principles DFT calculations were also carried out for a range of model structures to aid interpretation of the experimental data. The results are consistent with a model for hydrous wadsleyite whereby hydrogen bonds to the O1 site to form hydroxyl groups that are charge balanced by cation vacancies on the Mg3 site. Structural models containing cation vacancies on the Mg2 site are found to be energetically less favourable and calculated NMR parameters show poor agreement with the experimental data. Disorder was also observed in the hydrous wadsleyite samples, and ¹H and ²H NMR are consistent with not only Mg–O1–H but also more strongly hydrogen-bonded Si–O–H environments. These silanol protons can be incorporated into the structure with only a small increase in energy. Two-dimensional ¹H–²⁹Si and ¹H–¹⁷O NMR correlation experiments confirm that the additional resonances do not correspond to Mg–OH protons and enable the identification of ²⁹Si and ¹⁷O species within the Si–OH groups. This assignment is also confirmed by first-principles DFT calculations of NMR parameters. Silanol protons within Mg3 vacancies could account for up to 20% of the protons in the structure.

---

Introduction

The Earth's mantle to a depth of 660 km is primarily composed of iron-bearing magnesium silicates, which undergo a number of phase transitions with increasing depth owing to changes in temperature and pressure. At a depth of 410 km, the main constituent of the upper mantle, olivine (α-(Mg,Fe)₂SiO₄), transforms to wadsleyite, (β-(Mg,Fe)₂SiO₄).¹ Wadsleyite is the main component of the so-called transition zone between the upper and lower mantle, until a depth of ∼530 km where it transforms to ringwoodite (γ-(Mg,Fe)₂SiO₄). Although making up a relatively small proportion of the Earth's mantle, wadsleyite has received intense interest as a potential host for hydrogen, as hydroxyls, commonly termed water, in the inner-Earth.^1–4 Whilst nominally anhydrous, this mineral can accommodate up to 3.3 wt% water.^2,5,6 Over the volume of the Earth's transition zone, this represents a potentially vast amount of water (if fully hydrated, the amount of hydrogen stored would be approximately four times the amount present in the oceans and atmosphere)³ with significant implications for mantle properties such as conduction,⁷ phase relations⁸ and elastic properties.⁹

The structure of Fe-free wadsleyite (β-Mg₂SiO₄), shown in Fig. 1a, has orthorhombic symmetry with the space group Imma.¹⁰ The structure is made up of Si₂O₇ (pyrosilicate) groups comprising a single crystallographic Si site, a bridging oxygen, O2, and two crystallographically distinct non-bridging silicate oxygens, O3 and O4. The structure also contains an oxygen site, O1, which is not bonded to silicon but instead is coordinated to five Mg²⁺ cations. This environment has a low apparent Pauling bond-strength sum, making it ‘underbonded’ relative to conventional divalent oxygen species. Each of the three crystallographically distinct Mg species is approximately octahedrally coordinated to six surrounding oxygens. Local coordination environments for each species are shown in ESI.†

Fig. 1 (a) Crystal structure of anhydrous wadsleyite with the four distinct O sites and three distinct Mg sites indicated. (b and c) Hypothetical ordered structures for fully hydrated hydrous wadsleyite obtained through full substitution of Mg2 and Mg3, respectively. Mg vacancies are indicated by dashed circles.

Despite its importance as a potential water reservoir in the mantle, the exact way in which hydrogen is substituted into the wadsleyite structure is not fully understood. Hydrogen can be incorporated into anhydrous silicates through the formation of OH⁻ groups, which are charge balanced by cation vacancies or coupled substitutions.^11,12 For hydrous wadsleyite, the incorporation of hydrogen atoms is balanced by the removal of magnesium, with the maximum effective H₂O content of 3.3 wt% corresponding to the removal of two magnesium cations per unit cell. In principle, cation vacancies can be located at any of the Mg1, Mg2 or Mg3 sites. Immediately surrounding each of these vacancies, there are eight oxygen atoms to which the incorporated hydrogen can bond. This means that there are several possible locations for hydrogen close to each vacancy and a number of different possibilities for the ordering of vacancies in the structure.

Several theoretical studies have identified the O1 site as being particularly susceptible to protonation due to its underbonded state.^2,3,13–17 Using simple ionic constraints and consideration of electrostatic potentials for the different oxygen sites, Smyth proposed a hypothetical ordered structure whereby O1 is fully protonated, with the O–H bond vectors oriented parallel to the c-axis, and the incorporation of H charge balanced by vacancies on the Mg2 site.³ This model, shown in Fig. 1b, corresponds to a theoretical maximum H₂O content of 3.3 wt%, which is in good agreement with a range of experimental measurements.^2,5,6 Recently, Tsuchiya and Tsuchiya performed a first-principles density functional theory (DFT) study of model structures for hydrous wadsleyite.¹⁷ Fully hydrated structures with vacancies on the Mg2 site (including the Smyth structure) were found to be stable; however, structures with full hydration of O1 balanced by vacancies on the Mg3 site, such as the structure shown in Fig. 1c, were found to be energetically more favourable. Other theoretical studies have identified favourable locations for protonation close to other oxygen sites in the structure. On the basis of electrostatic calculations, Downs suggested that the O2 site is a favourable location for protonation,¹⁸ while Ross et al. performed electron density calculations for wadsleyite and found favourable docking sites close to all oxygens in the structure.¹⁹ However, these studies did not account directly for the presence (and position) of cation vacancies in the structure.

Experimental studies of wadsleyite with high H₂O contents have generally indicated that the main mechanism for hydrogen incorporation is through vacancies on the Mg3 site. Indeed, X-ray diffraction suggests that most protons are located around the edges of vacant Mg3 octahedra.^20–23 A recent neutron diffraction study of a sample containing 1.6 wt% H₂O found the main location of deuterium atoms to be between the O1 and O4 oxygens,²⁴ as in the lowest energy Mg3-vacancy structures identified by Tsuchiya and Tsuchiya.¹⁷ However, larger numbers of hydrogen sites have been suggested for samples with lower H₂O concentrations. Kohn et al. used ¹H solid-state NMR and Fourier-transform infra-red (FTIR) spectroscopy to identify at least 14 different proton environments in samples with hydration levels between 0.8 and 1.5 wt% H₂O. It was suggested that O1 is no longer the main protonation site at 1.5 wt% H₂O.²⁵ Jacobsen et al. used polarised FTIR spectroscopy to study a series of samples with hydration levels up to 1 wt% and assigned OH bands to protons situated along the O1⋯O1, O1⋯O3 and O1⋯O4 vectors.²⁶ However, Deon et al. recently performed a combined XRD and FTIR study of samples containing 0.8 and 1.6 wt% H₂O and suggested that most hydrogen is located along the O1⋯O4 and O3⋯O4 edges of vacant Mg3 octahedra.²⁷

The sensitivity of NMR to the local structural environment makes it a potentially powerful complementary method to diffraction and FTIR for probing the structure of hydrous wadsleyite. NMR is an excellent probe of structure and dynamics in both crystalline and disordered materials, providing information with no requirement for long-range order. However, the synthesis of high-pressure minerals for NMR studies can be very challenging. The low natural abundances of the NMR-active nuclei (²⁵Mg (I = 5/2), ¹⁷O (I = 5/2) and ²H (I = 1)) mean that isotopic enrichment is often required for enhancement of the NMR signal. Furthermore, the high pressures (15–20 GPa) that are needed to synthesise mantle transition zone phases often greatly restrict the amount of sample that can be produced. However, despite the difficulties associated with NMR studies of high-pressure minerals, technological and methodological advances are enabling an increasing amount of structural insight to be obtained. The development of high-field NMR spectrometers and experimental methodologies such as DFS, WURST and QCPMG^28–30 has opened the way for the study of “difficult” nuclei such as ²⁵Mg and ¹⁷O, which can suffer from poor receptivity (even when isotopically enriched) owing to the quadrupolar broadening of spectral resonances. Furthermore, sophisticated experimental methods such as two-dimensional multiple-quantum (MQ)³¹ and satellite-transition (ST) MAS^32,33 experiments have been applied to achieve resolution of distinct resonances that are overlapped due to second-order quadrupolar broadening in conventional MAS NMR spectra.^34–38 Indeed, the STMAS method offers particular advantages in the study of high-pressure minerals, as sensitivity is typically 2–8 times higher than with MQMAS.³³

Another recent advance that has greatly complemented experimental solid-state NMR methods is the development of DFT codes that utilise periodic boundary conditions. These codes enable the efficient calculation of NMR parameters of solids with high accuracy by exploiting the inherent periodicity associated with crystalline systems. In particular, codes employing the gauge including projector augmented wave (or GIPAW)³⁹ approach, such as CASTEP⁴⁰ have seen widespread application for a large range of crystalline systems. More recently, a number of studies have demonstrated how this approach can also provide valuable insight in the study of structure, disorder and dynamics in inner-Earth minerals.^37,41–47

In the study of wadsleyite, NMR investigations have been relatively scarce to date. ¹⁷O and ²⁹Si NMR spectra for anhydrous wadsleyite have been obtained^48–50 and resonances assigned to distinct sites in the structure using first-principles calculations.⁴¹ For hydrous wadsleyite, in addition to the ¹H NMR study by Kohn et al.,²⁵ recent studies by Stebbins et al. used ²⁹Si enrichment to obtain structural information and were able to observe the effect on ²⁹Si NMR spectra of trace impurities of paramagnetic transition metal ions in the structure.^51,52

Here, we present a full multinuclear study of all the NMR-active nuclei present in anhydrous and hydrous wadsleyite. For the inherently insensitive nuclei ²⁵Mg, ¹⁷O and ²H, isotopic enrichment is used for the acquisition of high-quality NMR spectra. A variety of experimental methods are employed, including two-dimensional ¹⁷O STMAS and ¹H double-quantum (DQ) MAS NMR approaches, which provide a direct insight into the mechanism of hydration and enable the identification of distinct types of hydrated cation vacancies. These methods are complemented by first-principles calculations performed for a series of recently proposed model structures containing a range of different cation vacancy configurations. Using this approach, we are able to identify which models provide a better description of the overall structure in terms of both energetics and predicted NMR parameters. Additional calculations for a series of alternative defect structures together with heteronuclear correlation experiments provide further insight into the disorder that is observed to be present, leading to a more detailed picture of the local structure of this important mineral.

Experimental and computational methods

Synthesis

¹⁷O-enriched SiO₂ and Mg(OH)₂ were prepared from the reaction of 75%-enriched H₂¹⁷O with SiCl₄ and Mg₃N₂, respectively.³⁴ Mg(¹⁷OH)₂ was dehydrated to give Mg¹⁷O. Mg(O²H)₂ was prepared by the reaction of ²H₂O with Mg₃N₂. 98%-enriched ²⁵MgO was used without further modification. Relevant starting materials were mixed, in some cases with non-enriched oxides, in the correct proportions to give Mg_1.77H_0.46Si¹⁷O₄ (∼3 wt% H₂¹⁷O), Mg_1.77²H_0.46SiO₄ (∼3 wt% ²H₂O), and ²⁵Mg₂SiO₄. Mg₂Si¹⁷O₄ was prepared previously (ref. 49). The compositions (20–30 mg in most cases) were sealed in welded Pt capsules, with an external diameter of 3 mm and length of ∼3.5 mm, which were inserted into a 25/15 assembly comprising a MgO sleeve and spacers, LaCrO₃ heater, ZrO₂ outer sleeve, and Cr₂O₃-doped MgO octahedron. The hydrous wadsleyite compositions were equilibrated at either 1100 °C and 14 GPa or 1200 °C and 14.5 GPa for 1–3 h, and the anhydrous composition at 1100 °C and 15 GPa for 2 h, using a split-cylinder 6–8 Kwai-type multi-anvil apparatus (Toshiba F grade tungsten carbide anvils and pyrophyllite gaskets) and 5000-tonne hydraulic press. Further details of the assembly and press are given in ref. 53.

X-ray diffraction

X-ray powder diffraction patterns were recorded using a PANalytical X'Pert PRO diffractometer equipped with a Cu tube operating at 45 kV and 40 mA, a primary monochromator, and a 2.1° position sensitive detector (Xcelerator). Lattice parameters were determined by Le Bail refinement using Topas v4.1 software.

FTIR spectroscopy

Unpolarised transmission FTIR spectra were recorded from irregular aggregates of powder, held by surface tension within the squares of a TEM grid, using a Bruker Hyperion 1000 FTIR microscope connected to a Bruker Tensor 27 FTIR spectrometer.

Solid-state NMR

Solid-state NMR experiments were performed using Bruker Avance III spectrometers operating at magnetic field strengths, B₀, of 14.1 T and 20.0 T, corresponding to ¹H Larmor frequencies of 600.1 and 850.2 MHz, respectively. All experiments at both magnetic fields were performed using a Bruker 2.5 mm probe, at a MAS frequency of 30 kHz, unless otherwise stated. ¹⁷O MAS NMR spectra were recorded using recycle intervals of 2 s or 30 s. Two-dimensional ¹⁷O STMAS NMR spectra were recorded using a phase-modulated split-t₁ pulse sequence, with a recycle interval of 2 s. A double-quantum filter (DQF) was also used in the STMAS experiments to ensure the removal of the undesirable autocorrelation diagonal.⁵⁴ For all STMAS experiments, the rotor angle was adjusted prior to the experiment (to within an estimated accuracy of ±0.002°) using Rb₂SO₄.^33,55 For ¹H–¹⁷O CP MAS and two-dimensional HETCOR NMR experiments, transverse magnetisation was obtained by cross polarisation (CP) from ¹H using a contact pulse duration of 500 μs (ramped for ¹H), and a recycle interval of 1.5 s. Typical radiofrequency field strengths of 50 kHz and 10 kHz were used for ¹H and ¹⁷O, respectively. Owing to the relatively low signal-to-noise for hydrous wadsleyite, these parameters were optimised using ¹⁷O-enriched Mg(OH)₂. ¹⁷O chemical shifts were referenced relative to H₂O (l) at 0 ppm.

²⁵Mg MAS NMR spectra were recorded using a spin-echo pulse sequence to avoid baseline distortions owing to the relatively short T₂ relaxation times. For the natural abundance samples an initial double frequency sweep (DFS) pulse was used to increase signal sensitivity.⁵⁶ Spectra were referenced relative to 11 M MgCl₂ using a secondary reference of MgO at 26 ppm.

The ¹H MAS NMR spectrum was recorded using the “Depth” pulse sequence in order to reduce background signals from the probe.⁵⁷ The two-dimensional homonuclear ¹H correlation experiment was carried out using the double-quantum (DQ) MAS pulse sequence in ref. 47 with two cycles of BABA⁵⁸ dipolar recoupling for DQ excitation and reconversion. Sign discrimination in the indirect dimension was achieved using the States, Haberkorn, Ruben method.⁵⁹ Recycle intervals of 2 s were used for all ¹H NMR experiments. Spectra were referenced relative to TMS using the CH₃ resonance of L-alanine at 1.1 ppm as a secondary reference.

²H MAS NMR spectra were recorded using a recycle interval of 5 s. Prior to each experiment, the rotor angle was adjusted (to within an estimated accuracy of ±0.01°) by minimising the linewidth of the OD resonance of d₄-malonic acid.

²⁹Si MAS NMR spectra were obtained by direct polarisation of ²⁹Si, with a recycle interval of 120 s. Although this duration is too short to allow full relaxation, no difference in the relative intensities of the Si resonances was observed at shorter or longer recycle intervals. For the ¹H–²⁹Si CP MAS NMR experiment, transverse magnetisation was obtained by cross polarisation from ¹H using a contact pulse duration of 6 ms (ramped for ¹H) and a recycle interval of 3 s. Typical radiofrequency field strengths of 70 kHz and 50 kHz were used for ¹H and ²⁹Si, respectively. Two-pulse phase modulation (TPPM) ¹H decoupling was applied during acquisition. For the ¹H–²⁹Si CP HETCOR NMR experiment, a contact pulse duration of 1 ms was used. Sign discrimination in the indirect dimension was achieved using the States, Haberkorn, Ruben method.⁵⁹ Spectra were referenced relative to TMS using the single resonance of forsterite (Mg₂SiO₄) at −62 ppm as a secondary reference. Further experimental details are given in the relevant figure captions.

DFT calculations

Calculations of total energies and NMR parameters were carried out using the CASTEP DFT code,⁴⁰ employing the GIPAW algorithm,³⁹ which allows the reconstruction of the all-electron wave function in the presence of a magnetic field. The generalised gradient approximation (GGA) PBE functional⁶⁰ was employed and core–valence interactions were described by ultrasoft pseudopotentials.^61,62 Total energies and NMR parameters were calculated using a planewave energy cut-off of 50 Ry (680 eV) and integrals over the Brillouin zone were performed using a k-point spacing of 0.05 Å⁻¹. Calculations generate the absolute shielding tensor (σ) in the crystal frame. Diagonalisation of the symmetric part of σ yields the three principal components, σ_XX, σ_YY and σ_ZZ. The isotropic shielding, σ_iso, is given by (1/3) Tr{σ}. The isotropic chemical shift, δ_iso, is given by −(σ_iso − σ_ref), where σ_ref is a reference shielding. For ¹⁷O and ²⁹Si, σ_ref values of 251.1 ppm and 314.7 ppm, respectively, were determined by comparison to the experimental spectrum for anhydrous wadsleyite. For ²⁵Mg a σ_ref value of 565.7 ppm was taken from a recent DFT study of MgSiO₃.⁴⁷ For ¹H a σ_ref value of 30.5 ppm was determined by comparison of the calculated and experimental chemical shifts for L-alanine.

The quadrupolar coupling constant, C_Q = eQV_ZZ/h and asymmetry parameter, η_Q = (V_XX − V_YY)/V_ZZ are obtained directly from the principal components of the electric field gradient (EFG) tensor, which are ordered such that |V_ZZ| ≥ |V_YY| ≥ |V_XX|, where Q is the nuclear quadrupole moment (for which experimentally determined values of 199.4 and −25.6 mb were used for ²⁵Mg and ¹⁷O, respectively).⁶³ In addition to the magnitude, the calculations also generate the sign of C_Q. However, the sign of C_Q cannot be determined from the experimental data presented in this work; therefore, when comparing calculated and experimental quadrupolar couplings, we refer only to the magnitude of the calculated C_Q.

For anhydrous wadsleyite, the initial atomic positions and unit cell parameters were taken from an experimental diffraction structure.¹⁰ For hydrous wadsleyite model structures, hydrated defects were introduced by the removal of magnesium atoms from anhydrous wadsleyite and manual insertion of two protons around the resulting vacancies. For the calculation of defects within ordered hydrous wadsleyite structures, a 2 × 1 × 1 supercell was used to isolate the defect from its periodic images. Prior to calculation of the NMR parameters, all structures were fully geometry-optimised with the unit cell parameters allowed to vary using a cut-off energy of 40 Ry and k-point spacing of 0.05 Å⁻¹. Calculations were carried out using CASTEP version 5.5 on a 198-node (2376 core) Intel Westmere cluster with 2 GB memory per core and QDR Infiniband interconnect at the University of St Andrews. Typical calculation wallclock times ranged from 0.5 to 2 h using 96 cores, depending on the size of the model unit cell being calculated.

Results

X-ray diffraction and FTIR spectroscopy

The phase purity of each sample was determined using powder XRD. The anhydrous, ¹⁷O-enriched sample was pure wadsleyite, while the synthesis using the ²⁵Mg-enriched starting materials produced a mixture of wadsleyite, MgO and an unidentified minor phase. The ¹⁷O-enriched hydrous wadsleyite sample (referred to hereafter as wads-H) was found to be phase pure, while the sample of deuterated hydrous wadsleyite (hereafter referred to as wads-D) contained ∼15 wt% clinoenstatite. It is known that the water content of hydrous wadsleyite can be determined from an empirical relationship between the hydration level and the ratio of the b and a lattice parameters.²⁶ Although anhydrous wadsleyite has orthorhombic symmetry (Imma), hydration results in a deviation of β from 90° and monoclinic (I2/m) symmetry.^21,64 The lattice parameters of the hydrous wadsleyite samples were refined in both space groups, and the average values are given in Table 1. From these values, water contents of 2.9 wt% for wads-H and 3.2 wt% for wads-D were estimated. These values are close to the maximum hydration level of 3.3 wt%. We note that the empirical relationship relating the water content to b/a relies on calibrations of infrared spectra that may not be appropriate; however, it allows relative water contents to be compared between studies, although the absolute error may be as high as 20%.²³

Table 1 Unit cell parameters for samples of hydrous wadsleyite and calculated water contents.²⁶ The error in the lattice parameters corresponds to the difference between refinements in Imma and I2/m. The value of β is for I2/m

Sample	a (Å)	b (Å)	c (Å)	β (°)	b/a	H2O (wt%)
a No correction was made for the difference in mass between ^1H and ^2H.
Wads-H	5.6646(4)	11.5818(5)	8.2388(3)	90.051	2.0446	2.9
Wads-D	5.6654(1)	11.6041(20)	8.2412(9)	90.176	2.0482	3.2^a

---

FTIR spectra of the O–H stretching region (shown in ESI†) are broadly consistent with previous results for ¹H (ref. 25, 26 and 65) and ²H (ref. 24) hydrous wadsleyite. The ²H/(¹H + ²H) ratio of wads-D was estimated from the relative intensities of the ¹H–O and ²H–O stretching bands near 3350 and 2475 cm⁻¹, respectively, to be ∼0.35 (noting that the absorption coefficient of ¹H–O is 1.89 times that of ²H–O).

Solid-state NMR spectroscopy

¹⁷O MAS NMR spectra of anhydrous wadsleyite and wads-H are compared in Fig. 2. As observed previously at lower magnetic field^49,50 for anhydrous wadsleyite, a sharp resonance is observed corresponding to the O1 species, which has a small quadrupolar interaction as a result of its relatively symmetric local environment. Intensity observed between 80 and 40 ppm corresponds to the silicate oxygens O2, O3 and O4, which have larger quadrupolar interactions, and for which the resonances are consequently overlapped in the spectrum. Resolution is increased in a ¹⁷O STMAS NMR spectrum, shown in Fig. 2b, where the O1 and O2 sites are well separated in the isotropic dimension. At 20.0 T, the resonances corresponding to the O3 and O4 silicate oxygens remain closely spaced in the δ₁ dimension. However, these resonances have been resolved and assigned in previous studies at lower magnetic field.^49,50 Experimental NMR parameters for the four distinct oxygen sites in anhydrous wadsleyite are summarised in Table 2.

Fig. 2 (a and c) ¹⁷O (20.0 T) MAS and (b and d) STMAS NMR spectra of (a and b) anhydrous wadsleyite and (c and d) wads-H. MAS NMR spectra are the result of coadding 360 transients separated by a recycle interval of 30 s. STMAS NMR spectra are the result of averaging (b) 1280 and (d) 512 transients separated by a recycle interval of 1 s for each of (b) 164 and (d) 128 t₁ increments of 43.06 μs. In each case an echo duration of 1.8 ms was used and the MAS rate was 30 kHz.

Table 2 Experimental and calculated ¹⁷O quadrupolar coupling constants, C_Q, asymmetry parameters, η_Q, and chemical shifts, δ_iso, for anhydrous wadsleyite

Site	C ^expQ/MHz	η ^expQ	δ ^expiso (ppm)	C ^calcQ/MHz	η ^calcQ	δ ^calciso (ppm)
a Estimated from the value of PQ (= CQ(1 + ηQ^2)^1/2) determined in ref. 49. b Determined in ref. 50.
O1	∼1.3(1)^a	n. d.	38(1)^b	1.56	0.45	36.9
O2	5.0(1)	0.9(1)	78(1)	5.16	0.94	78.3
O3	4.4(1)^b	0.2(1)	66(1)^b	4.78	0.19	68.6
O4	3.8(1)^b	0.3(1)	65(1)^b	4.13	0.28	66.5

---

Fig. 2c shows a ¹⁷O MAS NMR spectrum of wads-H. This spectrum has a similar overall appearance to that for anhydrous wadsleyite, featuring a sharp O1 resonance and broader intensity corresponding to overlap of signals from O2, O3 and O4. However, the relative intensity of the O1 resonance is significantly reduced, and expansion of the region between 30 and −20 ppm (shown in the inset) reveals an additional, much broader resonance. The width and position of this resonance is consistent with that expected for a hydroxyl oxygen, which, in silicates, typically exhibit large quadrupolar coupling constants of between 6 and 7 MHz.^32,66,67 The simultaneous reduction in relative intensity of the O1 resonance and observation of hydroxyl group resonances suggests that hydrogen has been incorporated into the structure by bonding to O1. In the ¹⁷O STMAS NMR spectrum of wads-H, shown in Fig. 2d, the hydroxyl resonance is visible at a δ₁ value of ∼20 ppm. The spectrum also exhibits significant broadening of the resonances in both dimensions. It has been shown in STMAS NMR studies of other hydrated silicates that resonances in STMAS NMR spectra can be broadened as a result of microsecond timescale dynamics.^42,68 However, a ¹⁷O triple-quantum MAS NMR spectrum of wads-H (shown in ESI†) was recorded and found to be identical in appearance to the ¹⁷O STMAS NMR spectrum. MQMAS NMR experiments are not sensitive to dynamics on the same timescale, and therefore the observation of broadening in both high-resolution spectra indicates the presence of positional disorder rather than dynamics in the material.

To help interpret the ¹⁷O NMR data, first-principles DFT calculations were carried out. As a starting point, NMR parameters were calculated for anhydrous wadsleyite and the six fully hydrated ordered model structures identified by Tsuchiya and Tsuchiya.¹⁷ In each of these structures, two Mg²⁺ cations per unit cell are substituted for four protons, giving a formula unit of Mg₇Si₄O₁₄(OH)₂. Models containing vacancies on the Mg2 and Mg3 sites are denoted by vMg2^a,b and vMg3^a–d, respectively. In the vMg2 structures, the O1–H bond vectors lie parallel to the crystallographic c axis, each pointing into the centre of four O4 sites. The vMg2^a structure (shown in Fig. 1b) is equivalent to that proposed by Smyth, while in vMg2^b (shown in ESI†) adjacent O1–H bond vectors point in opposite directions. In the vMg3 structures, removal of the Mg3 cation is balanced by the incorporation of hydrogen atoms on O1 that form O1–H⋯O4 hydrogen bonds along the longer O1⋯O4 edge (3.12 Å) of the vacant Mg3 octahedron (as shown for vMg3^a in Fig. 1c). The four vMg3 structures differ in the relative positions of the two Mg3 vacancies within the unit cell. All structures were fully geometry-optimised prior to calculation of the NMR parameters. Whilst in all cases the basic wadsleyite structure was preserved, geometry optimisation resulted in small changes to the bond distances in all structures and more significant local distortions of the structures around the hydrated defects. In the following discussions of hydrogen locations within the optimised structures, we therefore refer to O⋯O distances as given in the unoptimised anhydrous structure¹⁰ for clarity. Further details of the model structures used, and calculated ¹⁷O NMR parameters for all structures, are given in ESI.†

Simulated ¹⁷O (20.0 T) MAS NMR spectra based on the calculated NMR parameters for each model structure are shown in Fig. 3. For anhydrous wadsleyite, good agreement between the calculated and experimental NMR parameters is observed (as shown in Table 2), and the simulated ¹⁷O MAS NMR spectrum shown in Fig. 3a agrees well with the experimental spectrum in Fig. 2a. The simulated spectra for the model structures vMg2^a and vMg2^b show very poor agreement with the experimental ¹⁷O MAS NMR spectrum of wads-H. In these model structures, hydrogen bonding between the O1–H hydroxyl protons and O4 silicate oxygens significantly changes the chemical shift for the O4 species resulting in intensity between 90 and 70 ppm in the simulated spectra, which is not observed experimentally. This indicates that vacancies on the Mg2 site are not the main mechanism for hydration in wadsleyite. Better agreement with the experimental data is observed for the model structures vMg3^a–d. Although these structures also contain O1–H⋯O4 hydrogen bonds, the different geometries of the hydroxyl groups result in ¹⁷O NMR parameters for the silicate oxygens that are more consistent with the intensity observed experimentally, between 80 and 40 ppm. Furthermore, the calculated quadrupolar parameters for the hydroxyl oxygen yield a lineshape that agrees well with the experimental hydroxyl resonance.

Fig. 3 Simulated ¹⁷O (20.0 T) MAS NMR spectra for (a) anhydrous wadsleyite and (b–g) fully hydrated ordered model structures for hydrous wadsleyite based on calculated NMR parameters. Lorentzian line broadening factors of (a) 200 Hz and (b–g) 400 Hz were applied prior to Fourier transformation of the simulated FIDs.

Calculated unit cell parameters and total energies for the ordered model structures are summarised in Table 3. Total energies are given (in kJ per mole of fully hydrated wadsleyite (Mg₇Si₄O₁₄(OH)₂)) relative to the lowest energy structure. Further details of the calculation of these total energies are given in the ESI.† Considering the calculated total energies, the vMg3^a–d structures are found to be much more favourable, as was observed by Tsuchiya and Tsuchiya.¹⁷ The lowest energy structure, vMg3^a, is lower in energy than vMg2^a and vMg2^b by 132 and 187 kJ mol⁻¹, respectively. For vMg3^a and vMg3^d, the geometry-optimised structure exhibits a distortion of the unit cell from orthorhombic to monoclinic symmetry. This is consistent with the experimental diffraction studies that have observed an increase in the unit cell β angle from 90° with increasing H₂O content.^21,64,65 However, the reported (experimental) β angles range between ∼90.1° and 90.4°, which is less than the value of 92.82° predicted by the calculation for vMg3^a. It was suggested by Tsuchiya and Tsuchiya that the similarity in energy of the other vMg3 structures means that disorder of the Mg3 vacancies could be possible and may result in partial cancelling of the monoclinic distortion.¹⁷ This would also be consistent with the disorder observed in the ¹⁷O STMAS NMR spectrum of wads-H.

Table 3 Unit cell parameters and calculated total energies relative to the lowest energy structure, E^calc_rel, for fully ordered model structures for hydrous wadsleyite

	vMg2^a	vMg2^b	vMg3^a	vMg3^b	vMg3^c	vMg3^d
a/Å	5.82	5.82	5.71	5.71	5.74	5.72
b/Å	11.56	11.56	11.70	11.69	11.77	11.71
c/Å	8.29	8.34	8.30	8.31	8.21	8.25
β (°)	90	90	92.82	90	90	92.24
E ^calcrel/kJ mol^−1	132.15	187.46	0.00	14.40	33.12	44.17

---

²⁵Mg MAS NMR spectra of ²⁵Mg-enriched anhydrous wadsleyite and wads-H are shown in Fig. 4. A ²⁵Mg MAS NMR experiment carried out for the anhydrous sample used for ¹⁷O NMR (which is natural abundance in ²⁵Mg) was unsuccessful owing to the very small quantity of sample. In the ²⁵Mg MAS NMR spectra, distinct magnesium sites are unresolved and the observation of broadened intensity extending to lower frequency indicates some disorder in the structures. For wads-H, this is consistent with the disorder observed in the ¹⁷O NMR spectra. For the ²⁵Mg-enriched anhydrous wadsleyite sample, the additional impurity phases that are known to be present in the sample may contribute to the broadening observed. However, we note that the dominant impurity, MgO, is not observed in the spectrum, probably owing to the very long T₁ relaxation time for this phase (∼60 s) compared to the short recycle interval (0.5 s) used in the experiment.

Fig. 4 ²⁵Mg (20.0 T) MAS NMR spectra of (a) ²⁵Mg-enriched anhydrous wadsleyite and (b) wads-H. Spectra are the result of coadding (a) 109 552 and (b) 163 840 transients separated by a recycle interval of 0.5 s. For wads-H an initial DFS pulse was used to increase signal sensitivity. In both cases the MAS rate was 30 kHz.

The similarity in appearance of the experimental ²⁵Mg NMR spectra for anhydrous wadsleyite and wads-H suggests that ²⁵Mg NMR is not very sensitive to the structural changes that take place upon hydration. However, simulated ²⁵Mg NMR spectra based on calculated NMR parameters for anhydrous wadsleyite and the six ordered model structures, shown in Fig. 5, indicate that it should be possible to distinguish between fully hydrated structures with Mg2 vacancies and Mg3 vacancies. Indeed, reasonable agreement between the simulated and experimental spectra is observed for anhydrous wadsleyite. The superposition of relatively sharp and broad second-order quadrupolar lineshapes in each case gives spectra that exhibit decreasing intensity to lower frequency, as seen in the experimental spectrum. In contrast, simulated ²⁵Mg NMR spectra for vMg2^a and vMg2^b, shown in Fig. 5b and c, are significantly different in appearance to the experimental spectrum for wads-H, with two distinct features clearly observed. The simulated spectra for vMg3^a–d show better agreement, each exhibiting one main feature with broadened intensity extending to low frequency. Even in the presence of disorder resulting in a broadening of the experimental lineshape, it should be possible to identify spectral features indicative of the fully hydrated vMg2 structure if they were present in significant amounts. The ²⁵Mg NMR data are therefore consistent with the ¹⁷O NMR spectrum that supports the presence of Mg3 vacancies. The calculated ²⁵Mg NMR parameters for the six fully hydrated ordered model structures are given in ESI.†

Fig. 5 Simulated ²⁵Mg (20.0 T) MAS NMR spectra for (a) anhydrous wadsleyite and (b–g) fully hydrated ordered model structures for hydrous wadsleyite based on calculated NMR parameters. In each case a Lorentzian line broadening factor of 400 Hz was applied prior to Fourier transformation of the simulated FID.

¹H solid-state NMR offers a direct insight into the local environment of the hydrogen atoms in the structure of hydrous wadsleyite. A ¹H MAS NMR spectrum of wads-H is shown in Fig. 6a. The spectrum exhibits an intense resonance at ∼4 ppm, together with a broad ‘shoulder’ at approximately 2 ppm. These chemical shifts are consistent with other measurements of hydroxyl protons in Mg–OH environments,^69,70 and are therefore consistent with the main mechanism of hydrogen atom incorporation being protonation of the O1 site. However, in addition to this main region of intensity, weaker resonances are also observed between approximately 6 and 10 ppm. These higher chemical shifts indicate the presence of protons that are in different (i.e., not Mg–OH) environments. A fit of the experimental spectrum assuming four individual Lorentzian lineshapes (and including spinning sidebands which are outside of the displayed spectral region) is shown underneath the experimental spectrum in red, with the individual components shown in blue. Integrated peak intensities obtained from the fit are summarised in Table 4. It can be seen that the resonances with chemical shifts greater than 6 ppm account for ∼17% of the total intensity, indicating that the protons in non-Mg–OH environments represent a small but significant proportion of the total number of protons in the sample. A two-dimensional ¹H DQMAS NMR spectrum, shown in Fig. 6b, correlates homonuclear dipolar-coupled spin pairs enabling the identification of protons that are in close proximity to each other. The two-dimensional spectrum provides higher resolution and confirms the presence of a number of distinct H sites. The main region of high intensity is revealed to be composed of two distinct species with chemical shifts of δ_SQ = 4.1 and 3.9 ppm. A weak autocorrelation signal is also observed at δ_SQ = 1.2 ppm. This resonance does not correlate with any other resonances in the spectrum, indicating that it corresponds to H species that are either more remote within the structure or related to a background signal from the rotor, as has been observed in another ¹H NMR study of high-pressure minerals.⁷¹ The spectrum exhibits a considerable spread along the δ_DQ = 2δ_SQ diagonal, indicating a distribution of hydroxyl proton environments. In addition to the Mg–OH resonances, correlations involving the protons with higher chemical shift are also observed. The resonances at δ_SQ = 8.6 and 6.7 ppm correlate with each other, and that at δ_SQ = 8.6 ppm correlates with the resonance at δ_SQ = 3.9 ppm. This confirms that protons with both high and low chemical shifts belong to the same phase, and indicates that multiple types of proton environments can exist for each hydrated cation vacancy.

Fig. 6 (a) A ¹H (14.1 T) MAS NMR spectrum of wads-H. The spectrum is the result of coadding 16 transients separated by a recycle interval of 10 s. A deconvolution of the experimental spectrum is shown below the MAS lineshape in red, with individual components shown in blue. (b) A rotor-synchronised ¹H (14.1 T) DQMAS NMR spectrum of wads-H recorded using two cycles of BABA recoupling.⁵⁸ DQ correlations are indicated by dashed lines. The diagonal line shows the axis δ₁ = 2δ₂ around which symmetrical correlation peaks are expected to appear. The ¹H DQMAS NMR spectrum is the result of coadding 32 transients separated by a recycle interval of 2 s for each of the 100 t₁ increments of 33.33 μs. Both spectra were recorded at a MAS rate of 30 kHz.

Table 4 Experimental ¹H and ²H chemical shifts, δ_iso, quadrupolar coupling constants, C_Q, and asymmetry parameters, η_Q, and relative intensities for H sites in hydrous wadsleyite samples obtained from fits to ¹H and ²H MAS NMR spectra shown in Fig. 6a and 7a

Wads-H			Wads-D
Site	δ iso ^1H (ppm)	Rel. int. (%)	δ iso ^2H (ppm)	Rel. int. (%)	C Q ^2H/kHz	η Q
1	1.1	19	2.8	13	240(10)	0.1(1)
2	3.4	64	4.6	57	223(10)	0(1)
3	6.7	10	7.9	9	184(10)	0.2(1)
4	8.6	7	9.7	21	148(10)	0.3(1)

---

A rotor-synchronised ²H MAS NMR spectrum of wads-D is shown in Fig. 7a. This spectrum has a similar overall appearance to the ¹H MAS NMR spectrum of wads-H, but is better resolved owing to the smaller dipolar coupling for ²H. The spectrum exhibits an intense resonance at 4.6 ppm with a shoulder at 2.8 ppm, as well as two lower-intensity resonances at 7.9 and 9.7 ppm. These values are slightly higher than the ¹H chemical shifts found for wads-H, although this could be due to the difference in hydrogen-bonding strength between ¹H and ²H, and also possibly due to small differences in referencing. We note that a ¹H MAS NMR spectrum of the residual protons in wads-D (shown in ESI†) exhibits very similar chemical shifts to those observed for wads-H. As well as providing higher resolution, ²H MAS NMR can be a sensitive probe of microsecond timescale dynamics, as modulation of the ²H quadrupolar coupling by dynamic processes can lead to a temperature-dependent broadening of the MAS sidebands.^45,68,72 However, a second ²H MAS NMR spectrum recorded at 373 K (shown in ESI†) showed no significant differences in the spectrum to that recorded at ambient temperature, confirming that microsecond timescale dynamics do not appear to be present.

Fig. 7 (a) Rotor-synchronised and (b) wide-spectral width ²H (14.1 T) MAS NMR spectra of wads-D. A deconvolution of the experimental spectrum in (a) is shown below the MAS lineshape in red, with individual components shown in blue. Spectra are the result of coadding (a) 4126 and (b) 12 378 transients separated by recycle intervals of 5 s. MAS rates were (a) 12.5 kHz and (b) 20 kHz.

Fig. 7b shows a ²H MAS NMR spectrum of wads-D recorded with a wider spectral width. In this spectrum, the first-order quadrupolar broadening of the ²H NMR resonances results in the observation of a spinning sideband manifold across a frequency range of approximately 200 kHz. ²H quadrupolar parameters obtained from fits for each of the four sites are summarised in Table 4. For the resonances with the lower chemical shifts, C_Q values of 240 and 223 kHz, and η_Q values of 0.09 and 0.00 are consistent with deuterons in Mg–OH environments.⁴⁵ However, the ²H species with higher chemical shifts have smaller C_Q values of 184 and 148 kHz and slightly higher η_Q values of 0.17 and 0.27. This further indicates that these resonances do not correspond to deuterons in Mg–OD environments.

Calculated ¹H chemical shifts for the ordered model structures are summarised in Table 5. For vMg2^a, the values of 3.6 and 3.5 ppm are within the distribution of the highest intensity observed in the ¹H DQMAS NMR spectra. For vMg2^b, the calculated chemical shift of 1.3 ppm for H2 is consistent with the low intensity resonance observed at 1.2 ppm. For the vMg3 structures, it can be seen that the arrangement of the Mg3 vacancies affects the calculated ¹H chemical shift, with predicted values between 3.6 and 5.2 ppm for the four structures. The disordered co-existence of these different arrangements could give rise to the broad region of intensity observed around δ_SQ = 4 ppm in the ¹H DQMAS NMR spectrum. However, none of the model structures adequately explain the resonances with higher chemical shift observed between 6 and 9 ppm. The observation of these resonances suggests the presence of protons in more strongly hydrogen-bonded environments.

Table 5 Calculated ¹H and ²⁹Si chemical shifts, δ^calc_iso, for anhydrous wadsleyite and fully ordered model structures for hydrous wadsleyite

δ ^calciso (ppm)
Site	Anhyd.	vMg2^a	vMg2^b	vMg3^a	vMg3^b	vMg3^c	vMg3^d
H1	—	3.6	3.9	4.2	3.6	4.6	5.2
H2	—	3.5	1.3	4.2	3.6	4.6	5.2
Si1a	–79.0	–80.7	–80.0	–76.8	–77.2	–77.8	–78.2
Si1b	—	–80.6	–80.8	–76.9	–78.9	–78.1	–78.2
Si1c	—	—	—	–78.4	—	—	—
Si1d	—	—	—	–78.4	—	—	—

---

To obtain further insight into the nature of the proton environments, ²⁹Si solid-state NMR experiments were performed. ²⁹Si MAS NMR spectra for anhydrous wadsleyite and wads-H are compared in Fig. 8a and b. For anhydrous wadsleyite, the observation of a single sharp resonance at −79 ppm is consistent with the single crystallographic Si site in the crystal structure, and is in agreement with previous work.^48,50–52 For wads-H, the ²⁹Si MAS NMR spectrum appears very similar to that obtained for anhydrous wadsleyite, with an intense resonance observed at −78.8 ppm. However, a lower intensity ‘shoulder’ is also observed at approximately −75 ppm. In a ²⁹Si CP MAS NMR spectrum, shown in Fig. 8c, the relative intensity of the shoulder is significantly increased and the position of the main resonance is shifted slightly to −78.2 ppm. The increased intensity of the additional resonance indicates that it corresponds to a silicon species that is closer to hydrogen in the structure than those that correspond to the main resonance. In a recent study by Stebbins et al., the observation of resonances around −75 ppm in ²⁹Si CP MAS NMR spectra of hydrous wadsleyite was attributed to the presence of a significant impurity of phase B, a dense hydrous magnesium silicate phase that was known to be present in the sample.⁵² However, no evidence of this (or any other) phase was observed in X-ray diffraction measurements of the sample used in the current study. Furthermore, for phase B, a second resonance corresponding to a Si^VI site is expected at −166 ppm.^71,73 A Si^VI resonance was observed in a ²⁹Si CP MAS NMR spectrum of a mixed phase sample known to contail a significant proportion of a related material, superhydrous phase B (shown in ESI†). However ²⁹Si CP MAS NMR spectra recorded for wads-H with contact times of up to 10 ms (shown in ESI†) did not show any evidence for resonances between ¬165 and ¬170 ppm that would indicate the presence of phase B or superhydrous B. This indicates that the additional resonance at −75 ppm corresponds to a silicon species within the hydrous wadsleyite structure itself.

Fig. 8 ²⁹Si (14.1 T) MAS NMR spectra of (a) anhydrous wadsleyite and (b) wads-H, and (c) a ¹H–²⁹Si (14.1 T) CP MAS NMR spectrum of wads-H. (d) A ¹H–²⁹Si (14.1 T) CP HETCOR NMR spectrum of wads-H. MAS NMR spectra are the result of coadding (a) 136 and (b) 1576 transients separated by a recycle interval of 120 s. The ¹H–²⁹Si CP MAS NMR spectrum was recorded using a contact pulse duration of 6 ms and is the result of coadding 2400 transients separated by a recycle interval of 3 s. The HETCOR spectrum is the result of coadding 2720 transients separated by a recycle interval of 1.5 s for each of the 28 t₁ increments of 50 μs. Polarisation transfer was achieved using a contact pulse duration of 1 ms. Spectra were recorded at MAS rates of (a and d) 20 kHz, (b) 30 kHz and (c) 12.5 kHz.

Further insight is obtained from a ¹H–²⁹Si two-dimensional HETCOR correlation spectrum of wads-H, shown in Fig. 8d. This spectrum was recorded using a relatively short contact time of 1 ms in order to favour short through-space proximities. In this spectrum, a high-intensity correlation peak is observed between the ²⁹Si resonance at −78.2 ppm and the ¹H resonances around 4 ppm. This is consistent with magnetisation transfer between Mg–OH hydroxyl protons and nearby pyrosilicate silicon species in the structure. However, a second low-intensity correlation is also observed between the ²⁹Si resonance at −75.0 ppm and the protons at chemical shifts between 6 and 10 ppm. This confirms that the additional ²⁹Si resonance is unlikely to correspond to phase B or superhydrous phase B, since a correlation with Mg–OH protons at lower chemical shift would be expected. Indeed, a ¹H DQMAS NMR spectrum of a sample containing superhydrous phase B (shown in ESI†) exhibits just two resonances with chemical shifts of 4.2 and 3.8 ppm (in good agreement with previous ¹H NMR studies of superhydrous phase B^71,73). Therefore, if phase B or superhydrous B were present in wads-H, the ¹H–²⁹Si HETCOR spectrum would be expected to exhibit a correlation between the ²⁹Si resonance at −75 ppm and proton resonances at lower chemical shift.

Calculated ²⁹Si chemical shifts for anhydrous wadsleyite and the ordered fully hydrated model structures are summarised in Table 5. For the model structures, a loss of symmetry upon incorporation of H into the structure leads to the structures having two or four crystallographically distinct silicon sites in the unit cell. The calculated ²⁹Si chemical shift of −79 ppm for the single crystallographic Si site in anhydrous wadsleyite is in good agreement with the experimental value. For vMg2^a and vMg2^b, the calculated chemical shifts show the opposite behaviour to those observed experimentally, being shifted downfield slightly to –80.0 and −80.7 ppm. The calculated ²⁹Si chemical shifts for vMg3^a–d show better agreement with the experimental values, with shifts predicted between −76.8 and −78.9 ppm. Although the exact values of calculated shifts would not necessarily be expected to be in perfect agreement with experimental values, calculated changes in shift (for ²⁹Si) have been shown to be extremely reliable.⁷⁴ The calculated shifts lie within the range covered by the main resonance in the experimental spectrum and therefore do not fully account for the additional signal intensity between −72.5 and −76 ppm in the experimental CP MAS and HETCOR spectra.

Discussion

The multinuclear experimental NMR data are generally consistent with a model for the structure of hydrous wadsleyite in which most of the hydrogen is located on the O1 site, with the substitution charge balanced by Mg3 cation vacancies. Considering the ¹⁷O NMR data for wads-H, the simultaneous observation of a resonance consistent with a hydroxyl oxygen and reduced intensity of the O1 resonance is a strong indication that hydrogen bonds to the O1 site to form Mg–OH hydroxyl groups. The presence of hydroxyl groups is further indicated by the ¹H and ²H NMR spectra, which show high intensity resonances with chemical shifts that are consistent with protons and deuterons in Mg–OH environments. Calculated ¹⁷O and ²⁵Mg NMR spectra for fully hydrated ordered model structures give much better agreement with the experimental data for structures containing Mg3 vacancies than for structures containing Mg2 vacancies. The validity of the model structures with Mg3 vacancies is also supported by the significantly lower calculated energies as compared to those with Mg2 vacancies. These findings are consistent with a number of experimental X-ray diffraction studies of hydrous wadsleyite which have observed high concentrations of Mg3 vacancies together with the shortening of the O1–O4 distance, indicating that the proton sits on the edge of the octahedral vacancy.^20,22,23,27 Additionally, a recent neutron powder diffraction study located deuterium in an O1–D⋯O4 hydrogen bond along the Mg3 octahedral edge.²⁴

However, the models with ordered Mg3 cation vacancies do not provide a complete explanation for all the experimental NMR data. In particular, the observation of resonances with chemical shifts between 6 and 9 ppm in the ¹H NMR spectrum, and a ²⁹Si resonance with a chemical shift of −75 ppm in ²⁹Si CP MAS NMR and ¹H–²⁹Si HETCOR spectra are not consistent with any of the fully hydrated ordered model structures. It is possible that, while a large proportion of the hydrogen is located in environments such as those described by the model structures vMg3^a–d, a smaller number are present in defects with different proton arrangements, or are centred around vacancies on different cation sites. Indeed, a number of other hydrogen locations have been proposed in the literature. In particular, FTIR and neutron powder diffraction measurements have been interpreted in terms of a bent O1–H⋯O3 hydrogen bond along the edge of a vacant Mg3 octahedron.^24,26 Recently, Deon et al. suggested that protonation occurs along the O3–O4 edge of the vacant Mg3 octahedron (in addition to O1–O4), with random protonation of either two O1, two O3, or one O1 and one O3.²⁷ Diffraction studies have generally reported that concentrations of cation vacancies on the Mg2 and Mg1 sites are low. However, it may be possible that low levels of hydrated Mg1 and Mg2 defects could contribute to the low-intensity signals observed in the NMR spectra.

To investigate the relative stabilities of alternative hydrated defects within the hydrous wadsleyite structure, further DFT calculations were carried out on additional model structures. A set of 24 additional structures was constructed, with each structure based upon a 2 × 1 × 1 supercell of the lowest energy ordered vMg3 structure, vMg3^a. In each supercell, a single Mg3 vacancy was altered such that the proton configuration was changed, or it was replaced by a vacancy on another cation site. In this way, the models simulate an alternative hydrated defect within an otherwise ordered fully hydrated structure. For alternative defects based around Mg2 and Mg3 vacancies, configurations were considered that contained either a single hydroxyl proton and a single silanol proton, or two silanol protons. For configurations based around a vacancy on the Mg1 site, the relatively large distance from O1 meant that only defects containing two silanol protons were considered. Further details of all the structural models used are given in ESI.† After full geometry optimisation of each structure, the total internal energy and NMR parameters were calculated.

Calculated total energies for the supercell defect structures are compared with energies for the ordered model structures in Fig. 9. The structures are ranked in terms of increasing total energy for each type of alternative defect and the oxygen sites to which the protons are bonded within the alternative defect are indicated. The results show that the fully ordered vMg3^a structure still remains the lowest energy of all the structures considered. However, the energies for the alternative defect structures show that in many cases altering the proton configuration within one of the Mg3 vacancies in this structure, or replacing it with a vacancy in another location only leads to a relatively small increase in the total energy. For the structures where the alternative defect remains around Mg3 and simply differs in the proton configuration, five structures have energies of less than 23 kJ mol⁻¹ greater than vMg3^a. These structures each have a Mg3 vacancy defect containing a single hydroxyl and a single silanol proton. In each of these alternative defects the hydroxyl proton forms an O1–H⋯O4 hydrogen bond along the longer (3.12 Å) octahedral edge, as in the fully hydrated model structures. The silanol protons were found to form hydrogen bonds along the O3–H⋯O4 (2.91 Å), O3–H⋯O3 (2.85 Å) and O4–H⋯O1 (3.12 Å) edges of the vacant Mg3 octahedron. We note that structures containing defects with a proton situated in a bent O1–H⋯O3 (2.99 Å) hydrogen bond configuration (as has been suggested in the literature^24,26) were found to be unstable and always optimised to the O1–H⋯O4 (3.12 Å) position. Furthermore, structures with protons situated in hydrogen bonds along the O1⋯O1 (2.90 Å) and shorter O1⋯O4 (2.79 Å) edges of the vacant Mg3 octahedron, which have also been suggested in the literature,²⁶ were also found to be unstable, and similarly optimised consistently to the longer O1–H⋯O4 (3.12 Å) position.

Fig. 9 Calculated total energies for fully hydrated ordered model structures (represented by empty and filled blue diamonds) and structures containing a hydrated defect at an alternative cation site (represented by squares, triangles and crosses). For the defect model structures, the oxygen sites to which the hydrogen atoms are bonded within the alternative defect are indicated. Energies are shown relative to the lowest energy structure, vMg3^a.

Three other structures with Mg3 vacancy defects containing two silanol protons have energies between 37 and 55 kJ mol⁻¹ greater than vMg3^a. The slightly higher energies of these structures indicate that protonation of the O1 site is favoured over protonation of silicate oxygens. However, the calculated energies for the structures containing defects centred around Mg1 (which all contain two silanol protons) all fall within 30 kJ mol⁻¹ of vMg3^a. For structures containing Mg2 vacancy defects, proton configurations including one or two O1–H hydroxyl groups are more favourable, although energies are higher in general than for the alternative Mg1 and Mg3 defects. Comparing the calculated energies with those determined for the other ordered fully hydrated structures, the energies for the alternative defect structures are significantly less than for the ordered structures vMg2^a and vMg2^b. This analysis does not provide a complete picture of the energetics of hydrated defects in wadsleyite as not all possible proton configurations have been considered. Furthermore, the calculated energies do not account for finite temperature and entropic effects, which will be important in determining whether the types of defects considered can be stabilised under the high-temperature and/or high-pressure synthesis conditions. However, the calculations for the 24 additional model structures serve to illustrate that alternative types of defect including silanol protons can be accommodated within the fully hydrated structure with only a small effect on the total energy.

Calculated ¹H chemical shifts for the ordered model structures and alternative defect structures are plotted for each type of ¹H environment in Fig. 10a. For O1–H hydroxyl protons, calculated chemical shifts fall within the range 5.2–0.7 ppm, with an average shift (indicated by the dotted line) of 3.8 ppm. This is still within the range of the broad region of high signal observed in the experimental ¹H DQMAS NMR spectrum of wads-H, indicating that the incorporation of the alternative defects in the fully hydrated model structures does not have a significant effect on the chemical shifts of surrounding hydroxyl protons. In contrast, for protons bonded to silicate oxygens O2, O3 and O4, significantly higher chemical shifts are predicted, with values in the range 7.5–13.9 ppm. These values are generally higher than the experimental values for the high chemical shift resonances of 8.7 and 6.7 ppm. However, the calculated values indicate that significantly higher chemical shifts are expected for silanol protons, and therefore offer a possible explanation for the high chemical shift resonances observed experimentally. We note that a tendency for the overestimation of ¹H chemical shifts for hydrogen-bonded protons has been observed in other GIPAW studies.^74–76

Fig. 10 Calculated (a) ¹H chemical shifts, (b) ²H quadrupolar coupling and (c) ²⁹Si chemical shifts for all H and Si sites in the ordered and defect-containing model structures, grouped by local bonding environment. Average values for each group of parameters are indicated by dashed lines.

Calculated ²H C_Q values for the ordered model structures and the alternative defect structures are plotted for each type of ²H environment in Fig. 10b. The calculations predict C_Q values for O1–H hydroxyl deuterons in the range 212–280 kHz, with an average value of 233 kHz. This range is consistent with the values of 223 and 240 kHz measured for the deuterons with low chemical shift in the ²H MAS NMR spectrum shown in Fig. 7b. For O2–H deuterons, large C_Q values are also predicted, with an average value of 228 kHz. This makes it unlikely that the resonances with high chemical shift correspond to hydrogen in O2–H environments, since smaller C_Q values of 148 and 184 kHz were measured experimentally. However, for silanol O3–H and O4–H deuterons, distinctly smaller C_Q values in the range 66–212 kHz are predicted, with average values of 134 and 162 kHz, respectively. These ranges and average values are in good agreement with the experimental C_Q values measured for the ²H species with high chemical shift. This further indicates that the resonances at higher chemical shift observed in the ¹H and ²H NMR data correspond to silanol O3–H and O4–H.

Calculated ²⁹Si chemical shifts for different types of silicon environments in the ordered fully hydrated model structures and the alternative defect structures are plotted in Fig. 10c. For silicon species in non-protonated silicate SiO₄ environments, the calculated chemical shifts lie between −73.1 and −81.1 ppm with an average value of −78.2 ppm. This value is in good agreement with the experimental chemical shift of the most intense resonance in the ²⁹Si CP MAS NMR spectrum of wads-H. Significant shifts are also predicted for Si–OH environments, depending on the oxygen site that is protonated. For silicon species directly bonded to a protonated O2 oxygen, a downfield shift is predicted, with an average value of −79.1 ppm. For silicon species directly bonded to protonated O3 and O4 oxygens, upfield shifts are predicted with average values of −75.0 and −76.2 ppm, respectively. The close proximity of the silicon species in these environments to the nearby silanol protons would favour their observation in ²⁹Si CP MAS NMR spectra over SiO₄ silicon species that are slightly further away from protons in the structure. The increased intensity of the resonance at around −75 ppm in the ²⁹Si CP MAS NMR spectrum of wads-H is therefore consistent with the presence of Si–O3–H and Si–O4–H silanol silicon species in the structure. Increased intensity in the region around −79.1 ppm is not observed experimentally, indicating that silicon species in Si–O2–H environments are not present in significant quantities and that protonation of O2 is not extensive.

The ¹H and ²⁹Si solid-state NMR data are consistent with a structural model for hydrous wadsleyite whereby most hydrogen is incorporated as hydroxyl groups in Mg3 cation vacancies, while low levels of silanol O3–H and O4–H groups are also present. To obtain further evidence for the existence of silanol groups in the structure, we may consider what NMR parameters should be expected for ¹⁷O species within the silanol groups. Fig. 11a plots calculated ¹⁷O C_Q values for all hydroxyl and silanol oxygen species in the ordered model structures and the 24 defect model structures considered in this study. In general, lower C_Q values are calculated for oxygens in O3–H and O4–H oxygens. However, the results suggest that it would be difficult to distinguish these from the O1–H hydroxyl oxygens, as there is considerable overlap in the ranges of calculated C_Q values.

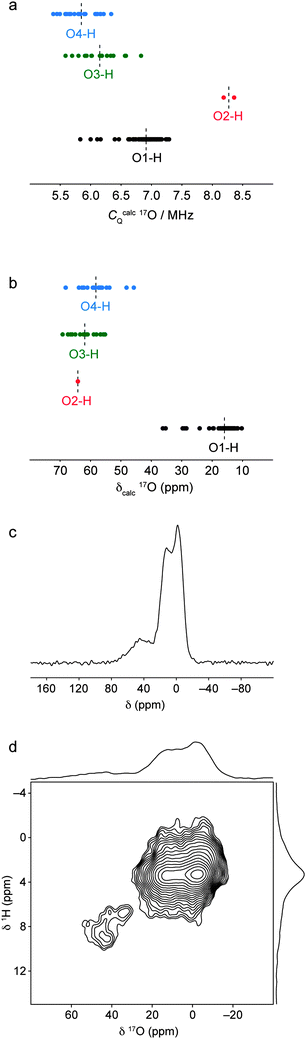Fig. 11 Calculated (a) ¹⁷O quadrupolar coupling constants and (b) chemical shifts for all O sites in the ordered and defect-containing model structures, grouped by local bonding environment. Average values for each group of parameters are indicated by dashed lines. (c) ¹H–¹⁷O (20.0 T) CP MAS NMR spectrum of wads-H obtained by coadding 3752 transients separated by a recycle interval of 1.5 s. (d) ¹H–¹⁷O CP HETCOR NMR spectrum of wads-H, obtained by coadding 400 transients separated by a recycle interval of 1.5 s for each of the 90 t₁ increments of 33.33 μs. The ¹H–¹⁷O CP MAS and HETCOR NMR spectra were both recorded at a MAS rate of 30 kHz, with polarisation transfer achieved using a contact time of 500 μs.

Calculated values for O2–H oxygens are significantly larger, although this also means they will be more difficult to observe experimentally. However, a plot of calculated isotropic chemical shift for each type of oxygen environment, shown in Fig. 11b, shows that the silanol oxygens have significantly higher chemical shifts and should be distinguishable from the hydroxyl oxygens on this basis. The calculations predict that the silanol oxygens should fall in the same region as the silicate oxygen resonances, making them difficult to observe in ¹⁷O MAS, MQMAS and STMAS NMR spectra. Instead, it is possible to favour the observation of oxygens that are close to protons by using a ¹H–¹⁷O CP MAS NMR experiment. A ¹H–¹⁷O CP MAS NMR experiment was performed on wads-H using a contact time of 500 μs to ensure selective transfer between protons and nearby oxygens. This is slightly longer than contact times employed in other selective ¹H–¹⁷O CP MAS NMR experiments;⁷⁷ however, the faster MAS frequency of 30 kHz used in this experiment (to maximise ¹H resolution) necessitates longer contact times to achieve magnetisation transfer. In the ¹H–¹⁷O CP MAS NMR spectrum, shown in Fig. 11c, a strong resonance corresponding to the hydroxyl oxygen species is observed owing to the close ¹H–¹⁷O proximity (approximately 1 Å as determined from the optimised model structures) and high proportion of hydroxyl groups in the structure. In addition to the hydroxyl oxygen resonance, additional weak intensity is observed at higher chemical shift. In a ¹H–¹⁷O heteronuclear correlation spectrum recorded using the same 500 μs contact time, shown in Fig. 11d, this resonance is observed to correlate with only the protons with higher chemical shifts between 6–9 ppm, while the intense hydroxyl oxygen resonance correlates only with protons around 4 ppm. This confirms that those protons with high chemical shift are in close proximity to oxygen species that are not in Mg–OH environments. The position of the observed resonance is instead consistent with the calculated ¹H and ¹⁷O NMR parameters for oxygens in Si–OH environments.

Conclusions

The multinuclear NMR data point towards a structural model for hydrous wadsleyite that is consistent with those proposed in recent studies whereby a large proportion of the cation vacancies are located on the Mg3 site, and protonation takes place along the longer O1⋯O4 (3.12 Å) edges of the vacant Mg3 octahedron. An expanded view of this hydrated defect structure is shown in Fig. 12a. DFT calculations indicate that fully ordered structures containing hydrogens in locations such as this are the most stable; however, the incorporation of alternative defects containing either one or two Si–OH protons (such as those shown in Fig. 12b and c) can be achieved with only a small increase in energy. These findings are consistent with the recent work by Deon et al.,²⁷ where it was proposed that the main sites for protonation are along the longer O1⋯O4 (3.12 Å) and shorter O3⋯O4 (2.91 Å) edges of vacant Mg3 octahedra. In addition, DFT calculations also indicate that the O3⋯O3 edge of the vacant Mg3 octahedron is a stable location for a hydrogen atom to be incorporated (as shown in Fig. 12b). The calculated NMR parameters for Si–OH silicons, oxygens and protons within Mg3 vacancies are consistent with those observed experimentally. The experimental ¹H MAS NMR spectra indicate that silanol protons within Mg3 vacancies could account for up to approximately 20% of the protons in the structure.

Fig. 12 Expanded views of proposed models for hydrated defects surrounding the vacant Mg3 octahedron (shown in green) in the structure of hydrous wadsleyite. Vacancies are shown containing (a) two hydroxyl, (b) one hydroxyl and one silanol, and (c) two silanol protons. Oxygen, silicon and hydrogen atoms are represented by red, blue and black spheres, respectively. The nomenclature of the oxygen species is as given in the anhydrous crystal structure.¹⁰

Previous studies have also identified the locations described above as potential sites for protonation, together with other sites such as the O1⋯O1 (2.90 Å) edge and shorter O1⋯O4 (2.79 Å) edge of the vacant Mg3 octahedron, and the O4⋯O4 (2.72 Å) tetrahedral edge of the Si₂O₇ group.^24–26 Our results suggest that many of these additional locations are highly unstable and fail to optimise in the DFT calculations. However, we have found that hydrated defects located around Mg1 and Mg2 vacancies can also be incorporated into the fully hydrated structure with only a small increase in energy. Although only low concentrations of Mg1 and Mg2 vacancies have been measured in diffraction studies, calculated NMR parameters for silicons, oxygens and protons within some of these types of defects are consistent with those observed experimentally, with the exception of ²H and ²⁹Si NMR parameters for Si–O2–H groups.

Although this work has focussed on Fe-free silicates, natural minerals do contain small amount of Fe. This would, of course increase the disorder present, but we anticipate that the major conclusions of this work would be very similar, as previous work on mantle silicates has shown IR spectra of Fe-free and Fe-bearing minerals to be essentially the same. Any effect of Fe incorporation, however, does offer an interesting and extremely challenging area for future investigation.

This work has provided direct insight into the location of hydrogen within hydrous wadsleyite, using only milligram quantities of synthetic sample. We envisage that the methods employed in this work will be applicable in a wider context for further structural characterisation of both this mineral and other important silicate phases, enabling a deeper understanding of the locations and distribution of hydrogen in the Earth's mantle.

Acknowledgements

We are grateful to the Leverhulme Trust (Grant number F/00268/BJ) and to the research councils for a RCUK academic fellowship to S.E.A. We thank EaStCHEM for computational support through the EaStCHEM Research Computing Facility. We thank Jens Najorka for assistance with the diffraction experiments and the lattice parameter refinements. High-pressure experimentswere performed at the Bayerisches Geoinstitut under the EU “Research Infrastructures: Transnational Access” Programme (Contract no. 505320 (RITA) – High Pressure). The UK 850 MHz solid-state NMR Facility used in this research was funded by EPSRC and BBSRC, as well as the University of Warwick including via part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (EDRF).

Notes and references

1. T. Katsura and E. Ito, J. Geophys. Res., 1989, 94, 15663.
2. J. R. Smyth, Am. Mineral., 1987, 72, 1051.
3. J. R. Smyth, Am. Mineral., 1994, 79, 1021.
4. N. Bolfan-Casanova, H. Keppler and D. C. Rubie, Earth Planet. Sci. Lett., 2000, 182, 209.
5. T. Inoue, H. Yurimoto and Y. Kudoh, Geophys. Res. Lett., 1995, 22, 117.
6. D. L. Kohlstedt, H. Keppler and D. C. Rubie, Contrib. Mineral. Petrol., 1996, 123, 345.
7. X. Huang, Y. Xu and S. Karato, Nature, 2005, 434, 746.
8. J. Chen, T. Inoue, H. Yurimoto and D. J. Weidner, Geophys. Res. Lett., 2002, 29, 1875.
9. S. D. Jacobsen, Rev. Mineral. Geochem., 2006, 62, 321.
10. H. Horiuchi and H. Sawamoto, Am. Mineral., 1981, 66, 658.
11. A. J. Berry, H. St. C. O'Neill, J. Hermann and D. R. Scott, Earth Planet. Sci. Lett., 2007, 261, 134.
12. A. M. Walker, J. Hermann, A. J. Berry and H. St. C. O'Neill, J. Geophys. Res.: Atmos., 2007, 112, B05211.
13. B. Winkler, V. Milman, B. Hennion, M. C. Payne, M.-H. Lee and J. S. Lin, Phys. Chem. Miner., 1995, 22, 461.
14. K. Wright and C. R. A. Catlow, Phys. Chem. Miner., 1996, 23, 38.
15. M. Haiber, P. Ballone and M. Parrinello, Am. Mineral., 1997, 82, 913.
16. A. M. Walker, S. Demouchy and K. Wright, Eur. J. Mineral., 2006, 18, 529.
17. J. Tsuchiya and T. Tsuchiya, J. Geophys. Res.: Atmos., 2009, 114, B02206.
18. J. W. Downs, Am. Mineral., 1989, 74, 1124.
19. N. L. Ross, G. V. Gibbs and K. M. Rosso, Am. Mineral., 2003, 88, 1452.
20. Y. Kudoh, T. Inoue and H. Arashi, Phys. Chem. Miner., 1996, 23, 461.
21. Y. Kudoh and T. Inoue, Phys. Chem. Miner., 1999, 26, 382.
22. C. M. Holl, J. R. Smyth, S. D. Jacobsen and D. J. Frost, Am. Mineral., 2008, 93, 598.
23. Y. Ye, J. R. Smyth, A. Hushur, M. Manghani, D. Lonappan, P. Dera and D. J. Frost, Am. Mineral., 2010, 95, 1765.
24. A. Sano-Furukawa, T. Kuribayashi, K. Komatsu, T. Yagi and E. Ohtani, Phys. Earth Planet. Inter., 2011, 189, 56.
25. S. C. Kohn, R. A. Brooker, D. J. Frost, A. E. Slesinger and B. J. Wood, Am. Mineral., 2002, 87, 293.
26. S. D. Jacobsen, S. Demouchy, D. J. Frost, T. Boffa-Ballaran and J. Kung, Am. Mineral., 2005, 90(1), 61.
27. F. Deon, M. Koch-Müller, D. Rhede, M. Gottschalk, R. Wirth and S.-M. Thomas, Am. Mineral., 2010, 95, 312.
28. F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Neilsen, J. Magn. Reson., 1998, 131, 144.
29. L. A. O'Dell and R. W. Schurko, Chem. Phys. Lett., 2008, 464, 97.
30. D. Iuga, H. Schafer, R. Verhagen and A. P. M. Kentgens, J. Magn. Reson., 2000, 147, 192.
31. L. Frydman and J. S. Harwood, J. Am. Chem. Soc., 1995, 117, 5367.
32. Z. Gan, J. Am. Chem. Soc., 2000, 122, 3242.
33. S. E. Ashbrook and S. Wimperis, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 53.
34. S. E. Ashbrook, A. J. Berry and S. Wimperis, Am. Mineral., 1999, 84, 1191.
35. S. E. Ashbrook, A. J. Berry and S. Wimperis, J. Am. Chem. Soc., 2001, 123, 6360.
36. S. E. Ashbrook, A. J. Berry and S. Wimperis, J. Phys. Chem. B, 2002, 106, 773.
37. S. E. Ashbrook, A. J. Berry, D. J. Frost, A. Gregorovic, J. E. Readman and S. Wimperis, J. Am. Chem. Soc., 2007, 129, 13213.
38. M. C. Davis, W. Brouwer, A. S. Lipton, Z. Gan and K. T. Mueller, Am. Mineral., 2010, 95, 1601.
39. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
40. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
41. S. E. Ashbrook, L. Le Pollès, C. J. Pickard, A. J. Berry, S. Wimperis and I. Farnan, Phys. Chem. Chem. Phys., 2007, 9, 1587.
42. J. M. Griffin, S. Wimperis, A. J. Berry, C. J. Pickard and S. E. Ashbrook, J. Phys. Chem. C, 2009, 113, 465.
43. L. S. Cahill, J. V. Hanna, A. Wong, J. C. C. Freitas, J. R. Yates, R. K. Harris and M. E. Smith, Chem.–Eur. J., 2009, 15, 9785.
44. P. J. Pallister, I. L. Moudrakovski and J. A. Ripmeester, Phys. Chem. Chem. Phys., 2009, 11, 11487.
45. J. M. Griffin, A. J. Miller, S. Wimperis, A. J. Berry and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2010, 12, 2989.
46. J. M. Griffin, J. R. Yates, A. J. Berry, S. Wimperis and S. E. Ashbrook, J. Am. Chem. Soc., 2010, 132, 15651.
47. J. M. Griffin, A. J. Berry and S. E. Ashbrook, Solid State Nucl. Magn. Reson., 2011, 40, 91.
48. J. F. Stebbins and M. Kanzaki, Science, 1991, 251, 294.
49. S. E. Ashbrook, A. J. Berry, W. O. Hibberson, S. Steuernagel and S. Wimperis, J. Am. Chem. Soc., 2003, 125, 11824.
50. S. E. Ashbrook, A. J. Berry, W. O. Hibberson, S. Steuernagel and S. Wimperis, Am. Mineral., 2005, 90, 1861.
51. J. F. Stebbins, W. Panero, J. R. Smyth and D. J. Frost, Am. Mineral., 2009, 94, 626.
52. J. F. Stebbins, J. R. Smyth, W. R. Panero and D. J. Frost, Am. Mineral., 2009, 94, 905.
53. D. J. Frost, B. T. Poe, R. G. Tronnes, C. Liebske, A. Duba and D. C. Rubie, Phys. Earth Planet. Inter., 2004, 143/144, 507.
54. H.-T. Kwak and Z. Gan, J. Magn. Reson., 2003, 164, 369.
55. S. E. Ashbrook and S. Wimperis, J. Magn. Reson., 2002, 156, 269.
56. D. Iuga, H. Schäfer, R. Verhagen and A. P. M. Kentgens, J. Magn. Reson., 2000, 147, 192.
57. D. G. Cory and W. M. Ritchey, J. Magn. Reson., 1988, 80, 128.
58. W. Sommer, J. Gottwald, D. E. Demco and H. W. Spiess, J. Magn. Reson., Ser. A, 1995, 113, 131.
59. D. J. States, R. A. Haberkorn and D. J. Ruben, J. Magn. Reson., 1982, 48, 286.
60. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
61. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
62. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
63. P. Pyykkö, Mol. Phys., 2008, 106, 1965.
64. J. R. Smyth, T. Kawamoto, S. D. Jacobsen, R. J. Swope, R. L. Hervig and J. R. Holloway, Am. Mineral., 1997, 82, 270.
65. Z. Mao, S. D. Jacobsen, F. M. Jiang, J. R. Smyth, C. M. Holl, D. J. Frost and T. S. Duffy, Earth Planet. Sci. Lett., 2008, 268, 540.
66. E. R. H. Van Eck, M. E. Smith and S. C. Kohn, Solid State Nucl. Magn. Reson., 1999, 15, 181.
67. S. E. Ashbrook and M. E. Smith, Chem. Soc. Rev., 2006, 35, 718.
68. S. E. Ashbrook, S. Antonijevic, A. J. Berry and S. Wimperis, Chem. Phys. Lett., 2002, 364, 634.
69. X. Xue and M. Kanzaki, J. Am. Ceram. Soc., 2009, 92, 2803.
70. C. Chizallet, H. Petitjean, G. Costentin, H. Lauron-Pernot, J. Maquet, C. Bonhomme and M. Che, J. Catal., 2009, 268, 175.
71. X. Xue, M. Kanzaki and A. Shatskiy, Am. Mineral., 2008, 93, 1099.
72. M. Cutajar, S. E. Ashbrook and S. Wimperis, Chem. Phys. Lett., 2006, 423, 276.
73. B. L. Phillips, P. C. Burnley, K. Worminghaus and A. Navrotsky, Phys. Chem. Miner., 1997, 24, 179.
74. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 11, 5733.
75. A.-C. Uldry, J. M. Griffin, J. R. Yates, M. Pérez-Torralba, M. D. Santa Maria, A. L. Webber, M. L. L. Beaumont, A. Samoson, R. M. Claramunt, C. J. Pickard and S. P. Brown, J. Am. Chem. Soc., 2008, 130, 945.
76. A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, J. Phys. Chem. A, 2010, 114, 10435.
77. L. Peng, Y. Liu, N. Kim, J. E. Readman and C. P. Grey, Nat. Mater., 2005, 4, 216.

---

Footnote

† Electronic supplementary information (ESI) available: FTIR spectra of hydrous wadsleyite, a comparison of ¹⁷O MQMAS and STMAS NMR spectra, structural models used for DFT calculations, calculated ¹⁷O and ²⁵Mg NMR parameters (and total energies) for structural models, ¹H MAS and variable-temperature ²H MAS of wads-D, ²⁹Si and ¹H solid-state NMR of phase B. See DOI: 10.1039/c3sc21892a

---