Vibrationally resolved dynamics of the reaction of Cl atoms with 2,3-dimethylbut-2-ene in chlorinated solvents†
Fawzi
Abou-Chahine
a,
Stuart J.
Greaves‡
a,
Greg T.
Dunning
a,
Andrew J.
Orr-Ewing
*a,
Gregory M.
Greetham
b,
Ian P.
Clark
b and
Michael
Towrie
b
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK. E-mail: a.orr-ewing@bris.ac.uk; Fax: +44 (0)117 9277985; Tel: +44 (0)117 9287672
bCentral Laser Facility, Research Complex at Harwell, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Didcot, Oxfordshire, OX11 0QX, UK
First published on 15th October 2012
Abstract
Broadband transient infra-red absorption measurements are reported that contrast the dynamics of reaction of Cl atoms with 2,3-dimethylbut-2-ene and n-pentane in chlorinated solvents. In both cases, H-atom transfer produces HCl and a hydrocarbon radical, but the energy release in the former reaction is greater because of the formation of a resonance-stabilized allylic radical. The reaction of Cl atoms with n-pentane in solution in CH2Cl2 forms HCl exclusively in its lowest vibrational level (v = 0), and our measured rate coefficient agrees with a prior report by Sheps et al., J. Phys. Chem. A, 2006, 110, 3087. The time-dependence of the growth of intensity in the HCl fundamental absorption band shows two domains of reaction: a prompt rise is associated with reaction of the photolytically generated Cl atoms with n-pentane molecules lying within the first solvent shell, whereas a slower further rise is attributed to reaction following diffusion through the solution. For the reaction of Cl atoms with 2,3-dimethylbut-2-ene, these two domains of reaction are also observed, and fitting to a kinetic model incorporating these components gives bimolecular rate coefficients for formation of HCl of (1.7 ± 1.4) × 1010 M−1 s−1 in CDCl3 and (3.4 ± 1.2) × 1010 M−1 s−1 in CCl4. However, an additional transient absorption is observed ∼115 cm−1 lower in wavenumber than the fundamental HCl absorption band and is assigned to the v = 2 ← v = 1 hot band of HCl. The absorption by the nascent HCl(v = 1) peaks after ∼20 ps and subsequently decays to baseline levels because of vibrational relaxation, which is shown to be enhanced by energy transfer to 2,3-dimethylbut-2-ene. In solution in CDCl3, the fraction of HCl formed initially in v = 1 is determined to be 0.24 ± 0.04 and in CCl4 it is 0.15 ± 0.02. The branching to HCl(v = 1) for these reactions in solution is significantly lower than the 0.48 ± 0.06 fraction reported for reaction of Cl atoms with propene in the gas phase [Pilgrim and Taatjes, J. Phys. Chem. A, 1997, 101, 5776]. This comparison between similar bimolecular reactions in solution and in the gas phase therefore identifies changes to the dynamics caused by interaction with the solvent. Solvent friction experienced by the separating products of the reaction is considered more likely to be responsible for the lower vibrational excitation of the nascent HCl than is solvent modification of the topology of the potential energy surface in the vicinity of the transition state. Possible consequences of addition of Cl to the unsaturated bond in 2,3-dimethylbut-2-ene are also discussed.
Introduction
The reactions of chlorine atoms with organic molecules, forming HCl and an organic radical, reveal rich dynamical behaviour when subjected to detailed study in the gas phase under conditions of isolated collisions.1,2 Direct abstraction of an H atom is observed for reactions of Cl atoms with alkanes,3–5 whereas reactions with alkenes show competition between direct abstraction and addition–elimination pathways.6–8 Reactions of Cl atoms with simple alcohols, amines, haloalkanes and ethers exhibit similar abstraction dynamics,9–15 with further interaction of the separating products after the transition state (TS) also influencing the scattering.1,2,16 An extensive body of experimental and computational work has connected the observed kinetics and dynamics with the topology of the potential energy surfaces for representative reactions.2,16–18 Here, we seek to compare the mechanisms of such reactions taking place in liquid solutions with the better known gas-phase behaviour to extract information about how the solvent influences the chemical dynamics.In the gas phase, exothermic chemical reactions with an early TS are known to couple the available energy efficiently into certain vibrational motions of the reaction products.19,20 Hammond's postulate, that the TS for an exothermic reaction resembles the reagents,21,22 provides a simple interpretation: for a direct abstraction reaction with an early TS, the new bond is formed extended beyond its equilibrium separation. In recent experimental and theoretical studies of reactions of CN radicals with cyclohexane, tetramethylsilane and tetrahydrofuran, we demonstrated that this behaviour can persist in solution in liquids.23–25 Although the solvent quenches vibrational excitation of the product HCN (or DCN) on timescales of tens to hundreds of picoseconds, at shorter times, mode-specific excitation of the bending and C–H stretching vibrational modes was observed. We now aim to establish whether such behaviour extends to reactions of other atomic or radical species in solution. Most reactions of Cl atoms with hydrocarbons are, at best, only mildly exothermic and therefore strongly favour production of HCl(v = 0).2 However, those forming resonance stabilized radicals can produce significant fractions of HCl(v = 1), as illustrated by the reaction with propene to form an allyl radical:6
Cl + CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 → HCl + ˙CH2–CH CH2 → HCl + ˙CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ΔrH = −59.8 ± 2.5 kJ mol−1 CH2, ΔrH = −59.8 ± 2.5 kJ mol−1 | (1) |
From infra-red absorption measurements of reaction (1) in the gas phase (for which the quoted enthalpy change applies), Pilgrim and Taatjes reported that (48 ± 6)% of the HCl products are formed in their v = 1 level (requiring 34.5 kJ mol−1 of vibrational excitation), with the remainder in v = 0.6
The current work translates a variant of reaction (1) from the gas phase to solution in chlorinated organic solvents. The chosen reaction is
Cl + (CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2 → HCl + (˙H2C)(CH3)C C(CH3)2 → HCl + (˙H2C)(CH3)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2 C(CH3)2 | (2) |
Experimental
Steady-state infra-red band positions and shapes were measured for solutions of HCl in various solvents at ambient temperature using Fourier transform infra-red (FTIR) spectroscopy. FTIR absorption spectra of HCl in solution in CCl4, CDCl3, CHCl3 and CH2Cl2 (all solvents >99% purity, Sigma Aldrich, and dried using a molecular sieve before use) were obtained using a Nicolet Nexus spectrometer operating at 1 cm−1 resolution. Solvent samples were degassed on a vacuum line and then exposed to 1 atm of HCl (Aldrich, 99+%). Dissolution of the HCl in the solvent was found to be improved if the glass finger containing both was immersed in liquid nitrogen and then allowed to warm to room temperature. Samples of the HCl solutions were pipetted into a Harrick cell with CaF2 windows separated by 1 mm using a Teflon spacer. The cell was then sealed to prevent loss of HCl and uptake of water. Spectra of the pure solvents were also obtained using the same cell and subtraction from the HCl/solvent spectra allowed identification of HCl features.Simulations of the HCl fundamental band in solution were carried out using the PGOPHER spectral simulation program.31 Rotational constants, vibrational frequencies and anharmomic corrections were taken from the NIST Webbook,26 the P and R-branch structure was simulated using a first rank T10 spherical tensor transition moment term, and a T00 tensor moment term was incorporated to simulate the Q-branch seen in this and other work, which is forbidden for an electric dipole transition in gas-phase molecules.32 Rotational structure in the bands was then broadened by use of a 50–100 cm−1 Gaussian or Lorentzian lineshape to simulate the collisional environment in solution, with collisions every ∼100 fs. By scaling the relative magnitudes of the T10 and T00 terms, simulated spectra could be made to reproduce general features of the HCl vibrational band shapes observed in solution.
Time-resolved infra-red absorption spectra were obtained using the ULTRA Facility at the Central Laser Facility of the Rutherford Appleton Laboratory. Details of the laser systems, sample handling and accumulation of spectra have been provided elsewhere,23,25 and only a brief summary is given here. Room temperature samples were circulated through a Harrick cell with CaF2 windows spaced by 0.35 mm, using a peristaltic pump and Teflon tubing. All these components and all solvents were thoroughly dried before use. Two types of experiment were conducted: (i) IR pump and IR probe of HCl to measure vibrational relaxation rates of HCl(v = 1) in various solvents; and (ii) UV pump and IR probe to study the bimolecular reaction of Cl atoms with selected organic molecules. Both made use of a ∼500 cm−1 bandwidth mid-IR probe laser pulse of duration ∼50 fs to probe simultaneously absorptions by HCl(v = 0) and HCl(v = 1) via their Δv = +1 bands centred at 2832 cm−1 and 2720 cm−1 respectively for solutions in CCl4. These bands shifted by 15 and 38 cm−1 to lower wavenumber in CDCl3 and CH2Cl2 respectively. Following transmission through the sample, IR probe pulses were dispersed onto a pair of 128-pixel mercury cadmium telluride (MCT) array detectors and the outputs were digitized for subsequent analysis. The detectors were calibrated by passing the same probe pulses through thin samples of 1,4-dioxane and referencing absorption features to the known FTIR spectrum of this molecule.
The IR pump and IR probe experiments employed solutions of HCl in chlorinated solvents prepared as described above. HCl molecules were pumped to v = 1 using a linearly polarized IR excitation pulse of bandwidth ∼12 cm−1 and duration <2 ps. An IR probe pulse, also linearly polarized, then measured the absorption by HCl(v = 0 and 1) at time delays from 0–250 ps. Difference spectra, obtained by subtraction of IR-pump laser off from IR-pump laser on measurements, showed transient absorption via the v = 2 ← v = 1 band and an associated bleach of the v = 1 ← v = 0 band (the amplitude of which is determined by the change in population difference between v = 0 and v = 1 levels), both of which decayed in amplitude with time. These two bands are henceforth denoted as (2–1) and (1–0) respectively.
The UV pump and IR probe experiments were conducted on solutions of 0.25 M, 0.5 M and 0.75 M DMB (Sigma Aldrich, >99.9%) in CCl4 or CDCl3. A ∼50 fs duration, ∼1 μJ energy UV pump pulse of wavelength 267 nm was gently focused into the centre of the Harrick cell to generate Cl atoms by 2-photon excitation of the solvent.28,29 At time delays from 0–1000 ps, the broadband IR probe pulse then probed reactive formation of HCl(v = 1 and 0) and any vibrational relaxation to the ground state. Subtraction of spectra obtained without from those with the UV laser pulses was used to identify transient HCl absorptions. Similar experiments were conducted for solutions of n-pentane in place of DMB.
The lasers operated at repetition rates of 10 kHz, and rapid circulation of solutions and rastering of the position of the Harrick cell were used to ensure a fresh solution sample was probed with each absorption measurement. Time delays between the pump and probe pulses were controlled using linear motorized translation stages, with random variation of the order of the delay times from a user-selected list. Features in the absorption spectra resulting from bands of the solvent or the DMB were identified using published IR spectra and FTIR analysis of static samples.
Results
The objective of the current study is to resolve vibrational quantum-state specific dynamics for HCl formation from reaction (2) of Cl atoms with 2,3-dimethylbut-2-ene in selected organic solvents. As a first necessary step towards this objective, we examine the spectroscopic signatures for HCl(v = 0 and 1) in solution and determine the timescale for vibrational relaxation to HCl(v = 0) (Section A). We then develop a model to understand the dynamics of reaction of Cl atoms with pentane (Section B.1), as a representative bimolecular reaction immune from any complexity associated with branching between HCl(v = 1) and HCl(v = 0) vibrational levels. Finally, in Section B.2, we draw on these outcomes to interpret the results for Cl atom reaction with DMB.A. IR-pump and IR-probe of HCl in solution
Absorption spectra of HCl in solution in a variety of fluids (e.g. rare gases,33–36 CO,37,38 and SF6 (ref. 39)) exhibit residual rotational branch structure that has been the subject of extensive analysis. In solution in CCl4, the fundamental band of HCl shows a pronounced sharp feature between the broad P and R-branch contours40 that is generally referred to as a Q-branch. This feature is dipole forbidden for an isolated molecule, but is attributed to interaction of HCl with the solvent.32,34,41Fig. 1 compares our FTIR absorption spectra of HCl in solution in various chlorinated solvents, and the spectrum obtained in CCl4 is accompanied by a simulation obtained using the PGOPHER program.31 The band centres shift to lower wavenumber with increasing dielectric constant of the solvent, while the Q-branch feature broadens and the residual P and R branch features become less distinct.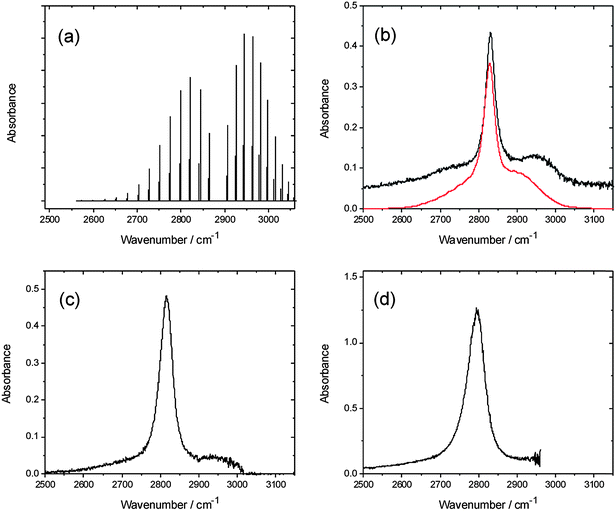 | ||
| Fig. 1 Panel (a) shows a simulation of the gas phase spectrum of HCl.31 The remaining panels show absorption spectra of HCl in solution in (b) CCl4, (c) CDCl3, and (d) CH2Cl2. The red line in panel (b) is a simulation of the condensed phase spectrum based on the gas-phase spectral simulation as described in the text. | ||
In transient IR-pump and IR-probe experiments in which the HCl is excited on the fundamental absorption band by a ∼2 ps IR pulse, the considerable widths of the P and R-branch structure of the (2–1) and (1–0) bands means there is some overlap of the observed absorption and bleach features despite the large anharmonic shift. The shapes of transient spectra observed in IR pump and probe experiments depend on the central wavenumber chosen for the pump laser, and thus the region of the HCl band excited. Here, we focus on IR pump and IR probe spectra in which the pump laser was tuned close to the Q-branch feature, and Fig. 2 shows example data. By integrating the intensities of the transient absorption and bleach features evident in such spectra at each time delay, decays of the transient population in v = 1 and recovery of the population in v = 0 can, in principle, be fitted separately to derive vibrational relaxation time constants. For solutions of HCl in solution in CCl4, CDCl3, CHCl3 and CH2Cl2, after a fast initial drop in intensity lasting only ∼7 ps, little or no further decay was observed of the transient features over the time delays of up to 250 ps used in our experiments. Exponential functions could therefore not be fitted accurately to the data, but the slow relaxation times are consistent with the 4.7 ± 0.3 ns time constant reported by Knudston and Stephenson42 for relaxation of HCl(v = 1) in solution in CCl4. The transition dipole moments for P,R and for Q-branch excitation lie orthogonal to one another in freely rotating HCl, and the fast decay at early times may reflect a loss of initial polarization of the sample caused by the polarized pump laser excitation on the Q-branch.
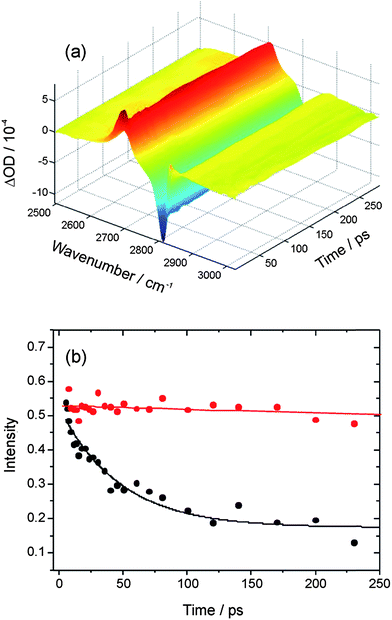 | ||
| Fig. 2 (a) Time resolved IR pump and IR probe spectra for HCl (∼0.15 M) dissolved in CDCl3. The spectra are presented as differences with and without the IR pump laser, so the negative signal is the bleach of the HCl (1–0) fundamental band and the positive signal is transient absorption on the HCl (2–1) hot band. (b) Decays of the wavenumber-integrated intensity of the transient HCl (2–1) band in solution in CDCl3 without (red) and with (black) added DMB (∼1 M). The solid lines are an overlay of an exponential decay with 4.7 ns time constant (red) and an exponential fit (black) for which the time constant is 47 ± 6 ps. | ||
Upon addition of DMB to the HCl solution in CDCl3 to give a concentration in the 1 ml volume of the Harrick cell of ∼1 M DMB, transient features associated with HCl(v = 1) and the bleach of the fundamental absorption band of HCl(v = 0) decayed with the much shorter relaxation time constant of 50 ± 13 ps (reported as an average and 1 standard deviation uncertainty from 3 measurements, one of which is illustrated in Fig. 2(b)). The DMB has a C–H stretching band with onset above 2820 cm−1 and near-resonant vibrational-to-vibrational energy transfer associated with this vibrational mode may shorten the lifetime of the vibrationally excited HCl molecules.
When the time-dependent IR absorption spectra are presented as differences between measurements made with the IR pump laser on and off, such as in Fig. 2(a), the magnitudes of the bleach of the fundamental (1–0) band and of the (2–1) hot band are observed to be almost the same for any particular time delay. The intensities of these spectral features depend upon the population difference between the lower and upper levels connected by the IR transition, and the transition dipole moments μ10 and μ21 for the two bands. If n molecules are excited from v = 0 to v = 1 then the ratio of magnitudes of intensities in the difference spectra is (I2–1/I1–0) = (nμ212/2nμ102) ≈ 1, suggesting that the ratio of transition moments for the two bands is (μ21/μ10)2 ≈ 2, as expected for a harmonic oscillator.43
B. Reactions of Cl atoms in solution
In this section, results are contrasted for the reaction of Cl atoms with n-pentane:| Cl + n-C5H12 → HCl + n-C5H11, ΔrH = −8.4 or −22.2 kJ mol−1 | (3) |
 | ||
| Fig. 3 Time-dependence of integrated absorption intensity on the fundamental band of HCl following initiation of reaction of Cl atoms with n-pentane in solution in dichloromethane. Circles are experimental data and solid lines are fits to a kinetic model described in the main text. Panel (a): experimental data from Sheps et al. reported in ref. 28, black = 0.15 M, red = 0.3 M, blue = 0.6 M n-pentane solutions. Panel (b): data from the current study, black = 0.2 M n-pentane solution. The inset shows the data on the same time axis as panel (a). | ||
A simple bimolecular reaction scheme, Cl + pentane → HCl + pentyl radical, was inadequate to describe the observed time-dependence of HCl formation. We therefore fitted the rises in HCl(v = 0) absorption on its fundamental band to the following scheme (with RH denoting n-pentane):
 | (4a) |
 | (4b) |
 | (4c) |
 | (4d) |
| Kinetic parameter | k/M−1 s−1 | τ d/ps |
|---|---|---|
| a Experimental data from Sheps et al.28 b Experimental data from the current work. | ||
| 0.15, 0.3, 0.6 M n-pentane in CH2Cl2a | (1.19 ± 0.11) × 1010 | 12.3 ± 6.0 |
| 0.2 M n-pentane in CH2Cl2b | (1.12 ± 0.14) × 1010 | 22 ± 14 |
The bimolecular rate coefficients derived from this analysis agree with the value of (9.5 ± 0.7) × 109 M−1 s−1 reported by Sheps et al.28 for reaction (3) in CH2Cl2 using a Smoluchowski model to fit their data. The fast initial rise in the production of HCl, evident in Fig. 3, is attributed to prompt reaction of some fraction of those Cl atoms that are formed from photolysis of CH2Cl2 molecules that have one or more n-pentane molecules present in their first solvation shells. The rate of this initial rise may also be influenced by the competitive loss of Cl atoms by geminate recombination with the CH2Cl radicals also formed by the solvent photolysis, but this process does not affect the analysis and interpretation that follows. We note that our constraint on the kc values to scale linearly with n-pentane concentration fits the data in Fig. 3 well at early times (with respective time constants for 0.15, 0.3 and 0.6 M solutions of 122, 61 and 30 ps), suggesting that the geminate recombination is less important than prompt in-cage reaction with n-pentane in accounting for the early time loss of Cl atoms. As Sheps et al. discussed, the contribution to the observed HCl signals from Cl atom reactions with the solvent is negligible, even for the lowest n-pentane concentrations because of a much lower bimolecular rate coefficient of k (Cl + CH2Cl2) = (1.36 ± 0.06) × 107 M−1 s−1.28,29
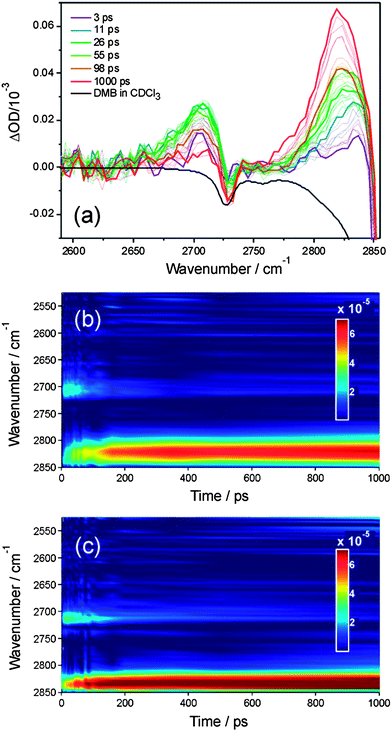 | ||
| Fig. 4 Transient IR spectra obtained in the 2500–2850 cm−1 region following initiation of reaction (2) in solution at time t = 0 ps. Panel (a): transient spectra for reaction (2) in CDCl3 for numerous time delays from 0–1000 ps. Time delays associated with the thicker lines are indicated in the inset key. The black line is a portion of an FTIR absorption spectrum of DMB in CDCl3 (inverted for clarity). Panel (b) the transient IR data from panel (a) replotted to show the time evolution of the spectra, with a colour scale ranging from dark blue (zero signal) to dark red (maximum signal) as shown in the inset key. Panel (c) shows data for reaction (2) in solution in CCl4 in the same format as for panel (b). All spectra have been curtailed at 2850 cm−1 to avoid the strongly negative signal resulting from an absorption band of DMB, the onset of which is evident in panel (a). | ||
Certain aromatic molecules, when excited with UV light at wavelengths around 267 nm are known to undergo photoinduced Cl-atom transfer reactions with chlorinated solvents.47 We observed strong transient IR bands in the 2800 cm−1 region that arise from such a mechanism when we replaced DMB with 1,3,5-trimethylbenzene. However, the assignment of the transient features in Fig. 4 at ∼2700 cm−1 to a comparable reaction can be discounted because (as we verified by UV spectroscopy) the DMB UV absorption band lies to much shorter wavelength than those of molecules such as 1,3,5-trimethylbenzene containing an aromatic chromophore, and shows a much smaller extinction coefficient at 267 nm. Under our experimental conditions, the absorbance by DMB in solution in CDCl3 or CCl4 at 267 nm was ADMB ≤ 0.1, and any photoexcitation to the S1 state is expected to be followed by relaxation on <100 fs timescales back to the S0 electronic state via a conical intersection, as is observed for UV excitation of ethene.48
The time-dependent integrated intensities of the bands assigned as HCl (1–0) fundamental and (2–1) hot band transitions were derived by summing intensities over 4 pixels (∼20 cm−1), and Fig. 5 displays representative outcomes for DMB solutions in CCl4 and CDCl3. The HCl (1–0) bands show a rapid growth over the first ∼20 ps followed by slower increases out to time delays of 1500 ps that approximately mirror the decline in intensity of the (2–1) bands. It is therefore tempting to assign the slower growth of HCl(v = 0) to vibrational relaxation of the HCl(v = 1) products of reaction (2). However, two pieces of evidence caution against this assignment. Firstly, the same division into prompt and slower formation of HCl is observed in the Cl + n-pentane data for which HCl(v = 1) is not a significant product. As noted earlier, Crim and co-workers analysed this time dependence for reaction (3) and several other examples in terms of a Smoluchowski model for the reaction in solution,28,29,46 and we have successfully employed the model summarized in eqn (4a–d). Secondly, if the time-dependent HCl (1–0) band intensities are fitted to a simple bi-exponential rise, the time constants for the more slowly rising component increase with increasing concentration of the DMB, and have values consistent with a diffusion-limited reaction. This observation indicates that much of the more slowly rising HCl(v = 0) signal results from bimolecular reactions forming HCl(v = 0) directly.
 | ||
| Fig. 5 Integrated intensities of the HCl(1–0) (black) and HCl(2–1) (red) absorption bands plotted against time delay between initiation of reaction (2) of Cl atoms with DMB, and measurement of the product HCl absorption spectrum. The top row shows data for reaction (2) in solution in CDCl3 and the bottom row is for solutions in CCl4. The right hand column shows expanded views of the first 200 ps of the data sets presented in the left hand column. Data are shown for various concentrations of DMB: filled circles are for 0.5 M, open circles for 0.25 M and open triangles for 0.75 M solutions. Solid lines are fits to the data using the kinetic model described in the text. | ||
As was the case for reaction of Cl atoms with n-pentane discussed in Section B.1, the two distinct timescales for reactive production of HCl suggest contributions from a prompt reaction of Cl atoms with DMB in the immediate vicinity of their points of formation (in-cage), and a slower diffusion mediated pathway after escape of Cl atoms into the bulk solvent. Any Cl atoms that avoid prompt reaction with nearby DMB molecules may complex with a molecule of the chlorinated solvent,49–51 in which case the diffusion will be of these complexes, not bare Cl atoms. The timescales for diffusive in-bulk reaction appear to be similar to those for vibrational relaxation of the HCl(v = 1), which complicates the kinetic analysis that follows.
Based on the above discussion, the following extension of reaction scheme (4) is proposed for analysis of the time-dependent data, with RH now denoting DMB and subscripts c and b again indicating in-cage and in-bulk species. This scheme is summarized pictorially in Fig. 6.
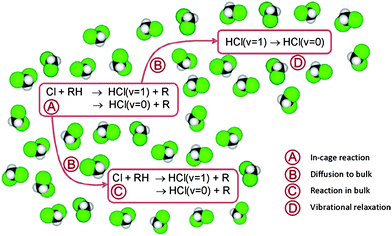 | ||
| Fig. 6 Pictorial representation of the mechanism used for analysis of the experimental observations. RH denotes the DMB molecule. | ||
In-cage reaction and relaxation
 | (5a) |
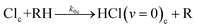 | (5b) |
 | (5c) |
Diffusion from cage to bulk
 | (5d) |
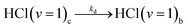 | (5e) |
 | (5f) |
In-bulk reaction and relaxation
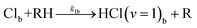 | (5g) |
 | (5h) |
 | (5i) |
The kic and kib (i = 1 or 0 denoting production of HCl(v = 1) or HCl(v = 0) respectively) are pseudo-first order rate coefficients that can be converted to bimolecular rate coefficients by division by the concentration of the DMB, which is in considerable excess over the Cl atoms. We implicitly consider the solution to be homogeneous, but recognize that there may instead be some clustering of the DMB molecules at the concentrations used. The first order rate coefficient kr accounts for vibrational relaxation of HCl(v = 1), but is likely to depend on the concentration of DMB (see Section A). To keep the fits tractable, rate coefficients for diffusion from in-cage to in-bulk are taken to be the same for all species. This is recognized to be an approximation because, as noted earlier, Cl atoms are known to form complexes with chlorinated solvent molecules,50,51 which will affect their diffusion rates.
In the model of eqn (5a–i), we neglect loss of Cl atoms by reaction with the solvent or recombination with CCl3 or CDCl2 radicals also formed by the UV laser pulses. As was discussed in Section B.1, the rates of these loss processes have been measured by Sheps et al. using transient UV absorption features assigned to charge transfer from solvent bands and are slow in comparison with the reactive losses discussed here. Moreover, the initial rise times of HCl signals evident in the expanded plots in Fig. 5 show a dependence on DMB concentration that would not be expected for rates dominated by geminate recombinative loss of Cl atoms. These processes are therefore not expected to impact significantly on our analysis. Any fitting of time dependent HCl (1–0) and (2–1) band intensities to derive populations of HCl(v = 0) and (v = 1) must take into account that these band intensities depend on the population difference between vibrational levels connected by the transition, and that the transition dipole moments for the two bands (μ10 and μ21 respectively) will differ. There is insufficient (or barely sufficient) energy available to form HCl(v = 2) products, and no transient absorption features are seen that might be assigned to the HCl (3–2) band, so the intensity of the (2–1) band is taken to be proportional to the population of HCl(v = 1). However, significant population of v = 1 will affect the observed intensity of the HCl(1–0) absorption band and the fitting incorporates this.
Reactions of Cl atoms with alkenes are known to exhibit competition between direct H-atom abstraction and addition of Cl to form an adduct, denoted here as {Cl–RH}.6,52,53 Under isolated collision conditions in molecular beam experiments, the energised adduct can eliminate HCl,7 and if this process is very rapid for our experimental conditions, kinetic scheme (5) remains valid, with reactions (5a), (5b), (5g) and (5h) encompassing both direct and addition/elimination mechanisms. However, if the adduct does not promptly eliminate HCl, it is likely to be stabilized by collisions with the solvent and will not be a source of HCl on the timescale of our experiments. Such collision-stabilized adducts have been observed, for example, for reaction of Cl atoms with isoprene in the gas phase at pressures as low as 10 Torr and have lifetimes of microseconds or longer.53 The consequences of stabilized adduct formation for the analysis of our experimental data are reserved for further discussion in the (ESI†).
Fitting individual data sets to the kinetic model of eqn (5a–5i) did not produce consistent outcomes for different concentrations of DMB or between independent sets of data for the same concentration, because of the large number of fit parameters. Constraints were therefore imposed using procedures explained in the ESI.† The constrained fits were performed simultaneously to HCl(1–0) and HCl(2–1) band data sets for two different DMB concentrations, and the only independent parameters floated were k1c, k0c, k1b, k0b and kd. Examples of the outcomes are shown by the solid lines in Fig. 5, and illustrate that the kinetic model provides a good account of the forms of the data. For experiments in both CDCl3 and CCl4, time-resolved spectral data were accumulated twice for each of the 0.25, 0.5 and 0.75 M solutions, and the above analysis was conducted independently for both of these data sets to check for consistency. Table 2 summarizes the values of the fit parameters derived from experiments in CDCl3 and CCl4. Values reported are the averages of separate analysis of two independent sets of data, and uncertainties are 1 SD, propagated from errors from the individual data set fits. Although values of pseudo-first order rate coefficients reported are appropriate for 0.5 M DMB solutions, they were derived from simultaneous fits to data for pairs of concentrations (0.25 and 0.5 M or 0.5 and 0.75 M) as illustrated in Fig. 5. Values of kd are expected to be independent of DMB concentration.
| 0.5 M DMB in CDCl3 | 0.5 M DMB in CCl4 | |
|---|---|---|
| a Fixed in the fits. | ||
| k 1c/ps−1 | 0.048 ± 0.006 | 0.044 ± 0.006 |
| k 0c/ps−1 | 0.155 ± 0.015 | 0.268 ± 0.027 |
| k 1b/ps−1 | 0.0018 ± 0.0006 | 0.0064 ± 0.0030 |
| k 0b/ps−1 | 0.0065 ± 0.0043 | 0.011 ± 0.005 |
| k rc/ps−1 | 0.0000a | 0.0000a |
| k rb/ps−1 | 0.010a | 0.010a |
| k d/ps−1 | 0.047 ± 0.013 | 0.103 ± 0.037 |
| (μ21/μ10)2 | 2.0a | 2.0a |
The time constants for diffusion from the initial cage to the bulk, as estimated from the mean values of kd, are 21 ± 6 ps and 9.7 ± 3.5 ps for CDCl3 and CCl4. These values are broadly in agreement with those obtained for the reaction of Cl atoms with n-pentane in CH2Cl2 reported in Table 1. Table 2 also demonstrates that there is good correspondence between values of parameters derived from analysis of the data for reactions in CCl4 and CDCl3.
Further manipulation of the values summarized in Table 2 gives estimates for the bimolecular rate coefficients and branching into HCl(v = 1), here expressed as a ratio Γ(v = 1) defined as:
 | (6) |
Specifically, Γ(v = 1) was estimated from the ratios of rate coefficients (k1c + k1b)/(k1c + k1b + k0c + k0b), and the bimolecular rate constant for production of HCl from reaction (2) in bulk solution was calculated using (k1b + k0b) × 1012/[DMB] from knowledge of the DMB concentration. The outcomes are summarized in Table 3. The values of Γ(v = 1) obtained from this analysis were largely insensitive to the constraints imposed in the fitting of time-dependent integrated band intensity data, but did depend on the choice of (μ21/μ10)2. Further exploration of the effects of this choice included allowing (μ21/μ10)2 to take values of 2.5 and 1.4 but resultant values of Γ(v = 1) did not exceed 0.3 and were mostly within the range of the uncertainties specified in Table 3. For reasons that are discussed in the ESI,† together with the procedures used, the values of Γ(v = 1) were also estimated from the relative amplitudes of signals for HCl(v = 1) and HCl(v = 0) during the first 55 ps of reaction. The results, Γ(v = 1) = 0.27 ± 0.02 and 0.18 ± 0.02 for CDCl3 and CCl4 solutions, are in good accord with those obtained from the rate coefficient ratios described above.
The values listed in Table 3 derive from fitting to two data sets for each of two concentrations of DMB and incorporate propagation of the uncertainties listed in Table 2, but not the consequences of our choice of fit constraints. The derived rate coefficients k will depend quite sensitively on other parameters in the fit, including the choice of krb made with guidance from the IR-pump and IR-probe experiments (see ESI†), and their values must therefore be treated with caution. The large uncertainties in these parameters could be reduced with inclusion of more data points at time delays >200 ps in the experimental measurements.
The gas phase rate coefficient for reaction of Cl atoms with propene, the nearest analogue to reaction (4) for which such data are available, is kgas = (2.2 ± 0.4) × 1010 M−1 s−1 at 293 K,6 and the values reported in Table 3 are in reasonable accord with this number. The magnitudes of the rate coefficients indicate close to diffusion limited behaviour, which would be consistent with a negligible activation barrier for this exothermic reaction.
Pilgrim and Taatjes obtained Γ(v = 1) = 0.48 ± 0.06 for the Cl + propene reaction, which is significantly higher than the branching fractions we derive for solution phase experiments on the Cl + DMB reaction. This comparison must be tempered by the fact that the two reactions are not identical, although both involve abstraction of an H-atom from a –CH3 group to form an allylic radical. However, we conclude that there is evidence for the branching to HCl(v = 1) being reduced in the presence of solvent, indicating some modification to the reaction dynamics of the H-atom abstraction pathway. The solvent pertubation is not, however, sufficient to damp completely the formation of vibrationally excited HCl and a significant fraction is still formed in v = 1. There also appears to be a systematic difference between measurements carried out in CCl4 and CDCl3 with the former solvent having a more pronounced effect in suppressing the branching to HCl(v = 1). This observation is consistent with the higher viscosity of CCl4, which might result in greater solvent friction, but this bulk property does not appear to affect the bimolecular rate coefficients for reaction, at least within the uncertainties in our reported values. The lower branching to HCl(v = 1) in CCl4 than in CDCl3 may also be a consequence of greater spectral overlap of the HCl fundamental band (centred at 2832 cm−1 in CCl4 and 2817 cm−1 in CDCl3) with the absorption band of DMB located above 2830 cm−1, leading to more efficient coupling to the bath of solution modes.
As was noted above, the kinetic model of eqn (5) used to analyse our data does not consider competition between the direct H-atom abstraction pathway and {Cl–DMB} adduct stabilization or HCl formation via an addition–elimination pathway. The latter mechanism is not considered to be a significant source of HCl, and the consequences for the analysis of instead forming a collision-stabilized adduct are discussed in the ESI.† However, our experimental results contain no clear-cut evidence for participation of such an adduct. For example, we were not able to observe any transient signatures of possible association complexes when the probe laser and detector were tuned to the 1200–1800 cm−1 wavenumber range which includes the region of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond stretching frequencies. Absolute yields of HCl from reactions with n-pentane and DMB under otherwise identical conditions were similar, suggesting no significant new sink for photolytically generated Cl atoms. Perhaps the steric bulk of the four –CH3 groups in DMB hinders the approach of a Cl atom to the centrally located C
C bond stretching frequencies. Absolute yields of HCl from reactions with n-pentane and DMB under otherwise identical conditions were similar, suggesting no significant new sink for photolytically generated Cl atoms. Perhaps the steric bulk of the four –CH3 groups in DMB hinders the approach of a Cl atom to the centrally located C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond to form an addition complex, and the ready availability of the H-atoms at the periphery of the molecule and the low energy barrier for abstraction may instead promote the direct reaction to form HCl.
C bond to form an addition complex, and the ready availability of the H-atoms at the periphery of the molecule and the low energy barrier for abstraction may instead promote the direct reaction to form HCl.
Our prior calculations of the potentials of mean force for reactions of CN radicals with organic molecules such as cyclohexane in solution suggested that chlorinated solvents such as CDCl3 or CCl4 only weakly perturbed the energy surface and the nuclear dynamics for isolated (i.e. non-solvated) reactions.54,55 It is therefore likely that the observed vibrational excitation of the HCl product of reaction (2) in solution, which is lower than expected under gas-phase conditions, is a consequence of solvent friction acting on the separating products in the post-TS region of the reaction pathway, instead of significant solvent modification of the potential energy hypersurface in the vicinity of the transition state. Fast coupling of vibrational energy from the nascent HCl to the modes of the (CH2)(CH3)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2 radical co-product may also occur within a solvent cage before diffusive separation, as we observed for CN radical reactions.55 Furthermore, the solvent might play a role in selecting between competing reaction mechanisms: as was discussed earlier, the collisional environment of a liquid should suppress the addition–elimination pathway known to occur in Cl + alkene reactions in the gas phase.7 However, statistical decomposition of an addition complex is expected to disfavour HCl(v = 1) products, unless the transition state involves an extended H–Cl configuration. Solvent induced closure of this channel, leaving the direct abstraction pathway dominant, is therefore unlikely to be the cause of our observed reduction in branching to HCl(v = 1).
C(CH3)2 radical co-product may also occur within a solvent cage before diffusive separation, as we observed for CN radical reactions.55 Furthermore, the solvent might play a role in selecting between competing reaction mechanisms: as was discussed earlier, the collisional environment of a liquid should suppress the addition–elimination pathway known to occur in Cl + alkene reactions in the gas phase.7 However, statistical decomposition of an addition complex is expected to disfavour HCl(v = 1) products, unless the transition state involves an extended H–Cl configuration. Solvent induced closure of this channel, leaving the direct abstraction pathway dominant, is therefore unlikely to be the cause of our observed reduction in branching to HCl(v = 1).
Conclusions
Transient IR absorption studies of the reactions of Cl atoms with n-pentane and 2,3-dimethylbut-2-ene in solution in chlorinated organic solvents, performed with ∼1 ps time resolution, reveal considerable detail about the dynamics of these bimolecular reactions. The Cl atoms were produced by UV photolysis of the solvent, defining the zero of time in the experiments. The reactions form HCl products, and the rates of growth of absorption on the fundamental HCl (1–0) band distinguish two timescales, corresponding to prompt reaction of Cl atoms with a partner hydrocarbon most likely located within the immediate solvent shell, and slower reaction following diffusion into the bulk solvent. Fits to data for the Cl + n-pentane reaction, employing numerical integration of a simple kinetic model distinguishing reaction in the initial solvent cage and the bulk solution, give bimolecular rate coefficients of (1.19 ± 0.11) × 1010 M−1 s−1 that agree well with a prior analysis using a model based on Smoluchowski theory of reactions in solution.28 For this reaction, we only observe transient IR signals corresponding to HCl absorption on the (1–0) fundamental band, but for the more exothermic reaction of Cl atoms with DMB, a further transient IR feature is seen that is assigned to the HCl (2–1) hot band, indicating production of HCl(v = 1). This feature grows within ∼20 ps and decays within ∼200 ps, the latter timescale deriving from a balance between continual diffusive production of HCl(v = 1) and vibrational relaxation to HCl(v = 0) in the presence of DMB.Infra-red pump and probe experiments were independently used to measure the vibrational relaxation rates for HCl solution in CCl4 and CDCl3 and outcomes are consistent with prior measurements of decay time constants of ∼ 4 ns.42 However, upon addition of DMB to the HCl solutions, the vibrational relaxation time shortens to 50 ± 13 ps (for a ∼1 M solution of DMB in CDCl3) indicating an efficient energy transfer from HCl(v = 1) to the DMB. This information was used to constrain the fits to the production and relaxation of HCl(v = 1) from reaction of Cl atoms with DMB in solution in both CDCl3 and CCl4. These fits employed an extension of the model used to analyse Cl + n-pentane data, with inclusion of vibrational state resolved production of HCl(v = 1) and (v = 0) and relaxation of the former to the latter. The outcomes of these fits indicate nascent branching fractions to HCl(v = 1) of 0.24 ± 0.04 in CDCl3 and 0.15 ± 0.02 in CCl4 that can be compared with the previously reported 0.48 ± 0.06 fraction of HCl(v = 1) formed from reaction of Cl atoms with propene in the gas phase.6 Both the Cl + DMB and Cl + propene reactions form an allylic radical by abstraction of an H-atom from a methyl group adjacent to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The balance between HCl formation via direct abstraction and addition–elimination pathways may be altered in going from the gas phase to reactions in bulk liquids, but we favour a different interpretation for the observed differences in HCl(v = 1) branching fractions. Our results suggest that the dynamics leading to vibrationally excited HCl are partially, but incompletely suppressed by the presence of a solvent, either through modification to the potential energy surface for the reaction, or because of solvent coupling to the nuclear motion degrees of freedom of the reacting molecules from the transition state onwards. In the current case, this effect appears to be more pronounced in CCl4 than in CDCl3, perhaps reflecting greater overlap of the frequencies of the HCl fundamental band and a C–H stretching mode of DMB in the former solvent.
C bond. The balance between HCl formation via direct abstraction and addition–elimination pathways may be altered in going from the gas phase to reactions in bulk liquids, but we favour a different interpretation for the observed differences in HCl(v = 1) branching fractions. Our results suggest that the dynamics leading to vibrationally excited HCl are partially, but incompletely suppressed by the presence of a solvent, either through modification to the potential energy surface for the reaction, or because of solvent coupling to the nuclear motion degrees of freedom of the reacting molecules from the transition state onwards. In the current case, this effect appears to be more pronounced in CCl4 than in CDCl3, perhaps reflecting greater overlap of the frequencies of the HCl fundamental band and a C–H stretching mode of DMB in the former solvent.
The results presented here extend our recent studies of vibrationally state resolved dynamics in solution in organic liquids from reactions of CN radicals23–25,54,55 to include exothermic Cl atom reactions. Several general conclusions are emerging from these combined studies. In particular, many features of the gas-phase dynamics of exothermic reactions involving transfer of an H (or D) atom persist when the reactions take place in these organic solvents. Thus, for example, reactions with an early barrier on the PES will still produce nascent products that are vibrationally excited, consistent with Hammond's postulate and Polanyi rules for chemical dynamics, despite the very short time intervals between collisions with solvent molecules. The experimental studies, supported by our previous computational investigations of solution phase reaction dynamics, can distinguish solvent modifications to the PES over the course of the reaction from solvent interaction with the products after the reaction by examining nascent vibrational energy distributions. The measurements and calculations also distinguish between reaction within the initial solvent cage in which reactive species are first generated photolytically, and reaction following diffusion into the bulk solvent environment.
Acknowledgements
The Bristol group gratefully acknowledges financial support from the EPSRC Programme Grant EP/G00224X and the ERC Advanced Grant 290966 CAPRI. S.J.G. thanks the EPSRC for a Career Acceleration Fellowship (EP/J002534/1). Access to the ULTRA laser complex at the Central Laser Facility, Rutherford Appleton Laboratory is funded by STFC (Facility Grant ST/501784). We thank Drs T.J. Preston and M.P. Grubb for valuable comments, M. Dawson for help with acquiring the FTIR spectra of HCl in solution and Dr C.M. Western for discussions about their simulation.References
- C. Murray, J. K. Pearce, S. Rudic, B. Retail and A. J. Orr-Ewing, J. Phys. Chem. A, 2005, 109, 11093–11102 CrossRef CAS.
- C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435–482 CrossRef CAS.
- M. J. Bass, M. Brouard, C. Vallance, T. N. Kitsopoulos, P. C. Samartzis and R. L. Toomes, J. Chem. Phys., 2003, 119, 7168 CrossRef CAS.
- A. D. Estillore, L. M. Visger and A. G. Suits, J. Chem. Phys., 2008, 132, 164313 Search PubMed.
- R. A. Rose, S. J. Greaves and A. J. Orr-Ewing, J. Chem. Phys., 2010, 132, 244312 CrossRef.
- J. S. Pilgrim and C. A. Taatjes, J. Phys. Chem. A, 1997, 101, 5776–5782 CrossRef CAS.
- A. D. Estillore, L. M. Visger and A. G. Suits, J. Chem. Phys., 2010, 133, 074306 CrossRef.
- J. S. Pilgrim and C. A. Taatjes, J. Phys. Chem. A, 1997, 101, 4172–4177 CrossRef CAS.
- C. Murray, A. J. Orr-Ewing, R. L. Toomes and T. N. Kitsopoulos, J. Chem. Phys., 2004, 120, 2230–2237 CrossRef CAS.
- C. Murray, B. Retail and A. J. Orr-Ewing, Chem. Phys., 2004, 301, 239–249 CrossRef CAS.
- J. K. Pearce, S. J. Greaves, B. Retail, R. A. Rose and A. J. Orr-Ewing, J. Phys. Chem. A, 2007, 111, 13296–13304 CrossRef CAS.
- S. Rudic, D. Ascenzi and A. J. Orr-Ewing, Chem. Phys. Lett., 2000, 332, 487–495 CrossRef CAS.
- S. Rudic, C. Murray, D. Ascenzi, H. Anderson, J. N. Harvey and A. J. Orr-Ewing, J. Chem. Phys., 2002, 117, 5692–5706 CrossRef CAS.
- S. Rudic, C. Murray, J. N. Harvey and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2003, 5, 1205–1212 RSC.
- R. L. Toomes, A. J. van den Brom, T. N. Kitsopoulos, C. Murray and A. J. Orr-Ewing, J. Phys. Chem. A, 2004, 108, 7909–7914 CrossRef CAS.
- S. Rudic, C. Murray, J. N. Harvey and A. J. Orr-Ewing, J. Chem. Phys., 2004, 120, 186–198 CrossRef CAS.
- S. J. Greaves, A. J. Orr-Ewing and D. Troya, J. Phys. Chem. A, 2008, 112, 9387–9395 CrossRef CAS.
- A. J. Orr-Ewing, D. R. Glowacki, S. J. Greaves and R. A. Rose, J. Phys. Chem. Lett., 2011, 2, 1139–1144 CrossRef CAS.
- Tutorials in Molecular Reaction Dynamics, ed. M. Brouard and C. Vallance, Royal Society of Chemistry, Cambridge, 2010 Search PubMed.
- J. C. Polanyi, Acc. Chem. Res, 1972, 5, 161 CrossRef CAS.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- J. E. Leffler, Science, 1953, 117, 340–341 CAS.
- S. J. Greaves, R. A. Rose, T. A. A. Oliver, D. R. Glowacki, M. N. R. Ashfold, J. N. Harvey, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, Science, 2011, 331, 1423–1426 CrossRef CAS.
- R. A. Rose, S. J. Greaves, F. Abou-Chahine, D. R. Glowacki, T. A. A. Oliver, M. N. R. Ashfold, I. P. Clark, G. M. Greetham, M. Towrie and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2012, 14, 10424–10437 RSC.
- R. A. Rose, S. J. Greaves, T. A. A. Oliver, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, J. Chem. Phys., 2011, 134, 244503 CrossRef.
- NIST Chemistry Webbook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899 (retrieved 12 June 2012) Search PubMed.
- D. Raftery, M. Iannone, C. M. Phillips and R. M. Hochstrasser, Chem. Phys. Lett., 1993, 201, 513–520 CrossRef CAS.
- L. Sheps, A. C. Crowther, S. L. Carrier and F. F. Crim, J. Phys. Chem. A, 2006, 110, 3087–3092 CrossRef CAS.
- L. Sheps, A. C. Crowther, C. G. Elles and F. F. Crim, J. Phys. Chem. A, 2005, 109, 4296–4302 CrossRef CAS.
- C. G. Elles and F. F. Crim, Annu. Rev. Phys. Chem., 2006, 57, 273–302 CrossRef CAS.
- C. M. Western, PGOPHER, a Program for Simulating Rotational Structure, University of Bristol, 2010, http://pgopher.chm.bris.ac.uk/ Search PubMed.
- D. Robert and L. Galatry, Chem. Phys. Lett., 1967, 1, 399–403 CrossRef CAS.
- A. Medina, J. M. M. Roco, A. Calvo Hernandez, S. Velasco, M. O. Bulanin, W. A. Herrebout and B. J. van der Veken, J. Chem. Phys., 2002, 116, 5058–5065 CrossRef CAS.
- A. Padilla, J. Perez, W. A. Herrebout, B. J. Van der Veken and M. O. Bulanin, J. Mol. Struct., 2010, 976, 42–48 CrossRef CAS.
- J. Perez, A. Padilla, W. A. Herrebout, B. J. Van der Veken, A. Calvo Hernandez and M. O. Bulanin, J. Chem. Phys., 2005, 122, 194507 CrossRef CAS.
- K. S. Rutkowski and S. Melikova, J. Mol. Struct., 1998, 448, 231–237 CrossRef CAS.
- S. Melikova, K. S. Rutkowski, P. Lipkowski, D. N. Shchepkin and A. Koll, J. Mol. Struct., 2000, 844–845, 64–69 Search PubMed.
- K. S. Rutkowski, S. Melikova, D. N. Shchepkin, P. Lipkowski and A. Koll, Chem. Phys. Lett., 2000, 325, 425–432 CrossRef CAS.
- A. Padilla, J. Perez, K. Kerl and M. O. Bulanin, J. Mol. Struct., 2003, 651–653, 561–566 CrossRef CAS.
- W. West and R. T. Edwards, J. Chem. Phys., 1937, 5, 14–22 CrossRef CAS.
- D. Robert and L. Galatry, J. Chem. Phys., 1971, 55, 2347–2359 CrossRef CAS.
- J. T. Knudtson and J. C. Stephenson, Chem. Phys. Lett., 1984, 107, 385–388 CrossRef CAS.
- P. W. Atkins and R. Friedman, Molecular Quantum Mechanics, Oxford University Press, Oxford, 4th edn, 2005 Search PubMed.
- M. Tachiya, Radiat. Phys. Chem., 1983, 21, 167–175 CrossRef CAS.
- S. A. Rice, Comprehensive Chemical Kinetics, Vol.25: Diffusion-Limited Reactions, Elsevier, Amsterdam, 1985 Search PubMed.
- C. G. Elles, M. J. Cox, G. L. Barnes and F. F. Crim, J. Phys. Chem. A, 2004, 108, 10973–10979 CrossRef CAS.
- K. Iwata and H. Takahashi, J. Mol. Struct., 2001, 598, 97–102 CrossRef CAS.
- H. Tao, T. K. Allison, T. W. Wright, A. M. Stooke, C. Khurmi, J. van Tilborg, Y. Liu, R. W. Falcone, A. Belkacem and T. J. Martinez, J. Chem. Phys., 2011, 134, 244306 CrossRef CAS.
- J. Chateauneuf, J. Org. Chem., 1999, 64, 1054–1055 CrossRef CAS.
- J. Chateauneuf, J. Am. Chem. Soc., 1990, 112, 442–444 CrossRef CAS.
- J. Chateauneuf, Chem. Phys. Lett., 1989, 164, 577–580 CrossRef CAS.
- M. Ezell, W. Wang, A. Ezell, G. Soskin and B. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2002, 4, 5813–5820 RSC.
- I. Suh and R. Zhang, J. Phys. Chem. A, 2000, 104, 6590–6596 CrossRef CAS.
- D. R. Glowacki, A. J. Orr-Ewing and J. N. Harvey, J. Chem. Phys., 2011, 134, 204311 CrossRef.
- D. R. Glowacki, R. A. Rose, S. J. Greaves, A. J. Orr-Ewing and J. N. Harvey, Nat. Chem., 2011, 3, 850–855 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sc21267f |
| ‡ Current address: Department of Chemistry, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. |
| This journal is © The Royal Society of Chemistry 2013 |
