View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C3RP00043E (Paper) Chem. Educ. Res. Pract., 2013, 14, 421-430

Modeling meaningful learning in chemistry using structural equation modeling

Alexandra R. Brandrieta, Rose Marie Wardb and Stacey Lowery Bretz*a
aMiami University, Department of Chemistry and Biochemistry, Oxford, OH 45056, USA. E-mail: bretzsl@miamioh.edu
bMiami University, Department of Kinesiology and Health, Oxford, OH 45056, USA

Received 19th March 2013 , Accepted 24th April 2013

First published on 9th May 2013

Abstract

Ausubel and Novak's construct of meaningful learning stipulates that substantive connections between new knowledge and what is already known requires the integration of thinking, feeling, and performance (Novak J. D., (2010), Learning, creating, and using knowledge: concept maps as facilitative tools in schools and corporations, New York, NY: Routledge Taylor & Francis Group.). This study explores the integration of these three domains using a structural equation modeling (SEM) framework. A tripartite model was developed to examine meaningful learning through the correlational relationships among thinking, feeling, and performance using student responses regarding Intellectual Accessibility and Emotional Satisfaction on the Attitudes toward the Subject of Chemistry Inventory version 2 (ASCI V2) and performance on the American Chemical Society exam. We compared the primary model to seven alternatives in which correlations were systematically removed in order to represent a lack of interconnectedness among the three domains. The tripartite model had the strongest statistical fit, thereby providing statistical evidence for the construct of meaningful learning. Methodological issues associated with SEM techniques, including problems related to non-normal multivariate distributions (an assumption of traditional SEM techniques), and causal relationships are considered. Additional findings include evidence for weak configural invariance in the pre/post implementation of the ASCI(V2), mainly due to the poor structure of the pretest data. The results are discussed in terms of their implications for teaching and learning.

Introduction

Ausubel and Novak's construct of meaningful learning provides insight into human acquisition of knowledge that is substantive and anchored in prior understanding (Ausubel, 1963, 1968; Novak, 2010). When students learn, new ideas are attended to based upon their relevance to prior knowledge; this process is known as Ausubel's assimilation theory (Bretz, 2001; Novak, 2010). New information interacts with and is shaped by, prior knowledge, often increasing its stability (Ausubel, 2000). Such meaningful learning stands in contrast to rote-memorization in which information is simply and arbitrarily memorized (Mintzes et al., 1997). Memorized information is often quickly forgotten and difficult to transfer to other situations (Driscoll, 2005). However, if connections are made between prior knowledge and new information in a substantial way, then meaningful learning can take place (Cardellini, 2004).

In the classroom, meaningful learning engages students in three domains of experience: thinking, feeling, and performance (Novak, 2002). Not only must all three domains be part of the learning experience, but there must also be an active integration among students' thinking, feeling, and doing:

“…successful education must focus upon more than the learner's thinking. Feelings and actions are also important. We must deal with all three forms of learning. These are acquisition of knowledge (cognitive learning), change in emotions or feelings (affective learning) and gain in physical or motor actions or performance (psychomotor learning) that enhance a person's capacity to make sense out of their experiences.” (Novak, 2010, p. 13, italics original)

A key point in Novak's theory is that the interaction of thinking and performance is necessary, but not sufficient, for meaningful learning to occur. Consider a student in the chemistry laboratory who may be able to execute a titration with extreme precision and accuracy. This does not mean that the student has meaningfully learned about the particulate interactions of the acid–base chemistry that cause the indicator to change color or even what information can be learned from a titration. If a student performs the task perfunctorily with no appreciation for when and why chemists perform titrations, then meaningful learning will not occur. Previous studies have typically investigated learning in chemistry with regard to either thinking or feeling, but have not examined the integration of thinking and feeling and performance.

For example, a large body of literature exists regarding student misconceptions that form when new information interacts with prior knowledge structures (Banerjee, 1991; Garnett and Treagust, 1992; Nakhleh, 1992; Taber, 2002; Stefani and Tsaparlis, 2009; Davidowitz et al., 2010; Bretz and Linenberger, 2012; McClary and Bretz, 2012; Naah and Sanger, 2012). In addition to knowledge acquisition, metacognition is an intellectual skill in which students are required to think about their own thinking and is an important construct for understanding how students learn chemistry (Cooper et al., 2008; Cooper and Sandi-Urena, 2009).

Students' feelings with regard to learning chemistry (e.g., students' attitudes, self-concept, and motivation) have been investigated largely through the use of self-report surveys (Pintrich and Johnson, 1990; Bennett et al., 2001; Bauer, 2005, 2008; Barbera et al., 2008). Xu and Lewis (2011) created a shortened version of the Attitude towards the Subject of Chemistry Inventory (ASCI) originally proposed by Bauer (2008). This instrument, referred to as the ASCI(V2), stems from social psychology theories in which attitudes are grounded in a tripartite model of responses: cognitive, affective, and behavioral (Rosenberg and Hovland, 1960). ASCI(V2) measures students' thinking about the Intellectual Accessibility of chemistry and their feelings about the Emotional Satisfaction of learning chemistry. Instruments of this nature can be used as diagnostic measures in the chemistry classroom and laboratory (Brandriet et al., 2011) to explore the interaction between thinking and feeling that impacts students' willingness to choose to learn the content in a meaningful manner. The National Research Council (2012) report on Discipline-Based Education Research (DBER) has recommended that more research is needed to examine the affective domain and its relationships to other outcomes such as knowledge (thinking) and skills (performance).

While performance in learning chemistry typically conjures up images of students in the laboratory (e.g., Mattox et al., 2006; Poock et al., 2007; Lawrie et al., 2009; Sandi-Urena et al., 2011), this third element of meaningful learning has also been investigated in classroom settings by examining constructs such as problem solving, chemistry expectations, and scientific reasoning (Tobin and Capie, 1981; Grove and Bretz, 2007; Holme et al., 2010). Numerous studies have explored factors that influence performance using American Chemical Society examinations that are nationally normed in the United States (Lewis and Lewis, 2005, 2007; Bunce et al., 2006; Cracolice et al., 2008).

Students' abilities to perform algorithmic problems without demonstrating a strong conceptual understanding have been investigated (Nakhleh and Mitchell, 1993; Zoller et al., 1995) and are typical of research that examines dyads, i.e., relationships among two variables such as thinking and performing. For example, Lewis et al. (2009) and Xu and Lewis (2011) used student performance on an ACS exam to characterize the thinking-performance dyad and the feeling-performance dyad. Very recently, a study by Xu et al. (2013) used structural equation modeling (SEM) to identify pre-instruction predictors (prior knowledge, math ability, and attitude as measured by the ASCIV2) for student performance on an ACS exam. However, this study did not simultaneously examine thinking, feeling, and performance in chemistry as the essential elements of Novak's construct of meaningful learning.

Methodological considerations

Chemistry education research has typically examined thinking or feeling or performance in the chemistry classroom by identifying relationships through the use of bivariate correlations (which can only test dyadic relationships) and/or regression techniques (which assume an independent/dependent association between variables). Fig. 1 shows a regression model in which three independent variables influence a single dependent variable. This research study fills a gap in the literature by simultaneously investigating the relationships among thinking, feeling, and performance in chemistry through the use of SEM which simultaneously estimates the relationships among variables so that each variable competes for shared variance with the other variables in the model. In other words, each equation in the model is necessarily influenced by the system of equations that surrounds it. Therefore, each dyad in meaningful learning (e.g., thinking–feeling) will be influenced by the other dyads in the model (i.e., thinking-performance and feeling-performance). SEM also improves upon the statistical techniques used in previous research by considering not only the measurement error, but also the variance associated with latent structures (Raykov and Marcoulides, 2006).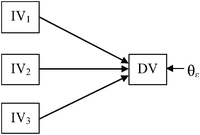
Independent-dependent relationships in regression analysis. Independent variable (IV) and dependent variable (DV).
Fig. 1 Independent-dependent relationships in regression analysis. Independent variable (IV) and dependent variable (DV).

Extensive literature has identified the relationships between student attitude and science achievement (Steinkamp and Maehr, 1983; Turner and Lindsay, 2003; Kan and Akbas, 2006; Nieswandt, 2007). However, discrepancies exist regarding the exact nature of the attitude–achievement relationship. Researchers often use statistical techniques that assume directional relationships between variables (e.g., attitude is an independent variable that influences the dependent variable of chemistry achievement). Whereas this can be a legitimate assumption when temporal relationships exist between variables (e.g., attitude is established first and then subsequently influences achievement), this argument is not always viable for cross-sectional studies (Bullock et al., 1994). Hence, the question of whether achievement influences attitude must also be considered. For example, students who do well may improve in attitude, while the attitudes of students who underperform may decline.

In a study recently published by Xu et al. (2013) students' pre-instruction “thinking” and “feeling” were used as predictors of student performance. While Xu et al. (2013) contribution to the body of literature is profound, our work adds to this previous literature by being strongly grounded not only in previous literature but also analyzed through the use of a theoretical lens. While situating a research study within the context of previous literature is important, the confirmatory approach of SEM requires a priori stipulation of a theoretical model (Kline, 2011). In the absence of theory, SEM may identify multiple patterns that can exist in the data and can be confirmed by a variety of models that fit the data well. Using a theoretical lens to formulate testable hypotheses reduces the occurrence of type 1 or 2 error (Kline, 2011). Novak himself cautions against method driven, rather than theory driven, research (Novak, 2010, p. 20). The research described below emerged from Novak's construct of meaningful learning, tested a simple model that was thoughtfully built to reflect this theoretical framework, and contributes to the body previously published research by simultaneously testing all three dyads within Novak's domains of meaningful learning. Furthermore, the design of this study contrasted the theorized model with multiple, other plausible models in order to provide evidence that any good statistical fit stemmed from confirmation of the theory, rather than patterns in the data.

Research questions

In addition to simultaneously investigating the interrelationships among thinking, feeling, and performance in chemistry, this study also provides insight into a complex statistical technique that can be useful for numerous research questions, but is not yet commonly used in chemistry education research. In this study, SEM was used to provide construct validity for the ASCI(V2), probe for structural invariance across pretest and posttest implementations of the ASCI(V2), discuss the implications of independent/dependent assumptions in SEM, and provide evidence for a model of meaningful learning. The study specifically explored answers to two questions:

(1) What evidence exists for a mutually dependent relationship across thinking, feeling, and performance for meaningful learning?

(2) Is the ASCI(V2) structurally invariant across pretest and posttest implementations?

Methodology

Participants

The student sample in this study was a group of first year chemistry students at a Midwestern university in the United States. Prior to beginning the first semester, student understanding of algebra was assessed via a university sponsored placement exam. Historical university data had shown that students who scored poorly on this exam were more likely to fail or withdraw from first year chemistry and were considered to be an “at-risk” student population. These students were placed into a separate general chemistry course that covered the same content as the traditional general chemistry courses at the university. However, in addition to the typical three hours of lecture and three hours of laboratory per week, the at-risk students were required to enroll in an additional one hour “recitation section” structured around a Process-Oriented Guided Inquiry Learning (POGIL) activity (Spencer, 1999; POGIL, 2012). These students were asked to complete the ASCI(V2) at the beginning of the semester and again at the end of the semester. Given the brevity of the instrument, students with missing data were removed from analysis based on the assumption that these students may not have read and considered the items thoroughly. Final data analysis was conducted with a sample of 123 students for the pretest and 89 students for the posttest. The pretest sample consisted of 58.5% female and 39.0% male (gender demographics were missing for 3 students in the pretest sample), whereas the posttest consisted of 59.6% female and 40.4% male. This is consistent with the overall university demographics that indicate that the university has a larger population of females than males. Though demographics for ethnicity were not collected for this sample, the university is composed of over 80% Caucasian students.

Data collection

Students answered an online version of the ASCI(V2) during the first two weeks of the fall semester (pretest) and again during the last ten days of the same fall semester (posttest) in 2009. On average, the ASCI(V2) required less than 2 minutes to complete, and students received 2 points of extra credit for participation (less than 1% of the total course grade). Students also were required to take the ACS first semester general chemistry exam (American Chemical Society, 2012) as a graded final exam for the course.

Instruments

ASCI(V2). The ASCI(V2) is a shortened version of the five-factor, 20-item Attitude towards the Subject of Chemistry Inventory (ASCI) originally proposed by Bauer (2008). Xu and Lewis (2011) created the ASCI(V2) by refining the ASCI into two-factors: Intellectual Accessibility (IA) and Emotional Satisfactions (ES), with each factor consisting of 4 items. The IA factor measures what students think about chemistry as a discipline to be learned, while the ES factor measures how students feel about chemistry. The ASCI(V2) does not contain a performance dimension because concrete behaviors are difficult to measure accurately on a self-reporting instrument (Xu and Lewis, 2011). The IA and ES factors have been chosen as the measures of Novak's constructs of “thinking” and “feeling” for this study.

The response options for the ASCI(V2) are on a semantic differential scale of polar adjectives with the stem “Chemistry is…”. The items are measured on a 7-point scale where a positive response (e.g., chemistry is easy) is scored as a 7 while the polar adjective (e.g., chemistry is hard) is scored as 1. Four items on the ASCI(V2) require reverse coding. ASCI(V2) has strong internal consistency and greater construct validity than the original ASCI (Brandriet et al., 2011; Xu and Lewis, 2011).

ACS exam. The ACS General Chemistry First Term 2005 exam is a nationally normed assessment used to measure students' performance. The exam asks students to solve problems regarding content taught in a first-semester university course such as stoichiometry, oxidation–reduction reactions, and Lewis structures. The exam consists of 70 multiple-choice questions to be answered in 120 minutes. Student scores range from 0–70 points, based on the number of correctly answered items. National data provides evidence of high internal consistency amongst the items with a KR-21 value of 0.90 (American Chemical Society, 2012). Novak's tripartite model of meaningful learning draws a distinction between knowing chemistry and the ability to perform in a classroom setting: “…you can relate what you know to how that knowledge operates” (Novak, 2010, p. 38). Hence scores on the ACS exam were used to measure Novak's construct of “performance.”

Analysis

SEM models

To examine the associations among thinking, feeling, and performance, SEM was used to test a model of meaningful learning and compare it to several alternative models. Theory describes that not only must the elements of thinking, feeling, and performance be present, but they also need to be integrated for meaningful experiences to occur (Novak, 1998). The theorized model represented the framework of meaningful learning in which thinking and feeling latent constructs covary with each other and with the performance variable (Fig. 2, model a). This theorized model of meaningful learning was compared to two competing models in which the thinking and feeling constructs had independent and dependent relationships with ACS exam score (Fig. 2, models b and c).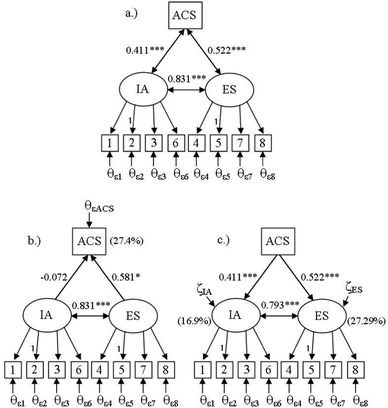
Directional models tested through structural regression modeling. Standardized parameter estimates for the theorized and comparison models (N = 89): meaningful learning (a), attitude influence success (b), and success influences attitude (c). Theta (θε) represents error associated with an observed variable and zeta (ζ) represents error associated with a latent variable. All paths leaving error are set to 1. IA, ES, and ACS are Intellectual Accessibility, Emotional Satisfaction, and ACS exam score, respectively. *p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.001.
Fig. 2 Directional models tested through structural regression modeling. Standardized parameter estimates for the theorized and comparison models (N = 89): meaningful learning (a), attitude influence success (b), and success influences attitude (c). Theta (θε) represents error associated with an observed variable and zeta (ζ) represents error associated with a latent variable. All paths leaving error are set to 1. IA, ES, and ACS are Intellectual Accessibility, Emotional Satisfaction, and ACS exam score, respectively. *p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.001.

To provide evidence that the elements of thinking, feeling, and performance must not only exist in the model but also be interdependent, the model of meaningful learning (Fig. 2, model a) was compared to seven alternative models in which individual bidirectional paths were successively removed from between the thinking, feeling, and performance variables (Fig. 3, models 1–7). Furthermore, configural invariance of the ASCI(V2) was assessed to test for equivalence of its two-factor structure across both pretest and posttest implementations of the instrument. This was done to identify whether the ASCI(V2) factor structure is equivalent across the pretest and posttest implementations for the at-risk students in this study, and thus, provide some insight into the construct validity of the data produced by the instrument within this study. If the factor structure is not similar across the pretest and posttest implementation of the instrument, caution is advised when comparing the results of the two implementations.


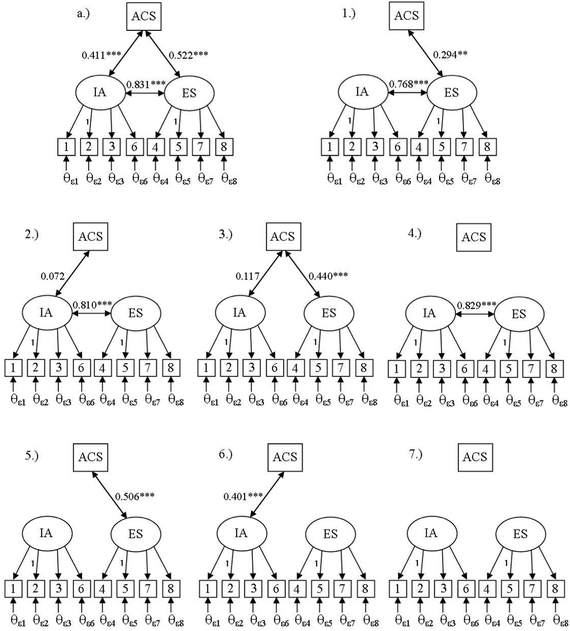Theorized and alternative models of meaningful learning standardized parameter estimates for the theorized (a) and alternate models (1–7) (N = 89). Theta (θ) represents error associated with an observed variable and zeta (ζ) represents error associated with a latent variable. All paths leaving errors are set to 1. *p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.001.
Fig. 3 Theorized and alternative models of meaningful learning standardized parameter estimates for the theorized (a) and alternate models (1–7) (N = 89). Theta (θ) represents error associated with an observed variable and zeta (ζ) represents error associated with a latent variable. All paths leaving errors are set to 1. *p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.001.

SEM assumptions and fit statistics

This study reinvestigated the measurement model of the ASCI(V2) with the Midwestern data set from Brandriet et al. (2011). Maximum Likelihood (ML) is the default parameter estimation method for most SEM analysis software. However, this method requires multivariate normal data. When the ML method is used on data that lacks multivariate normal distributions, inflation of the χ2 fit statistic can occur which leads to increased Type I error rates and means a greater chance of rejecting a correctly specified model (Hancock and Mueller, 2006; Byrne, 2012). An inflated χ2 will influence the results of some of the other fit statistics. The authors hypothesize that the lack of multivariate normality may explain the increased χ2 value (and corresponding decreased p-value) originally proposed in Brandriet et al. (2011). In this study, all data analysis was conducted using Mplus 5.21 (Muthén and Muthén, 1998–2010) using the Maximum Likelihood estimator (MLR) with robust standard errors. The MLR estimator used a Yuan–Bentler correction for non-normal data, and it works well with small sample sizes (Bentler and Yuan, 1999; Yuan and Bentler, 2000). When sample sizes are small, the probability of accepting a false model increases. Therefore, statistical power for the models was assessed post-hoc.

Based on recommendations of Hu and Bentler (1999), χ2 and the associated p-value, Comparative Fit Index (CFI), and Standardized Root Mean Square Residual (SRMR) were used to evaluate model fit. The χ2 goodness-of-fit test compares the proposed covariance structure of the theorized model with that of the sample data. In order to retain the null hypothesis, i.e., the theorized and sample covariance matrices are equal, a p-value would need to be greater than 0.05. Another indication that the proposed model fits the data well is when the χ2 per degrees of freedom (χ2/df) is lower than 2.00; however, this value should be interpreted with caution since it is considered a “rough rule of thumb” (Tabachnick and Fidell, 2007). Due to small sample considerations, the model fit was based on analysis of the CFI (>0.95) and SRMR (<0.06) statistics as proposed by Hu and Bentler (1999). The CFI is an incremental fit index that measures the relative improvement of the fit in the model in comparison to a model that assumes that none of the variables covary; this is known as the independence or null model. Large CFI values indicate a substantial improvement of the proposed model relative to the independence model. The SRMR is a standardized index based on the difference in covariance of the residuals between the predicted and the observed models. Small values indicate that the residuals of the theorized model reflect those in the sample data (Kline, 2011). The Root Mean Square Error Approximation (RMSEA) and the Tucker–Lewis Fit Index (TLI) are also provided as output by Mplus, but these indices tend to overreject true-population models when the sample sizes are small (Hu and Bentler, 1999). Therefore, the RMSEA and TLI indices were not used in this analysis as indicators of model fit.

Results and discussion

Descriptive statistics

The means and standard deviations for the pretest and posttest implementations of the ASCI(V2) are shown in Table 1. All items, except item 8, fell below the midpoint of the Likert scale, indicating less favorable student responses for both IA and ES. Both factors are internally consistent (pretest: αIA = 0.82, αES = 0.78; posttest: αIA = 0.85, αES = 0.79). The ACS exam mean ([X with combining macron] = 47.37, sx = 8.68) for the first year chemistry students was at the 69th percentile per the nationally normed statistics for the exam (American Chemical Society, 2012).
Table 1 Descriptive statistics for ASCI(V2) responses
Item Item #a Pre mean (SD) (N = 123) Post mean (SD) (N = 89)
a Items that required reverse coding are labeled ‘r’.
Intellectual accessibility (IA)     — — —
Easy Hard 1r 2.92 (1.28) 2.78 (1.43)
Complicated Simple 2 2.64 (1.29) 3.06 (1.61)
Confusing Clear 3 3.36 (1.37) 3.53 (1.55)
Challenging Unchallenging 6 2.20 (1.06) 2.43 (1.36)
Emotional satisfaction (ES)     — — —
Comfortable Uncomfortable 4r 3.61 (1.37) 3.74 (1.56)
Satisfying Frustrating 5r 3.72 (1.56) 3.37 (1.77)
Pleasant Unpleasant 7r 3.90 (1.24) 3.64 (1.37)
Chaotic Organized 8 4.40 (1.40) 4.34 (1.54)

Multivariate normality was assessed using the Mardia's normalized estimate of multivariate kurtosis using AMOS 20 (Mardia, 1970). Values greater 5.00 indicate that the data may lack a multivariate normal distribution (Byrne, 2010). The Mardia normalized coefficient was assessed prior to running analyses on each model. All values were greater than 7.00; therefore, the models were outside the bounds of multivariate normality. Another consideration of the authors was the small sample size; therefore, a post-hoc power analysis was conducted based on the RMSEA of close fit (MacCallum et al., 1996). Power was established to be greater than 0.80, and thus, sufficient to detect statistical differences.

Measurement models

Before running structural regression analyses, the fit of the measurement model (as shown in Fig. 4) for the pretest and posttest ASCI(V2) was examined. Items 1, 2, 3, and 6 were fixed to load on the IA factor, while items 4, 5, 7, and 8 were fixed to load on the ES factor. Items 2 and 5 had the greatest correlation with the other items within each of their respective factors and, thus, were set as scaling factors for this model. The scaling factor was necessary in order to measure the variance associated with the IA and ES factors (Kline, 2011).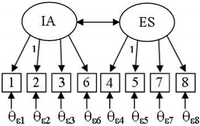
Measurement model for ASCI(V2). Theta (θε) represents measurement error in model. Paths leaving error are set to 1 but removed for simplicity of image. IA and ES are Intellectual Accessibility and Emotional Satisfaction, respectively.
Fig. 4 Measurement model for ASCI(V2). Theta (θε) represents measurement error in model. Paths leaving error are set to 1 but removed for simplicity of image. IA and ES are Intellectual Accessibility and Emotional Satisfaction, respectively.

The fit indices for the pretest measurement model were χ2(19, N = 123) = 77.177, p ≤ 0.001, CFI = 0.832, and SRMR = 0.078, while the fit indices for the posttest measurement model were χ2(19, N = 89) = 27.657, p = 0.0903, CFI = 0.958, and SRMR = 0.051. Based on the Hu and Bentler (1999) criteria, the posttest measurement model was determined to have a strong fit, while the pretest model was poor. In order to assess whether the two-factor structure of the ASCI(V2) was stable across pre and post chemistry instruction, configural invariance testing was performed on the data. The structure was found to vary across implementations with fit indices of χ2(50) = 121.482, p ≤ 0.001, CFI = 0.868, and SRMR = 0.079. Results show that the pretest data contributed to the overall χ2 value more than the posttest (χ2pretest = 76.964, χ2posttest = 44.518). Since a large χ2 is associated with a smaller p-value, this result is indicative of the poor fit in the pretest model. This was likely a consequence of the diversity of students' prior experiences with chemistry before college instruction (e.g., secondary school chemistry). Students with varying prior experiences may respond differently, and thus, result in inconsistent responses and poor model fit. However, the two-factor structure did fit the posttest data well. This result may be founded in the students now having a shared experience, and therefore, shared understanding of chemistry.

Because the strong fit in the ASCI(V2) measurement model provides evidence of high construct validity (based on the fit indices), the posttest data was used for the remaining analyses. All pretest and posttest items had large and significant loading on their respective factors, as indicated in Table 2. The correlation between the IA and ES factors was determined to be large and significant (rpretest = 0.759, p ≤ 0.001; rposttest = 0.828, p ≤ 0.001).

Table 2 Table of standardized parameters for pretest and posttest ASCI(V2) measurement model
ASCI(V2) items Factor loadings Error variance
Pretest Posttest Pretest Posttest
a p ≤ 0.01.b p ≤ 0.001.
Intellectual accessibility          
1r 0.700b 0.736b 0.511b 0.458b
2 0.755b 0.822b 0.429b 0.324a
3 0.857b 0.840b 0.265b 0.294b
6 0.577b 0.655b 0.667b 0.571b
Emotional satisfaction          
4r 0.787b 0.824b 0.381b 0.320b
5r 0.808b 0.783b 0.348b 0.387b
7r 0.787b 0.630b 0.381b 0.603b
8 0.418b 0.552b 0.826b 0.696b

Considering directionality between variables

The posttest ASCI(V2) data was collected within the last ten days of the fall semester and the ACS exam was given as the final course exam. By this point in the semester, students had already taken four course examinations, and therefore, we can assume that students' thinking and feeling towards chemistry was fairly stable within this ten day period. Because the ACS final exam was also given within this time period, we can also assume that this study is cross-sectional in nature. Although SEM is often referred to as ‘causal modeling’ (e.g., Schreiber et al., 2006), no statistical technique can actually establish causal relationships if the design of the study does not warrant such (Bullock et al., 1994). Three minimum conditions must be satisfied in order to establish independent/dependent associations among variables: (1) association between variables, (2) isolation of the effect, and (3) temporal ordering (Bullock et al., 1994). Based on the cross-sectional nature of this study (lack of temporal ordering of variables), independent/dependent associations amongst variables cannot be presumed. Further, the theory of meaningful learning describes a relationship in which all three variables influence each other with no specific directional relationship among the thinking, feeling, and performance domains (Novak, 2010). For this reason, it was best not to specify an exact directional relationship as we wanted to compare our theorized model that allowed for bidirectional relationships among thinking, feeling, and performance (Fig. 2, model a) with models in which thinking and feeling influence performance and vice versa (Fig. 2, models b and c), as has been shown in previously described literature.

Both the theorized and the alternate models had identical and good fit: χ2(25, N = 89) = 35.985, p = 0.0718, χ2/df = 1.44, CFI = 0.955, and SRMR = 0.052. The Akaike Information Criteria (AIC) takes into account model fit and parsimony and is generally used to compare non-nested models (one model is nested in another when the only difference between models is that individual paths in one model are removed) (Kline, 2011; Byrne, 2012). However, since models a–c had the same level of parsimony (df = 25) and similar fit, the AIC was equivalent across the three models (AIC = 2962.265). Based purely on statistical fit, we could not rule out any of the proposed non-nested models. All significant parameter estimates for models a–c were large (see Fig. 2).

Given that all the models had identical and good statistical fit, the best fitting model could not be determined based on empirical evidence alone. If we had tested only one of these models without comparing it to the fit of the other theoretically viable models, an incomplete account of the relationships could have been proposed. Once again, SEM models should always be based on theory and compared to other theoretically viable models. When model specification is based only on empirical evidence and not upon theoretical consideration, the likelihood of a significant or non-significant path due to chance (type I or type II error) is of great concern (Kline, 2011). For this reason, the model of best-fit was chosen upon the basis of the theoretical framework of meaningful learning (Fig. 2, model a). Feedback on assessment of student performance may also influence students' thinking and feeling, much like students' thinking and feeling affects their performance. If one were to accept one of the other models (Fig. 2, model b or c) based only on empirical evidence, they would fail to maximize the quality of student learning by not taking into account the tripartite equilibrium that exists between thinking, feeling, and learning. Remaining analyses were based upon this model due to theoretical implications of meaningful learning and the temporality of variables consideration.

Comparing nested models

In order to provide additional evidence for the tripartite model of meaningful learning, Fig. 2 model ‘a’ (also shown in Fig. 3, model a) was compared to three similar models in which one of the bidirectional paths were successively removed. These alternate models depicted the absence of any connection between two of the domains of meaningful learning (Fig. 3, models 1–3). The theorized model was also compared to three models in which two of the correlational paths were removed (Fig. 3, models 4–6), i.e., one of the domains was modeled as having no relationship with the other two domains. The final alternate model included all three domains, but considered none of them to be related to any of the others (Fig. 3, model 7).

As shown in Table 3, the theorized model of meaningful learning had a much stronger fit than the seven alternate models. The chi-square fit statistic was influenced by the number of degrees of freedom in the model, so that more parsimonious models (more degrees of freedom) were less likely to emulate the covariance matrix and were easier to reject than less parsimonious models (fewer degrees of freedom) (Raykov and Marcoulides, 2006). Since the alternate models were more parsimonious than the meaningful learning model, a chi-square difference test was used to determine if constraining correlational paths to zero (i.e., removing a path and increasing the degrees of freedom) in the alternate models did, in fact, reduce the fit of the model.

Table 3 Indicators of model fit and chi-square difference values associated with the nested theorized and alternate models
Nested models χ2[thin space (1/6-em)]a ΔTb Δdf χ2/df CFI SRMR
a Satorra–Bentler chi-square corrected for non-normal data.b Satorra–Bentler chi-square difference value corrected by scaling factor.c p < 0.01.d p < 0.001.
Meaningful learning 35.985 — — 1.44 0.955 0.052
Alternate 1 47.143c 14.83d 1 1.69 0.913 0.117
Alternate 2 53.529c 17.54d 1 2.06 0.887 0.133
Alternate 3 78.864d 37.95d 1 3.03 0.783 0.255
Alternate 4 54.608c 21.34d 2 2.02 0.877 0.141
Alternate 5 80.239d 47.28d 2 2.97 0.782 0.260
Alternate 6 85.528d 44.72d 2 3.17 0.760 0.265
Alternate 7 96.722d 63.02d 3 3.45 0.718 0.278

When using the MLR method for parameter estimation, the chi-square values were corrected for non-normality in the data through the use of a scaling correction factor (Muthén and Muthén, 2010). Due to this correction, the chi-square value no longer followed a normal chi-square distribution so the difference between values alone had very little meaning. The Satorra–Bentler scaled chi-square difference test (ΔT) was used to take into account the scaling factor of the chi-square value (Mplus, 2012; Satorra and Bentler, 2001).

Table 3 provides the ΔT and associated p-values between the meaningful learning model and each of the seven alternate models. The theorized meaningful learning model showed a significantly better fit than any of the alternate models, providing evidence that a tripartite relationship exists between the thinking, feeling, and performance elements of meaningful learning. In alternate models 2 and 3 (Fig. 3) it is noted that the relationships between IA and ACS exam score is non-significant but in the meaningful learning model the equivalent relationship is strong and significant. A similar result occurred in the alternate model in Fig. 2, model b. From these results, it is possible to conclude that the relationship between thinking and performance was the weakest relationship in the models. A slight positive skew (students responded that chemistry was hard, complicated, challenging, and confusing) in the IA items likely reduced the associated variance, and since the SEM paths are measured simultaneously, the influence of the ES-ACS exam path may be so great that it suppressed the variance associated with the IA-ACS exam path in Fig. 2, model b and Fig. 3, model 2 and 3 (Velicer, 1978; Maassen and Bakker, 2001). However, since the fit of the theorized model was greater than either model 2 or 3 in Fig. 3, the conclusion can be drawn that a relationship does exist between thinking and performance. Based on both theory and the results of this analysis, evidence has been generated that not only do thinking, feeling, and performance each need to be present, but that each domain also needs to be interconnected or integrated into an educational experience as originally theorized.

Implications for research and teaching

Based on careful theoretical and methodological considerations, an SEM model of meaningful learning has been established using the ASCI(V2) and ACS Exam scores in the posttest. There is frequently an emphasis in the literature to focus on encouraging positive student attitudes which will in turn help to stimulate student achievement in the classroom. However, as this study demonstrates, instructors need to be aware of the interdependent nature of this relationship. Instructors should consider providing positive affective experiences by using formative assessment in the classroom by using assessment as a meaningful experience to help students learn from their mistakes and build greater confidence in the material. Tools such as clickers and concept inventories may help faculty assess students' thinking in order to help motivate students to continue to work through the course material and build upon and change their understandings. Without meaningful assessment of their chemistry understanding, students may continue to struggle on summative assessments (i.e., exams) and leave university chemistry courses with a negative feeling regarding the academic subject of chemistry.

Instructors face the challenge of maintaining an equilibrium across thinking, feeling, and performance so that all domains co-exist and are integrated into a meaningful experience. In a chemical equilibrium, increasing the concentration of the reactants will shift the equilibrium to the right so that the concentration of the products also increases. LeChatelier's principle does not apply, however, to the model of meaningful learning. That is to say, emphasis of thinking and performance in the chemistry classroom is necessary, but not sufficient, to improve feeling. In fact, in this study the weakest association was between thinking and performance in the meaningful learning model, further emphasizing that feeling is vital for students to have meaningful experiences. Teachers must help students grow in the affective domain. Chemistry students' affective ideas are built through teacher and student interactions with thinking and performance (Novak, 2010). By sharing and discussing their thinking with the instructor or through inquiry-based teaching strategies, students can build their own ideas about how chemical principles relate to them and their understanding of the world. By providing contextual examples of chemical concepts, students may be able to assimilate news ideas with their prior understanding. We suggest that future research replicate this study with different samples in order to further generalize Novak's model to a larger population, as well as test different types of measures of thinking, feeling and performance under Novak's model.

In this study, the model of meaningful learning had strong statistical fit for the posttest data, but the fit for the pretest data was poor. One explanation for this result is that students at the beginning of the semester have not yet had a meaningful experience to integrate their thinking, feeling, and performance, and therefore, meaningful learning of chemistry could not have possibly occurred yet. However, after a semester of chemistry lecture, laboratory, and POGIL-based recitation sections, the thinking, feeling, and performance of these students are more meaningfully integrated. Our data suggest that meaningful learning does not exist at the beginning of general chemistry for these students. More research is needed to explore how thinking, feeling, and performance change at multiple points in time across a semester in order to understand the implications of the lack of invariance across the pretest and posttest measurement model. However, based on the results of this study, educators and researchers should proceed cautiously when designing studies that compare the results of self-report data over time. The pretest results in this study are likely a consequence of the diversity of (if not lack thereof) student prior experiences with chemistry before university instruction. The thinking, feeling, and performance of students with varying prior experiences may well differ, especially when measured at the beginning of a semester before the students have a chance to share a common meaningful experience.

Acknowledgements

This material is based upon work supported by the National Science Foundation under the Graduate Research Fellowship Program and the NSF-DUE collaborative project Grant No. 0817297.

References

  1. American Chemical Society, (2012), American Chemical Society Division of Chemical Education Examination Institute Retrieved Nov., 2012, from http://chemexams.chem.iastate.edu/.
  2. Ausubel D. P., (1963), The psychology of meaningful verbal learning; an introduction to school learning, New York, NY: Grune & Stratton.
  3. Ausubel D. P., (1968), Educational psychology; A cognitive view, New York, NY: Holt, Rinehart, and Winston Inc.
  4. Ausubel D. P., (2000), The acquisition and retention of knowledge: a cognitive view, Dordrecht, Boston: Kluwer Academic Publishers.
  5. Banerjee A. C., (1991), Misconceptions of students and teachers in chemical equilibrium, Int. J. Sci. Educ., 13(4), 487–494.
  6. Barbera J., Adams W. K., Wieman C. E. and Perkins K. K., (2008), Modifying and validating the Colorado Learning Attitudes about Science Survey for use in chemistry, J. Chem. Educ., 85(10), 1435–1439.
  7. Bauer C. F., (2005), Beyond student attitudes: chemistry self-concept inventory for assessment of the affective component of student learning, J. Chem. Educ., 82(12), 1864–1870.
  8. Bauer, C. F., (2008), Attitudes towards chemistry: a semantic differential instrument for assessing curriculum impact, J. Chem. Educ., 85(10), 1440–1445.
  9. Bennett J., Rollnick M., Green G. and White M., (2001), The development and use of an instrument to assess students' attitude to the study of chemistry, Int. J. Sci. Educ., 23(8), 833–845.
  10. Bentler P. M. and Yuan K. H., (1999), Structural equation modeling with small samples: test statistics, Multivariate Behav. Res., 34(2), 181–197.
  11. Brandriet A. R., Xu X. Y., Bretz S. L. and Lewis J. E., (2011), Diagnosing changes in attitude in first-year college chemistry students with a shortened version of Bauer's semantic differential, Chem. Educ. Res. Pract., 12(2), 271–278.
  12. Bretz S. L., (2001), Novak's theory of education: human constructivism and meaningful learning, J. Chem. Educ., 78(8), 1107.
  13. Bretz S. and Linenberger K., (2012), Development of the enzyme-substrate interactions concept inventory, Biochem. Mol. Biol. Educ., 40(4), 229–233.
  14. Bullock H. E., Harlow L. L. and Mulaik S. A., (1994), Causation issues in structural equation modeling research, Struc. Equ. Modeling, 1(3), 253–267.
  15. Bunce D. M., VandenPlas J. R. and Havanki K. L., (2006), Comparing the effectiveness on student achievement of a student response system versus Online WebCT quizzes, J. Chem. Educ., 83(3), 488–493.
  16. Byrne B. M., (2010), Structural equation modeling with AMOS: basic concepts, applications, and programming, 2nd edn, New York: Routledge.
  17. Byrne B. M., (2012), Structural equation modeling with Mplus: basic concepts, applications, and programming, New York: Routledge.
  18. Cardellini L., (2004), Conceiving of concept maps to foster meaningful learning: an interview with Joseph D. Novak, J. Chem. Educ., 81(9), 1303–1308.
  19. Cooper M. M. and Sandi-Urena S., (2009), Design and validation of an instrument to assess metacognitive skillfulness in chemistry problem solving, J. Chem. Educ., 86(2), 240–245.
  20. Cooper M. M., Sandi-Urena S. and Stevens R., (2008), Reliable multi method assessment of metacognition use in chemistry problem solving, Chem. Educ. Res. Pract., 9(1), 18–24.
  21. Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: a cognitive difference, J. Chem. Educ., 85(6), 873–878.
  22. Davidowitz B., Chittleborough G. and Murray E., (2010), Student-generated submicro diagrams: a useful tool for teaching and learning chemical equations and stoichiometry, Chem. Educ. Res. Pract., 11(3), 154–164.
  23. Driscoll M. P., (2005), Psychology of learning for instruction, 3rd edn, Boston: Pearson Allyn and Bacon.
  24. Garnett P. J. and Treagust D. F., (1992), Conceptual difficulties experienced by senior high school students of electrochemistry: electric circuits and oxidation–reduction equations, J. Res. Sci. Teach., 29(2), 121–142.
  25. Grove N. and Bretz S. L., (2007), CHEMX: an instrument to assess students' cognitive expectations for learning chemistry, J. Chem. Educ., 84(9), 1524–1529.
  26. Hancock G. R. and Mueller R. O., (2006), Structural equation modeling: a second course, Greenwich, CT: Information Age Publishing Inc.
  27. Holme T., Bretz S. L., Cooper M., Lewis J., Paek P., Pienta N., Stacey A., Stevens R. and Towns M., (2010), Enhancing the role of assessment in curriculum reform in chemistry, Chem. Educ. Res. Pract., 11(2), 92–97.
  28. Hu L. and Bentler P. M., (1999), Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives, Struc. Equ. Modeling, 6(1), 1–55.
  29. Kan A. and Akbas A., (2006), Affective factors that influence chemistry achievement (attitude and self efficacy) and the power of these factors to predict chemistry achievement—I, J. Turk. Sci. Educ., 3(1), 76–85.
  30. Kline R. B., (2011), Principles and practice of structural equation modeling, in Kenny D. A. (ed.), New York, NY: The Guildford Press.
  31. Lawrie G., Adams D., Blanchfield J. and Gahan L., (2009), The CASPiE Experience: Undergraduate Research in 1st Year Chemistry Laboratory. Paper presented at the UniServe Science Conference, The University of Sydney, Australia.
  32. Lewis S. E and Lewis J. E., (2005), Departing from lectures: an evaluation of a peer-led guided inquiry alternative, J. Chem. Educ., 82(1), 135–139.
  33. Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
  34. Lewis S. E., Shaw J. L., Heitz J. O. and Webster G. H., (2009), Attitude counts: self-concept and success in general chemistry, J. Chem. Educ., 86(6), 744–749.
  35. Maassen G. H. and Bakker A. B., (2001), Suppressor variables in path models, Soc. Meth. Res., 30, 241–270.
  36. MacCallum R. C., Browne M. W. and Sugawara H. M., (1996), Power analysis and determination of sample size for covariance structure modeling, Psychol. Meth., 1(2), 130–149.
  37. Mardia K. V., (1970), Measures of multivariate skewness and kurtosis with applications, Biometrika, 57(3), 519–530.
  38. Mattox A. C., Reisner B. A. and Rickey D., (2006), What happens when chemical compounds are added to water? An introduction to the Model-Observe-Reflect-Explain (MORE) Thinking Frame, J. Chem. Educ., 83(4), 622–624.
  39. McClary L. and Bretz S., (2012), Development and Assessment of a Diagnostic Tool to Identify Organic Chemistry Students' Alternative Conceptions Related to Acid Strength, Int. J. Sci. Educ., 34(15), 2317–2341.
  40. Mintzes J. J., Wandersee J. H. and Novak J. D., (1997), Meaningful Learning is Science: The Human Constructivist Perspective, in Phye G. D. (ed.), Handbook of Academic Learning Construction of Knowledge, San Diego, CA: Academic Press Inc., pp. 405–451.
  41. Mplus, (2012), Chi-square difference testing using the Satorra–Bentler scaled chi-square. Retrieved Nov., 2012, from http://www.statmodel.com/chidiff.shtml.
  42. Muthén L. K. and Muthén B. O., (1998–2010), Mplus User's Guide, 6th edn, Los Angeles, CA: Muthén & Muthén.
  43. Naah B. M. and Sanger M. J., (2012), Student misconceptions in writing balanced equation for dissolving ionic compounds in water, Chem. Educ. Res. Pract., 13(3), 186–194.
  44. Nakhleh M. B., (1992), Why some students don't learn chemistry: chemistry misconceptions, J. Chem. Educ., 69(3), 191–196.
  45. Nakhleh M. B. and Mitchell R. C., (1993), Concept learning versus problem solving: there is a difference, J. Chem. Educ., 70(3), 190–192.
  46. National Research Council, (2012), Discipline-based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, in Singer S. R., Nielsen N. R. and Schweingruber H. A. (ed.), Committee on the Status, Contributions, and Future Direction of Discipline-based Education Research. Board on Science Education, Division of Behavioral and Social Sciences and Education, Washington, DC: The National Academies Press.
  47. Nieswandt M., (2007), Student affect and conceptual understanding in learning chemistry, J. Res. Sci. Teach., 44(7), 908–937.
  48. Novak J. D., (1998), Learning, creating, and using knowledge: concept maps as facilitative tools in schools and corporations, Mahwah, N.J.: L. Erlbaum Associates.
  49. Novak J. D., (2002), Meaningful learning: the essential factor for conceptual change in limited or inappropriate propositional hierarchies leading to empowerment of learners, Sci. Educ., 86(4), 548–571.
  50. Novak J. D., (2010), Learning, creating, and using knowledge: concept maps as facilitative tools in schools and corporations, New York, NY: Routledge Taylor & Francis Group.
  51. Pintrich P. R. and Johnson G. R., (1990), Assessing and improving students' learning strategies, New Dir. Tech. Learn., 42, 83–92.
  52. POGIL, (2012), Process-Oriented Guided Inquiry Learning, (last accessed July, 2012, from http://www.pogil.org).
  53. Poock J. R., Burke K. A., Greenbowe T. J. and Hand B. M., (2007), Using the science writing heuristic in the general chemistry laboratory to improve students' academic performance, J. Chem. Educ., 84(8), 1371–1379.
  54. Raykov T. and Marcoulides G. A., (2006), A first course in structural equation modeling, 2nd edn, Mahwah, N.J.: Lawrence Erlbaum Associates.
  55. Rosenberg M. J. and Hovland C. I., (1960), Cognitive, affective, and behavioral components of attitude, in Rosenberg M. J. and Hovland C. I. (ed.), Attitude organization and change, New Haven, CT: Yale University Press, pp. 1–14.
  56. Sandi-Urena S., Cooper M. M., Gatlin T. A. and Bhattacharyya G., (2011), Students' experience in a general chemistry cooperative problem based laboratory, Chem. Educ. Res. Pract., 12(4), 434–442.
  57. Satorra A. and Bentler P. M., (2001), A scaled difference chi-square test statistic for moment structure analysis, Psychometrika, 66(4), 507–514.
  58. Schreiber J. B., Nora A., Stage F. K., Barlow E. A. and King J., (2006), Reporting structural equation modeling and confirmatory factor analysis results: a review, J. Educ. Res., 99(6), 323–337.
  59. Spencer J. N., (1999), New directions in teaching chemistry: a philosophical and pedagogical basis, J. Chem. Educ., 76, 566–569.
  60. Stefani C. and Tsaparlis G., (2009), Students' levels of explanations, models, and misconceptions in basic quantum chemistry: a phenomenographic study, J. Res. Sci. Teach., 46(5), 520–536.
  61. Steinkamp M. W. and Maehr M. L., (1983), Affect, ability, and science achievement: a quantitative synthesis of correlational research, Rev. Educ. Res., 53(3), 369–396.
  62. Tabachnick B. G. and Fidell L. S., (2001), Using multivariate statistics, 5th edn, Boston, MA: Pearson Education.
  63. Taber K. S., (2002), Conceptualizing quanta: illuminating the ground state of student understanding of atomic orbitals, Chem. Educ. Res. Pract., 3(2), 145–158.
  64. Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
  65. Turner R. C. and Lindsay H. A., (2003), Gender differences in cognitive and noncognitive factors related to achievement in organic chemistry, J. Chem. Educ., 80(5), 563–568.
  66. Velicer W. F., (1978), Suppressor variables and the semipartial correlation coefficient, Educ. Psychol. Meas., 38, 953–958.
  67. Xu X. and Lewis J. E., (2011), Refinement of a chemistry attitude measure for college students, J. Chem. Educ., 88(5), 561–568.
  68. Xu X., Villanfane S. M. and Lewis J. E., (2013), College students' attitudes towards chemistry, conceptual knowledge and achievement: structural equation model analysis, Chem. Educ. Res. Pract., 14(2), 188–200.
  69. Yuan K. H. and Bentler P. M., (2000), Three likelihood-based methods for mean and covariance structure analysis with nonnormal missing data, Soc. Meth., 30, 165–200.
  70. Zoller U., Lubezky A., Nakhleh M. B., Tessier B. and Dori Y. J., (1995), Success on algorithmic and LOCS vs. conceptual chemistry exam questions, J. Chem. Educ., 72(11), 987–989.
This journal is © The Royal Society of Chemistry 2013