Hungarian university students' misunderstandings in thermodynamics and chemical kinetics

Abstract

The misunderstandings related to thermodynamics (including chemical equilibrium) and chemical kinetics of first and second year Hungarian students of chemistry, environmental science, biology and pharmacy were investigated. We demonstrated that Hungarian university students have similar misunderstandings in physical chemistry to those reported in published research papers. We also found that there are significant differences between the misunderstandings in physical chemistry of the students who have had very different levels of chemistry studies at the university. However, there is no significant difference between the four student groups in misunderstandings brought from secondary education. Behind the students' misunderstandings found in this survey there are some common reasons, like using everyday analogies in solving scientific problems, assuming macroscopic properties at the particulate level, reducing proportionality to direct proportionality, and mixing the concepts of thermodynamics and reaction kinetics.

---

Introduction

In the last two years several articles ( e.g., Radnóti, 2010; Tóth, 2010) demonstrated that in Hungary the knowledge of first year university students in chemistry is not sufficient. In these papers it was reported that the students not only know few facts, but also have misunderstandings in several areas of chemistry. We are interested in the misunderstandings in physical chemistry of the students who have studied this discipline during several previous semesters. The misunderstandings related to thermodynamics (including chemical equilibrium) and chemical kinetics of first and second year students of chemistry, environmental science, biology and pharmacy were investigated. The following hypotheses were tested in this research:

1. The Hungarian university students have similar misunderstandings in physical chemistry to those published in the literature.

2. There are significant differences between the misunderstandings in physical chemistry of the students who have had very different levels of chemistry study at university.

3. Some common reasons for students' misunderstandings in physical chemistry can be identified.

4. Some of the misunderstandings are rooted in secondary school education.

Theoretical background

What are the misunderstandings?

The misunderstandings are imaginations, notions and interpretations that are scientifically incorrect. It is known that there are several names (misconceptions, alternative conceptions, alternative frameworks etc.) used in the literature for students' misunderstandings. The widely, but not unambiguosly used term is ‘misconception’. Several authors agree that the word ‘misconception’ is not the most appropriate in the research of students' understanding (e.g., Gunstone, 1989). In agreement with Sözbilir and Bennett (2006) the word ‘misunderstanding’ is preferred to the word of ‘misconception’, because the students' explanations are mostly spontaneous constructions, which might or might not be compatible with the present level of science.

The misunderstandings are sometimes similar to out-of-date theories, which are well known from the history of science, like the phlogiston theory or the concept of continuous matter from Aristotle (e.g., Barke et al., 2009). Some theories interpret the emergence of misunderstandings as a way of learning (e.g., Johnstone, 2000). According to the constructivist theory of learning, misunderstandings appear when the new information (the new notion to be learned) does not agree with the already known system of knowledge, but the association occurs in such a way that the new information gets distorted (Osborne et al., 1983; Nahalka, 1997). As an example, the student may originally assume that the structure of matter is continuous, and then, as a result of education, accepts that the matter consists of atoms, molecules and ions. However, the student still supposes that these particles have exactly the same properties (colour, density, hardness) like those of the original bulk matter (e.g., Johnson, 1998).

Among the cognitive resources of misunderstandings in science, phenomenological primitives (p-prims) must be emphasized. P-prims are simple abstractions of personal common everyday experiences, and support the development of ideas that are intuitively accepted. Phenomenological primitives were proposed by diSessa (diSessa, 1993), and were used mainly in physics (e.g., diSessa, 1993; Hammer, 1996). Werby (2010) qualified a p-prim as follows: (a) it is not a formally learned concept; (b) it describes a phenomenon; (c) it is a bit of knowledge based on personal observations; (d) it may be a useful problem-solving tool as a cognitive shortcut. Taber (2008) and his co-workers studied the role for p-prims in learning chemistry (García-Franco and Taber, (2009); Taber and García-Franco, 2009, 2010).

According to other theories (Solomon, 1993; Talanquer, 2006), the origin of problems people have when studying chemistry (or another branch of science) is that they keep the everyday way of thinking when they handle scientific concepts. The thinking of most people can be characterized as naïve realism, which means that they rely on observations, even though the non-scientific observations may have shortcomings (inaccurate observations, excessive generalization, and selective cognition). The two most important categories of this theory are experimental assumptions and reasoning heuristics (Talanquer, 2006). Experimental assumptions are beliefs that originate from the experiences obtained from the surrounding world by an ordinarily thinking (‘common sense’) person. It's most important elements are continuity, substantialism, essentialism, mechanical causality, and teleology. Reasoning heuristics is a shortcut thinking scheme that is frequently used in quick decision making. Its main elements are association, reduction, fixation and linear sequencing.

Most of the misunderstandings are created during education via the transfer of the misunderstandings of the teachers, or as a consequence of improper teaching methods (‘school-made misconceptions’, e.g., Barke et al., 2009). It is especially characteristic for chemistry education, since the basic concepts of chemistry are scientific; most people do not have direct experience with its concepts and they meet them in the school only. The basic concepts of chemistry, like physical and chemical changes, atoms, molecules, ions, elements, compounds, mixtures and amount of matter, belong to this category (Taber, 2002). One of the sources of the problems is that chemistry interprets the matter and the notions simultaneously at three levels: at the macro, particle and symbolic levels (Johnstone, 2000). In the cases of some concepts of chemistry, the outdated name refers to the original meaning while the meaning itself has been changed (e.g., Schmidt, 1997). Such notions are the oxidation, neutralization or the periodic table of elements. Some concepts are not well-defined or their interpretation depends on the context (e.g., proton or concentration). Also, several theoretical models of chemistry are simultaneous models that complement each other. Examples are the acid–base models and the interpretation of redox reactions (e.g., Taber, 2002). These two features naturally lead to the emergence of misunderstandings (e.g., Barke et al., 2009; Taber, 2002). Misunderstandings have been identified in all branches of chemistry and discussed in several books and reviews (e.g., Garnett et al., 1995; Taber, 2002; Kind, 2004; Horton, 2007; Barke et al., 2009, etc.).

Students' misunderstandings in thermodynamics and chemical kinetics

In the international chemistry education literature, there have been numerous studies concentrating on the students' misunderstandings related to thermodynamics (including chemical equilibrium) and chemical kinetics (e.g., Garnett et al., 1995; Taber, 2002; Kind, 2004; Horton, 2007; Barke et al., 2009 and references therein).

The most frequently described misunderstanding is that the students are unable to distinguish between how far a reaction goes (thermodynamics) and how fast it is (chemical kinetics). Sözbilir et al. (2010) studied Turkish prospective chemistry teachers' conceptions of chemical thermodynamics and kinetics. They found six major misunderstandings about the difference between the concepts of chemical thermodynamics and kinetics, e.g., ‘Dissolving rate of a gas in water decreases with increasing temperature’ (79%), ‘The larger the equilibrium constant, the faster a reaction occurs’ (52%), ‘The rate of a forward reaction decreases with increasing temperature for an exothermic reaction’ (57%) (p. 113). They stated that the Turkish ‘prospective chemistry teachers attempted to interpret the kinetics of several phenomena by using thermodynamic data’ (p. 111). Several papers deal with chemistry teachers' misunderstandings in physical chemistry (e.g., Kolomuc and Tekin, 2011; Cheung et al., 2009). These studies show that the teachers' misunderstandings are the same as those of the students'.

Other papers on students' misunderstandings about chemical equilibrium (Quílez, 2004; Erdemir et al., 2000; Kousathana and Tsaparlis, 2002; Özmen, 2008; Pedrosa and Dias, 2000), entropy (Sozbilir, 2003; Sözbilir and Bennett, 2007), reaction rate (Cakmakci et al., 2006), enthalpy and spontaneity (Sozbilir and Bennett, 2006a, 2006b), and Gibbs free energy (Sozbilir, 2002) have also been published.

The effectiveness of teaching and learning methods on teaching and learning physical chemistry is a subject of several studies. Sözbilir, (2004) tried to answer the question what physical chemistry makes difficult. He examined student and lecturer perceptions of students' learning difficulties and he also proposed possible solutions. His findings suggest that students and lecturers perceive the learning difficulties differently. Among others, he suggested that ‘problems could first be asked that are answerable in qualitative terms; only later, when there is a reasonable understanding of the meanings attached to the chemical entity, should derivations and numerical calculations be introduced' (p. 578). Bilgin et al. (2009) studied the effect of problem-based learning instruction on students' performance of conceptual and quantitative problems in gas concepts. Their results showed that students in experimental groups have better performance on conceptual problems, but there was no significant difference between the experimental and the control groups in students' performance of quantitative problems. A study on teaching gases through problem-based learning showed significant effect on the development of students' skills such as self-directed learning, critical thinking and cooperative learning (Senocak et al., 2007). A similar effect of the problem-based learning was found during a physical chemistry laboratory course (Gürses et al., 2007). Evidence-informed instruction was found to be effective in teaching chemical kinetics (Cakmakci and Aydogdu, 2011). Students in the experimental group achieved significantly higher results in chemical kinetics and were more likely to use their knowledge across different contexts than students in the control group. The positive effect of conceptual change of pedagogy on the students' conceptions of reaction rate (Calik et al., 2010), chemical equilibrium and chemical kinetics (van Driel, 2002), and chemical thermodynamics (Le Maréchal and El Bilani, 2008) is presented by several authors. There is a wide range of publications on teaching problems and possibilities of chemical equilibrium in the literature (e.g., Banerjee, 1991, 1995; Ben-Zvi et al., 1993; Hackling and Garnett, 1985; Quílez and Solaz, 1995; Quílez, 2004; Rollnick et al., 2008; van Driel, Verloop and de Vos, 1998; van Driel, de Vos, Verloop and Dekkers, 1998).

Method

Instrument

A task sheet was assembled for the investigation of the misunderstandings of students in physical chemistry that contained 10 tasks in the fields of thermodynamics and reaction kinetics. Special attention was paid to the misunderstandings that are coming from mixing up chemical kinetics and thermodynamic notions. The task sheet was designed to test for the presence of known common misunderstandings instead of factual knowledge. The problems were solved by university students after the conclusion of their thermodynamics and chemical kinetics studies.

Questions were taken from the literature and from the educational experience of the authors. The validity of the questions was checked by the authors, and some of them were also tested in pilot studies among secondary school and university students.

The correlation of the result of each task with the results of the whole task sheet is given in Table A1. The correlation coefficients (at 0.01 significance level) indicate strong or moderately strong correlations, except for task 2 that has a weak correlation. The reliability of the task sheet was characterized with Cronbach-alpha. The obtained value is α = 0.758, which is an acceptable reliability value.

Sample

Between April and November, 2009, the task sheet was given to the following students of the Eötvös University (ELTE; Budapest, Hungary): Environmental Science BSc, Biology BSc, and Chemistry BSc. According to an inter-university agreement, the students of pharmacy of the Semmelweiss University (SOTE; Budapest, Hungary) study general, analytical and physical chemistry at the Eötvös University and they also were asked to answer the questions on the task sheet. All in all, 424 students sit the test; the distribution of the majors is indicated in Fig. 1. The results of the test contributed to the students' marks in physical chemistry, so they considered it seriously. There was no time limit for answering the questions. The number of female students (288) was almost double that of male students (136), but the gender ratio was very different in the different courses, as indicated in Table A2.

Fig. 1 The fraction of students participating in this study according to their majors.

It is noted that the chemistry students have learned much more chemistry (including physical chemistry) than the other students. The students of pharmacy are next according to the extent of their chemistry prestudies. The students of environmental science had the least studies in physical chemistry; in the form of lectures they had only 21 hours of physical chemistry and 12 hours on physical chemistry measurement methods (see Table A3).

Data analysis

Data were analysed both quantitatively and qualitatively. For each task, 2 points were given for a perfect answer and 0 for a wrong answer. Accordingly, the maximum score was 20 points. Fractional points were given for some answers as discussed below. During the qualitative analysis, the students' responses were categorized and the typical wrong answers were collected.

Results

The overall quantitative view of the results

The histogram given in Fig. 2 shows the results that the students achieved. The average score is very low: 4.00 ± 3.64 points, which is only 20% of the maximum. Fig. 3 compares the results of the various courses. The result of the chemistry students is the best (43.0%), followed by the students of pharmacy (24.5%), biology (17.2%), and environmental science (5.3%). This order correlates with the number of hours of their previous chemistry studies, but such a strong separation between the results of the four groups had not been expected; it is clear from Fig. 3 that the 95% confidence limits of the scores do not overlap.

Fig. 2 Histogram of the results. The solid line belongs to normal distribution corresponding to the calculated average and variance.

Fig. 3 Comparison of the results of the students of various courses. The squares denote the mean values of the results and the error bars correspond to 95% confidence limits.

Students of pharmacy and biology responded to the task sheet together with their written exam in thermodynamics and reaction kinetics. Fig. 4 shows that there is a very week correlation between the results of the exam and the task sheet (r = 0.184 at level p = 0.01). This means that the result of the task sheet cannot be interpreted as an assessment of the level of factual knowledge in physical chemistry. It is well known from the literature (e.g., Taber, 2002; Barke et al., 2009) that ‘traditional’ lectures focusing only on the scientific subject are not effective in changing misunderstandings.

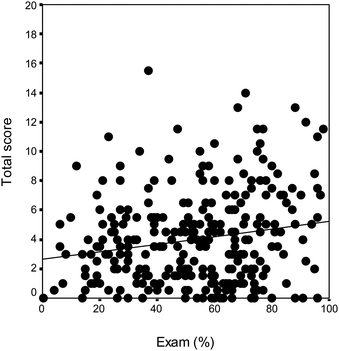Fig. 4 The results of the physical chemistry exam (%) vs. the score of the present task sheet for each student of biology and pharmacy. There is only a weak correlation between the two results.

Previous investigations on the level of knowledge in chemistry of first year university students have indicated (Radnóti, 2010; Tóth, 2010) that male students achieved significantly better results. In this case, we also found that the results of the male students was significantly (p = 0.001) better than those of the female students (see Fig. 5). The gender ratio was different in the different courses (see Table A2), and the results depended very much on the courses (see Fig. 3), therefore, special attention was paid to compensate this effect. The exam results of biology and pharmacy students in physical chemistry was almost identical for the male and female students (average points for males: 51.97; females: 50.62; p = 0.702).

Fig. 5 Comparison of the results of male and female students.

Discussion of the results by individual tasks

The average point obtained for each task is shown in Fig. 6. The easiest problems were tasks 10, 4, and 8 with successive ratios of about 35%. The hardest problems were tasks 2 and 3, where the average result was less than 5%. The detailed results are given in Tables 1 and 2 for tasks 1 to 5 and 6 to 10, respectively.

Fig. 6 The average result of each task.

Table 1 Summarized results for tasks 1 to 5 (Good solution is emphasised by italics, wrong answer with typical misunderstanding is emphasised by bold.)

Task	Answer	Chemistry	Pharmacy	Biology	Environmental science
1	Good solution	56%	13%	8%	4%
	(a) In the wet air there are…
	- less molecules	0%	1%	7%	8%
	- same number of molecules	79%	48%	34%	13%
	- more molecules	13%	20%	40%	30%
	(b) The wet air is…
	- lighter	56%	13%	11%	5%
	- of the same weight	2%	4%	2%	1%
	- heavier	25%	35%	59%	33%
	No answer	6%	27%	14%	49%
2	Good answer	2%	0%	4%	0%
	The rate of reaction…
	- decreases	50%	60%	50%	15%
	- does not change	2%	2%	2%	1%
	- increases	40%	21%	36%	38%
	No answer	6%	18%	9%	46%
3	Good answer (e) with justification	31%	4%	1%	0%
	Share of the solutions:
	- (a)	2%	19%	23%	5%
	- (b)	6%	28%	37%	23%
	- (c)	2%	4%	4%	1%
	- (d)	33%	16%	20%	4%
	- (e) without justification	15%	10%	9%	5%
4	Perfect solution	38%	10%	6%	5%
	Partially good answer: [A]e = [B]e	48%	66%	51%	19%
	Totally bad solution	13%	11%	28%	19%
	No answer	2%	13%	16%	58%
5	Good answer	60%	33%	27%	6%
	Typical wrong answer (6 moles)	17%	21%	24%	10%
	Other wrong answer	17%	24%	27%	16%
	No answer	6%	22%	21%	68%

---

Task 1

(a) Which gas contains more molecules, the dry air or the air saturated with water vapour? Assume that the volumes, temperatures and pressures are identical and the gas mixtures can be considered as ideal gases. (b) Which mixture has a higher weight and why?

Good answer: (a) According to the ideal gas law (and also according to Avogadro's law) the numbers of molecules are identical (1 point). (b) The relative molecular weight of air is about 29, while that of water is 18, therefore the air saturated with water vapour is lighter (1 point).

Typical wrong answers:

- Dry air contains N₂ and O₂ molecules, but if the air is saturated with water vapour, it also contains H₂O molecules. Therefore, it contains more molecules and it has a higher weight. The origin of this wrong answer is the misunderstanding of the structure of gases and gas laws.

- Analogy from everyday life: wet cloth is heavier than the dry one; therefore wet air is heavier than dry.

- Assumption of a continuous matter: liquids are heavier than gases; therefore the molecules of liquids also must have higher weight than those of gases. Several students stated that the numbers of molecules are identical in both cases, and the air containing water vapour is heavier, if the molar weight of the H₂O is higher than the molar weight of N₂ and O₂. Then they concluded that the relative mass of H₂O molecules is 18, while the relative masses of N₂ and O₂ molecules, are 28 and 32, respectively, thus the water molecule is heavier. They distorted the outcome of a perfect reasoning to obtain the desired result.

Only 14% of the students gave a good answer. According to 22% of the students the air saturated with water vapour contains more molecules, and therefore, the wet air is heavier. 15% of the students knew that there are identical number molecules in the two gases, but considered the air saturated with water vapour is heavier. The trend in these results is similar to those obtained from a test of secondary school students. The share of these answers of secondary school students were the following: 15%, 43%, 15%, respectively (Tóth, 2004). Some of the secondary school students explained that when they speak about a H₂O particle (that is, a H₂O molecule) they imagine it as a small water droplet. We did not meet this reasoning among the university students. It is noted that the literature reports several examples of retaining alternative conceptions commonly found among secondary school students (e.g., Taber and Tan, 2011).

The detailed results are summarized in Table 1. The ratio of good answers decreases, while the ratio of wrong answers with typical misunderstandings increases in order from ‘Chemistry’ to ‘Environmental Science’ supporting our hypothesis No. 2.

Based on the students' wrong answers we could detected two major reasons behind these misunderstandings: (1) using everyday analogy in solving a scientific problem, and (2) assuming macroscopic properties at particulate level.

Note that this question can be found in different context on the internet (e.g., Haby, no date).

Task 2

How does the rate of an exothermic reaction change if the initial temperature increases?

Good answer: Increasing the temperature, the rate of an exothermic reaction may decrease, remain constant or increase (2 points). There is no relation between the sign of the reaction enthalpy and the change of the reaction rate due to the increase of temperature.

Typical wrong answers:

- The rate of the reaction decreases. Some of the wrong answers originated from mixing up thermodynamic and reaction kinetic notions. For example, several students described that, according to the Le Châtelier principle, when increasing the temperature in exothermic reactions the reactants are favoured. This means that increasing the temperature the rate of production of products will decrease. In this case a thermodynamic principle, valid for equilibrium only, is used incorrectly for a chemical kinetic problem.

- The rate of the reaction increases. This typical wrong answer is based on several secondary school textbooks. These textbooks claim (referring to the everyday experience that perishable food should be kept in a fridge) that increasing the temperature, the rates of all chemical reactions increase. Some of the students mentioned that a typical exothermic reaction is the combustion, and the rates of all combustion reactions increase with temperature. This statement is simply wrong. The rates of many complex reactions decrease when the temperature increases. A usual example is the low temperature combustion of hydrocarbons that have a negative temperature coefficient (NTC) regime in a range of temperature (e.g., Zádor et al., 2011). Also, the rates of many enzymatic reactions decrease when the temperature exceeds 40 °C due to the change of the structure of the enzyme. The rate of an elementary reaction always increases with increasing temperature, if there is a single transition state and if there is a nonzero energy barrier. (For simplicity, let us neglect the effect of tunnelling.) A typical setup relating to the emergence of negative activation energy in an elementary reaction is when there are two energy barriers, passing through the second barrier is the rate limiting, and the height of the second barrier is lower than the energy level of the reactants. In the typical textbook examples, however, gas phase elementary reactions usually have a single transition state and positive energy barrier, which misguides the students.

This task shows that it is not easy to change the information during university education that was taught in secondary schools. Therefore, it is an important task for secondary school teachers to deliver the notions (in this case the temperature dependence of reaction rate) in a more subtle way. Some secondary school textbooks in Hungary include statements that “the reaction rate usually increases with temperature” or that “the rates of most chemical reactions increase with increasing temperature”, but these cautious sentences are not enough, and examples should be given for secondary school students to show that the reaction rate may decrease with temperature. Enzymatic reactions could be used as good examples.

The success rate of task 2 is detailed in Table 1. It can be seen that the occurrence of the misunderstanding related to mixing up thermodynamics and reaction kinetics depends on the level of chemistry studies at the university. On the contrary, the frequency of secondary school related misunderstandings is basically the same in the various students' groups.

Task 3

How does the rate of reaction N₂ + 3H₂ → 2NH₃ change if the initial concentration of the hydrogen gas is doubled? The temperature and the initial concentrations of N₂ and NH₃ remain identical. Indicate the correct answer and give a justification.

(a) The rate of the reaction remains identical;

(b) The rate of the reaction is doubled;

(c) The rate of the reaction is increased by a factor of 3;

(d) The rate of the reaction is increased by a factor of 8;

(e) The data provided are not sufficient to answer this question.

The good answer is (e). Reaction N₂ + 3H₂ → 2NH₃ is surely not an elementary reaction, because 4 molecules cannot collide at the same time. If this is not an elementary reaction, then the law of mass action is not applicable, therefore, we cannot state anything about the rate law. The students knew that in a gas phase elementary reaction more than two species never collide simultaneously, and they also knew that the law of mass action is applicable in all cases for elementary reactions only. However, they could not interconnect these two pieces of information.

Typical wrong answers:

- Some students assume that the reaction rate is always a linear function of concentrations. This would mean that doubling the reactant concentration the reaction rate is also doubled; therefore, the correct answer is (b).

- According to the law of mass action the rate of the reaction is v = k[N₂][H₂]³. If all other conditions are identical and the concentration of H₂ is doubled, then the rate of the reaction should increase by a factor of 2³ = 8, which means that the answer is (d).

The latter wrong answer may be typical for the Hungarian students. In most Hungarian secondary school textbooks, equilibrium is introduced through the rates of a pair of fast reactions having opposite direction (Tóth, 1999). The usual examples are equilibrium reaction H₂ + I₂ ⇌ 2HI or symbolic reaction aA + bB ⇌ cC + dD, and therefore, most students have the impression that the rate equation can always be obtained from the stoichiometric chemical equation.

Task 4

Plot a concentration (c)–time (t) diagram that indicates how the concentrations of reactant A and product B change, when reaction A ⇌ B reaches equilibrium. The initial concentration of A is not zero and that of B is zero. Let the horizontal and vertical axes represent time, t, and concentration, c, respectively!

Good answers: The concentration curves of both [A] and [B] should approach a vertical line. The sum of the equilibrium concentrations of [A]_e and [B]_e should be equal to [A]₀. In the general case the equilibrium concentrations of A and B are not equal to each other, since [A]_e = K [B]_e and [A]_e = [B]_e only if K = 1.

Typical wrong answer: Most students drew a figure in which the concentration curves [A] and [B] approach the same vertical line. Some students even explain that in equilibrium the rates of the forward and backward reactions are equal to each other, and the condition of it is that the equilibrium concentrations [A]_e and [B]_e are equal. Scoring: Any good figure is 2 points, in which equilibrium concentrations [A]_e ≠ [B]_e. Point 1 was given for all otherwise good figures in which the equilibrium concentrations are equal.

The answer that equilibrium concentrations [A]_e and [B]_e are equal to each other is a common misunderstanding. It is known from international studies (e.g., Garnett et al., 1995; Taber, 2002; Kind, 2004; Horton, 2007; Barke et al., 2009 and references therein) that, according to some students, in equilibrium the concentrations (or the amounts of matter) of the reactants and products should be equal to each other. This misunderstanding is amplified by analogies like the condition of the equilibrium of a scale is that the masses are equal on both sides. Also, most secondary school textbooks in Hungary do not show concentration–time curves, only reaction rate–time curves at the discussion of the equilibria. In these figures the reaction rates become equal after longer times.

Task 5

The stoichiometric mixture of hydrogen and oxygen gases—called detonating gas—explodes after ignition and forms the product water. How many moles of H₂ molecules are present in 3 moles of molecules in detonating gas?

Good answer: In the detonating gas the molar ratio of H₂ and O₂ molecules is 2 : 1. This means that 3 moles of molecules in detonating gas contain 2 moles of H₂ molecules and 1 mole of O₂ molecules.

Typical wrong answer: In the detonating gas the molar ratio of H₂ and O₂ is 2 : 1. This means that 3 moles of detonating gas contains 3 × 2 = 6 moles H₂.

The students know and use equations and n_i = x_in,, where n is the total number of moles in a mixture, n_i is the number of moles of species i, and x_i is the mole fraction of species i. However, they could not use the concept of the number of moles in a gas mixture on a given example. Very likely this task interfered with the usual task of the calculation of the number of moles of elements in a compound, like calculating the number of moles of hydrogen atoms in 3 moles of water molecules.

Task 6

Give the reaction equation of the process that has an enthalpy change equal to the enthalpy of formation of methanol (CH₃OH) at room temperature and 1 bar pressure!

Good answer: C(graphite) + 2H₂(g) + 0.5O₂(g) → CH₃OH(l)

Typical wrong answer: Several students suggested equations CH₃OH + 3/2O₂ → CO₂ + 2H₂O or CH₄ + 1/2O₂ → CH₃OH. In the examples of thermochemistry, most equations are related to combustion, and probably this is the reason for these incorrectly suggested chemical equations.

Results are summarized in Table 2. Almost all students know that the enthalpy of formation of a compound is equal to the reaction enthalpy of the formation from reference state elements. However, many students could not interpret this statement for an actual compound.

Table 2 Summarized results for tasks 6–10. (Good solution is emphasised by italics, wrong answer with typical misunderstanding is emphasised by bold.)

Task	Answer	Chemistry	Pharmacy	Biology	Environmental science
6	Good answer	40%	12%	4%	0%
	Wrong answer	23%	23%	18%	4%
	No answer	38%	64%	78%	96%
7	Good answer	6%	2%	0%	0%
	Typical wrong answer	35%	47%	23%	1%
	Other wrong answer	42%	16%	39%	3%
	No answer	17%	35%	52%	96%
8	Good answer	56%	50%	29%	5%
	Wrong answer	33%	33%	38%	13%
	No answer	10%	17%	32%	83%
9	Perfect solution (24.3)	17%	0%	0%	0%
	Good approximate answer (27)	13%	12%	11%	6%
	Typical wrong answer (9)	10%	23%	36%	13%
	Other wrong answer	23%	19%	23%	9%
	No answer	38%	45%	29%	73%
10	Good answers…
	- (a)	40%	22%	25%	6%
	- (b)	71%	44%	39%	10%
	- (c)	46%	22%	22%	5%
	- (d)	75%	61%	57%	31%
	No answer	2%	10%	4%	39%

---

Task 7

Which enthalpies of formation should be known to calculate the standard reaction enthalpy of the reaction between magnesium metal and 0.1 M hydrogen chloride solution?

Good solutions: There are no HCl molecules in a 0.1 M hydrogen chloride solution, but it contains hydrated ions of H⁺ and Cl⁻. Therefore, the chemical reaction is

Mg(s) + 2H⁺(aq) = Mg²⁺(aq) + H₂(g)

Mg(s) and H₂(g) are reference state elements and the corresponding enthalpies of formation are zero. Therefore, the standard molar enthalpies of formation of ions H⁺(aq) and Mg²⁺(aq) should be known at the conditions of reaction (2 points). Usually the relative enthalpies of formation of ions are considered, and the standard molar enthalpy of formation of H⁺(aq) is assigned to zero. Therefore, an alternative good answer is that only the enthalpy of formation of Mg²⁺(aq) relative to H⁺(aq) should be known (2 points). However, it is possible to determine the absolute standard molar enthalpy of formation of H⁺(aq), (see Tissandier et al., 1998). Note, that the enthalpies of formation of ions in water depend also on the type and concentration of the other ions present.

The typical wrong answer was that the chemical equation is Mg + 2HCl = MgCl₂ + H₂. Mg(s) and H₂(g) are reference state elements having zero standard molar enthalpies of formation. Therefore, the enthalpies of formation of HCl and MgCl₂ should be known. In this case the students did not consider that species HCl and MgCl₂ are not present in the solution. However, 1 point was given if the student realized that Mg(s) and H₂(g) are reference state elements having zero enthalpy of formation.

Assumption of the presence of HCl molecules in a 0.1 M hydrogen chloride solution is clearly a misunderstanding. A possible source of it is that in the laboratories, labels HCl and MgCl₂ are used also for the solutions of these compounds. Another possible reason for this misunderstanding is that the answers of students may depend on the subject. In an analytical chemistry test, the students might have written up ion equations, but in a physical chemistry test they were thinking in overall reactions of the compounds.

Task 8

The thermochemical equation of the combustion of carbon monoxide is the following:

2CO(g) + O₂(g) → 2CO₂(g) Δ_rH = −566 kJ mol⁻¹

Calculate the amount of heat that is released during the combustion of 0.500 mole of CO molecules.

The chemical equation is related to the enthalpy change of 2 moles CO molecules, which is four times more than 0.5 mole of CO molecules. The good answer is 566/4 kJ = 141.5 kJ (2 points).

Many students assume that reaction enthalpy always refers to the transformation of one mole of reactant, therefore, a frequent wrong answer is 566/2 kJ = 283 kJ. The dimension of reaction enthalpy is “energy divided by amount of matter” and the usual SI physical unit is kJ mol⁻¹, which is a frequent source of misunderstanding in secondary schools. Most students assume that this unit means that the reaction enthalpy belongs to one mole of one of the reactants or products. Some secondary school textbooks try to avoid this source of misunderstanding by using unit “kJ”, but it is not correct and it only disguises the problem. In general and physical chemistry classes, more attention should be paid to the clarification of the meaning of reaction enthalpy.

Task 9

The rate of a chemical reaction increases by a factor of 3 if the temperature is increased from 25 °C by 5 °C. How many times the rate of this reaction increases if the temperature is increased from 25 °C by 15 °C?

The good answer is that in a narrow temperature range, the change of the reaction rate with temperature can usually be described by the Arrhenius equation k = A exp(−E/RT). The reaction rate was tripled when temperature was increased from T₁ = 298.15 K to T₂ = 303.15 K, which allows the calculation of activation energy

The reaction rate increases by factor x if the temperature is increased from T₁ = 298.15 K to T₃ = 313.15 K:

The calculation above gives x = 24.3. (2 points)

A good estimation is that increasing the temperature by 5 °C increases the value of k by a factor of 3. This means that another 5 °C increase in temperature (2 × 5 °C = 10 °C) increases k by a factor of 3² = 9 and yet another 5 °C increase (3 × 5 °C = 15 °C) increases k by a factor of 3³ = 27 (2 points).

The typical wrong answer is that increasing the temperature by 5 °C increases the value of k by a factor of 3. This means that increasing temperature by 3 × 5 °C = 15 °C should increase k by a factor of 3 × 3 = 9. Most students (similarly to most persons-on-the-street) assume that all functions are linear, and make estimations of the results of exponential processes by assuming linear relations. The chemistry students have solved several numerical problems related to the application of the Arrhenius equation, and this is the reason why they had a better performance.

Task 10

Indicate if the statements below are true or false. Give also a short justification!

(a) The combustion of carbon is not a spontaneous process, because it has to be ignited.

(b) The solubility of sugar in water can be increased by stirring.

(c) The higher the equilibrium constant is, the faster the equilibrium is reached.

(d) Using a proper catalyst, higher conversion can be achieved than without the application of a catalyst.

Good answers (each good answer is 0.5 point):

(a) False. There is oxidation even at room temperature, but the reaction is slow at low temperature.

(b) False. The rate of solution can be increased by stirring, but the maximum concentrations remain identical. We must assume that stirring itself does not change the temperature and that we compare the equilibrium states before and after the stirring.

(c) False. The magnitude of the equilibrium constant and the time needed to reach the equilibrium are not related.

(d) False. A catalyst may increase the rate of reaction but cannot increase the conversion.

Typical wrong answers:

(a) Yes, the combustion of coal requires ignition. The origin of this wrong answer is that a kinetic notion (the rate of a process) is mixed up with a thermodynamic notion (spontaneous process). The students should have investigated which is the thermodynamically stable state of the coal + air system.

(b) Yes, the solubility of sugar in water can be increased by stirring. An everyday experience is that fast solution requires stirring. Maybe high solubility was mixed up with fast solution.

(c) Yes, a higher equilibrium constant means reaching the equilibrium state faster.

These students did not take into account that the equilibrium constant is the ratio of two rate coefficients. The same equilibrium constant can be obtained from rate coefficients having very different orders of magnitude.

(d) Yes, a catalyst may change the equilibrium composition.

Most of the good answers were given for question (d), because this topic had extensively been discussed in the secondary school and in university lectures. Many good answers were given for question (b). Here the students properly distinguished a kinetic process (rate of solution) and a thermodynamic controlled issue (the maximal concentration in a solution). Students who gave a good answer might have remembered that solubility is related to the chemical potential of the dissolved compound, which is entirely determined by the state variables.

Conclusions

The results basically supported our initial hypotheses. We demonstrated that Hungarian university students have similar misunderstandings in physical chemistry to those reported in several recent research papers (e.g., Garnett et al., 1995; Taber, 2002; Kind, 2004; Horton, 2007; Barke et al., 2009 and references therein). However, we had not expected that university science students are not able to apply knowledge (e.g., the number of molecules in special volumes of ideal gases) that is part of the basic curriculum in the secondary school. Many students could not determine if a given task belongs to thermodynamics or chemical kinetics. They tried to apply thermodynamic reasoning for solving kinetic problems or vice versa. Results of several tasks indicated that even if they knew well the facts (such as the interpretation of a gas mixture or definition of the enthalpy of formation), the students could not apply this knowledge for a given problem. We received wrong answers when the task was not echoing a learned definition, but the application of it for a specific problem. On the contrary, we received a high ratio of good answers when the question was directly related to factual knowledge.

It has been well known from teaching experiences that there are significant differences between the chemical knowledge of students of chemistry, pharmacy, biology and environmental science (decreasing in this order). However, the results of the administration of the task sheet were surprising for the authors of the present paper. It had not been expected that such a difference in the number of good answers could be obtained from the different courses for each task. The difference is related not only to the different amount of previous chemistry study, but also, it seems, to the motivation of the students towards studying chemistry. The different levels of motivation may be indicated by the ratio of the missing answers for a task; in this case the student did not attempt to give any answer. Remarkably, there is no significant difference between the four students' groups in misunderstandings that we consider to be brought from secondary education.

Students' misunderstandings found in this survey can be attributed to the following general reasons:

- Using everyday analogy in solving the tasks (misunderstandings in tasks 1 and 4).

- Assuming macroscopic properties at particulate level (misunderstanding in task 1).

- Reducing proportionality to direct proportionality (misunderstandings in tasks 3 and 9).

- Mixing concepts in thermodynamics and reaction kinetics (misunderstandings in tasks 2 and 10).

- Misunderstandings brought from the secondary education (misunderstandings in tasks 2, 3 and 4).

Our conclusion is that lecturers need to be alert to the possible misinterpretations of the subject matter of the lectures so that the chance of emerging misunderstandings should be decreased. Introduction of definitions should always be followed by showing applications on specific problems and the discussion of common misunderstandings. Active learning methods based on constructivist theory should be used more frequently. These measures may lead to an improved and more effective education of physical chemistry.

Appendices

Tables A1–A3

Table A1 Correlation of the score of the individual tasks with that of the whole task sheet

Task No.	1	2	3	4	5	6	7	8	9	10
Correlation coefficient	0.712	0.253	0.453	0.671	0.648	0.642	0.567	0.600	0.426	0.655

---

Table A2 The gender of the students in the different courses

Course	Males	Females
Chemistry	62%	38%
Environmental science	36%	64%
Pharmacy	25%	75%
Biology	27%	73%
All students	32%	68%

---

Table A3 The university chemistry studies of the students in different majors prior to writing the task sheet. The figures are hours per week within a semester: lecture + problem solving class + laboratory practice. Biology students wrote the test in the 2nd semester, students of all other courses wrote it in the 3rd semester

Subject	1st semester	2nd semester	3rd semester
Chemistry (C)
General chemistry	4 + 2 + 3
Inorganic chemistry	2 + 0 + 0	3 + 0 + 6
Physical chemistry		3 + 1 + 0	2 + 1 + 4
Organic chemistry		4 + 0 + 0	3 + 0 + 4
Analytical chemistry		4 + 0 + 0	4 + 0 + 4
Colloid- and surface chemistry			2 + 0 + 0
Pharmacy (P)
General and inorganic chemistry	4 + 1 + 5	3 + 0 + 0
Analytical chemistry		2 + 0 + 5	2 + 0 + 5
Physical chemistry			3 + 1 + 0
Environmental science (E)
Introduction to Chemistry
(general and physical chemistry)		3 + 0 + 0
Organic chemistry			3 + 0 + 0
Analytical chemistry			2 + 0 + 2
Physical chemistry measurement methods			1 + 0 + 0
Biology (B)
General chemistry	4 + 0 + 2
Organic chemistry		3 + 0 + 0
Physical chemistry		3 + 0 + 0

---

Acknowledgements

The support of OTKA grants K84054 and K105262 is gratefully acknowledged. The authors are indebted for the useful comments of Prof. Ernő Keszei, Dr Tibor Nagy, Dr Judit Zádor and Dr István Gy. Zsély. Suggestions of the reviewers are also acknowledged.

References

1. Banerjee, A. C. (1995), Teaching Chemical Equilibrium and Thermodynamics to undergraduate general chemistry classes. Journal of Chemical Education,72(10), 879–887.
2. Banerjee, A. C. (1991), Misconceptions of students and teachers in chemical equilibrium. International Journal of Science Education,13, 487–494.
3. Barke, H.-D., Hazari, A. and Yitbarek, S. (2009), Misconceptions in chemistry. Addressing perceptions in chemical education. Springer-Verlag, Berlin, Heidelberg.
4. Ben-Zvi, R., Silberstein, J. and Mamlok, R. (1993), A model of thermal equilibrium. A tool for the introduction of thermodynamics. Journal of Chemical Education,70(1), 31–34.
5. Bilgin, I., Senocak, E., and Sözbilir, M. (2009), The effects of problem-based learning instruction on university students' performance of conceptual and quantitative problems in gas concepts. Eurasia Journal of Mathematics, Science and Technology Education,5, 153–164.
6. Cakmakci, G., and Aydogdu, C. (2011), Designing and evaluating an evidence-informed instruction in chemical kinetics. Chemistry Education Research and Practice,12, 15–28.
7. Cakmakci, G., Leach, J., and Donnelly, J. (2006), Students' ideas about reaction rate and its relationship with concentration or pressure. International Journal of Science Education,28, 1795–1815.
8. Calik, M., Kolomuc, A., and Karagölge, Z. (2010), The effect of conceptual change pedagogy on students' conceptions of rate of reaction. Journal of Science Educational Technology,19, 422–433.
9. Cheung, D., Ma, H.-J., and Yang, J. (2009), Teachers' misconceptions about the effects of addition of more reactants or products on chemical equilibrium. International Journal of Science and Mathematics Education,7, 1111–1133.
10. diSessa, A. A. (1993), Towards an epistemology of physics. Cognition and Instruction,10(2–3), 105–225.
11. Erdemir, A., Geban, Ö., and Uzuntiryaki, E. (2000), Freshman dtudents' misconceptions in chemical equilibrium. Hacettepe Üniversitesi Egitim Facültesi Dergisi,18, 79–84.
12. García-Franco, A. and Taber, K. S. (2009), Secondary students' thinking about familiar phenomena: student explanations in a curriculum context where ‘particles’ is a key idea for organizing teaching and learning. International Journal of Science Education,31(15), 1917–1952.
13. Garnett, P., Garnett P. and Hackling, M. (1995), Students' alternative conceptions in chemistry: A review of research and implications for teaching and learning. Studies in Science Education,25, 69–95.
14. Gunstone, R. F. (1989), A comment on “The problem of terminology in study of student conceptions in science”. Science Education,73, 643–646.
15. Gürses, A., Acikyildiz, M., Dogar, C., and Sözbilir, M. (2007), An investigation into the effectiveness of problem-based learning in a physical chemistry laboratory course. Research in Science and Technological Education,25, 99–113.
16. Haby, J. (no date), Why is moist air less dense than dry air at same temperature.www.theweatherprediction.com/habyhints/260/; Retrieved date: 25.10.2012.
17. Hackling, M. W. and Garnett, P. J. (1985), Misconceptions of chemical equilibrium. European Journal of Science Education, 7, 205–214.
18. Hammer, D. (1996), Misconceptions or p-prims: how may alternative perspectives of cognitive structure influence instructional perceptions and intentions? The Journal of Learning Sciences, 5(2), 97–127.
19. Horton, C. (2007), Student preconceptions and misconceptions in chemistry (Student alternative conceptions in chemistry). www.daisley.net/hellevator/misconceptions/misconceptions.pdf; Retrieved date: 07.02.2011.
20. Johnson, P. M. (1998), Progression in children's understanding of a ‘basic’ particle theory: A longitudinal study. International Journal of Science Education,20, 393–412.
21. Johnstone, A. H. (2000), Teaching chemistry – logical or psychological? Chemistry Education Research and Practice in Europe,1, 9–15.
22. Kind, V. (2004), Beyond appearances: Students' misconceptions about basic chemical ideas.http://www.rsc.org/images/Misconceptions_update_tcm18-188603.pdf; Retrieved date: 07.02.2011.
23. Kolomuc, A., and Tekin, S. (2011), Chemistry teachers' misconceptions concerning concept of chemical reaction rate. Eurasian Journal of Physics and Chemistry Education,3, 84–101.
24. Kousathana, M., and Tsaparlis, G. (2002), Students' errors in solving numerical chemical-equilibrium problems. Chemistry Education: Research and Practice in Europe,3, 5–17.
25. Le Maréchal, J.-F., and El Bilani, R. (2008), Teaching and learning chemical thermodynamics in school. International Journal of Thermodynamics,11, 91–99.
26. Nahalka I. (1997), Konstruktív pedagógia – egy új paradigma a láthatáron (III) (Constructive pedagogy − a new paradigm is ahead). Iskolakultúra,7, 3–20 (in Hungarian).
27. Osborne, R. J., Bell, B. F. and Gilbert, J. K. (1983), Science teaching and children's views of the world. European Journal of Science Education,5, 1–14.
28. Özmen, H. (2008), Determination of students' alternative conceptions about chemical equilibrium: a review of research and the case of Turkey. Chemistry Education Research and Practice,9, 225–233.
29. Pedrosa, M. A., and Dias, M. H. (2000), Chemistry textbook approaches to chemical equilibrium and student alternative conceptions. Chemistry Education: Research and Practice in Europe,1, 227–236.
30. Quílez, J. (2004), A historical approach to the development of chemical equilibrium through the evolution of the affinity concept: some educational suggestions. Chemistry Education: Research and Practice,5(1), 69–87.
31. Quílez, J. (2004), Changes in concentration and in partial pressure in chemical equilibria: students' and teachers' misunderstandings. Chemistry Education: Research and Practice in Europe,5, 281–300.
32. Quílez, J. and Solaz, J. J. (1995), Students' and teachers' misapplication of the Le Chatelier's principle. Implications for the teaching of chemical equilibrium. Journal of Research in Science Teaching,33(9), 939–957.
33. Radnóti K. (2010), Felmérés az elsőéves hallgatók kémiatudásáról (Exploring the chemical knowledge of first year university students). Magyar Kémikusok Lapja,65, 158–192 (in Hungarian).
34. Rollnick, M., Bennett, J., Rhemtula, M., Dharsey, N. and Ndlovu, T. (2008), The place of subject matter knowledge in pedagogical content knowledge: A case study of South African teachers teaching the amount of substance and chemical equilibrium. International Journal of Science Education,30(10), 1365–1387.
35. Schmidt, H.-J. (1997), Students' misconceptions – looking for a pattern. Science Education,81, 123–135.
36. Senocak, E., Taskesenligil, Y., and Sozbilir, M. (2007), A study on teaching gases to prospective primary science teachers through problem-based learning. Research of Science Education, 37, 279–290.
37. Solomon, J. (1993), The social construction of children's scientific knowledge. In Black, P. and Lucas, A.M. (Eds), Children's informal ideas in science. London: Routledge, 85–101.
38. Sozbilir, M. (2002), Turkish chemistry undergraduate students' misunderstandings of Gibbs free energy. University Chemistry Education,6, 73–83.
39. Sozbilir, M. (2003), What students' understand from entropy?: A review of selected literature. Journal of Baltic Science Education, 21–27.
40. Sözbilir, M. (2004), What makes physical chemistry difficult? Journal of Chemical Education,81, 573–578.
41. Sozbilir, M., and Bennett J. M. (2006a), Turkish prospective chemistry teachers' misunderstandings of enthalpy and spontaneity. The Chemical Educator,11, 355–363.
42. Sozbilir, M., and Bennett, J. M. (2006b), Turkish prospective chemistry teachers' misunderstandings of enthalpy and spontaneity. Chemistry Educator, 11, 355–363.
43. Sözbilir, M., and Bennett, J. M. (2007), A study of Turkish chemistry undergraduates' understandings of entropy. Journal of Chemical Education,84, 1204–1208.
44. Sözbilir, M., Pinarbasi, T., and Canpolar, N. (2010), Prospective chemistry teachers' conceptions of chemical thermodynamics and kinetics. Eurasia Journal of Mthematics, Science and Technology Education,6, 111–120.
45. Taber, K. (2002), Chemical misconceptions – prevention, diagnosis and cure. Volume I: theoretical background. Royal Society of Chemistry, London.
46. Taber, K. S. (2008), Conceptual resources for learning science: issues of transience and grain-size in cognition and cognitive structure. International Journal of Science Education,30(8), 1027–1053.
47. Taber, K. S. and García-Franco, A. (2009), Intuitive thinking and learning chemistry. Education in Chemistry, 46 (2), 57–60.
48. Taber, K. S. and García-Franco, A. (2010), Learning processes in chemistry. Drawing upon cognitive resources to learn about the particulate structure of matter. Journal of the Learning Sciences,19(1), 99–142.
49. Taber, K. S., and Tan, K. Ch. D. (2011), The insidious nature of, hard-core' alternative conceptions: implications fort he constructivist research programme of patterns in high school students' and pre-service teachers' thinking about ionisation energy. International Journal of Science Education,33, 259–297.
50. Talanquer, V. (2006), Commonsense chemistry: A model for understanding students' alternative conceptions. Journal of Chemical Education,83, 811–816.
51. Tissandier, M. D., Cowen, K. A., Yong Feng, W., Gundlach, E., Cohen, M. H., Earhart, A. D., Coe, J. V. and Tuttle, T. R., Jr. (1998), The proton's absolute aqueous enthalpy and Gibbs free energy of solvation from cluster-ion solvation data, Journal of Physical Chemistry A,102, 7787–7794.
52. Tóth, Z. (1999), Egy kémiai tévképzet nyomában. Az egyensúlyi állandó bevezetésének lehetőségei és problémái (Tracing a chemical misconception. The challenges and problems of the introduction of the chemical equilibrium constant). Iskolakultúra,9, 108–112 (in Hungarian).
53. Tóth, Z. (2004), Exploring students' ideas on particles. Education in Chemistry,41, 10.
54. Tóth, Z. (2010), Kémia, vegyészmérnöki és biomérnöki alapképzésüket kezdő egyetemi hallgatók kémiai alapismereteinek vizsgálata (Investigation of the basic chemistry knowledge of chemist, chemical engineer and bioengineer freshers). Középiskolai Kémiai Lapok,37, 62–79; 299–320 (in Hungarian).
55. van Driel, J. H., De Vos, W., Verloop, N. and Dekkers, H. (1998), Developing secondary students' conceptions of chemical reactions: the introduction of chemical equilibrium. International Journal of Science Education, 20(4), 379–392.
56. van Driel, J. H., Verloop, N. and de Vos, W. (1998). Developing Science Teachers' Pedagogical Content Knowledge. Journal of Research in Science Teaching,35(6), 673–695.
57. van Driel, J. H. (2002), Students' corpuscular conceptions in the context of chemical equilibrium and chemical kinetics. Chemistry Education: Research and Practice in Europe,3, 201–213.
58. Werby, O. (2010), What is a p-prim? www.interfaces.com/blog/2010/10/what-is-a-p-prim/; Retrieved date: 25.10.2012.
59. Zádor, J., Taatjes, C. A., and Fernandes, R. X. (2011), Kinetics of elementary reactions in low-temperature autoignition chemistry. Progress in Energy and Combustion Science, 37, 371–421.

---