Fullerene filling modulates carbon nanotube radial elasticity and resistance to high pressure

Abstract

The high pressure behavior of carbon nanotubes (CNTs) filled with fullerenes (C₆₀@CNTs) is investigated systematically using molecular mechanics and molecular dynamics simulations. It is shown that the C₆₀ filling can increase the transition pressure (P_c) of intrinsic CNTs and optimize the radial elasticity of CNTs. The C₆₀ filling increases the P_c of CNT(17, 0) by a factor of ∼25, and the P_c of CNT(10, 10) by a factor of ∼5. An inelastic CNT(17, 0) can be transformed into a superelastic CNT(17, 0) by filling C₆₀ into CNTs. Moreover, C₆₀@CNTs with larger diameters (21.76 Å > d > 13.56 Å) show the better radial elasticity compared with intrinsic CNTs. These characteristics can make C₆₀@CNTs possess potential applications in pressure sensors, electromechanical oscillators, nanotube memory etc. In addition, C₆₀@CNTs with larger diameters (21.76 Å > d > 13.56 Å) undergo two structure transitions under high pressure, which is well in agreement with the experimental results. The Lennard–Jones potential can describe the interaction between C₆₀ and CNT well and explain radial collapse and recovery properties of C₆₀@CNT completely, which can provide theoretical guidance for experimental results.

---

I. Introduction

Since the discovery of carbon nanotubes (CNTs),¹ people have found that CNTs possess remarkable electrical and mechanical properties, which enable them to be used for the development of superconductive devices for nanoelectromechanical system applications.

Theoretical calculations and experimental studies have shown that CNTs can undergo significant plastic deformation under hydrostatic pressure.^2–8 It is shown that the radial deformation of small CNTs whose diameters are smaller than ∼6.78 Å are reversible.^9,10 Of particular interest is that the band-gap of CNTs can vary with radial deformation and eventually closes or opens at a critical deformation.^11–13 This electronic-structure transformation has an important implication for device applications, such as pressure sensors, electromechanical oscillators, nanotube memory and nanosprings, etc. However, the deformation of larger tubes could be irreversible and a collapsed state is metastable or even absolutely stable.¹⁴ Our group found that the collapsed state of the armchair CNT was metastable and collapsed states of other chiral and modified CNTs were energetically favorable.^15,16 The stable collapsed state of CNTs makes them lose radial elasticity, which will confine the development of CNT-based superconductive devices for nanoelectromechanical system applications. Therefore, improving the CNT's radial elasticity under hydrostatic pressure remains a major challenge.

The introduction of “foreign” materials can significantly alter the mechanical, electronic or conducting behavior of CNTs.^17–25

For example, C₆₀ filling not only can modulate the energy band gap and electronic properties of CNT,²⁶ but also can change the CNT's mechanical properties such as resistance to high hydrostatic pressure.^27–30 The experimental results show that the first transition pressure of CNT filled with C₆₀ is lower than that of intrinsic CNT, but the second transition pressure is much higher than that of intrinsic CNT.²⁹ It is expected that the experimental data will feed theoretical models that will in turn advance the understanding of the effect of C₆₀ filling on the high-pressure effects on CNT.²⁹ In addition, it is not clear enough if C₆₀ filling can influence the radial elasticity of CNT. The radial elasticity upon unloading have much influence on the application of CNTs filled with C₆₀ (C₆₀@CNTs) nanocomposites in electromechanical system.

In this paper, using molecular mechanics (MM) and molecular dynamics (MD) simulations we investigate the radial collapse process of C₆₀@CNTs and construct theoretical model based on Lennard–Jones potential to disclose the physical mechanism of collapse. It is shown that filling C₆₀ can modulate the CNT's (d = 13.56 Å) radial elasticity and resistance to high pressure. An inelastic CNT(17, 0) can be transformed into a superelastic CNT(17, 0) by filling C₆₀ into CNTs. In addition, the C₆₀@CNTs with larger diameters (21.76 Å > d > 13.56 Å) undergo two structure transitions under high pressure, which are in very agreement with the experimental results. What's more, the C₆₀ filling can improve the radial elasticity of CNTs. However, for CNT with d > 21.76 Å, C₆₀ filling deteriorates the radial elasticity of CNT.

Both C₆₀ filling²⁶ and radial deformation¹¹⁻¹³ can modulate the energy band gap of CNT, and further change the electronic properties of CNT. Therefore, our findings can provide a basis for further investigating the electromechanical properties of C₆₀@CNTs and developing nanoelectronics devices using C₆₀@CNTs such as pressure sensor, electromechanical oscillator, nanotube memory used in electromechanical system. In addition, the resistance to high pressure can also make C₆₀@CNTs an ideal filler for nanocomposites for high load mechanical support.

II. Computational methods

The simulations have been carried out using a commercial software package called Materials Studio (MS) developed by Accelrys Software, Inc. The condensed-phase optimized molecular potential for atomistic simulation studies (COMPASS) force field method is chosen to model the atomic interaction.³¹ The COMPASS force-field is a parameterized, tested, and validated first ab initio force-field, which enables an accurate prediction of various gas-phase and condensed-phase properties of most of the common organic and inorganic materials.^32,33 Moreover, it has been shown to be applicable in describing the mechanical properties of CNT.^34,35

The systems considered in this work are the C₆₀@CNTs with the length of 73.5 Å. The CNT diameter ranges from 13.56 to 27.76 Å. In simulations, periodic boundary conditions are employed. MM and MD simulations are performed to simulate the filling of C₆₀ into CNTs. In order to avoid the metastable phase of C₆₀, the C₆₀@CNTs systems relax 40 ps under 300 K firstly, and then cool to 1 K slowly. Finally, when the total energy of C₆₀@CNTs reaches a minimum, the systems have stable structure.

In order to investigate the radial collapse of all systems, every system's structure is initially optimized at atmospheric pressure and subsequently subjected to step-wise monotonically hydrostatic pressure increments with FORCITE code. Then, after each pressure increment the unit cell volume is allowed to equilibrate for at least 30 ps at each step in the NPT ensemble, and a fixed time step size of 1 fs is used in all cases. The simulations are carried out at a temperature of 1 K to avoid the thermal effect, and the interactions are determined within a cut-off distance of 9.5 Å. The reduced volume (V/V₀), where V and V₀ are the unit cell volumes at an applied pressure and atmospheric pressure, respectively, was measured as a function of applied hydrostatic pressure.

III. Results and discussion

III.I. The filling of C₆₀ into CNT (10, 10)

Fig. 1(a–g) show the longitudinal snapshots of C₆₀-filled CNT(10, 10) (from no full to full).²⁷ For full-filled CNT (7C₆₀@CNT(10, 10)), as shown in Fig. 1(g), the investigation has revealed that C₆₀ molecules align periodically along with the CNT axis. To investigate the structure of 7C₆₀@CNT(10, 10), the concentration profiles of 7C₆₀@CNT(10, 10) along z and y axes are shown in Fig. 2. From Fig. 2(a), we can find that the mean of a constant spacing between two C₆₀ molecules was found to be 3.25 Å which is close to interlayer distance of graphite (3.4 Å), which shows that there exists a strong attractive van der Waals (vdW) interaction among C₆₀ molecules along z axes. Herein, considering the diameter (7.10 Å) of C₆₀, we can determine 10.35 Å as the average intermolecular distance center to center of C₆₀ molecules. In addition, Fig. 1(h) shows the transverse snapshots of the 7C₆₀@CNT(10, 10). We can observe that the inter wall spacing between C₆₀ and CNT(10, 10) is homogeneous. This is verified according to the concentration profiles of 7C₆₀@CNT(10, 10) along y axes, as shown in Fig. 2(b). One can observe that both left and right inter wall spacing between the C₆₀ and CNT along y axes are 3.77 Å, which are close to interlayer distance of graphite (3.4 Å). The result shows that there exists the homogeneous attractive vdW interaction between C₆₀ and CNT(10, 10). The result is in agreement with previous theoretical studies^36,37 and experimental observations.^38,39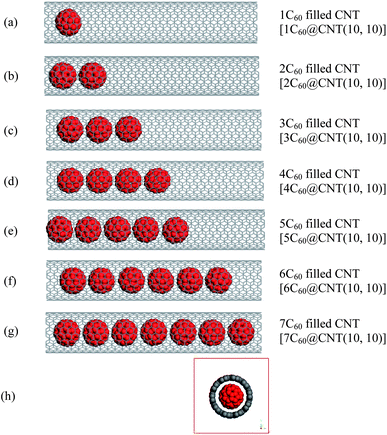

Fig. 1 Longitudinal and transverse snapshots of C₆₀@CNT(10, 10). (a–g) Longitudinal snapshots of C₆₀(1−7)@CNT(10, 10), and (h) transverse snapshots of 7C₆₀@CNT(10, 10).

Fig. 2 Concentration profiles of 7C₆₀@CNT(10, 10). (a) Concentration profiles of 7C₆₀@CNT(10, 10) along z axes; the inset is the longitudinal snapshot of 7C₆₀@CNT(10, 10), and (b) concentration profiles of 7C₆₀@CNT(10, 10) along y axes; the inset is the transverse snapshot of 7C₆₀@CNT(10, 10).

III.II. Effect of CNT chirality on the high pressure behavior of C₆₀@CNTs

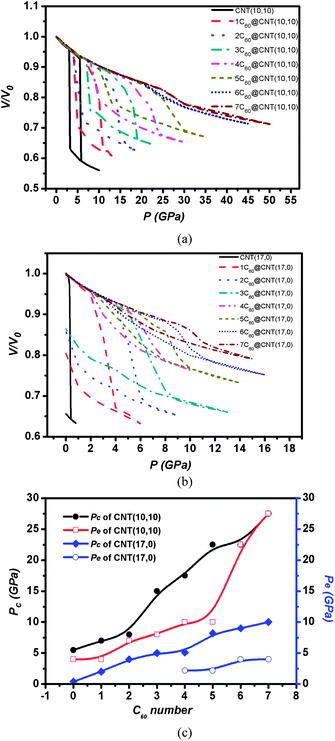
We investigated the high pressure behavior of 1C₆₀@CNT(10, 10) firstly, as shown in Fig. 3(a). Herein, the applied pressure is hydrostatic pressure which is different from the pressure applied in one end of open tube.⁴⁰ In addition, the periodic boundary conditions are employed in simulations. All the systems are infinitely extended along the axial direction. Therefore, C₆₀ molecules can't be released by CNT.

Fig. 3 (a) Loading and unloading curves of CNT(10, 10) and 1C₆₀@CNT(10, 10), the insets are transverse snapshots of CNT(10, 10) and longitudinal snapshots of 1C₆₀@CNT (10, 10), and (b) the mechanical model and the force between 1C₆₀ and CNT.

Fig. 3(a) shows the loading and unloading curves of CNT(10, 10) and 1C₆₀@CNT(10, 10); the insets are transverse snapshots of CNT(10, 10) and longitudinal snapshots of 1C₆₀@CNT(10, 10).

The simulations show that when a CNT(10, 10) deforms under pressure, it undergoes two shape transitions: (1) changing from a cycle to an oval (a continuous transition); and (2) changing from an oval to collapse (an abrupt transition).^41,42 Here, we define two critical pressures, P_e and P_c, where P_e is the pressure at which the collapsed shape returns to the circle shape upon unloading, its value can characterize the radial elasticity of CNT; and P_c is the pressure to collapse CNT upon loading, its value can characterize the CNT's resistance to high pressure. From Fig. 3(a), it is found that the loading curve of 1C₆₀@CNT(10, 10) is smooth while the loading curve of intrinsic CNT(10, 10) has a sudden change at 5.5 GPa. In other words, the 1C₆₀@CNT(10, 10) shows the better resistance to high pressure compared with intrinsic CNT(10, 10).

Physically, the structural transformation of CNT is determined by the competition among the interaction forces experienced, the stress of CNT and the applied external force. Herein, we present a mechanical model for the specific 1C₆₀@CNT(10, 10) based on Lennard–Jones potential.⁴³Fig. 3(b) shows that the mechanical model and the force between C₆₀ and CNT. Where R is the distance between an atom of CNT and the centre of the C₆₀, F is the interaction force between the atom of CNT and the C₆₀. When R is in the region of [0, R₀], the value of F is positive which shows the interaction force is a repulsive force; when R is in the region of [R₀, R_f], the value of F is negative which shows that the interaction force is an attractive force; when R is in the region of [R_f, +∞], the interaction force is extremely weak. We can find that the carbon atoms at the end of CNT near the C₆₀ will endure an attractive force from the C₆₀. When the CNT is subjected to an applied pressure, the carbon atoms at the end of CNT near the C₆₀ are easier to be in the region of [0, R₀] so that there exists a repulsive vdW force between the C₆₀ and the carbon atoms of the end of CNT near the C₆₀, which can prevent the end of CNT to deform and further influence the whole CNT's collapse gradually. Therefore, when the applied pressure is up to 5.5 GPa 1C₆₀@CNT undergoes a gradual collapse and its the loading curve doesn't demonstrate a sudden change, as shown in Fig. 3(a).

In addition, we can observe that upon unloading the unloading curve of 1C₆₀@CNT(10, 10) shows also a hysteresis but its P_e is larger than that of intrinsic CNT(10, 10), which indicates that the origin state of 1C₆₀@CNT(10, 10) can be recovered more quickly and 1C₆₀@CNT(10, 10) shows a better radial elasticity compared with intrinsic CNT(10, 10). From Fig. 3(b), we can find that after 1C₆₀@CNT(10, 10) collapses the major CNT(10, 10) transforms into a linked double graphene layers paralleling to the plane like a ribbon, there exists a larger attractive vdW interaction between the double graphene layers. Upon unloading, the attractive vdW interaction can lead to the hysteresis of curve.⁴⁴ However, upon unloading the repulsive force between the C₆₀ and the carbon atoms of the end of CNT near the C₆₀ can promote the system recover to the origin state quickly. Therefore the radial elasticity of 1C₆₀@CNT(10, 10) is superior to that of intrinsic CNT(10, 10).

The effect of C₆₀ number on the radial collapse and elasticity of CNT(10, 10) is investigated. Fig. 4(a) shows the loading and unloading curves of CNT(10, 10) and C₆₀@CNT(10, 10). We can observe easily that both P_c and P_e of C₆₀@CNT(10, 10) can increase as the number of C₆₀ increases and both P_c and P_e of 7C₆₀@CNT(10, 10) achieve 27.5 GPa, as shown in Fig. 4(c). It indicates that C₆₀@CNT(10, 10) can support higher pressure than the corresponding individual CNTs and show super radial elasticity. In addition, we can find that the value of P_c and P_e of 6/7C₆₀@CNT(10, 10) is consistent and their hysteresis in the unloading curves disappear, as shown in Fig. 4(a). After 6/7C₆₀@CNT(10,10) collapse, little part of opposite walls of CNT(10, 10) can contact with each other, which indicates that there exists a very small attractive vdW interaction between the opposite walls. If there is little vdW interaction, the hysteresis will disappear and the loading and unloading curves are superposed.⁴⁵ Therefore, the hysteresis in the unloading curve of 6/7C₆₀@CNT(10, 10) nearly disappears. Herein, we can conclude that the C₆₀ filling can increase the P_c of intrinsic CNT(10, 10) and optimize the radial elasticity of CNT(10, 10). What's more, the C₆₀ filling number can modulate the P_c and radial elasticity of CNT(10, 10). The filling C₆₀ increases the P_c of CNT(10, 10) by a factor of ∼5.

Fig. 4 (a) Loading and unloading curves of CNT(10, 10) and (1−7)C₆₀@CNT(10, 10), and (b) loading and unloading curves of CNT(17, 0) and (1−7)C₆₀@CNT(17, 0), and (c) P_c and P_e of CNT(10, 10) and CNT(17, 0) filled with different C₆₀ number.

As shown in Fig. 4(a and b), compared with the curves of intrinsic CNT(10, 10) and (17, 0), we can observe that the P_c of CNT(17, 0) is always considerably lower than that of CNT(10, 10); the intrinsic CNT(17, 0) has a negligible pressure capacity, which has been investigated in our former research.¹⁵ The C₆₀ filling can effectively improve the pressure capacity. Fig. 4(b) presents the loading and unloading curves of C₆₀@CNT(17, 0), which show that C₆₀ filling can increase the P_c of intrinsic CNT(17, 0) and improve its radial elasticity. As shown in Fig. 4(c), we can observe that C₆₀ filling increases the P_c of CNT(17, 0) by a factor of ∼25, from 0.4 to 10.0 GPa; what's more, when C₆₀ number is equal or greater than four, the CNT(17, 0) recovers the radial elasticity, and an inelastic CNT(17, 0) can be transformed into a superelastic CNT by filling C₆₀ into CNT with P_e ranging from 0 to 4.8 GPa.

III.III. The high pressure behavior of 7C₆₀@CNTs with different diameters

According to the experimental results, the inhomogeneous filling of C₆₀ into CNTs can introduce inhomogeneity and consequently instability of CNTs toward collapse at lower pressure.^28–30 From this section, we begin to investigate the filling of C₆₀ into CNTs with different diameters and the radial collapse and elasticity of C₆₀@CNTs.

To assess the diameter dependence of high pressure behavior of 7C₆₀@CNTs with different diameters, we investigated the high pressure behavior of the intrinsic CNTs with different diameters firstly, as shown in Fig. 5(a–d). P_c of the CNTs with different diameters is shown in Table 1. We can find that the values of P_c of CNT(12, 12), CNT(14, 14), CNT(16, 16) and CNT(20, 20) are 4.0, 2.8, 1.1 and 0.6 GPa, respectively. It indicates that the P_c decreases with increasing CNT diameter. Moreover, when the diameter is larger than a threshold, the loading and unloading curves of CNTs can't shape a hysteresis loop. In other words, their collapsed states are favorable. Herein, we can introduce the specific energy for different compression ratios of round tubes to explain the mechanism of high pressure behavior of the CNTs with different diameters. The relationship of specific energy correlated with the D/t ratio and compression ratio δ/D can be written as:⁴⁶

where D is the diameter of the CNT, t (3.4 Å) is the thickness of the wall, and δ is the compression strain of the CNT. Herein, the specific energy expresses the energy absorbing capacity of the CNT. It is clear that the energy absorbing capacity of a CNT exponentially decreases rapidly with the increase of D/t ratio at first and infinitely approaches zero after a threshold which depends upon its thickness. In other words, only a little energy can induce the variation of the compression ratio when the diameter of the CNT is larger than the threshold. Thus, the CNTs with large diameters collapse easily and their collapsed states are favorable; a critical diameter value exists when the CNT suffers a given external force. Our results are in agreement with ref. 47.

We investigate the effect of the diameter on the high pressure behavior of 7C₆₀@CNTs, as shown in Fig. 5(a–d). We can find that the 7C₆₀@CNTs with larger diameter undergoes two abrupt transitions under pressure. Herein, P_c1 is the first transition pressure; P_c2 is the second transition pressure. The P_c1 and P_c2 of 7C₆₀@CNTs are shown in Table 1. We can find that P_c1 is lower than that of intrinsic CNT while P_c2 is higher than that of intrinsic CNT. We studied the relationship between the collapse pressures (P_c1 and P_c2) of filled CNT and diameter D, and find that P_c1 ∼ D^−4.25, P_c2 ∼ D^−2.39. Compared with the relationship between the collapse pressure P_c and diameter D of CNT (P_c ∼ D⁻³),⁴⁷ we can draw a conclusion that the filled tubes behave the different relationship between the transition pressure (P_c1 or P_c2) and D, which may be caused by the heterogeneous interaction between the C₆₀ and CNT wall. The experiments have yet shown two pressures induced transitions in the bundle CNT.²⁸ Take the loading and unloading processes of the 7C₆₀@CNT(16, 16) as an example. We show the concentration profiles of the structure 7C₆₀@CNT(16, 16) along y axes, as shown in Fig. 5(e). We can observe that when 7C₆₀ moleculars are filled in CNT(16, 16), the closest distance between the C₆₀ and CNT is 3.056 Å, which indicates that there exists a strong attractive vdW interaction between C₆₀ and one side of CNT(16, 16) wall. Therefore, the 7C₆₀ moleculars are attracted to the side of CNT(16, 16) wall, and can lead to an inhomogeneous interaction between C₆₀ and CNT(16, 16) wall, which can make CNT(16, 16) structure change at lower pressure. So the first transition of 7C₆₀@CNT(16, 16) occurs at 0.7 GPa which is less than that of intrinsic CNT(16, 16). When the applied pressure continues to increase, the second transition takes place at 3.0 GPa which is larger than that of the intrinsic CNT(16, 16) due to the repulsive force between 7C₆₀ and CNT which is stated in former section. In addition, we can observe that the unloading curve of 7C₆₀@CNT(16, 16) shows the hysteresis due to the stronger attractive vdW interaction between opposite walls after 7C₆₀@CNT(16, 16) collapses completely. Finally, we can find that the 7C₆₀@CNT(16, 16) can return to its original state quickly compare with the intrinsic CNT(16, 16) due to the repulsive force between C₆₀ and CNT under higher pressure.

Fig. 5 Loading and unloading curves of 7C₆₀@CNTs with different diameters. (a–d) Loading and unloading curves of 7C₆₀@CNT(12, 12)/CNT(14, 14)/CNT(16, 16)/CNT(20, 20), the insets are transverse snapshots of 7C₆₀@CNTs. (e) Concentration profiles of 7C₆₀@CNT(16, 16) along z axes, the inset is transverse snapshot of 7C₆₀@CNT(16, 16).

Table 1 Collapse pressure P_c of armchair CNTs and filled-CNTs with different diameters

Armchair CNT	P c (GPa)	Filled-CNT	P c1 (GPa)	P c2 (GPa)
(12,12)	4.0	7C60@(12,12)	2.5	7.0
(14,14)	2.8	7C60@(14,14)	1.5	4.0
(16,16)	1.1	7C60@(16,16)	0.7	3.0
(20,20)	0.6	7C60@(20,20)	0.3	2.0

---

Then, we investigate the high pressure behavior of 7C₆₀@CNT(12, 12), CNT(14, 14), CNT(20, 20), as shown in Fig. 5(a, b and d). For 7C₆₀@CNT(12, 12) and 7C₆₀@CNT(14, 14), we can find that upon loading the 7C₆₀@CNT(12, 12) and 7C₆₀@CNT(14, 14) undergo two transitions under pressure, and upon unloading the hysteresises in unloading curves of two systems disappear and they return to their original state. After CNTs collapse, the partial opposite walls contact each other, which indicates that there exists a weak vdW interaction force between the opposite walls of collapsed CNT. Upon unloading, the weak vdW interaction force is not large enough to make the unloading curves of two systems show the hysteresis. For 7C₆₀@CNT(20, 20), it undergoes two transitions under the external pressure clearly; the unloading curve of 7C₆₀@CNT shows a tendency of returning to its original state compared to the intrinsic CNT(20, 20), as shown in Fig. 5(d). The results indicate that the 7C₆₀@CNTs with larger diameters undergo two transitions under high pressure; P_c1 is lower than that of intrinsic CNT but the C₆₀ filling improves the radial elasticity of the intrinsic CNTs.

III.IV. The mechanism for the high pressure behavior of 7C₆₀@CNTs

Based on the above discussion, we can find that the 7C₆₀@CNTs can't be sufficiently deformed by the vdW force between C₆₀ and CNTs, but the vdW interaction force plays a major role in the high pressure behavior of 7C₆₀@CNTs. In order to better understand the high pressure behavior of 7C₆₀@CNTs with different diameters, we present a mechanical model for the specific 7C₆₀@CNTs with different diameters based on Lennard−Jones potential,⁴³ as shown in Fig. 6. As shown in Fig. 6(a), where dλ is the radial differential unit of CNT, S is the closest distance between 7C₆₀ and dλ. F is the vdW interaction force between the 7C₆₀ and dλ. Herein, we take the two differential units of CNT which are marked for dλ₁ or dλ₂, respectively; S₁ and S₂ are the closest distances between dλ₁ or dλ₂ and 7C₆₀, respectively; F₁ and F₂ are the vdW interaction forces between dλ₁ or dλ₂ and 7C₆₀, respectively. When S is in the region of [0, S₀], the value of F is positive which shows the interaction force is the repulsive force; when S is in the region of [S₀, S_f], the value of F is negative which shows that the interaction force is the attractive force; when S is in the region of [S_f, +∞], the interaction force is extremely weak. We roughly obtain the trend in the variation of F vs. S, which is illustrated in Fig. 6(b) with a plot of the force distribution at different points around the 7C₆₀. The force distribution indicates that when CNT and 7C₆₀ are next to each other, they will approach each other until the interaction reaches minimum (F = 0). We assume that M is the bending modulus, a threshold that can just start the deformation of CNT. When the difference of forces (dF = F₁ – F₂) in the adjacent different unit dλ is larger than M, the CNTs will deform. The mechanical relationship can be described as follows:

|dF/ds| > M (2)

where |dF/ds| denotes the difference of the endured force per unit distance. When the CNT is in the region of [S₀, S_f], the variation of F along with S is relatively large. The abrupt curves in the regions indicate the value of |dF/ds| is large enough and the eqn (2) will be easily satisfied. The CNTs will deform with the interaction force between CNT and 7C₆₀.

Fig. 6 (a) The scheme of the mechanical model. (b) The variation of the interaction force between the differential unit of CNT and 7C₆₀ with their distance.

According to former section's discussion, the closest distance between the C₆₀ and CNT is 3.056 Å, which indicates that there exists a strong attractive vdW interaction between C₆₀ and dλ closest to 7C₆₀. Due to the attractive vdW interaction a lower pressure can make the partial CNT near 7C₆₀ be easily in the region of [S₀, S_f], undergo deformation and coat the surface of 7C₆₀, and the first collapse of CNT occurs, as shown in Fig. 5(a–d). Therefore, the P_c1 is lower than that of the intrinsic CNT. In other words, the inhomogeneous filling can introduce inhomogeneity and consequently instability toward collapse. When the applied pressure continues to increase, the carbon atoms coated surface of 7C₆₀ approach to the 7C₆₀ sequentially so that there exists a larger repulsive vdW interaction between the 7C₆₀ and CNT, which can prevent the CNT further collapse and the P_c2 is higher than P_c of the intrinsic CNT. Upon unloading, the repulsive force between 7C₆₀ and CNT can promote the CNT to return to its origin state quickly, so the radial elasticity of 7C₆₀@CNTs is superior to that of intrinsic CNTs.

III.V. Effect of CNT diameter on the high pressure behavior of C₆₀@CNTs

Fig. 7 shows the longitudinal and transverse snapshots of different diameter CNTs fully filled with C₆₀. With increasing CNT diameter different ordered phases of C₆₀ molecules inside the CNT were observed. The arrangement pattern of C₆₀ in CNT(10, 10) is linear, which has been demonstrated; the arrangement patterns of C₆₀ in CNT(12, 12) and (14, 14) are zigzag; the arrangement pattern of C₆₀ in CNT(16, 16) is double helix. The results are in agreement with the reference results.⁴⁸

Fig. 7 Longitudinal and transverse snapshots of C₆₀@CNTs with different diameters. (a–d) 7C₆₀@CNT(10, 10), 8C₆₀@CNT(12, 12), 10C₆₀@CNT(14, 14) and 19C₆₀@CNT(16, 16).

The high pressure behaviors of these systems are investigated. Fig. 8 shows that the loading and unloading curves of 8C₆₀@CNT(12, 12), 10C₆₀@CNT(14, 14) and 19C₆₀@CNT(16, 16). For 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14), we can observe that the systems take place two structure transitions. Table 2 summarizes the P_c values of CNTs as a function of the filler C₆₀. The P_c1 of 8C₆₀@CNT(12, 12) is not easy to be observed, but at 2.0 GPa V/V₀ has been lower than that of intrinsic CNT(12, 12). Therefore, we considered that the P_c1 of 8C₆₀@CNT(12, 12) is 2.0 GPa, and P_c1 of 10C₆₀@CNT(14, 14) is 0.8 GPa; P_c2 of 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14) are 12.0 and 13.0 GPa respectively. Obviously, it is shown that the P_c1 of 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14) is lower than that of intrinsic CNT(12, 12) and (14, 14) and P_c2 are much higher than that of intrinsic CNT(12, 12) and (14, 14).

Fig. 8 Loading and unloading curves of C₆₀@CNTs with different diameters. (a–c) Loading and unloading curves of 8C₆₀@CNT(12, 12),10C₆₀@CNT(14, 14) and 19C₆₀@CNT(16, 16), the insets are transverse snapshots of 8C₆₀@CNT(12, 12), 10C₆₀@CNT(14, 14) and 19C₆₀@CNT(16, 16).

Table 2 P _c for CNT as a function of the filler C₆₀

	Filler	P ^CNTc (GPa)	P ^filledc1 (GPa)	P ^filledc2 (GPa)	ΔPc = P^filledc1 − P^CNTc (GPa)	ΔPc = P^filledc2 − P^CNTc (GPa)
CNT(10,10)	C60	5.5	25.0		+19.5	+19.5
CNT(12,12)	C60	4.0	2.0	12.0	−2.0	+8.0
CNT(14,14)	C60	2.8	0.8	13.0	−2.0	+10.2
CNT(16,16)	C60	1.1	7.5	17.5	+6.4	+16.4

---

The experimental results demonstrate that the first structure transition of CNTs bundle filled with C₆₀ (mean diameter 1.35 ± 0.1 nm) takes place at a lower pressure of 2–2.5 GPa; the second transition takes place at a higher pressure of 10–30 GPa. In our simulation, the diameters of CNT(12, 12) and CNT(14, 14) are a little larger than 1.35 ± 0.1 nm; therefore, the P_c1 and P_c2 is a little lower than that of experimental results. Simulation results are in the range of experimental results^28,29 and confirm the validity of simulation method used here.

For CNT(12, 12) and CNT(14, 14), the zigzag layout of C₆₀ inside CNTs, which is different from the linear layout of C₆₀ inside CNT(10, 10), provide inhomogeneous filling. According to the mechanical model based on Lennard–Jones potential, upon loading inhomogeneous filling induces the inhomogeneous attractive vdW interaction between C₆₀ and CNT and further leads to CNT mechanical instability at lower pressure. Further loading, the repulsive vdW interaction between C₆₀ and CNT reinforces the resistance to high pressure. Therefore, 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14) take place two structure transitions. The mechanical model can well explain the experimental results and confirm the validity of simulation method used here again.

For CNT(16, 16), the double helix-filling of 19C₆₀ into CNT(16, 16) can be considered to provide an approximate homogeneous tube filling consolidating mechanical stability of CNT(16, 16) approximately. Therefore, both P_c1 and P_c2 of the 19C₆₀@CNT(16, 16) can increase compared with that of CNT(16, 16).

The radial elasticity of C₆₀@CNTs is a significant issue to be investigated. As shown in Fig. 8(a and b), upon unloading 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14) return to origin state quickly compared with intrinsic CNT. It shows that the radial elasticity of 8C₆₀@CNT(12, 12), 10C₆₀@CNT(14, 14) is superior to that of intrinsic CNTs. The repulsive vdW attraction between C₆₀ and CNT makes 8C₆₀@CNT(12, 12) and 10C₆₀@CNT(14, 14) return to their origin state quickly and optimize the radial elasticity of CNTs.

However, after 19C₆₀@CNT(16, 16) collapses, C₆₀ molecules occur the relative slippage and the all C₆₀ molecules realign in the plane, as shown in Fig. 8(c). Upon unloading the attractive vdW interaction among C₆₀ molecules make all C₆₀ be constrained in the plane and the attractive interaction between C₆₀ molecules and CNT can prevent the CNT return to the original state, so the 19C₆₀@CNT(16, 16) shows the worse radial elasticity compared with intrinsic CNT(16, 16).

We can conclude that filling C₆₀ into CNTs with larger diameters (21.76 Å > d > 13.56 Å) can introduce inhomogeneity and consequently instability of CNTs toward collapse at lower pressure compared with intrinsic CNTs, but the P_c2 increases and the radial elasticity of the system became better compared with intrinsic CNTs. However, the filling C₆₀ into CNTs with much larger diameters (d > 21.76 Å) can make P_c of CNTs increase but the radial elasticity of CNTs becomes worse compared with intrinsic CNTs.

Conclusions

In summary, we have shown that the C₆₀ filling can increase P_c of intrinsic CNTs and optimize the radial elasticity of intrinsic CNTs while making the CNTs recover quickly and maintaining the structural integrity of CNTs upon unloading. The filling increases P_c of CNT(17, 0) by a factor of ∼25, and P_c of CNT(10, 10) by a factor of ∼5. The C₆₀ filling number can modulate CNT's radial elasticity. An inelastic CNT(17, 0) can be transformed into superelastic CNTs by filling C₆₀ into CNT(17, 0). Moreover, C₆₀@CNTs with larger diameters (21.76 Å > d > 13.56 Å) show better radial elasticity compared with intrinsic CNTs. It is well known that both radial deformation and filling can change the electrical properties of CNT. In view of the recoverability of C₆₀@CNT upon unloading, C₆₀@CNT can be used to develop nanoelectronic devices such as pressure sensors, electromechanical oscillators, nanotube memory used in the nanoelectromechanical systems.

In addition, C₆₀@CNTs with larger diameters (21.76 Å > d > 13.56 Å) undergo two structure transitions under pressure; P_c2 of C₆₀@CNTs is higher than that of the intrinsic CNTs. The Lennard–Jones potential can describe the interaction between C₆₀ and the CNT wall and explain radial collapse of C₆₀@CNT completely, which can provide theoretical guidance for experimental results.

However, for CNT with diameter d > 21.76 Å, upon unloading the vdW interaction among C₆₀ molecules influences the radial elasticity of CNT and makes the radial elasticity of CNT become worse. The irreversibility of C₆₀@CNT will make it lose application in electromechanical systems.

Acknowledgements

This work is supported by the Natural Science Foundation of China (11374372, 41330313), Taishan Scholar Foundation (ts20130929), the Fundamental Research Funds forthe Central Universities (13CX06004A,14CX02018A and 14CX02025A), and the Qingdao Science&Technology Program (12-1-4-7-(1)-jch).

References

1. S. Lijima, Nature, 1991, 354, 56–58.
2. P. Tangney, R. B. Capaz, C. D. Spataru, M. L. Cohen and S. G. Louie, Nano Lett., 2005, 5, 2268–2273.
3. N. M. Pugno, J. Mech. Phys. Solids, 2010, 58, 1397–1410.
4. J. A. Elliott, J. K. W. Sandler, A. H. Windle, R. J. Young and M. S. P. Shaffer, Phys. Rev. Lett., 2004, 92, 095501.
5. X. Yang, G. Wu and J. Dong, Appl. Phys. Lett., 2006, 89, 113101.
6. V. Gadagkar, P. K. Maiti, Y. Lansac, A. Jagota and A. K. Sood, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085402.
7. P. Puech, E. Flahaut, A. Sapelkin, H. Hubel, D. Dunstan, G. Landa and W. S. Bacsa, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 233408.
8. C. Caillier, A. Ayari, V. Gouttenoire, A. S. Miguel, V. Jourdain, M. Picher and J. L. Sauvajol, Appl. Phys. Lett., 2010, 97, 173111.
9. P. E. Lammert, P. Zhang and V. H. Crespi, Phys. Rev. Lett., 2000, 84, 2453–2456.
10. M. Hasegawa and K. Nishidate, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115401.
11. M. S. C. Mazzoni and H. Chacham, Appl. Phys. Lett., 2000, 76, 1561–1563.
12. O. Gulseren, T. Yildirim, S. Ciraci and C. Kilic, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155410.
13. J. Q. Lu, J. Wu, W. Duan, F. Liu, B. F. Zhu and B. L. Gu, Phys. Rev. Lett., 2003, 90, 156601.
14. L. X. Benedict, V. H. Crespi, N. G. Chopra, A. Zettl, M. L. Cohen and S. G. Louie, Chem. Phys. Lett., 1998, 286, 490–496.
15. C. C. Ling, Q. Z. Xue, L. Y. Chu, N. N. Jing and X. Y. Zhou, RSC Adv., 2012, 2, 12182–12189.
16. C. C. Ling, Q. Z. Xue, N. N. Jing and D. Xia, Nanoscale, 2012, 4, 3894–3900.
17. E. Borowiak-Palen, E. Mendoza, A. Bachmatiuk, M. H. Rummeli, T. Gemming, J. Nogues, V. Skumryev, R. J. Kalenczuk, T. Pichler and S. R. P. Silva, Chem. Phys. Lett., 2006, 421, 129–133.
18. K. Svensson, H. Olin and E. Olsson, Phys. Rev. Lett., 2004, 93, 145901.
19. X. P. Gao, Y. Zhang, X. Chen, G. L. Pan, J. Yan, F. Wu, H. T. Yuan and D. Y. Song, Carbon, 2004, 42, 47–52.
20. Q. Wang, K. M. Liew and V. K. Varadan, Appl. Phys. Lett., 2008, 92, 043120.
21. L. Wang, H. W. Zhang, Z. Q. Zhang, Y. G. Zheng and J. B. Wang, Appl. Phys. Lett., 2007, 91, 051122.
22. B. Ni, S. B. Sinnott, P. T. Mikulski and J. A. Harrison, Phys. Rev. Lett., 2002, 88, 205505.
23. Q. Wang, Carbon, 2011, 49, 729–732.
24. F. W. Sun and H. Li, Carbon, 2011, 49, 1408–1415.
25. D. J. Hornbaker, S. J. Kahng, S. Misra, B. W. Smith, A. T. Johnson, E. J. Mele, D. E. Luzzi and A. Yazdan, Science, 2002, 295, 828–831.
26. S. Okada, S. Saito and A. Oshiyama, Phys. Rev. Lett., 2001, 86, 3835–3838.
27. N. M. Pugno and J. A. Elliott, Physica E, 2012, 944–948.
28. Ch. Caillier, D. Machon, A. S. Miguel, R. Arenal, G. Montagnac, H. Cardon, M. Kalbac, M. Zukalova and L. Kavan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125418.
29. A. L. Aguiar, A. San-Miguel, E. B. Barros, M. Kalb, D. Machon, Y. A. Kim, H. Muramatsu, M. Endo and A. G. Souza Filho, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195410.
30. C. A. Kuntscher, A. Abouelsayed, A. Botos, A. Pekker and K. Kamaras, Phys. Status Solidi B, 2011, 248, 2732–2735.
31. D. Rigby, H. Sun and B. E. Eichinger, Polym. Int., 1997, 44, 311–330.
32. H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246.
33. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
34. Q. Wang, W. H. Duan, K. M. Liew and X. Q. He, Appl. Phys. Lett., 2007, 90, 033110.
35. Q. B. Zheng, Y. Geng, S. J. Wang, Z. G. Li and J. K. Kim, Carbon, 2010, 48, 4315–4322.
36. S. Okada, S. Saito and A. Oshiyama, Phys. Rev. Lett., 2001, 86, 3835–3838.
37. M. Hodak and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 075419.
38. B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323–324.
39. K. Hirahara, S. Bandow, K. Suenaga, H. Kato, T. Okazaki, H. Shinohara and S. Lijima, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115420.
40. M. Chen, J. Zang, D. Q. Xiao, C. Zhang and F. Liu, Nano Res., 2009, 2, 938–944.
41. J. Zang, A. Treibergs, Y. Han and F. Liu, Phys. Rev. Lett., 2004, 92, 105501.
42. D. Y. Sun, D. J. Shu, M. Ji, F. Liu, M. Wang and X. G. Gong, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165417.
43. J. E. Lennard-Jones, Proc. Phys. Soc., 1931, 43, 461–482.
44. P. Tangney, R. B. Capaz, C. D. Spataru, M. L. Cohen and S. G. Louie, Nano Lett., 2005, 5, 2268–2273.
45. S. Lebedkin, K. Arnold, O. Kiowski, F. Hennrich and M. M. Kappes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094109.
46. N. K. Gupta, G. S. Sekhon and P. K. Gupta, Thin Wall Struct., 2005, 43, 895.
47. V. Gadagkar, S. Saha, D. V. S. Muthu, P. K. Maiti, Y. Lansac, A. Jagota, A. Moravsky, R. O. Loutfy and A. K. Sood, J. Nanosci. Nanotechnol., 2007, 7, 1753.
48. M. Hodak and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 075419.

---