Defective modelling of chaotic motions on empirical potential energy surfaces

Abstract

The progression from regular to chaotic behaviour with increasing vibrational energy is examined for two unimolecular reactions, CH₃NC ⇌ CH₃CN and NCNC ⇌ NCCN. The potential energy surfaces used are, respectively, a piecewise empirical construction and an ab initio numerical surface. It is found that in the former case, the motions never become chaotic in the appropriate energy range, but in the latter, they seem to be approaching that ideal condition. The reasons for this difference are subject to speculation at the present time, but there seems to be a strong impediment to randomisation of energy in one case that is not present in the other. An attempt is made to formulate a semi-quantitative measure of chaotic behaviour in these reactions. Until this problem with synthetic potential energy surfaces can be resolved, these results have important consequences for the numerical modelling of larger polyatomic systems, up to and including such problems as protein folding.

---

Introduction

A cornerstone of the theory of unimolecular reactions is that in the reactive energy range, the internal motions of the atoms are random, or that all energy states are equally probable, or some other statement implying totally chaotic motion. A second cornerstone is that states depleted by reaction are replaced on a time scale much faster than the decay processes; in the case of a single molecule, or at the low-pressure limit, this randomisation process must be first-order, although it may have a second-order component at higher pressures.^1,2 The mechanism of this process may be envisaged as follows: we start from a ground-state molecule, for which the internal motions are regular and vibrational spectra can be observed, but as the energy rises, due to anharmonicities, a pair of spectral lines will merge, i.e. have the same energy, and the wave function becomes indeterminate. The higher the energy, the more crossings there will be, and the degree of chaos increases. For small (triatomic) molecules, there may be no crossings, or else very few, and so their reactions do not fall within the realm of traditional (RRKM) unimolecular reaction theory; on the other hand, large molecules will have many crossings and readily fulfil the requirement of chaotic motion at reaction energies. Of the two isomerisation reactions chosen for this study, the first is generally regarded as falling into the large-molecule class, whereas the other, containing only four atoms, has to be regarded as a borderline example.

In previous studies,³ we had observed that for the isomerisation reaction NCNC ⇌ NCCN, the calculated lifetimes obeyed microscopic reversibility, i.e.

ρ(E)_CN/[small tau, Greek, macron]_CN = ρ(E)_NC/[small tau, Greek, macron]_NC

where [small tau, Greek, macron] is the ensemble average lifetime and ρ(E) is the density of states at the given energy E; however for the reaction CH₃NC ⇌ CH₃CN, this was not true, with a discrepancy of about an order of magnitude, but improving slowly with increasing energy. The study presented here attempts to understand this departure from one of the fundamental principles of statistical mechanics.

Computational procedure

The computational methods used have been described extensively in previous publications:^3,4 briefly, to follow each trajectory by using a simple fourth-order Runge–Kutta start-up procedure followed by a fifth-order Adams–Mouton predictor-corrector.⁵ For a given value of the energy, trajectories were started from the equilibrium internuclear configuration of either NCNC or NCCN with quasi-random momenta assigned to each of the 12 degrees of freedom (or 18 for the CH₃NC or CH₃CN cases); a portable random number generator (ran1.for)⁵ was used to create these random initial conditions. A time step-length of 0.1 fs was used throughout, and values of all internuclear distances for the 4- and 6-atom reactions were tabulated at δt = 5 fs intervals.

Each of the (r − r_e)^N_(i,t) vectors for trajectory N, i = 1,i_max, t = 1,t_max, (i_max = 14 and t_max = 16 384δt in this study – see below), was subjected to a Fourier transform algorithm⁵ to extract the characteristic frequencies; however, the individual frequencies themselves are of minor importance because, separately, they contain no angle information, but they do provide an intuitive feel for the connections of specific motions with particular spectral frequencies.

It is a simple matter, for the 4-atom case, to see that a vector containing the sum of all 6 distances at each time step contains all the information, internuclear distances, bond and dihedral angles, and gives the full spectrum.

The 6-atom case is more complicated: there are 15 inter-atomic distances, but there are only (3n − 6), i.e. 12 internal degrees of freedom when n = 6. Thus, by using all 15 distances, the system would appear to be over-specified, but not so: it is feasible, but not trivial, to transform these 15 vectors into 12 vectors, each representing one normal mode, but complicated further because there are 4 doubly-degenerate as well as 4 non-degenerate modes. Moreover, the concept of a normal mode only has meaning for low energies where the motions are regular, and it is unclear how instructive such calculations would be when applied to partially or completely chaotic motions, so this avenue was not explored further.

A useful contraction is to impose the constraint that all three H atoms are grouped with one C atom to give a pseudo-molecule N–C¹–C²–M where M represents the centre of mass of the three H atoms; as before, N–C¹–C²–M has 6 inter-particle distances, and the 4-atom group C²H₃ contains another 6, making 12; however, the rotation of the CH₃ group when N–C¹–C²–M is non-linear is not defined, and it needs distances from any one of the H atoms to C¹ and to N to specify the dihedral angles completely, making 14 in all. It was thought that this parallelism between the two systems might be of help in their comparison.

The calculations are subject to two constraints: (a) that the trajectory shall be long enough to contain a large number of vibrational periods, and (b) that the sampling width for the Fourier transform (FFT) algorithm shall be wide enough to give a good resolution. With time intervals of 5 fs, a choice of 256-point sampling width gave reasonable results; this leads to a 16 384-length vector for each variable, and a time length of 81.92 ps.

At energies near the higher limit of these calculations, there are often many more than 50 crossings and recrossings of the energy barrier on this time scale,⁶ whereas only trajectories with no (or very few) crossings are suitable for this experiment; for example, in one of the two sets of high-energy (7.3 eV) calculations, out of 1000 trajectories not one lives for this length of time without a crossing, and only one at 7.0 eV.

The potential energy surfaces used were: for CH₃NC ⇌ CH₃CN, the empirical surface constructed by Sumpter and Thompson;⁷ and for NCNC ⇌ NCCN, an 870-point “clamped-nuclei” MP2/6-31G* ab initio potential surface.^6,8

Fig. 1 shows the key properties of the two potential energy surfaces. Since the energy difference between the minima of the CH₃NC and CH₃CN potentials is almost exactly 1 eV, it is convenient to use electron volts in these calculations: 1 eV = 23.06 kcal mol⁻¹ = 96.5 kJ mol⁻¹ = 8066 cm⁻¹; in what follows (except for Fig. 5) energies are uniformly measured from the global minimum, i.e. NCCN or CH₃CN. The zero-point energy (zpe) for either CH₃NC or CH₃CN is 1.3 eV, so that the highest energy, 7.3 eV, is 5 eV above the CH₃NC zpe, i.e. 115 kcal mol⁻¹, which is far above the activation of 38.2 kcal mol⁻¹.⁹ Likewise, the NCNC minimum is about 1.38 eV above the global minimum and the zero-point energies for both NCNC and NCCN are 0.42 eV; this makes the topmost energy tested of 4 eV approximately 2.2 eV above the NCNC zpe.

Fig. 1 Relative energy levels, in eV, for the reactions CH₃NC ⇌ CH₃CN and NCNC ⇌ NCCN: the bottom-most thick horizontal line denotes the potential minimum for each molecule, and zpe denotes its zero-point energy; TS_cl and TS_qu are, respectively, the classical saddle points on the clamped-nuclei surfaces without vibration, and with the vibrational “correction” usually introduced in transition state theory.

Numerical results: CH₃NC and CH₃CN

At energies near the zpe, the resolved spectral lines are very sharp. but they grow in width with increasing energy. Fig. 2 shows the degree of variation for two individual Fourier transforms, (a) for R(N–C) and (b) for R(C–C). There is a slight shift in frequency of the single peak in the former case, but no evidence of contamination from other frequencies in the system; in the other, in addition to the broadening, there is an apparent shift of about 400 cm⁻¹ of one peak to higher frequencies. This implies that there is virtually no significant coupling of R(N–C) with any of the other motions in the molecule, even when the total internal energy is 5 eV greater. For the R(C–C) case, there is evidence of anharmonicity, but at higher energy, one would expect the energy levels to be closer together, and not further apart.†

Fig. 2 Fourier transforms of two individual distances at the zpe and at (zpe + 5 eV): for (a) R(N–C) and (b) R(C–C); the very sharp peaks at 600 cm⁻¹ and 2150 cm⁻¹ are for the zpe and the broad peaks for the (zpe + 5 eV) motions.

Fig. 3 gives two more examples: there are 3 R(C–H) motions and 3 R(H–H) motions, and the members of each set are almost indistinguishable from each other; panel (a) shows the R(C–H) behaviour, and (b), that of the R(H–H) motions. These spectra show much more evidence of mixing and chaotic behaviour, and of frequency shifts in the expected direction. Fig. 4 compares the total spectra of two trajectories. For the 2.3 eV case, these spectra are very similar for each individual trajectory, but vary in the observed intensities due to the differences in starting momenta in each calculation. However, for the higher energy spectra, these are almost identical for trajectories with no (or only a few) CH₃NC ⇌ CH₃CN crossings; since each of these trajectories starts from a different set of momenta, this sameness suggests comparable degrees of chaos in two isolated regions of phase space.

Fig. 3 Fourier transforms of the relative separations R(C–H) and R(H–H) at an energy of (zpe + 5 eV); there are 3 such (almost identical) spectra for (a) and for (b).

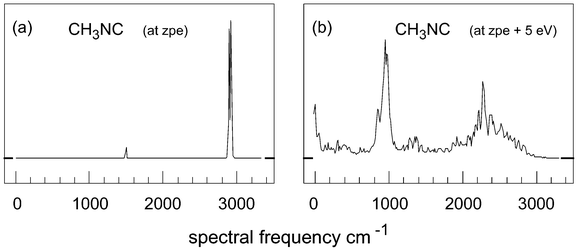Fig. 4 Complete spectral plots, i.e. Fourier transforms of Σr^N_(i,j), at energies of (a) zpe and of (b) (zpe + 5 eV); in (a), for this particular trajectory, the doublet near 3000 cm⁻¹ is very prominent.

A semi-quantitative measure of the degree of chaos?

If the extent of the chaos revealed by a spectrum such as Fig. 4(b) were perfect, the spectrum would be a flat line over the whole range, with the total signal strength residing at zero frequency. This plot shows some of the required characteristics: there is a long low signal between 200 cm⁻¹ and 800 cm⁻¹, and a longer one between 1200 cm⁻¹ and 2000 cm⁻¹, which could be characterised as something analogous to “white light”; also, there is a hint of the expected rise near zero frequency.

However, there are “blockages” between these two regions of “almost-chaos” – a large one near 1000 cm⁻¹ and a weaker one near 1300 cm⁻¹, which are frequencies associated with R(C–C) and R(H–H) motions in Fig. 2 and 3. At the present time, the exact cause of these impediments to the onset of chaos throughout the system are yet to be understood.

Examining the complete spectra extracted from non-crossing trajectories for all four of the molecules studied in this paper, it appears that there is a relationship between the total area under the curve and the energy: this is shown for CH₃NC in Fig. 5(a). Even though there is a large scatter in the data, it is clear that there is something like a linear correlation between the area and the energy; the area units are arbitrary, as each point is simply the sum of the 256 values of the strength given by the Fourier transform algorithm for each individual trajectory. The straight line is simply a guess, drawn by eye, and it does not start at the origin, as it probably should; in fact, at very low energies (e.g. in the classical region below the zero-point energy), the motions are too feeble for the Fourier transform algorithm to extract any frequency peaks, due to insufficient arithmetic precision. The large scatter also arises from a combination of the limitation in the trajectory length and in the sampling width, whence the whole frequency range from zero to slightly over 3300 cm⁻¹ is covered with only 256 points.

Fig. 5 (a) Total area under spectral curve (vertical units arbitrary); (b) fraction of total spectral intensity residing below 250 cm⁻¹.

As energy is removed from the regular to the chaotic regime, the area under the regular spectrum will decline, and be transferred to the feature near zero frequency. To test this hypothesis, an arbitrary division was chosen at 250 cm⁻¹ (just under the lowest bending frequency of 263 cm⁻¹ in CH₃NC) and the area below that was compared with the total. For both CH₃NC and CH₃CN trajectories having no or few crossings, values of less than 0.1% were found at the lowest energies and up to around 10% at very high energy. This is shown in Fig. 5(b) which exhibits similar scatter, and for the same reasons.

If it were possible to reduce the scatter of these plots, a more accurate relationship between the energy and the area under the spectrum would ensue, and the percentage of the total area residing below some cut-off frequency would yield an acceptable measure of the chaos in the internal motions for each trajectory. This is not quite as straightforward as it may seem: first, it would be necessary to use a larger sampling width, say 512 or 1024, which would necessitate the construction of, respectively, (14 × 32 768) or (14 × 65 536) matrices of interparticle distances as a function of time. This cannot be done by extending the time span because already (see above) very few trajectories of higher energy live for 81.92 ps without a crossing, so the time intervals must be reduced. That will make the inter-atomic differences at each step smaller, with loss of precision, and may require quadruple (32 decimal place) precision, especially at the lower energies.

Numerical results: NCNC and NCCN

The results for trajectories of these molecules are quite similar to those described above at low energies, as shown in Fig. 6; if we label the atoms in this molecule as N₁C₁N₂C₂, then panel (a) represents the transform on R(C₁–C₂) and (b) on R(N₁–C₂). For NCCN at 2.0 eV, the average percentage of the total area for the 0–250 cm⁻¹ range in 13 trajectories having zero or one crossing is 10.8%, and for NCNC over 11 low-crossing trajectories, 24.6%. At energies greater than 3.0 eV above the NCCN minimum, there are very few low-crossing trajectories in an ensemble of 100, with percentage for the 0–250 cm⁻¹ range being (for 2 trajectories in each case) 13% and 25%, respectively. An example of one of these spectra is shown in Fig. 7(a): the signals around 1000 and 2000 cm⁻¹ from Fig. 6 still persist, but are hardly perceptible on the scale of this diagram: the feature between 400 and 800 cm⁻¹ is probably the remnants of a bending process.¹⁰

Fig. 6 Fourier transform of two individual atom-separations for NCNC at the zpe.

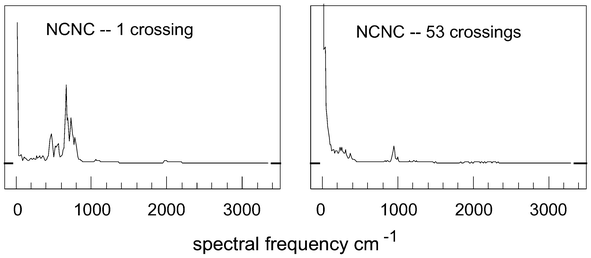Fig. 7 Complete spectral plots, i.e. Fourier transforms of Σr^N_(i,j), at energies of (zpe + 2.2 eV): (a) low-crossing case; (b) high-crossing case.

Usually, there are very many crossings at these energies for each trajectory, typically in the range 50–60,⁶ and the outcomes are quite different. For example, Fig. 7(b) shows the result for a trajectory with 53 crossings over the 81.92 ps period: here, one finds a truly random result – with in excess of 99% of the signal strength concentrated below 250 cm⁻¹. Moreover, the feature near 1000 cm⁻¹ is probably associated with the crossing frequency: of the 53 crossings, 15 are spread fairly evenly between 9 and 11 ps, i.e. mean separation of 0.13 ps; two other bursts of crossings have mean lifetimes of 0.17 ps, hence, the mean there-and-back crossing time is about 0.3 ps, corresponding to a frequency near 1000 cm⁻¹.

Earlier spectra purporting to show ergodicity, e.g. Noid, Koszykowski and Marcus,¹¹ are remote from the asymptotic behaviour of Fig. 7(b) here.

Discussion

The results of this study show conclusively that the synthetic potential surface for the CH₃NC ⇌ CH₃CN reaction in rotational state J_x = J_y = J_z = 0 is deficient because there is some obstacle to randomisation. Calculations with non-zero J are very little different because the rotational broadening of the lines is minimal, and the rotations don't add significantly to the probability of eigenvalue crossings. The simplest way to describe it would be to say that if the three R(C–H) spectra for J_x = J_y = J_z = 0, one of which is shown in Fig. 3(a), and the corresponding three for (say) J_x = J_y = J_z = 10 for the same energy and initial conditions, were laid out on the desk, one could not guess which ones went with which J; likewise for the three R(H–H) spectra, one of which is shown in Fig. 3(b).

As we have noted previously,^3,4,12 the calculated rate constant for the isomerisation of CH₃NC is about a factor of 20 below the observed reaction rate, and a similar discrepancy of a factor of 20 was found by Stimac and Barker¹³ during the simulation of the CH₃–O–ON–O radical thermal dissociation into CH₃O + NO₂, using a similarly constructed potential energy surface. In addition, their ensemble decay resembles that of a small molecule like HNC,¹⁴ instead of a first-order process like that for CH₃NC.¹⁵

That these deficits are due to insufficient mixing has been demonstrated by adding more coupling between the vibrations: this was done by either using coupling constants published by Sumpter and Thompson,⁷ or by an artificial coupling procedure in which some momenta were reversed every 0.1 ps¹² mimicking, crudely, collisions at very high pressure, or black-body radiation³ in a collisionless environment. However, there is no way of knowing, beforehand, how much coupling to add, as the reaction rate can be driven too high, especially just above threshold, as shown in Fig. 6 of ref. 12.

Beyond that, there are other issues that need to be resolved. For example, in the light of Fig. 4(b), why does the decay of an ensemble of 1000 trajectories behave in a perfectly logarithmic fashion¹⁵ when there are two isolated quasi-chaotic regions of phase space? This could only be true if molecules trapped on either side of the blockage decayed with the same intrinsic rate.

This raises the question how much chaos is needed for there to be a first-order decay? Both CH₃NC and NCNC exhibit first-order ensemble decay,^8,15 but in the first case, the distribution of states is far from chaotic, whereas in the second it seems to be approaching total chaos: thus, first-order decay does not imply a proper chaotic distribution among the reactant states. On the other hand, microscopic reversibility, which fails badly in the first case, but not in the second, seems to be a more reliable indicator.

Finally, does microscopic reversibility guarantee the calculation of the correct rate constant? We know that for the isomerisation of CH₃NC where there is a discrepancy of about an order of magnitude,⁴ the calculation of the rate fails badly; unfortunately, there are no experimental data available for the NCNC isomerisation, as it polymerises readily at 193 K,¹⁶ so we may never know.

Recently, Sutcliffe and Woolley¹⁷ have pointed out that clamped-nuclei potential energy surfaces are inconsistent with quantum mechanics and cannot give a correct representation of the transition state problem; however, the Eyring–Polanyi concept of the transition state as a saddle-point on a potential energy surface has been a powerful visualisation tool, and one would expect the numerical errors to be comparable with those usually assosciated with the Born–Oppenheimer approximation. Thus, it is important to determine how well the classical treatment of motion on a clamped-nuclei potential energy surface can match the experimental behaviour.

The smallest molecules for which extensive experimental isomerisation data are available are methyl isocyanide^18,19 and cyclopropane,²⁰ 6-atom and 9-atom molecules respectively. Calculation of ab initio clamped-nuclei potential energy surfaces for the former reaction, perhaps even the latter, are within the bounds of modern computing power,²¹ whence it would be possible to test the predictive accuracy of two methods: first, the classical trajectory method used here; and second, a wave-packet method²² which is essentially a wave-mechanical version of the same classical method.‡ The possibility of an “exact” solution, based on Sutcliffe and Woolley's analysis, seems to be further into the future.

Finally, from time to time, Ehrenfest's Theorem and/or the correspondence principle are mentioned in connection with such trajectory calculations. In the quantum sense, this association is meaningless because as the energy rises and the first eigenvalue crossing occurs, the adiabatic principle is violated. But the present calculations show that such crossings are nowhere nearly as frequent as one might expect, and often the ground-state vibrational frequencies persist up to very high energies. To resolve this paradox, it should be possible to construct an arbitrary 3-atom potential energy surface with anharmonicities chosen in such a way that the vibrational frequencies will cross at some energy. At this point, what happens? Do they become one more complex motion, is there an avoided crossing, or do they simply cross and continue unchanged?

If either of the last two, by analogy with the high-energy behaviour of a harmonic oscillator,²⁴ success may be interpreted as a multi-dimensional extension of the correspondence principle²⁵ with a collection of weakly dependent anharmonic oscillators whose wave functions are similar to those of a simple harmonic oscillator, but with asymmetric distortions.²⁶

Conclusion

Classical trajectory calculations for two unimolecular isomerisation reactions, NCNC ⇌ NCCN using a rudimentary ab initio potential energy surface, and CH₃NC ⇌ CH₃CN using an empirical potential energy surface, have been examined. These surfaces are quite primitive, but exhibit correct asymptotic behaviour and approximately correct energy values for the stationary states. No effort was made to calculate rate constants, only to examine the difference in behaviour with respect to microscopic reversibility between the two different basic types of potential energy surface.

It was shown, convincingly, that the primitive ab initio surface allowed the atomic motions to become almost chaotic, as required by unimolecular reaction theory, but that the empirical surface did not. The details of this failure were not revealed by these calculations, but (quoting Bowman et al.²¹) “simple functional forms are highly problematic” and it may be a consequence of the use of switching functions in the empirical surface.

If this difficulty can be resolved, and if classical trajectory calculations can give satisfactory reaction rates for one, or more, of the reactions^17–20,23 noted above, it could reveal how to create semi-empirical potential energy surfaces that would allow the prediction of useful rate constants for complex reactions such as occur in combustion, or in biological systems.

Acknowledgements

I wish to thank Dr S. R. Vatsya for valuable advice and comments. I also acknowledge the privilege of publication in the Journals of this Society since 1950.

References

1. H. O. Pritchard, Can. J. Chem., 1980, 58, 2236–2245.
2. H. O. Pritchard, Quantum Theory of Unimolecular Reactions, Cambridge University Press, Cambridge, 1984, Chapter 7.
3. H. O. Pritchard, S. R. Vatsya and D. Shen, J. Chem. Phys., 1999, 110, 9384–9389.
4. H. O. Pritchard, Cent. Eur. J. Chem., 2011, 9, 753–760.
5. W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, Cambridge, 1985.
6. H. O. Pritchard, J. Phys. Chem. A, 2005, 109, 1400–1404.
7. B. G. Sumpter and D. L. Thompson, J. Chem. Phys., 1987, 87, 5809–5819.
8. D. Shen and H. O. Pritchard, J. Chem. Soc., Faraday Trans., 1996, 92, 4357–4360.
9. J. L. Collister and H. O. Pritchard, Can. J. Chem., 1976, 54, 2380–2384.
10. F. Stroh, B. P. Winnewisser, M. Winnewisser, H. P. Reisenauer, G. Maier, S. J. Goede and F. Bickelhaupt, Chem. Phys. Lett., 1989, 160, 105–112.
11. D. W. Noid, M. L. Koszykowski and R. A. Marcus, J. Chem. Phys., 1977, 67, 404–408 , Fig. 5.
12. D. Shen and H. O. Pritchard, J. Chem. Soc., Faraday Trans., 1996, 92, 1297–1304.
13. P. J. Stimac and J. R. Barker, J. Phys. Chem. A, 2008, 112, 2553–2562.
14. W.-T. Chan, D. Shen and H. O. Pritchard, J. Chem. Soc., Faraday Trans., 1995, 91, 1717–1721.
15. D. Shen and H. O. Pritchard, Int. J. Chem. Kinet., 1994, 26, 729–736.
16. L. W. Jenneskens, J. W. G. Mahy, E. J. Vlietstra, S. J. Goede and F. Bickelhaupt, J. Chem. Soc., Faraday Trans., 1994, 90, 327–332.
17. B. T. Sutcliffe and R. G. Woolley, J. Chem. Phys., 2012, 137, 22A544-1–22A544-8.
18. F. W. Schneider and B. S. Rabinovitch, J. Am. Chem. Soc., 1962, 84, 4215–4230 , 1963, 85, 2365–2370.
19. C. K. Yip and H. O. Pritchard, Can. J. Chem., 1970, 48, 2942–2944.
20. H. O. Pritchard, R. G. Sowden and A. F. Trotman-Dickenson, Proc. R. Soc. London, Ser. A, 1953, 217, 563–571.
21. J. M. Bowman, B. J. Braams, S. Carter, C. Chen, G. Czakó, B. Fu, X. Huang, E. Kamarchik, A. R. Sharma, B. C. Shepler, Y. Wang and Z. Xie, J. Phys. Chem. Lett., 2010, 1, 1866–1874.
22. R. Schork and H. Köppel, J. Chem. Phys., 2001, 115, 7907–7923.
23. J. E. Douglas, B. S. Rabinovitch and F. S. Looney, J. Chem. Phys., 1955, 23, 315–323.
24. L. Pauling and E. B. Wilson, Introduction to Quantum Mechanics, McGraw Hill, New York, 1935, p. 76.
25. E. C. Kemble, The Fundamental Princples of Quantum Mechanics, Dover, New York, 1937, p. 375.
26. H. O. Pritchard, J. Phys. Chem., 1961, 65, 504–510 , Fig. 1.

---

Footnotes

† It should also be noted that in all these spectral plots, the vertical axis is linear in the strength, not logarithmic as is the normal way of representing experimental data.

‡ A third option might be the cis-trans isomerisation of 1,2-dideuterioethylene where, due to symmetry, generation of the ab initio potential surface is simpler, but the experimental data²³ are less extensive.

---