DOI:
10.1039/C2RA22164K
(Paper)
RSC Adv., 2013,
3, 221-227
Dielectric properties of polymethacrylate-grafted carbon nanotube composites†
Received
14th September 2012
, Accepted 27th October 2012
First published on 15th November 2012
Abstract
The dielectric properties of a series of multi-walled carbon nanotubes on which poly(cyclohexyl methacrylate)s were densely grafted (PCHMA-CNTs) were systematically characterized over the broad frequency range of 10−2–108 Hz. PCHMA-CNT was used as an ideal polymer/CNT nanocomposite system in which the CNT is homogeneously dispersed and the polymer/CNT interface is strong. When the volume fraction of the CNT ΦCNT < 0.1 PCHMA-CNT exhibited a relatively high dielectric constant ε′r and a quite low dielectric loss factor ε′′r, while when ΦCNT > 0.1 a very large ε′r was observed at low frequencies. The Cole–Cole relaxation model was applied to the impedance spectra of PCHMA-CNT in order to investigate the correlation between the tunneling conduction and the very large ε′r. Also, from thus-obtained relaxation frequencies, the inter-nanotube distance in the PCHMA-CNT system was estimated. As a result, a new mechanism was proposed for the very large ε′r: the locally enhanced electric field by the tunneling conduction results in the very large ε′r at the low frequencies along with the increase in ε′′r. Furthermore, the CNT was demonstrated to be five times more effective than barium titanate (BT) for the enhancement in ε′r of polymer materials because of the higher electric field enhancement effect of the CNT than that of the BT.
Introduction
Dielectric materials are mainly used to store electrical energy as capacitors nowadays.1 Among the dielectric materials, polymer materials have the advantages of high flexibility, lightness, durability, and processability. Highly flexible dielectrics are also promising for other applications such as dielectric actuators and sensors.2–6 However, the low dielectric constant ε′r of the polymer materials strongly limits the extent of the applications. Because of the high ε′r of ceramic materials, therefore, polymer/ceramic composite materials have been much developed over the last few decades.7–11 Barium titanate (BT), one of the ferroelectric metal oxides, is most widely used for enhancing ε′r. For practical use, however, over 50 vol% of the BT is often required to be added despite the high ε′r of the BT. Such high BT loading spoils the superior properties of polymeric materials described above.
Recently, polymer/carbon nanotube (CNT) nanocomposites have received much attention as dielectric materials.12–23 A very large ε′r was often observed at low frequencies with only a small percentage volume of CNT loading.12–21 According to the previous studies, it is considered that the very large ε′r is attributed to space charge polarization and/or interface polarization between the CNT and the polymer matrix.13,14,17,18,23 However, almost no evidence of such polarizations has been reported. Because the dielectric behavior of the polymer/CNT nanocomposites strongly depends on the dispersivity of the CNT and/or the interface interaction between the CNT and the polymer matrix, fundamental understanding of the mechanism of the increase in ε′r remains unclear. This is a serious issue that needs to be overcome for material design of the polymer/CNT nanocomposites. We suggest that the ideal polymer/CNT nanocomposite in which the CNT is homogeneously dispersed and the polymer/CNT interface is strong should give a much better understanding of the very large ε′r.
The second issue in the polymer/CNT nanocomposites is a great increase in dielectric loss factor ε′′r along with the increase in ε′r.12–21 The increase in ε′′r mainly results from a leak current passing through the nanocomposites. The polymer/CNT nanocomposites become conductive owing to the formation of a three-dimensional conductive network of the CNT within the polymer matrix when the CNT content exceeds a critical value, known as a percolation threshold.24–26 At over the percolation threshold, the CNTs approach each other within several nanometers, allowing efficient electron hopping between the nanotubes (tunneling conduction).15,27–29 The tunneling conduction causing the leak current cannot be avoided even if the CNT is covered with an organic layer having a thickness of a few nanometers.13,19,29 To impede the tunneling current, Nan et al. covered CNTs with a thick polymer shell. The physically adsorbed polymer chain on the CNT brings a low ε′′r as well as a relatively high ε′r and breakdown strength.22,23
Another simple method to perfectly prevent the tunneling conduction of the polymer/CNT nanocomposites is polymer grafting on the surface of the CNT.29–33 Unlike a physically adsorbed polymer chain, the covalently attached polymer chain would be more effective in the insulation of the CNT. We have recently developed a surface-initiated atom-transfer radical polymerization (ATRP) method using an originally designed ATRP initiator, p-(bromomethyl)benzyl 2-bromoisobutylate.34,35 The ATRP initiator moiety was covalently attached on the surface of the CNT (CNT-Br), and high molecular weight poly(cyclohexyl methacrylate)s were densely grafted on the CNT-Br (PCHMA-CNTs).29 It was characteristic that all the polymer chains were tethered on the CNT in the PCHMA-CNT system, and the grafted polymer chains served as a matrix, implying that the CNT should be homogeneously dispersed in the polymer matrix. The electrical resistance of PCHMA-CNT under direct current (DC) was compared to that of two types of conventional nanocomposites prepared by blending PCHMA with the CNT or CNT-Br (PCHMA/CNT and PCHMA/CNT-Br). At a comparable volume fraction of the CNT, DC volume resistivity of PCHMA-CNT was 14 orders of magnitude higher than that of PCHMA/CNT. This is because the grafted polymer with a combination of high molecular weight and high grafting density isolates individual CNTs at a long distance in the PCHMA-CNT system. In addition, it was indicated that PCHMA-CNT had a strong polymer/CNT interface according to dynamic mechanical analysis.
We believe our PCHMA-CNT system is the best candidate of the ideal polymer/CNT nanocomposite as mentioned above, and the most suitable for the characterization of the dielectric behavior. In this study, therefore, the dielectric properties of PCHMA-CNT are systematically characterized over the broad frequency range of 10−2–108, and compared to that of PCHMA/CNT-Br. The Cole–Cole relaxation model is applied to the impedance spectra of the composites in order to obtain information of the tunneling conduction. From the information, the inter-nanotube distance is also estimated. As a result, a new mechanism is proposed for the very large ε′r. Furthermore, the performance of PCHMA-CNT as a dielectric material is evaluated by comparing with that of a BT-filled PCHMA composite (PCHMA/BT).
Results and discussion
A series of PCHMA-CNTs with various molecular weights from 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 190
000 to 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 are listed in the ESI.† Conventional nanocomposites (PCHMA/CNT and PCHMA/CNT-Br) were designed to have the same volume fraction of CNT, ΦCNT, as PCHMA-CNT. In the blending procedure, a preliminary blending method using freeze-drying was used in order to obtain as good dispersion of the CNTs as possible.35 These nanocomposite samples were molded by compression of 10 MPa at 130 °C prior to electrical measurements. The dispersivity of the CNT in the polymer matrix for the three types of nanocomposites thus produced was observed using a scanning electron microscope (SEM). In this observation, the surfaces of the nanocomposites had been slightly etched with oxygen plasma in order that the PCHMA polymer on the surface was removed. Fig. 1 shows SEM images of the nanocomposites with ΦCNT = 0.055. For PCHMA/CNT and PCHMA/CNT-Br, the CNTs are inhomogeneously dispersed at a submicron scale. This inhomogeneity is typical of polymer/CNT composites prepared by blending, owing to the poor polymer/CNT compatibility. In contrast, the dispersivity of the CNT is surprisingly good for PCHMA-CNT. In the PCHMA-CNT system, the PCHMA matrix cannot be separated from the CNT because all the PCHMA chains are tethered on the CNT. The excellent CNT dispersivity for PCHMA-CNT is also confirmed by an SEM image with low magnification (ESI†). We suggest polymer-grafting should be the best method of producing the perfectly homogeneous dispersion of CNT in a polymer matrix.
000 are listed in the ESI.† Conventional nanocomposites (PCHMA/CNT and PCHMA/CNT-Br) were designed to have the same volume fraction of CNT, ΦCNT, as PCHMA-CNT. In the blending procedure, a preliminary blending method using freeze-drying was used in order to obtain as good dispersion of the CNTs as possible.35 These nanocomposite samples were molded by compression of 10 MPa at 130 °C prior to electrical measurements. The dispersivity of the CNT in the polymer matrix for the three types of nanocomposites thus produced was observed using a scanning electron microscope (SEM). In this observation, the surfaces of the nanocomposites had been slightly etched with oxygen plasma in order that the PCHMA polymer on the surface was removed. Fig. 1 shows SEM images of the nanocomposites with ΦCNT = 0.055. For PCHMA/CNT and PCHMA/CNT-Br, the CNTs are inhomogeneously dispersed at a submicron scale. This inhomogeneity is typical of polymer/CNT composites prepared by blending, owing to the poor polymer/CNT compatibility. In contrast, the dispersivity of the CNT is surprisingly good for PCHMA-CNT. In the PCHMA-CNT system, the PCHMA matrix cannot be separated from the CNT because all the PCHMA chains are tethered on the CNT. The excellent CNT dispersivity for PCHMA-CNT is also confirmed by an SEM image with low magnification (ESI†). We suggest polymer-grafting should be the best method of producing the perfectly homogeneous dispersion of CNT in a polymer matrix.
 |
| | Fig. 1 SEM images of three types of nanocomposites with ΦCNT = 0.055: (a) PCHMA/CNT, (b) PCHMA/CNT-Br, (c) PCHMA-CNT. | |
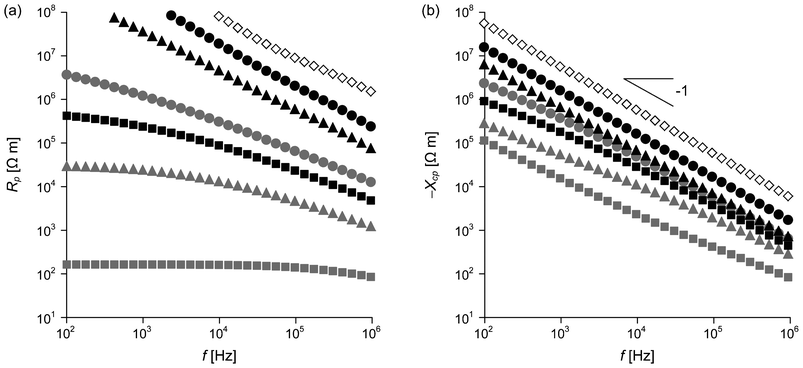
Electrical impedance Z depends on the frequency f of an applied electric field. The magnitude of impedance |Z| for the three types of nanocomposites is plotted as a function of f in the range of 102–106 Hz in Fig. 2. PCHMA/CNT with ΦCNT = 0.055 shows very low |Z|, independent of f over the frequency range. This is typical behavior of conductive polymer/CNT nanocomposites. Due to the coating of the CNT with the organic thin layer (≈2 nm), PCHMA/CNT-Br has much higher |Z| than PCHMA/CNT at ΦCNT = 0.055. However, |Z| of PCHMA/CNT-Br is rapidly decreased with the increase in ΦCNT, indicating that such a thin layer on the CNT in PCHMA/CNT-Br easily allows the tunneling conduction.29 At ΦCNT = 0.094, no frequency dependence of |Z|, conductor behavior, is observed in the low frequency range of 102–103 Hz. In comparison at the same ΦCNT, |Z| of PCHMA-CNT is higher than that of PCHMA/CNT-Br, because the CNT is covered with the thick polymer shells in the PCHMA-CNT system. At ΦCNT = 0.055 and 0.094, |Z| of PCHMA-CNT linearly increased with the decrease in f in all of the frequency range, similar to that of PCHMA. On the other hand, weak frequency dependence of |Z| is observed for PCHMA-CNT with ΦCNT = 0.14 at below 104 Hz. Further characterization of these electrical behaviors was carried out by the introduction of the real and imaginary parts of Z. Because a material can be simply modeled as the electric circuit composed of a resistor and a capacitor connected in parallel, we can divide Z into the resistance Rp and the capacitive reactance Xcp as:
| | | 1/Z = 1/Rp + 1/(jXcp); −Xcp = 1/(2πfCp), | (1) |
where
j is the imaginary unit and
Cp is the capacitance. The two components,
Rp and −
Xcp for PCHMA/CNT-Br and PCHMA-CNT are shown in
Fig. 3. Notice that
Xcp has a minus sign. The corresponding
spectra of PCHMA/CNT cannot be exhibited because the reactance component for PCHMA/CNT was too small to be measured precisely. For PCHMA-CNT with
ΦCNT = 0.094, −
Xcp is much smaller than
Rp in all the frequency range, which means almost all electric current is passed through the capacitor in the parallel resistor-capacitor (RC) circuit. That is, the PCHMA-CNT composite is a dielectric. In addition, −
Xcp of the composite has a relationship described by −
Xcp ∝
f−1 because
Cp is almost constant. Similar dielectric behavior is also observed for PCHMA and PCHMA-CNT with
ΦCNT = 0.055. Unlike these PCHMA-CNT composites, PCHMA-CNT with
ΦCNT = 0.14 has a transition from a dielectric (
Rp > −
Xcp) to a conductor (
Rp < −
Xcp) at ∼10
3 Hz. This is because
Rp at
ΦCNT = 0.14 is small especially at the low frequencies due to the tunneling conduction. In our previous study, the dominant tunneling conduction was clarified for PCHMA-CNT with
ΦCNT over 0.1.
29
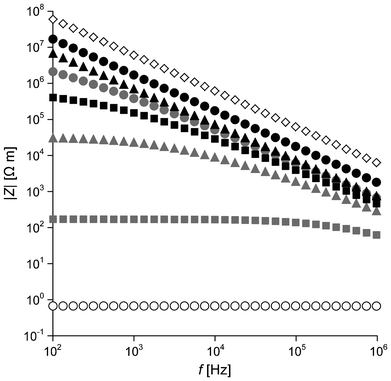 |
| | Fig. 2 Frequency f dependence of magnitude of impedance |Z| of PCHMA (diamond) and three types of nanocomposites with ΦCNT = 0.055 (circles), ΦCNT = 0.094 (triangles), and ΦCNT = 0.14 (squares). White symbols, PCHMA/CNT; gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT. | |
 |
| | Fig. 3
f dependence of (a) resistance Rp and (b) capacitive reactance Xcp of PCHMA (diamond) and two types of nanocomposites with ΦCNT = 0.055 (circles), ΦCNT = 0.094 (triangles), and ΦCNT = 0.14 (squares). Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT. | |
The transition from a dielectric to a conductor results from a Z relaxation related to the tunneling conduction that occurs at a microcapacitor formed between two CNT electrodes.15 To characterize the Z relaxation in detail, we again assume the parallel RC circuit with a resistance R and a capacitance C. Z is expressed using the Cole–Cole model as:36
| | | Z = R∞ + R/{1+(jω/ω0)β}; ω = 2πf, | (2) |
where
R∞ is the resistance at infinite frequency, and
ω0 is the relaxation frequency of the RC circuit. The exponent parameter
β (0 <
β ≤ 1) indicates stretching of the relaxation. When
β = 1,
eqn (2) denotes a single relaxation, the Debye relaxation.
Table 1 summarizes parameters obtained by fitting
eqn (2) to the experimental results. Examples of the Cole–Cole plots are shown in the ESI.
† The fitting was not applicable to PCHMA-CNT with
ΦCNT below 0.1, because
ω0 was too low to be observed. At
ΦCNT = 0.14, PCHMA-CNT has low
ω0 than PCHMA/CNT-Br, resulting from the difference of magnitude of
R. Assuming that the relaxation of
Z is the Debye relaxation, the relationship
ω0 = 1/(
RC) is concluded. Therefore, we can estimate the average value of the internanotube distance
d of the microcapacitor with a tunneling resistance
Rt and a capacitance
Cμ using the following equation:
15,37| | 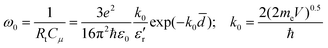 | (3) |
where
e is the charge of the electron,
ħ is the Planck constant,
ε0 is the dielectric constant of vacuum,
ε′
r is the dielectric constant of a matrix
polymer, and
me is the electron mass.
k0 describes the potential barrier with a potential height of
V against the electron. The average internanotube distance
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
calculated using the potential height of 0.2 eV
38 and
ε′
r of 2.7 is plotted in
Fig. 4.
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
decreases with the increase in
ΦCNT (
Fig. 4a), which is reasonable and consistent with a previous result that has been reported by Klüppel
et al.15 It is more important that
R is exponentially increased with the increase in
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
at such nanometer scale (
Fig. 4b), which is well-known as a quantum effect. This fact means that if many microcapacitors with different
d are connected in a series like a real composite system, the applied voltage is concentrated at some of the microcapacitors with the longest
d; in a series circuit, the applied voltage is distributed to the microcapacitors in proportion to their tunneling resistance
Rt. This locally amplified electric field would give an apparent increase in the total capacitance of the composite. In the case of the corresponding macroscale capacitors, the electric field is not amplified because the resistance is proportional to the gap width between the electrodes.
Table 1 Parameters of the Cole–Cole relaxation equation for two series of PCHMA/CNT-Br and PCHMA-CNT
| Sample |
Φ
CNT
|
ω
0 [rad s−1] |
R [Ω m] |
β
|
| PCHMA/CNT-Br |
0.020 |
8.2 × 10−1 |
1.9 × 109 |
0.69 |
| |
0.055 |
6.6 × 101 |
1.2 × 107 |
0.72 |
| |
0.094 |
1.3 × 104 |
3.3 × 104 |
0.70 |
| |
0.143 |
2.0 × 106 |
1.8 × 102 |
0.72 |
| PCHMA-CNT |
0.112 |
8.2 × 10−2 |
7.2 × 109 |
0.72 |
| |
0.124 |
6.3 × 100 |
1.1 × 108 |
0.71 |
| |
0.143 |
1.2 × 103 |
6.4 × 105 |
0.68 |
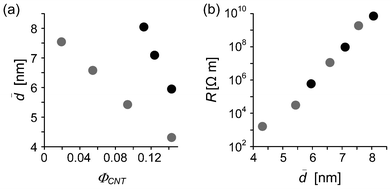 |
| | Fig. 4 Relationships of the average internanotube distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) for two types of nanocomposites to (a) ΦCNT and (b) R. Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT. for two types of nanocomposites to (a) ΦCNT and (b) R. Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT. | |
The apparent enhanced capacitance implies an increase in ε′r. Fig. 5 shows frequency dependence of ε′r and ε′′r of PCHMA/CNT-Br and PCHMA-CNT in the wide range of 10−2–108 Hz. For PCHMA/CNT-Br, ε′r and ε′′r are significantly increased with the decrease in f. These behaviors of ε′r and ε′′r at the lower frequencies than ω0 were consistent with the theoretical curves calculated from eqn (2).
| | | ε′r = sin(πβ/2)/Rε0ω0βω1−β + ε′r∞, | (4) |
| | | ε′′r = 1/Rε0ω + cos(πβ/2)/Rε0ω0βω1−β, | (5) |
where
ε′
r∞ is the dielectric constant at infinite frequency. At the higher frequencies than
ω0, however,
eqn (4) and (5) were not consistent with the experimental spectra (ESI
†). This could be attributed to negligible tunneling conduction, because −
Xcp of the
polymer bulk between the CNTs is lower than
Rt at the higher frequencies than
ω0. In other words, the electric current is mainly passed through the
polymer matrix, not through the tunneling conduction.
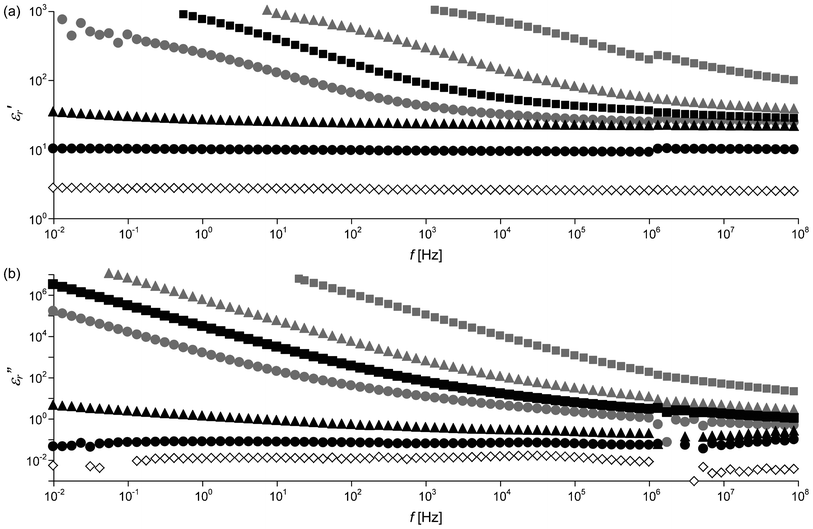 |
| | Fig. 5
f dependence of (a) dielectric constant ε′r and (b) dielectric loss factor ε′′r of PCHMA (diamonds) and two types of nanocomposites with ΦCNT = 0.055 (circles), ΦCNT = 0.094 (triangles), and ΦCNT = 0.14 (squares). Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT. | |
From the obtained results mentioned above, the relaxation related to the tunneling conduction at the microcapacitor is understood as follows. At the much higher frequencies than ω0, Z of the polymer bulk determines the overall Z of the composite because −Xcp of the polymer matrix between the CNTs is much lower than Rt. Therefore, the tunneling conduction can be ignored. As the −Xcp is increased with the decrease in f, the −Xcp becomes equal to Rt. The microcapacitors with the smaller d (with the smaller Rt) are electrically connected by the tunneling conduction. These short circuits give the system the apparent enhanced capacitance because the electric field becomes concentrated only at the residual microcapacitors with longer d. Finally, at the much lower frequencies than ω0, Rt of the microcapacitor with the longest d dominates Rp, resulting in no frequency dependence of Rp (= R). In many previous studies on polymer/CNT nanocomposites, the very large ε′r at low frequencies has been attributed to space charge polarization and/or interface polarization between the CNT and the polymer matrix.13,14,17,18,23 Therefore, it has also been suggested that the interaction at the polymer/CNT interface and the dispersivity of the CNT in the polymer matrix are important for the enhancement in ε′r.13,16,18,19,23 However, the discrepant phenomena have been found for our PCHMA-CNT system. ε′r of PCHMA-CNT with ΦCNT = 0.055 is almost independent of f even at the low frequency although the dispersivity of the CNT is surprisingly good (Fig. 1c). Furthermore, the polymer/CNT interface should be strong because of polymer grafting. On the other hand, PCHMA-CNT with ΦCNT = 0.14, where the tunneling conduction is observed, exhibits very large ε′r at the low frequencies, as previously reported. As a result, we suggest that the increase in ε′r should result from not the interface polarization and/or the space charge polarization but the apparently enhanced capacitance by locally amplified electric field mentioned above. This explanation is consistent with no increase in ε′r at the low frequencies for PCHMA-CNT with ΦCNT = 0.055. Also, this electric field enhancement effect can account for the increase in ε′r∞ of the polymer/CNT composites relative to the neat polymer (ESI†). In this case, the electric field enhancement originates from the heterogeneity of the polymer/CNT composite regardless of the tunneling conduction. In other words, a large electric field fluctuation originally exists in the polymer/CNT composites. The field fluctuations in composite materials have been demonstrated using simulated methods.39,40
For the PCHMA/CNT-Br system, Rp is usually much smaller than −Xcp, suggesting that the microcapacitor is a resistor rather than a capacitor, i.e., it is a conductor. In contrast, PCHMA-CNTs with ΦCNT = 0.055 and 0.094 have very low ε′′r in all the frequency range (Fig. 5b). This is because d is large enough to prevent the tunneling conduction. ε′r and the dissipation factor (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = ε′′r/ε′r) of PCHMA/CNT-Br and PCHMA-CNT at 1 MHz are plotted in Fig. 6. For PCHMA-CNT, tan
δ = ε′′r/ε′r) of PCHMA/CNT-Br and PCHMA-CNT at 1 MHz are plotted in Fig. 6. For PCHMA-CNT, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is below 0.01 when ΦCNT is less than 0.1. At ΦCNT = 0.094, ε′r of 22.5 and tan
δ is below 0.01 when ΦCNT is less than 0.1. At ΦCNT = 0.094, ε′r of 22.5 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of 0.010 are obtained. This tan
δ of 0.010 are obtained. This tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value is small even compared with low-loss polymer/CNT composites that have been reported.19–23 The dielectric property of the low-loss PCHMA-CNT is comparable to that of PCHMA filled with barium titanate (PCHMA/BT). In Fig. 7a, the plots of log
δ value is small even compared with low-loss polymer/CNT composites that have been reported.19–23 The dielectric property of the low-loss PCHMA-CNT is comparable to that of PCHMA filled with barium titanate (PCHMA/BT). In Fig. 7a, the plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε′rversus ΦCNT and ΦBT show linear relationships for both the composites. The slope of the relationship for PCHMA-CNT is five times larger than those for PCHMA/BT, implying the CNT has higher electric field enhancement effect than the BT owing to the high aspect ratio of the CNT.39 This finding is a major advantage of PCHMA-CNT over PCHMA/BT for polymer material design. According to Fig. 7a, if ε′r of PCHMA-CNT is enhanced by about ten times, it can be achieved with only 10 vol% of the CNT. In addition, tan
ε′rversus ΦCNT and ΦBT show linear relationships for both the composites. The slope of the relationship for PCHMA-CNT is five times larger than those for PCHMA/BT, implying the CNT has higher electric field enhancement effect than the BT owing to the high aspect ratio of the CNT.39 This finding is a major advantage of PCHMA-CNT over PCHMA/BT for polymer material design. According to Fig. 7a, if ε′r of PCHMA-CNT is enhanced by about ten times, it can be achieved with only 10 vol% of the CNT. In addition, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of PCHMA-CNT is as low as that of PCHMA/BT (Fig. 7b), and PCHMA-CNT has smaller frequency dependence of the dielectric properties than PCHMA/BT (Fig. 7c). For PCHMA/BT, due to the dielectric relaxation related to the BT particle, tan
δ of PCHMA-CNT is as low as that of PCHMA/BT (Fig. 7b), and PCHMA-CNT has smaller frequency dependence of the dielectric properties than PCHMA/BT (Fig. 7c). For PCHMA/BT, due to the dielectric relaxation related to the BT particle, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is much increased at the low frequencies.
δ is much increased at the low frequencies.
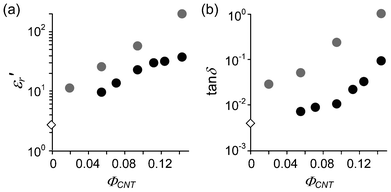 |
| | Fig. 6 (a) ε′r and (b) dissipation factor (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of PCHMA (diamonds) and two types of nanocomposites (circles) at 1 MHz as a function of ΦCNT. Gray circles, PCHMA/CNT-Br; black circles, PCHMA-CNT. δ) of PCHMA (diamonds) and two types of nanocomposites (circles) at 1 MHz as a function of ΦCNT. Gray circles, PCHMA/CNT-Br; black circles, PCHMA-CNT. | |
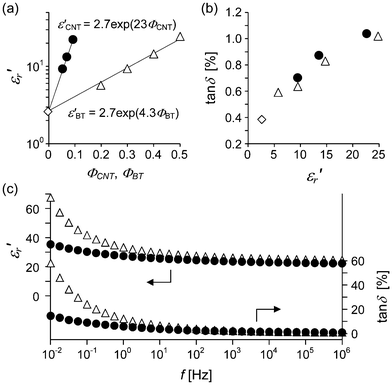 |
| | Fig. 7 Comparison of dielectric properties between PCHMA-CNT (black circle) and PCHMA/BT (white triangles). (a) ε′r as a function of ΦCNT and ΦBT, and (b) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ/ε′r plot at 1 MHz. The values for PCHMA are plotted with diamond symbols. (c) f dependence of ε′r and tan δ/ε′r plot at 1 MHz. The values for PCHMA are plotted with diamond symbols. (c) f dependence of ε′r and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of PCHMA-CNT with ΦCNT = 0.094 and PCHMA/BT with ΦBT = 0.50. δ of PCHMA-CNT with ΦCNT = 0.094 and PCHMA/BT with ΦBT = 0.50. | |
In summary, the dielectric properties of PCHMA-CNT were systematically characterized by focusing on the tunneling conduction. When ΦCNT < 0.1, PCHMA-CNT exhibited relatively high ε′r and quite low ε′′r, while when ΦCNT > 0.1, a very large ε′r was observed at low frequencies. The Cole–Cole relaxation model was applied to the impedance spectra of PCHMA-CNT, and from the obtained relaxation frequencies, the average internanotube distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) in the PCHMA-CNT system was estimated. The relationship between
in the PCHMA-CNT system was estimated. The relationship between ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and the resistance R of PCHMA-CNT strongly supports the tunnneling conduction that occurs in the PCHMA-CNT system when ΦCNT > 0.1. As a result, a new mechanism is proposed for the very large ε′r; the locally enhanced electric field by the tunneling conduction results in the very large ε′r at the low frequencies along with the increase in ε′′r. Furthermore, we have demonstrated that the CNT is five times more effective than the BT for the enhancement in ε′r of polymer materials because of the higher electric field enhancement effect of the CNT than that of the BT.
and the resistance R of PCHMA-CNT strongly supports the tunnneling conduction that occurs in the PCHMA-CNT system when ΦCNT > 0.1. As a result, a new mechanism is proposed for the very large ε′r; the locally enhanced electric field by the tunneling conduction results in the very large ε′r at the low frequencies along with the increase in ε′′r. Furthermore, we have demonstrated that the CNT is five times more effective than the BT for the enhancement in ε′r of polymer materials because of the higher electric field enhancement effect of the CNT than that of the BT.
Experimental
Sample preparation
MWCNTs with an average diameter and length of 10 nm and 1.5 μm, respectively, were obtained from Nanocyl SA. ATRP-initiator-modified MWCNT (CNT-Br) was synthesized as reported previously.29 For the synthesis of PCHMA-CNT, the surface-initiated polymerization was carried out. For example, N,N-dimethylacetamide (DMAc) (20 ml) was added to CNT-Br (0.188 g) and CuBr (7.2 mg, 50 μmol) in a vacuum. After sonication of the mixture, 2,2′-bipyridyl (bpy) (15.6 mg, 100 μmol) in cyclohexyl methacrylate (10 ml, CHMA) was added, and the solution was kept at 60 °C for 6 h. The resultant polymer mixture was precipitated in methanol and freeze-dried by benzene. Conventional nanocomposites (PCHMA/CNT, PCHMA/CNT-Br and PCHMA/BT) were prepared by blending PCHMA with CNT, CNT-Br, or BT, where BT particle with an average size of less than 100 nm (Aldrich) was used. First, the PCHMA and the CNTs or the BT were added in benzene and dispersed by sonication. The dispersion was quickly frozen by liquid nitrogen, and then freeze-dried under vacuum. Thus-obtained composite samples were crushed into powders. These nanocomposite samples were molded into 15 mm square specimens with a thickness of ∼0.9 mm by compression of 10 MPa at 130 °C. For impedance measurements in the frequency range of 10−2–106 Hz, two gold electrodes 11 mm square were deposited on the top and bottom of the specimen at a distance of 2 mm from the edge of the specimen.
Measurements
The specimens were observed using a scanning electron microscope (JEOL, JEM-2100F) operated at an accelerating voltage of 2 kV. For impedance measurement, three types of impedance analyzers, Solartron 126096W, Agilent E4980A, and Agilent E4991A, were used depending on the frequency range, 10−2–102 Hz, 102–106 Hz, and 106–108 Hz, respectively.
Acknowledgements
SEM observations were carried out by Ms Yoriko Matsuoka at Toyota Central R&D Labs Inc., and impedance measurement was supported by Dr Kensuke Wada at Toyota Central R&D Labs Inc. The author appreciates their help.
References
-
H. Nalwa, Handbook of Low and High Dielectric Constant Materials and Their Applications, Academic Press, London, UK, 1999 Search PubMed.
- P. Brochu and Q. B. Pei, Macromol. Rapid Commun., 2010, 31, 10 CrossRef CAS.
- S. Risse, B. Kussmaul, H. Krüger and G. Kofod, Adv. Funct. Mater., 2011, 21, 4589 CrossRef.
- B. Kussmaul, S. Risse, G. Kofod, R. Wache, M. Wegener, D. N. McCarthy, H. Krüger and R. Gerhard, RSC Adv., 2012, 2, 9029 RSC.
- S. C. B. Mannfleld, B. C.-K. Tee, R. M. Stoltenberg, C. V. H.-H. Chen, S. Barman, B. V. O. Muir, A. N. Sokolov, C. Reese and Z. Bao, Nat. Mater., 2010, 9, 859 CrossRef.
- D. J. Cohen, D. Mitra, K. Peterson and M. M. Maharbiz, Nano Lett., 2012, 12, 1821 CrossRef CAS.
- H. M. Jung, J.-H. Kang, S. Y. Yang, J. C. Won and Y. S. Kim, Chem. Mater., 2010, 22, 450 CrossRef CAS.
- M.-F. Lin, V. K. Thakur, E. J. Tan and P. S. Lee, RSC Adv., 2011, 1, 576 RSC.
- L. Xie, X. Huang, C. Wu and P. Jiang, J. Mater. Chem., 2011, 21, 5897 RSC.
- Z.-M. Dang, J.-K. Yuan, J.-W. Zha, T. Zhou, S.-T. Li and G.-H. Hu, Prog. Mater. Sci., 2012, 57, 660 CrossRef CAS.
- Y. Song, Y. Shen, H. Liu, Y. Lin, M. Li and C.-W. Nan, J. Mater. Chem., 2012, 22, 16491 RSC.
- L. Wang and Z.-M. Dang, Appl. Phys. Lett., 2005, 87, 042903 CrossRef.
- Z.-M. Dang, L. Wang, Y. Yin, Q. Zhang and Q.-Q. Lei, Adv. Mater., 2007, 19, 852 CrossRef CAS.
- J. Zhang, M. Mine, D. Zhu and M. Matsuo, Carbon, 2009, 47, 1311 CrossRef CAS.
- J. Fritzsche, H. Lorenz and M. Klüppel, Macromol. Mater. Eng., 2009, 294, 551 CrossRef CAS.
- R. R. Kohlmeyer, A. Javadi, B. Pradhan, S. Pilla, K. Setyowati, J. Chen and S. Gong, J. Phys. Chem. C, 2009, 113, 17626 CAS.
- Z.-M. Dang, S.-H. Yao, J.-K. Yuan and J. Bai, J. Phys. Chem. C, 2010, 114, 13204 CAS.
- J.-K. Yuan, S.-H. Yao, Z.-M. Dang, A. Sylvestre, M. Genestorux and J. Bai, J. Phys. Chem. C, 2011, 115, 5515 CAS.
- T. Zhou, J.-W. Zha, Y. Hou, D. Wang, J. Zhao and Z.-M. Dang, ACS Appl. Mater. Interfaces, 2011, 3, 4557 CAS.
- H. Wu, A. Gu, G. Liang and L. Yuan, J. Mater. Chem., 2011, 21, 14838 RSC.
- J. Chang, G. Liang, A. Gu, S. Cai and L. Yuan, Carbon, 2012, 50, 689 CrossRef CAS.
- C. Yang, Y. Lin and C.-W. Nan, Carbon, 2009, 47, 1096 CrossRef CAS.
- H. Liu, Y. Shen, Y. Song, C.-W. Nan, Y. Lin and X. Yang, Adv. Mater., 2011, 23, 5104 CrossRef CAS.
- J. N. Coleman, U. Khan and Y. K. Gun'ko, Adv. Mater., 2006, 18, 689 CrossRef CAS.
- J. Li, P. C. Ma, W. S. Chow, C. K. To, B. Z. Tang and J. K. Kim, Adv. Funct. Mater., 2007, 17, 3207 CrossRef CAS.
- Z. Spitalsky, D. Tasis, K. Paragelis and G. Costas, Prog. Polym. Sci., 2010, 35, 357 CrossRef CAS.
- B. E. Kilbride, J. N. Coleman, J. Fraysse, P. Fournet, M. Cadek, A. Drury, S. Hutzler, S. Roth and W. J. Blau, J. Appl. Phys., 2002, 92, 4024 CrossRef CAS.
- H.-C. Li, S.-Y. Lu, S.-H. Syue, W.-K. Hsu and S.-C. Chang, Appl. Phys. Lett., 2008, 93, 033104 CrossRef.
- K. Hayashida and H. Tanaka, Adv. Funct. Mater., 2012, 22, 2338 CrossRef CAS.
- Z. Yao, N. Bradiy, G. A. Botton and A. Adronov, J. Am. Chem. Soc., 2003, 125, 16015 CrossRef CAS.
- D. Baskaran, J. W. Mays and M. S. Bratcher, Angew. Chem., Int. Ed., 2004, 43, 2138 CrossRef CAS.
- S. Qin, D. Qin, W. T. Ford, D. E. Resasco and J. E. Herrera, Macromolecules, 2004, 37, 752 CrossRef CAS.
- H. Kong, C. Gao and D. Yan, Macromolecules, 2004, 37, 4022 CrossRef CAS.
- K. Hayashida, H. Tanaka and O. Watanabe, Polymer, 2009, 50, 6228 CrossRef CAS.
- K. Hayashida, H. Tanaka and O. Watanabe, Polym. Int., 2011, 60, 1194 CrossRef CAS.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- J. G. Meier, J. W. Mani and M. Klüppel, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054202 CrossRef.
- P. Sheng, E. K. Sichel and J. I. Gittleman, Phys. Rev. Lett., 1978, 40, 1197 CrossRef CAS.
- H. Cheng and S. Torquato, Phys. Rev. B: Condens. Matter, 1997, 56, 8060 CrossRef CAS.
- J. Y. Li, C. Huang and Q. Zhang, Appl. Phys. Lett., 2004, 84, 3124 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Characteristics of a series of PCHMA-CNTs, SEM and TEM images of PCHMA-CNT, Cole–Cole plots of the impedance spectra, comparison between the experimental and theoretical spectra, and mechanism of the increase ε′r in the polymer/CNT system. See DOI: 10.1039/c2ra22164k |
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 190
000 to 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 are listed in the ESI.† Conventional nanocomposites (PCHMA/CNT and PCHMA/CNT-Br) were designed to have the same volume fraction of CNT, ΦCNT, as PCHMA-CNT. In the blending procedure, a preliminary blending method using freeze-drying was used in order to obtain as good dispersion of the CNTs as possible.35 These nanocomposite samples were molded by compression of 10 MPa at 130 °C prior to electrical measurements. The dispersivity of the CNT in the polymer matrix for the three types of nanocomposites thus produced was observed using a scanning electron microscope (SEM). In this observation, the surfaces of the nanocomposites had been slightly etched with oxygen plasma in order that the PCHMA polymer on the surface was removed. Fig. 1 shows SEM images of the nanocomposites with ΦCNT = 0.055. For PCHMA/CNT and PCHMA/CNT-Br, the CNTs are inhomogeneously dispersed at a submicron scale. This inhomogeneity is typical of polymer/CNT composites prepared by blending, owing to the poor polymer/CNT compatibility. In contrast, the dispersivity of the CNT is surprisingly good for PCHMA-CNT. In the PCHMA-CNT system, the PCHMA matrix cannot be separated from the CNT because all the PCHMA chains are tethered on the CNT. The excellent CNT dispersivity for PCHMA-CNT is also confirmed by an SEM image with low magnification (ESI†). We suggest polymer-grafting should be the best method of producing the perfectly homogeneous dispersion of CNT in a polymer matrix.
000 are listed in the ESI.† Conventional nanocomposites (PCHMA/CNT and PCHMA/CNT-Br) were designed to have the same volume fraction of CNT, ΦCNT, as PCHMA-CNT. In the blending procedure, a preliminary blending method using freeze-drying was used in order to obtain as good dispersion of the CNTs as possible.35 These nanocomposite samples were molded by compression of 10 MPa at 130 °C prior to electrical measurements. The dispersivity of the CNT in the polymer matrix for the three types of nanocomposites thus produced was observed using a scanning electron microscope (SEM). In this observation, the surfaces of the nanocomposites had been slightly etched with oxygen plasma in order that the PCHMA polymer on the surface was removed. Fig. 1 shows SEM images of the nanocomposites with ΦCNT = 0.055. For PCHMA/CNT and PCHMA/CNT-Br, the CNTs are inhomogeneously dispersed at a submicron scale. This inhomogeneity is typical of polymer/CNT composites prepared by blending, owing to the poor polymer/CNT compatibility. In contrast, the dispersivity of the CNT is surprisingly good for PCHMA-CNT. In the PCHMA-CNT system, the PCHMA matrix cannot be separated from the CNT because all the PCHMA chains are tethered on the CNT. The excellent CNT dispersivity for PCHMA-CNT is also confirmed by an SEM image with low magnification (ESI†). We suggest polymer-grafting should be the best method of producing the perfectly homogeneous dispersion of CNT in a polymer matrix.



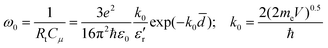
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) calculated using the potential height of 0.2 eV38 and ε′r of 2.7 is plotted in Fig. 4.
calculated using the potential height of 0.2 eV38 and ε′r of 2.7 is plotted in Fig. 4. ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) decreases with the increase in ΦCNT (Fig. 4a), which is reasonable and consistent with a previous result that has been reported by Klüppel et al.15 It is more important that R is exponentially increased with the increase in
decreases with the increase in ΦCNT (Fig. 4a), which is reasonable and consistent with a previous result that has been reported by Klüppel et al.15 It is more important that R is exponentially increased with the increase in ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) at such nanometer scale (Fig. 4b), which is well-known as a quantum effect. This fact means that if many microcapacitors with different d are connected in a series like a real composite system, the applied voltage is concentrated at some of the microcapacitors with the longest d; in a series circuit, the applied voltage is distributed to the microcapacitors in proportion to their tunneling resistance Rt. This locally amplified electric field would give an apparent increase in the total capacitance of the composite. In the case of the corresponding macroscale capacitors, the electric field is not amplified because the resistance is proportional to the gap width between the electrodes.
at such nanometer scale (Fig. 4b), which is well-known as a quantum effect. This fact means that if many microcapacitors with different d are connected in a series like a real composite system, the applied voltage is concentrated at some of the microcapacitors with the longest d; in a series circuit, the applied voltage is distributed to the microcapacitors in proportion to their tunneling resistance Rt. This locally amplified electric field would give an apparent increase in the total capacitance of the composite. In the case of the corresponding macroscale capacitors, the electric field is not amplified because the resistance is proportional to the gap width between the electrodes.

![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) for two types of nanocomposites to (a) ΦCNT and (b) R. Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT.
for two types of nanocomposites to (a) ΦCNT and (b) R. Gray symbols, PCHMA/CNT-Br; black symbols, PCHMA-CNT.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = ε′′r/ε′r) of PCHMA/CNT-Br and PCHMA-CNT at 1 MHz are plotted in Fig. 6. For PCHMA-CNT, tan
δ = ε′′r/ε′r) of PCHMA/CNT-Br and PCHMA-CNT at 1 MHz are plotted in Fig. 6. For PCHMA-CNT, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is below 0.01 when ΦCNT is less than 0.1. At ΦCNT = 0.094, ε′r of 22.5 and tan
δ is below 0.01 when ΦCNT is less than 0.1. At ΦCNT = 0.094, ε′r of 22.5 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of 0.010 are obtained. This tan
δ of 0.010 are obtained. This tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value is small even compared with low-loss polymer/CNT composites that have been reported.19–23 The dielectric property of the low-loss PCHMA-CNT is comparable to that of PCHMA filled with barium titanate (PCHMA/BT). In Fig. 7a, the plots of log
δ value is small even compared with low-loss polymer/CNT composites that have been reported.19–23 The dielectric property of the low-loss PCHMA-CNT is comparable to that of PCHMA filled with barium titanate (PCHMA/BT). In Fig. 7a, the plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε′rversus ΦCNT and ΦBT show linear relationships for both the composites. The slope of the relationship for PCHMA-CNT is five times larger than those for PCHMA/BT, implying the CNT has higher electric field enhancement effect than the BT owing to the high aspect ratio of the CNT.39 This finding is a major advantage of PCHMA-CNT over PCHMA/BT for polymer material design. According to Fig. 7a, if ε′r of PCHMA-CNT is enhanced by about ten times, it can be achieved with only 10 vol% of the CNT. In addition, tan
ε′rversus ΦCNT and ΦBT show linear relationships for both the composites. The slope of the relationship for PCHMA-CNT is five times larger than those for PCHMA/BT, implying the CNT has higher electric field enhancement effect than the BT owing to the high aspect ratio of the CNT.39 This finding is a major advantage of PCHMA-CNT over PCHMA/BT for polymer material design. According to Fig. 7a, if ε′r of PCHMA-CNT is enhanced by about ten times, it can be achieved with only 10 vol% of the CNT. In addition, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of PCHMA-CNT is as low as that of PCHMA/BT (Fig. 7b), and PCHMA-CNT has smaller frequency dependence of the dielectric properties than PCHMA/BT (Fig. 7c). For PCHMA/BT, due to the dielectric relaxation related to the BT particle, tan
δ of PCHMA-CNT is as low as that of PCHMA/BT (Fig. 7b), and PCHMA-CNT has smaller frequency dependence of the dielectric properties than PCHMA/BT (Fig. 7c). For PCHMA/BT, due to the dielectric relaxation related to the BT particle, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is much increased at the low frequencies.
δ is much increased at the low frequencies.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of PCHMA (diamonds) and two types of nanocomposites (circles) at 1 MHz as a function of ΦCNT. Gray circles, PCHMA/CNT-Br; black circles, PCHMA-CNT.
δ) of PCHMA (diamonds) and two types of nanocomposites (circles) at 1 MHz as a function of ΦCNT. Gray circles, PCHMA/CNT-Br; black circles, PCHMA-CNT.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ/ε′r plot at 1 MHz. The values for PCHMA are plotted with diamond symbols. (c) f dependence of ε′r and tan
δ/ε′r plot at 1 MHz. The values for PCHMA are plotted with diamond symbols. (c) f dependence of ε′r and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of PCHMA-CNT with ΦCNT = 0.094 and PCHMA/BT with ΦBT = 0.50.
δ of PCHMA-CNT with ΦCNT = 0.094 and PCHMA/BT with ΦBT = 0.50.![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) in the PCHMA-CNT system was estimated. The relationship between
in the PCHMA-CNT system was estimated. The relationship between ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and the resistance R of PCHMA-CNT strongly supports the tunnneling conduction that occurs in the PCHMA-CNT system when ΦCNT > 0.1. As a result, a new mechanism is proposed for the very large ε′r; the locally enhanced electric field by the tunneling conduction results in the very large ε′r at the low frequencies along with the increase in ε′′r. Furthermore, we have demonstrated that the CNT is five times more effective than the BT for the enhancement in ε′r of polymer materials because of the higher electric field enhancement effect of the CNT than that of the BT.
and the resistance R of PCHMA-CNT strongly supports the tunnneling conduction that occurs in the PCHMA-CNT system when ΦCNT > 0.1. As a result, a new mechanism is proposed for the very large ε′r; the locally enhanced electric field by the tunneling conduction results in the very large ε′r at the low frequencies along with the increase in ε′′r. Furthermore, we have demonstrated that the CNT is five times more effective than the BT for the enhancement in ε′r of polymer materials because of the higher electric field enhancement effect of the CNT than that of the BT.