Phase evolution and oxide ion conduction behavior of Dy_1−xBi_xO_1.5 (0.00 ≤ x ≤ 0.50) composite system

Abstract

A series of Dy_1−xBi_xO_1.5 (0.00 ≤ x ≤ 0.50) compositions were prepared by conventional solid state reactions of Bi₂O₃ and Dy₂O₃. X-ray diffractometry, ac-impedance spectroscopy and scanning electron microscopy were used to characterize the structure and properties of these compositions. All the compositions except x = 0.44 exist as composites of either rhombohedral and C-type rare-earth oxide phases or rhombohedral and fluorite type phases. At x = 0.44, a rhombohedral phase is observed which can broadly be explained on a sub cell with unit cell parameters: a_sub = 3.7728(1) Å and c_sub = 9.5541(5) Å, V = 117.77(1) ų, Z = 3. The exact structure is a super lattice of this unit cell. The unit cell of the super- and sub structures are related as: a_super = b_super ∼ 4 × a_sub and c_super ∼ 2 × c_sub. The studied Bi₂O₃–Dy₂O₃ systems showed an oxide anionic conductivity and the conductivity increases with the increase in Bi concentration as well as temperature. Typical activation energies of all compositions are within 1.1 to 1.2 eV. At 800 K, the highest conductivity is observed for the composition Dy_0.50Bi_0.50O_1.50 in the series. The observed maximum conductivity is lower than δ-Bi₂O₃, but significantly higher than the stabilized zirconia.

---

I Introduction

Bi₂O₃ and cation substituted Bi₂O₃ have been of interest for a long time due to their high oxide ion conductivity at relatively lower temperature compared to many other known oxide ion conductors.^1–3 For example, Bi₂O₃ shows conductivity two orders of magnitude higher than zirconia–based electrolytes such as yttria stabilized ZrO₂ (YSZ) at relatively lower temperatures.² At ambient temperature, Bi₂O₃ exists in monoclinic (α) form and transforms to cubic (δ) fluorite type structure above 1003 K which exhibit significantly higher oxide ion conductivity. The fluorite type δ phase remains stable from 1003 K to its melting temperature (1098 K). Besides, on cooling the δ phase transforms to α- phase through several intermediate phases. Depending on the temperature, heating and cooling procedures, a number of polymorphs, namely β, γ, δ, ε and ω etc have been reported in literature.^1,4 Due to the potential of δ-Bi₂O₃ as electrolytes in solid oxide fuel cells (SOFC) and oxygen sensors,^5,6 major research attention has been focused on its stabilization and conduction behavior. It has been concluded that a partial substitution of Bi³⁺ by iso- or heterovalent cations can stabilize the δ-Bi₂O₃ phase at ambient temperature.^1,2 In particular, the rare-earth doped Bi₂O₃ has been more extensively studied due to the similar charge and properties of Bi³⁺ and Ln³⁺.^6–10 A number of structural studies have been carried out to understand the origin of the high oxygen ion conduction behavior of such stabilized δ phase. The high oxygen ion conduction behavior of δ-Bi₂O₃ has been explained on the basis of significant amounts of intrinsic oxygen vacancies and asymmetric arrangements of anions due to the lone pair (6s²) of Bi³⁺ ions.^2,11

Despite the superior ion conduction properties, the lower structural stability and higher reactivity of Bi₂O₃ remained a limitation for their practical usage in SOFCs. Similar to the ceria based electrolytes, the Bi₂O₃ based electrolytes are unstable under reducing environments. Even at 600 °C, a rapid degradation of electrolyte has been observed at an oxygen partial pressure (p_O2) of about 10⁻¹³ atm.¹² In order to overcome the problem of reduction induced degradation of electrolytes, the concept of using a thin layer of stable oxide ion conductors like YSZ to avoid the direct contact of electrolyte and fuel has been proposed. However such an approach can not prevent the reaction of the electrolytes which leads to several undesirable phases of Bi₂O₃ and ZrO₂.^13,14 Thus the practical electrolytes should have a reduced contribution from the reactive Bi₂O₃; a possible approach is to develop newer electrolytes with Bi deficient compositions. In order to attain such electrolytes, the Bi deficient compositions in the Bi₂O₃–Ln₂O₃ (Ln = Lanthanides) can be considered as potential candidates. In such Bi deficient systems, several ordered lattices with open channels for oxygen migration have been reported.^14,15 The ordering of cations and anions impart more structural and chemical stability compared to the δ-Bi₂O₃ phases. In an optimum concentration of Bi₂O₃, a significant improvement in the stability at the expense of partial loss of conductivity can thus be achieved. In order to study the potential of Bi₂O₃ deficient compositions as electrolytes, we have investigated the phase evolution and conductivity properties in Dy_1−xBi_xO_1.5 (0.0 ≤ x ≤ 0.50) system. The details of structural changes and oxygen ion conductivity of this system are explained in this manuscript.

II Experimental

A series of compositions with stoichiometry Dy_1−xBi_xO_1.50 (0.00 ≤ x ≤ 0.50) were prepared by solid state reaction of appropriate amounts of component binary oxides (Dy₂O₃, 99.9%, Aldrich, Bi₂O₃, 99.9%, Aldrich). In order to remove any carbonate, hydroxide and adsorbed water molecules in the starting materials, Dy₂O₃ and Bi₂O₃ were heated at 1073 and 773 K, respectively. Appropriate amounts of Bi₂O₃ and Dy₂O₃ were thoroughly homogenized and pressed into pellets of 1 cm diameter and 2 to 3 mm height. The pellets were heated at 973 K for 24 h in platinum crucible. The pellets were re-homogenized, pelletized and then sintered at 1173 K for 24 h. The sintered products were characterized by powder XRD patterns recorded on a Panalytical Powder X-ray diffractometer (X'Pert-Pro) using monochromatic Cu-Kα radiation. The observed powder XRD data were analyzed by Rietveld refinements using Fullprof2000 and GSAS software packages.^16,17 The microstructures of the sintered samples were studied using scanning electron microscopy (Mini-SEM, Model SNE 3000M). For impedance study, the parallel faces of cylindrical sintered pellets were coated with platinum paste. The impedance measurements were carried in the frequency range of 0.1 Hz to 10 MHz using a Solartron impedance analyzer (Model 1290). The impedance data were collected while cooling the sample from 973 K.

III Results and discussions

The powder XRD patterns of all the sintered samples are depicted in Fig. 1. The powder XRD data of one end member, x = 0.00 (i.e. Dy₂O₃), shows the characteristic reflection of cubic C-type rare-earth oxide lattice. All the observed reflections could be indexed on the body centered cubic lattice with unit cell parameter a = 10.6606(2) Å, which is in agreement with that reported earlier for Dy₂O₃ (JCPDS-PDF: 43-1006). As the Bi³⁺ content in the nominal composition Dy_1−xBi_xO_1.5 increases, several new reflections in addition to the reflections attributable to Dy₂O₃ but different from the Bi₂O₃ have appeared. With the increase in Bi concentration, a systematic increase in intensity of the reflections of the new phase with a concomitant decrease in intensity of the reflections of Dy₂O₃ type phase was observed. The reflections attributable to the Dy₂O₃ type phase observed in different nominal compositions were indexed on similar body centered cubic lattices and the refined unit cell parameters are given in Table 1. Further details of the phases were obtained from the analyses of the unit cell parameters and refinement of the powder XRD data.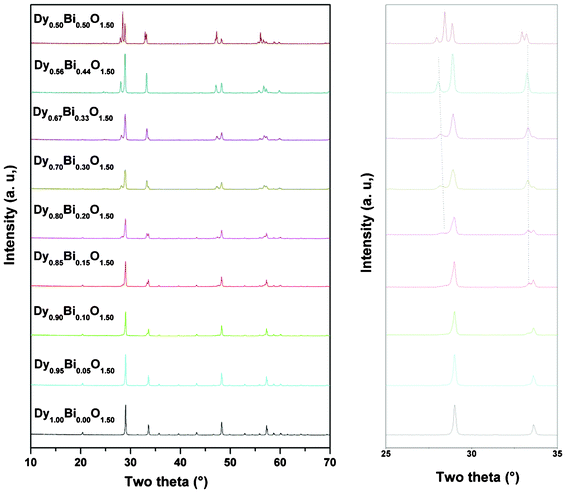

Fig. 1 Powder XRD patterns of nominal compositions Dy_1−xBi_xO_1.5.

Table 1 Details of phase analysis of Dy_1−xBi_xO_1.5 system

x	Nominal compositions	Phases identified
			a/Å	c/Å	V (Å)^3	Z
a C = Cubic C-type rare-earth oxides type. b R = Rhombohedral. c F = δ-Bi2O3 type (fluorite). d * Not determined due to very weak reflections.
0.00	Dy1.00Bi0.00O1.50	C^a	10.6606(2)	-	1211.57(3)	32
0.05	Dy0.95Bi0.05O1.50	C^b	10.6630(2)	-	1212.39(4)	32
		R	*^d	-	-	3
0.10	Dy0.90Bi0.10O1.50	C	10.6639(2)	-	1212.67(4)	32
		R	*	-	-	3
0.15	Dy0.85Bi0.15O1.50	C	10.6644(2)	-	1212.87(4)	32
		R	3.7817(3)	3.4080(10)	116.52(2)	3
0.20	Dy0.80Bi0.20 O1.50	C	10.6619(3)	-	1212.01(5)	32
		R	3.7780(3)	9.4773(9)	117.15(2)	3
0.30	Dy0.70Bi0.30 O1.50		10.6629(5)	-	1212.36(10)	32
		R	3.77C58(2)	9.4912(7)	117.19(1)	3
0.33	Dy0.67Bi0.33O1.50	C	10.6612(7)	-	1211.78(13)	32
		R	3.7744(2)	9.4914(8)	117.10(1)	3
0.44	Dy0.66Bi0.44O1.50	R	3.7728(1)	9.5541(6)	117.77(1)	3
0.50	Dy0.50Bi0.50O1.50	R	3.7722(2)	9.5713(7)	117.95(1)	3
		F^c	5.4366(3)	-	160.69(1)	4

---

From the XRD data and unit cell parameters of C-type phases in the studied compositions, it is observed that the unit cell parameter has an increasing trend with the increasing values of x in Dy_1−xBi_xO_1.5, up to x = 0.15. This suggests that Bi³⁺ is partially incorporated in the Dy₂O₃ lattice. However, the non linear variation of the unit cell parameter suggests a possible inter-diffusion Bi³⁺ ion in between the two coexisting phases leading to a variable concentration of Bi³⁺ ion incorporation in them.

The crystal structure and crystal chemistry of A₂O₃ type sesquioxides have been a subject of research interest for a long time. It has been well understood that the structure is mainly governed from the ionic radii of the A³⁺ ion.¹⁸ A₂O₃ compositions with r_A³⁺ ≤ 0.7 Å, mainly crystallize in the corundum type structure where the trivalent cations form ideal octahedra. However, compounds with larger r_A³⁺ crystallize in various rare-earth oxide type structures, where the cations have distorted octahedral or seven or eight fold coordination. These structures can be grouped to three categories, namely hexagonal (A-type), monoclinic (B-type), and cubic (C-type).¹⁹ In addition, several other distinct structure types have been observed in various A₂O₃ type compounds. Depending on the composition and external variables such as pressure or temperature, a number of structural variants are known and they have been recently reviewed by Manjon and Errandonea.²⁰ The structure of lighter rare-earth oxides have cubic lattice (C-type) which is closely related to the fluorite type lattice with ¼ of oxygen sites vacant. The ordered arrangement of the vacancies leads to two different site symmetries for the cations, which lower the symmetry of the lattice from cubic Fm3m to Ia3̄. Almost all the heavier lanthanides, In₂O₃ and Mn₂O₃ exist in such C-type structures, which can be explained as distorted LnO₆ octahedra. As mentioned in the introduction section, the structure of other end member, Bi₂O₃ can exists in a number of structure types. The ambient temperature, α-Bi₂O₃ has a monoclinic structure where the lattice is formed by stacking of layers of Bi³⁺ and O⁻² ions. This arrangement results a distorted trigonal bipyramidal configuration where the 6s² lone pair of Bi³⁺ and two oxygen atoms at shorter Bi–O bond length form the basal triangle and other two oxygen atoms at longer Bi–O bond lengths form apices.²¹ This structure is also a closely related to fluorite lattice with ¼ of anions sites vacant. At higher temperature, Bi₂O₃ transforms to a cubic fluorite type (δ-Bi₂O₃) structure by complete disordering of anion and vacant sites. In addition to these ionic structures, several molecular structures are also known for some lone pair containing A₂O₃ type compounds, viz. Sb₂O₃, As₂O₃etc.(Ref. 22 and references therein) Due to the complexity of the crystal chemistry of A₂O₃ type compounds, ordered lattices and different polymorphs can be easily expected in Dy_1−xBi_xO_1.5 system.

In addition, the stabilized fluorite phases often show anion or cation ordering which lead to various ordered lattices.³ Thus the possibility of getting ordered phases is very common in the cation substituted Bi₂O₃ lattices. Hence weak peaks and profiles of the XRD patterns were carried out. The analyses of the XRD data of compositions with 0.0 ≤ x < 0.44 revealed no distortion or ordering in the C-type phase. Watanabe et al.²³ have reported a gradual transformation of fluorite-type stabilized face centered cubic lattice of Bi_0.68Dy_0.32O_1.5 to a body centered cubic lattice (I2₁3) with unit cell parameter a = 10.987 Å. The disordered anions of the δ-Bi₂O₃ type phase slowly relaxed to ordered sites of such body centered cubic lattice. The authors also suggested that the transformed body centered cubic lattice is closely related to the C-type rare-earth oxide lattice. However, the occupation of oxygen in two non-equivalent sites lower the symmetry in stabilized body centered cubic lattice of the rare-earth doped Bi₂O₃ compared to the C-type lattice. The maximum observed unit cell parameter of the present study (a = 10.6644(2) Å for x = 0.15) is only marginally higher than that of pure Dy₂O₃. The larger ionic radii and highly asymmetric electron configuration of Bi³⁺ may be a plausible reason for very low solubility of Bi³⁺ in the Dy₂O₃ lattice. Besides, no additional reflections attributable to the low symmetry (I2₁3) lattice or any other polymorph of A₂O₃ type compounds are observed in XRD patterns of any Dy_1−xBi_xO_1.5 compositions. The limited solubilities of Bi₂O₃ in rare-earth oxide lattice retaining the C-type structure have been reported earlier in literature.^24–26 The maximum solubility of Bi₂O₃ (∼15 mol %) has been reported in Gd₂O₃, while the solubility decreases with increasing or decreasing the ionic radii of the rare-earth ions with respect to Gd³⁺, viz. about 8 mol % in hexagonal Pr₂O₃ and about 2 mol % in cubic Yb₂O₃. From the variation of unit cell parameters of the present investigation it can be suggested that the solid solubility of Dy₂O₃ remains within 2 mole % as in the cases of Yb₂O₃.

In order to understand the nature of the new coexisting phase, the diffraction data observed for the higher Bi³⁺ containing composition, viz. x = 0.33 to 0.50 were compared. The reflections attributable to the above mentioned C-type phase are not observed at the composition with x = 0.44 (Fig. 1). All the observed intense reflections observed for the Dy_0.56Bi_0.44O_1.5 composition could be indexed on a rhombohedral lattice with unit cell parameters as a = 3.772 and c = 9.5482 Å. The unit cell parameters of this rhombohedral phase identified in the studied nominal compositions are summarized in Table 1. The formation of the rhombohedral phase in the bismuth rich (viz. x > 0.65) compositions of Bi₂O₃–Ln₂O₃ systems have been reported earlier.^3,6,26 Typical unit cell parameters of such rhombohedral phase can be compared to the present observed parameters as: a ∼ a_h and c ∼ 3 × c_h (where a_h and c_h are present observed unit cell parameters). A comparison of the unit cell parameters of the rhombohedral phase observed in various nominal composition indicates that the a-axis systematically decreases with the increase in the concentration of Bi³⁺ while the c-axis show an increasing trend. A wide homogeneity range of Bi³⁺ and Dy³⁺ with a concomitant cation distribution in the lattice may be the reason for such variation of unit cell parameters. By considering both the rhombohedral and C-type phases, all the compositions for 0.00 < x < 0.44 can be explained as a composite system.

In all these rhombohedral phases, appreciably lower ionic conductivities are observed compared to the δ-Bi₂O₃ type phases, which have been explained by the ordering of anions.^2,3 Later a number of reports dealing with structural and phase transition aspects of such rhombohedral phases are available in literature.³ Most of these rhombohedral phases show homogeneity ranges which depend on the ionic radii of the rare-earth ions. Besides, two different types rhombohedral phases, namely β1 and β2 have been reported in literature, which have almost identical XRD patterns and unit cell parameters.^3,26 However, the difference of the two types of rhombohedral phases has been concluded from the thermodynamic stability and nature of temperature induced phase transitions.³ Further investigations by electron microscopy revealed two different types of modulated structures in such bismuth rich rhombohedral phases.^27,28 However, the phases observed in rare-earth rich compositions have diversified symmetry. Extensive structural reports on the Ln₂O₃ rich compositions in Bi₂O₃–La₂O₃/Nd₂O₃ systems have been available.^27–33 An orthorhombic tunnel like structure has been reported for a definite Bi₈Ln₁₀O₂₇ composition with only La as rare-earth cation.^14,15 Horlyn et al.³⁰ investigated a series of Bi₃Ln₅O₁₂, for Ln = La to Lu compositions and assigned rhombohedral lattices to all of them. The rhombohedral unit cell parameters observed in the present study are similar to those reported by Horlyn et al.³⁰ Chen et al.²⁹ and Walcryz et al.^31,32 have reported a monoclinic (C2/m) lattice for Bi₂La₄O₉ and Bi₂Nd₄O₉ compositions. The reported monoclinic cell is very closely related to the rhombohedral lattice of the present study as well as that reported by Horlyn et al.³⁰ Drache et al.³ have explained a close relation of the rhombohedral and monoclinic lattice with fluorite-type lattice of δ-Bi₂O₃.

Further conclusions about the observed rhombohedral phase were obtained from the detailed structural investigations on Dy_0.56Bi_0.44O_1.50 composition. The average structure for the rhombohedral phase observed at Dy_0.56Bi_0.44O_1.5 was obtained by the Rietveld refinement of the powder XRD data using a cation disorder model reported earlier for such non-stoichiometric rhombohedral phases.^31–33 In this initial structural model, Bi and Dy are statistically occupied on 3a (0,0,0) sites (occ. Dy : Bi = 0.56 : 0.44) while anions are occupied on 6c (0,0,z) sites (occ. = 0.75) of space group R3̄m. The refined unit cell parameters are: a = 3.7728(1) Å and c = 9.5541(5) Å, V = 117.77(1) ų, Z = 3, (the corresponding rhombohedral unit cell parameters are: a = 3.8584(2) and α = 58.538(2)°, Z = 1) and final refined oxygen positions coordinates are: (0,0, 0.251(2)). The refined structural parameters and observed and calculated XRD patterns for Dy_0.56Bi_0.44O_1.5 are shown in Fig. 2. The equivalent volume fluorite (Fm3m) lattice of the present observed composition can be transformed to a rhombohedral (R3̄m) lattice with unit cell parameter (a_r = 3.818 Å and α = 60°). A comparison of the unit cell parameters of the observed rhombohedral lattice with the corresponding volume cubic lattice (see ESI†), suggests that the fluorite lattice is stretched along <111> direction. Besides, the oxygen sub lattice remains defective, similar to the δ-Bi₂O₃ lattice.

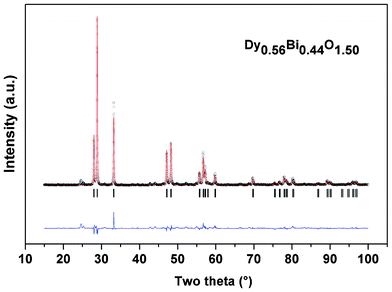Fig. 2 Rietveld refinement data for the powder XRD data of Dy_0.56Bi_0.44O_1.5 with the average structure. (Rp: 12.4, Rwp: 17.8, χ²: 6.07, R_B: 6.38 and R_F: 4.96).

It can be mentioned here that the above assigned rhombohedral unit cell cannot index a number of weak reflections observed in the XRD pattern of Dy_0.56Bi_0.44O_1.50. Thus the exact structure is a superstructure of this rhombohedral lattice. All the observed weak reflections could be indexed on rhombohedral lattice with unit cell parameters: a = 15.21 and c = 19.67 Å, which can be related to the basis rhombohedral cell as: a ∼ 4 × a_h and c ∼ 2 × c_h. The typical observed and calculated reflections of the rhombohedral sub and super structure are tabulated in the ESI.† The formation of super structure have been reported for several rare-earth oxide rich compositions, viz. Watanabe³⁴ has reported a hexagonal super structure with unit cell parameters, a = 22.865 and c = 19.036 Å for the compositions Bi_0.425Y_0.575O_0.15; Walcryz et al.³¹ have reported a rhombohedral super structure with unit cell parameters, a = 31.67 and c = 19.93 Å for Bi₂La₄O₉. In addition to such hexagonal super lattices, several other distorted monoclinic and triclinic lattices are also assigned for similar rare-earth rich compositions.^27,32,33 Earlier, a possible anion ordering has been mentioned for the average rhombohedral structure of Bi₃Ln₅O₁₂ (Ln = Rare-earth ions),³⁰ Bi₂La₄O_4.5³¹etc. It has also been mentioned that the structure of rhombohedral phase is closely related to the structure of fluorite type δ-Bi₂O₃ and hexagonal (A-type) La₂O₃ and acts as a bridge between fluorite to La₂O₃ type structural transition. The unit cell parameters reported for the rhombohedral super structure observed by Wolcyrz et al. can be related to the presently observed unit cell parameter of the rhombohedral super cell of Dy_0.56Bi_0.44O_1.5 by doubling the a- and b-axes. However no structural details for such super structures have been reported in the literature, and thus the direct refinement of observed XRD data could not be carried out in the present study. The detailed analyses of crystal structure are being carried out and they will be reported elsewhere.

The observed powder XRD pattern of the compositions with x = 0.50 indicates several intense reflections in addition to the reflections due to the above mentioned rhombohedral lattice (Fig. 1). These extra reflections could be indexed on a fluorite-type lattice, with unit cell parameter a = 5.437 Å. Earlier studies of Verkerk and Burggraaf ⁹ on bismuth rich compositions of the Bi₂O₃–Dy₂O₃ system indicate that with 25–52 mole % Dy₂O₃ the fluorite type δ-Bi₂O₃ can be stabilized at ambient temperature. The authors have also observed that for lower Dy₂O₃ (i.e. below 25 mol %) compositions, the fluorite type δ-Bi₂O₃ phase can also be stabilized by quenching from higher temperature. In order to determine the cation ratio and phase fraction Rietveld refinement of the XRD data were carried out by GSAS software package.¹⁷ The earlier mentioned rhombohedral phase with the composition Dy_0.50Bi_0.50O_1.5 and fluorite type phase with stoichiometry Dy_0.5Bi_0.5O_1.5 were as initial structural model for Rietveld refinement. The refined unit cell parameters for the rhombohedral phase are: a_h = 3.7722(2), c_h = 9.5715(7) Å, V = 117.95(1) Å ³ and those of fluorite type phase are: a = 5.4366(2) Å, V = 160.69(1) Å ³. The details of other structural parameters are given in Table 2. The final Rietveld refinement plot for Dy_0.5Bi_0.5O_1.5 composition is shown in Fig. 3. A comparison of the unit cell parameter observed for fluorite type δ-Bi₂O₃ with those reported by Verkerk and Burggraaf ⁹ suggests that the composition of the fluorite phase is close to nominal composition Dy_0.5Bi_0.5O_1.50. Further occupation of the cation sites of the fluorite type phase was refined by constraining the total metal ion at 4a site to unit. The cation ration do not show appreciable variation from that expected for Dy_0.50Bi_0.50O_1.50. Thus it can be suggested that the rhombohedral and fluorite type δ-Bi₂O₃ phases are stable competing phases at x = 0.50 and later is more preferred phase for x ≥ 0.50. Further it can be mentioned here that no triclinic phase similar to BiYbO₃³³ is formed in the adopted preparation condition.

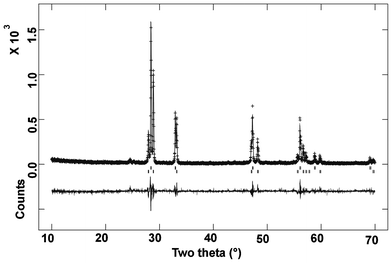Fig. 3 Rietveld refinement plot for Dy_0.50Bi_0.50O_1.5 composition (rhombohedral: lower vertical marks and fluorite: upper vertical marks).

Table 2 Refined structural details for nominal composition Dy_0.5Bi_0.5O_1.5

Rhombohedral		Cubic
Rp: 0.17, Rwp: 0.22, χ^2 = 1.95.
a = 3.7722(2) Å		a = 5.4366(2) Å
c = 9.5715(7) Å
V = 117.95(1) Å^3		V = 160.69(1) Å^3
Dy/Bi	3a: 0,0,0	Dy/Bi	4a: 0,0,0
(occ. 0.49 : 051)	U iso = 0.023(2) Å^2	(occ. 0.50 : 050)	U iso = 0.031(1) Å^2
O	6c: 0,0, 0.243(2);	O	8c: 0.25,0.25,0.25;
(occ. 0.75)	U iso = 0.016(11) Å^2	(occ. 0.75)	U iso = 0.067(14) Å^2
Wt fractions	48.6(4) %	51.4(4) %

---

In summary, it can be concluded that the Dy_1−xBi_xO_1.5 (0.00 < x ≤ 0.50) system has three different phases, namely, a feebly Bi doped rare-earth oxide type, a fluorite related rhombohedral and a fluorite type phases. Both the rare-earth oxide type and rhombohedral phases have a homogeneity range as observed from the variation of unit cell parameters. All the compositions, except x = 0.44 exists as a composite of two phases.

The SEM micrographs of representative samples obtained after sintering at 1173 K are shown in Fig. 4. A comparison of the SEM micrographs shows very well developed grains for the compositions with higher Bi³⁺ content compared to the lower Bi³⁺ ones. These features corroborate to the findings of the XRD study. The poor sinterability is evident for the C-type phases having excess of Dy₂O₃, which can be attributed to the higher melting temperature of rare-earth oxides. The compositions of metal ions of some representative compositions were verified by point EDX scanning and are given in the ESI† (S-III). The homogeneous distributions of elements are confirmed by liner EDX scan. The elemental profiles along the line are shown in S-IV to S-VI of the ESI.†

Fig. 4 SEM images of Dy_1−xBi_xO_1.5 (A: x = 0.05; B: x = 0.20; C: x = 0.33 and D: x = 0.50) pellets recorded at different magnifications. (Left column is at 3 K and right column is at 5 K magnification).

In order to understand the electrical properties, the ac conductivities of all of the compositions were studied from ambient temperature to 973 K. At ambient temperature, the impedance spectra show noisy features, indicating highly resistive behavior and impedance beyond the measurable limit of the instrument. Proper semicircles displaying real and imaginary part of impedance could be obtained only above 673 K. So the data measured above this temperature were used for extracting the conductivity information. Typical Cole–Cole plots for some representative compositions at a temperature are shown in Fig. 5. In the frequency range of 0.1 Hz to 10 MHz, two overlapping semicircles are observed for all the compositions. However, two distinct semicircles indicating two different types of relaxation phenomena are observed for the composition with x = 0.20. As observed from the XRD data, the rhombohedral phase is appreciably developed along with the cubic C-type phase at this composition. This may result in two different conduction procedures leading to two distinct semicircles in the Cole–Cole plot. At the low frequency end, the spike like features attributable to electrode phenomena or semicircle attributable to other contributions were not observed.

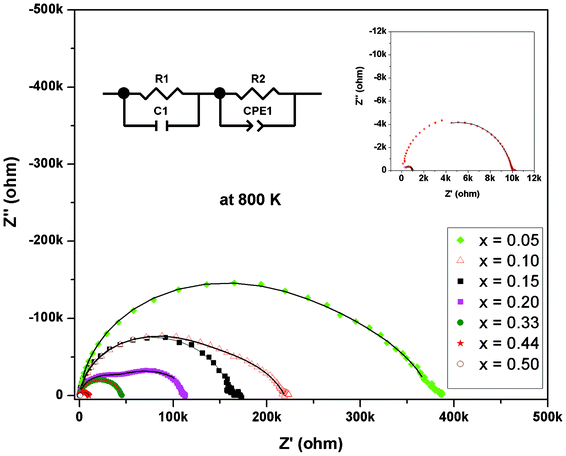Fig. 5 Typical Cole–Cole plots of some representative compositions in Dy_1−xBi_xO_1.50 at 800 K (insets shows expanded data observed for x = 0.50 and 0.44). (Solid lines indicate fit data of equivalent circuits).

The analyses of the impedance were carried out by considering equivalent circuit models using ZView ver. 3.1 (Scribner Associates, Inc.). The impedance data observed between 1 kHz to 1 MHz were used for the non linear least square fitting. The impedance data observed at higher temperature could be modelled by using one RC and one R-CPE (R = resistance, C = capacitance and CPE = constant phase element) circuits in series configuration. The equivalent circuit and the corresponding fit data are shown in Fig. 5. The total conductivity (σ) was calculated using the relation σ = (1/R)l/a, where R = total resistance, l and A are thickness and cross sectional area of sample pellets. The conductivities of the samples were extracted from the observed resistances at different temperatures and they are depicted in Fig. 6. The temperature dependent conductivity of various samples could be fitted with Arrhenius relations: lnσ = lnσ₀ − E_a/kT, (where σ₀ = pre-exponential factor, E_a = activation energy, k = Boltzmann's constant). The pre-exponential factor and activation energy for different compositions as obtained from the Arrhenius relation are given in Table 3. The typical conductivities of Dy_1−xBi_xO_1.5 compositions at 800 K are also included in Table 3. Typical activation energy for all the studied compositions is marginally different and they all remain within 1.1 to 1.2 eV. However, the pre-exponential factor increases systematically with the increase in Bi³⁺ content and a sharp rise in pre-exponential factor is observed for the composition with x = 0.50.

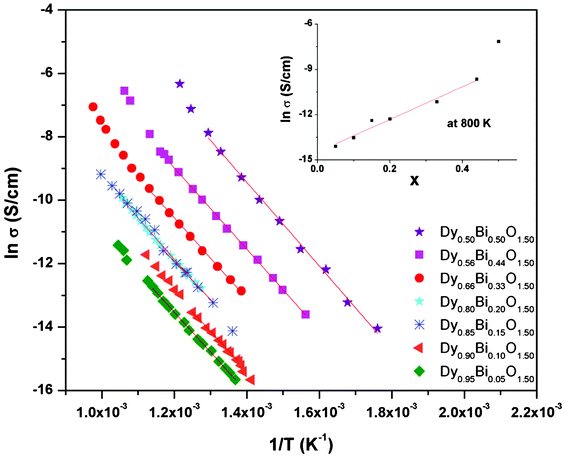Fig. 6 Variation of conductivity of Dy_1−xBi_xO_1.50 with temperature (variation of conductivity with composition x at 800 K is shown as inset).

Table 3 Activation energy, pre-exponential factor and typical conductivity at 800 K of Dy_1−xBi_xO_1.50 compositions

x	Composition	E a(ev)	σ 0 (ohm^−1 cm^−1)	σ (ohm^−1 cm^−1) at 800 K
0.05	Dy0.95Bi0.05O1.50	1.11	7.30	7.5 × 10^−7
0.10	Dy0.90Bi0.10O1.50	1.14	23.44	1.3 × 10^−6
0.15	Dy0.85Bi0.15O1.50	1.13	48.312	4.2× 10^−6
0.20	Dy0.80Bi0.20 O1.50	1.17	92.636	4.6 × 10^−6
0.33	Dy0.67Bi0.33O1.50	1.20	519.80	1.4 × 10^−5
0.44	Dy0.66Bi0.44O1.50	1.18	1957.43	6.4 × 10^−5
0.50	Dy0.50Bi0.50O1.50	1.19	23 837.85	8.1 × 10^−4

---

From Fig. 5, it can also be seen that the radius of the semicircle decreases systematically with the increasing values of x in Dy_1−xBi_xO_1.5, which indicates a systematic increase in conductivity with increase in x values. A comparison of the conductivity of the investigated compositions suggests that at any temperature conductivity increases with increasing Bi³⁺ content (inset in Fig. 6 and Table 3). Typical conductivity of Dy_0.95Bi_0.05O_1.50 and Dy_0.80Bi_0.20O_1.50 at 800 K are: 7.5 × 10⁻⁷ and 4.6 × 10⁻⁶ S cm⁻¹, respectively. However, those of Dy_0.56Bi_0.44O_1.50 and Dy_0.50Bi_0.50O_1.50 are about 6.4 × 10⁻⁵ and 8.1 × 10⁻⁴ S cm⁻¹, respectively. The lower conductivity in low Bi containing samples can be attributed to poor oxygen transport in C-type cubic lattice. However, as the bismuth content increases in composition, the contribution from the rhombohedral phase becomes appreciable and that enhances the net conductivity. The conductivity of the rhombohedral phase is about one order higher than that of the C-type cubic phases. The variation of the pre-exponential factor of the rhombohedral dominating compositions (Table 3) suggests that the excessive Bi containing phases favor ionic conduction. This can be attributed the under occupied disordered anion sites of rhombohedral phase compared to the fully occupied ordered anion sites of the C-type cubic phases. Besides, the rhombohedral phase has layers of disordered anions with vacancies, which can favor anion migration due to unhindered two dimensional channels in a layer. Also it is important to note here that the all the compositions have identical oxygen stoichiometry due to the isovalent character of Bi³⁺ and Dy³⁺. Thus the increasing ion mobility might be related to the facile percolation pathway in the rhombohedral structures. In addition, better grain growth of the composites phases are observed for the Bi³⁺ rich compositions, which favor creating channels for anion migration.

The significantly higher conductivity at the composition with x = 0.50 can be attributed to the coexisting fluorite type phases δ-Bi₂O₃ phase. As mentioned earlier, the δ-Bi₂O₃ and rare-earth doped stabilized δ-Bi₂O₃ type phases phase are fast oxide ion conductors due to excessive anion vacancy and disordered lattices. Though the electrical conductivity is appreciably high, the thermal and electrical stability of this composition will be limited due to the metastable nature of fluorite type phase. However, the identified rhombohedral phase has lower conductivity compared to the δ-Bi₂O₃ type phase but it has significantly higher conductivity compared to zirconia based ionic conductors. Besides, the ordered arrangements as concluded from the super structure reflections may render better structural stability compared to δ-Bi₂O₃ type phases. Further investigation on structural stability and the conduction mechanism will be useful for delineating the potential of this ordered phase.

IV Conclusions

Detailed analysis of phases in Dy_1−xBi_xO_1.50 (0.00 ≤ x ≤ 0.50) systems revealed a composite systems with coexisting C-type cubic and rhombohedral or rhombohedral and δ-Bi₂O₃ type phases in all composition except x = 0.44. A minute amount of bismuth incorporation in the Dy₂O₃ lattice and a wider homogeneity of Bi and Dy, is concluded from the variation of unit cell parameters. The non linear variations of the unit cell parameters of the C-type and rhombohedral phases suggest a possible inter-diffusion of Bi³⁺ between these two phases. Around Dy_0.56Bi_0.44O_1.50, a single phasic rhombohedral ordered phase is identified. The ionic conductivity studies revealed a systematically increasing trend with temperature and Bi³⁺ content. The activation energies obtained by the Arrhenius equation are marginally different in all studied compositions, while the pre-exponential factor increases with Bi⁺³ content. The ordered rhombohedral phase show appreciably higher ionic conductivity at relatively lower temperature (∼800 K). The observed conductivity rhombohedral phases at 800 K but about two order lower than the Dy³⁺ stabilized Bi₂O₃ phases but significantly higher compared zirconia based electrolytes.

Acknowledgements

The Department of Atomic Energy's Science Research Council (DAE-SRC) is sincerely acknowledged for supporting this work via sanction number 2010/21/9-BRNS/2025. The authors also thank Dr D. Das, Head, Chemistry Division and Dr G. P. Kothiyal, Head, Glass and Advanced Ceramic Division, BARC, for their interest in this work.

References

1. N. M. Sammes, G. A. Tompestt, H. Nafe and F. Aldinger, J. Eur. Ceram. Soc., 1999, 19, 1801.
2. S. Hull, S. T. Norberg, M. G. Tucker, S. G. Eriksson, C. E. Mohn and S. Stølen, Dalton Trans., 2009, 8737.
3. M. Drache, P. Roussel and J. P. Wignacourt, Chem. Rev., 2007, 107, 80.
4. H. A. Harwig and A. G. .Gerards, J. Solid State Chem., 1978, 26, 265.
5. S. Kostantonis and J. A. Kilner, Solid State Ionics, 2011, 192, 168.
6. T. Takahashi, H. Iwahara and T. Arao, J. Appl. Electrochem., 1975, 5, 187.
7. S. Nakyama, Ceram. Int., 2002, 28, 907.
8. S. Ekhelikar and G. K. Bichile, Bull. Mater. Sci., 2004, 27, 19.
9. M. J. Verkerk and A. J. Burggraaf, J. Electrochem. Soc., 1981, 128, 75.
10. S. Boyapati, E. D. Wachsman and B. C. Chakoumakos, Solid State Ionics, 2001, 138, 293.
11. C. E. Mohn, S. Stølen, S. T. Norberg and S. Hull, Phys. Rev. Lett., 2009, 102, 155502.
12. T. Takahashi, T. Esaka and H. Iwahara, J. Appl. Electrochem., 1977, 7, 299.
13. I. Abrahams, A. J. Bush, S. C. M. Chan, F. Krok and W. Wrobel, J. Mater. Chem., 2001, 11, 1715.
14. C. Michel, V. Caignaert and B. Raveau, J. Solid State Chem., 1991, 90, 296.
15. Y. Li, T. P. Hutchinson, X. Kuang, P. R. Slater, M. R. Johnson and I. R. Evans, Chem. Mater., 2009, 21, 4661.
16. J. Rodriguez-Carvajal, Multi-Pattern Rietveld Refinement Program FullProf .2k .ver. 3.30, June, 2005, -LLB.
17. A. C. Larson and R. B. van Dreele, GSAS: General Structure Analysis System, Los Alamos National Laboratory, Report LA-UR 86-748, 2000.
18. A. F. Wells, Structural Inorganic Chemistry, 3rd edn Oxford Press, 1962.
19. P. P. Fedorov, M. V. Nazarkin and R. M. Zakalyukin, Crystallogr. Rep., 2002, 47, 281.
20. F. J. Manjón and D. Errandonea, Phys. Status Solidi B, 2009, 246, 9.
21. H. A. Harwig, Z. Anorg. Allg. Chem., 1978, 444, 151.
22. A. L. J. Pereira, L. Gracia, D. Santamarıa-Perez, R. Vilaplana, F. J. Manjon, D. Errandonea, M. Nalin and A. Beltran, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174108.
23. A. Watanabe, J. Solid State Chem., 1995, 120, 30.
24. Y. Jinling, L. Jingkui, T. Weihua, S. Ying, C. Xiaolong and R. Guanghui, J. Alloys Compd., 1997, 252, 143.
25. X. L. Chen, F. F. Zhang, Y. M. Shen, J. K. Liang, W. H. Tang and Q. Y. Tu, J. Solid State Chem., 1998, 139, 398.
26. M. Drache, S. Obbade, J. P. Wignacourt and P. Conflant, J. Solid State Chem., 1999, 142, 349.
27. S. Obbade, M. Drache, P. Conflant and E. Suard, J. Solid State Chem., 2001, 162, 10.
28. S. Obbade, M. Huve, E. Suard, M. Drache and P. Conflant, J. Solid State Chem., 2002, 168, 91.
29. X. L. Chen, W. Eysel and J. Q. Li, J. Solid State Chem., 1996, 124, 300.
30. R. Horyń, M. Wolcyrz and A. Wojakowski, J. Solid State Chem., 1995, 116, 68.
31. M. Wolcyrz, L. Kepinski and R. Horyn, J. Solid State Chem., 1995, 116, 72.
32. M. Wołcyrz, R. Horyn and F. Bouree, J. Phys.: Condens. Matter, 1999, 11, 5757.
33. M. Drache, P. Roussel, P. Conflant and J.-P. Wignacourt, Solid State Sci., 2005, 7, 269.
34. A. Watanabe, Solid State Ionics, 1996, 86–88, 1427.

---

Footnote

† Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra21352d

---