Exploration of conformational flexibility and hydrogen bonding of xylosides in different solvents, as a model system for enzyme active site interactions

Abstract

The predominantly populated conformation of carbohydrates in solution does not necessarily represent the biologically active species; rather, any conformer accessible without too large an energy penalty may be present in a biological pathway. Thus, the conformational preferences of a naphthyl xyloside, which initiates in vivo synthesis of antiproliferative glycosaminoglycans, have been studied by using NMR spectroscopy in a variety of solvents. Equilibria comprising the conformations ⁴C₁, ²S_O and ¹C₄ were found, with a strong dependence on the hydrogen bonding ability of the solvent. Studies of fluorinated analogues revealed a direct hydrogen bond from the hydroxyl group at C2 to the fluorine atom at C4 by a ^1hJ_F4,HO2 coupling. Hydrogen bond directionality was further established via comparisons of fluorinated levoglucosan molecules.

---

Introduction

In recent years the impact of carbohydrate ring flexibility on biological systems has become even more apparent. Conformational aspects in enzyme–substrate complexes and reaction intermediates are of great importance for ligand recognition and stereochemical outcomes.¹ Studies with a focus on the potential energy and/or free energy of carbohydrate systems in solution and in the gas phase have been performed experimentally and computationally. For example, quantum mechanical calculations by Rovira and co-workers describe free energy landscapes for the ring conformations of gluco-² and manno-pyranosides,³ displaying local minima for conformers not detectable in solution, but found in enzyme–substrate complexes. An interpretation of this is that the predominantly populated conformation in solution does not necessarily represent the biologically active species; instead, a conformer accessible without too large an energy penalty can exist in a biological pathway. It was further established that the suggested conformers made the molecule at hand more apt to undergo reaction, e.g., increasing the tendency for aglycon dissociation by increasing the C1–O1 bond distance in mannose upon a transition from the ⁴C₁ to the ¹S₅ ring conformation. Recent experiments performed with xylose analogues locked in the ^2,5B conformation⁴ displayed enhanced glycolysis and glycosylation rates, thus confirming these calculations.

One major difference between solution conformation in an aqueous environment and the ligand bound to the active site of a protein lies in the polarity. For example, the active site of a xylan-hydrolyzing enzyme has been found to have a polarity between benzene and tetrahydrofuran,⁵ which have ε_r-values ∼75 units lower than water, on a scale covering ∼107 units (pentane–formamide) at ambient temperature.⁶ In solution, the impact of the polarity, i.e., the solvent properties, on the conformation of a solute occurs in various ways; e.g., by affecting the intramolecular charge–dipole and dipole–dipole interactions as well as the exposed surface area. Regarding carbohydrate structures, the anomeric effect has been shown to be of greater significance in solvents of low polarity.⁷ The preference to form intramolecular hydrogen bonds is also anticipated to increase in non-polar solvents.

Recent research indicates that the pathobiology of cancer progression is dependent on the expression of glycosaminoglycan (GAG) chains.^8–11 These long, unbranched polyanionic carbohydrate chains are covalently attached to proteins to form proteoglycans (PG). The biosynthesis of GAG starts from the coupling of the carbohydrate xylose to a serine residue of the protein followed by the formation of a linker tetrasaccharide. This tetrasaccharide is a biosynthetic branching point, and the linker is elongated by the addition of repeating disaccharides. The growing chain is later on modified by epimerization and sulfation reactions, resulting in extensive structural diversity. Simple xylosides, carrying an aromatic aglycon, can enter cells and serve as primers for GAG formation and the composition of GAG depends on the structure of the aglycon. Xylosides carrying an aromatic aglycon have shown very promising tumor selective and antiproliferative properties in vitro as well as in vivo.^12–14 The knowledge of structure recognition of the antiproliferative GAG is still scarce due to the lack of effective molecular tools to identify and correlate specific structures with functions. It is reasonable that the flexibility of xylose, in comparison to, for example, glucose and due to the lack of a primary hydroxymethyl group, controls the growing GAG chain. In a recent study of xylose derivatives by using NMR spectroscopy in a methanol-d₄ solution, the expected ⁴C₁ conformer was found to be predominant, accompanied by minor contributions of the ²S_O conformation.¹⁵ The goal of this study is to gain information on conformational equilibria of carbohydrates in different solvents, as models for different enzyme active site polarities.

Results and discussion

¹H NMR spectra of compound 1¹⁵ (Fig. 1) were recorded in 14 deuterated solvents (Table 1), ranging from highly polar (dimethyl sulfoxide-d₆, N,N-dimethylformamide-d₇) containing hydrogen bond accepting and/or donating functionalities to non-polar solvents (benzene-d₆, chloroform-d). Chemical shifts and ⁿJ_HH coupling constants were extracted in different solvents utilizing the PERCH NMR spin simulation software¹⁶ (Table S1†). The measured ³J_HH coupling constants were compared to calculated coupling constants based on molecular models built from canonical ring conformations using molecular mechanics and the generalized Haasnoot–Altona Karplus-type equations,¹⁷ in the same manner as previously described.¹⁵ A three-state model comprising chair and skew conformers, viz., ⁴C₁, ²S_O and ¹C₄, gave the best agreement in the fitting procedure. The incorporation of other skew conformers in the model gave negligible or no contribution to the equilibrium.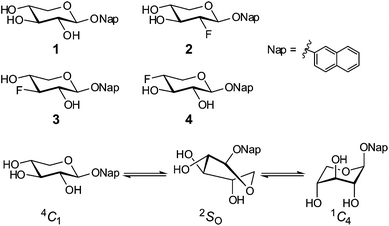

Fig. 1 Compounds 1–4 and the conformational equilibrium.

Table 1 Solvent parameters, dielectric constant (ε_r), hydrogen bond accepting parameter (β), and conformation populations for 1–4, given in %, for the different solvents

Solvent	ε r	β	ln(εr + 100β)	1			2			3			4
				^4C1	^2SO	^1C4	^4C1	^2SO	^1C4	^4C1	^2SO	^1C4	^4C1	^2SO	^1C4
a Solvent parameters for non-isotopically labeled compounds at 20 or 25 °C, obtained from CRC Handbook of chemistry and physics, 67th edition, and CRC Handbook of solubility parameters and other cohesion parameters, 2nd edition.
Dimethyl sulfoxide-d6	46.6	0.76	4.81	95	5	0
Methanol-d4	32.63	0.66	4.59	94	6	0	95	5	0	92	8	0	86	14	0
N,N-Dimethylformamide-d7	36.7	0.76	4.72	93	7	0
Pyridine-d5	12.3	0.64	4.33	93	7	0
Acetone-d6	20.7	0.43	4.15	88	12	0							84	16	0
Nitromethane-d3	39.4	0.06	3.82	88	12	0
Tetrahydrofurane-d8	7.61	0.55	4.14	88	12	0
Aniline-d7	6.89	0.5	4.04	87	13	0
Phenol-d6	10.0	0.3	3.69	86	14	0
Dichloromethane-d2	9.08	0.1	2.95	77	22	1
Chloroform-d	4.81	0.1	2.70	71	22	7	76	24	0	75	20	5	58	16	26
Toluene-d8	2.4	0.11	2.60	65	16	19							62	15	23
Chlorobenzene-d5	5.6	0.07	2.53	69	22	9
Benzene-d6	2.28	0.1	2.51	64	20	15	83	17	0				59	22	19

---

The ⁴C₁ conformational state is the most highly populated of 1 in all solvents although the amount decreases, primarily favoring ²S_O, with decreasing solvent polarity (Table 1). In solvents with a good capability of accepting hydrogen bonds (all except benzene-d₆, toluene-d₈, chloroform-d and dichloromethane-d₂), a slight positive slope of the amount of ⁴C₁versus the dielectric constant, ε_r, is observed with the ⁴C₁ population decreasing from 95% to 86% when ε_r is lowered. In non-hydrogen bonding solvents the ⁴C₁ population is more drastically diminished with a minimum for benzene-d₆ (64%). The dielectric constant of dichloromethane-d₂ is higher than those of tetrahydrofuran-d₈ and aniline-d₇, but the population of the ⁴C₁ conformer of 1 is significantly smaller in the former one compared to the latter two. Evidently the solvent polarity is not sufficient to describe these observations. When comparing the different populations to the hydrogen-bond accepting parameter, β,¹⁸ derived by Kamlet and Taft, a similar pattern is observed. Benzene-d₆, chloroform-d and dichloromethane-d₂ share the same β value (0.1) but differ in their distributions of conformations. In a study of hydroxymethyl group rotation and hydrogen bonding as a function of solvation by Dix and co-workers,¹⁹ a linear combination of the empiric solvent parameter E_T(30) and β, i.e., E_T(30) + 100β, was used to describe the experimental data. By applying a similar relationship, with ε_r replacing E_T(30), a clear trend between this combined parameter and the population of ⁴C₁ was observed. The natural logarithm of the combined parameter, i.e., ln(ε_r + 100β), gave a linear relationship to the population distributions of ⁴C₁ (r² = 0.95), ²S_O (r² = 0.87) and ¹C₄ (r² = 0.63), which is displayed in Fig. 2. Consequently, both the dielectric constant and the hydrogen bond accepting ability of the solvent have a major influence on the solution state conformational equilibrium.

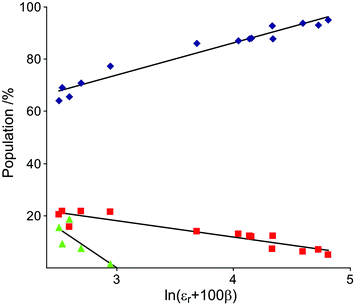Fig. 2 Conformer distributions of 1, ⁴C₁ (blue diamonds), ²S_O (red squares) and ¹C₄ (green triangles) versus the combined solvent parameter.

It is, as stated in the Introduction, established that the influence of the anomeric effect is favored by diminished solvent polarity.⁷ The axial orientation of the aglycon in the ¹C₄ conformation should thereby be favored in the solvents of lower polarity. However, the non-existence of the ¹C₄ conformation in solvents of low polarity but with a hydrogen bonding ability, e.g., tetrahydrofuran-d₈, shows that this is not enough to describe the whole picture.

To investigate possible hydrogen bonds and their directionality, the conformations of three n-deoxy,n-fluoro-analogues of 1, compounds 2–4¹⁵ (Fig. 1), were also investigated. These were fully characterized by ¹H, ¹³C and ¹⁹F NMR spectroscopy in methanol-d₄, chloroform-d and benzene-d₆ solutions (Table 2), and subjected to conformational analysis. Attempts at deploying ³J_FH Karplus-type equations, based on either five-membered fluorosubstituted rings²⁰ or fluoroalkanes,²¹ in the conformational analysis were not successful; supposedly due to the difficulty of describing such couplings based solely on dihedral angles and the lack of transferability between different classes of compounds. Instead the ³J_HH coupling constants were used in the analysis in the same way as for compound 1. The fluorinated compounds follow the same trend as compound 1 regarding solvent and conformation, although deviations occur (vide infra).

Table 2 δ _H, (ⁿJ_HH), δ_F, [ⁿJ_FH] of compounds 2–5, and δ_C, {ⁿJ_FC} for compound 5, at 37 °C. For methylene groups the ¹H chemical shift, ³J_HH and ⁿJ_FH of the pro-R proton is given prior to that of the pro-S proton

Compound	Solvent	1	2	3	4	5	HO2	HO3	HO4
2	Methanol-d4	5.268	4.286	3.714	3.646	3.988, 3.482
		(7.346)	(8.757)	(8.871)	(5.389, 10.158)	(−11.508)
			−200.43
		[3.519]	[−51.113]^a	[15.424]	[−0.118]	[1.322, 0.451]
	Chloroform-d	5.306	4.523	3.908	3.858	4.181, 3.541		2.703	2.417
		(6.342)	(7.794)	(7.892)	(4.759, 8.651)	(−11.875)		(4.003)	(4.485)
			−202.02
		[4.666]	[−49.889]	[13.866]	[−0.097]
	Benzene-d6	4.946	4.373	3.389	3.292	3.680, 2.969		1.839	1.582
		(6.738)	(8.204)	(8.282)	(5.017, 9.233)	(−11.578)		(3.929)	(4.272)
			−200.68
		[4.337]	[−50.564]	[14.577]	[−0.262]	[1.133]
3	Methanol-d4	5.064	3.742	4.346	3.865	3.999, 3.467
		(7.530)	(8.805)	(8.553)	(5.719, 10.274)	(−11.667)
				−195.48
		[0.562]	[13.931]	[−52.427]	[13.275]	[−5.827, −0.998]
	Chloroform-d	5.162	4.064	4.550	3.989	4.196, 3.510	2.710		2.382
		(6.335)	(7.801)	(7.405)	(4.897, 8.548)	(−12.009)	(4.107)		(4.584)
				−198.50
			[11.853]	[−50.994]	[11.651]	[−5.308]
4	Methanol-d4	5.108	3.572	3.756	4.487	4.165, 3.680
		(7.127)	(9.196)	(8.009)	(5.569, 8.935)	(−11.721)
					−199.42
			[−0.693]	[16.742]	[−50.361]	[6.296, 6.466]
	Acetone-d6	5.222	3.626	3.816	4.539	4.161, 3.731	4.682	4.802
		(7.146)	(9.185)	(7.948)	(5.315, 8.693)	(−11.787)	(3.655)	(3.598)
					−198.29
			[−1.226]	[17.475]	[−50.496]	[7.332, 7.196]
	Chloroform-d	5.316	3.847	4.022	4.660	4.266, 3.751	2.647	2.915
		(5.397)	(7.051)	(6.142)	(4.043, 6.649)	(−12.593)	(6.142)	(5.173)
					−198.98
			[−0.695]	[12.542]	[−48.500]	[17.798, 9.500]	[2.703]
	Toluene-d8	4.900	3.431	3.595	4.169	3.707, 3.157	2.052	2.194
		(5.586)	(7.424)	(6.643)	(4.201, 6.590)	(−12.460)	(6.236)	(4.913)
					−196.56
			[−0.226]	[13.873]	[−49.086]	[17.370, 9.953]	[2.212]
	Benzene-d6	4.965	3.509	3.666	4.223	3.716, 3.167	2.096	2.239
		(5.641)	(7.528)	(6.693)	(4.211, 6.672)	(−12.454)	(5.820)	(4.791)
					−196.86
			[−0.505]	[13.937]	[−49.098]	[16.972, 9.832]	[2.011]

---

		1	2	3	4	5	6	HO3	HO4
a Negative signs are assumed for ^2J and ^4J.
5	Chloroform-d	5.493	4.229	3.912	3.557	4.528	4.101, 3.723	2.068	2.493
		(2.042, −1.653, −0.950 (pro-S)	(1.685, −1.267)	(2.728, −2.083)	(1.673, −5.576)	(0.939, 5.522)	(−7.589)	(6.299)	(10.389)
			−190.64
		[2.189]	[−45.359]	[15.913]	[−0.181]
		99.46	87.99	71.34	70.75	76.88	65.53
		{−27.69}	{182.48}	{−25.88}	{3}

---

In the ¹H NMR spectrum of 4 in a benzene-d₆ solution a scalar coupling between HO2 and F4 of 2.01 Hz was present. This coupling was verified by a ¹⁹F-decoupled ¹H NMR spectrum (Fig. 3a and 3b). The respective nuclei are separated by five covalent bonds through which mediation of a scalar coupling of this magnitude is highly unlikely. This finding rather suggests the presence of an intramolecular hydrogen bond, with HO2 as the hydrogen bond donor and F4 as the acceptor, in an arrangement which is only accessible in the ¹C₄ conformation (Fig. 5). The magnitude of the coupling is in agreement with previously reported through-space ^1hJ_FH coupling constants,^22,23 considering that the ¹C₄ conformation is populated ∼20% of the time. The populations of 4 in benzene-d₆, toluene-d₈ and chloroform-d display a linear correlation of the amount of the ¹C₄ conformation vs. the magnitude of ^1hJ_F4,HO2 (Tables 1 and 2), i.e., 2.0 Hz to 2.7 Hz from 19% to 26%. In compound 2, neither coupling between HO4 and F2 nor the ¹C₄ conformation was observed. Partial isotopic labeling of the hydroxyl groups by the addition of a droplet containing H₂O–D₂O in a ratio of 2 : 1 to the benzene-d₆ solutions of 2 and 4 caused a downfield shift of 0.07 ppm in the ¹H-decoupled ¹⁹F spectrum of 4 (Fig. 3d) for the deuterium-containing molecules, with peak area ratios matching the isotope ratio of the added droplet, whereas the corresponding spectrum of 2 was unaffected (Fig. 3c). This observation, with δ_F⋯H upfield of δ_F⋯D, corresponds to an unsymmetrical hydrogen bond with the hydrogen atom located closer to the donor²⁴ in 4. The population distribution of 3 in chloroform-d contains some amount of ¹C₄ (Fig. 4), since an HO4–HO2 hydrogen bond is accessible. The diminished amount of the ¹C₄ conformation for 3 in comparison with 1 and 4 may be attributed to the replacement of a hydrogen bond donor at C3. In the latter two compounds HO3 could interact favorably with the exo-anomeric oxygen atom, which may act as a hydrogen bond acceptor. This interaction appears to be of less significance than that between the substituents at C2 and C4, according to the observed data.

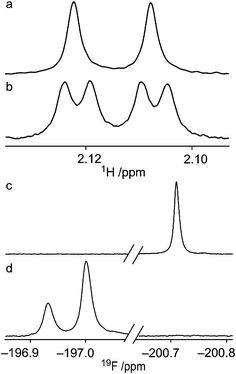Fig. 3 (a) ¹⁹F-decoupled ¹H NMR spectrum and (b) ¹H NMR spectrum of the HO2-resonance from 4 in a benzene-d₆ solution: J_F4,HO2 = 2.01 Hz and J_H2,HO2 = 5.82 Hz. (c) ¹⁹F NMR spectra in a benzene-d₆ solution with the addition of one drop of H₂O–D₂O in a ratio of 2 : 1 to compound 2 and (d) to compound 4, with the isotope effect causing a downfield shift of 0.07 ppm.

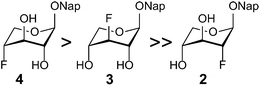Fig. 4 The relative stabilities of the ¹C₄ conformations of n-deoxy,n-fluoro xylosides 2–4 in a chloroform-d solution.

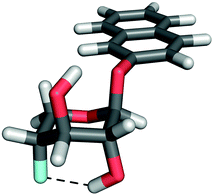Fig. 5 Compound 4 with the observed F4⋯HO2 hydrogen bond displayed.

When comparing the equilibrium populations of 1 to 4 by changing solvents from polar hydrogen bonding to nonpolar non-hydrogen bonding ones, their behaviors are found to be very similar. Thus, substitution of OH by F is an excellent probe to investigate conformationally dependent hydrogen bond interactions when the conformational equilibrium is not perturbed (Table 1). In 4 a hydrogen bond between HO2 and F4 was unequivocally proven via the experimentally observed ^1hJ_F4,HO2. Upon a comparison of the chemical shifts of the hydroxyl group protons of 1 in different solvents (Table 3), increased differences (Δδ) between δ_HO2 and δ_HO4, and δ_HO3 and δ_HO4, are observed in solvents where the ¹C₄ conformation is present. The chemical shift of HO4 is typically 0.4 ppm upfield of HO2 when the ¹C₄ conformation is absent and 0.6 ppm upfield of HO2 when it is present, where a downfield shift corresponds to increased hydrogen bonding.²⁵ A reasonable interpretation of this is that the substituent at C4 acts as a hydrogen bond acceptor, in both 1 and 4. The downfield chemical shift of HO2 in 1 (Table 3) compared to 4 (Table 2) may be attributed to increased hydrogen bond strength in 1, where the hydrogen bond donor and acceptor are more closely related in pK_a,²⁶ and compared to the weaker hydrogen bonding accepting ability of covalently bonded fluorine.²⁷ For compounds 1 and 4vs.2 in a benzene-d₆ solution, δ_HO3 differ significantly, being 2.316, 2.239, and 1.839 respectively, with an apparent dependence on favorable hydrogen bonding geometry, displaying a downfield shift in 1 and 4, both of which enter the ¹C₄ conformation.

Table 3 δ _H, (³J_HH) and Δδ for the hydroxyl groups of 1. For the solvents below the dashed line the ¹C₄ conformation of 1 is significantly populated, i.e., >5%

Solvent	HO2	HO3	HO4	ΔδHO2,HO3	ΔδHO2,HO4	ΔδHO3,HO4
a n.d. = not determined.
Pyridine-d5	n.d.^a	7.243	7.112	n.d.	n.d.	0.131
	(4.802)	(4.314)	(4.476)
Nitromethane-d3	3.422	3.318	3.067	0.104	0.355	0.251
	(3.797)	(1.575)	(4.210)
Tetrahydrofurane-d8	4.643	4.398	4.282	0.245	0.361	0.116
	(4.461)	(3.771)	(3.918)
Dichloromethane-d2	2.860	2.832	2.426	0.028	0.434	0.406
	(4.005)	(3.882)	(3.754)
Chloroform-d	2.704	2.768	2.266	−0.064	0.438	0.502
	(4.198)	(3.736)	(3.447)
Toluene-d8	2.299	2.278	n.d.	0.021	n.d.	n.d.
	(5.133)	(4.233)	(3.020)
Chlorobenzene-d5	2.625	2.626	2.071	−0.001	0.554	0.555
	(4.603)	(4.251)	(3.621)
Benzene-d6	2.301	2.316	1.582	−0.015	0.719	0.734
	(5.150)	(4.611)	(3.787)

---

To address the absence of the ¹C₄ conformation in compound 2, the hydrogen bond geometries in 1–4 in their potential energy minimized ¹C₄ conformations were analyzed. The H⋯acceptor distances were ∼2.0–2.2 Å and the donor-H⋯acceptor angles were ∼140–130°, where the most favorable interaction occurs for compound 4 for which a hydrogen bond was detected based on the scalar coupling interaction. However, the hydrogen bond geometries were all similar and although small differences may add up to observed differences in conformational equilibria, additional reasons may be of importance. To gain further insights into the hydrogen bonding pattern the conformationally locked 2-deoxy-2-fluoro-levoglucosan 5 (Fig. 6) was synthesized in order to be compared with the 4-deoxy-4-fluoro-levoglucosan 6 (Fig. 6) in which an intramolecular hydrogen bond between HO2 and F4 has been displayed via a ^1hJ_F4,HO2 coupling of 1.8 Hz in a chloroform-d solution.^28,29

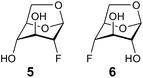Fig. 6 1,6-Anhydro-compounds.

Initial attempts towards 1,6-anhydro-2-deoxy-2-fluoro-β-D-glucopyranose 5 were made starting from D-glucal, using Selectfluor™ as a fluorinating agent.³⁰ However, the resulting 1 : 3 mixture of 5 and 1,6-anhydro-2-deoxy-2-fluoro-β-D-mannopyranose was found to be inseparable. Thus, the fluorinating agent was changed to KHF₂ in ethylene glycol,³¹ using the commercially available 1,6:2,3-dianhydro-β-D-mannopyranose 7 as a starting point (Scheme 1). To avoid the well-known Payne rearrangement,³² the mixture was acetylated before treatment with KHF₂ in ethylene glycol at 198 °C. Again, an inseparable product mixture was formed. Despite the risk of rearrangement, the same conditions were used on the unprotected 7, which gave a mixture of 5 and 1,6-anhydro-3-deoxy-3-fluoro-β-D-mannopyranose, 9, together with a small amount of rearranged product 8. Controlled benzoylation of the mixture of 9 and 5 at 0 °C resulted in a separable mixture of the mono-benzoylesters 10³³ and 11. Saponification of 11 under Zemplén conditions gave the pure compound 5 in a yield of 70%.

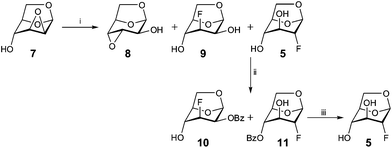Scheme 1 Reagents and conditions: (i) KHF₂, ethylene glycol, 198 °C, 2 h, 8 (3%), 9 + 5 (40%); (ii) BzCl, pyridine, CH₂Cl₂, 0 °C, 12 h, 10 (24%), 11 (19%); (iii) NaOMe, MeOH, 3 h, 5 (70%).

Compound 5 was characterized with respect to chemical shifts and coupling constants (Table 2), but no ^1hJ_F2,HO4 coupling was observed in the chloroform-d solution, despite the fact that the interatomic distances for energy minimized models of compounds 5 and 6 are similar. The ³J_H4,HO4 coupling of 10.4 Hz in 5 suggests a torsion angle close to 0° or ±150°, according to the Karplus-type relationship for ³J_HCOH couplings in carbohydrates developed by Serianni et al.³⁴ The reported ³J_H2,HO2 coupling for compound 6 is 11.5 Hz,²⁸ while a 4-deoxygenated levoglucosan, i.e., a compound without the possibility of a 1,3-diaxial intramolecular hydrogen bonding, has a ³J_H2,HO2 coupling of 10.2 Hz.²⁸ It may be reasonable to assume that the HO2 hydroxyl proton of compound 5 and the above mentioned 4-deoxy compound is oriented towards O5. The difference between regioisomers 5 and 6 may be attributed to the anti-periplanar relationship of F2 to both the exo-anomeric oxygen and O3 in 5, by which the partial electron depletion of the fluorine atom should render it less suited as a hydrogen bond acceptor, in comparison with F4 in 6, where the fluorine atom has only one oxygen in an anti-periplanar relationship. Takagi et al. observed a ^1hJ_F2,HO4 coupling in a 2-deoxy-2-fluoro-α-L-talopyranoside derivative,³⁵ further discussed by Vasella et al.,²⁸ in which the C3-substituent is oriented equatorially, hence being in a gauche relationship to the fluorine atom and not participating as strongly in the electron depletion of it. Based on this finding it is valid to assume that compound 2 would not engage a hydrogen bond between F2 and HO4 in the ¹C₄ conformation, thus raising the potential energy for this conformer. Furthermore, the shift of the conformational equilibrium in compound 4 toward the ¹C₄ conformation compared to 2 may in part be driven by a stronger gauche effect with the fluorine substituent at C4 being gauche to O5 and the anti-bonding orbital of the C4–F bond being stabilized by hyperconjugation from the axial C5–H_pro-R bond. A corresponding situation for the C2–F bond is not favored in the ¹C₄ conformation due to the axially positioned oxygen atoms at both C1 and C3 disfavoring the conformational shift in compound 2. The magnitude of the gauche effect for 1,2-difluoroethane is slightly larger (∼1.0 kcal mol⁻¹)³⁶ than for ethylene glycol (∼0.7 kcal mol),³⁷ which may explain the increased preference for ¹C₄ conformation of 4 as compared to 1 in benzene-d₆ and chloroform-d solutions.

Conclusions

The goal of this study was to gain information on conformational equilibria of carbohydrates in different solvents, as models for different enzyme active site polarities. In conclusion, the conformational dynamics of a xyloside and three fluorosubstituted derivatives, bearing a naphthyl aglycon, have been found to reside in two- or three-state equilibria, with population dependences on solvent polarity and hydrogen bond accepting ability (Fig. 7). In non-hydrogen bonding environments the ¹C₄ conformation of compounds 1 and 4 is stabilized by an internal hydrogen bond between the C2 and C4 substituents, with the latter acting as the hydrogen bond acceptor. Directionality for the formation of intramolecular hydrogen bonds in xylosides, and probably glucosides, in the ¹C₄ conformation is suggested, based on the analysis of the fluorinated levoglucosans 5 and 6. It is highly reasonable that conformations higher in potential energy, such as the ¹C₄ conformation, are important for xylose-containing compounds in the non-polar environment of an enzyme active site,⁵ similar to three-dimensional arrangements proposed in xylanases.³⁸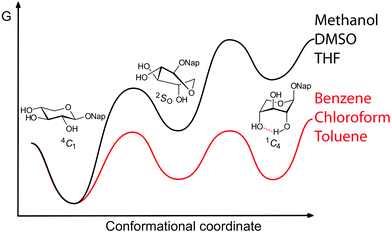

Fig. 7 Schematic representation of conformational equilibria of naphthyl xylosides in different solvents.

Experimental section

NMR spectroscopy and molecular modeling

NMR experiments for conformational analysis were performed on four different spectrometers: a Bruker Avance III 600 MHz spectrometer equipped with a 5 mm PFG triple resonance probe, a Bruker AVANCE 500 MHz spectrometer and a Bruker AVANCE III 700 MHz spectrometer; the latter two equipped with 5 mm TCI Z-Gradient CryoProbes. The ¹⁹F experiments were performed at 376 MHz on a Bruker Avance II 400 MHz spectrometer equipped with a 5 mm BBO probe. Chemical shifts are reported in ppm using residual solvent signals (Table S2†) as references in ¹H and ¹³C spectra, and internal hexafluorobenzene (δ_F −164.90) as a reference in ¹⁹F spectra. NMR samples were prepared by dissolving 1–2 mg of the xylosides in 0.5 mL of the respective deuterated solvents (99.9%, purchased from Sigma-Aldrich). ¹H and ¹³C NMR chemical shift assignments were performed at 37 °C using 2D ¹H,¹H-TOCSY,³⁹¹H,¹³C-HSQC,⁴⁰¹H,¹³C-H2BC,⁴¹ and ¹H,¹³C-HMBC⁴² experiments. ¹⁹F chemical shifts were assigned at 25 °C. ¹H spectra with ¹⁹F decoupling were performed with an inverse gated decoupling sequence, with a broadband decoupling pulse of 30 dB. ¹H chemical shifts and ⁿJ_HH and ⁿJ_FH coupling constants of compounds 1–5 were determined with the aid of the PERCH NMR spin simulation software (PERCH Solutions Ltd, Kuopio, Finland). Chemical shifts and coupling constants were altered iteratively until the simulated and experimental spectra appeared highly similar according to visual inspection and the total root-mean-square value was close to or below 0.1%. ²J_HH and ⁴J_HH were assumed to have negative signs whereas ²J_FH have a positive sign.^43,44 3D models of compounds 1–6 were built using Vega ZZ software (release 2.3.1.2).⁴⁵ The molecular structures were energy minimized, using algorithms included in the program, in the consecutive order (i) steepest descent, (ii) conjugate gradient and (iii) truncated Newton. Calculated ⁿJ_HH coupling constants for the different ring conformations of compounds 1–5 were based on the Karplus-type relationships proposed by Haasnoot et al.¹⁷ as implemented in Janocchio software.⁴⁶

General synthesis methods

NMR spectra were recorded with a Bruker Avance II operating at 294 K. ¹H NMR spectra were assigned using COSY (2D homonuclear shift correlation) with a gradient selection. ¹H NMR chemical shifts are given in ppm downfield from Me₄Si, with reference to residual CHCl₃ (δ_H 7.26) or MeOH-d₄ (δ_H 3.31). ¹³C NMR chemical shifts are given in ppm downfield from Me₄Si, with reference to residual CDCl₃ (δ_C 77.16) or MeOH-d₄ (δ_C 49.00). The ¹⁹F NMR chemical shifts were indirectly referenced from Me₄Si using γ(¹⁹F)/γ(¹H). Coupling constant values are given in Hz. Mass spectra were recorded on a Micromass Q-Tof micro™ instrument. Optical rotations were measured on a Perkin Elmer polarimeter (model 341). Reactions were monitored by TLC using alumina plates coated with silica gel and visualized using UV light or by charring with para-anisaldehyde. Preparative chromatography was performed with silica gel (35–70 μm, 60 Å). All the solvents were dried prior to use unless otherwise stated. The purchased reagents were used without further purification.

1,6-Anhydro-2-O-benzoyl-3-deoxy-3-fluoro-β-D-mannopyranose (10) and 1,6-anhydro-4-O-benzoyl-2-deoxy-2-fluoro-β-D-glucopyranose (11). KHF₂ (0.25 g, 3.2 mmol) was added to a stirred solution of 1,6:2,3-dianhydro-β-D-mannopyranose 7 (0.10 g, 0.69 mmol) in ethylene glycol (3.0 mL) at rt before heating to 198 °C. After 2 h, the reaction mixture was let to reach rt before the addition of sat. NaHCO₃ (aq) and SiO₂ followed by the removal of solvent under reduced pressure. The dry SiO₂ was applied to a column and a mixture of 1,6:3,4-dianhydro-β-D-altropyranose 8,⁴⁷ 1,6-anhydro-3-deoxy-3-fluoro-β-D-mannopyranose 9 and 1,6-anhydro-2-deoxy-2-fluoro-β-D-glucopyranose 5 was eluted with toluene–EtOAc (1 : 9). The mixture was purified again by column chromatography (SiO₂, CH₂Cl₂–MeOH 96 : 4) to give 8 (3 mg, 3%) followed by an inseparable mixture of 9 and 5 (45 mg, 40%). The mixture of 9 and 5 (0.45 mg, 0.27 mmol) was dissolved in CH₂Cl₂ (2.0 mL) and cooled to 0 °C followed by the addition of benzoyl chloride (0.03 mL, 0.27 mmol) and pyridine (0.40 mL, 5.0 mmol). After 12 h, toluene was added and the solvent was removed under reduced pressure. The crude mixture was purified by column chromatography (SiO₂, petroleum ether–diethyl ether 6 : 4 → 1 : 1) to give 10 (18 mg, 24%), 11 (14 mg, 19%) as pure fractions and a recovered mixture of 9 and 5 (15 mg, 33%). Compound 10: [α]²⁰_D −100 (c 1.5, CDCl₃); ¹H NMR (CDCl₃, 400 MHz) δ 8.13–8.10 (m, 2H, ArH), 7.62–7.57 (m, 1H, ArH), 7.48–7.44 (m, 2H, ArH), 5.61 (s, 1H, C1-H), 5.11 (ddd, 1H, J = 1.6, 4.4, 24.8 Hz, C2-H), 5.07–4.93 (m, 1H, C3-H), 4.64 (d, 1H, J = 5.6 Hz, C5-H), 4.25 (d, 1H, J = 7.6 Hz, C6-H), 4.08 (br s, 1H, C4-H), 3.95–3.90 (m, 1H, C6-H), 2.60 (d, 1H, J = 6.8 Hz, C4-OH); ¹³C NMR (CDCl₃, 100 MHz) δ 165.9, 133.8, 130.2, 129.1, 128.6, 99.7, 88.4 (J = 185.8 Hz), 75.9, 70.3 (J = 25.8 Hz), 68.3 (J = 15.0 Hz), 65.1 (J = 5.9 Hz); HRMS calc. for C₁₃H₁₄O₅F: 269.0825; found: 269.0843. ¹⁹F NMR (CDCl₃) δ −200.63 (dddd, J = 3.4, 10.5, 24.8, 48.5 Hz). Compound 11: [α]²⁰_D −111 (c 0.9, MeOH); ¹H NMR (CDCl₃, 400 MHz) δ 8.11–8.08 (m, 2H, ArH), 7.62–7.58 (m, 1H, ArH), 7.49–7.45 (m, 2H, ArH), 5.64 (d, 1H, J = 4.0 Hz, C1-H), 4.87 (t, 1H, J = 1.4 Hz, C4-H), 4.75 (d, 1H, J = 4.8 Hz, C5-H), 4.38 (d, 1H, J = 46.4 Hz, C2-H), 4.21 (dd, 1H, J = 0.8, 7.6 Hz, C6-H), 4.13–4.07 (m, 1H, C3-H), 3.85–3.81 (m, 1H, C6-H); ¹³C NMR (CDCl₃, 100 MHz) δ 166.5, 133.8, 130.1, 129.3, 128.7, 99.6 (J = 29.2 Hz), 88.7 (J = 182.0 Hz), 74.6, 73.9 (J = 5.7 Hz), 69.9 (J = 28.3 Hz), 66.1; HRMS calc. for C₁₃H₁₄O₅F: 269.0825; found: 269.0848. ¹⁹F NMR (CDCl₃) δ −187.95 (ddd, J = 4.1, 19.2, 46.3 Hz).

1,6-Anhydro-2-deoxy-2-fluoro-β-D-glucopyranose (5). 1 M NaOMe (5 μL, 5 μmol) was added to a stirred solution of 11 (14 mg, 0.01 mmol) in MeOH (0.2 mL) at rt. After 3 h, conc. AcOH was added until neutral pH followed by removal of solvent under reduced pressure. The crude residue was purified by column chromatography (SiO₂, CH₂Cl₂–MeOH 96 : 4) to give 5 (6 mg, 70%) as white crystals. [α]²⁰_D −75 (c 1.2, MeOH); ¹H NMR (MeOH-d₄, 400 MHz) δ 5.43 (d, 1H J = 4.8 Hz, C1-H), 4.49 (dd, 1H, J = 1.4, 5.8 Hz, C5-H), 4.14 (dt, 1H, J = 1.2, 46.4 Hz, C2-H), 4.02 (dd, 1H, J = 1.2, 7.2 Hz, C6-H), 3.74 (dt, 1H, J = 1.2, 19.2 Hz, C3-H), 3.68–3.64 (m, 1H, C6-H), 3.50 (s, 1H, C4-H); HRMS calc. for C₆H₉O₄FNa: 187.0383; found: 187.0410.

Acknowledgements

This work was supported by grants from the Swedish Research Council, The Knut and Alice Wallenberg Foundation, The Crafoord Foundation, and The Royal Physiographic Society in Lund. We thank Agata Ochocinska and Markus Ohlin for initial studies.

References

1. D. J. Vocadlo and G. J. Davies, Curr. Opin. Chem. Biol., 2008, 12, 539–555.
2. X. Biarnés, A. Ardèvol, A. Planas, C. Rovira, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2007, 129, 10686–10693.
3. A. Ardèvol, X. Biarnés, A. Planas and C. Rovira, J. Am. Chem. Soc., 2010, 132, 16058–16065.
4. L. Amorim, F. Marcelo, C. Rousseau, L. Nieto, J. Jiménez-Barbero, J. Marrot, A. P. Rauter, M. Sollogoub, M. Bols and Y. Blériot, Chem.–Eur. J., 2011, 17, 7345–7356.
5. S. P. George and M. B. Rao, Eur. J. Biochem., 2001, 268, 2881–2888.
6. R. C. Weast, M. J. Astle and W. H. Beyer, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, Florida, 67th edn, 1987, pp. E49–E53.
7. K. B. Wiberg and M. Marquez, J. Am. Chem. Soc., 1994, 116, 2197–2198.
8. G. W. Yip, M. Smollich and M. Gotte, Mol. Cancer Ther., 2006, 5, 2139–2148.
9. M. M. Fuster and J. D. Esko, Nat. Rev. Cancer, 2005, 5, 526–542.
10. R. Sasisekharan, Z. Shriver, G. Venkataraman and U. Naryanasami, Nat. Rev. Cancer, 2002, 2, 521–528.
11. D. Liu, Z. Shriver, G. Venkataraman, Y. El Shabrawi and R. Sasisekharan, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 568–573.
12. K. Mani, M. Belting, U. Ellervik, N. Falk, G. Svensson, S. Sandgren, F. Cheng and L.-Å. Fransson, Glycobiology, 2004, 14, 387–397.
13. M. Jacobsson, U. Ellervik, M. Belting and K. Mani, J. Med. Chem., 2006, 49, 1932–1938.
14. U. Nilsson, R. Johnsson, L.-Å. Fransson, U. Ellervik and K. Mani, Cancer Res., 2010, 70, 3771–3779.
15. A. Siegbahn, U. Aili, A. Ochocinska, M. Olofsson, J. Rönnols, K. Mani, G. Widmalm and U. Ellervik, Bioorg. Med. Chem., 2011, 19, 4114–4126.
16. R. Laatikainen, M. Niemitz, U. Weber, J. Sundelin, T. Hassinen and J. Vepsäläinen, J. Magn. Reson., Ser. A, 1996, 120, 1–10.
17. C. A. G. Haasnoot, F. A. A. M. De Leeuw and C. Altona, Tetrahedron, 1980, 36, 2783–2792.
18. M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383.
19. C. Beeson, N. Pham, G. Shipps and T. A. Dix, J. Am. Chem. Soc., 1993, 115, 6803–6812.
20. C. Thibaudeau, J. Plavec and J. Chattopadhyaya, J. Org. Chem., 1998, 63, 4967–4984.
21. J. W. Emsley, L. Phillips and V. Wray, Prog. Nucl. Magn. Reson. Spectrosc., 1976, 10, 83–115.
22. I. Alkorta, J. Elguero and G. S. Denisov, Magn. Reson. Chem., 2008, 46, 599–624.
23. A. Mele, B. Vergani, F. Viani, S. V. Meille, A. Farina and P. Bravo, Eur. J. Org. Chem., 1999, 187–196.
24. H.-H. Limbach, G. S. Denisov and N. S. Golubev, Isotope Effects in Chemistry and Biology, ed. A. Kohen and H.-H. Limbach, CRC Press, Boca Raton, Florida, 1st edn, 2006, ch. 7.
25. G. Gunnarsson, H. Wennerström, W. Egan and S. Forsén, Chem. Phys. Lett., 1976, 38, 96–99.
26. S. Shan, S. Loh and D. Herschlag, Science, 1996, 272, 97–101.
27. W. Caminati, J. Mol. Spectrosc., 1982, 92, 101–116.
28. B. Bernet and A. Vasella, Helv. Chim. Acta, 2007, 90, 1874–1888.
29. It should be noted that the bicyclic system of the levoglucosan structures forces the 1,3-diaxial ring substituents to be further apart, thus decreasing the strength of the hydrogen bond and the magnitude of the resulting scalar coupling, compared to that of e.g. compound 4 in the ¹C₄ conformation.
30. J. Ortner, M. Albert, H. Weber and K. Dags, J. Carbohydr. Chem., 1999, 18, 297–316.
31. A. D. Barford, A. B. Foster, J. H. Westwood, L. D. Hall and R. N. Johnson, Carbohydr. Res., 1971, 19, 49–61.
32. G. B. Payne, J. Org. Chem., 1962, 27, 3819–3822.
33. D. V. Yashunsky, Y. E. Tsvetkov, M. A. J. Ferguson and A. V. Nikolaev, J. Chem. Soc., Perkin Trans. 1, 2002, 242–256.
34. H. Zhao, Q. Pan, W. Zhang, I. Carmichael and A. S. Serianni, J. Org. Chem., 2007, 72, 7071–7082.
35. Y. Takagi, H. Sohtome, T. Tsuchiya, S. Umezawa and T. Takeuchi, J. Antibiot., 1992, 45, 355–362.
36. L. Goodman, H. Gu and V. Pophristic, J. Phys. Chem. A, 2005, 109, 1223–1229.
37. G. Widmalm and R. W. Pastor, J. Chem. Soc., Faraday Trans., 1992, 88, 1747–1754.
38. M. E. F. Soliman, G. D. Ruggiero, J. J. Ruiz Pernía, I. R. Greig and I. H. Williams, Org. Biomol. Chem., 2009, 7, 460–468.
39. L. Braunschweiler and R. R. Ernst, J. Magn. Reson., 1983, 53, 521–528.
40. T. Parella, F. Sánchez-Ferrando and A. Virgili, J. Magn. Reson., 1997, 126, 274–277.
41. B. O. Petersen, E. Vinogradov, W. Kay, P. Würtz, N. T. Nyberg, J. Ø. Duus and O. W. Sørensen, Carbohydr. Res., 2006, 341, 550–556.
42. A. Bax and M. F. Summers, J. Am. Chem. Soc., 1986, 108, 2093–2094.
43. L. D. Hall and J. F. Manville, Carbohydr. Res., 1969, 9, 11–19.
44. M. Michalik, M. Hein and M. Frank, Carbohydr. Res., 2000, 327, 185–218.
45. A. Pedretti, L. Villa and G. Vistoli, J. Mol. Graphics Modell., 2002, 21, 47–49.
46. D. A. Evans, M. J. Bodkin, S. R. Baker and G. Sharman, J. Magn. Reson. Chem., 2007, 45, 595–600.
47. M. Džoganováa, M. Černýb, M. Buděšínskýa, M. Dračínskýa and T. Trnka, Collect. Czech. Chem. Commun., 2006, 71, 1497–1515.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1 and S2 and ¹H and ¹³C NMR spectra of compounds 1–5 and 10–11. See DOI: 10.1039/c3ob40991k

---