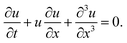Soliton-like thermophoresis of graphene wrinkles

Abstract

We studied the thermophoretic motion of wrinkles formed in substrate-supported graphene sheets by nonequilibrium molecular dynamics simulations. We found that a single wrinkle moves along applied temperature gradient with a constant acceleration that is linearly proportional to temperature deviation between the heating and cooling sides of the graphene sheet. Like a solitary wave, the atoms of the single wrinkle drift upwards and downwards, which prompts the wrinkle to move forwards. The driving force for such thermophoretic movement can be mainly attributed to a lower free energy of the wrinkle back root when it is transformed from the front root. We establish a motion equation to describe the soliton-like thermophoresis of a single graphene wrinkle based on the Korteweg–de Vries equation. Similar motions are also observed for wrinkles formed in a Cu-supported graphene sheet. These findings provide an energy conversion mechanism by using graphene wrinkle thermophoresis.

---

1 Introduction

Graphene, one of the thinnest elastic films in the world, exhibits exceptional mechanical,^1–3 thermal^4–6 and electronic properties.^7–9 Wrinkles and ridges have usually been observed in graphene sheets, which were obtained by mechanical exfoliation on SiO₂,¹⁰ chemical vapor deposition (CVD) growth on Cu foils¹¹ and SiC epitaxial growth,^12,13 mainly due to compressive effects from substrates and the low bending rigidity of graphene. Such structural corrugations have a remarkable impact on the electronic conductivity and quantum transport properties of graphene.^14–16 On the other hand, wrinkled graphene leads to new physical phenomena and is playing an increasingly important role in developing novel nano electromechanical systems. For example, wrinkled graphene sheets have recently been shown to be useful in flexible electronic sensors by cooperating with substrate morphology,¹⁷ and successfully employed to fabricate well-aligned graphene nanoribbons.¹⁸

How to manipulate and control wrinkle morphology is a key issue for utilizing wrinkled graphene characteristics to design functional devices. Previous experiments have shown that the geometry of pre-existing wrinkles or ridges in graphene sheets can be modified using atomic force microscopy (AFM) tips.^12,15 Moreover, thermally induced compressive strain creates periodic graphene wrinkles with controllable wavelength and amplitude.^19,20 During the working process of graphene-based devices, temperature might vary in different parts of the graphene. Wrinkles are actually hard to avoid in the graphene plane while the physical properties of graphene are closely related to its structure. However, the effects of temperature change on wrinkle structure and dynamic behaviors, to our best knowledge, are seldom considered in previous studies. On the other hand, thermal load, such as thermophoresis caused by temperature gradient, is a commonly used way to explore thermally actuated phenomena at the nanoscale, and also useful for converting thermal energy into desired mechanical energy.^21–25 Further investigations on the response of wrinkles to thermal influence are therefore necessary for actual applications of wrinkled graphene.

In this study, we show by nonequilibrium molecular dynamics (MD) simulations that a single wrinkle formed in a substrate-supported graphene sheet will move from hot to cold regions when subjected to a temperature gradient. Thermophoresis of the wrinkle is a constant acceleration motion, and its acceleration increases linearly with increasing the temperature deviation between the heating and cooling sides of the sheet. The atoms of the single wrinkle drift upwards and downwards, moving the wrinkle forwards. This kind of motion is similar to the dynamic behaviors of a solitary wave or single-soliton described by the Korteweg–de Vries (KdV) equation, where the solitary wave is localized and travels with unchanged shape.^26,27 The driving force for such thermophoretic movement can be attributed to the fact that the front root of the wrinkle transforming into the back root will have a lower free energy. Based on the KdV equation, we establish a motion equation to describe the soliton-like thermophoretic movement of a single graphene wrinkle. Furthermore, similar accelerated motion has been observed for two wrinkles formed in a Cu-supported graphene sheet, which move together from the hot to cold regions, but the wrinkle in the hotter region has a higher acceleration than that of the wrinkle in the cooler region. Our results unveil a novel energy conversion through thermophoresis of a graphene wrinkle.

2 Model and method

Here we choose an AB stacking graphite of three-layer as the substrate, of which the bottom layer is fixed in our simulations. The length and width of the substrate are 29.5 nm and 6.4 nm, respectively. A graphene sheet with the same size is placed on the substrate surface. The periodic boundary condition is applied in the width direction to avoid edge effect. Due to structural buckling, a wrinkle is created in the graphene sheet when a uniaxial compression applied at the left and right sides, as shown in Fig. 1(a). This kind of wrinkle has been experimentally realized by the compression from the AFM tips and substrates. Because of the large size scale for the considered system, the influence from interlayer registry and atom arrangement between the wrinkled graphene and substrate is slight. Nonequilibrium MD simulations²⁸ are performed by using the adaptive intermolecular reactive bond order (AIREBO) potential²⁹ to account for C–C interactions and the 6–12 Lennard-Jones (L-J) potential for nonbonding van der Waals interactions, which are implemented in the LAMMPS package.³⁰ The AIREBO potential has been shown to provide an accurate account of the chemical and mechanical behaviors of carbon materials.^31–34 The whole system is first relaxed in a canonical ensemble (NVT) at 300 K by a Nose–Hoover thermostat^35,36 for 200 ps, and the time step is 1 fs. Then two slabs with a length of 1.35 nm at the left and right sides of the sheet are chosen to model the heat source [red color in Fig. 1(a)] and heat sink (gray color) by increasing and decreasing the temperature around 300 K, respectively. The graphene sheet between the heat source and sink regions is relaxed again in a microcanonical ensemble (NVE) under a given temperature difference. As a result, a temperature gradient is established along the sheet with the average temperature between the heat source and sink keeping at 300 K. Such kind of setting for achieving thermal gradient has been widely employed in thermophoresis and heat transfer simulations.^21,37,38 Because of weak interlayer interactions, the substrate plays a role in stabilizing the wrinkle structure.

Fig. 1 (a) A wrinkle is created by applying a −6.1% uniaxial compression in the x direction of the graphene sheet supported by the graphite substrate (top), and a snapshot of the thermophoretic movement of the wrinkle under a temperature deviation of 100 K between the heating and cooling regions (bottom). (b) The temperature distribution along the graphene sheet averaged from 20 to 100 ps before the wrinkle starts to move. Here l is the length of the graphene sheet between the heating and cooling regions. The averaged temperature along the graphene sheet is about 300 K.

3 Results and discussion

We first consider a single wrinkle, which is formed by applying a uniaxial compression of ε = −6.1% on the graphene sheet, in the presence of the heat source and heat sink. For a given temperature deviation ΔT = 100 K between the heating and cooling slabs, the wrinkle firstly stays at its initial position and the whole sheet will be relaxed to build a temperature gradient along its longitudinal direction before the wrinkle movement, as shown by the averaged temperature profile in Fig. 1(b). Once the thermal gradient ΔT/l in the inner region is established after 100 ps, the wrinkle starts to run toward the cold side. Fig. 1(a) presents a MD snapshot of the wrinkle motion under ΔT = 100 K. This wrinkle will finally stop and stay at the cold end. To obtain the wrinkle motion characteristics, we record the translational displacements in the x direction under various ΔT, and the variations of the thermophoretic motion with time are plotted in Fig. 2(a). To simplify, we set the time to zero when the wrinkle begins to move. It is shown that this thermally activated motion depends on the temperature deviation between the heat source and sink. Higher temperature difference leads to a larger thermal gradient. The wrinkle is running faster under higher ΔT. Surprisingly, all the motion data can be well fitted by a quadratic polynomial: , here x is the translational displacement of the wrinkle and t is the time, and a_w, b_w, are the fitting parameters. In term of this equation, we can deduce . This indicates that the wrinkle runs with a constant translational acceleration. Moreover, the height and width of the wrinkle are approximately unchanged during its movement, suggesting an identical wrinkle effective mass. So we can assume that there is a force F acting on the wrinkle and satisfying F = M_ea_w, here M_e is the effective mass of the wrinkle. To further understand the thermal effect on the wrinkle, Fig. 2(b) presents the variations of the acceleration a_w with temperature gradient ΔT/l. The acceleration linearly increases with increasing temperature gradient. Therefore, the thermophoretic motion of the wrinkle can be described by Newton's second law of motion.

Fig. 2 (a) Translational displacement of the wrinkle of ε = −6.1% as a function of time under different temperature deviations ΔT. Here we set the time to zero when the wrinkle begins to move. The solid lines are the quadratic polynomial fits to the MD data. The inset shows the structure between the back root rb and front root rf of the wrinkle. (b)The variation of the translational acceleration a_w with temperature gradient ΔT/l.

Temperature also varies along the wrinkle, and the atoms at higher temperature possess higher potential energies. The translational movement of the wrinkle is actually activated by its carbon atoms detaching from substrate (ascending in the z direction) and attaching (descending) with substrate under the temperature gradient. Fig. 3(a) and (b) show some snapshots of the motion trajectory of the chosen atoms (cyan color) at the wrinkle front root under ΔT = 100 K (ΔT/l = 3.84 K nm⁻¹). The atoms at the front root firstly rise up and transform into the wrinkle top, then they fall down to the substrate and become the back root. This kind of motion is similar to the behavior of a solitary wave. The displacements of the chosen atoms in the z and x directions with time are shown in Fig. 3(c). Besides the vibration in the z direction, the atoms are also moving forwards along the x direction. The translational displacement in the x direction for the atoms completing the transition from the front root to the back root is just the value of the wrinkle length subtracting its width, while the wrinkle is moving forward with a distance equal to the wrinkle length. The corresponding free energies that are the sum of kinetic and potential energies for the chosen atoms are shown in Fig. 3(d). The energy increases as the atoms at the front root rise up, as denoted by the red arrow in Fig. 3(d), which means that the ascending process is endothermic. On the contrary, the energy decreases when the wrinkle top becomes the back root, and the descending process is exothermic. It is clearly shown in Fig. 3(d) that the energy change ΔE_b between the wrinkle top and back root is larger than that of ΔE_f between the top and front root, here ΔE_b = E_top − E_rb and ΔE_f = E_top − E_rf. The atoms at the wrinkle front root move forward to a colder region when they transform into the back root, as shown by the x displacements in Fig. 3(c), so that E_rb is lower than the initial E_rf. As a result, the thermophoresis of the wrinkle can occur only if ΔE_b > ΔE_f. The energy difference between E_rb and E_rf depends on the magnitude of the temperature gradient, which is the main driving force for the thermophoretic motion of the graphene wrinkle.

Fig. 3 The chosen carbon atoms highlighted by a cyan circle (a) ascend and (b) descend when the wrinkle is moving forward under ΔT/l = 3.84 K nm⁻¹. The black arrows denote the locations of these atoms, and the horizontal arrows show the translational direction of the wrinkle. (c) The displacements in the z and x directions, and (d) the free energy with time for the chosen atoms shown in (a) and (b). The shaded region represents the descending of the chosen atoms. E_rf, E_rb and E_top are the free energies for the chosen atoms located at the front root, back root and top of the wrinkle, respectively. Here we set the time to zero when the atom begins to move.

With increasing compression on the graphene sheet, the wrinkle height and length increase but the width decreases, and the shape of the wrinkle is changed as well, as shown by the insets in Fig. 4. Applying the thermal difference of ΔT = 200 K (ΔT/l = 7.69 K nm⁻¹) can still motivate the wrinkle to move from the hot site to the cold site. Similarly, all the MD motion data can be well fitted by a quadratic polynomial (Fig. 4), but the translation acceleration decreases with the strain increase. This is because the change of wrinkle shape increases its effective mass and extends the time for the front root transforming into the back root. However, the thermally driven motion will be halted when the highly deformed wrinkle is formed. Under ε = −21.2%, the front and back bottoms of the wrinkle bind together by non-bonding van der Waals interactions. This wrinkle cannot move in the presence of ΔT = 200 K or even higher, as the interlayer relative friction between the wrinkle bottoms is large enough to lock its movement.

Fig. 4 Translational displacements of the wrinkles of ε = −10.6% and −19.7% as a function of time under ΔT/l = 7.69 K nm⁻¹. The solid lines are quadratic polynomial fits of to the MD data. The insets show the structures of the wrinkles.

The thermophoretic movement and structural shape of the graphene wrinkles are very similar to a solitary wave and its motion characteristics. The motion equation of a single-soliton is usually described by the KdV equation:^26,39

One solution to this equation is: , here c is considered to be the velocity of the soliton. According to our MD simulation results and fitted quadratic polynomial, we assume that the wrinkle at different positions has a structural form: u_w = 3c_wsec h²ξ, here . c_w, a and b are constants, and c_w can be adjusted to make u_w consistent with the shape of the wrinkle. Then we can demonstrate that the u_w satisfies the motion equation below:

As the shape of the wrinkle is unchanged during traveling, the wrinkle motion can be considered as a kind of single-soliton. Compared with the KdV equation, there is an additional item . This is the driving force from thermal gradient for the accelerated motion of the wrinkles. The Hamiltonian of this soliton derived from the motion equation is:

here and A is a constant. The item is the kinetic energy, so should be the effective mass of the soliton. The effective mass increases with increasing the wrinkle height. It is also concluded from those equations that the acceleration decreases with increasing the effective mass under the same thermal gradient. The theoretical prediction from the motion equation coincides with the MD simulation results.

To understand the effect of substrate, we have studied thermophoretic motion of a wrinkle formed in a Cu-supported graphene sheet. We chose a graphene sheet with a length of 58.8 nm placed on a (100) Cu substrate. The C–C and Cu–Cu interactions are described by the AIREBO potential and embedded atom method (EAM) potential,⁴⁰ respectively. Here we use the 6–12 L-J potential to describe the C–Cu interaction with parameters σ_c–cu = 3.225 Å and ε_c–cu = 0.019996 eV, which have been proved to be valid for non-bonding C–Cu interaction.^41,42 The interlayer interaction between the graphene and the Cu substrate is stronger than that between two graphene sheets. A wrinkle is created by applying a uniaxial compression of −5.4%. Being the same as previous case, the wrinkle starts to move after a temperature gradient is established. Fig. 5 shows the variation of the translational displacement of the wrinkle with time under ΔT/l = 7.05 K nm⁻¹. All the motion data can be well fitted by the quadratic polynomial: . Therefore, soliton-like thermophoresis is also available for a single graphene wrinkle on Cu substrate.

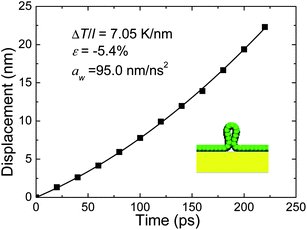Fig. 5 Translational displacement of the wrinkle of ε = −5.4% formed in Cu-supported graphene sheet as a function of time under ΔT/l = 7.05 K nm⁻¹. The solid lines are quadratic polynomial fits to the MD data. The inset shows the structure of the wrinkle.

Furthermore, we have studied thermophoretic motion of two graphene wrinkles on Cu substrate. The two wrinkles are created by applying a uniaxial compression of −10.88% with imposing a constraint in the middle part of the sheet. Then the whole system is relaxed without this constraint under 300 K for 200 ps. The two wrinkles are quite stable in the Cu-supported graphene, as shown in Fig. 6(a). The same simulation setting (Fig. 1) is applied for this system and a temperature gradient of ΔT/l = 3.53 K nm⁻¹ is formed along the sheet before the wrinkles move. Fig. 6(b) shows the displacements of the two wrinkles with time. The wrinkle (W1) in the hotter region comes into motion first, and the second wrinkle (W2) in the cooler region begins to move after an approximate 120 ps delay. Both the W1 and W2 motion data are well fitted by the quadratic polynomial: . The corresponding accelerations for the W1 and W2 are 122 and 112 nm ns⁻², respectively. This is because that the size and mass of wrinkle 1 are smaller than that of wrinkle 2. Due to a larger acceleration, the W1 moves faster than the W2 so that they crash with each other after 260 ps. The strong interaction between the crashed wrinkles leads to a structure shift, so the movement of the stacked wrinkles under thermal gradient is different from that of a single wrinkle, and finally they stay at the cooler site. These results indicate that the thermal gradient can drive graphene wrinkles moving to the cooler region and forming a tightly stacking wrinkle structure [the top inset in Fig. 6(b)] on a metal substrate. When the same system is put on a flat graphite substrate, owing to the weaker interlayer interaction it is difficult to stabilize two such wrinkles in the graphene plane, which will transform into one big wrinkle after structural relaxation at 300 K.

Fig. 6 (a) Two wrinkles are created by applying a uniaxial compression of ε = −10.88% in the x direction of the graphene sheet supported by Cu substrate. (b) Displacements of the two wrinkles W1 and W2 in the x direction as a function of time under ΔT/l = 3.53 K nm⁻¹. The solid lines are the quadratic polynomial fits of to the MD data before the wrinkles crash. The insets show the MD snapshots of the wrinkles at 120 and 260 ps.

4 Conclusion

The wrinkles in a substrate-supported graphene sheets subjected to thermal gradients will move from the hot to the cold region with constant accelerations. This thermophoresis obeys Newton's second law of motion and is described by our established motion equation based on the KdV equation of soliton. The wrinkle thermophoretic motion is mainly due to the atoms constituting the wrinkle front root having lower free energy when they transform into the back root. The soliton-like thermophoresis of wrinkles opens up a possibility of utilizing graphene wrinkles to design a thermal motor, and can be used for controllable manipulation of functional graphene-based devices.

Acknowledgements

This work is supported by the 973 Program (2013CB932604, 2012CB933403), the NSF (91023026, 11072109), and the Fundamental Research Funds for the Central Universities (no. NE2012005). We thank Prof. Tienchong Chang from Shanghai University and Dr Zhuhua Zhang for their helpful discussions.

References

1. J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank and D. M. Tanenbaum, et al. , Science, 2007, 315, 490.
2. C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
3. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60.
4. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan and F. Miao, et al. , Nano Lett., 2008, 8, 902.
5. J. H. Seol, I. Jo, A. L. Moore, L. Lindsay, Z. H. Aitken and M. T. Pettes, et al. , Science, 2010, 328, 213.
6. W. W. Cai, A. L. Moore, Y. Zhu, X. Li, S. Chen and L. Shi, et al. , Nano Lett., 2010, 10, 1645.
7. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson and I. V. Grigorieva, et al. , Nature, 2005, 438, 197.
8. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
9. F. Miao, S. Wijeratne, Y. Zhang, U. C. Coskun, W. Bao and C. N. Lau, Science, 2007, 317, 1530.
10. K. Xu, P. G. Cao and J. R. Heath, Nano Lett., 2009, 9, 4446.
11. X. Li, W. Cai, J. An, S. Kim, J. Nah and D. Yang, et al. , Science, 2009, 324, 1312.
12. G. F. Sun, J. F. Jia, Q. K. Xue and L. Li, Nanotechnology, 2009, 20, 355701.
13. G. Prakash, Mi. A. Capano, M. L. Bolen, D. Zemlyanov and R. G. Reifenberger, Carbon, 2010, 48, 2383.
14. K. Kim, Z. Lee, B. D. Malone, K. T. Chan, B. Alemán and W. Regan, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245433.
15. A. P. Barboza, H. Chacham, C. K. Oliveira, T. F. Fernandes, E. H. Ferreira and B. S. Archanjo, et al. , Nano Lett., 2012, 12, 2313.
16. W. Zhu, T. Low, V. Perebeinos, A. A. Bol, Y. Zhu and H. Yan, et al. , Nano Lett., 2012, 12, 3431.
17. Y. Wang, R. Yang, Z. Shi, L. Zhang, D. Shi and E. Wang, et al. , ACS Nano, 2011, 5, 3645.
18. Z. Pan, N. Liu, L. Fu and Z. Liu, J. Am. Chem. Soc., 2011, 133, 17578.
19. W. Bao, F. Miao, Z. Chen, H. Zhang, W. Jang and C. Dames, et al. , Nat. Nanotechnol., 2009, 4, 562.
20. Z. J. Li, Z. G. Cheng, R. Wang, Q. Li and Y. Fang, Nano Lett., 2009, 9, 3599.
21. A. Barreiro, R. Rurali, E. R. Hernandez, J. Moser, T. Pichler, L. Forro and A. Bachtold, Science, 2008, 320, 775.
22. H. Somada, K. Hirahara, S. Akita and Y. Nakayama, Nano Lett., 2009, 9, 62.
23. V. R. Coluci, V. S. Timoteo and D. S. Galvao, Appl. Phys. Lett., 2009, 95, 253103.
24. Z. Guo, T. Chang, X. Guo and H. Gao, J. Mech. Phys. Solids, 2012, 60, 1676.
25. S. Chen, Q. Li, Q. Zhang, Y. Qu, H. Ji, R. S. Ruoff and W. Cai, Nanotechnology, 2012, 23, 365701.
26. P. G. Drazin and R. S. Johnson, Solitons: An Introduction, Cambridge University Press, 1989.
27. A. La Magna, R. Pucci, G. Piccitto and F. Siringo, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15273.
28. F. M. Plathe, J. Chem. Phys., 1997, 106, 6082.
29. D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783.
30. S. Plimpton, J. Comput. Phys., 1995, 117, 1.
31. W. L. Guo, C. Z. Zhu, T. X. Yu, C. H. Woo, B. Zhang and Y. T. Dai, Phys. Rev. Lett., 2004, 93, 245502.
32. C. D. Reddy, A. Ramasubramaniam, V. B. Shenoy and Y. W. Zhang, Appl. Phys. Lett., 2009, 94, 101904.
33. Z. Wang, M. Devel, B. Dulmet and S. Stuart, Fullerenes, Nanotubes, Carbon Nanostruct., 2009, 17, 1.
34. H. Zhao, K. Min and N. R. Aluru, Nano Lett., 2009, 9, 3012.
35. S. Nose, J. Chem. Phys., 1984, 81, 511.
36. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
37. P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144306.
38. N. Wei, L. Q. Xu, H. Q. Wang and J. C. Zheng, Nanotechnology, 2011, 22, 105705.
39. D. J. Korteweg and F. de Vries, Philos. Mag., 1895, 39, 422.
40. J. B. Adams, S. M. Foiles and W. G. Wolfer, J. Mater. Res., 1989, 4, 102.
41. S. P. Huang, D. S. Mainardi and P. B. Balbuena, Surf. Sci., 2003, 545, 163.
42. C. M. Fuentes, B. H. Rhodes, J. D. Fowlkes, B. A. López, H. Terrones and M. L. Simpson, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041603.

---