1,2,4-Triazine-picolinamide functionalized, nonadentate chelates for the segregation of lanthanides(III) and actinides(III) in biphasic systems

Abstract

A novel family of nonadentate ligands based on the (5,6-diphenyl-1,2,4-triazin-3-yl)-picolinamide donor moiety has been synthesized from simple starting materials in high yield and purity. This group of ligands is an addition to the neutral nonadentate group but the first to incorporate 1,2,4-triazine. Their ability to extract a select group of lanthanides from acidic aqueous solution has been correlated to their ability to meet the ideal trigonal tricapped prismatic geometry that is seen by lanthanides and actinides in aqueous solution. The rate of metallation was determined using UV/VIS spectroscopy with pseudo first order conditions and showed similar behaviour to literature examples. Theoretical calculations were used to probe the bonding structure with lanthanides and actinides to predict the potential Ln/An segregating ability of the new ligands.

---

Introduction

The energy needs of human populations are growing with increases in population size. The necessity for clean, sustainable power is becoming an ever present topic of discussion in scientific circles and the media. Nuclear power generation is often proposed as a power source with a small carbon footprint compared to fossil fuel based energy production but as a source of power it brings substantial challenges to its environmental viability. With recent catastrophic events, future power plant builds may be limited but an issue exists with the quantity of high level waste already generated from domestic nuclear power production over the last six decades. Currently in the United States 60% of nuclear power plants have reached their capacity for storage in spent nuclear fuel pools and are storing the waste by alternate methods.¹

Nuclear fuel has a life time of approximately three years in a typical light water reactor before it is retired or recycled.² The spent nuclear fuel (SNF) is stored in cooling pools to allow the shortest lived radionuclides to dissipate. After this time, the waste constituents are a cocktail of various fission products containing approximately 95% of the parent ²³⁸U while the remaining 5% is a mixture of lanthanides (3.1%), plutonium (0.9%), minor actinides (0.1%), and other short and long lived fission products.³ Realistic storage and treatment strategies demand efficient segregation of the long-lived actinides (An) from the lanthanides (Ln). Though the quantity of americium and curium may seem initially insignificant relative to the scale of the industrial operation, these nuclides are significantly dangerous for 1 × 10⁶ years⁴ and given that a typical 1 Gigawatt reactor produces approximately 30 tonnes of waste per annum⁵ the worldwide production of these elements is actually quite substantial. The necessity for efficient separation of Ln and An arises due to the Ln large neutron cross section. This characteristic impedes transmutation treatment strategies for minimization of waste volume.⁶

At present industrial scale operations are in place for separation of U and Pu from acidic waste streams in the PUREX process (Plutionium Uranium Extraction). This method employs tri-n-butyl phosphate as extractant. Organophosphorous compounds are commonly employed for trivalent lanthanide (Ln³⁺) and trivalent actinide (An³⁺) separations. The PUREX process can be followed by other biphasic extractions upon the waste stream (DIAMEX, TRUEX, SANEX, TALSPEAK) to segregate specific substituents. The selective separation of Ln and An remains elusive as both groups of metals are classified as hard acids (all in the +3 oxidation state),⁷ they have minimal deviation in ionic radius,⁸ and they commonly take on the same coordination geometries and coordination numbers (8–12).⁹

It is theorized that the two groups of metals could be segregated by exploiting ligands with softer donor groups, in effect increasing the covalency of the M–L bonding. Recent work has demonstrated, by modulation of the donor character from hard to soft, an increased affinity of An³⁺ as compared to Ln³⁺.^10–13 In a telling recent study,¹⁴ three dichalcogen–phosphinic acid derivatives were compared with changing from a O/O, O/S, and S/S donor set. The solution structures were compared by X-ray fine structure (EXAFS) to determine an inherent difference between the exceptional ability of dithiophosphinic acid to coordinate An³⁺ compared to other extractants. The other derivatives generated various structures in solution including dimers and hydrogen bonded monodentate structures, dithiophosphnic acid (DTPA) took exclusively the ML₃ form in solution with a bidentate binding mode for all ligands. The authors concluded that increased covalency was the origin of the increased selectivity. Importantly, there was no clear shortening the bond lengths coupled to increases in stability in the dithiophosphinic acid complexes, an observation made previously with An³⁺ complexes with other ligands.¹⁵

A heterocyclic based extractant that has received wide attention is the 2,6-bis(5,6-dialkyl-1,2-4-triazin-3-yl)pyridines (BTP) originally discovered by Kolarik and co-workers^16,17 to have very high distribution ratios from highly acidic aqueous phases. BTP was shown to form ML₃ type structures in solution with An(III) and Ln(III) of similar ionic radii and M–L bond lengths but a much larger excess of ligand was necessary for Ln(III) to form exclusively ML₃ complexes.¹⁸ In competition experiments between U(III) and Ce(III), BTP completely formed U(BTP)₃³⁺ in solution by ¹H-NMR before any signal from the Ce(BTP)_x³⁺ was observed.¹⁹ More recently, the study of 1,2,4-triazine based extractants has expanded into bipyridine and phenanthroline systems.^20–22

By coupling the known selectivity of the 1,2,4-triazine moiety into a higher order chelate, the present study was undertaken to synthesize extractants that could be effective An³⁺/Ln³⁺ separators. These ligands would also offer other advantages in that may avoid hydrolytic and radiolytic stability problems commonly encountered with BTP.^23,24 To this end a new family of preorganized chelates has been synthesized bearing 1,2,4-triazine picolinamide arms tethered to a triphenoxymethane scaffold generating nonadentate, neutral ligands. The synthesis is reported along with the extraction properties into dichloromethane (DCM) from 1 M nitric acid aqueous solutions. The kinetics of metallation is presented along with a computational comparison of BTP with the presented donor sets.

Experimental

General considerations

¹H and ¹³C NMR spectra were recorded on a Gemini300, Varian300, or Mercury300 NMR instrument at 299.99 MHz for the proton channel and 75.47 MHz for the carbon channel. All UV/VIS spectra were recorded on a Varian Cary 50 spectrophotometer. Each sample analyzed by mass spectrometry was dissolved in appropriate solvent and underwent direct-injection through an autosampler, followed by ESI or APCI analysis with methanol (with or without 0.2% acetic acid) as mobile phase. The ions were detected with the Agilent 6210 TOF-MS while the data was processed with the MassHunter™ software. Elemental analyses were performed at the in-house facilities at the University of Florida. All solvents, unless otherwise noted, were used as received and either HPLC or ACS grade. Metal solutions were made using 18 MΩ Millipore deionized water and TraceMetal grade HNO₃ (Fisher Scientific). Arsenazo(III) dye (Alfa Aesar) was used as a UV/VIS sensitizer for all metal extraction experiments. Lanthanide nitrate and triflate salts were purchased from Sigma Aldrich and used as received as was 6-methyl-picolonitrile. Compounds 6, 7, and 8 were prepared as previously described.²⁵

For all UV/VIS experiments a quartz cuvette with a 1 cm path length was used along with dry, deoxygenated acetonitrile (MeCN) or tetrahydrofuran (THF) to allow for analysis down to λ = 240 nm. Ligand aliquots (3 mL) at approximately 7 × 10⁻⁵ M were pipetted into the cuvette using an automatic pipettor. The background consisted of 1 × 10⁻² M tetrabutylammonium nitrate ([NBu₄](NO₃)).

For kinetics measurements, pseudo first order conditions were used. The Yb solution concentration was 2.10 × 10⁻² M. The spike volume was adjusted to generate M : L ratios of approximately 15 : 1, 30 : 1, and 65 : 1. The spike was administered with an automatic pipettor and the solution was transferred back and forth three times with a glass pipette for mixing which lasted 2 to 3 seconds. The spectra were then collected at a gradient time scale for 80 minutes.

The procedure for metal extraction experiments followed a previous literature report.²⁶ 4 mL solutions of ligand in the chosen organic solvent were contacted with 4 mL of the 1 M nitric acid aqueous phase containing the metal at 1 × 10⁻⁴ M in 20 mL borosilicate scintillation vials with plastic cone lined urea caps (Fisher Scientific). Each extraction was performed in triplicate. The vials were sealed and contacted for 16 hours on a shaker table. The vials were then allowed 2 hours for phase separation. Then, aliquots of 1 mL of the aqueous phase were extracted with an automatic pipettor and placed in 25 mL volumetric flasks and diluted with formic acid/sodium formate with 2.5 mL of the Arsenazo(III) dye added. The UV/VIS absorption was collected at λ = 655 nm. The result was compared against the spectrum of the stock metal solution with no extraction according to the formula: E% = 100*[(A₁ − A)/(A₁ − A₀)] where A is the absorbance of the extracted aqueous phase, A₁ is the absorbance of the untreated metal solution, and A₀ is the absorbance of the metal free nitric acid solution diluted in the buffer. Distribution ratios (D) were defined as: D = Σ[M_org]/Σ[M_aq]. [M_org] is the concentration of the metal in the organic phase and [M_aq] is the corresponding concentration of the remaining metal in the aqueous phase. D was calculated based on the extraction efficiency: D = E%/(100 − E%). The final descriptor used was the separation factor which is a measure of the selectivity of a ligand for one metal as compared to another metal under the same extraction conditions and this is calculated by: SF_m/n = D_m/D_n.

Theoretical calculations

All density functional theory (DFT) calculations were carried out with the Gaussian' 03 software suite.²⁷ Spin-unrestricted multiplicities were used to account for the formal fⁿ configurations for the Ln and An. Each geometry optimization utilized the B3LYP functional and the 6-31G* basis set for C, H, O, and N. A small-core relativistic effective core potential (RSC ECP) was used for Eu, Am, and Cm. The RECP was taken from the EMSL basis set library which used work from the Stuttgart and Dresden groups.^28,29 The full geometry optimizations for each structure converged to within 2 kcal mol⁻¹ of the C₃ or D₃ symmetric complexes.

Single point energy calculations were performed to determine the Mulliken population analysis and the output was processed by the AOMix program package.^30,31 Spin contamination was closely monitored and found to remain near accepted levels. Orbital pictures were generated with Gabedit.³²

X-Ray structure solution

X-Ray intensity data was collected at 100 K on either a Bruker DUO or Bruker SMART diffractometer using MoKα radiation (λ = 0.71073 Å) or CuKα (λ = 1.54178 Å) and an APEXII CCD area detector. Raw data frames were read by program SAINT and integrated using 3D profiling algorithms. The resulting data was reduced to produce hkl reflections, intensities, and estimated standard deviations. Structures were solved and refined in SHELXTL6.1,^33,34 using full-matrix least-squares refinement. Where necessary, the program SQUEEZE, a part of the PLATON package³⁵ of crystallographic software, was used to calculate the solvent disorder area and remove its contribution to the overall intensity data. Solvent removed per project – La9: the solvent area included three ether and six methanol molecules, for Er9: five ether and three methanol molecules, for Yb9: three ether and three methanol molecules, for Yb10: four and a half ether and three methanol molecules, for Yb11: two and a half pentane and three ethanol molecules, and for Yb53: one MTBE molecule. Where necessary, disordered regions were refined in two, and sometimes in three, parts and refined with their site occupation factors dependently refined. Disordered parts' site occupation factors also were in some instances fixed after proper refinement.

Synthetic procedures

Compound 1. A 4.05 g portion of 6-methylpicolonitrile (34.3 mmol) was added to a flask with 65% hydrazine aqueous solution (65 mL) and heated to 70 °C for 4 hours during which time all the 6-methylpicolonitrile dissolved. The solution was cooled to room temperature and then placed in a refrigerator overnight. The resulting crystals were collected by filtration and dried under reduced pressure to yield 1 as white crystals (4.28 g, 83%). ¹H NMR (CDCl₃) δ ppm 2.53 (s, 3H), 3.97 (br s, 2H), 5.37 (br s, 2H), 7.10 (d, J = 7.4 Hz, 1H), 7.55 (t, J = 7.8 Hz, 1H), 7.79 (d, J = 7.9 Hz, 1H). ¹³C–{¹H} NMR, δ 24.2, 116.5, 123.2, 136.6, 149.0, 149.8, 156.7. HRMS-ESI: calcd for [M + H]⁺: m/z 151.0907. Found: m/z 151.0978. Anal. calcd for C₇H₁₀N₄: C, 55.98; H, 6.71; N, 37.31. Found: C, 55.65; H, 6.92; N, 37.54.

Compound 2. Compound 1 (1.50 g, 10.0 mmol) was combined with benzil (2.10 g, 10.0 mmol) in 150 mL of ethanol (EtOH). The mixture was heated to reflux for 4 hours before cooling to room temperature. The solvent was removed under reduced pressure and the residue was recrystallized from isopropanol to yield 2 as yellow crystals (3.08 g, 95%). ¹H NMR (CDCl₃) δ ppm 2.76 (s, 3H), 7.30–7.48 (m, 7H), 7.60–7.74 (m, 4H), 7.80 (t, J = 7.8 Hz, 1H), 8.47 (d, J = 7.6 Hz, 1H). ¹³C–{¹H} NMR, δ ppm 24.83, 121.31, 125.14, 128.44, 128.54, 129.48, 129.93, 130.65, 135.33, 135.63, 137.07, 152.31, 155.94, 156.18, 159.40, 160.83. HRMS-ESI: calcd for [M + H]⁺: m/z 325.1448; [2M + H]⁺: m/z 649.2828; [3M + H]⁺: m/z 973.4203. Found: m/z 325.1433, 649.2828, 973.4179. Anal. calcd for C₂₁H₁₆N₄: C, 77.76; H, 4.97; N, 17.27. Found: C, 77.50; H, 4.94; N, 17.36.

Compound 3. Compound 2 (5.31 g, 16.4 mmol) was dissolved in 175 mL of 1,4-dioxane and selenium dioxide (9.1 g, 81 mmol) was added to the reaction vessel which was then heated to reflux overnight. The reaction was cooled to room temperature and placed in the refrigerator for 1 hour. Solid impurities were removed by filtration and the solvent was removed under reduced pressure. The residue was dissolved in hot dimethylsulfoxide (100 °C) and the solution was cooled to room temperature. Cold water was added which caused 3 to precipitate as a pale yellow solid. The mixture was placed in the refrigerator for 2 additional hours and the resulting precipitate was collected by filtration and used without further purification. The main by-product was the overoxidized compound, 4, and further purification would reduce the overall yield of 4. ¹H NMR (CDCl₃) δ ppm 7.32–7.51 (m, 6H), 7.68 (dd, J = 16.8, 6.9 Hz, 4H), 8.08–8.20 (m, 2H), 8.91 (dd, J = 6.9, 1.6 Hz, 1H), 10.33 (s, 1H). ¹³C–{¹H} NMR, δ ppm 122.85, 128.02, 128.61, 128.65, 129.51, 129.89, 129.94, 130.99, 134.96, 135.29, 138.24, 153.21, 153.43, 156.29, 156.76, 159.81, 193.33.

Compound 4. A slurry was made by the addition of the residue of 3 to 175 mL of acetonitrile. Silver nitrate (13.9 g, 81 mmol) was dissolved in water (30 mL) and added to the reaction mixture which resulted in the complete dissolution of 3. Solid sodium hydroxide (4.9 g, 121 mmol) was added and the resulting black solution was stirred for 2 days. The pH of the solution was adjusted to approximately 3 by addition of 10% HCl solution. DCM was added (100 mL) and both layers were filtered over a Buchner funnel. The organic layer was separated and the aqueous layer was extracted with DCM (2 × 50 mL). The combined organics were washed with brine, dried with magnesium sulphate and the solvent removed under reduced pressure. The residue was stirred in a minimal amount of refluxing methanol which was then allowed to cool to room temperature. The resulting mixture was passed over a fritted filter to yield 4 as a pale yellow solid (4.80 g, 83%, based on 2). ¹H NMR (CDCl₃) δ ppm 3.28–3.61 (m, 3H), 7.34–7.54 (m, 6H), 7.57–7.72 (m, 4H), 8.14 (t, J = 7.8 Hz, 1H), 8.41 (d, J = 7.6 Hz, 1H), 8.88 (d, J = 7.9 Hz, 1H). ¹³C–{¹H} NMR, δ ppm 126.30, 126.97, 128.69, 129.47, 129.75, 130.13, 131.24, 134.57, 134.86, 139.12, 147.86, 151.01, 156.59, 157.10, 159.04, 165.19. HRMS-ESI: calcd for [MH]⁺: m/z 355.1190. Found: m/z 355.1206. Anal. calcd for C₂₂H₁₈N₄O₃: C, 68.38; H, 4.70; N, 14.50. Found: C, 68.21; H, 4.53; N, 14.66.

Compound 5. A 0.75 g portion of 4 (2.1 mmol) was combined with thionyl chloride (3.1 mL, 42 mmol) in 100 mL of chloroform and heated to reflux for 3 hours. The solvent was removed under reduced pressure to remove remaining thionyl chloride. The residue was dissolved in 100 mL of fresh chloroform and cooled to 0 °C. Dimethylaminopyridine (1.3 g, 10.5 mmol) was added and then di-sec-butylamine (1.10 mL, 6.3 mmol). The solution was warmed to room temperature and stirred overnight. The solvent was washed with 10% HCl solution (3 × 40 mL) followed by 1 M NaOH (40 mL) and brine (40 mL). The organics were dried with sodium sulphate and removed under reduced pressure. The residue was recrystallized from EtOH to yield yellow crystals of 5 (0.73 g, 74%). ¹H NMR (CDCl₃) δ ppm 0.77 (d, J = 6.5 Hz, 6H), 1.03 (d, J = 6.8 Hz, 6H), 1.88 (spt, J = 7.1 Hz, 1H), 2.21 (spt, J = 6.5 Hz, 1H), 3.44 (d, J = 7.6 Hz, 2H), 3.63 (d, J = 7.6 Hz, 2H), 7.30–7.50 (m, 6H), 7.61–7.74 (m, 4H), 7.82–7.89 (m, 1H), 8.00 (t, J = 7.9 Hz, 1H), 8.67 (dd, J = 7.8, 1.0 Hz, 1H). ¹³C–{¹H} NMR, δ 19.9, 20.3, 26.7, 27.9, 53.8, 56.4, 124.3, 125.7, 128.4, 128.7, 129.5, 129.8, 130.0, 130.9, 135.3, 135.5, 137.8, 151.1, 155.8, 156.2, 160.4, 168.6. HRMS-ESI: calcd for [M + H]⁺: m/z 466.2601. Found: m/z 466.2597. Anal. calcd for C₂₉H₃₁N₅O: C, 74.81; H, 6.71; N, 15.04. Found: C, 74.50; H, 6.74; N, 15.06.

Compound 9. A sample of 4 (1.51 g, 4.3 mmol) and thionyl chloride (6.2 mL, 85 mmol) were added to 100 mL of chloroform and the mixture was heated to reflux for 2 hours. The solvent was removed under reduced pressure to afford the crude acid chloride. This material was dissolved in 100 mL of fresh chloroform and cooled to 0 °C. A 0.60 g portion of 6 (0.95 mmol) and 2.32 g of 4-dimethylaminopyridine (DMAP) (19 mmol) were dissolved in a small amount of chloroform and injected into the reaction vessel drop wise. The reaction was then allowed to warm to room temperature and stirred overnight. The organic phase was washed with 40 mL of 10% HCl solution three times followed by washing with 1 M NaOH. The organics were dried with sodium sulphate and allowed to sit on the bench top for 1 hour, resulting in precipitation of the sodium salt of 4. The precipitate was removed by filtration along with the desiccant. The organics were then removed under reduced pressure. The final purification was accomplished by silica gel column chromatography using 1 : 4 : 1 DCM  : THF  : hexanes to afford 9 as a pale yellow solid (1.43 g, 91%). ¹H NMR (CDCl₃) δ ppm 1.06–1.31 (m, 27H), 2.17 (s, 9H), 3.61–3.71 (m, 6H), 3.76 (br q, J = 5.0, 5.0, 5.0 Hz, 6H), 6.92 (s, 3H), 6.98–7.14 (m, 10H), 7.21–7.43 (m, 15H), 7.45–7.58 (m, 12H), 7.78 (t, J = 7.8 Hz, 3H), 8.09 (d, J = 7.9 Hz, 3H), 8.41 (d, J = 7.9 Hz, 3H), 9.09 (t, J = 5.6 Hz, 3H). ¹³C–{¹H} NMR, δ 17.0, 31.4, 34.2, 40.1, 71.0, 123.6, 125.5, 125.7, 126.1, 128.3, 128.5, 129.5, 129.6, 129.8, 130.3, 130.6, 135.2, 135.2, 136.4, 137.8, 145.5, 150.9, 151.2, 152.8, 155.7, 156.1, 159.7, 164.1. HRMS-ESI: calcd for [M + H + K]⁺: m/z 840.3741. Found: m/z 840.3719.

Compound 10. A sample of 4 (1.55 g, 4.37 mmol) and thionyl chloride (3.17 mL, 44 mmol) were combined in 100 mL of chloroform and heated to reflux for 2 hours. The solvent was removed under reduced pressure to afford the crude acid chloride. The residue was dissolved in 100 mL of chloroform and cooled to 0 °C. A 0.74 g portion of 7 (0.97 mmol) and 2.38 g of DMAP (19.4 mmol) were dissolved in a small amount of chloroform and injected into the reaction vessel dropwise. The reaction was then allowed to warm to room temperature and stirred overnight. The organic phase was washed with 40 mL of 10% HCl three times followed by washing with 40 mL of 1 M NaOH three times. The organics were dried with sodium sulphate and allowed to sit on the bench top for 1 hour resulting in precipitation of the sodium salt of 4. The precipitate was removed by filtration along with the desiccant. The organics were then removed under reduced pressure. Final purification was accomplished by passing the residue over a plug of silica gel eluting with THF and removal of solvents under reduced pressure affording 10 as a pale yellow solid (1.19 g, 67%). ¹H NMR (CDCl₃) δ ppm 1.19 (s, 27H), 1.26 (s, 27H), 3.74–3.86 (m, 6H), 3.90–4.08 (m, 6H), 6.59–6.63 (m, 1H), 7.15 (dd, J = 9.6, 2.0 Hz, 6H), 7.22–7.42 (m, 18H), 7.50 (d, J = 7.4 Hz, 6H), 7.57 (d, J = 7.6 Hz, 6H), 7.84 (t, J = 7.8 Hz, 3H), 8.27 (d, J = 7.6 Hz, 3H), 8.54 (d, J = 7.6 Hz, 3H), 9.00 (t, J = 5.9 Hz, 3H). ¹³C–{¹H} NMR, δ 31.3, 31.5, 34.4, 35.4, 40.2, 67.9, 122.2, 123.8, 126.0, 126.8, 128.4, 129.5, 129.6, 129.9, 130.7, 135.1, 135.4, 137.7, 137.9, 141.9, 144.4, 150.9, 151.5, 153.3, 155.9, 156.1, 160.2, 164.3. Anal. calcd for C₁₁₂H₁₁₅N₁₅O₆: C, 76.12; H, 6.56; N, 11.89. Found: C, 75.81; H, 6.60; N, 11.73.

Compound 11. A sample of 4 (2.56 g, 7.22 mmol) and thionyl chloride (10.5 mL, 144 mmol) were combined in 120 mL of chloroform and heated to reflux for 2 hours. The solvent was removed under reduced pressure to afford the crude acid chloride. The residue was dissolved in 100 mL of chloroform and cooled to 0 °C. 8 (1.41 g, 1.61 mmol) and DMAP (3.92 g, 32 mmol) were dissolved in a small amount of chloroform and injected into the reaction vessel drop wise. The reaction was then allowed to warm to room temperature and stirred overnight. The organic phase was washed with 75 mL of 10% HCl three times followed by washing with 75 mL of 1 M NaOH three times. The organics were dried with sodium sulphate and allowed to sit on the bench top for 1 hour resulting in precipitation of the sodium salt of 4. The precipitate was removed by filtration along with the desiccant. The organics were then removed under reduced pressure. The residue was recrystallized from EtOH (35 mL) to afford 11 as yellow crystals (2.31 g, 76%).¹H NMR (CDCl₃) δ ppm 0.46 (t, J = 7.3 Hz, 9H), 0.54 (t, J = 7.3 Hz, 9H), 1.12 (br s, 18H), 1.25 (br s, 18H), 1.47 (q, J = 7.0 Hz, 6H), 1.62 (q, J = 7.0 Hz, 6H), 3.79 (br s, 6H), 3.93–4.27 (m, 6H), 6.56 (s, 1H), 7.02 (d, J = 10.0 Hz, 6H), 7.21–7.42 (m, 18H), 7.47 (d, J = 7.0 Hz, 6H), 7.56 (d, J = 7.0 Hz, 6H), 7.84 (t, J = 7.8 Hz, 3H), 8.28 (d, J = 7.6 Hz, 3H), 8.53 (d, J = 7.3 Hz, 3H), 9.20 (br t, J = 4.8, 4.8 Hz, 3H). ¹³C–{¹H} NMR, δ 9.1, 9.5, 28.5, 29.3, 34.8, 36.9, 37.5, 39.1, 40.1, 70.4, 124.0, 124.6, 125.9, 127.4, 128.4, 129.5, 129.6, 129.9, 130.7, 135.1, 135.3, 137.9, 139.8, 142.4, 151.1, 151.3, 153.2, 155.9, 156.1, 160.1, 164.4. HRMS-APCI: calcd for [M + H]⁺: m/z 1851.0167. Found: m/z 1851.0208; calcd for [M + Na]⁺: m/z 1872.9986. Found: m/z 1872.9987. Anal. calcd for C₁₁₈H₁₂₇N₁₅O₆: C, 76.55; H, 6.91; N, 11.35. Found: C, 76.61; H, 7.05; N, 11.35.

General procedure for metal complex synthesis

A portion of the appropriate ligand (approximately 0.2 g) was dissolved in a minimal amount of ethyl acetate until completely dissolved. Two equivalents of the metal salt were dissolved in 5–10 mL of ethyl acetate and pipetted into the reaction vessel, commonly inducing immediate precipitation. The reaction was stirred for 1–2 hours to ensure complete reaction. The solid was collected by filtration.

[La9][La(NO₃)₆]. X-ray quality crystals were grown by diffusion of diethyl ether into methanol. ¹H NMR (OC(CD₃)₂) δ ppm 1.19 (s, 27H), 2.25 (s, 9H), 2.56–2.73 (m, 3H), 2.89–2.98 (m, 3H), 3.97 (br t, J = 9.7, 9.7 Hz, 3H), 4.52–4.75 (m, 3H), 6.94 (d, J = 7.2 Hz, 3H), 7.09 (s, 3H), 7.15–7.19 (m, 1H), 7.29 (s, 6H), 7.35–7.48 (m, 9H), 7.51–7.59 (m, 3H), 7.61–7.69 (m, 6H), 8.43–8.55 (m, 3H), 8.67 (d, J = 8.0 Hz, 3H), 9.18 (d, J = 7.6 Hz, 3H), 9.75 (d, J = 9.2 Hz, 3H). Anal. calcd for C₁₀₃H₉₇La₂N₂₁O₂₄: C, 54.00; H, 4.27; N, 12.84. Found: C, 49.81; H, 4.08; N, 11.78.

[Er9][NO₃]₃. X-ray quality crystals were grown by diffusion of diethyl ether into methanol. ¹H NMR (CD₃OD) δ ppm 2.37 (s, 27H), 3.82–4.08 (m, 9H), 6.89–7.27 (m, 4H), 7.68–7.83 (m, 4H), 7.91 (br s, 10H), 8.57 (br s, 9H), 8.89–9.14 (m, 4H), 9.14–9.41 (m, 6H), 9.90–10.12 (m, 4H), 10.47–10.90 (m, 6H). Sample analyzed as [Er(9)][Er(NO₃)₆·(CH₃OH)₄]. The sample that was analyzed by single crystal X-ray diffraction and the one analyzed by elemental analysis were collected at different times but under the same conditions. It is unclear what causes the change from compositions with free nitrates versus with metal coordinated nitrates as the anion. Anal. calcd for C₁₀₇H₁₁₃Er₂N₂₁O₂₈: C, 51.91; H, 4.60; N, 11.88. Found: C, 51.31; H, 4.08; N, 11.92.

[Yb9][Yb(NO₃)₄·(CH₃OH)₂][(NO₃)₂]. X-ray quality crystals were grown by diffusion of diethyl ether into methanol. ¹H NMR (CD₃OD) δ ppm 2.17 (s, 27H), 3.64 (s, 9H), 4.89–5.06 (m, 6H), 5.10–5.23 (m, 3H), 5.25–5.41 (m, 3H), 6.49–6.66 (m, 3H), 6.88–7.03 (m, 3H), 7.66–7.86 (m, 10H), 8.31 (d, J = 2.0 Hz, 3H), 8.41 (br d, J = 7.0 Hz, 6H), 8.70 (t, J = 7.6 Hz, 3H), 8.88 (t, J = 6.8 Hz, 6H), 9.41–9.53 (m, 3H), 9.76–9.93 (m, 6H). Sample analyzed as [Yb(9)][Yb(NO₃)₄·(CH₃OH)₂][(NO₃)₂]. Anal. calcd for C₁₀₅H₁₀₅Yb₂N₂₁O₂₆: C, 52.04; H, 4.37; N, 12.14. Found: C, 51.63; H, 4.40; N, 11.64.

[Yb10][NO₃]₃. X-ray quality crystals were grown by diffusion of diethyl ether into methanol. ¹H NMR (CD₃OD) δ ppm 1.89 (s, 27H), 1.99–2.15 (m, 27H), 4.53–4.77 (m, 3H), 5.47–5.81 (m, 6H), 6.05–6.39 (m, 6H), 6.42–6.69 (m, 3H), 7.49–7.80 (m, 9H), 7.93–8.43 (m, 18H), 8.52–8.78 (m, 6H), 8.96–9.19 (m, 3H), 12.84 (br s, 3H), 13.72 (br s, 1H). Sample analyzed as [Yb(10)][(NO₃)₃·(CH₃OH)₃]. Anal. calcd for C₁₁₅H₁₂₇YbN₁₈O₁₈: C, 62.15; H, 5.76; N, 11.34. Found: C, 61.84; H, 5.47; N, 11.39.

[Yb11][SO₃CF₃]₃. X-ray quality crystals were grown by diffusion of pentane into acetone. ¹H NMR (CD₃OD) δ ppm 1.09 (br t, J = 7.2, 7.2 Hz, 3H), 1.21 (br t, J = 7.3, 7.3 Hz, 9H), 1.82 (s, 9H), 1.89 (m, J = 9.2 Hz, 18H), 2.14 (d, J = 3.4 Hz, 9H), 2.16–2.31 (m, 6H), 2.53–2.78 (m, 6H), 4.55–4.74 (m, 3H), 5.39–5.55 (m, 3H), 5.55–5.73 (m, 3H), 6.04–6.23 (m, 3H), 6.23–6.41 (m, 3H), 6.47–6.67 (m, 3H), 7.53–7.64 (m, 6H), 7.68 (d, J = 7.3 Hz, 3H), 7.97–8.11 (m, 9H), 8.19 (m, J = 7.3 Hz, 3H), 8.27 (t, J = 7.0 Hz, 6H), 8.62 (d, J = 6.7 Hz, 6H), 8.92 (s, 3H), 12.50–12.90 (m, 3H), 13.50–13.73 (m, 1H). Anal. calcd for C₁₂₁H₁₂₇F₉N₁₅O₁₅S₃Yb: C, 58.80; H, 5.18; N, 8.50. Found: C, 59.07; H, 5.27; N, 8.47.

[Yb5₃][SO₃CF₃]₃. X-ray quality crystals were grown by diffusion of methyl-tert-butyl-ether into a saturated solution in methanol. ¹H NMR (OC(CD₃)₂) δ ppm −23.98–−23.66 (m), −21.75–−21.48 (m), −19.06–−18.69 (m), −16.47–−16.12 (m), −14.42–−14.18 (m), −14.01–−13.73 (m), −12.51 (d, J = 5.5 Hz), −10.91–−10.59 (m), −10.28–−9.90 (m), −8.93 (d, J = 6.0 Hz), −8.79–−8.58 (m), −8.54–−8.33 (m), −8.25–−7.97 (m), −5.73 (d, J = 6.0 Hz), −5.07 (br s), −4.10 (br s), −2.94 (d, J = 6.0 Hz), −1.86 (br s), −1.72–−1.48 (m), −0.11 (d, J = 5.5 Hz), 0.19 (br s), 1.34–1.69 (m), 2.34–2.62 (m), 2.83 (br s), 3.09 (br s), 3.18–3.56 (m), 4.12–4.35 (m), 4.33–4.54 (m), 4.57–4.68 (m), 4.73–5.27 (m), 5.40–5.73 (m), 6.32 (br s), 6.52–6.71 (m), 6.80 (s), 7.15 (s), 7.22–7.49 (m), 7.58–7.92 (m), 7.86–8.09 (m), 8.32 (br s), 8.56 (d, J = 7.3 Hz), 9.34 (s), 9.45–9.66 (m), 9.63–9.93 (m), 10.40–10.66 (m), 10.99 (d, J = 6.9 Hz), 11.19–11.47 (m), 11.62–11.85 (m), 12.13 (s), 12.71 (s), 16.51–16.96 (m), 17.84–18.16 (m), 19.15–19.44 (m), 19.44–19.74 (m), 22.20–22.56 (m), 25.06–25.41 (m), 25.46–25.82 (m). Sample analyzed as [Yb5₃][(SO₃CF₃)₃·(CH₃OH)₂]. Anal. calcd for C₈₆H₈₉F₉N₁₅O₁₄S₃Yb: C, 51.73; H, 4.49; N, 10.52. Found: C, 51.84; H, 4.46; N, 10.04.

[Yb12₃][SO₃CF₃]₃·(CH₃OH)₃. X-ray quality crystals were grown by diffusion of diethyl ether into methanol. ¹H NMR (CD₃OD) δ ppm 0.69–0.85 (m, 2H), 1.08–1.21 (m, 1H), 8.09–8.27 (m, 6H), 9.40 (d, J = 3.7 Hz, 4H), 9.72–9.88 (m, 2H), 10.22 (br s, 4H), 13.11–13.33 (m, 4H). Sample analyzed as [Yb(12)₃][(SO₃CF₃)₃]. Anal. calcd for C₁₀₈H₆₉F₉N₂₁O₉S₃: C, 57.78; H, 3.10; N, 13.10. Found: C, 57.50; H, 3.03; N, 12.81.

Results and discussion

Synthesis of tris-picolinamide triphenoxymethane ligands

Numerous studies with BTP in solution and solid-state have shown the unique ML₃ metal to ligand stoichiometry with a coordination number of nine for lanthanides and actinides even in the presence of the strongly competing nitrate anion.^19,36–38 In this investigation, the design strategy centred on incorporation of the 1,2,4-triazine moiety into a scaffold that could preorganize nine donors. It was thought that tethering all nine donors onto one scaffold would generate efficient extractants by limiting the rearrangement energy upon complexation of the metal ion. The triphenoxymethane platform was chosen because it maintains the ‘all up’ conformation which has been verified by solid-state structural analysis and theoretical calculations (Fig. 1).^39–43 Additionally, the triphenoxymethane scaffold allows facile synthetic modulation of the alkyl substitution on the platform by choice of 2,4-substituted phenol.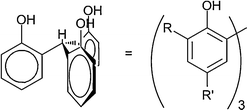

Fig. 1 Conformation maintained by the triphenoxymethane platform in solution and the solid state.

Incorporation of the 1,2,4-triazine moiety into a nonadentate extractant was accomplished by initially synthesizing 6-(5,6-diphenyl-1,2,4-triazin-3-yl)-2-picolinic acid (4) (Scheme 1). Insertion of hydrazine into the cyano group of 6-methyl-2-picolonitrile allowed formation of the hydrazonoimine (1).⁴⁴ Compound 1 can be combined with α-diketones for facile synthesis of 1,2,4-triazines with the alkyl substitution originating in the α-diketone. In this instance, benzil was used to install phenyl groups into the 5 and 6 position of the triazine ring. Protons in positions α to these ring positions are known to lead to multiple degradation pathways when BTP has been used in actinide extractions.⁴⁵ The use of benzil allowed for omission of problematic protonation in those positions and also incorporation of phenyl groups which in some studies have increased stability to gamma radiation.⁴⁶ The methyl group of 2 was then oxidized to the corresponding aldehyde (3) which was used immediately in the next reaction. ¹H-NMR showed the main ‘impurity’ in the residue to be a small amount of the carboxylic acid (4).⁴⁷ A second oxidation using silver nitrate and sodium hydroxide allowed isolation of pure 6-(5,6-diphenyl-1,2,4-triazin-3-yl)-2-picoinic acid (4).⁴⁸

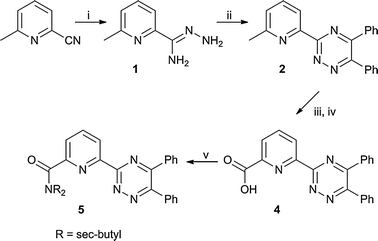Scheme 1 Synthesis of 1,2,4-triazine–picolinamide donor arm. (i) hydrazine–hydrate; (ii) benzil, EtOH; (iii) SeO₂, 1,4-dioxane; (iv) AgNO₃, NaOH, H₂O/THF; (v) HNCH₂CH(CH₃)₂, DMAP, CHCl₃.

Coupling of 4 to the triphenoxymethane scaffolds (6–8, Scheme 2) or sec-butyl amine was completed by initial formation of the acyl chloride derivative of 4, which was assumed quantitative. This was followed by combination of the isolated residue with the appropriate amine and DMAP to afford 5, and 9–11 in high yield and purity with an overall yield of 43–59% relative to 6-methylpicolonitrile.

Scheme 2 Synthesis of tris-(1,2,4-triazin-3-yl)picolinamide–triphenoxymethanes 9–11. Key (i) SOCl₂, CHCl₃; (ii) DMAP, CHCl₃.

Solid state structure analysis

Metal complexes were synthesized with various Ln (La, Er, Yb) for comparison of the ability of 9–11 to meet the preferred trigonal tricapped prismatic geometry. More closely meeting TTP geometry should produce more stable structures and preferential coordination. These structures were compared against the solid-state crystal structures of the terdentate derivative of the triazine–picolinamide complex [Yb5₃][(SO₃CF₃)₃] and against [Yb12₃3][(SO₃CF₃)₃] (12 = bis-(5,6-diphenyl-1,2,4-triazin-3-yl)-pyridine). The synthesis of BTP ligand 12 has been previously reported.⁴⁹

Shown in Fig. 2 is the structure for [La9][La(NO₃)₆] which is representative for all other nonadentate ligand–metal complexes (Er9, Yb9, Yb10, Yb11). All crystal structures indicate the ligands coordinate the La³⁺ ion through nine donors in distorted TTP geometry via three 1,2,4-triazine nitrogen atoms (N4, N5, N6), three pyridine nitrogen atoms (N1, N2, N3), and three amide–carbonyl oxygen atoms (O1, O2, O3). Twist angles are defined as the dihedral angle between associated donor atoms in the top and bottom plane of the trigonal prism made by the ligand (Fig. 2, right). The axis for the dihedral angle was chosen as the center of gravity of the plane made by the three donors on top and bottom of the trigonal prism (not shown). Inspection of the three structures with ligand 9 indicates a decrease in the twist angle as the Ln (La > Er > Yb) ionic radius decreases. The change in the bond lengths tracks very closely with the decrease in the ionic radii.⁸ These distances are summarized in Table 2 and complete listings of all crystal parameters can be found in Table 1.

Fig. 2 (Left) X-ray crystal structure of [La(9)][La(NO₃)₆]. (Right) View down the crystallographic c-axis highlighting the distortion from TTP geometry (black bonds are drawn only as a guide for the eye). Metal centers and their immediate coordination spheres are represented by 50% probability ellipsoids, all others are shown at standard radii. Hydrogens and disordered atoms have been removed for clarity.

Table 1 X-ray data for the crystal structures for La9, Er9, Yb9, Yb10, Yb11, Yb5₃, and Yb12₃3

	[La9][La(NO3)6]^a	[Er9] [NO3]3^a	[Yb9][Yb(NO3)4·(CH3OH)2][NO3]2^a	[Yb10][NO3]3^a^,^c	[Yb11][SO3CF3]3^a	[Yb53][SO3CF3]3^b^,^c	[Yb123][SO3CF3]3·(CH3OH)3^a
R 1 = Σ(∥Fo|−|Fc∥)/Σ|Fo|, wR2 = [Σ[w(Fo^2−Fc^2)^2]/Σ[w(Fo^2)^2]]^1/2.a MoKα radiation (λ = 0.71073 Å).b CuKα radiation (λ = 1.54178 Å).c Flack parameters of Yb10 and Yb53 are 0.402(17) and 0.008(5), respectively (racemic twinning applied).
Empirical formula	C121H151La2N21O33	C126H159ErN18O23	C120H145N21O32Yb2	C133H159N18O22.50Yb	C139H175F9N15O18S3Yb	C95H105F9N15O13S3Yb	C111H83F9N21O13S3Yb
Total reflections	40185	54385	18761	5536	125559	37661	66571
Uniq. reflections/reflections I > 2σ(I)	22967/20200	30261/22824	9684/8278	5536/4482	31899/22963	12824/12386	23419/20763
Collection range (°)	1.12 to 25.00	0.79 to 22.50	1.01 to 18.76	1.48 to 27.50	1.52 to 27.50	3.17 to 66.50	1.50 to 27.50
M r	2704.45	2460.97	2739.65	2542.82	2784.16	2105.16	2359.20
Crystal system	Triclinic	Triclinic	Triclinic	Cubic	Triclinic	Monoclinic	Triclinic
Space group	P1̄	P1̄	P1̄	P213	P1	Cc	P1̄
Z	2	4	2	4	2	4	2
a (Å)	18.2537(10)	21.310(2)	17.6026(14)	23.7722(9)	14.8807(3)	24.8539(6)	13.6476(9)
b (Å)	18.390(1)	21.575(2)	17.8227(15)		20.2373(4)	13.9870(3)	16.3938(10)
c (Å)	20.7899(12)	25.924(2)	20.5821(17)		24.8721(6)	28.8206(6)	23.0054(14)
α (°)	74.209(1)	82.036(2)	81.5270(10)		95.009(2)		88.036(1)
β (°)	89.492(1)	86.570(1)	81.6540(10)		101.027(2)	107.791	89.204(1)
γ (°)	87.577(1)	84.975(1)	88.4920(10)		107.138(1)		82.558(1)
V c (Å^3)	6709.5(6)	11744.8(19)	6318.9(9)	13434.1(9)	6942.5(3)	9687.0(4)	5100.5(6)
D c (g cm^−3)	1.139	1.392	1.440	1.257	1.332	1.443	1.530
F(000)	2408	5172	2816	5332	2914	4332	2388
μ[Mo-Kα] (mm^−1)	0.709	0.795	1.555	0.769	0.799	3.120	1.071
R 1[I > 2σ(I)data]	0.0395	0.0567	0.0470	0.0580	0.0469	0.0284	0.0324
wR 2[I > 2σ(I)data]	0.1082	0.1521	0.1348	0.1645	0.1025	0.0679	0.0833
GoF	1.101	1.093	1.092	1.090	0.914	1.055	1.044
Largest peak, deepest trough (e Å^−3)	+1.800, −1.233	+1.929, −1.785	+1.032, −1.037	+1.434, −0.625	+0.980, −1.133	+0.747, −0.695	+1.904, −1.056

---

Table 2 Bond length data for [La9][La(NO₃)₆], [Er9][(NO₃)₃], [Yb9][Yb(NO₃)₄ (CH₃OH)₂][(NO₃)₂], [Yb10][(NO₃)₃], [Yb11][(SO₃CF₃)₃], [Yb5₃][(SO₃CF₃)₃], and [Yb12₃][(SO₃CF₃)₃]. The complexes are labelled in the table with only the metal and ligand shown

		La9	Er9	Yb9	Yb10	Yb11	Yb53	Yb123
a Radii from Shannon, Acta Crystallogr. A, 1976, 32, 751. for coordination number 8.
M–NTriazine	(Å)	2.702(2)	2.526(5)	2.523(7)	2.521(6)	2.531(3)	2.474(3)	2.482(2)
M–NPyridine	(Å)	2.692(2)	2.489(5)	2.472(7)	2.472(6)	2.476(3)	2.470(3)	2.459(2)
M–O	(Å)	2.454(2)	2.319(4)	2.298(6)	2.279(5)	2.301(2)	2.271(2)
Twist angle	(°)	22.1	12.8	11.6	12.5	13.0	9.9	10.5
Ion. rad.^a	(Å)	1.30	1.14	1.13	1.13	1.13	1.13	1.13

---

The largest twist angle of 22.1° was found for La9, while an angle of 12.8° and 11.6° was found for Er9 and Yb9, respectively. This equates to a difference of 9.3° between the La and Er structures. The solid-structure of Yb5₃ shows a twist angle 9.9°, which was the smallest measured and smaller than the comparable terdentate BTP complex. Ligand 5 has no scaffold to constrain its movement and has the ability to settle into the most stable orientation implying that the triphenoxymethane scaffold does not substantially constrain the movement of the donor arms. A non-linear decrease is seen in the twist angle which roughly follows the change in extraction ability in biphasic systems. This data is in contrast to 5 which has the smallest twist angle, which shows only nominal ability to extract Ln with no preference for any specific Ln (see extraction data below).

Extraction behaviour for 9, 10, and 11

The ability of 9, 10, and 11 to extract a select group of Ln ions from an acidic aqueous phase into organic phases was explored to determine preferential extraction. The extraction experiments were carried out with DCM or 1-octanol as the organic phase and 1 M HNO₃ as the aqueous phase containing the chosen metal ion with a metal to ligand ratio of 1 : 10. The metal concentration was 1 × 10⁻⁴ M and the ligand was 1 × 10⁻³ M. The phase contact time was approximately 16 hours with two hours allowed for phase separation. The results for DCM are depicted in Fig. 3. In extraction experiments under the same conditions using 1-octanol the ligands showed no ability to remove any tested Ln from the organic phase presumably due to insolubility of the metal–ligand complex.

Fig. 3 Extraction data for ligands 5, 9, 10, and 11 from 1 M nitric acid into DCM for a select group of lanthanides. The contact time was 12 h and the [L] = 1 × 10⁻³ M for 9–11 and 3 × 10⁻³ M for 5 and [M³⁺] = 1 × 10⁻⁴ M for all Ln.

For all nonadentate ligands a subtle preference was observed for the heavier, smaller lanthanides. For 11, which exhibited the largest difference in distribution ratios, the separation factor between Yb and La was approximately 2. The increased steric bulk in 11, though impinging upon the flexibility of the donor arms, also increases the solubility in organic solvents. This effect is also proportional to the solubility of the extracted metal complex as each ligand is expected to have the same general formula for the extracted species, ML(NO₃)₃.

For comparison, the terdentate derivative of the picolinamide donor arm, 5, was also tested under the same conditions as the nonadentate ligands with the only difference being an increased ligand concentration, 3 × 10⁻³ M, to have a comparable number of available donors. This ligand essentially showed no selectivity (Fig. 3) for any metals within the lanthanide series tested and a diminished ability to extract relative to its preorganized congeners. This leads to the conclusion that the restriction of movement arising from the triphenoxymethane platform imbues some modest selectivity that is not inherently shown by the donor atoms themselves.

Metallation rate analysis

A necessary property for industrial applications of biphasic extractants is fast kinetics of metallation, and often large, preorganized ligands can exhibit slow binding kinetics in comparison to small mono or bidentate analogues. The rates of metallation of 11 were measured using UV/VIS spectroscopy and pseudo first order kinetics conditions since this sterically demanding; nonadentate ligand was expected to have the slowest kinetics.

The experiment was performed by adding spikes of large excess of Yb(NO₃)₃·5H₂O relative to 11 (approximately 15 : 1, 30 : 1, and 65 : 1), mixing for approximately three seconds and then measuring the UV/VIS spectrum at predetermined time intervals. Experiments were run in THF as it gave the best balance of solubility and measureable reaction time. Methanol is the most common solvent in the literature for these types of experiments but due to limited solubility of the ligand in methanol this solvent was not employed.⁵⁰

A collection of UV/VIS spectra are shown in Fig. 4 (left) for the 30 : 1 addition showing the change over time for the expected metallation reaction defined in eqn (1) (2 minute intervals). On the right of Fig. 4 is a plot of the change at λ = 305 nm, the wavelength with the largest change over time and used in all analysis. Spectra were treated according to eqn (2) from which k_obs was extracted as the slope of the plot of ln(A_∞− A_t) versus time. The linearity of these plots and the clear isosbestic points indicate that the metallation reaction is pseudo-first order. The results of the kinetic analysis are collected in Table 3 for compound 11 and all metal solution additions.⁵⁰ The rate constant for the reaction (k) was determined as the slope of the plot of k_obsversus [M³⁺] according to eqn (3), assuming a simple 1 : 1 metal : ligand interaction. As expected, the more sterically bulky, higher denticity ligands in this study were approximately 4 to 5 orders of magnitude slower than their terdentate counterparts in forming 1 : 1 metal to ligand complexes as reported by Hubscher-Bruder et al.⁵⁰

M³⁺_aq + 3NO_{3 aq}⁻ + L_org → ML(NO₃)_3org (1)

ln(A_∞ − A_t) = −k_obst + ln(A_∞ − A₀) (2)

k_obs = k[M³⁺] (3)

Theoretical descriptions of ML₃ complex analogues

To gain insight into the preferential bonding of bis-(1,2,4-triazin-3-yl)-pyridines (BTP) compared to other similar terdentate nitrogen donor ligands, the investigation was extended to incorporate theoretical calculations to explore the role of increased covalency in An complexes versus Ln complexes as a source of selectivity. This approach remains a challenging task due to the paucity of theoretical data limiting calibration and causing analysis to remain ambiguous.^51,52 The limited experimental data available for the hazardous and rare An further complicates calculations.

Fig. 4 Representative plot of UV/VIS spectra for titration of 11 with a 30 : 1 excess of Yb at varying time intervals and (inset) absorbance change over time plot at λ_max = 305 nm. [L] = 2.10 × 10⁻⁵ M in THF.

Table 3 Experimentally determined k_obs and k for 11 with Yb(NO₃)₃·5H₂O in THF

M to L	k obs (s^−1)	k (M^−1 s^−1)
15 : 1	1.28 × 10^−3	4.12
30 : 1	2.20 × 10^−3	3.60
65 : 1	4.87 × 10^−3	3.71

---

Theoretical approaches are especially important in cases where similar bond lengths are found between Ln(BTP)₃³⁺ complexes and An(BTP)₃³⁺ complexes, but in extraction experiments, there is observed selectivity for An. BTP and DTPA both show excellent selectivity for Cm(III) over Eu(III) in biphasic extraction systems, but according to EXAFS data on the solution structure, there are negligible differences between the complexes.^14,18

In the work reported here, systems were evaluated from three different approaches. First, target structures were optimized at the DFT level (Fig. 5). Second, the electronic structure of the simplified target ligand arms were analyzed for characteristic electronic properties and the results compared to those of a BTP derivative. Third, the orbital population of the ML₃ complexes were analyzed and compared to determine the extent of covalent bonding interactions. Similar calculations were performed on BTP complexes for comparison to literature examples and solid-state structures collected in house with synthesized BTP derivatives.

Fig. 5 BTP derivatives and simplified 1,2,4-triazine–picolinamide used as the basis of theoretical calculations.

Geometry optimizations

Terdentate heterocyclic ligands frequently show monomeric structures unless combined with large excesses of ligand and this is especially true when combined with the smaller Ln (Sm–Lu).^53–56 Terpyridine only attains the ML₃ structure when in the presence of excess ligand and very weakly coordinating anions.⁵⁴ These literature results make BTP more striking in its coordination chemistry. Even addition of 1 : 1 combinations of BTP–Pr to An(III) in the presence of the strongly competitive nitrate (NO₃⁻) anion forms preferentially the ML₃ structure.³⁶

Validation of the theoretical method was done by comparison of geometry optimization of Cm(BTP–H)₃³⁺ to solution-state EXAFS data for Cm(BTP–Pr)₃³⁺ reported by Denecke and co-workers¹⁸ along with calculations in that same report¹⁸ and the calculations results of Maldivi and co-workers.⁵⁷ The calculation method reported herein deviated from the earlier works in that a less verbose basis set was used to obtain similar geometries and that the geometries were not constrained to D₃ or C₃. The results are summarized in Table 4. The treatment used in this report shows a similar overestimation of the M–N bond lengths for both the pyridine and the 1,2,4-triazine moieties in BTP.

Table 4 Summary of theoretical data for Cm(BTP–H)₃³⁺ with experimental data for Cm(BTP–Pr)₃³⁺ and two different literature calculations

		Exp.^a	Calc.^a	Calc.^b	Calc.^c
a Data from ref. 18. b Data from ref. 57. c This work.
M–NTriazine	(Å)	2.57 ± 0.01	2.636	2.61	2.631
M–NPyridine	(Å)	2.57 ± 0.01	2.646	2.61	2.643

---

Geometry optimizations were carried out for BTP–H and TPAm with Eu, Cm, and Am. The value for M–N_Triazine is the average of all six bonds in the BTP based structures and the average of three bonds in the 1,2,4-triazine–picolinamide based structures. The relevant bond lengths and twist angles are collected in Table 5.

Table 5 Complete geometry optimization results for ML₃ complexes with M = Eu, Am, and Cm and L = BTP–H or TPAm

		Eu(BTP–H)3^3+	Am(BTP–H)3^3+	Cm(BTP–H)3^3+	Eu(TPAm)3^3+	Am(TPAm)3^3+	Cm(TPAm)3^3+
M–NTriazine	(Å)	2.60	2.62	2.63	2.65	2.69	2.67
M–NPyridine	(Å)	2.61	2.64	2.64	2.62	2.66	2.67
M–O	(Å)				2.39	2.43	2.44
Twist	(°)	16.69	17.95	17.80	16.99	17.47	18.99

---

Ligand orbital comparison

The energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) has been used previously to determine the absolute hardness of donating ligands.⁵⁸ The absolute hardness for ligands of BTP–H and TPAm were evaluated with this approach. The ligands were treated as a fragment made up of three ligands (3L) and the HOMO–LUMO energy gap measured for the combined fragment.

For BTP–H, the donating nitrogen lone pairs are accumulated in the HOMO orbitals of the 3L fragment. The LUMO is comprised of the π* of the triazine aromatic system. It is thought that softer donors can increase the level of covalent character in the bonding with an appropriate metal that has orbitals of the proper energy and symmetry.

The selectivity of BTP–H for An has been well documented, but the driving force for selectivity is still unclear.^19,38 A recent theoretical analysis was carried out by Petit and co-workers⁵⁹ in a manner similar to that described above. A comparison was made between BTP–H, the methylated derivative (BTP–Me), and terpyridine as L₃ fragments. The authors pointed out that though terpyridine has the lowest energy for its donating electrons, its LUMO (π* character) was at a much higher energy. BTP–H and BTP–Me had slightly higher energy donating orbitals, but the LUMO of each was significantly closer in energy to the HOMO compared to terpyridine.⁵⁹ Predictably, BTP–H has the smallest energy gap (88.1 kcal) as it contains six softer donor 1,2,4-triazine rings within the fragment. TMAm contains an amide carbonyl oxygen donor and this causes and increase to 91.1 kcal, yet this amounted to only a 3 kcal increase in the energy separation.

ML₃³⁺ electronic structure

The extent of 5f-orbital contribution to bonding in complexes is commonly analyzed for comparison to the 4f-orbital contribution. It has been observed numerous times that the 5f are more radially extended and available to generate covalent interactions. In many cases, the extent of bonding of the s, p, and d orbitals in covalency is similar and therefore cannot be the differentiating factor.¹³ It should be noted that recently this approach was succinctly critiqued by Kaltsoyannis as that report focused on electron density build up at a bond critical point using the QTAIM method as opposed to orbital mixing arguments.⁶⁰

Bis-(1,2,4-triazin-3-yl)-pyridine molecular orbital descriptions. Eu(BTP–H)₃³⁺, Am(BTP–H)₃³⁺, and Cm(BTP–H)₃³⁺ were all treated with the same theoretical method to give a baseline for comparison to other literature studies with the same systems. The europium in Eu(BTP–H)₃³⁺ showed minimal covalent interaction with the ligand orbitals. Only one interaction of Eu f-orbitals was seen in the HOMO[−35] which consisted of 3.4% f-orbital and 47.1% of the ligand HOFO[−19]. This molecular orbital is severely buried in energy and should not be deemed indicative of a frontier orbital interaction. There is also one molecular orbital each for the metal d-orbitals and s-orbitals with contributions of 3.2% and 2.2% respectively. Overall, this is insignificant relative to the electrostatic interactions that dominate the bonding picture.

Am(BTP–H)₃³⁺ on the other hand had noteworthy orbital interactions within an array of molecular orbitals. Contributions from the f-orbitals are seen in four different molecular orbitals (HOMO[−9], [−10], [−11], and [−13]) with metal contributions of 39.2%, 25.1%, 36.3%, and 44.6%, respectively and an average ligand contribution of 26.6% (Fig. 6, Fig. S10, Chart S2, ESI†). (The full orbital breakdown can be found in the ESI†)

Fig. 6 Three dimensional representation of Am(BTP–H)₃³⁺ molecular orbital HOMO[−9]. Example of a M–L covalent interaction.

The valence orbital structure of Cm(BTP–H)₃³⁺ has a significantly different energetic profile when contrasted with the structure of Am(BTP–H)₃³⁺. The highest occupied orbitals in Am(BTP–H)₃³⁺ are metal centered (HOMO[0] to HOMO[−14]) and contain the f-electrons (f⁶ electron configuration) but the analogous orbitals in Cm(BTP–H)₃³⁺ (f⁷) are set within the molecular orbital manifold from HOMO[−12] to HOMO[−29]. This clearly shows the energetic recession of the f-orbitals moving from left to right across the actinide series.^61,62

An analysis of the orbital structure of Cm(BTP–H)₃³⁺ shows a diminished but existent f-orbital contribution compared with Am(BTP–H)₃³⁺. Three interactions between Cm f-orbitals and ligand orbitals (HOMO[−33], [−43], [−44]) with an average metal contribution of 17.0% and ligand contribution of 31.6% were calculated (Fig. S9, ESI†). It is interesting to note that HOMO[−43] and HOMO[−44] of Cm(BTP–H)₃³⁺ show interaction of the metal f-orbital with the triazine rings while for Am there are three molecular orbitals with interactions with the ligand triazine rings.

BTP–H is predicted to interact with An with a degree of covalency that other terdentate N-donor ligands cannot. Also, according to the calculation results, it is implied that f-orbital contributions could be the determining factor in why BTP–H is able to selectively coordinate An over Ln. Only the f-orbitals show any real deviation from complex to complex while the s, d, and p orbitals all exhibit similar, small percentages (<4%) in a small number of molecular orbitals.

(1,2,4-Triazin-3-yl)picolinamide molecular orbital descriptions. A similar comparison was made between Eu(TPAm)₃³⁺, Am(TPAm)₃³⁺, and Cm(TPAm)₃³⁺. In each structure, the total number of covalent interactions between the metal f-orbitals with ligand orbitals decreased relative to M(BTP–H)₃³⁺ which was expected as the total number of triazine rings decreased from 6 in the BTP–H structures to 3 in the TPAm structures.

The expected bonding picture for Eu(TPAm)₃³⁺ was congruent to Eu(BTP–H)₃³⁺ in that there were only three molecular orbitals that contained positive interactions: one with d-orbital character, one with s/p mixing, and one with s-orbital character. The maximum percentage contribution was only 2.8% and the average donation was on the order of 2% which resided in the HOMO[−16], HOMO[−29], and HOMO[−56] indicating insignificant covalent interaction. The f-orbital density resided in the filled HOMO[−35] to HOMO[−50] with with no indication of covalent overlap with the ligands.

The case of Am(TPAm)₃³⁺ was more complex. The HOMO[0] to HOMO[−4] orbitals were on average 75% metal f-orbital with no overlap with ligand orbitals. These molecular orbitals represent the non-interacting f-orbital electrons as Am(III) has an f⁶ configuration. Three orbitals showed significant overlap with f-orbital density with a contribution of 8.4% in the HOMO[−5], 8.6% in the HOMO[−20], and 2.7% in the HOMO[−26] for an average donation of 6.6%. As predicted, there is a sharp decline relative to BTP–H but it was not expected that the drop off would be larger than 50% and that the total number of interactions would decrease. For An affinity to be seen for 9, 10, and 11 the preorganization of donors and constriction of movement will have to be the driving force if there is to be any observed selectivity to the ligands according to these results.

The Cm(TPAm)₃³⁺ case was more divergent than the Am case. Similar to Cm(BTP–H)₃³⁺, the orbitals containing the non-interacting f-electrons reside at lower energies and are within the molecular orbital manifold from HOMO[−8] to HOMO[−30]. There is one small s-orbital contribtion in the HOMO[−36] of 1.6% and a d-orbital contribution to the HOMO[−15] of 2.0%.

The f-orbital contribution resides in only two molecular orbitals, the HOMO[−24] and the HOMO[−30] (Fig. 7) with large contributions of 43.7% and 43.1%, respectively with an average of 19.7% donation arising from the ligands. Upon close inspection, the donation in HOMO[−24] is clearly coming from the oxygen of the amide carbonyl and in HOMO[−30] the donation arises from the pyridine nitrogen lone pairs. Therefore, even though two strong covalent interactions are predicted with an average of 43.4% f-orbital contribution, upon visual inspection of the orbitals all interaction with ligand orbitals on the triazine rings were lost. The triazine rings are the source of selectivity in BTP so, as a purely empirical conclusion, these ligands are not predicted to show the same selectivity for Cm as BTP type ligands. The results of this theoretical approach seem to support the experimental observation that BTP type ligands have a greater ability to interact with An³⁺ than many other similar type, terdentate ligands. However, the efficacy of this approach needs to be substantiated with experimental results. The authors would like to note that purely f-orbital mixing based arguments could lead to erroneous conclusions as the mixing could be due simply to energy match of metal based orbitals and ligand based orbitals and not truely imply a ‘orbital mixing’. This is duely noted but a deeper analysis in that respect is beyond the scope of this work.^63–65

Fig. 7 Visualization of Cm(TPAm)₃³⁺ molecular orbitals HOMO[−24] (left) and HOMO[−30] (right). Note interaction with the carbonyl oxygens for HOMO[−24] and the pyridine nitrogen in HOMO[−30].

Conclusions

A new family of ligands has been synthesized based on the 1,2,4-triazine–picolinamide donor moiety preorganized into a nonadentate chelate. The ligand design centred on paralleling terdentate, bis-1,2,4-triazine based extractants that are highly selective for An over Ln while increasing the denticity and stability of complexes. These ligands were observed to have a modest ability to extract lanthanides from 1 M nitric acid aqueous phases into DCM but not into 1-octanol. This extraction efficiency seems to be highly dependent on the solubility of the ML(NO₃)₃S_x complex in the organic phase. For large, preorganized chelates the reported compounds had moderately fast extraction kinetics. These extractants have potential to proficiently remove the minor actinides from acidic aqueous phases. Further experiments are needed to verify their selectivity characteristics.

Theoretical calculations on the simplified structure of BTP indicated a clear increase in the interaction of f-orbitals in the molecular orbitals of ML₃³⁺ type complexes as has been seen in the literature previously. The same methodology was applied to simplified versions of the synthesized structures. The 1,2,4-triazine–picolinamide donor arm shows a measurable covalent interaction with the f-orbitals of Am and Cm though substantially diminished with respect to BTP–H and also orbital interaction with the triazine ring is removed. This implies that these extractants may not show the same selectivity characteristics as BTP for An over Ln but this fact must be verified with future experimental work.

Acknowledgements

This research was supported by the University of Florida and the Department of Energy. This research was also supported by the National Science Foundation (NSF) while MJS served as a program officer and we thank the IR/D program at NSF.

Notes and references

1. OECD/NEA, Nuclear Fuel Cycle Transition Scenario Studies Status Report, Nuclear Energy Agency, Paris, 2009.
2. F. Roelofs, J. Hart and A. van Heek, Nucl. Eng. Des., 2011, 241, 2307–2317.
3. R. G. Bennett, in NAE National Meeting Symposium in Honor of Foreign Secretary Harold. K. Forsen, Idaho National Engineering and Environmental Laboratory, 2003.
4. J. Magill, V. Berthou, D. Haas, J. Galy, R. Schenkel, H.-W. Wiese, G. Heusener, J. Tommasi and G. Youinou, J. Nucl. Energy, 2003, 42, 263–277.
5. B. A. Lindley and G. T. Parks, Ann. Nucl. Energy, 2012, 40, 106–115.
6. G. Gryntakis, D. E. Cullen and G. Mundy, Thermal Neutron Cross Sections and Infinite Dilution Resonance Integrals, Handbook on Nuclear Activation Data, IAEA Technical Report Series, 1987.
7. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539.
8. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
9. G. Choppin, J. Commun. Met., 1983, 93, 323–330.
10. L. Karmazin, M. Mazzanti, C. Gateau, C. Hill and J. Pecaut, Chem. Commun., 2002, 2892–2893.
11. M. Mazzanti, R. Wietzke, J. Pecaut, J.-M. Latour, P. Maldivi and M. Remy, Inorg. Chem., 2002, 41, 2389–2399.
12. L. Karmazin, M. Mazzanti, J.-P. Bezombes, C. Gateau and J. Pecaut, Inorg. Chem., 2004, 43, 5147–5158.
13. A. J. Gaunt, S. D. Reilly, A. E. Enriquez, B. L. Scott, J. A. Ibers, P. Sekar, K. I. M. Ingram, N. Kaltsoyannis and M. P. Neu, Inorg. Chem., 2008, 47, 29–41.
14. M. P. Jensen and A. H. Bond, J. Am. Chem. Soc., 2002, 124, 9870–9877.
15. N. L. Banik, B. Schimmelpfennig, C. M. Marquardt, B. Brendebach, A. Geist and M. A. Denecke, Dalton Trans., 2010, 39, 5117.
16. Z. Kolarik, U. Mullich and F. Gassner, Solvent. Extr. Ion Exch., 1999, 17, 1155–1170.
17. Z. Kolarik, U. Müllich and F. Gassner, Solvent. Extr. Ion Exch., 1999, 17, 23–32.
18. M. A. Denecke, A. Rossberg, P. J. Panak, M. Weigl, B. Schimmelpfennig and A. Geist, Inorg. Chem., 2005, 44, 8418–8425.
19. P. B. Iveson, C. Riviere, M. Nierlich, P. Thuery, M. Ephritikhine, D. Guillaneux and C. Madic, Chem. Commun., 2001, 1512–1513.
20. F. W. Lewis, L. M. Harwood, M. J. Hudson, M. G. B. Drew, J. F. Desreux, G. Vidick, N. Bouslimani, G. Modolo, A. Wilden, M. Sypula, T.-H. Vu and J.-P. Simonin, J. Am. Chem. Soc., 2011, 133, 13093–13102.
21. M. Steppert, I. Císařová, T. Fanghänel, A. Geist, P. Lindqvist-Reis, P. Panak, P. Štěpnička, S. Trumm and C. Walther, Inorg. Chem., 2012, 51, 591–600.
22. F. W. Lewis, L. M. Harwood, M. J. Hudson, P. Distler, J. John, K. Stamberg, A. Núńez, H. Galán and A. G. Espartero, Eur. J. Org. Chem., 2012, 1509–1519.
23. C. Hill, D. Guillaneux, L. Berthon and C. Madic, JAERI-Conf, 2002, 2002–2004, 573–578.
24. M. Nilsson, S. Andersson, C. Ekberg, M. R. S. Foreman, M. J. Hudson and G. Skarnemark, Radiochim. Acta, 2006, 94, 103–106.
25. M. B. Dinger and M. J. Scott, Eur. J. Org. Chem., 2000, 2467–2478.
26. S. Barboso, A. G. Carrera, S. E. Matthews, F. Arnaud-Neu, V. Bohmer, J.-F. Dozol, H. Rouquette and M.-J. Schwing-Weill, J. Chem. Soc., Perkin Trans. 2, 1999, 719–724.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gauessian 09, Revision A.1, Gaussian Inc., Wallingford, CT, 2009.
28. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
29. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
30. S. I. Gorelsky and A. B. P. Lever, J. Organomet. Chem., 2001, 635, 187–196.
31. S. I. Gorelsky, AO Mix, Version 6.36, 2007.
32. A.-R. Allouche, J. Comput. Chem., 2010, 32, 174–182.
33. SHELKTL6 (2000). Bruker-AXS, Masison, WI, USA.
34. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
35. P. Van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 194–201.
36. M. G. B. Drew, D. Guillaneux, M. J. Hudson, P. B. Iveson, M. L. Russell and C. Madic, Inorg. Chem. Commun., 2001, 4, 12–15.
37. J.-C. Berthet, C. Riviere, Y. Miquel, M. Nierlich, C. Madic and M. Ephritikhine, Eur. J. Inorg. Chem., 2002, 1439–1446.
38. J.-C. Berthet, Y. Miquel, P. B. Iveson, M. Nierlich, P. Thuery, C. Madic and M. Ephritikhine, J. Chem. Soc., Dalton Trans., 2002, 3265–3272.
39. M. B. Dinger and M. J. Scott, Eur. J. Org. Chem., 2000, 2467–2478.
40. M. B. Dinger and M. J. Scott, Inorg. Chem., 2001, 40, 856–864.
41. K. Matloka, A. Gelis, M. Regalbuto, G. Vandegrift and M. J. Scott, Dalton Trans., 2005, 3719–3721.
42. K. Matloka, A. K. Sah, M. W. Peters, P. Srinivasan, A. V. Gelis, M. Regalbuto and M. J. Scott, Inorg. Chem., 2007, 46, 10549–10563.
43. K. Matloka, A. Gelis, M. Regalbuto, G. Vandegrift and M. J. Scott, Sep. Sci. Technol., 2006, 41, 2129.
44. E. Sagot, A. Le Roux, C. Soulivet, E. Pasquinet, D. Poullain, E. Girard and P. Palmas, Tetrahedron, 2007, 63, 11189–11194.
45. C. Hill, D. Guillaneux, L. Berthon and C. Madic, J. Nucl. Sci. Technol., 2002, 309–312.
46. M. J. Hudson, C. E. Boucher, D. Braekers, J. F. Desreux, M. G. B. Drew, M. R. S. J. Foreman, L. M. Harwood, C. Hill, C. Madic, F. Marken and T. G. A. Youngs, New J. Chem., 2006, 30, 1171–1183.
47. G. Ulucçam, N. Beynek, Z. Seller, G. Akalın, G. Turan and K. Benkli, Phosphorus, Sulfur Silicon Relat. Elem., 2008, 183, 2237–2247.
48. W. Yu, E. Wang, R. J. Voll, A. H. Miller and M. M. Goodman, Bioorg. Med. Chem., 2008, 16, 6145–6155.
49. M. J. Hudson, M. R. S. J. Foreman, C. Hill, N. Huet and C. Madic, Solvent. Extr. Ion Exch., 2003, 21, 637–652.
50. V. Hubscher-Bruder, J. Haddaoui, S. Bouhroum and F. Arnaud-Neu, Inorg. Chem., 2010, 49, 1363–1371.
51. R. J. Strittmatter and B. E. Bursten, J. Am. Chem. Soc., 1991, 113, 552–559.
52. D. Guillaumont, J. Phys. Chem. A, 2004, 108, 6893–6900.
53. M. G. B. Drew, M. J. Hudson, P. B. Iveson, M. L. Russell, J.-O. Liljenzin, M. Sklberg, L. Spjuth and C. Madic, J. Chem. Soc., Dalton Trans., 1998, 2973–2980.
54. L. I. Semenova and A. H. White, Aust. J. Chem., 1999, 52, 507–517.
55. P. C. Leverd, M.-C. Charbonnel, J.-P. Dognon, M. Lance and M. Nierlich, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 368–370.
56. S. A. Cotton and P. R. Raithby, Inorg. Chem. Commun., 1999, 2, 86–88.
57. P. Maldivi, L. Petit, C. Adamo and V. Vetere, C. R. Chim., 2007, 10, 888–896.
58. R. G. Pearson, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8440–8441.
59. L. Petit, C. Daul, C. Adamo and P. Maldivi, New J. Chem., 2007, 31, 1738–1745.
60. N. Kaltsoyannis, Inorg. Chem., 2012 DOI:10.1021/ic3006025.
61. B. E. Bursten, L. F. Rhodes and R. J. Strittmatter, J. Am. Chem. Soc., 1989, 111, 2756–2758.
62. K. I. M. Ingram, M. J. Tassell, A. J. Gaunt and N. Kaltsoyannis, Inorg. Chem., 2008, 47, 7824–7833.
63. I. Prodan, G. Scuseria and R. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033101.
64. M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6719–6725.
65. D. Girnt, P. W. Roesky, A. Geist, C. M. Ruff, P. J. Panak and M. A. Denecke, Inorg. Chem., 2010, 49, 9627–9635.

---

Footnotes

† This article is included in the All Aboard 2013 themed issue.

‡ Electronic supplementary information (ESI) available: NMR spectra, theoretical calculation output files, crystallographic information files. CCDC 889301 (La9), 889302 (Er9), 889303 (Yb9), 889304 (Yb10), 889305 (Yb11), 889306 (Yb5₃), 889307 (Yb12₃). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2nj40586e

---