Logical modelling of Drosophila signalling pathways

Abstract

A limited number of signalling pathways are involved in the specification of cell fate during the development of all animals. Several of these pathways were originally identified in Drosophila. To clarify their roles, and possible cross-talk, we have built a logical model for the nine key signalling pathways recurrently used in metazoan development. In each case, we considered the associated ligands, receptors, signal transducers, modulators, and transcription factors reported in the literature. Implemented using the logical modelling software GINsim, the resulting models qualitatively recapitulate the main characteristics of each pathway, in wild type as well as in various mutant situations (e.g. loss-of-function or gain-of-function). These models constitute pluggable modules that can be used to assemble comprehensive models of complex developmental processes. Moreover, these models of Drosophila pathways could serve as scaffolds for more complicated models of orthologous mammalian pathways. Comprehensive model annotations and GINsim files are provided for each of the nine considered pathways.

---

Introduction

Deciphering the regulatory mechanisms enabling the development of sophisticated multicellular animals and plants from a single cell (a fertilised egg or seed) constitutes one of the most intriguing and challenging tasks in biology. In this respect, the use of Drosophila as a model system has been particularly fruitful in molecular genetic and more recent genomic studies. This has revealed a blueprint for animal development, leading to the identification of crucial regulatory components, from homeobox transcriptional factors to signalling pathways, which turn out to be highly conserved throughout metazoans.^1–3

Such studies have progressively led to the delineation of large intertwined regulatory networks underlying developmental processes, whose properties are difficult to grasp intuitively due to the inherent pleiotropy, cross-talk and redundancy within these systems. To deal with this complexity, diverse mathematical approaches are increasingly used to study developmental networks, ranging from statistical or probabilistic methods to mine large data sets, to dynamical modelling frameworks to integrate relevant components into full fledged mechanistic and predictive models.

Early Drosophila development has been the focus of a large number of dynamical modelling studies, often using differential equations (see e.g.ref. 4–10 and references therein). However, these studies have typically considered relatively limited numbers of regulatory components and required a quantitative determination of poorly documented parameters. In this context, formal qualitative modelling approaches constitute an interesting alternative, at least as a first step towards more quantitative modelling. In particular, logical modelling (Boolean or multilevel) has been applied to various regulatory networks of increasing sizes (see e.g.ref. 11–26 and references therein). Logical models have been proposed for several Drosophila developmental processes, focusing on early stages of embryo segmentation,^27–31 on boundary and compartment formation in imaginal discs,^32,33 and also on the specification of the mesoderm during stages 8 to 10 of Drosophila development (Mbodj et al., in prep.). Because signalling pathways are known to play important roles in these developmental processes (see e.g.ref. 34–38 and references therein), these models contain several signalling components (e.g. Wg, Hh, Notch, and a limited number of downstream components) belonging to different signalling pathways.

Noticeably, although Drosophila has been a prominent model system to decipher cell signalling, in particular in the context of development, bona fide dynamical models for these pathways are still largely lacking. Furthermore, information about pathway organisation and function is spread across many publications and various databases (for links pointing to Drosophila signalling pathways in public knowledge repositories, see Table 1). In particular, Flybase and Interactive Fly provide rich textual descriptions of each pathway. However, computational biologists must perform substantial analyses to convert this vast array of information into a format that can be used to derive formal graphical and dynamical models. There is thus a clear need for reference models for each of the recurrently used signalling pathways in Drosophila, which would undoubtedly constitute a valuable resource for the modelling of developmental networks.

Table 1 Main public information resources regarding Drosophila developmental pathways

Database	Drosophila pathways	URL
KEGG	Notch Wg Hh JAK/STAT	http://www.genome.jp/dbget-bin/www_bget?dme04330 http://www.genome.jp/dbget-bin/www_bget?dme04310 http://www.genome.jp/dbget-bin/www_bget?dme04340 http://www.genome.jp/dbget-bin/www_bget?dme04630
Wikipathway	Notch Wg Dpp Hh	http://www.wikipathways.org/index.php/Pathway:WP208 http://www.wikipathways.org/index.php/Pathway:WP97 http://www.wikipathways.org/index.php/Pathway:WP230 http://www.wikipathways.org/index.php/Pathway:WP492
Reactome	Notch Wg Dpp FGF EGF	http://www.reactome.org/entitylevelview/PathwayBrowser.html (select Drosophila as organism and browse pathways)
InteractiveFly	Dpp Wg Hh JAK/STAT	http://www.sdbonline.org/fly/aignfam/sgmtplty.htm#Dpp http://www.sdbonline.org/fly/aignfam/sgmtplty.htm#Wingless http://www.sdbonline.org/fly/aignfam/sgmtplty.htm#Hedgehog http://www.sdbonline.org/fly/aignfam/jakstat.htm
SignaLink	Notch Wg Hh EGF Dpp JAK/STAT FGF	http://signalink.org/protein/P07207 http://signalink.org/protein/P09615 http://signalink.org/protein/Q02936 http://signalink.org/protein/P04412 http://signalink.org/protein/P07713 http://signalink.org/protein/Q24592 http://signalink.org/protein/P04412

---

To address this issue, we have developed reference logical models for the major Drosophila developmental pathways, with extensive references as hyperlinks to relevant articles and database entries. These pathway models can be used as building blocks to assemble more comprehensive models, as we are currently doing for mesoderm specification during Drosophila embryogenesis (Mbodj et al., in prep.). As they represent a manually curated collection of the current knowledge on each signalling cascade, they can also be used for teaching purposes.

Hereafter, we first introduce the logical framework used to define the qualitative dynamical models of Drosophila signalling pathways (see Methods), which are then briefly described in the following section (Results). As comprehensive descriptions of each of the nine presented models would be very lengthy, these are provided in ESI.† The last section (Conclusions and prospects) is devoted to the evocation of further developments and potential exploitations of this model collection.

Methods

Logical modelling is adapted to the qualitative nature of genetic data. It can offer a global view on the dynamics of large systems. The logical modelling approach has been introduced in genetics by Stuart Kauffman^39,40 and René Thomas.^41,42 Here, we used an extension of Thomas' original Boolean approach, which enables the consideration of multi-level components, e.g. to account for differential effects of different signal levels on their targets.^11,42–44

In short, regulatory networks and their dynamics can be represented using two kinds of graphs called logical regulatory graphs (model structure) and state transition graphs (dynamical behaviour).

In a logical regulatory graph, nodes (or vertices) usually denote regulatory components or their targets. They can represent different types of biomolecules (genes, mRNA, proteins, complexes, etc.) or functional processes (e.g. entry in a specific cell cycle phase). A logical function (or a logical rule) is associated with each regulatory component. By default, a node can have two alternative levels: active (1) or inactive (0). However, more levels can be considered when justified by available data. When all entities take their values within the [0, 1] interval, the model is said to be Boolean.

Signed arcs connecting graph components denote regulatory interactions. Positive or negative signs denote activatory or inhibitory effects on their targets, respectively. Multiple arcs between a pair of nodes can be used to account for dual regulatory interactions, or for differential qualitative effects of increasing regulator concentrations. When a source node may take more than two levels, a threshold (1 per default for the Boolean case) must be further associated with each outgoing arc.

Arcs may represent different types of influences, from transcriptional regulation (e.g. the activation or the repression of the transcription of a particular gene), to biochemical reactions (de/phosphorylation or degradation of a protein, etc.), to subtler situations (e.g. modulation of the activity of another component, co-factors participating in a complex, regulation through implicit components, etc.).

The regulatory graph allows a first glance at a logical model, but a logical model fundamentally consists of a set of logical rules associated with the components, thereby enabling qualitative simulations. Logical rules combine positive and negative influences using NOT, AND and OR operators and define the target value of a component depending on the values of its regulators.^11,15,16

The dynamical behaviour of a logical model is represented in terms of state transition graphs, where each node corresponds to a state of the system, i.e. a vector giving the levels of all the components of the regulatory graph (integers between 0 and the corresponding maximal levels). Arcs connecting states represent transitions enabled by the logical rules. More precisely, starting from a given initial state (or a set of initial states), the successor states are computed by comparing the values of the different components for the current state with those returned by the logical rules. Whenever the current value of a component differs from that returned by its logical rule, there is an updating call on this component. The computation of the next state(s) then depends on the updating mode. In biology, only unitary changes (+1 or −1) are usually considered, while two main updating modes are generally used. According to the synchronous mode,⁴⁰ all updating calls are considered simultaneously. Network behaviour is then deterministic since each state can have at most one successor state (although several paths may lead to the same state). In the case of the asynchronous mode,¹¹ updating calls are considered individually. A successor state is then created for each updating call.

Various solutions have been proposed to refine logical simulations and avoid the complexity of fully asynchronous schemes, for example by distinguishing between fast and slow subnetworks simulated sequentially,³⁰ or by grouping transitions into ranked (a) synchronous classes.¹⁵

A simulation can lead to a stable state, i.e. a state without successor. From a biological point of view, a stable state may correspond to a specific cell type. Alternatively, a simulation can lead to a (simple or complex) cyclic attractor, which may denote periodic behaviour, as in the case of the cell cycle.¹⁶

Whatever the updating mode, a logical model keeps the same stable states, but cyclic attractors may differ. Interestingly, powerful algorithms have been recently proposed to compute stable states in large regulatory networks.^45,46

To ease the simulation of large networks, we have developed a flexible model reduction method, which allows hiding selected components of the regulatory graph. Reduction is then applied in an iterative way to hide multiple components. When a component is masked, the effects of its regulators are transferred to its targets, for which new logical functions are then computed. By avoiding the masking of auto-regulated components, most essential dynamical properties, including the stable states, are preserved upon model reduction.⁴⁷

The software GINsim (for Gene Interaction Network simulation) implements the logical formalism and various analysis tools, including stable state computation and model reduction.⁴⁸GINsim further supports the annotation of regulatory graphs with free text and URLs, thereby enabling extensive documentation of the considered regulatory elements and interactions. Once a model is defined, the user can launch simulations, which are presented in the form of state transition graphs. GINsim also allows blocking the expression levels of specific components to simulate different types of perturbations (e.g. loss-of-function, gain-of-function, and combinations thereof).

All signalling pathway models described hereafter have been implemented and annotated using GINsim. Extensive documentation is provided in ESI† for each of the nine pathway models. Furthermore, we are providing these models in a dedicated repository, in the form of an archive file that can be opened using GINsim (release 2.4 or higher), which can be downloaded from the GINsim web site (http://ginsim.org).

Results

Table 2 lists the nine main Drosophila signalling pathways covered by this study, namely Wg, Hh, Notch, JAK/STAT, Dpp, EGF, FGF, VEGF, and Toll pathways, mentioning the main ligands, receptors, and effectors, along with reference developmental processes. Based on an extensive literature analysis, and predominantly focusing on the roles of signalling pathways during Drosophila embryonic development, we have developed a logical model for each of these pathways. Hereafter, for sake of space, a general presentation of these models is given, complemented by a more detailed presentation provided in ESI.† The number of components considered in the model is mentioned in the last column of Table 2, along with some key model properties.

Table 2 Main signalling pathways involved in the control of cell differentiation during Drosophila development. For each of the nine pathways currently considered, signals, ligands, receptors, effectors (transcription factors) are listed, along with a description of developmental processes under their control, and a brief description of the corresponding logical model proposed in this study

Pathway	Ligands	Receptors	Effectors	Biological processes	Logical models
Wg	WG	FZ ARR	PAN	Wg is involved in cell specification, cell proliferation and cell polarity during development.	26 components (all Boolean). The receptors Frizzled 1 and 2 are modeled by a single node Fz. Activatory (ARM, Pan, CBP, Hyx, BCL9 and Pygo) and inhibitory complexes (ARM, Pan and Gro) are implicitly modelled.
Hh	HH	PTC	CI (act, rep)	Hh is required during embryo segmentation, imaginal disc patterning, establishment of cell polarity and eye development.	24 components (all Boolean). CI processing into activatory and inhibitory variants is explicitly modelled.
Notch	DL SER SCA	NOTCH	NICD	Notch is required during tissue development, cell fate determination, cell proliferation, lateral inhibition, cell differentiation, apoptosis, and wing patterning.	14 components (12 Boolean, 2 ternary). Absence of Nicd and Da ON: high Twi. Presence Nicd and Da ON: medium Twi. Presence Nicd and Da OFF: Twi OFF.
Dpp	DPP	SAX TKV	MAD/MED	Dpp is responsible for dorsal/ventral polarity and controls the growth of the wing imaginal disc.	15 components (13 Boolean, 2 ternary). Logical rules account for homodimer and heterodimer formation. Morphogen gradient establishment is implicitly modelled by multi-level components.
JAK/STAT	OS UPD2 UPD3	DOME	STAT92E	JAK/STAT pathway is involved in embryo segmentation, eye development, cell growth, sex determination, hematopoiesis, spermatogenesis, oogenesis, and signal transduction in larva and adult.	17 components (15 Boolean, 2 ternary). Binding of three different ligands, as well as the effects of many inhibitors are modelled. The model also takes into account the two forms of Stat92E, the normal form and the truncated form (Nstat92E).
EGF	VN SPI KRN GRK	DER	PNT RL	EGF pathway is involved in embryogenesis, oogenesis, sex-determination, tissue specification, tissue differentiation, patterning of wing and eye imaginal discs, in adult abdomen, brain and leg development.	25 components (16 Boolean, 9 ternary). Gradient establishment through cell secreting or receiving signal implicitly modelled.
FGF	PYR THS BNL	BTL HTL	PNT RL	FGF regulates branching morphogenesis during embryogenesis (e.g. tracheal system), cell migration and differentiation, and CNS development.	23 components (all Boolean). Absence of ligand: targets OFF. Binding of one ligand and Sty OFF: targets ON. Presence of Sty (ligand ON or OFF): targets OFF.
VEGF	PVF1 PVF2 PVF3	PVR	PNT RL	VEGF regulates cell migration (e.g. hematocytes, salivary gland cells), cell size and differentiation, metamorphosis, morphogenesis, dendritogenesis and neurogenesis.	18 components (all Boolean). Absence of ligand: targets OFF. Binding of one ligand and Sty OFF: targets ON. Presence of Sty (ligand ON or OFF): targets OFF.
Toll	SPZ	TOLL	DORSAL DIF	Toll is implicated in early dorso-ventral embryonic differentiation, eye, motoneuron and muscle development, hematopoiesis, and immune response.	11 components (all Boolean). Absence of ligand: targets OFF. Binding of ligand: targets ON.

---

The regulatory graphs corresponding to the nine considered pathways are displayed in Fig. 1–4, using similar conventions. In all regulatory graphs, ellipses denote Boolean components (i.e. components with two possible values, 0 or 1, standing for absent/inactive or present/active, respectively), while rectangular contours denote multi-level components (here all ternary, i.e. taking three possible values, 0, 1 and 2, corresponding to low/insignificant, middle and high activity levels, respectively); furthermore, components with yellow background denote molecules (e.g. signals) acting from the exterior of the cell considered.

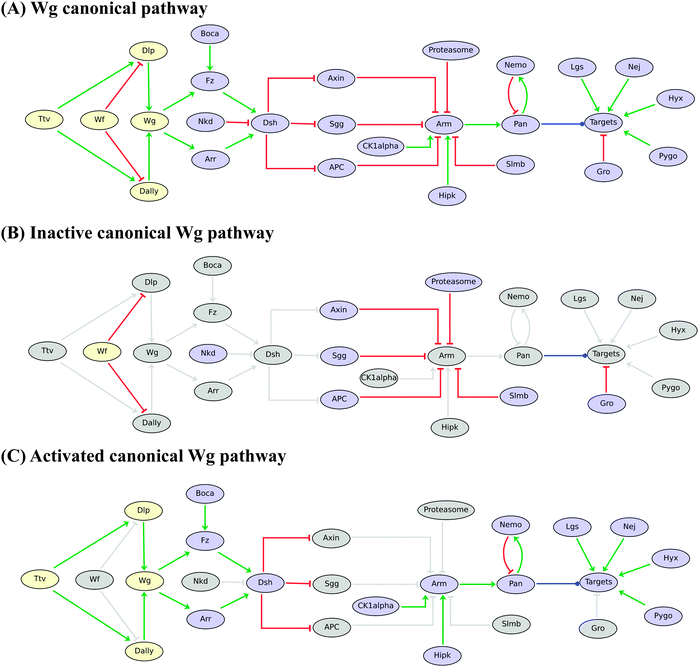Fig. 1 Boolean model for the Drosophila Wingless (Wg/Wnt) pathway. (A) Wg pathway is displayed from regulatory (Wf, Dly and Dally) and ligand (Wg) components on the left to the main downstream effectors (Dsh, Arm, Pan) and a generic “Targets” node, along with inhibitory and activatory partners on the right. Red blunt and green normal arrows denote activatory and inhibitory interactions, respectively. The blue dot arrow denotes the fact that Pangolin (Pan) can activate or inhibit different sets of target genes. (B) In the absence of Wg binding to its receptors, Arm is phosphorylated by the Axin–Sgg–APC complex and degraded by the proteasome; Pan then forms a complex with Gro, which inhibits target genes. (C) Binding of Wg to Arrow or Frizzled triggers the accumulation of Arm, which forms a complex with Pan and other cofactors (Lgs, Nej, Hyx and Pygo) for transcription activation. Grey nodes and arcs denote the lack of activity or influence depending on Wg pathway activity. Note that both inhibitory and activatory complexes are modelled implicitly by considering interactions from their components onto their targets and using proper logical rules (i.e. using the AND operator).

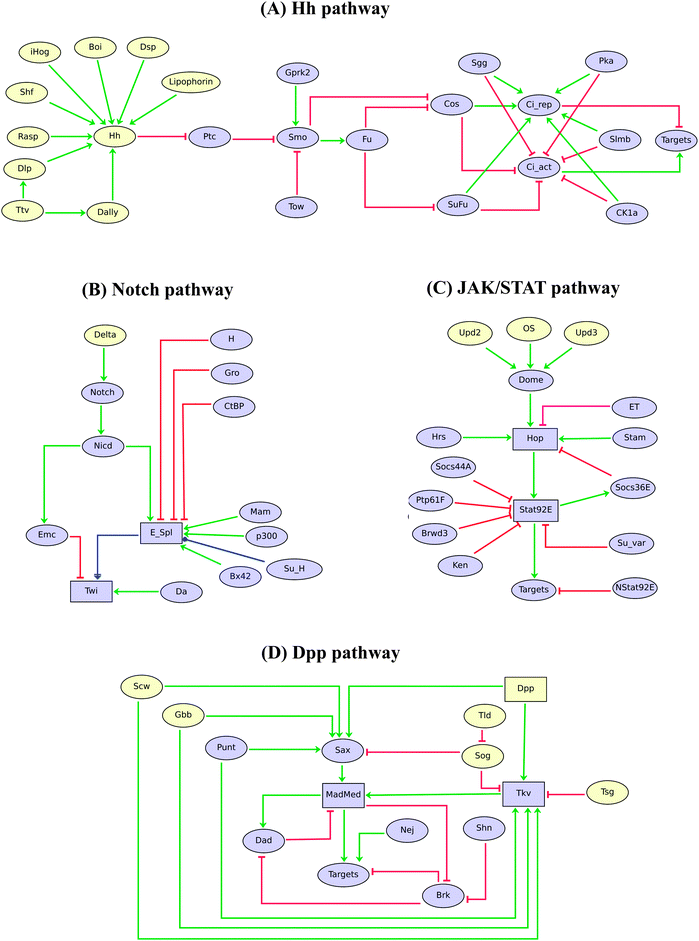Fig. 2 Logical models of Drosophila Hh, Notch, JAK/STAT and Dpp signalling pathways. Ellipses and rectangles denote Boolean and multilevel nodes, respectively. Red blunt and green normal arrows denote activatory and inhibitory interactions, respectively, while the blue dot arrows denote dual effects of the source nodes on their targets.

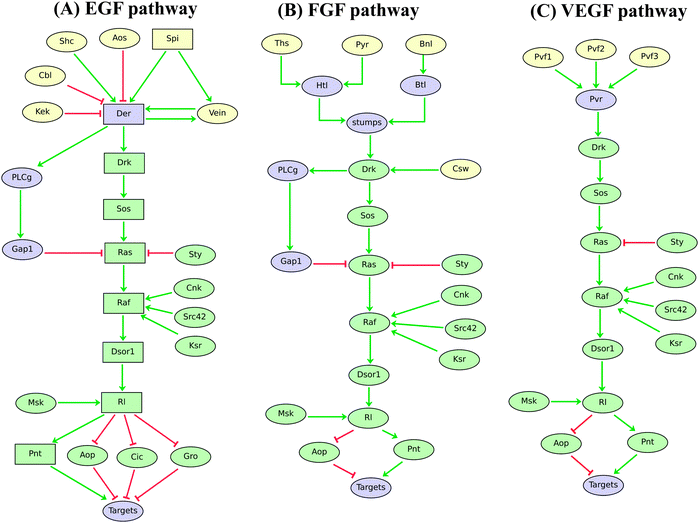Fig. 3 Logical models of Drosophila EGF, FGF, and VEGF signalling pathways. Ellipses and rectangles denote Boolean and multilevel nodes, respectively. Red blunt and green normal arrows denote activatory and inhibitory interactions, respectively. By comparing these regulatory graphs, one can easily detect the overlapping core pathway, emphasised in green. To account for differential effects of SPI and VEIN on EGF target genes, we are using ternary components for the DRK–PNT signalling cascade. Indeed, a gradient of SPI (we distinguish low, medium and high levels) can activate the pathway at medium or high levels, while VEIN is known to activate the pathway only at medium levels.

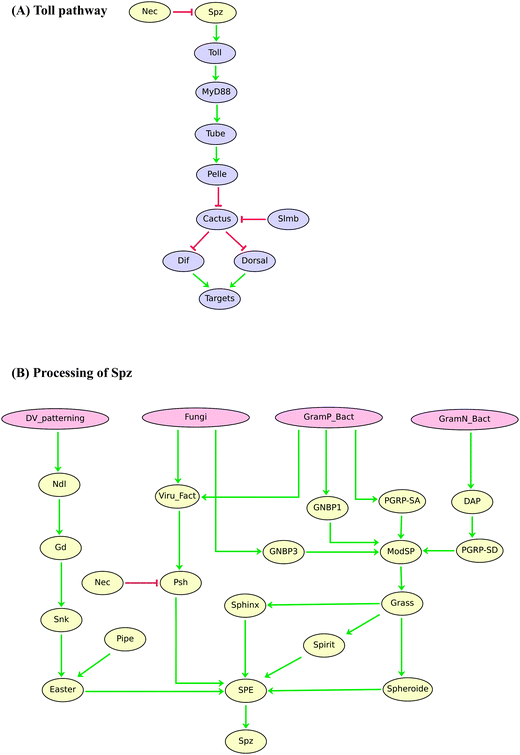Fig. 4 Boolean model of the Drosophila Toll signalling pathway. (A) Regulatory graph for Toll signalling upon activation by the ligand Spz. (B) Processing of Toll ligand Spz depending on the developmental process or type of pathogen. Red blunt and green normal arrows denote activatory and inhibitory interactions, respectively.

Logical rules have been defined for the components of these models, so that they qualitatively recapitulate the effect of the reported perturbations (effects of loss-of-function or gain-of-function of pathway components).

Note that in all cases, only single signalling components are explicitly modelled, while associations in complexes are implicitly modelled by arcs outgoing from complex partners onto their targets, along with adequate logical rules (using the AND operator).

When one of these models is used to simulate the behaviour of the pathway for various input configurations (potentially in the presence of genetic perturbations such as loss-of-function or gain-of-function), the levels/activities of pathway components are encoded into a discrete vector or a logical state, while temporal changes are represented by state transitions (cf. Methods). Such simulations can be reproduced using the GINsim files provided in ESI.† Hereafter, we focus on a limited number of representative results.

Fig. 1A displays the logical regulatory graph for the Wingless (Wg) pathway, which acts recurrently during Drosophila development.^49,50

In the absence of Wingless, the protein complex composed of Axin (AXN), Shaggy (SGG or ZW3) and APC sequesters Armadillo (ARM), enabling its ubiquitination and a Slimb-dependent degradation by the proteasome. This absence of ARM facilitates the formation of a Pangolin (PAN)–Groucho (GRO) inhibitory complex, leading to the inhibition of Wg target genes. This corresponds to the situation shown in Fig. 1B (an inactive Wg pathway), where inactive (or irrelevant) regulatory components and interactions are shown in grey.

In the presence of its co-receptor Frizzled (FRZ), binding of Wingless (the ligand) to its receptor Arrow (ARR) triggers a set of reactions, starting with the activation of Dishevelled, which in turn inhibits the AXN–SGG–APC complex;⁵¹ this leads (with the help of HIPK) to the stabilization and accumulation of ARM. Next, ARM translocates into the nucleus, where it can form an activatory complex with PAN and other co-factors (LGS, NEJ, PYGO and HYX), leading to the activation of WG target genes. This situation (an activated Wg pathway) is illustrated in Fig. 1C.

Fig. 2 shows the logical models for the Hedgehog (Hh), Notch, JAK/STAT, and Decapentaplegic (Dpp) pathways, which are also recurrently used during Drosophila development.^34,52–60

The Hh pathway (Fig. 2A) consists of a regulatory cascade leading to the activation of the pathway effectors encoded by the gene cubitus interruptus (ci). CI can be released in a full-length CI[act] form, which functions as a transcriptional activator, or in a truncated CI[rep] form, which functions as a repressor. The processing of CI is regulated by several kinases (cf.ref. 56).

The Hh and Wg pathways both play key roles in the antero-posterior segmentation of the Drosophila embryo (many of their signalling components are encoded by the so called “segment polarity” genes). Consequently, they have been considered in several models for Drosophila embryo segmentation, although in very simplified ways.^6,29–31

In this context, the more comprehensive pathway models presented here may serve as references to extend already published models, e.g. to recapitulate a broader collection of experimental data, or yet to better ground the simplifications made (e.g. applying model reduction tools to extended pathway modules to obtain consistent simplified models).

The Notch pathway (Fig. 2B) is required during tissue development, cell fate determination, cell proliferation (lateral inhibition), cell differentiation, apoptosis, wing patterning and development. Here, we particularly refer to its role in the specification of the mesoderm, where it contributes to modulate the level of Twist (TWI).³⁵

The JAK/STAT pathway (Fig. 2C) is involved in various developmental processes, including eye development, cell growth, sex determination, hematopoiesis, spermatogenesis, oogenesis, and signal transduction in larva and adult.^34,52,60 Our model considers three different ligands (OS, UPD2 and UPD3), several inhibitors, as well as the differential action of the two forms of STAT92E, the normal form and the truncated form (NSTAT92E).

Turning to the Dpp pathway (Fig. 2D), our model recapitulates the establishment of the morphogen gradient, by the implicit modelling (using proper logical rules) of different homodimers of DPP itself, Screw (SCW) and Glass-bottom-boat (GBB), which are involved in relatively low signalling, as well as of heterodimers (DPP/SCW, DPP/GBB, SCW/GBB), which are responsible for high signalling.

Dpp and Notch pathways both play important roles in the delineation of boundaries and compartments in Drosophila imaginal discs, which prefigure the organisation of adult structures such as the wings, legs or eyes. Consequently, these pathways have been implemented, albeit in very simplified ways, in models of these differentiation processes (see e.g.ref. 32, 61 and 62).

Fig. 3 shows the logical models derived for the EGF, FGF and VEGF signalling pathways.^63–67 For sake of simplicity, the processing of the EGF ligand Spitz (SPI) is not modelled. Noticeably, only two ligands have been selected when several redundant ligands have been characterised (e.g. Gurken, Keren). Various inhibitors known to function in the establishment of a signalling gradient between expressing cells and receiving cells are explicitly considered (Sprouty, Argos, Kekkon, etc.).

From these graphical representations, one can easily see that the three pathways share an extensive core cascade (MAPK cascade) encompassing eight components, including homologs of the notorious vertebrate oncogenic factors RAS and RAF (components coloured with light green). This emphasises the fact that the same signalling cascade can respond to different signals, with contextual regulatory variations, to finally affect target genes through common effectors (i.e. the transcriptional factors AOP and PNT). Examples of simulation results for EGF and FGF pathway models are given in Table 3.

Table 3 Sample results from simulations of EGF and FGF pathway models. For each initial or final state, only active components are listed (omitted components are thus absent or inactive). In the case of multi-level (ternary) components, high levels (value 2) are specified whenever it is used under initial conditions or reached at final states; when not otherwise specified, the listed components are set to the value 1. In all simulations, all internal nodes were set to zero at the initial states. Significant changes in activity levels between initial conditions or between initial and final states are emphasised in bold. Regarding EGF signalling (upper part), three simulations are shown, which correspond to wild-type pathway activity in the absence of ligand, in the presence of medium levels, and in the presence of high levels of Spi, respectively. Note the difference of levels of activation of the core components between the two latter situations. Next, the results of the simulations of Sprouty inhibition, of cnk loss-of-function, and of aop gain-of-function (each time in the presence of a high signal) are shown. Note that Pnt gets expressed at a medium level in the first case, whereas inhibitors get expressed in the latter cases. These results qualitatively recapitulate published data.^79,80 Regarding FGF signalling (bottom part), three reference wild-type simulations are shown, corresponding to ligand absence, to the activation of Htl by Ths and Pyr, and to the activation of Btl by Bnl, respectively. In the first situation, the inhibitor Aop gets expressed and the target genes are consequently repressed, whereas the pathway and target genes become activated in the two later cases. The last two rows recapitulate the effect of Htl loss-of-function, as well as of the (ectopic activatory) effect of Ras gain-of-function combined with a Stumps loss-of-function^81,82

	Initial state	Final (stable) state
EGF signalling pathway
No ligand	Shc, Cnk, Src42, Ksr, Msk	Shc, Cnk, Src42, Ksr, Msk, Aop, Cic, Gro
Medium Spi	Spi, Shc, Cnk, Src42, Ksr, Msk	Spi, Vein, Shc, Der, Drk, Sos, Ras, PLCg, Gap1, Raf, Cnk, Src42, Ksr, Dsor, Rl, Msk, Pnt, Targets
High Spi	Spi (2), Shc, Cnk, Src42, Ksr, Msk	Spi (2), Vein, Shc, Der (2), Drk (2), Sos (2), Ras (2), PLCg, Gap1, Raf, Cnk, Src42, Ksr, Dsor1 (2), Rl (2), Msk, Pnt (2), Targets
High Spi in the presence of Sprouty (Sty)	Spi (2), Shc, Cnk, Src42, Ksr, Msk, Aop, Cic, Gro	Spi (2), Vein, Shc, Der (2), Drk (2), Sos (2), Ras, PLCg, Gap1, Sty, Raf, Cnk, Src42, Ksr, Dsor1, Rl, Msk, Pnt, Targets
cnk loss-of-function	Spi (2), Shc, Src42, Ksr, Msk	Spi (2), Vein, Shc, Der (2), Drk (2), Sos (2), Ras (2), PLCg, Gap1, Src42, Ksr, Msk, Aop, Cic, Gro
aop gain-of-function in the presence of high Spi	Spi (2), Shc, Cnk, Src42, Ksr, Msk, Aop	Spi (2), Vein, Shc, Der (2), Drk (2), Sos (2), Ras (2), PLCg, Gap1, Raf (2), Cnk, Src42, Ksr, Dsor1 (2), Rl (2), Msk, Pnt (2), Aop
FGF signalling pathway
No ligand	Csw, Cnk, Src42, Ksr, Msk	Csw, Cnk, Src42, Ksr, Msk, Aop
Htl activation	Ths, Pyr, Csw, Cnk, Src42, Ksr, Msk	Ths, Pyr, Htl, Stumps, Drk, Csw, Sos, Ras, PLCg, Gap1, Raf, Cnk, Src32, Ksr, Dosr1, Msk, Rl, Pnt, Targets
Btl activation	Bnl, Csw, Cnk, Src42, Ksr, Msk	Bnl, Btl, Stumps, Drk, Csw, Sos, Ras, PLCg, Gap1, Raf, Cnk, Src42, Ksr, Dsor1, Msk, Rl, Pnt, Targets
Inhibition by Sprouty (Sty) in the presence of all ligands	Ths, Pyr, Bnl, Csw, Sty, Cnk, Src42, Ksr, Msk	Ths, Pyr, Htl, Bnl, Btl, Stumps, Drk, Csw, Sos, PLCg, Gap 1, Sty, Cnk, Src42, Ksr, Msk, Aop
Htl loss-of-function in the presence of Pyr and Ths	Ths, Pyr, Csw, Cnk, Src42, Ksr, Msk	Ths, Pyr, Csw, Cnk, Src42, Ksr, Msk, Aop
Ras gain-of-function combined with stumps loss-of-function in the presence of Ths and Pyr	Ths, Pyr, Csw, Cnk, Src42, Ksr, Msk	Ths, Pyr, Htl, Csw, Ras, Raf, Cnk, Src32, Ksr, Dosr1, Msk, Rl, Pnt, Targets

---

Finally, Fig. 4A shows our current logical model for the Drosophila Toll signalling pathway,^68,69 which is involved in early dorso-ventral embryo differentiation. The Toll pathway also plays a key role in innate immunity. Indeed, it can be activated upon infection by various kinds of pathogens, a process involving complex signals converging onto the production of Spaetzle (SPZ), the main ligand of Toll in Drosophila (Fig. 4B). At this stage, however, our logical model does not yet account for potential differential effects of SPZ depending on immunological challenges.

All nine pathway models are provided in ESI† (ZGINML files, which can be opened using the public software GINsim), along with extensive documentation (included in the model files, but also provided in html and pdf formats). To ease simulations, each model file includes sample parametrisations for typical signalling situations.

Conclusions and prospects

We have presented a collection of logical models for the prominent signalling pathways involved in Drosophila development. Each of these models can be considered as a building block to assemble more complex models for specific developmental processes. In their present form, these logical modules can be used to extend recent models for pattern formation in Drosophila embryo^30,31 or in imaginal discs.^32,62

Overall, although the nine pathway models reported here will require refinements as new data are gathered, or depending on specific applications, they already constitute a comprehensive knowledge repository that should facilitate the delineation of sophisticated models by combining inter-cellular signalling and other regulatory modules involved in Drosophila development. In this respect, simplified versions of seven of these signalling modules have been integrated in a novel model for mesoderm specification (Fig. 5), which will be reported in detail elsewhere (Mbodj et al., in prep.).

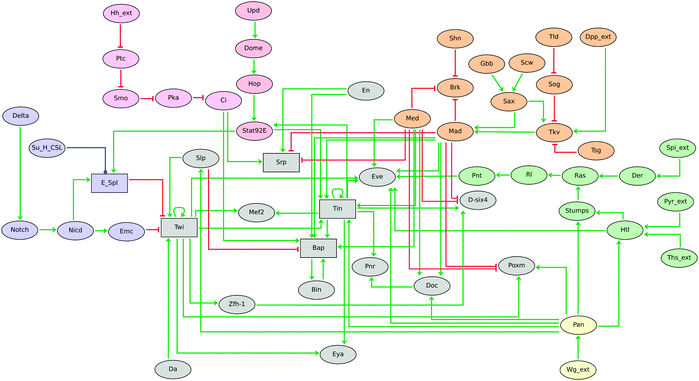Fig. 5 Logical model for Drosophila mesoderm specification at embryonic developmental stages 8–10, showing the combinatorial control of this developmental process by seven signalling pathways, each represented here in a simplified way for sake of clarity. Notch, Hh, Dpp, Wg, EGF + FGF, and JAK/STAT signalling modules are emphasised with different colours. Although the majority of the components are modelled by Boolean variables (denoted by ellipsoid nodes), the five rectangles denote multilevel components. Red blunt and green normal arrows denote activatory and inhibitory interactions, respectively. This model is described in detail elsewhere (Mbodj et al., in prep.).

Several studies indicate that the proteins implicated in these pathways are shared between species.^70–75 Our collection of pathway modules could thus be used to perform comparative analyses or to build models of orthologous pathways in other model organisms.

By and large, our modelling work mainly relied on genetic data (gene expression patterns and mutant phenotypes). As can be seen in Table 2 and Fig. 1–4, we modelled most signalling components by Boolean variables. This is certainly an oversimplification, which could be refined as novel data become available, thanks to the recent technological advances (transcriptomics, proteomics, interactomics, or high-throughput functional assays such as RNAi screens).

Furthermore, the mutant developmental phenotypes used to identify pathway components may only reflect extreme situations (loss-of-function or gain-of-function). This presumably led to overlook many potential unknown pathway actors and regulators, which can now be identified using high-throughput methods.⁷⁶

The pace of acquisition, the quantity and the nature of the resulting data pose novel challenges to biologists. Indeed, efficient exploitation of the resulting datasets and their integration with relevant lower-throughput results is far from trivial. To do so, several groups set to progressively complete and extend canonical pathways with novel interactions and components identified by large-scale interaction screens.^77,78 Although still in its infancy, there is no doubt that integration of large-scale datasets along with more detailed molecular studies will open novel avenues for signalling pathway mapping and modelling. In this respect, the collection of signalling pathways proposed here may be considered as seeds to build more comprehensive maps and ultimately delineate more quantitative and predictive models.

Acknowledgements

This work is supported by the “Agence Nationale de la Recherche” as a partner of the ERASysbio+ initiative supported under the EU ERANET Plus scheme in FP7 (ModHeart Project). We warmly thank Laurent Perrin, Krzysztof Jagla and Johannes Jaeger for insightful discussions and suggestions.

References

1. P. A. Lawrence and G. Morata, Nature, 1992, 356, 107–108.
2. E. Wolpert, L. Beddington, R. Brockes, J. Jessell, T. Lawrence and P. Meyerowitz, Principles of Development, Oxford Univ. Press, 2002.
3. S. Gilbert, Developmental Biology, Sinauer, 9th edn, 2010.
4. H. Meinhardt, Models of Biological Pattern Formation, Academic Press Inc., 1982.
5. H. Meinhardt, Curr. Top. Dev. Biol., 2008, 81, 1–63.
6. G. von Dassow, E. Meir, E. M. Munro and G. M. Odell, Nature, 2000, 406, 188–192.
7. J. Jaeger, M. Blagov, D. Kosman, K. N. Kozlov, Manu, E. Myasnikova, S. Surkova, C. E. Vanario-Alonso, M. Samsonova, D. H. Sharp and J. Reinitz, Genetics, 2004, 167, 1721–1737.
8. L. Calzone, D. Thieffry, J. J. Tyson and B. Novak, Mol. Syst. Biol., 2007, 3, 131.
9. Manu, S. Surkova, A. V Spirov, V. V. Gursky, H. Janssens, A.-R. Kim, O. Radulescu, C. E. Vanario-Alonso, D. H. Sharp, M. Samsonova and J. Reinitz, PLoS Comput. Biol., 2009, 5, e1000303.
10. A. Crombach, K. R. Wotton, D. Cicin-Sain, M. Ashyraliyev and J. Jaeger, PLoS Comput. Biol., 2012, 8, e1002589.
11. R. Thomas, R. D'Ari, Biological Feedback, CRC Press, 1990.
12. L. Mendoza, D. Thieffry and E. R. Alvarez-Buylla, Bioinformatics, 1999, 15, 593–606.
13. J. Saez-Rodriguez, L. Simeoni, J. A. Lindquist, R. Hemenway, U. Bommhardt, B. Arndt, U.-U. Haus, R. Weismantel, E. D. Gilles, S. Klamt and B. Schraven, PLoS Comput. Biol., 2007, 3, e163.
14. J. Saez-Rodriguez, L. G. Alexopoulos, M. Zhang, M. K. Morris, D. A. Lauffenburger and P. K. Sorger, Cancer Res., 2011, 71, 5400–5411.
15. A. Fauré, A. Naldi, C. Chaouiya and D. Thieffry, Bioinformatics, 2006, 22, e124–e131.
16. A. Fauré, A. Naldi, F. Lopez, C. Chaouiya, A. Ciliberto and D. Thieffry, Mol. Biosyst., 2009, 5, 1787–1796.
17. S. Bornholdt, J. R. Soc. Interface, 2008, 5, S85–S94.
18. D. J. Irons, J. Theor. Biol., 2009, 257, 543–559.
19. O. Sahin, H. Fröhlich, C. Löbke, U. Korf, S. Burmester, M. Majety, J. Mattern, I. Schupp, C. Chaouiya, D. Thieffry, A. Poustka, S. Wiemann, T. Beissbarth and D. Arlt, BMC Syst. Biol., 2009, 3, 1.
20. L. Calzone, L. Tournier, S. Fourquet, D. Thieffry, B. Zhivotovsky, E. Barillot and A. Zinovyev, PLoS Comput. Biol., 2010, 6, e1000702.
21. L. Mendoza and F. Pardo, Theory Biosci., 2010, 129, 283–293.
22. A. Naldi, J. Carneiro, C. Chaouiya and D. Thieffry, PLoS Comput. Biol., 2010, 6, e1000912.
23. M. K. Morris, J. Saez-Rodriguez, P. K. Sorger and D. A. Lauffenburger, Biochemistry, 2010, 49, 3216–3224.
24. A. Ryll, R. Samaga, F. Schaper, L. G. Alexopoulos and S. Klamt, Mol. Biosyst., 2011, 7, 3253–3270.
25. J. Huard, S. Mueller, E. D. Gilles, U. Klingmüller and S. Klamt, FEBS J., 2012, 279, 3290–3313.
26. A. Garg, K. Mohanram, G. De Micheli and I. Xenarios, Methods Mol. Biol., 2012, 786, 397–443.
27. L. Sánchez and D. Thieffry, J. Theor. Biol., 2001, 211, 115–141.
28. L. Sánchez and D. Thieffry, J. Theor. Biol., 2003, 224, 517–537.
29. R. Albert and H. G. Othmer, J. Theor. Biol., 2003, 223, 1–18.
30. M. Chaves, R. Albert and E. D. Sontag, J. Theor. Biol., 2005, 235, 431–449.
31. L. Sánchez, C. Chaouiya and D. Thieffry, Int. J. Dev. Biol., 2008, 52, 1059–1075.
32. A. Gonzalez, C. Chaouiya and D. Thieffry, Genetics, 2006, 174, 1625–1634.
33. A. Gonzalez, C. Chaouiya and D. Thieffry, Bioinformatics, 2008, 24, i234–i240.
34. N. Denef and T. Schüpbach, Curr. Biol., 2003, 13, R388–R390.
35. A. Tapanes-Castillo and M. K. Baylies, Development, 2004, 131, 2359–2372.
36. D. Sims, P. Duchek and B. Baum, Genome Biol., 2009, 10, R20.
37. A. McMahon, G. T. Reeves, W. Supatto and A. Stathopoulos, Development, 2010, 137, 2167–2175.
38. N. Perrimon, C. Pitsouli and B.-Z. Shilo, Cold Spring Harbor Perspect. Biol., 2012, 4, a005975.
39. S. A. Kauffman, J. Theor. Biol., 1969, 22, 437–467.
40. S. A. Kauffman, The Origins of Order – Self-Organization and Selection in Evolution, Oxford University Press, 1993.
41. R. Thomas, J. Theor. Biol., 1973, 42, 563–585.
42. R. Thomas, J. Theor. Biol., 1991, 153, 1–23.
43. R. Thomas, D. Thieffry and M. Kaufman, Bull. Math. Biol, 1995, 57, 247–276.
44. C. Chaouiya, E. Remy, B. Moss and D. Thieffry, Lect. Notes Control Inf. Sci., 2003, 294, 119–126.
45. A. Naldi, Decision Diagrams for the Representation and Analysis of Logical Models of Genetic Networks, Lect. Notes Comput. Sci., 2007, 4695, 233–247.
46. A. Garg, A. Di Cara, I. Xenarios, L. Mendoza and G. De Micheli, Bioinformatics, 2008, 24, 1917–1925.
47. A. Naldi, E. Remy, D. Thieffry and C. Chaouiya, Theor. Comput. Sci., 2011, 412, 2207–2218.
48. C. Chaouiya, A. Naldi and D. Thieffry, Methods Mol. Biol., 2012, 804, 463–479.
49. J. Klingensmith and R. Nusse, Dev. Biol., 1994, 166, 396–414.
50. A. M. Michelson, Sci. STKE, 2003, PE30.
51. C. M. Chen and G. Struhl, Development, 1999, 126, 5441–5452.
52. X. S. Hou and N. Perrimon, Trends Genet., 1997, 13, 105–110.
53. H. Tanimoto, S. Itoh, P. ten Dijke and T. Tabata, Mol. Cell, 2000, 5, 59–71.
54. A. Eldar, R. Dorfman, D. Weiss, H. Ashe, B.-Z. Shilo and N. Barkai, Nature, 2002, 419, 304–308.
55. S. J. Bray, Nat. Rev. Mol. Cell Biol., 2006, 7, 678–689.
56. R. A. Aikin, K. L. Ayers and P. P. Thérond, EMBO Rep., 2008, 9, 330–336.
57. Y. Kamiya, K. Miyazono and K. Miyazawa, FEBS Lett., 2008, 582, 2496–2500.
58. K. L. Ayers and P. P. Thérond, Trends Cell Biol., 2010, 20, 287–298.
59. O. Wartlick, P. Mumcu, A. Kicheva, T. Bittig, C. Seum, F. Jülicher and M. González-Gaitán, Science, 2011, 331, 1154–1159.
60. V. M. Wright, K. L. Vogt, E. Smythe and M. P. Zeidler, Cell. Signalling, 2011, 23, 920–927.
61. J. Buceta, H. Herranz, O. Canela-Xandri, R. Reigada, F. Sagués and M. Milán, PLoS One, 2007, 2, e602.
62. A. Gonzalez, C. Chaouiya and D. Thieffry, Bioinformatics, 2008, 24, i234–i240.
63. P. Duchek, K. Somogyi, G. Jékely, S. Beccari and P. Rørth, Cell, 2001, 107, 17–26.
64. B.-Z. Shilo, Development, 2005, 132, 4017–4027.
65. B.-Z. Shilo and N. Barkai, Curr. Biol., 2007, 17, R1038–R1041.
66. S. Yogev, E. D. Schejter and B.-Z. Shilo, EMBO J., 2008, 27, 1219–1230.
67. S. Tulin and A. Stathopoulos, BMC Dev. Biol., 2010, 10, 83.
68. K. Takeda, T. Kaisho and S. Akira, Annu. Rev. Immunol., 2003, 21, 335–376.
69. S. Valanne, J. H. Wang and M. Ramet, J. Immunol., 2011, 186, 649.
70. A. Bauer-Mehren, L. I. Furlong and F. Sanz, Mol. Syst. Biol., 2009, 5, 290.
71. A. L. Blasius and B. Beutler, Immunity, 2010, 32, 305–315.
72. M. Tian, J. R. Neil and W. P. Schiemann, Cell. Signalling, 2011, 23, 951–962.
73. A. Mikryukov and T. Moss, PLoS One, 2012, 7, e43330.
74. J. Roma, A. Almazán-Moga, J. Sánchez de Toledo and S. Gallego, Sarcoma, 2012, 2012, 695603.
75. C. W. Tan, B. S. Gardiner, Y. Hirokawa, M. J. Layton, D. W. Smith and A. W. Burgess, PLoS One, 2012, 7, e31882.
76. A. Friedman and N. Perrimon, Cell, 2007, 128, 225–231.
77. E. Glaab, A. Baudot, N. Krasnogor and A. Valencia, BMC Bioinf., 2010, 11, 597.
78. D. C. Kirouac, J. Saez-Rodriguez, J. Swantek, J. M. Burke, D. A. Lauffenburger and P. K. Sorger, BMC Syst. Biol., 2012, 6, 29.
79. I. Rebay and G. M. Rubin, Cell, 1995, 81, 857–866.
80. G. Laberge, M. Douziech and M. Therrien, EMBO J., 2005, 24, 487–498.
81. F. Imam, D. Sutherland, W. Huang and M. A. Krasnow, Genetics, 1999, 152, 307–318.
82. V. Muha and H. A. Müller, Int. J. Mol. Sci., 2013, 14, 5920–5937.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3mb70187e

---