Bridging the layers: towards integration of signal transduction, regulation and metabolism into mathematical models

Abstract

Mathematical modelling is increasingly becoming an indispensable tool for the study of cellular processes, allowing their analysis in a systematic and comprehensive manner. In the vast majority of the cases, models focus on specific subsystems, and in particular describe either metabolism, gene expression or signal transduction. Integrated models that are able to span and interconnect these layers are, by contrast, rare as their construction and analysis face multiple challenges. Such methods, however, would represent extremely useful tools to understand cell behaviour, with application in distinct fields of biological and medical research. In particular, they could be useful tools to study genotype–phenotype mappings, and the way they are affected by specific conditions or perturbations. Here, we review existing computational approaches that integrate signalling, gene regulation and/or metabolism. We describe existing challenges, available methods and point at potentially useful strategies.

---

Introduction

The functioning of a cell requires multiple processes to work in an orchestrated manner. Basic properties of cellular life, such as proliferation, macromolecule synthesis and degradation, and cellular metabolism, have to be tightly controlled. Failure in the regulation of these cellular functions, for example through mutations of specific genes, can result in another cellular phenotype and, eventually at the organism level, in severe diseases such as cancer.¹

Cellular metabolism comprises catabolic pathways, which break down molecules to produce energy, and anabolic reaction routes, which provide the essential building blocks required by the cell to synthesise the molecules it consists of and, thus, to enable homeostasis and growth. The required enzymes catalysing these metabolic processes are encoded in the genome and are translated from the intermediate messenger RNA (mRNA). A cell needs to control and adapt its enzyme production and behaviour depending on its requirements. This is achieved through diverse regulation mechanisms at the level of transcription (where DNA is copied into RNA) and translation (where mRNA is decoded into proteins).² Finally, the cell has to sense its environment to react accordingly via signal transduction mechanisms that are closely related to regulatory mechanisms through signalling cascades.³

All these processes are clearly interconnected (as illustrated in Fig. 1) but have usually been studied separately in distinct sub-disciplines of cellular biology. While all types of biological molecules and interactions directly or indirectly influence all processes, there are three main layers with distinct characteristics: (i) metabolism: the production and consumption of diverse small molecules (metabolites) in enzyme-driven metabolic reactions, (ii) gene regulation: the control of the abundance and translation of transcripts (mRNA) and consequently proteins, and (iii) signalling: the interaction of proteins that generate and process flows of information.

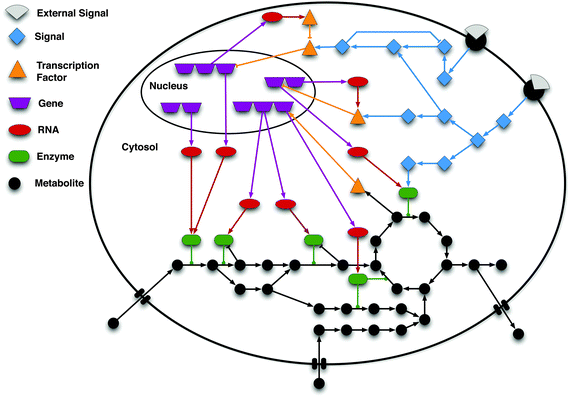Fig. 1 Schematic of the interconnection among signalling, gene regulation and metabolism. In a cell, signalling networks are activated by external signals, e.g. ligands (grey shapes) binding to a receptor (black semi-circles) located in the cell membrane. The signal is then internally propagated in the cell by means of e.g. protein phosphorylation cascades. These cascades may lead to alterations in the expression of genes by activating or inhibiting transcription factors (TFs). Gene regulatory networks control the transcriptional level of genes, and thus the production of messenger RNA molecules, which are subsequently translated into proteins. These proteins are in turn involved in cellular functions, including signal transduction and the catalysis of metabolic reactions. Specific metabolites are known to affect proteins' activity (e.g. binding to the allosteric site) and can also influence gene regulation. As illustrated in the scheme, signalling, gene regulation, and metabolism are tightly interconnected showing that the systems' behaviour can only be accurately modelled and understood by properly integrating the sub-systems. The interactions between the molecules are represented by edges: arrow shaped edges represent activating interactions; blunt edges represent inhibitory interactions; and edges with a circle on the top end depict enzyme reaction catalyses.

The phenotype of a cell results from the interoperation of the three different layers of biological processes since, as stated above, they are linked through diverse types of interactions. An important, well-known example is the regulation of blood sugar in humans.⁴ The liver regulates the level of sugar in the blood by releasing or storing it in the form of glycogen. Glucose levels are exquisitely regulated by complex control mechanisms driven by extracellular signals. The main hormonal drivers are insulin and glucagon, both being synthesised and released from specialised pancreatic cells in a glucose-dependent manner. The information contained in these extracellular signals is decoded and translated by liver cells via signalling and regulatory processes.

Complex diseases are systemic phenomena affecting multiple cellular processes. For example, cancer is characterised by a deregulation of the mechanisms that govern transduction of extracellular signals into the gene expression system, but also by an impaired functioning of its metabolic machinery.⁵ Hence, only an integrated view of the processes involved can lead to a comprehensive understanding that may shed new light on the development of these diseases and, therefore, provide new treatment opportunities.

Mathematical modelling has become a key methodology for gaining a deeper understanding of complex biological phenomena and for predicting phenotypes under different conditions. Similarly to what happens in experimental studies, signalling, gene expression, and metabolism are often modelled separately and integrated models are still scarce. Accordingly, mathematical formalisms have been developed independently, tailored to the nature of the biochemical interactions and molecules involved, and to the specific features of the processes in each domain. Some efforts have attempted to connect these different processes, both experimentally and computationally. Given the complexity of the task, studies in this direction so far have been limited in number and scope.⁶

We believe that the time has come to address this challenge. The main motivation, in our opinion, is the rapid development of high-throughput measurement techniques for these different types of data, associated with the corresponding ‘omics’ label: in historical order, genomics, transcriptomics (gene expression), proteomics and metabolomics. While there are undoubtedly many challenges, modelling approaches that leverage these data, as well as improved parameter optimisation algorithms⁷ and high-performance computing, should be a major avenue of research in the coming years in systems biology. This should lead to a broad range of potential applications in biotechnology, biomedicine, and pharmaceutical research.

In this review, after a brief summary of existing modelling approaches for signalling, metabolic, and gene regulatory processes, we describe recent efforts to connect these layers (Fig. 2).

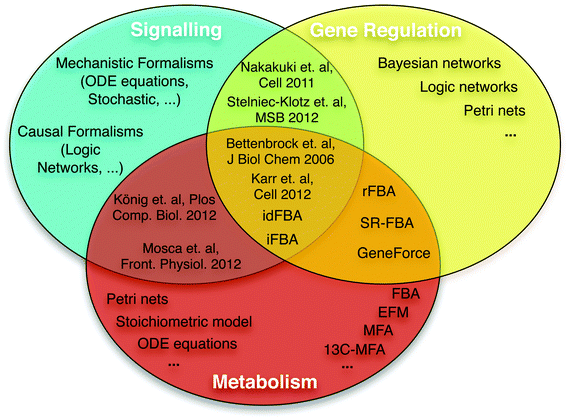Fig. 2 Overview of formalisms for modelling signalling, gene regulatory, and metabolic networks. Multiple formalisms and simulation methods can be used to model and analyse each biological system. Due to specific biological features, some mathematical formalisms are more suitable for specific systems (see main text). Some methods can model different types of systems, using either different (e.g. SR-FBA⁴⁰) or the same mathematical formalism.⁴⁷ Specific references are only used for the cases where a general term is not available; see main text for more references. Bettenbrock et al.,⁴⁴ iFBA,⁴⁹ idFBA⁵⁰ and Karr et al.⁶ represent the first efforts to integrate the three different systems. König et al.⁴⁷ and Mosca et al.⁴⁸ presented a metabolic ODE model approximately integrating the hormonal control via insulin, glucagon and epinephrine as underlying signalling networks are not incorporated.

Different layers are modelled with different mathematical formalisms

All cellular processes, from the basic to the most complex, result from the interaction of a large number of biological molecules. On a structural basis, these interactions can be described as networks, usually as graphs or, more generally, hypergraphs. Graphs are composed of nodes (e.g. proteins) that are connected via edges, the latter representing some relationship between pairs of nodes. Hypergraphs, additionally, facilitate the representation of relationships with more than two interacting components; for instance, in the case of a reaction with two reactants and one product.⁸ As stated in the introductory section, previous modelling approaches have distinguished among metabolic, signalling, and gene regulatory networks. In this section, we will give a brief overview of these networks and the corresponding modelling formalisms, pointing the interested reader to dedicated reviews for further information on these topics. Importantly, we will focus on modelling formalisms that are based on networks. These can be used to simulate perturbations (such as stimuli, mutations, or drug treatments), thus predicting how these alterations affect the network elements.

There is currently no single modelling formalism that can cover all biological aspects. Different types of biological networks are modelled using different formalisms that properly suit and represent their behaviour and specific properties. On the one hand, ordinary differential equations (ODEs) describing the underlying biochemistry are often used, as they are detailed and have high explanatory power. However, their applicability is limited due to the difficulty to obtain the necessary model parameters. They also have limited scalability, and thus they are, in general, not applicable to genome-scale models and simulations. On the other hand, less detailed approaches like Boolean networks and constraint-based models have been used in larger networks. Choosing the best modelling formalism is a trade-off between detail and complexity.

Signalling networks

Signal transduction pathways define the cellular response to external stimuli, which often reach the cell in the form of small chemical compounds, such as hormones. These molecules typically bind to proteins in the cell membrane, known as receptors, and trigger the activation of signalling pathways. These pathways are interconnected via crosstalk mechanisms, leading to complex networks that process, spread, and amplify extracellular information, finally altering gene expression, cell proliferation, differentiation and apoptosis, as well as metabolism.^9,10

Signalling networks can be mathematically represented using different types of formalisms. One can roughly distinguish between a mechanistic (biochemical) description, based on the chemical reactions that underlie signal transduction, and a causal description, where connections between nodes (typically proteins) correspond to a node's effect on the other, without describing these processes in molecular detail.⁹

Within the causal set of formalisms, arguably the simplest modelling approach is the Boolean representation of networks, identifying a node's state to be either active/on or inactive/off. Boolean networks can be modelled as dynamic systems, following the state of nodes over a (discrete) time range,¹¹ or by studying their basic input–output behaviour based on logical steady-states.¹² Despite their simplicity, Boolean models can reveal important structural features of signalling pathways.^13–15 Moreover, they can be refined or extended in various ways including multi-level logic, fuzzy logic, probabilistic Boolean networks, and logical ODEs.¹³

Mechanistic formalisms benefit from describing the process details, although this increases the model complexity. Mechanistic models are most commonly modelled as a set of biochemical reactions.¹⁰ A more sophisticated and principled way consists of writing rules describing the interactions among the different proteins that are then instantiated into biochemical reactions.¹⁶ In both cases, one often generates ODEs to be simulated, while in some cases (in particular when one simulates individual molecules), stochastic formalisms are used. Finally, spatial localisation in the cell is very important for signal transduction, and is sometimes explicitly considered when building models.¹⁰

Gene regulation

Gene regulatory networks are responsible for the control of gene expression and, therefore, have direct impact on virtually all processes in the cell. It is vital that certain genes are kept at their adequate expression levels at specific times and in certain cell types, in order to assure correct cell function and survival.^17,18 Broadly speaking, the process of gene expression/activation encompasses gene transcription into an mRNA molecule, which is subsequently translated into a protein. The encoded proteins may then take part in the metabolic network by catalysing chemical reactions, act as transcription factors (TFs) responsible for inducing and suppressing gene expression, or simply transduce post-receptor signalling via enzymatic cascades. Many different mechanisms can be involved in regulation, working both at the level of transcription or at the post-transcriptional or post-translational levels. Although the main molecules involved in these processes are arguably TFs and sigma factors, other molecules such as riboswitches or microRNAs may also take part.^19,20 Direct enzyme regulation by metabolites is also possible.

Given this large set of possible interactions, the construction of regulatory networks is far from trivial and our knowledge is still very limited. Indeed, substantial work has been devoted to reverse-engineer these networks from experimental data,^21,22 mainly at the gene expression level, but also considering, for instance, transcription factor binding sites and protein–DNA interactions. Popular methods to reconstruct these networks include Bayesian inference, approaches based on mutual information, and modular approaches to reduce the problem's complexity.²² These have resulted in a few genome-scale models, mostly restricted to transcriptional regulatory networks, for well studied microbes such as Escherichia coli, as well as numerous other networks of small/medium scale for sub-systems of interest in biomedical research.

Similarly to the signal transduction networks, formalisms for representing regulatory networks range from Boolean approaches for larger-scale networks to ODEs for small/medium-sized networks.¹⁸

Metabolism

A key difference between gene regulatory/signalling and metabolic networks is that the former carry signal flows, whereas metabolic pathways generate mass flows. For this reason, logical or Boolean networks are not suitable for describing metabolic networks.

Large-scale metabolic networks have been used for some years now, being usually represented as biochemical (mechanistic) networks solely based on the stoichiometry and reversibility of the reactions involved.²³ By assuming pseudo steady-state conditions, i.e. the concentrations of all intracellular compounds remain constant, various functional properties and capabilities of metabolic networks can be explored and phenotypes can be predicted under different environmental and genetic conditions. Most of the techniques belong to the class of constraint-based methods which include flux balance analysis, metabolic flux analysis, pathway analysis by elementary modes or extreme pathways.²⁴ There is a rapidly increasing number of stoichiometric genome-scale metabolic models that have been reconstructed and verified using such methods, including organisms like Escherichia coli,²⁵ yeast²⁶ or human.²⁷ Stoichiometric models and constraint-based techniques have also been used to compute intervention strategies for Metabolic Engineering^28–30 or to tackle biomedical issues related to biological discovery including elucidation³¹ and targeting³² of cancer mechanisms.

Regarding kinetic models of metabolism, only small-scale metabolic networks are usually modelled using ODEs and only a few with a larger size exist.^33–35 Simulation of large metabolic models requires a huge computational effort, therefore model reduction is often used to reduce the size of the model and consequently the complexity of the mathematical problem.³⁶

In eukaryotic cells, compartmentalization represents an important issue that has to be properly addressed for developing predictive models.³⁷ Division of the cell into different compartments enabled specialization of organelles for carrying out specific metabolic functions. Important conditions for the performance of metabolic enzymes such as pH, energy, cofactors or, generally, metabolite concentrations have been evolutionary optimized and are specific for the metabolic role of the compartment. Current genome-scale stoichiometric models already include compartmentalization.^25–27

Integrating different layers: the challenge and state of the art

Building an integrated model that accounts for interactions from all three layers and merges signalling, gene regulatory and metabolic networks could, in principle, be achieved by writing down the underlying biochemical reactions and transforming them into ODEs; such an approach has been already used to model any of the layers separately. At the level of state variables, ODEs do not distinguish between metabolites, genes, or signalling molecules. Furthermore, any interaction type (e.g., a metabolic conversion of a metabolite or ligand binding to a receptor) can be formally described by suitable kinetic rate laws. The integration of the different layers into ODE models would be computationally very challenging due to the different time scales of the processes (from seconds to a few minutes for signalling and metabolism to hours for gene regulation) giving rise to stiff ODEs. These problems might become tractable by suitable numerical methods. However, as mentioned above, building models of larger integrated networks requires a level of information that is very rarely available, even for a single layer. Therefore, it is not expected that fully mechanistic ODE models integrating all layers will become available in the near future.

In the case of qualitative modelling, formalisms have been developed tailored to the different types of large-scale networks, but their integration is not straightforward. At least for signalling and regulatory networks, similar modelling formalisms (e.g. logical models) can often be used, as signal flows are a key characteristic of both network categories. In those cases, model merging becomes, in principle, feasible but is actually rarely done. The reasons for this lack of integrated models might be the lack of knowledge about the molecular interfaces between the layers, and the absence of suitable data simultaneously at both levels. Furthermore, as stated above, different time scales need to be considered for each layer, which is often difficult in qualitative models. Connecting gene regulation or signalling with metabolism is additionally hampered by the different types of interactions (signal flows vs. mass flows) that imply different semantics in model descriptions.

To summarise, no single mathematical formalism currently seems capable of simulating the phenotype of a cell taking signalling, gene regulation and metabolic systems into account. In previous work, several methods have been presented to integrate two of these layers. We review these cases in the next sections, and in the last section efforts to address integrated models covering the three layers are described.

Metabolism and regulation

In this section, strategies to connect regulatory networks (represented as Boolean or probabilistic models) with metabolic networks (described as stoichiometric/constraint-based models) will be discussed. Regulatory FBA (rFBA)³⁸ was one of the first attempts to integrate a regulatory layer, represented as a Boolean model, with a metabolic model. The regulatory Boolean network specifies the set of “inactive” enzymes for a given environment and a cellular state. This information is then used to constrain the fluxes of the respective reactions in the metabolic layer, simulated using FBA. This framework was used to simulate growth in batch cultures of Escherichia coli,³⁹ using the first genome-scale integrated model including metabolic and regulatory layers. The model was used to predict dynamic flux profiles by a series of steady-state simulations of the metabolism, assuming that the regulation layer works at a slower time scale, and is approximately constant within those intervals.

A similar strategy, named steady-state regulated FBA (SR-FBA),⁴⁰ introduced a unified constraint-based approach. Here, a mixed integer linear programming (MILP) formulation was used to address the underlying optimisation problem. The formulation combined binary variables for the regulatory layer and real valued variables for the reaction fluxes. It also included distinct types of constraints representing the metabolic layer (from FBA) and the regulation interactions, all integrated in a single framework. This revealed feasible combined regulatory and metabolic states. Both rFBA and SR-FBA simulate the metabolic phenotype of a metabolic network under different environmental and genetic conditions (e.g. after knockout of certain genes). Besides having a higher predictive power than FBA, they also reveal insights into novel types of regulatory mechanisms. However, despite their added value, these approaches have two main weaknesses. As the regulatory interactions are represented using Boolean logic, the metabolic reactions are limited to a binary response (on vs. off). Furthermore, rFBA and SR-FBA encounter problems with cyclic networks and cannot account for regulatory feedbacks from the metabolic back to the regulatory layer. These feedbacks can take place, for example, when certain metabolites (or metabolite concentrations) affect the transcription of certain genes.

PROM (probabilistic regulation of metabolism)⁴¹ is another method proposed for connecting transcriptional regulatory networks with metabolism. Here, regulatory networks are represented by a probabilistic model, which is inferred (for a given organism) from gene expression data. Thus, PROM allows for a more quantitative description of regulatory events, instead of simple on/off rules. However, it may also have problems when closing back the circuit from the metabolic to the regulatory layer.

Another approach capable of directly integrating high-throughput measurements with metabolic network models is integrative omics-metabolic analysis (IOMA) which quantitatively integrates proteomic and metabolomic data with genome-scale metabolic models.⁴² The method formulates a quadratic programming (QP) problem to search for a steady-state flux distribution in which flux through reactions with measured proteomic and metabolomic data is as consistent as possible with kinetically derived flux estimations. Hyduke et al. provides an overview on methods for interpreting omics data with stoichiometric models.⁴³

Some other efforts focused on integrating modules of metabolic and gene regulatory processes at the level of ODEs. A larger example of such a model was presented by Bettenbrock and colleagues,⁴⁴ who quantitatively described the regulation of uptake and metabolism of various carbohydrates in Escherichia coli. By incorporating regulatory and metabolic events and by fitting the kinetic model against a large set of measurements, a complex phenomenon such as catabolite repression could be adequately described in a dynamic and quantitative manner. As stated above, such a fully mechanistic description based on ODEs does not seem feasible for large-scale networks.

Signalling and gene regulation

As mentioned above, similar modelling formalisms are often used for signalling and regulatory networks (e.g. logical models or influence graphs). At the technical level, it should therefore be relatively straightforward to merge models from the two different layers.

However, this is actually rarely done, possibly because the interfaces between these two layers are not well characterised. These interfaces are actually not simple; Stelniec-Klotz and colleagues⁴⁶ recently inferred jointly a signalling and regulatory network, identifying complex relationships between these layers. Accordingly, there are only a few examples of models linking signalling with gene regulation, and these are on a relatively small-scale level.^45,46

Signalling and metabolism

There are also a few simple models that account for both metabolism and signal transduction. Arguably, the low number of models in this case is due to the fact that a direct interaction from signalling to metabolism is rare, and most of the time occurs via gene regulation (e.g. signalling pathways affecting the expression of metabolic enzymes). König et al. presented a small dynamic model of the regulated hepatic glucose metabolism integrating insulin, glucagon, and epinephrine hormones and corresponding enzyme activity changes.⁴⁷ The model was set up using ODEs and the enzymes' phosphorylation state was formulated by directly mapping hormonal states into different kinetic functions for each state, without considering explicit signalling pathways.

Using a similar approach, Mosca et al. presented a dynamic metabolic model in which the cellular metabolic steady state condition was adapted to present two different phenotypes in HeLa cells.⁴⁸ These two phenotypes are due to the regulatory effect of the PI3K/AKT/mTOR signalling pathway. The metabolic effects of the signalling pathway were modelled as modifications of the maximum rate (v_max) of distinct metabolic reactions. However, as in the previous model, the PI3K/AKT/mTOR signalling pathway was not described mathematically.

Integrated approaches: towards a whole-cell model

Some advanced approaches – integrated FBA (iFBA)⁴⁹ and integrated dynamic FBA (idFBA)⁵⁰ – have been proposed. Both methods are based on the rFBA approach and both are able to integrate signalling pathways with the metabolic and regulatory layers.

iFBA has been applied to integrate different formalisms to create a medium scale model of Escherichia coli: the rFBA model for selected pathways of E. coli, including FBA simulation for the metabolic layer and Boolean networks for the regulatory part, is combined with an ODE model of the phosphotransferase system. This approach demonstrated a strategy to integrate modules of ODE/Boolean representations of metabolic/regulatory processes with FBA models. Importantly, regulatory events (and thus the resulting reaction activities) are modelled as simple binary variables.

In contrast, idFBA requires an integrated stoichiometric reconstruction of the three layers, incorporating slow and fast reactions in the framework. Slow reactions are incorporated directly into the stoichiometric matrix with a time-delay, while fast reactions rely on the pseudo steady-state assumption of FBA. idFBA was applied to the analysis of a prototypic integrated system of yeast.⁵⁰

To the best of our knowledge, the largest integrated model that has been published so far is the whole-cell model of Mycoplasma genitalium,⁶ accounting for more than 500 genes. Consistent with our statement given above, the authors also concluded that no single formalism could capture the diverse types of cellular processes. Consequently, in their approach they divided the total functionality of the cell into 28 sub-modules. Each sub-module was modelled using a specific mathematical representation. For example, metabolism was modelled using flux-balance analysis, whereas RNA and protein degradation were modelled as Poisson processes. The integration of the sub-modules during the whole-cell simulation was done based on the assumption that they are approximately independent of short timescales (less than 1 s). Simulations were then performed in discrete time steps: at each step the sub-modules are run independently, but depend on the values of variables determined by the other sub-modules at the previous time step. Hence, the different modules work autonomously for one second and then exchange material and information according to given rules.

This hallmark study is a proof of concept showing that all the processes in a cell can be modelled in an integrated fashion, assuming different time-scales of operation.

Conclusion and future directions

We expect increasing interest in developing models and methods that can represent and predict the cell's phenotype, considering different types of biological interactions, in particular metabolism, gene regulation and signalling. Integrated computer models covering all sub-systems should eventually lead to an overall perspective of the molecular mechanisms of the cell.⁶ Importantly, many diseases involve different layers, and therefore such models should have a broad applicability in biomedicine. Insulin, the key hormone in diabetes development and treatment, controls signalling processes besides sugar metabolism. Also, recent work has shown that metabolism in cancer is partially controlled by signalling networks.^51–53 With the advent of high-throughput experimental data, network reconstruction is moving towards an integration of all kinds of biological molecules based on different types of ‘omics’ data.

To develop models that integrate different types of biological networks into models that can be simulated, three computational aspects need to be addressed: (i) a mathematical formalism has to be adopted to represent each layer; (ii) a simulation method capable of accounting for the different types of systems has to be developed; and (iii) the interactions among different layers have to be identified and modelled. The proper solution is dependent on the specific problem at hand. For example, small models can be integrated using differential equations (ODEs). In contrast, larger models can be integrated using formalisms and simulation methods that best fit each layer. When different layers are modelled/simulated with different formalisms and methods, interfaces among them need to be established. An important issue to take into account is the proper compartmentalization of each biological entity and interaction, which affects model predictive capabilities, but is still hard to achieve with current modelling tools.

The recent breakthrough by Karr and colleagues to assemble a predictive whole-cell model of a simple organism⁶ should inspire the development of similar models in more complex organisms. The complexity of a human cell (genome size and complex regulation, vast variety of biological molecules and interactions, etc.) is overwhelming, and our knowledge of many biological processes (e.g. RNA regulation) is still fairly limited. Whole-cell computational models for higher organisms and in particular humans are, in our opinion, still a long way away.

Nevertheless, these integrated models should be a long-term grand goal of systems biology as tools to enhance our understanding of biological complexity and human disease.

Acknowledgements

We acknowledge with thanks financial support from the EU through project “BioPreDyn” (ECFP7-KBBE-2011-5 Grant number 289434), the German Federal Ministry of Education and Research (initiative Virtual Liver, grants 0315762, 0315744) and from the Federal State of Saxony-Anhalt (Research Center “Dynamic Systems: Biosystems engineering”), ERDF – European Regional Development Fund through the COMPETE Programme (operational programme for competitiveness) and by National Funds through the FCT (Portuguese Foundation for Science and Technology) within projects ref. COMPETE FCOMP-01-0124-FEDER-015079 and PEst-OE/EEI/UI0752/2011. We thank Michael Rempel, Anne Bonin and Sophia Bongard for their support, and Kiran Patil and Aidan MacNamara for critical reading of this manuscript.

References

1. E. T. Liu and D. A. Lauffenburger, Systems Biomedicine, Academic Press, 2009.
2. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, ed. M. Anderson and S. Granum, Garland Pub, 2008.
3. J. Downward, The ins and outs of signaling, Nature, 2001, 411, 1–4.
4. F. Q. Nuttall, A. Ngo and M. C. Gannon, Regulation of hepatic glucose production and the role of gluconeogenesis in humans: is the rate of gluconeogenesis constant?, Diabetes/Metab. Res. Rev., 2008, 24(6), 438–458.
5. D. Hanahan and R. A. Weinberg, Hallmarks of cancer: the next generation, Cell, 2011, 144(5), 646–674.
6. J. R. Karr, J. C. Sanghvi, D. N. Macklin, M. V. Gutschow, J. M. Jacobs and B. Bolival Jr, et al. A Whole-Cell Computational Model Predicts Phenotype from Genotype, Cell, 2012, 150(2), 389–401.
7. J. R. Banga, Optimization in computational systems biology, BMC Syst. Biol., 2008, 2(1), 47.
8. S. Klamt, U.-U. Haus and F. Theis, Hypergraphs and cellular networks, PLoS Comput. Biol., 2009, 5(5), e1000385.
9. C. Terfve and J. Saez-Rodriguez, Modeling Signaling Networks Using High-throughput Phospho-proteomics, Adv. Exp. Med. Biol., 2012, 736, 19–57.
10. B. Kholodenko, M. B. Yaffe and W. Kolch, Computational approaches for analyzing information flow in biological networks, Sci. Signaling, 2012, 5(220), re1.
11. A. González, C. Chaouiya and D. Thieffry, Logical modelling of the role of the Hh pathway in the patterning of the Drosophila wing disc, Bioinformatics, 2008, 24(16), i234–i240.
12. S. Klamt, J. Saez-Rodriguez, J. A. Lindquist, L. Simeoni and E. D. Gilles, A methodology for the structural and functional analysis of signaling and regulatory networks, BMC Bioinf., 2006, 7, 56.
13. M. K. Morris, J. Saez-Rodriguez, P. K. Sorger and D. A. Lauffenburger, Logic-Based Models for the Analysis of Cell Signaling Networks, Biochemistry, 2010, 49(15), 3216–3224.
14. P. Ghazal, S. Watterson, K. Robertson and D. C. Kluth, The in silico macrophage: toward a better understanding of inflammatory disease, Genome Med., 2011, 3(1), 4.
15. R.-S. Wang, A. Saadatpour and R. Albert, Boolean modeling in systems biology: an overview of methodology and applications, Phys. Biol., 2012, 9(5), 055001.
16. W. S. Hlavacek, J. R. Faeder, M. L. Blinov, R. G. Posner, M. Hucka and W. Fontana, Rules for modeling signal-transduction systems, Sci. STKE, 2006, 2006(344), re6.
17. T. Schlitt and A. Brazma, Current approaches to gene regulatory network modeling, BMC Bioinf., 2007, 8(Suppl 6), S9.
18. G. Karlebach and R. Shamir, Modelling and analysis of gene regulatory networks, Nat. Rev. Mol. Cell Biol., 2008, 9(10), 770–780.
19. ENCODE Project Consortium, E. Birney, J. A. Stamatoyannopoulos, A. Dutta, R. Guigó and T. R. Gingeras, et al. Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project, Nature, 2007, 447(7146), 799–816.
20. Y. Wan, M. Kertesz, R. C. Spitale, E. Segal and H. Y. Chang, Understanding the transcriptome through RNA structure, Nat. Rev. Genet., 2011, 12(9), 641–655.
21. R. De Smet and K. Marchal, Advantages and limitations of current network inference methods, Nat. Rev. Microbiol., 2010, 8(10), 717–729.
22. M. Bansal, V. Belcastro, A. Ambesi-Impiombato and D. di Bernardo, How to infer gene networks from expression profiles, Mol. Syst. Biol., 2007, 3, 78.
23. A. M. Feist, M. J. Herrgård, I. Thiele, J. L. Reed and B. Ø. Palsson, Reconstruction of biochemical networks in microorganisms, Nat. Rev. Microbiol., 2009, 7(2), 129–143.
24. C. H. Schilling, D. Letscher and B. O. Palsson, Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective, J. Theor. Biol., 2000, 203(3), 229–248.
25. J. D. Orth, T. M. Conrad, J. Na, J. A. Lerman, H. Nam and A. M. Feist, et al. A comprehensive genome-scale reconstruction of Escherichia coli metabolism–2011, Mol. Syst. Biol., 2011, 7, 535.
26. B. D. Heavner, K. Smallbone, B. Barker, P. Mendes and L. P. Walker, Yeast 5 - an expanded reconstruction of the Saccharomyces cerevisiae metabolic network, BMC Syst. Biol., 2012, 6, 55.
27. N. C. Duarte, S. A. Becker, N. Jamshidi, I. Thiele, M. L. Mo and T. D. Vo, et al. Global reconstruction of the human metabolic network based on genomic and bibliomic data, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(6), 1777–1782.
28. K. R. Patil, I. Rocha, J. Forster and J. Nielsen, Evolutionary programming as a platform for in silico metabolic engineering, BMC Bioinf., 2005, 6, 308.
29. A. R. Zomorrodi, P. F. Suthers, S. Ranganathan and C. D. Maranas, Mathematical optimization applications in metabolic networks, Metab. Eng., 2012, 14(6), 672–686.
30. I. Rocha, P. Maia, P. Evangelista, P. Vilaça, S. Soares and J. P. Pinto, et al. OptFlux: an open-source software platform for in silico metabolic engineering, BMC Syst. Biol., 2010, 4, 45.
31. T. Shlomi, T. Benyamini, E. Gottlieb, R. Sharan and E. Ruppin, Genome-scale metabolic modeling elucidates the role of proliferative adaptation in causing the Warburg effect, PLoS Comput. Biol., 2011, 7(3), e1002018.
32. C. Frezza, L. Zheng, O. Folger, K. N. Rajagopalan, E. D. MacKenzie and L. Jerby, et al. Haem oxygenase is synthetically lethal with the tumour suppressor fumarate hydratase, Nature, 2011, 477(7363), 225–228.
33. K. Maier, U. Hofmann, M. Reuss and K. Mauch, Dynamics and control of the central carbon metabolism in hepatoma cells, BMC Syst. Biol., 2010, 4, 54.
34. C. Chassagnole, N. Noisommit-Rizzi, J. W. Schmid, K. Mauch and M. Reuss, Dynamic modeling of the central carbon metabolism of Escherichia coli, Biotechnol. Bioeng., 2002, 79(1), 53–73.
35. K. Smallbone, E. Simeonidis, N. Swainston and P. Mendes, Towards a genome-scale kinetic model of cellular metabolism, BMC Syst. Biol., 2010, 4, 6.
36. I. E. Nikerel, W. A. van Winden, P. J. T. Verheijen and J. J. Heijnen, Model reduction and a priori kinetic parameter identifiability analysis using metabolome time series for metabolic reaction networks with linlog kinetics, Metab. Eng., 2009, 11(1), 20–30.
37. J. Niklas, K. Schneider and E. Heinzle, Metabolic flux analysis in eukaryotes, Curr. Opin. Biotechnol., 2010, 21(1), 63–69.
38. M. W. Covert, C. H. Schilling and B. Palsson, Regulation of gene expression in flux balance models of metabolism, J. Theor. Biol., 2001, 213(1), 73–88.
39. M. W. Covert, E. M. Knight, J. L. Reed, M. J. Herrgård and B. Ø. Palsson, Integrating high-throughput and computational data elucidates bacterial networks, Nature, 2004, 429(6987), 92–96.
40. T. Shlomi, Y. Eisenberg, R. Sharan and E. A. Ruppin, A genome-scale computational study of the interplay between transcriptional regulation and metabolism, Mol. Syst. Biol., 2007, 3.
41. S. Chandrasekaran and N. D. Price, Probabilistic integrative modeling of genome-scale metabolic and regulatory networks in Escherichia coli and Mycobacterium tuberculosis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(41), 17845–17850.
42. K. Yizhak, T. Benyamini, W. Liebermeister, E. Ruppin and T. Shlomi, Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model, Bioinformatics, 2010, 26(12), i255–i260.
43. D. R. Hyduke, N. E. Lewis and B. Ø. Palsson, Analysis of omics data with genome-scale models of metabolism, Mol. BioSyst., 2013, 9(2), 167.
44. K. Bettenbrock, S. Fischer, A. Kremling, K. Jahreis, T. Sauter and E.-D. Gilles, A quantitative approach to catabolite repression in Escherichia coli, J. Biol. Chem., 2006, 281(5), 2578–2584.
45. T. Nakakuki, M. R. Birtwistle, Y. Saeki, N. Yumoto, K. Ide and T. Nagashima, et al. Ligand-specific c-Fos expression emerges from the spatiotemporal control of ErbB network dynamics, Cell, 2010, 141(5), 884–896.
46. I. Stelniec-Klotz, S. Legewie, O. Tchernitsa, F. Witzel, B. Klinger and C. Sers, et al. Reverse engineering a hierarchical regulatory network downstream of oncogenic KRAS, Mol. Syst. Biol., 2012, 8, 601.
47. M. König, S. Bulik and H. G. Holzhütter, Quantifying the Contribution of the Liver to Glucose Homeostasis: A Detailed Kinetic Model of Human Hepatic Glucose Metabolism, PLoS Comput. Biol., 2012, 8(6), e1002577.
48. E. Mosca, R. Alfieri, C. Maj, A. Bevilacqua, G. Canti and L. Milanesi, Computational modeling of the metabolic States regulated by the kinase akt, Front Physiol., 2012, 3, 418.
49. M. W. Covert, N. Xiao, T. J. Chen and J. R. Karr, Integrating metabolic, transcriptional regulatory and signal transduction models in Escherichia coli, Bioinformatics, 2008, 24(18), 2044–2050.
50. J. M. Lee, E. P. Gianchandani, J. A. Eddy and J. A. Papin, Dynamic Analysis of Integrated Signaling, Metabolic, and Regulatory Networks, PLoS Comput. Biol., 2008, 4(5), e1000086.
51. M. G. Vander Heiden, L. C. Cantley and C. B. Thompson, Understanding the Warburg effect: the metabolic requirements of cell proliferation, Science, 2009, 324(5930), 1029–1033.
52. R. A. Cairns, I. S. Harris and T. W. Mak, Regulation of cancer cell metabolism, Nat. Rev. Cancer, 2011, 11(2), 85–95.
53. A. Schulze and A. L. Harris, How cancer metabolism is tuned for proliferation and vulnerable to disruption, Nature, 2012, 491(7424), 364–373.

---