 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct prediction of the desalination performance of porous carbon electrodes for capacitive deionization†
S.
Porada
ab,
L.
Borchardt
c,
M.
Oschatz
c,
M.
Bryjak
b,
J. S.
Atchison
d,
K. J.
Keesman
ae,
S.
Kaskel
c,
P. M.
Biesheuvel
af and
V.
Presser
*dg
aWetsus, Centre of Excellence for Sustainable Water Technology, Agora 1, 8934 CJ Leeuwarden, The Netherlands
bDepartment of Polymers and Carbon Materials, Faculty of Chemistry, Wroclaw University of Technology, Wybrzeze Wyspianskiego 27, 50-370 Wroclaw, Poland
cDepartment of Inorganic Chemistry, Dresden University of Technology, Bergstraße 66, 01069 Dresden, Germany
dINM-Leibniz-Institute for New Materials, Energy Materials Group, 66123 Saarbrücken, Germany. E-mail: volker.presser@inm-gmbh.de
eBiomass Refinery & Process Dynamics, Wageningen University, Bornse Weilanden 9, 6708 WG Wageningen, The Netherlands
fDepartment of Environmental Technology, Wageningen University, Bornse Weilanden 9, 6708 WG Wageningen, The Netherlands
gSaarland University, Campus D2 2, 66123 Saarbrücken, Germany
First published on 14th August 2013
Abstract
Desalination by capacitive deionization (CDI) is an emerging technology for the energy- and cost-efficient removal of ions from water by electrosorption in charged porous carbon electrodes. A variety of carbon materials, including activated carbons, templated carbons, carbon aerogels, and carbon nanotubes, have been studied as electrode materials for CDI. Using carbide-derived carbons (CDCs) with precisely tailored pore size distributions (PSD) of micro- and mesopores, we studied experimentally and theoretically the effect of pore architecture on salt electrosorption capacity and salt removal rate. Of the reported CDC-materials, ordered mesoporous silicon carbide-derived carbon (OM SiC-CDC), with a bimodal distribution of pore sizes at 1 and 4 nm, shows the highest salt electrosorption capacity per unit mass, namely 15.0 mg of NaCl per 1 g of porous carbon in both electrodes at a cell voltage of 1.2 V (12.8 mg per 1 g of total electrode mass). We present a method to quantify the influence of each pore size increment on desalination performance in CDI by correlating the PSD with desalination performance. We obtain a high correlation when assuming the ion adsorption capacity to increase sharply for pore sizes below one nanometer, in line with previous observations for CDI and for electrical double layer capacitors, but in contrast to the commonly held view about CDI that mesopores are required to avoid electrical double layer overlap. To quantify the dynamics of CDI, we develop a two-dimensional porous electrode modified Donnan model. For two of the tested materials, both containing a fair degree of mesopores (while the total electrode porosity is ∼95 vol%), the model describes data for the accumulation rate of charge (current) and salt accumulation very well, and also accurately reproduces the effect of an increase in electrode thickness. However, for TiC-CDC with hardly any mesopores, and with a lower total porosity, the current is underestimated. Calculation results show that a material with higher electrode porosity is not necessarily responding faster, as more porosity also implies longer transport pathways across the electrode. Our work highlights that a direct prediction of CDI performance both for equilibrium and dynamics can be achieved based on the PSD and knowledge of the geometrical structure of the electrodes.
Broader contextCapacitive deionization (CDI) is one of the most important small-scale and low-energy alternatives to reverse osmosis for the desalination of brackish water. Key components of this electro-kinetic method of water treatment are porous carbon electrodes with well-developed porosity. However, until now, the exact correlation between CDI performance and material parameters of the electrodes has largely remained unknown. To guide the ongoing research and development, quantitative methods to predict the equilibrium and dynamic behavior of CDI cells are essential. For direct practical implementation, predictive tools have to include the salt adsorption capacity and desalination rate as functions of the pore size distribution of the carbon electrode material, and of the geometrical measures of the electrodes, such as interparticle porosity. We present such a method based on a two-dimensional porous electrode theory, in combination with a predictive salt adsorption capacity analysis based on the pore size distribution. A high correlation between salt adsorption and pore size data for more than 15 different carbon materials presents evidence that sub-nm micropores are essential to achieve a high salt storage capacity. The reported work serves as an important step in making CDI a predictable electro-kinetic method, presenting clear guidelines for electrode materials' choice, synthesis, and electrode design. |
1 Introduction
Providing access to affordable and clean water is one of the key technological, social, and economical challenges of the 21st century.1–3 For the desalination of water, commercially available methods include distillation,4 reverse osmosis,5 and electrodialysis.6 Novel approaches include ion concentration polarization in microporous media,7 systems based on batteries,8,9 forward osmosis,10 and capacitive deionization (CDI).11–15CDI is based on an electrochemical cell consisting of an open-meshed channel for water flow, in contact with sheets of porous electrodes on both sides. Upon applying a cell voltage between the two electrodes, ions become immobilized by an electrosorption process, that is, cations move into the cathode (the electrode into which negative electrical charge is transferred), while anions move into the anode (Fig. 1). After some time, when the electrodes reach their adsorption capacity (which depends on cell voltage), a discharge cycle is initiated by reducing or reversing the cell voltage, thereby releasing the salt as a concentrated stream. In the discharging step of the cell, energy recovery is possible.16,17
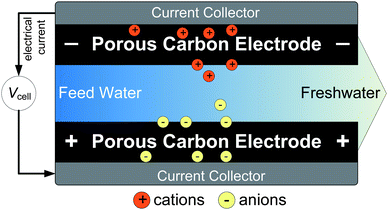 | ||
| Fig. 1 Schematic illustration of desalination via capacitive deionization (CDI). Upon applying a cell voltage between the two electrodes, anions and cations are electrosorbed within highly porous carbon electrodes to counterbalance the electrical charge. This immobilization of ions decreases the salt concentration in the flow channel, and results in the production of freshwater. | ||
Salt immobilization by CDI is considered an energy-efficient method for the desalination of water.15,18 Though typically applied to the desalination of brackish water sources, seawater can also be desalinated by CDI.19 In combination with ion-selective membrane layers placed in front of the electrodes, CDI can be used to selectively remove a certain ionic species from a mixture of salts or to harvest compounds such as acetic acid, sulphuric acid, insulin, and boron.20–26 Such separation processes may find use in the treatment of wastewater from agriculture (mining), industry, and hospitals.
Various configurations for the design, stacking, and water management of CDI cells are possible. Most studies consider a design where the salt water is directed parallel to two equal electrodes, while a constant cell voltage is maintained, see Fig. 1.13,27,28 However, stacks of electrodes do not necessarily have to consist of symmetrical cells and, instead, varying the carbon mass between the two electrodes provides the possibility to optimize the usable voltage window.29 Another approach utilizes carbon rods (called wires) which are sequentially dipped and taken out of the water, instead of using film electrodes forming a stack through which the water flows.30 Instead of using bare carbon electrodes, improved energy efficiency has been reported for membrane-CDI (MCDI), where ion-exchange membranes are placed in front of one or both of the electrodes.26,31–34 Further modifications are the use of constant current operation,33,35 directing the water flow straight through the electrodes,13,28 or the use of flowable electrode suspensions.19 Recently, CDI electrodes have also been used to produce energy from the controlled mixing of river and seawater, based on a reversal of the CDI process.36–42
Electrosorption of ions is an interfacial process and in order to have a maximum contact area between the electrode and the water, CDI employs high surface area porous carbon electrode materials. At the water–carbon interface, electrical double layers (EDLs) are formed in which ions are electrosorbed. It has been stated that for optimum performance, pores should be large enough to have only a weak EDL-overlap, that is, mesopores are to be preferred over micropores.43–45 However, some microporous carbons, such as activated carbons14,46 and carbide-derived carbons47 actually outperform mesoporous carbons. Recently, Porada et al.47 reported that CDI desalination capacity positively correlates with the volume of pores in the range below 1 nm, while obtaining a negative correlation with the total pore volume, or with the BET specific surface area (BET SSA, ref. 48). The importance of pores <1 nm has also been demonstrated for the capacitance of EDL-capacitor electrodes,49,50 for H2 gas storage,51 and for CO2 gas removal capacity.52 These results relate to equilibrium conditions, and micropores (<2 nm) and especially ultramicropores (<0.8 nm) can pose severe limitations to ion transport in CDI flow cells. Thus, porous electrodes that combine a large micropore volume (for a high deionization capacity) with a network of mesopores (between 2 and 50 nm) and macropores (>50 nm) may yield a highly efficient deionization process.43,53,54
For an optimum performance, the design of the various components of the CDI system must be tuned to achieve both high salt electrosorption capacity and fast kinetics at the same time. Desalination by porous electrodes is by nature a non-linear phenomenon. Classical transmission-line models applied to CDI are unsatisfactory as they predict zero salt electrosorption and assume a constant ionic resistivity in the electrode.15,55 Instead, when ions are being electrosorbed in the EDLs formed in intraparticle pores (within carbon particles), the interparticle pores (the pores in between the carbon particles) are subjected to ion starvation and the ionic conductivity will drop dramatically during desalination. This phenomenon results in an internal ionic electrode resistance that is much higher than expected on the basis of the performance derived for high salinity electrolytes, as common in EDLC research. EDLCs are specifically designed to operate at large salt concentrations to have a high ionic conductivity and maximum capacity. Such a free choice of electrolyte is obviously not possible for water desalination. Note that the effect of ion starvation and the temporal increase in local resistivity to ion transport in the interparticle pores is included in the porous electrode theory of our paper.
A variety of carbon materials, including activated carbons, carbon aerogels, carbon xerogels, and carbon nanotubes, have been studied for desalination by CDI.15,18 New developments of advanced CDI electrode materials include asymmetric electrodes made of activated carbon coated with alumina and silica nanoparticles,56 reduced graphene oxide and activated carbon composites,57 graphene electrodes prepared by exfoliation and reduction of graphite oxide,58 carbon nanotubes with polyacrylic acid,59 carbon fiber webs obtained from electrospinning,60,61 and mesoporous activated carbons.62 Templated carbons, although they require a more elaborate synthesis, are of particular interest as they provide additional means to precisely tailor the pore network, in order to combine a high electrosorption capacity with fast salt removal rates. A particularly high level of pore size control has been documented for carbons synthesized by selective etching of metal carbides with chlorine gas, called carbide-derived carbons, or CDCs.63 Lately, templated CDCs have been reported60,61 that combine a large micropore volume with hierarchic mesopores. Compared to conventional CDCs, templated ordered mesoporous CDCs (OM CDCs) show significantly larger specific surface areas (∼3000 m2 g−1) and total pore volumes (∼2 mL g−1).64 Furthermore, using foam-like CDCs, synthesized by the “high internal phase emulsion” (HIPE) approach, it is possible to obtain control over macropores. The resulting material has both high surface areas of up to 2300 m2 g−1 and extremely large pore volumes of up to ∼9 mL g−1.65
Despite many studies on various kinds of porous carbons, describing both equilibrium salt adsorption and the dynamics of the process, tools are not yet available to directly predict the performance of a certain carbon material and CDI design. The present work is aimed to be a first step towards a method for direct prediction of desalination performance in CDI. Our approach consists of two main routes.
(1) To extract data of the equilibrium salt adsorption and kinetics of CDI for carbon materials with precisely tailored and designed pore architectures. With these data we demonstrate how we can directly predict the desalination performance of a carbon material based on its pore size distribution (PSD).
(2) To use a two-dimensional porous electrode CDI transport model to predict the actual salt electrosorption kinetics. This model demonstrates how desalination kinetics depend not only on the intraparticle pore morphology, but also on the electrode thickness and interparticle porosity.
In the next sections we briefly describe the porous electrode transport theory, and discuss the synthesis of carbon materials and electrode architecture. We describe the salt adsorption performance in terms of equilibrium adsorption and kinetics, present a method to correlate equilibrium adsorption with PSD, and compare the dynamics of ion adsorption with theoretical predictions.
2 Theoretical section
To describe salt electrosorption and electrical current in porous carbon electrodes forming a CDI cell, we extend existing one-dimensional porous electrode theory to two dimensions, to consider both the flow direction of the aqueous solution through the spacer channel, and the movement of salt in and out of the electrodes. Within the electrodes, we consider simultaneously ion transport through the space between the carbon particles, that is, the large transport pathways across the electrode (interparticle pore volume), and the electrosorption of ions inside carbon particles (intraparticle pore volume). To describe the latter, a powerful and elegant approach is to assume that the EDLs inside the intraparticle pore volume are strongly overlapping and, therefore, that the potential in these pores does not vary with position in the pore. This is the common “Donnan” approach for charged porous materials. The electrical potential in the intraparticle pore volume is different from that in the interparticle pore volume (the transport pathways) by a value Δϕd. The direct Donnan approach is modified29,31,47 to consider the Stern layer located in between the electronic and ionic charge, and to include a chemical attraction energy for the ion when it transfers into the intraparticle pores, described by a term μatt.66 The modified Donnan (mD) model equals the limit situation of the Gouy–Chapman–Stern (GCS) theory when approaching full EDL overlap in micropores where the Debye length is of the order or larger than the pore size. In addition to GCS theory it includes the non-electrostatic adsorption energy μatt that reflects that also uncharged carbons adsorb some salt. A difference between the mD and GCS model is that in the mD model, EDL properties are described per unit pore volume, whereas in the GCS model charge and salt adsorption are described as functions of pore area. Numbers in either definition can be converted when the pore area/volume ratio is known.To describe the dynamics of ion transport and charge formation, we set up a two-dimensional porous electrode theory for a CDI cell consisting of two porous electrodes placed in parallel, with a flat planar slit, or transport channel, or spacer, in between. In the direction of flow, this transport channel is mathematically divided into M subsequent sub-cells, see Fig. 2.34 In the porous electrode, two coupled partial differential equations describe the salt concentration in the interparticle pores, the electrostatic potential there, ϕ, the charge density, and the salt electrosorption in the intraparticle pores as a function of time and depth in the electrode. The porous electrode transport theory requires various geometrical measures as inputs (thickness, porosity) that can be calculated from electrode dimensions. Besides, it requires an estimate of the diffusion coefficient of the ions in the macropores, which may be lower than the corresponding value in free solution. There are no other fitting functions. The present model neglects a transport resistance between interparticle pores and intraparticle pores, which can be incorporated, but requires an additional transport coefficient. Further details of the mD and transport model are provided in section 5 of the ESI.†
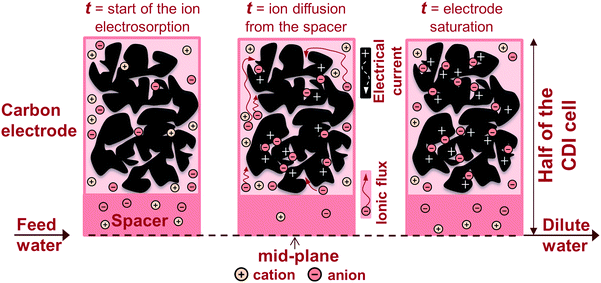 | ||
| Fig. 2 Schematic view of the time-dependent two-dimensional porous electrode model, combining a sequence of sub-cells in the flow direction, with ion fluxes into the electrode. A symmetric CDI geometry is assumed, thus only half of a cell is depicted. The electrode contains an electrolyte-filled volume allowing for ion transport, and carbon material in which ions and charge are stored. Electrical current (denoted by “+”) flows through the conductive carbon material. | ||
3 Experimental section
Electrodes from three different CDCs were prepared and compared to establish a basis of reference materials for further analysis of the salt electrosorption capacity. Details of material synthesis, electrode manufacturing and CDI testing are given in the ESI.† The synthesis methods are summarized in Fig. 3 for titanium carbide-derived carbon (TiC-CDC, Fig. 3A), ordered mesoporous silicon carbide derived carbon (OM SiC-CDC, Fig. 3B), and HIPE SiC-CDC (Fig. 3C).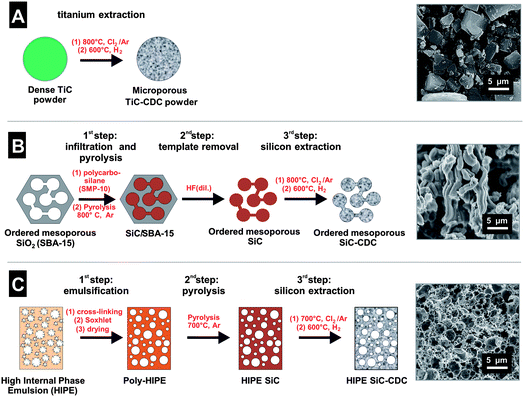 | ||
| Fig. 3 Schematic illustration and SEM images of the synthesis of (A) TiC-CDC, (B) OM SiC-CDC, and (C) HIPE SiC-CDC. | ||
Electrodes were prepared from these powders following the procedure outlined in ref. 47. A carbon slurry was prepared by mixing 85 mass% of CDC, 5 mass% of carbon black (Vulcan XC72R, Cabot Corp., Boston, MA), and 10 mass% of polyvinylidene fluoride (Kynar HSV 900, Arkema Inc., Philadelphia, PA); the latter was previously dissolved in N-methyl-2-pyrrolidone. Thus, the final electrode contains 85 mass% of porous CDC carbon. Electrodes were prepared by painting of the carbon slurry directly on one or both sides of a graphite current collector, taking care that approximately the same mass was coated on each side. Results for thickness and total electrode mass density are provided in Table S5.† Together with open-meshed porous spacer materials (thickness δsp = 350 μm) the current collector/electrode layers are stacked together forming three parallel cells (i.e., one stack).29,47 The flow of salt solution through the stack is kept constant, flowing first into a housing around the stack, entering the spacer layers from all four sides, and leaving via a centrally placed outlet to flow along a conductivity meter placed in-line.
An array of activated carbons and other carbon materials (see ESI†) were investigated along with the CDC materials for comparison. These materials were not painted, but prepared by a wet-casting technique following the procedure explained in ref. 47. In addition, carbon onions were tested as a representative of the class of fully graphitic, dense carbon nanoparticles (Fig. S9, ESI†) with no intraparticle porosity. The synthesis of carbon onions is based on the vacuum treatment of nanodiamonds at 1750 °C as outlined in more detail in the ESI.†
Ion electrosorption occurs when applying a cell voltage Vcell to each of the three cells, defined as the voltage difference between the positively and negatively polarized electrodes. At the end of the salt electrosorption step, the cell voltage is reduced to zero and ion desorption begins. The electrical current running from the cathode to the anode is measured and is integrated over time to provide a measure for the total charge transferred between the electrodes. This total charge is divided by the total electrode mass in the stack, mtot, to obtain the charge expressed in C g−1, see Fig. 5A, 7A and 8A. From the conductivity of the effluent solution, the salt concentration is calculated and, thus, by integrating over time, the salt electrosorbed, Γsalt, is calculated, see ref. 15 and 47. For each new experiment, the salt electrosorption/desorption cycle was repeated several times until the differences between cycles became negligible. We like to stress that in this work, the salt removal data are not obtained from the first cycle after a new condition has been applied, but instead are obtained when the system has reached the limit cycle, also called dynamic equilibrium (DE). This is the situation that the same amount of salt is electrosorbed during the adsorption step as is being removed in the desorption step of the cycle, as will be typical during practical long-term operation of a CDI system. All experiments were done using a c∞ = 5 mM NaCl-solution (290 ppm, 550 μS cm−1).
4 Results and discussion
4.1 Structure of the porous carbons
The CDC materials used for this study are produced from selective etching of silicon or titanium atoms out of a carbide precursor (SiC or TiC), a procedure which results in a material with a high BET SSA which, in the case of OM SiC-CDC, is as high as 2720 m2 g−1 (Table 1). Fig. 4 displays the cumulative pore volume of these materials, together with the salt adsorption capacity, or ζ(σ)-curve, which is discussed below.| Carbon material | Total pore volume (mL g−1) | BET SSA (m2 g−1) | QSDFT SSA (m2 g−1) | Average pore size d50 (nm) |
|---|---|---|---|---|
| TiC-CDC | 0.52 | 1309 | 1376 | 0.67 |
| OM SiC-CDC | 1.98 | 2720 | 2260 | 4.00 |
| HIPE SiC-CDC | 1.14 | 2351 | 2120 | 1.24 |
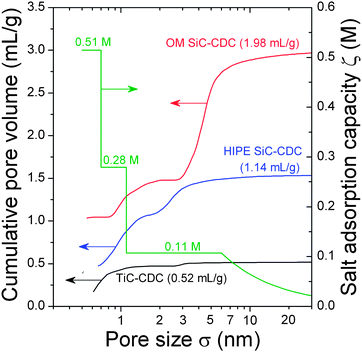 | ||
| Fig. 4 Cumulative pore size distributions calculated from QSDFT models of the three tested CDC-materials, as well as the suggested correlation function for the ion adsorption capacity, ζ(σ). PSD curves shifted up by 0.4 mL g−1 for HIPE SiC-CDC and 1.0 mL g−1 for OM SiC-CDC. | ||
All CDCs investigated in this study are predominantly amorphous, as evidenced by the broad D- and G-bands observed in Raman spectroscopy (see ESI†). TiC-CDC (Fig. 3A) powders are composed of anisometric particles with a size distribution ranging from approximately 1 to 10 μm and an average size of ∼5 μm. Compared to that, the structures of OM SiC-CDC and HIPE SiC-CDC differ in many aspects. HIPE SiC-CDC has a cellular pore structure as can be seen from Fig. 3C. Owing to the HIPE synthesis route, the material exhibits 2 to 4 μm sized cages that are interconnected by 300 to 500 nm sized windows. The walls are highly porous, but yet in the nanometer range. Thus, this material exhibits a hierarchical pore structure consisting of macro-, meso-, and micropores. For the other materials used in this study, macropores are only present in the form of large pores between carbon particles, but not within the porous particles themselves. OM SiC-CDC was synthesized as a powder of strand-like particles (Fig. 3B) having an average strand diameter of approximately 1 μm. These strands are built from nanorods which are arranged in a hexagonal ordered fashion and have very narrowly distributed mesopores located in between (Fig. 3B). The narrow distribution in the mesopore size is due to the method of nanocasting which employs ordered mesoporous silica templates as conformally corresponding exo-templates for the resulting CDC.64,67–71 Besides the ordered mesopores, micropores are also present in OM SiC-CDC. As a consequence, this material has a hierarchy of micro- and mesopores but no internal macropores.68
The data for cumulative pore volume, see Fig. 4, show a hierarchical pore size distribution (PSD) with contributions from micro- and mesopores for HIPE and OM SiC-CDC, while TiC-CDC is predominantly microporous: more than 90 vol% of the pores is smaller than 2 nm (see Table S1 in the ESI†). HIPE SiC-CDC shows a total percentage of 37 vol% of mesopores and for OM SiC-CDC the majority of the total pore volume is associated with mesopores (∼75 vol%). In that regard, HIPE SiC-CDC has the largest total micropore volume (0.72 mL g−1) of the CDC-materials. The hierarchic porosity of OM SiC-CDC is exemplified by its two narrow distribution maxima at approximately 1 nm and 4 nm. HIPE SiC-CDC does not show such a strongly pronounced bimodality, but it still exhibits two pore size distribution maxima at around 1 nm and another one at 2.4 nm.
4.2 Equilibrium desalination performance
Equilibrium data for salt adsorption and charge are presented in Fig. 5, based on underlying data for the desalination cycle for which examples given in Fig. S5 and S6 of the ESI,† using a symmetric CDI cell. Fig. 5A and B present data for salt adsorption and charge per gram of both electrodes, as functions of cell voltage. In Fig. 5B and C, the salt adsorption is presented relative to that at zero cell voltage in a two-electrode CDI cell. Fig. 5D presents the calculated total ion concentration in the pores (relative to an uncharged electrode), per mL intraparticle pore volume (for all pores below a size of 30 nm), as a function of the charge, also expressed per mL of intraparticle pores. The data for pore volume are given in Table 1 and Fig. 4. Fig. 5A and B show that the material with the highest capacitance (22.3 F g−1 at 5 mM NaCl, low-voltage limit), OM SiC-CDC, also has the highest salt adsorption capacity, 12.8 mg g−1 at a cell voltage of Vcell = 1.2 V. Per gram of carbon (not total electrode) the adsorption is 15.1 mg g−1 at 1.2 V.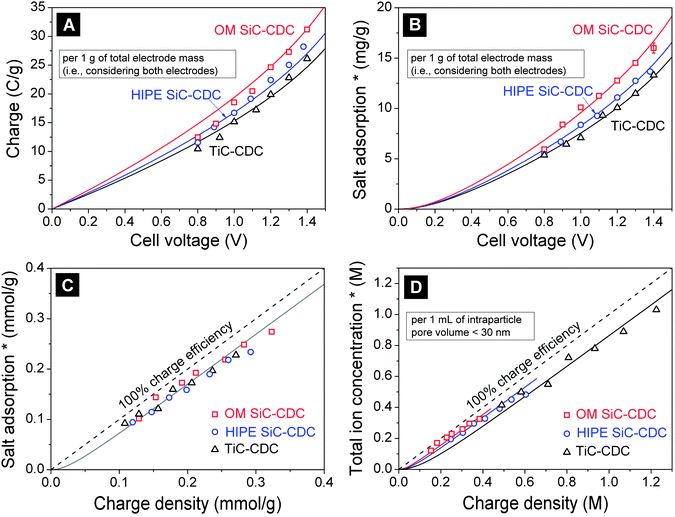 | ||
| Fig. 5 Equilibrium salt adsorption and charge in porous carbon electrodes prepared from OM SiC-CDC (squares), HIPE SiC-CDC (circles), and TiC-CDC (triangles). (A) Equilibrium charge ΣF and (B) equilibrium salt electrosorption Γsalt as functions of cell voltage, both per gram of both electrodes. (C) Charge and salt adsorption recalculated to mol g−1, and plotted one versus the other. (D) Total pore ion concentration vs. charge per unit intraparticle volume (<30 nm). Salt concentration c∞ 5 mM NaCl. Lines represent fits using the modified Donnan model with in (D), μatt,ref as the single fitting parameter. (*) Data relative to adsorption at Vcell = 0. | ||
Figs. 5A and B clearly show how with increasing cell voltage both charge and salt adsorption increase non-linearly. This is different from typical results for EDL capacitors where the charge increases linearly with voltage (see ref. 15). Fig. 5C plots salt adsorption vs. charge (both expressed in mol g−1; for salt by dividing the data of Fig. 5B by Mw,NaCl and for charge by dividing the results of Fig. 5A by Faraday's number), which is a novel representation, which shows how all three datasets overlap. Fig. 5C also shows that the total ion adsorption is always somewhat less than the charge, i.e., the charge efficiency (Λ = salt adsorption/charge) is below unity.73 The high suitability of the materials tested for CDI can be deduced from the fact how close the measured charge efficiency is to unity, with measured values of Λ generally beyond 0.85. Indeed, Fig. 5C shows how close the data points are to the “100% charge efficiency line”, the ideal limit where for each electron transferred one full salt molecule is removed. Interestingly, beyond the first data points (charge density ∼0.1 mmol g−1) the data run parallel to the “100% charge efficiency line” which demonstrate that in this range, for each additional electron transferred, a full salt molecule is adsorbed, i.e., the differential salt efficiency is unity.15,74Fig. 5C clearly makes the point that a strong correlation exists between the capacitance of a material (how much charge can be stored for a given cell voltage, typically evaluated under conditions of use for EDL capacitors) and desalination performance in CDI.47
Evaluating the data in Fig. 5B per unit pore volume (all pores <30 nm), one can calculate a salt adsorption of 0.39 M for TiC-CDC, 0.20 M for HIPE SiC-CDC, and 0.13 M for OM SiC-CDC, at a cell voltage of 1.2 V. This salt adsorption, SA, having dimension M, just as the ζ-function that will be discussed shortly, see Fig. 4, is equal to half the total ion concentration in the intraparticle pores (<30 nm) as given in Fig. 5D (relative to salt adsorption at zero voltage), evaluated for a symmetric two-electrode cell. Clearly, per unit pore volume the performance is decreasing in this order, which is opposite to the order when the more common metric of mg g−1 is used (as plotted in Fig. 5B). Careful assessment of the influence of pore size increments on desalination performance is required, and care must be taken in defining what is the “best” material, which may relate to electrode mass or volume, dependent on the final application.
Next, we define the performance ratio of a material, or PR. As we will take HIPE SiC-CDC as the reference, for HIPE this value is unity, PR = 1. For TiC-CDC, which has twice the desalination per unit pore volume compared to HIPE at the reference conditions, PR = 2. Likewise for OM SiC-CDC the value is PR = 0.66.
In a later section we will discuss how well the value of PR correlates with known data of the material's total pore volume, BET SSA, and full pore size distribution. If here a correlation can be found, this would allow one to estimate the PR of a new material when only the PSD is known, without having data of CDI experiments available. From the PR-value, desalination performance at the reference conditions of a symmetric CDI cell operating at Vcell = 1.2 V and for a salinity level of 5 mM NaCl can then be calculated. But in addition, knowing PR it will also be possible to calculate desalination at any other condition (different salinity, voltage, cell design), with the aid of the mD-model, which requires knowledge of the three parameters μatt, CSt,vol,0 and α that are used in the mD-model. Thus, we first address, when the value of PR is known, how we can calculate appropriate values to be used in the mD-model, which then predicts desalination, not only under the reference conditions as defined above, but also at other voltages (see Fig. 5B), other salinities, and very different CDI cell designs. The procedure that we propose is that relative to the reference material (HIPE SiC-CDC), for which the three parameters in the mD-model, being μatt, CSt,vol,0 and α, are determined as explained below, for materials with a different PR, the following rescalings are used: to μatt is added a term ln(PR), CSt,vol,0 is multiplied by PR, and α is divided by PR. This procedure is based on the finding that rescaling the total pore volume by PR gave a perfect match to the data. However, to avoid introducing the concept of a theoretical volume different from the actual one, for which there is no physical basis, the above procedure is proposed. In this way, once the value of PR of a new material is calculated (from the PSD data and using the ζ(σ)-curve), then by correlating to the known performance of HIPE SiC-CDC, its CDI performance can be directly predicted.
The values for μatt, CSt,vol,0, and α for HIPE SiC-CDC are calculated as follows. The novel representation in Fig. 5D is the starting point to derive by a structured method the parameters in the mD-model. Moreover the data in Fig. 5D can be fitted only by adjusting the value of μatt, without any influence of Stern layer properties on this fit, see eqn (S3) and (S4) in the ESI.† For HIPE an optimum value of μatt = 2.0 kT is found, in line with values used in previous work.29,30 Next, for HIPE the full data of Fig. 5A and B must be fitted by optimizing CSt,vol,0 and α, for which only one combination fits the curves well (namely, CSt,vol,0 = 72 MF m−3 and α = 50 F m3 mol−2). Having established all of these values, the curves for the other two materials in Fig. 5A, B, and D automatically follow, and a very satisfactory fit is obtained. Using a constant Stern layer capacity does not fit the data well, see Fig. S5 in the ESI† for a comparison with a calculation with α = 0.
4.3 Direct prediction of the desalination performance based on porosity analysis
We aim to find a method to correlate desalination performance in CDI to the porosity analysis of the carbon material. This is a hotly debated topic and the claim is often made that for CDI pores must be mesoporous (i.e., above 2 nm),43,44 or even beyond 20 nm (ref. 45) to avoid overlap of electrical double layers in the pores, an effect that is claimed to be deleterious for CDI. However, electrodes made of microporous AC and CDC powders showed very high performance in CDI, higher than electrodes based on mesoporous carbon aerogels.15,47,75 Also for the materials tested in this work, the predominantly microporous carbons (TiC-CDC, and HIPE SiC-CDC) show a general trend of higher salt adsorption per unit pore volume than the predominantly mesoporous OM SiC-CDC.One question remains: what porosity metrics are most suitable to predict CDI performance? In agreement with ref. 47, we find that desalination is positively correlated, even proportional, with the volume of pores smaller than 1 nm (see Fig. S3A and Table S1 in the ESI†), but only for materials that are mainly microporous. However, when including in the correlation materials with a significant portion of mesopores, such as HIPE SiC-CDC and even more so for OM SiC-CDC, for these materials a significant deviation from this proportionality (between salt adsorption and pore volume in pores <1 nm) is observed, with a much higher salt electrosorption than predicted based on this correlation, which can be explained by the contribution of mesopores to the ion immobilization. This contribution is not as high, per unit volume, as for micropores, but mesopores nevertheless also contribute to the ion electrosorption capacity. Thus, this measure of pore volume <1 nm cannot be the input parameter for a reliable predictive method. This situation is quite different from that in ref. 47 where it was demonstrated that for microporous carbons (AC and TiC-CDC), a positive correlation between the volume of pores smaller than 1 nm and the CDI performance could be established with a negative correlation of salt adsorption with BET SSA and with the total pore volume.
An appropriate metric based on PSD is not just correlated with salt adsorption, but ideally is proportional with desalination. Proportionality implies that the metric is a true measure of desalination, with an increase in this metric by a factor 2, resulting also in a two-times increased desalination. Such a metric is more likely to have a chemical–physical basis than a metric that is merely correlated with desalination. In Fig. S3 of ESI† we show four metrics based on the PSD and their proportionality with the salt adsorption performance: micropore volume <1 nm, <2 nm, total pore volume, and BET SSA. However, a satisfying fit is not observed in either case. Thus, we cannot establish a clear and unambiguous proportionality between the salt electrosorption capacity and either of these metrics (see Fig. S3 in the ESI†).
Still, porosity measurements present a very facile method to characterize porous carbons and it remains very attractive to base a predictive CDI performance method on porosity data. We, thus, propose a new approach to predict the CDI performance, based on considering the relevance to salt adsorption of each pore size increment, which we call “salt adsorption capacity analysis” (or, ζ-analysis), which determines the relevance of each size increment to the measured desalination under one reference condition (Vcell = 1.2 V, c∞ = 5 mM NaCl, symmetric cell). The function ζ is a property with dimension M and describes for the reference condition the contribution to desalination by a CDI cell of a certain pore size, σ, per unit pore volume (within the carbon in one electrode). Deriving the ζ(σ)-function is done by the simultaneous fit of the experimentally available PSD of a set of materials to their desalination performance. This analysis quantifies the fact that salt electrosorption depends not only on the total pore volume, but also on the pore size distribution: the volume associated with some pores contributes more to the total sorption capacity than other pores.
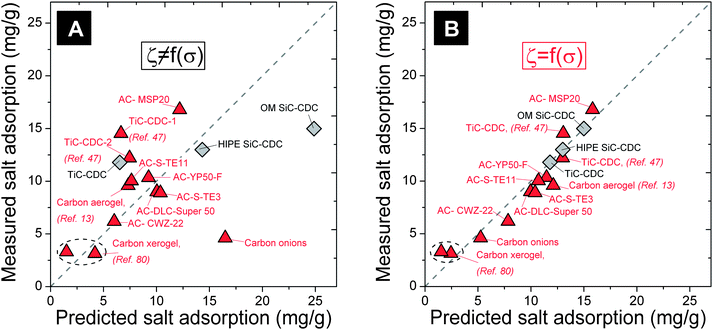
Mathematically, the aim of the analysis is to find the ζ(σ)-function, see Fig. 4, by which the salt adsorptions (SAs) of a set of materials (at the reference condition) predicted by eqn (1), fit as closely as possible the measured values of SA. Note that the ratio of this SA to the SA of our reference sample (HIPE SiC-CDC) is the performance ratio, PR. In the ζ(σ)-analysis, the total salt adsorption in mg g−1 of a symmetric two-electrode cell is given by eqn (1)
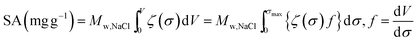 | (1) |
To find the optimum ζ(σ)-function we have used various methods, using e.g. predefined functions, but in the end we decided to use a “function-free” approach in which the value of ζ is adjusted separately for each increment in size σ, with the only imposed constraint that ζ must be decreasing with size σ.
Assuming, instead, as a first approximation ζ to be invariant with pore size σ, we obtain the parity plot of Fig. 6A, where for the three CDC-materials, and also for twelve other materials (listed in Table 2) we show the correlation between the predicted value of SA and the measured value. As can be observed in Fig. 6A, there is a large deviation between the measured and predicted salt adsorption when assuming ζ to be constant at ζ = 0.21 M and not varying with pore size.
 | ||
| Fig. 6 Parity plots for salt adsorption (c∞ = 5 mM, Vcell = 1.2 V) for three carbide-derived carbons (grey diamonds) and twelve other materials (red triangles) per gram of carbon in both electrodes combined. (A) Salt adsorption capacity ζ assumed independent of pore size σ. (B) Optimized ζ(σ)-function, see Fig. 4. | ||
| Cell voltage (V) | Salt concentration (mg L−1) | Γ salt (mg g−1) | Ref. | |
|---|---|---|---|---|
| CNT–RGO | 1.2 | ∼50 | 0.7 | 77 |
| 1.6 | ∼50 | 0.9 | ||
| MWCNTs | 1.2 | ∼3000 | 1.7 | 78 |
| RGO | 2.0 | ∼65 | 1.8 | 79 |
| Carbon xerogel | 1.2 | ∼260 | 3.1 | 80 |
| Carbon xerogel | 1.2 | ∼260 | 3.3 | 80 |
| Carbon onions | 1.2 | ∼290 | 3.9 | This work |
| CWZ-22 (AC) | 1.2 | ∼290 | 5.3 | This work |
| Carbon aerogel | 1.3 | ∼2000 | 7.1 | 75 |
| Mast carbon S-TE3 (AC) | 1.2 | ∼290 | 7.6 | This work |
| Norit DLC Super50 (AC) | 1.2 | ∼290 | 7.7 | This work |
| Mast carbon S-TE11 (AC) | 1.2 | ∼290 | 8.5 | This work |
| Kuraray YP50-F (AC) | 1.2 | ∼290 | 9.1 | This work |
| Microporous carbon aerogel monoliths | 1.25 | ∼2900 | 9.6 | 13 |
| TiC-CDC | 1.2 | ∼290 | 10.1 | This work |
| TiC-CDC | 1.2 | ∼290 | 10.4 | 47 |
| HIPE SiC-CDC | 1.2 | ∼290 | 11.1 | This work |
| ∼290 | 13.6 | |||
| TiC-CDC | 1.2 | ∼290 | 12.4 | 47 |
| OM SiC-CDC | 1.2 | ∼290 | 12.8 | This work |
| MSP-20 (AC) | 1.2 | ∼290 | 14.3 | This work, 81 |
Next we discuss our results of using a modified ζ(σ)-function. The optimized ζ(σ)-function is found by a least-square fitting procedure of the difference of predicted (see eqn (1) above) and measured desalination. Several a priori constraints are imposed:
(1) The full PSD curve is divided in short size ranges of 0.1 nm, for each of which the value of ζ can be adjusted by the optimization routine, independently of the others.
(2) With increasing size σ, ζ is not allowed to increase, but only to stay constant or decrease. Thus, we impose the rather stringent condition that the ζ(σ)-curve must monotonically decrease and the smallest pore size will have the highest ζ.
(3) We assume that beyond a certain size, when EDL overlapping starts to become minor, and desalination must be proportional with area, that desalination per unit volume must be inversely proportional with pore size. We impose this condition from a rather arbitrarily chosen point of a size of σ = 6 nm.
We apply this analysis method to the three CDC-materials discussed before, and we arrive at the ζ(σ)-curve as sketched in Fig. 4, where for a size σ from 1.1 to 6.0 nm a constant ζ is predicted of ζ = 0.11 M, from a size σ 0.7–1.1 nm we have ζ = 0.28 M and below σ = 0.7 nm ζ = 0.51 M. (Note that the computer routine predicts tiny variations within each “block”, and we removed these slight changes manually giving the ζ(σ)-curve plotted in Fig. 4, which was used as input in Fig. 6B). Next the optimized ζ(σ)-correlation function is validated by applying it to twelve different materials, see Fig. 6B. As can be observed, for the three CDC-materials the fit is now perfect, while also for the other materials, the fit between predicted desalination (x-axis) and actual desalination (y-axis) has improved substantially.
This analysis demonstrates that pores smaller than 1.1 nm contribute more substantially to desalination than larger pores. The finding of a very high value of the electrosorption capacity associated with these micropores is in good agreement with our previous study on a comparison of CDC and AC materials47 and is also in line with the data presented in Table 1 and Fig. S3A (see ESI).† It is closely related to the reported phenomenon of the anomalous increase in capacitance in EDL-capacitors in subnanometer-sized pores.49,76
In conclusion, the ζ(σ)-analysis gives the possibility to predict the CDI performance for both common and specialized carbons, purely based on easy-to-access cumulative PSD data. In contrast to this accuracy, our results (Fig. 6A and S3†) also underline that a convoluted, single value of pore analysis such as average pore size, total specific surface area, or total pore volume is not suited for direct prediction of the salt electrosorption capacity. Clearly, the complexity of carbon porosity must be appreciated and PSD data must be combined with consideration of the desalination efficiency of each pore size increment.
A spreadsheet file for the ζ-analysis based on arbitrary PSD-data is provided as ESI.†
4.4 Kinetics of salt electrosorption and charge transfer
Besides equilibrium electrosorption, the dynamics of ion sorption is of great importance for the practical application of CDI devices, and for a comprehensive understanding of differences between different porous carbon materials. In this section we apply for the first time a rigorous procedure based on a two-dimensional porous electrode theory that predicts the dynamical CDI behavior of a porous carbon electrode, see the ESI,† based on ion electrodiffusion through the interparticle pores in the electrodes, and ion electrosorption in the intraparticle pores. Electrosorption is described by the modified Donnan (mD) model for which appropriate parameter values for μatt, CSt,vol,0, and α were derived in Section 4.2 (see Fig. 5). The mD model not only predicts desalination at the reference condition of Vcell = 1.2 V and for c∞ = 5 mM NaCl, but also for other conditions, and in addition, also describes electrosorption in a dynamic calculation during which the salt concentration in the interparticle pores becomes significantly different from c∞, to drop for a short period during desalination, while increasing sharply, again only for a short period, during ion release.31 The only dynamic fitting parameter is the ion diffusion coefficient.As depicted in Fig. 7, the porous electrode theory describes the rate of salt electrosorption and charge accumulation in CDI electrodes very well for the materials with a fair amount of mesopores (HIPE SiC-CDC, and OM SiC-CDC). The only difference in the input values for these calculations is the electrode thickness and inter- and intraparticle porosity, all calculated from geometrical measurements (see also Tables 2 and S6 in the ESI†), and the parameters for the mD model obtained from the equilibrium analysis of Section 4.2. The dynamics are described by the ion diffusion coefficient, for which a value of D = 1.34 10−9 m2 s−1 is used for all materials (see ESI†).
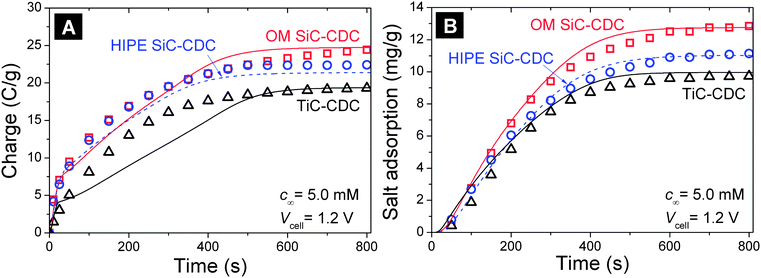 | ||
| Fig. 7 (A) Kinetics of charge transfer during the adsorption step and (B) salt electrosorption in CDI, as a function of time for OM SiC-CDC (squares), HIPE SiC-CDC (circles) and TiC-CDC (triangles). Lines are fits using two-dimensional porous electrode theory. | ||
While hierarchic porous carbons, that is, OM SiC-CDC and HIPE SiC-CDC, yield an excellent agreement between the measured and calculated dynamic behavior, for TiC-CDC which has practically no mesopores, and is much denser (Table S5 in ESI†), we do obtain a good fit of the salt electrosorption rate, but at the same time the charge accumulation rate (current) is underestimated initially. This possibly relates to a transport resistance from the interparticle space to the intraparticle space, see Section 5.3 in the ESI.†
4.5 Effect of electrode thickness on salt electrosorption and charge transfer
As we have seen, ion transport is strongly influenced by the structure of the pore network, with a very good description of the dynamics of desalination performance for the hierarchical materials, as shown in Fig. 7. To further validate the two-dimensional porous electrode theory for these hierarchical materials, electrodes characterized by the same mass density but different thicknesses were prepared from OM SiC-CDC. The choice of this material was motivated by the excellent correlation between data and model shown in Fig. 7. As shown in Fig. 8A and B, there is a very strong influence of the electrode thickness on both the salt electrosorption and the charge transfer rate. By increasing the thickness of the electrodes, the rate by which the maximum desalination is reached in the CDI process slows down, while as expected the final equilibrium values (defined per gram of material) remain exactly the same. We see that this applies for both the charge accumulation rate and the salt electrosorption rate. Fig. 8C and D analyze theoretically the effect of higher (or lower) electrode packing density (the overall electrode mass density, as presented in column 2 of Table S5†), by reducing the interparticle volume while keeping the mass and total intraparticle volume the same. Fig. 8D shows the interesting effect that a reduction of the interparticle volume is at first advantageous, with the time to reach 50% of the maximum desalination first decreasing (reaching a minimum value in the range of porosities between 30 and 60%), with this time increasing again for even lower porosities. The positive effect of a higher packing density of the electrode is that the length of the pathways for ions to traverse across the electrode goes down (the deepest regions of the electrode are more quickly reached), while the opposite effect at low porosity is because the transport pathways are being squeezed out of the electrode, with the apparent resistance for ion transport increasing (i.e., simply no transport pathways remain).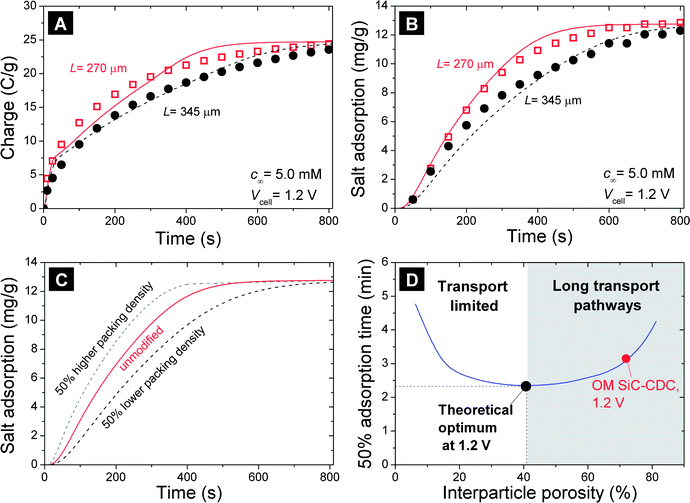 | ||
| Fig. 8 (A) Salt electrosorption and (B) charge transfer during the electrosorption step in CDI, as a function of time and electrode thickness, L, for electrodes made of OM SiC-CDC. Lines are predictions using two-dimensional porous electrode theory. (C and D) Calculation results as a function of electrode packing density. | ||
These observations have a number of important implications, because optimized kinetics are very important for actual CDI application. As Fig. 8 demonstrates, faster ion electrosorption (per unit mass of electrode) can be achieved by decreasing the electrode thickness and by optimizing the electrode porosity. Thus, our study demonstrates that it is not only important to appreciate the micro- and mesopores present inside a carbon particle, but also to understand the porous carbon electrode in its entirety. The latter also entails the pores in between the carbon particles, and the total thickness of an electrode.
5 Conclusions
We have studied capacitive deionization of water using three carbide-derived porous carbon materials with strongly varying contributions to the total pore volume originating from micro- and mesopores, and compared performance with various reference materials. We have demonstrated that there is no direct relationship between salt electrosorption capacity and typical pore metrics such as BET SSA and the total volume of pores. However, we have demonstrated that the salt electrosorption capacity can be predicted by analysis of the pore size distribution and the pore volume correlated with incremental pore size ranges, considering that differently sized pores exhibit a different electrosorption capacity for the removal of salt ions. This analysis has been validated by comparison to literature data and other carbon materials and we were able to quite reliably predict the CDI performance of a range of carbons used for CDI.Modeling is an important part of CDI performance analysis, not only to access information on the equilibrium salt removal capacity but also to gain understanding of the ion electrosorption process. Using the diffusion coefficient as the only dynamic fit parameter, two-dimensional porous electrode theory is capable of predicting the dynamics of charge accumulation and the resulting process of salt electrosorption for the CDC-materials with sufficient amounts of mesopores. For materials without pores in this size range, the theory underestimates the initial current. Although CDI is a complex process depending on various parameters, such as pore volume, pore size distribution and process parameters, our work demonstrates that prediction of the CDI dynamic equilibrium salt adsorption capacity and the kinetics for flow-by electrodes is feasible. These results will facilitate the rational development of carbon electrode designs for CDI. An important next step will be to adapt our model to more advanced CDI techniques, such as flow-through CDI,13,82 CDI using wires,30 or CDI using flowing electrodes.19
Acknowledgements
Part of this work was performed in the TTIW-cooperation framework of Wetsus, Centre of Excellence for Sustainable Water Technology. Wetsus is funded by the Dutch Ministry of Economic Affairs, the European Union Regional Development Fund, the Province of Friesland, the City of Leeuwarden, and the EZ/Kompas program of the “Samenwerkingsverband Noord-Nederland”. We thank the participants of the themes “Capacitive Deionization” and “Advanced Waste Water Treatment” for their involvement in this research. The authors also thank Matthew Suss (Stanford University, USA) and James London (University of Kentucky, USA) for providing pore size distribution data, and Taeyoung Kim for providing activated carbon sample called MSP-20. Dr Mesut Aslan and Dr Emilie Perre (both at INM) are thanked for their help with the gas sorption analysis. Rudolf Karos (INM) is thanked for his help with XRD analysis. VP acknowledges funding received from the Bayer Early Excellence in Science Award and Prof. Eduard Arzt (INM) is thanked for his continuing support.Notes and references
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- T. Humplik, J. Lee, S. C. O'Hern, B. A. Fellman, M. A. Baig, S. F. Hassan, M. A. Atieh, F. Rahman, T. Laoui, R. Karnik and E. N. Wang, Nanotechnology, 2011, 22, 292001 CrossRef CAS PubMed.
- http://www.un.org/News/Press/docs/2010/ga10967.doc.htm .
- A. D. Khawaji, I. K. Kutubkhanah and J.-M. Wie, Desalination, 2008, 221, 47–69 CrossRef CAS PubMed.
- L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Water Res., 2009, 43, 2317–2348 CrossRef CAS PubMed.
- H. Strathmann, Ion-Exchange Membrane Separation Processes, Elsevier, Amsterdam, 2004 Search PubMed.
- A. Mani and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061504 CrossRef.
- M. Pasta, C. D. Wessells, Y. Cui and F. La Mantia, Nano Lett., 2012, 12, 839–843 CrossRef CAS PubMed.
- M. Pasta, A. Battistel and F. La Mantia, Energy Environ. Sci., 2012, 5, 9487–9491 CAS.
- T. Y. Cath, A. E. Childress and M. Elimelech, J. Membr. Sci., 2006, 281, 70–87 CrossRef CAS PubMed.
- K.-L. Yang, T.-Y. Ying, S. Yiacoumi, C. Tsouris and E. S. Vittoratos, Langmuir, 2001, 17, 1961–1969 CrossRef CAS.
- C. J. Gabelich, T. D. Tran and I. H. M. Suffet, Environ. Sci. Technol., 2002, 36, 3010–3019 CrossRef CAS.
- M. E. Suss, T. F. Baumann, W. L. Bourcier, C. M. Spadaccini, K. A. Rose, J. G. Santiago and M. Stadermann, Energy Environ. Sci., 2012, 5, 9511–9519 CAS.
- H. Li, L. Zou, L. Pan and Z. Sun, Environ. Sci. Technol., 2010, 44, 8692–8697 CrossRef CAS PubMed.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 Search PubMed.
- O. N. Demirer, R. M. Naylor, C. A. Rios Perez, E. Wilkes and C. Hidrovo, Desalination, 2013, 314, 130–138 CrossRef CAS PubMed.
- P. Dlugolecki and A. van der Wal, Environ. Sci. Technol., 2013, 47, 4904–4910 CrossRef CAS PubMed.
- L. Zou, in Expanding Issues in Desalination, ed. R. Y. Ning, INTECH, 2011 Search PubMed.
- S.-I. Jeon, H.-R. Park, J.-G. Yeo, S. Yang, C. H. Cho, M. H. Han and D.-K. Kim, Energy Environ. Sci., 2013, 6, 1471–1475 CAS.
- H.-H. Jung, S.-W. Hwang, S.-H. Hyun, K.-H. Lee and G.-T. Kim, Desalination, 2007, 216, 377–385 CrossRef CAS PubMed.
- C.-H. Hou, T.-S. Patricia, S. Yiacoumi and C. Tsouris, J. Chem. Phys., 2008, 129, 224703 CrossRef PubMed.
- E. Avraham, M. Noked, A. Soffer and D. Aurbach, Electrochim. Acta, 2011, 56, 6312–6317 CrossRef CAS PubMed.
- R. Zhao, M. van Soestbergen, H. H. M. Rijnaarts, A. van der Wal, M. Z. Bazant and P. M. Biesheuvel, J. Colloid Interface Sci., 2012, 384, 38–44 CrossRef CAS PubMed.
- Y.-J. Kim and J.-H. Choi, Water Res., 2012, 46, 6033–6039 CrossRef CAS PubMed.
- S.-J. Kim, J.-H. Choi and J.-H. Kim, Process Biochem., 2012, 47, 2051–2057 CrossRef CAS PubMed.
- Y.-J. Kim, J.-H. Kim and J.-H. Choi, J. Membr. Sci., 2013, 429, 52–57 CrossRef CAS PubMed.
- A. M. Johnson and J. Newman, J. Electrochem. Soc., 1971, 118, 510–517 CrossRef CAS PubMed.
- Y. Bouhadana, E. Avraham, M. Noked, M. Ben-Tzion, A. Soffer and D. Aurbach, J. Phys. Chem. C, 2011, 115, 16567–16573 CAS.
- S. Porada, M. Bryjak, A. van der Wal and P. M. Biesheuvel, Electrochim. Acta, 2012, 75, 148–156 CrossRef CAS PubMed.
- S. Porada, B. B. Sales, H. V. M. Hamelers and P. M. Biesheuvel, J. Phys. Chem. Lett., 2012, 3, 1613–1618 CrossRef CAS.
- P. M. Biesheuvel, R. Zhao, S. Porada and A. van der Wal, J. Colloid Interface Sci., 2011, 360, 239–248 CrossRef CAS PubMed.
- J.-Y. Lee, S.-J. Seo, S.-H. Yun and S.-H. Moon, Water Res., 2011, 45, 5375–5380 CrossRef CAS PubMed.
- R. Zhao, P. M. Biesheuvel and A. Van der Wal, Energy Environ. Sci., 2012, 5, 9520–9527 CAS.
- R. Zhao, O. Satpradit, H. H. M. Rijnaarts, P. M. Biesheuvel and A. van der Wal, Water Res., 2013, 47, 1941–1952 CrossRef CAS PubMed.
- E. Garcia-Quismondo, R. Gomez, F. Vaquero, A. L. Cudero, J. Palma and M. A. Anderson, Phys. Chem. Chem. Phys., 2013, 15, 7648–7656 RSC.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef.
- B. B. Sales, M. Saakes, J. W. Post, C. J. N. Buisman, P. M. Biesheuvel and H. V. M. Hamelers, Environ. Sci. Technol., 2010, 44, 5661–5665 CrossRef CAS PubMed.
- D. Brogioli, R. Zhao and P. M. Biesheuvel, Energy Environ. Sci., 2011, 4, 772–777 CAS.
- F. Liu, O. Schaetzle, B. B. Sales, M. Saakes, C. J. N. Buisman and H. V. M. Hamelers, Energy Environ. Sci., 2012, 5, 8642–8650 CAS.
- R. A. Rica, R. Ziano, D. Salerno, F. Mantegazza and D. Brogioli, Phys. Rev. Lett., 2012, 109, 156103 CrossRef CAS.
- D. Brogioli, R. Ziano, R. A. Rica, D. Salerno, O. Kozynchenko, H. V. M. Hamelers and F. Mantegazza, Energy Environ. Sci., 2012, 5, 9870–9880 CAS.
- D. A. Vermaas, S. Bajracharya, B. B. Sales, M. Saakes, B. Hamelers and K. Nijmeijer, Energy Environ. Sci., 2013, 6, 643–651 CAS.
- L. Zou, L. Li, H. Song and G. Morris, Water Res., 2008, 42, 2340–2348 CrossRef CAS PubMed.
- L. Li, L. Zou, H. Song and G. Morris, Carbon, 2009, 47, 775–781 CrossRef CAS PubMed.
- C. J. Gabelich, P. Xu and Y. Cohen, Sustainability Science and Engineering, 2010, 2, 295–326 CrossRef.
- Z. Peng, D. Zhang, L. Shi and T. Yan, J. Mater. Chem., 2012, 22, 6603–6612 RSC.
- S. Porada, L. Weinstein, R. Dash, A. van der Wal, M. Bryjak, Y. Gogotsi and P. M. Biesheuvel, ACS Appl. Mater. Interfaces, 2012, 4, 1194–1199 CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- S. Kondrat, V. Presser, C. R. Perez, Y. Gogotsi and A. A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 CAS.
- Y. Gogotsi, C. Portet, S. Osswald, J. M. Simmons, T. Yildirim, G. Laudisio and J. E. Fischer, Int. J. Hydrogen Energy, 2009, 34, 6314–6319 CrossRef CAS PubMed.
- V. Presser, J. McDonough, S.-H. Yeon and Y. Gogotsi, Energy Environ. Sci., 2011, 4, 3059–3066 CAS.
- H. B. Li, T. Lu, L. K. Pan, Y. P. Zhang and Z. Sun, J. Mater. Chem., 2009, 19, 6773–6779 RSC.
- X. Wen, D. Zhang, L. Shi, T. Yan, H. Wang and J. Zhang, J. Mater. Chem., 2012, 22, 23835–23844 RSC.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef CAS.
- L. Han, K. G. Karthikeyan, M. A. Anderson, K. Gregory, J. J. Wouters and A. Abdel-Wahab, Electrochim. Acta, 2013, 90, 573–581 CrossRef CAS PubMed.
- H. Li, L. Pan, C. Nie, Y. Liu and Z. Sun, J. Mater. Chem., 2012, 22, 15556–15561 RSC.
- H. Wang, D. Zhang, T. Yan, X. Wen, L. Shi and J. Zhang, J. Mater. Chem., 2012, 22, 23745–23748 RSC.
- C. Nie, L. Pan, Y. Liu, H. Li, T. Chen, T. Lu and Z. Sun, Electrochim. Acta, 2012, 66, 106–109 CrossRef CAS PubMed.
- M. Wang, Z.-H. Huang, L. Wang, M.-X. Wang, F. Kang and H. Hou, New J. Chem., 2010, 34, 1843–1845 RSC.
- G. Wang, Q. Dong, Z. Ling, C. Pan, C. Yu and J. Qiu, J. Mater. Chem., 2012, 22, 21819–21823 RSC.
- G. Wang, B. Qian, Q. Dong, J. Yang, Z. Zhao and J. Qiu, Sep. Purif. Technol., 2013, 102, 216–221 CrossRef PubMed.
- V. Presser, L. Zhang, J. J. Niu, J. McDonough, C. Perez, H. Fong and Y. Gogotsi, Adv. Energy Mater., 2011, 1, 423–430 CrossRef CAS.
- P. Krawiec, E. Kockrick, L. Borchardt, D. Geiger, A. Corma and S. Kaskel, J. Phys. Chem. C, 2009, 113, 7755–7761 CAS.
- M. Oschatz, L. Borchardt, M. Thommes, K. A. Cychosz, I. Senkovska, N. Klein, R. Frind, M. Leistner, V. Presser, Y. Gogotsi and S. Kaskel, Angew. Chem., Int. Ed., 2012, 51, 7577–7580 CrossRef CAS PubMed.
- B. Kastening and M. Heins, Electrochim. Acta, 2005, 50, 2487–2498 CrossRef CAS PubMed.
- P. Krawiec, D. Geiger and S. Kaskel, Chem. Commun., 2006,(23), 2469–2470 RSC.
- E. Kockrick, C. Schrage, L. Borchardt, N. Klein, M. Rose, I. Senkovska and S. Kaskel, Carbon, 2010, 48, 1707–1717 CrossRef CAS PubMed.
- Y. Korenblit, M. Rose, E. Kockrick, L. Borchardt, A. Kvit, S. Kaskel and G. Yushin, ACS Nano, 2010, 4, 1337–1344 CrossRef CAS PubMed.
- M. Oschatz, E. Kockrick, M. Rose, L. Borchardt, N. Klein, I. Senkovska, T. Freudenberg, Y. Korenblit, G. Yushin and S. Kaskel, Carbon, 2010, 48, 3987–3992 CrossRef CAS PubMed.
- M. Rose, Y. Korenblit, E. Kockrick, L. Borchardt, M. Oschatz, S. Kaskel and G. Yushin, Small, 2011, 7, 1108–1117 CrossRef CAS PubMed.
- P. I. Ravikovitch and A. V. Neimark, Langmuir, 2006, 22, 11171–11179 CrossRef CAS PubMed.
- R. Zhao, P. M. Biesheuvel, H. Miedema, H. Bruning and A. van der Wal, J. Phys. Chem. Lett., 2010, 1, 205–210 CrossRef CAS.
- M. D. Levi, S. Sigalov, D. Aurbach and L. Daikhin, J. Phys. Chem. C, 2013, 117, 14876–14889 CAS.
- P. Xu, J. E. Drewes, D. Heil and G. Wang, Water Res., 2008, 42, 2605–2617 CrossRef CAS PubMed.
- R. K. Kalluri, M. M. Biener, M. E. Suss, M. D. Merrill, M. Stadermann, J. G. Santiago, T. F. Baumann, J. Biener and A. Striolo, Phys. Chem. Chem. Phys., 2013, 15, 2309–2320 RSC.
- H. Li, S. Liang, J. Li and L. He, J. Mater. Chem. A, 2013, 1, 6335–6341 CAS.
- K. Dai, L. Shi, J. Fang, D. Zhang and B. Yu, Mater. Lett., 2005, 59, 1989–1992 CrossRef CAS PubMed.
- Z. Wang, B. Dou, L. Zheng, G. Zhang, Z. Liu and Z. Hao, Desalination, 2012, 299, 96–102 CrossRef CAS PubMed.
- J. Landon, X. Gao, B. Kulengowski, J. K. Neathery and K. Liu, J. Electrochem. Soc., 2012, 159, A1861–A1866 CrossRef CAS PubMed.
- T. Kim and J. Yoon, J. Electroanal. Chem., 2013, 704, 169–174 CrossRef CAS PubMed.
- I. Cohen, E. Avraham, M. Noked, A. Soffer and D. Aurbach, J. Phys. Chem. C, 2011, 115, 19856–19863 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ee42209g |
| This journal is © The Royal Society of Chemistry 2013 |
