Decomposition kinetics of peroxynitrite: influence of pH and buffer

Abstract

The decay of ONOOH near neutral pH has been examined as a function of isomerization to H⁺ and NO₃⁻, and decomposition to NO₂⁻ and O₂via O₂NOO⁻. We find that in phosphate buffer k_{isomerization} = 1.11 ± 0.01 s⁻¹ and k_{disproportionation} = (1.3 ± 0.1) × 10³ M⁻¹ s⁻¹ at 25 °C and I = 0.2 M. In the presence of 0.1 M tris(hydroxymethyl)aminomethane (Tris), the decay proceeds more rapidly: k_{disproportionation} = 9 × 10³ M⁻¹ s⁻¹. The measured first half-life of the absorbance of peroxynitrite correlates with [Tris]₀·([ONOO⁻]₀ + [ONOOH]₀)², where the subscript 0 indicates initial concentrations; if this function exceeds 6.3 × 10⁻¹² M³, then Tris significantly accelerates the decomposition of peroxynitrite.

---

Introduction

Peroxynitrite† is formed from the reaction of NO˙ with O^˙−₂,³ which proceeds at a diffusion-controlled rate, k = 1.6 × 10¹⁰ M⁻¹ s⁻¹.^4,5 Because both NO˙ and O^˙−₂ are released by activated macrophages and neutrophils,^6–11 peroxynitrite can be formed in vivo.¹² Due to its oxidizing power and nitrating activity, peroxynitrite is cytotoxic and is associated with inflammatory diseases.¹³

ONOO⁻ is stable in a cold alkaline solution in the absence of carbonyl compounds and metals. The pK_a of ONOOH increases from 6.5 to 7.3 with increasing phosphate concentration.¹⁴ Isomerization of ONOOH to HNO₃,^15,16 reaction 1,‡ is first-order in ONOOH. Rate constants for the isomerization, obtained over a period of ca. 40 years, have slightly decreased, from 1.5 to 1.1 s⁻¹, most likely because of purer preparations of peroxynitrite (Table 1). ONOOH is a powerful one-electron and two-electron oxidant.^17,18 A review of the literature shows that evidence for the much-cited homolysis of ONOOH to HO˙ and NO^˙₂ is weak: at most 5% of ONOOH may undergo this reaction.¹⁹ In any case, the reaction of otherwise stable ONOO⁻ with CO₂ ²⁰ is far more relevant to biology (k = (3–5.8) × 10⁴ M⁻¹ s⁻¹)^21,22 as it yields, in part, very oxidising species, NO^˙₂ and CO^˙−₃ with E°(NO^˙₂/NO₂⁻) = 1.04 V²³ and E°(CO^˙−₃/CO₃²⁻) = 1.59 V.²⁴ These species are responsible for the higher yield of nitration of phenols compared to nitration by peroxynitrite alone (4–9% without and 14–19% with 20 mM HCO₃⁻).^22,25–27

Table 1 The literature values for rate constant k₁ of the isomerization of ONOOH at 25 °C

Year	Reference	k 1/s^−1	Remarks
a Ionic strength is not given. b At r.t. c At 37 °C.
1970	28	1.5	^,
1990	12	0.65 ± 0.05	^,
1992	17	1.3
1993	29	1.0 ± 0.2
1997	30	1.25
1997	14	1.20	I = 0.2 M
1998	31	1.20	I = 0.1 M
2003	32	1.10 ± 0.05	I = 0.9 M
2012	This work	1.11 ± 0.01	I = 0.2 M

---

Deviations from first-order behaviour³³ and formation of O₂ ³⁴ and NO₂⁻ in a 1 : 2 stoichiometric ratio³⁵ have been observed. Both phenomena can be explained with an additional reaction, namely between ONOOH and ONOO⁻, a disproportionation that, given a pK_a of ONOOH of nearly 7, is only relevant near and above neutral pH (Scheme 1). This disproportionation thus fits the observation that NO₂⁻ yields increase with pH and with peroxynitrite concentration.^36,37 Gupta et al.³⁸ showed that the disproportionation reaction yields initially O₂NOO⁻ and NO₂⁻. O₂NOOH has a pK_a of 5.9^39,40 and is relatively stable. When one compares the wavelengths of maximal absorptivity and the extinction coefficients of ONOO⁻ and O₂NOO⁻, one sees that these parameters are quite similar: O₂NOO⁻ absorbs with ε_max = 1650 M⁻¹ cm⁻¹ at 285 nm,³⁹ and ONOO⁻ with ε_max = 1705 M⁻¹ cm⁻¹ at 302 nm.⁴¹ Furthermore, the rates of decay of both ONOOH and O₂NOO⁻ are close to 1 s⁻¹ (see below). For these reasons O₂NOO⁻ went unnoticed as an intermediate during the decay of peroxynitrite. The decomposition of O₂NOO⁻ yields NO₂⁻ and O₂,³⁹ of which ca. 1–2% is in an excited (¹Δ_gO₂) state.⁴² Estimates for decomposition reaction 3 at 25 °C are k₃ = 1.0 ± 0.2 s⁻¹,³⁹ 1.35 ± 0.03 s⁻¹,⁴³ and 0.58 s⁻¹.³⁸k₄ and k₋₄ are estimated to be 1.05 ± 0.23 s^−1 43 and (4.5 ± 1.0) × 10⁹ M⁻¹ s⁻¹,³⁹ respectively. Redox reaction 5 is thermodynamically favoured, Δ_rxn5G°′ = −118 kJ mol⁻¹. Δ_fG⁰ (kJ mol⁻¹) values in aqueous solution are 62.5 for NO^˙₂,⁴⁴ 33.8 for O^˙−₂,⁴⁵ −38 for NO₂^− 23,44 and 16.4 for O₂;⁴⁶ the reaction proceeds with k₅ = 1 × 10⁸ M⁻¹ s⁻¹.⁴⁷ We emphasise that the formation of O₂NOO⁻, a reaction that is second-order in peroxynitrite, is biologically insignificant, because the concentration of peroxynitrite that may be generated by activated macrophages is very low. However, upon bolus additions of peroxynitrite during in vitro experiments that result in initial concentrations exceeding 0.1 mM, the formation of peroxynitrate should be taken into account.

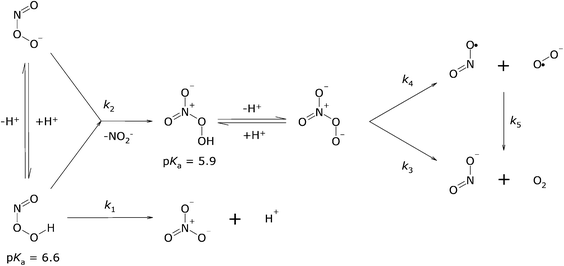Scheme 1

In neutral 0.1 M tris(hydroxymethyl)aminomethane (Tris) buffer, decomposition of peroxynitrite yields up to 40% peroxynitrate with k₂ = 3 × 10⁴ M⁻¹ s⁻¹.³⁸ Decomposition of peroxynitrite in various neutral amine buffers, e.g. 2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid (HEPES) or 1,4-piperazinediethanesulfonic acid (PIPES), yields an oxidant that was suggested to be H₂O₂.⁴⁸ However, it could well have been O₂NOOH. The pH of peroxynitrite containing samples is usually controlled by phosphate buffer, and rarely by Tris or HEPES buffer (e.g.ref. 49 and 50). At equal pH, similar initial peroxynitrite concentrations yield more NO₂⁻ in Tris buffer⁵⁰ than in phosphate buffer.³⁶ This indicates that a Tris-dependent conversion of peroxynitrite to NO₂⁻ takes place. The possibility that the buffer influences the course or result of a reaction has rarely been considered.^48,51 We therefore also compared decomposition kinetics of peroxynitrite at pH = 6.8 in buffers that contain variable concentrations of phosphate and Tris and refined the decomposition model by taking into account reactions (1)–(3).

Materials and methods

Materials

(Me₄N)OONO was prepared according to the work by Bohle et al.,⁵² dissolved in 0.01 M NaOH and frozen as 25 mM solutions. NaH₂PO₄·H₂O (s), Na₂HPO₄·12H₂O (s), H₂NC(CH₂OH)₃ (s), NaOH (s), 85% H₃PO₄ (aq), and 70% HClO₄ (aq), all of analytical grade, were purchased from Sigma-Aldrich/Fluka (Buchs, CH), Brenntag Schweizerhall AG (Basel, CH), Merck (Darmstadt, DE), Riedel-de Haën (Seelze, DE) and used as received. Ar and N₂, both of 99.995% purity, were taken from the in-house gas supply. All solutions were prepared in deionized water that was further purified by using a Milli-Q unit from Millipore AG (Zug, CH).

Preparation of solutions

All solutions were prepared, stored, transferred and mixed at room temperature in glass vessels under Ar or N₂ and used within one day. Because ONOO⁻ is sensitive to acid, heat and light, samples (1.4 g) of deeply frozen 25 mM (Me₄N)OONO (aq) were dissolved in ice-cold 20 mM aqueous NaOH to produce alkaline ONOO⁻ solutions that were stored and transferred at 0 °C and kept in the dark. The fresh alkaline ONOO⁻ solutions contained ONOO⁻, NO₂⁻ and NO₃⁻ in a molar ratio of 10 : 1 : 1 (see the section ‘Determination of peroxynitrite, nitrite and nitrate’). The impurity by NO₂⁻ and NO₃⁻ in the alkaline ONOO⁻ solutions is most probably formed during the thawing of frozen (Me₄N)OONO (aq).⁵³ Because the pK_a of ONOOH depends on the ionic strength of the medium,¹⁴ the ionic strength of the Tris buffers and the pH-varied 0.07 M phosphate buffers was adjusted to 0.2 M by the addition of NaClO₄, which we assume to be inert. Considering the ion-pairing of Na⁺ with HPO₄²⁻,⁵⁴ we calculated the ionic strength of our samples at pH 6–8 to be between 0.197 M and 0.206 M. The pK_a of ONOOH is 6.7 under these conditions.

Determination of peroxynitrite, nitrite and nitrate

The content of peroxynitrite and of its typical ionic decomposition products – NO₂⁻ and NO₃⁻ – were quantified for the lot of deeply frozen (Me₄N)OONO (aq) used for kinetics experiments as described before.³⁶ Briefly, a sample (1.4 g) of deeply frozen (Me₄N)OONO (aq) was subsequently weighted, dissolved in ice-cold 2 mM NaOH and analysed by spectrophotometry at 302 nm (Specord 250 from Analytik Jena AG, Jena, DE). To determine the content of NO₂⁻ and NO₃⁻, a sample (1.4 g) of deeply frozen (Me₄N)OONO (aq) was dissolved in 30 ml ice-cold 2 mM NaOH. 1 ml of this alkaline solution was added to 5 ml ice-cold 2 mM phosphoric acid to yield a mixture with pH = 3. In an acidic solution, peroxynitrite is mainly present as ONOOH, which isomerises to NO₃⁻. This acidic solution was neutralised after 5 min by the addition of 4 ml 2 mM NaOH and then analysed by ion chromatography (Super Sep IC Anion Column from Metrohm AG, Herisau, CH) with a phthalate eluent of pH = 4.7 and by conductometric detection (732 IC Detektor from Metrohm AG, Herisau, CH). To determine the content of NO₃⁻ in the (Me₄N)OONO (aq) sample, the peroxynitrite content was subtracted from the content of NO₃⁻, which resulted after isomerization of ONOOH. The amount of peroxynitrate was not determined because it decays very fast in an alkaline medium.

Stopped-flow experiments

The decay of peroxynitrite was initiated by a rapid 1 : 1 mixing of an alkaline ONOO⁻ solution with an acidic buffer solution in a thermostated (25 °C) stopped-flow unit (SX17MN) from Applied Photophysics (Leatherhead, UK) and observed for 10 s by spectrophotometry. Monochromatic light at the absorption maximum of ONOO⁻, 302 nm, was used.

For each sample the decay of the absorption was measured at least four times, and the decay traces were averaged before analysis. The initial absorption of each mixture was used to calculate [ONOO⁻]₀: the optical path length is 1 cm, and ε_{302 nm}(ONOO⁻) = 1705 M⁻¹ cm⁻¹.⁴¹

Prior to each decay experiment, the total initial peroxynitrite concentration in the sample, [ONOO⁻]_{0, total}, was derived from the absorbance of a 1 : 1 mixture of an alkaline ONOO⁻ solution with 20 mM NaOH. Then the experiments were carried out at the desired pH in a specific buffer. Prior to switching to another pH and buffer, the standardization with NaOH was repeated. For each mixture, the final pH value was measured by an Orion Microprocessor Ionalyzer 901 from Thermo Scientific after mixing, outside the stopped-flow apparatus. For the decay simulations, the pK_a of ONOOH was calculated from the measured pH, [ONOO⁻]₀ and [ONOO⁻]_{0, total} at pH = 6.8.

Computations

We assume that at pH < 6 ONOOH isomerises to NO₃⁻ and H⁺ exclusively; the decay of ONOOH was fitted to a single exponential function that resulted in k_obs. The rate constant k₁ was derived from k_obs, which is a function of pH, pK_a(ONOOH) and k₁:

Reactions (1)–(3)§ lead to rate laws 2 and 3 for peroxynitrite and peroxynitrate.

Given the pK_a values of ONOOH and O₂NOOOH, we calculated the time-dependent concentrations of the absorbing species ONOO⁻ and O₂NOO⁻.

With the extinction coefficients [ε_{302 nm}(ONOO⁻) = 1705 M⁻¹ cm⁻¹; ε_{302 nm}(O₂NOO⁻) = 1370 M⁻¹ cm⁻¹ from the spectrum in ref. 38], we reproduced the absorption trace of peroxynitrite solutions at 302 nm. The calculated absorbance trace was fitted to the measured absorbance trace by the variation of the rate constants according to the method of the least squares. All data analysis and model calculations were carried out in Microsoft Excel by macro programmes (which are available from the authors upon request). The kinetics of the mixed-order decomposition of peroxynitrite was quantitatively compared by the use of the first half-life of the absorbance.

Results

Computation of the decomposition rate constants of peroxynitrite in phosphate buffer

From the measurement of the initial absorbance at various pH values, we derive a pK_a(ONOOH) of 6.7 at I = 0.2 M which fits with the dependence of the pK_a on ionic strength.

A rate constant k₁ = 1.11 ± 0.01 s⁻¹ (n = 7, 95% confidence level) was determined by fitting absorbance traces at pH = 5.3 and I = 0.2 M in 70 mM phosphate buffer (see Fig. 1). At this pH, [ONOO⁻] is too low to contribute to significant disproportionation, and [HNO₂], from the nitrite present in the (Me₄N)OONO preparation, is too low to cause undesired reactions.

Fig. 1 Decomposition of 0.25 mM peroxynitrite at 25 °C and pH = 5.3 in 0.07 M phosphate buffer (I = 0.2 M) and simulation according to isomerization only with k₁ = 1.11 s⁻¹. (a) Actual decay curve measured (black) and simulated (yellow); (b) residuals (green) of the model.

It became clear that the results obtained at higher pH (Fig. 2) could not be fitted with k₁ = 1.11 s⁻¹ (Fig. 3). We therefore take into account an additional process, disproportionation of peroxynitrite to O₂NOO⁻ and NO₂⁻.³⁸ For the decay of O₂NOO⁻ to NO₂⁻ and O₂, we take a value of 1.35 s⁻¹.⁴³ The combination of these three processes allows us to fit the obtained results with significantly smaller errors (Fig. 4).

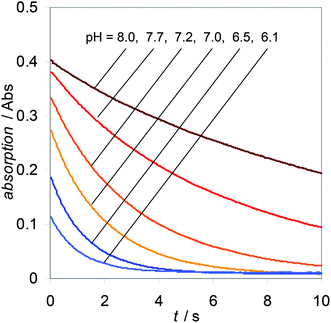Fig. 2 Four to six decay traces per pH value (0.25 mM peroxynitrite in 70 mM phosphate buffer at 25 °C and I = 0.2 M, see Table 2) were measured at 302 nm and averaged.

Fig. 3 Four to six decay traces per pH value (0.25 mM peroxynitrite in 70 mM phosphate buffer at 25 °C and I = 0.2 M, see Table 2) were averaged and fitted with k₁ = 1.11 s⁻¹. The residuals are much larger than in Fig. 4, the range of which is indicated by the two dashed lines.

Fig. 4 The same as Fig. 3, but fitted with k₁ = 1.11 s⁻¹ and k₃ = 1.35 s⁻¹.⁴³k₂ was varied to minimise the residuals shown here.

Fig. 5 shows an actual decay curve of 0.25 mM peroxynitrite at pH = 6.5 which was fitted according to rate laws 2 and 3 with k₁ = 1.11 s⁻¹ and k₃ = 1.35 s⁻¹.⁴³ In addition, the fit required that k₂ be 1163 M⁻¹ s⁻¹: the residuals are very small and do not show any systematic error. This procedure was repeated at various other pH values, and the results for k₂ are presented in Table 2.

Fig. 5 Decomposition of 0.25 mM peroxynitrite at 25 °C and pH = 6.5 in 0.07 M phosphate buffer (I = 0.2 M) and simulation according to rate laws 2 and 3 with k₁ = 1.11 s⁻¹ and k₃ = 1.35 s⁻¹,⁴³ resulting in k₂ = 1163 M⁻¹ s⁻¹. (a) Actual decay curve measured (black) and simulated (yellow); (b) residuals (green) of the model; (c) concentrations calculated for ONOO⁻ (blue) and O₂NOO⁻ (red), [ONOOH] is not shown.

Table 2 Decomposition of 0.25 mM ONOO⁻ at 25 °C in 0.07 M phosphate buffer, I = 0.2 M adjusted by NaClO₄, k₁ = 1.11 ± 0.01 s⁻¹, k₃ = 1.35 s⁻¹,⁴³n measurements. The error of 1 is based on all 27 measurements from pH 6.1 to 8.0 at the 95% confidence level

pH	First t1/2/s	k 2/(10^3 M^−1 s^−1)	n
5.3	0.69 ± 0.01	—	7
6.1	0.76 ± 0.04	0.9 ± 1.0	4
6.5	0.92 ± 0.03	1.3 ± 0.3	4
7.0	1.41 ± 0.02	1.7 ± 0.1	4
7.2	2.21 ± 0.06	1.1 ± 0.1	6
7.7	4.6 ± 0.1	1.4 ± 0.1	5
8.0	9.4 ± 0.1	1.7 ± 0.1	4
Over all pH values		1.3 ± 0.1	27

---

The first half-life of the absorbance increases with pH (Fig. 6) because ONOO⁻ is stable and the isomerization of ONOOH is the predominant decomposition pathway of peroxynitrite. The first half-life of the absorbance at pH 6–8 can be calculated according to rate laws 2 and 3 with k₁ = 1.11 s⁻¹, k₂ = 1.3 × 10³ M⁻¹ s⁻¹ and k₃ = 1.35 s⁻¹ much more accurately than by a model based on a first-order decay only.

Fig. 6 Decomposition of 0.25 mM peroxynitrite at pH = 5.3, 6.1, 6.5, 7.0, 7.2, 7.7 and 8.05 in 70 mM phosphate buffer (I = 0.2 M). The first half-life of the absorbance measured (+) and calculated (blue lines) based on the best fit of two decomposition models: (1) (dashed line) according to isomerization only with k₁ = 1.11 s⁻¹; (2) (solid line) according to rate laws 2 and 3 with k₁ = 1.11 s⁻¹, k₂ = 1.3 × 10³ M⁻¹ s⁻¹ and k₃ = 1.35 s⁻¹.

Decomposition of peroxynitrite in phosphate buffer and Tris buffer

The decomposition of peroxynitrite is decelerated by phosphate and accelerated by Tris: t_1/2 = 0.75–0.88 s in 0.1 M phosphate and 0.1 M Tris, t_1/2 = 1.33–1.42 s in 0.1 M phosphate only and t_1/2 = 0.63 s in 0.1 M Tris only (Tables 3 and 4, and Fig. 7).

Fig. 7 Decomposition of 0.047 mM (blue), 0.25 mM (green) and 0.34 mM (black) peroxynitrite at pH = 6.8 in 0.1 M phosphate buffers with varied Tris concentrations. The solid horizontal lines indicate the first half-life of the absorbance of peroxynitrite in the absence of Tris. When [Tris]₀·[ONOO⁻]_{0, total}² exceeds 6.3 × 10⁻¹² M³, Tris significantly catalyses the disproportionation.

Table 3 Decomposition of 0.25 mM peroxynitrite at 25 °C and pH = 6.8 in 0.1 M Tris buffers (I = 0.2 M) at various phosphate concentrations. n, the number of determinations

[Phosphate]/M	First t1/2/s	k 2/(10^3 M^−1 s^−1)	n
0	0.65 ± 0.00	14 ± 2	2
0.001	0.68 ± 0.02	13 ± 1	5
0.005	0.69 ± 0.09	13 ± 4	3
0.025	0.73 ± 0.04	12 ± 3	3
0.1	0.91 ± 0.02	9.3 ± 0.4	6

---

Table 4 Decomposition of 0.25 mM peroxynitrite at 25 °C and pH = 6.8 in 0.1 M phosphate buffers (I = 0.2 M) at various Tris concentrations

[Tris]/M	k 2 ^a/(10^3 M^−1 s^−1)	k 2 ^b/(10^3 M^−1 s^−1)
Initial total peroxynitrite concentration:a 260 μM andb 340 μM.c Not determined.
0	1.3	1.2
1 × 10^−4		1.3
3 × 10^−4	1.3	1.5
1 × 10^−3	1.5	2.0
3 × 10^−3	2.4	2.8
0.01	3.7	4.4
0.03	5.1	5.2
0.1	8.0	9.4

---

Interestingly, up to a certain concentration, Tris shows no significant influence on the decay of peroxynitrite. However, this concentration decreases with increasing initial peroxynitrite concentration. We find that the measured first half-life of the absorbance of peroxynitrite correlates with [Tris]₀·[ONOO⁻]_{0, total}²: if [Tris]₀·[ONOO⁻]_{0, total}² exceeds 6.3 × 10⁻¹² M³ (1 × 10^−11.2 M³), then Tris significantly accelerates the decomposition of peroxynitrite (Fig. 7).

Discussion

According to rate laws 2 and 3, absorption traces are fitted (e.g.Fig. 5) and values of the first half-life of the absorbance are simulated (Fig. 6) without a systematic error for the pH range 6–8. A model restricted to homolysis³⁷ does not simulate the decay of peroxynitrite in this pH range very well.

The first-order rate constant of the isomerization agrees with earlier results.

The disproportionation can be regarded as a two-step reaction: a reversible association and a subsequent irreversible conversion to the products:

Earlier estimates of the parameters of this sequence are listed in Table 5. The first two are in good agreement with the disproportionation rate constant determined here; however, the third estimate is higher.

Table 5 Rate constants of the decomposition of peroxynitrite into NO₂⁻ and O₂

k 6/(M^−1 s^−1)	k −6/(s^−1)	k 7/(s^−1)	k 2/(M^−1 s^−1)	Source
		0.20 ± 0.01	(2.0 ± 0.1) × 10^3	Decay modelling^14
2.5 × 10^5	25	0.2–0.3	(2–3) × 10^3	Decay modelling^36
1.7 × 10^4	0.025	0.05	1.1 × 10^4	Decay modelling^55
			(1.3 ± 0.1) × 10^3	This work

---

According to rate laws 2 and 3, the concentration of peroxynitrate reaches its concentration maximum ca. 1 s after the decay of peroxynitrite is initiated (Fig. 5c). After that peak concentration, the second-order disproportionation becomes negligible in comparison with first-order decay processes 1 and 3. Therefore, decay traces of peroxynitrite deviate from first-order kinetics in the first 1–2 s.³³

The decomposition model according to reactions (1)–(3)§ and (9) fails to reproduce the Tris-dependent first half-life of the absorbance. It fits the absorption curves with a residual that indicates a systematic error that increases with the Tris concentration (not shown). Moreover, it results in k₂ values that increase non-linearly with the Tris concentration if the latter is higher than 10⁻⁴ M (Table 4). Saturation may cause a non-linear dependence. The accelerating effect of Tris will be addressed in a future publication.

We find that k₂ is one order of magnitude lower in phosphate buffer (this work: 1.3 × 10³ M⁻¹ s⁻¹) than in Tris buffer (this work: 9 × 10³ M⁻¹ s⁻¹, Gupta et al.:³⁸ 3 × 10⁴ M⁻¹ s⁻¹, both in 0.1 M Tris) and that 0.25 mM peroxynitrite decomposes in 0.1 M Tris buffer twice as fast as it does in 0.1 M phosphate buffer. Therefore, Tris accelerates the disproportionation of peroxynitrite and thereby increases k₂. Indeed, the peroxynitrate yield is, being dependent on the square of the initial peroxynitrite concentration, 40 times higher in Tris buffer than it is in phosphate buffer.³⁸ The observed rate of decay of peroxynitrite accelerates with increasing Tris concentration (Fig. 7). Furthermore, the first half-life of the absorbance correlates with the concentration product [Tris]₀·[ONOO⁻]_{0, total}². The concentration product [Tris]·[ONOO⁻]_total² is likely part of the rate law of the additional Tris-dependent decomposition pathway. If the Tris concentration is high enough, this additional decomposition pathway contributes significantly to the overall decomposition. If Tris participates in the disproportionation according to reaction (9) and if k_{2, in Tris} = k₂ + k₉·[Tris], then we obtain an estimate of k₉ = (8–29) × 10³ M⁻² s⁻¹:

It is likely that a more accurate decomposition model can be achieved by considering a chain of association equilibria that involve peroxynitrite and Tris.

Peroxyacids, in general, decompose in reactions that are first-order in both the acid and its conjugate base: typically with rate constants of 1 × 10⁻³–1 × 10⁻¹ M⁻¹ s⁻¹.^56–59 These rate constants are much smaller than those found for peroxynitrite (1.3 × 10³–3 × 10⁴ M⁻¹ s⁻¹). However, in contrast to other peroxyacids, the atom attached to the OOH group of peroxynitrite has a lone pair that allows additional reactions – electrophilic attack and oxidative addition – that may allow faster decomposition (Scheme 2).

Scheme 2

At peroxynitrite concentrations >10⁻⁴ M, but at lower concentration in the presence of Tris, disproportionation of peroxynitrite in samples competes with reactions of peroxynitrite with target molecules and produces peroxynitrate that is an artificial reactive intermediate.

Acknowledgements

We thank the SNF and the ETH Zurich for financial support.

References

1. N. G. Connelly, T. Damhus, R. M. Hartshorn and A. T. Hutton, Nomenclature of Inorganic Chemistry. IUPAC Recommendations 2005, 2005.
2. W. H. Koppenol, Pure Appl. Chem., 2000, 72, 437–446.
3. N. V. Blough and O. C. Zafiriou, Inorg. Chem., 1985, 24, 3502–3504.
4. T. Nauser and W. H. Koppenol, J. Phys. Chem. A, 2002, 106, 4084–4086.
5. H. Botti, M. Möller, D. Steinmann, T. Nauser, W. H. Koppenol, A. Denicola and R. Radi, J. Phys. Chem. B, 2010, 114, 16584–16593.
6. S. Moncada, M. W. Radomski and R. M. J. Palmer, Biochem. Pharmacol., 1988, 37, 2495–2501.
7. J. B. Hibbs, R. R. Taintor, Z. Vavrin and E. M. Rachlin, Biochem. Biophys. Res. Commun., 1988, 157, 87–94.
8. M. R. Green, H. A. O. Hill, M. J. Okolow-Zubkowska and A. W. Segal, FEBS Lett., 1979, 100, 23–26.
9. R. J. Gryglewski, R. M. J. Palmer and S. Moncada, Nature, 1986, 320, 454–456.
10. T. B. McCall, N. K. Boughton-Smith, R. M. J. Palmer, B. J. R. Whittle and S. Moncada, Biochem. J., 1989, 261, 293–296.
11. Y. Xia, V. L. Dawson, T. M. Dawson, S. H. Snyder and J. L. Zweier, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 6770–6774.
12. J. S. Beckman, T. W. Beckman, J. Chen, P. A. Marshall and B. A. Freeman, Proc. Natl. Acad. Sci. U. S. A., 1990, 87, 1620–1624.
13. P. Pacher, J. S. Beckman and L. Liaudet, Physiol. Rev., 2007, 87, 315–424.
14. R. Kissner, T. Nauser, P. Bugnon, P. G. Lye and W. H. Koppenol, Chem. Res. Toxicol., 1997, 10, 1285–1292.
15. M. Anbar and H. Taube, J. Am. Chem. Soc., 1954, 76, 6243–6247.
16. J. D. Ray, J. Inorg. Nucl. Chem., 1962, 24, 1159–1162.
17. W. H. Koppenol, J. J. Moreno, W. A. Pryor, H. Ischiropoulos and J. S. Beckman, Chem. Res. Toxicol., 1992, 5, 834–842.
18. C. Kurz, X. Zeng, S. Hannemann, R. Kissner and W. H. Koppenol, J. Phys. Chem. A, 2005, 109, 965–969.
19. W. H. Koppenol, P. L. Bounds, T. Nauser, R. Kissner and H. Ruegger, Dalton Trans., 2012, 41, 13779–13787.
20. W. G. Keith and R. E. Powell, J. Chem. Soc. A, 1969, 90–90.
21. S. V. Lymar and J. K. Hurst, J. Am. Chem. Soc., 1995, 117, 8867–8868.
22. A. Denicola, B. A. Freeman, M. Trujillo and R. Radi, Arch. Biochem. Biophys., 1996, 333, 49–58.
23. D. M. Stanbury, Adv. Inorg. Chem., 1989, 33, 69–138.
24. R. E. Huie, C. L. Clifton and P. Neta, Radiat. Phys. Chem., 1991, 38, 477–481.
25. S. V. Lymar, Q. Jiang and J. K. Hurst, Biochemistry, 1996, 35, 7855–7861.
26. M. S. Ramezanian, S. Padmaja and W. H. Koppenol, Chem. Res. Toxicol., 1996, 9, 232–240.
27. J. N. Lemercier, S. Padmaja, R. Cueto, G. L. Squadrito, R. M. Uppu and W. A. Pryor, Arch. Biochem. Biophys., 1997, 345, 160–170.
28. F. Barat, L. Gilles, B. Hickel and J. Sutton, J. Chem. Soc. A, 1970, 1982–1986.
29. T. Løgager and K. Sehested, J. Phys. Chem., 1993, 97, 6664–6669.
30. B. Alvarez and R. Radi, First Int. Conf. Chemistry and Biology of Peroxynitrite, Ascona, 1997, 2–2.
31. W. H. Koppenol and R. Kissner, Chem. Res. Toxicol., 1998, 11, 87–90.
32. P. Maurer, C. F. Thomas, R. Kissner, H. Rüegger, O. Greter, U. Röthlisberger and W. H. Koppenol, J. Phys. Chem. A, 2003, 107, 1763–1769.
33. J. S. Beckman, H. Ischiropoulos, L. Zhu, M. van der Woerd, C. D. Smith, J. Chen, J. Harrison, J. C. Martin and M. Tsai, Arch. Biochem. Biophys., 1992, 298, 438–445.
34. R. Radi, J. S. Beckman, K. M. Bush and B. A. Freeman, Arch. Biochem. Biophys., 1991, 288, 481–487.
35. S. Pfeiffer, A. C. F. Gorren, K. Schmidt, E. R. Werner, B. Hansert, D. S. Bohle and B. Mayer, J. Biol. Chem., 1997, 272, 3465–3470.
36. R. Kissner and W. H. Koppenol, J. Am. Chem. Soc., 2002, 124, 234–239.
37. M. Kirsch, H.-G. Korth, A. Wensing, R. Sustmann and H. de Groot, Arch. Biochem. Biophys., 2003, 418, 133–150.
38. D. Gupta, B. Harish, R. Kissner and W. H. Koppenol, Dalton Trans., 2009, 5730–5736.
39. T. Løgager and K. Sehested, J. Phys. Chem., 1993, 97, 10047–10052.
40. S. Goldstein and G. Czapski, Inorg. Chem., 1997, 36, 4156–4162.
41. D. S. Bohle, B. Hansert, S. C. Paulson and B. D. Smith, J. Am. Chem. Soc., 1994, 116, 7423–7424.
42. S. Miyamoto, G. E. Ronsein, T. C. Corrêa, G. R. Martinez, M. H. G. Medeiros and P. Di Mascio, Dalton Trans., 2009, 5720–5729.
43. S. Goldstein, G. Czapski, J. Lind and G. Merényi, Inorg. Chem., 1998, 37, 3943–3947.
44. W. H. Koppenol, Inorg. Chem., 2012, 51, 5637–5641.
45. W. H. Koppenol, D. M. Stanbury and P. L. Bounds, Free Radical Biol. Med., 2010, 49, 317–322.
46. D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttal, J. Phys. Chem. Ref. Data, 1982, 11(Suppl. 2), 37–38.
47. P. Warneck and C. Wurzinger, J. Phys. Chem., 1988, 92, 6278–6283.
48. M. Kirsch, E. E. Lomonosova, H.-G. Korth, R. Sustmann and H. de Groot, J. Biol. Chem., 1998, 273, 12716–12724.
49. S. Kapiotis, M. Hermann, I. Held, A. Mühl and B. Gmeiner, FEBS Lett., 1997, 409, 223–226.
50. D. Tsikas, K. Denker and J. C. Frölich, J. Chromatogr., A, 2001, 915, 107–116.
51. E. Pollet, J. A. Martínez, B. Metha, B. P. Watts Jr. and J. F. Turrens, Arch. Biochem. Biophys., 1998, 349, 74–80.
52. D. S. Bohle, P. A. Glassbrenner and B. Hansert, Methods Enzymol., 1996, 269, 302–311.
53. P. Latal, R. Kissner, D. S. Bohle and W. H. Koppenol, Inorg. Chem., 2004, 43, 6519–6521.
54. R. M. Smith and A. E. Martell, Critical Stability Constants: Volume 4: Inorganic Complexes, 1976.
55. R. Kissner, T. Nauser, C. Kurz and W. H. Koppenol, IUBMB Life, 2003, 55, 567–572.
56. D. F. Evans and M. W. Upton, J. Chem. Soc., Dalton Trans., 1985, 1151–1153.
57. J. F. Goodman, P. Robson and E. R. Wilson, Trans. Faraday Soc., 1962, 58, 1846–1851.
58. E. Koubek, M. L. Haggett, C. J. Bataglia, K. M. Ibne-Rasa, H. Y. Pyun and J. O. Edwards, J. Am. Chem. Soc., 1963, 85, 2263–2268.
59. Z. Yuan, Y. Ni and A. R. P. van Heiningen, Can. J. Chem. Eng., 1997, 75, 37–41.

---

Footnotes

† “Peroxynitrite” refers to a mixture of ONOO⁻ and ONOOH, depending on the pH; “peroxynitrate” refers to a mixture of O₂NOO⁻ and O₂NOOH, depending on the pH. Buffers: Tris, tris(hydroxymethyl)aminomethane; Hepes, 2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid; Pipes, 1,4-piperazinediethanesulfonic acid. Formulae, trivial names and systematic names: ONOO⁻, peroxynitrite, (dioxido)oxidonitrate(1−); ONOOH, peroxynitrous acid, (hydridodioxido)oxidonitrogen; O₂NOO⁻, peroxynitrate, (dioxido)dioxidonitrate(1−); O₂NOOH, peroxynitric acid, (hydridodioxido)dioxidonitrogen; NO˙, nitric oxide, oxidonitrogen(˙) or nitrogen monoxide; O^˙−₂, superoxide, dioxide(˙1−) or dioxidanidyl; HNO₃, nitric acid, hydroxidodioxidonitrogen; HO˙, hydroxyl, hydridooxygen(˙) or oxidanyl; NO^˙₂, pernitric oxide, nitrogen dioxide or dioxidonitrogen(˙); CO₂, carbon dioxide, dioxidocarbon; CO^˙−₃, trioxidocarbonate(˙1−); CO₃²⁻, carbonate, trioxidocarbonate(2−); HCO₃⁻, hydrogencarbonate, hydridooxidodioxidocarbonate(1–); NO₂⁻, nitrite, dioxidonitrate(1−); O₂, dioxygen; H₂O₂, hydrogen peroxide or dioxidane.^1,2

‡ Reactions 1–5 are part of Scheme 1.

§ Reactions 1–5 are part of Scheme 1 with correspondingly numbered rate constants.

---