Structure and activity of iron-doped TiO₂-anatase nanomaterials for gas-phase toluene photo-oxidation

Abstract

The structural (from local to long range order) and electronic evolution of Fe-doped anatase nanomaterials is evaluated using in situ synchrotron based X-ray total scattering/diffraction and absorption techniques and Raman spectroscopy. These methods are combined with UV-visible spectroscopy and infrared diffuse reflectance (DRIFTS) to maximize the level of structural and morphological information regarding these materials. Fe doping of anatase nanomaterials generates solids having Fe at substitutional positions of the structure, and anion vacancies as charge neutrality entities. These structural modifications lead to materials with decreasing band gap energy as a function of Fe content. Concomitantly, mid-gap electronic states are observed to appear. At the same time, the presence of Fe alters the primary particle shape of the anatase without changing significantly the primary particle size. In contrast with previous results, analysis of the combined results strongly indicates that UV and visible photocatalytic activity are here dominated by morphological rather than structural/electronic issues.

---

Introduction

Nanostructured titanium dioxide (TiO₂) has become a standard photocatalyst for environmental cleanup and organic synthesis due to its low cost and physicochemical properties, e.g. high thermal and chemical stability, low toxicity, and relatively high photocatalytic activity.^1–4 Almost from the beginning of the field of photocatalysis, titanium oxide doping by transition metals has been employed in order to enhance the photocatalytic activity of TiO₂.^1–8 Iron is one of the most frequently used/examined dopants^1,2,9,10 due to the fact the ionic radius of six fold-coordinated Fe³⁺ (0.65 Å) is relatively similar to that of Ti⁴⁺ (0.605 Å). As such, it can be potentially incorporated into the crystal lattice of TiO₂.^11,12

The role of Fe doping ions in TiO₂ photoactivity is, however, controversial. It has been suggested that the Fe³⁺ behaves as an electron–hole recombination center and therefore inhibits photocatalytic activity.^13–17 Equally, it has been proposed that the presence of the Fe³⁺ centres favors electron–hole separation, and thus enhances photocatalytic activity.^12,18–25 These diametrically opposed opinions typically concern low loading (e.g. below 1 at%) catalysts and most likely have their origins in a number of preparation and experimental aspects. Firstly, Fe may occupy substitutional and/or (less frequently) interstitial positions at the anatase lattice.^1,10,22 Second, and possibly of more consequence, thus far no conclusive evidence of the corresponding charge neutrality vacancies for the most common substitutional doping position has been presented. Recent information regarding Fe-doped TiO₂ nanomaterials has provided evidence of cation vacancies²⁶ or has indicated the presence of anion vacancies.²⁷ This divergence can be understood by considering further information derived from bare TiO₂ nanomaterials which provides evidence of cation vacancies for samples with particle size well below ca. 10 nm and anion vacancies (typical of the bulk state) for samples above that size.^28,29 This appears intimately connected to the way nanoparticles can handle strain¹⁰ within the structure and indicates that size not only induces quantum and surface size-related electronic effects (particularly band gap magnitude but also the presence of electron-deficient under-coordinated species). Critically, in the case of titania, other mechanisms and species that can result in charge neutrality are size-dependent, and thus quite different electronic states with subsequent influence on photoactivity can exist. A third point, that is usually dismissed, is that the presence of heterocations may alter surface properties and, importantly, in the case of doping with Fe, primary particle shape.^1,10 As has been described in recent years, the reactivity of different surfaces of anatase nanoparticles appears quite different, with some general agreement in the fact that (100)/(001) surfaces are more active than (101) ones.³⁰ Although not without debate,³¹ this would mean that isotropic nanoparticle shapes would be more active than those most commonly found. These latter particles have bi-pyramidal shapes, elongated along the c crystallographic axis.^10,30,31 A last point to mention is the fact that liquid phase reactions concerning Fe-doped TiO₂ catalysts can also involve (if acid intermediates are present) lixiviation and subsequent re-adsorption of the heterocation at titania surfaces, with a potential homogeneous contribution to the activity which cannot be ignored.^32,33 The existence of such processes in the liquid case means that the partitioning of Fe between surface/bulk states could change during reaction and have resulting electronic/morphological/surface consequences, critical for catalytic purposes.^32–34

In this contribution we focus on analyzing the role of Fe-doped TiO₂ nanomaterials in the gas-phase elimination of toluene using both UV and (possibly of more general interest) solar light excitation. Note that this is a gas–solid phase reaction, free of some of the inherent possibilities mentioned above for liquid–phase reactions. Concerning the use of visible light sources for photocatalytic reactions, there is also considerable controversy regarding the effect of the Fe dopant on the TiO₂ band gap. While some authors describe, and theoretically support, a red-shift on the band gap energy and, consequently obtaining materials useful for application using visible light or sunlight,^35,36 others suggest that Fe only produces localized gap states whose effect on visible-light photoactivity remains unclear.³⁷ It is obvious that such differences may have their origin in structural variance between samples and thus call for a detailed characterization in order to interpret photoelimination properties. To shed light on this problem, we have analyzed the activity of a series of Fe-doped TiO₂ materials prepared by microemulsion, a method which allows careful control of all morphological properties of the solid.^5,38 We have studied the structural properties of the nanosolids, starting from the initial precursors, in order to obtain an accurate determination of the state and structure of the iron dopant and corresponding charge neutrality vacancy entities. This has been carried out using synchrotron-based X-ray total scattering/diffraction and absorption methods which are then complemented with other laboratory techniques. We show that our preparation method generates substitutional Fe–Ti mixed oxides having oxygen vacancies as the only (detectable) charge neutrality species. While such nanomaterials have different band gaps compared to titania which may permit visible-light absorption, other morphological modifications, particularly related to primary particle shape, appear to be of critical importance in understanding the final catalytic behavior of the samples.

Experimental section

Titania precursor materials were prepared using a microemulsion route by addition of titanium(IV) isopropoxide (Aldrich) to an inverse emulsion containing an aqueous phase (50 ml) dispersed in n-heptane (85/10 v/v vs. H₂O; Panreac), and using Triton X-100 (variable quantity; Aldrich) as surfactant, in 1-hexanol (105/100 v/v vs. surfactant; Aldrich).³⁹ Fe was introduced from Fe(NO₃)₃ (Aldrich) in the aqueous part of microemulsion to a final atomic content of x% (stoichiometry: Ti_1−xFe_xO_y). The resulting mixture was vigorously stirred for 24 h, centrifuged, decanted, and thoroughly rinsed under stirring with methanol in order to eliminate any portion from the organic and surfactant media. The resultant solids were then dried at 110 °C for 24 h. The composition of the catalysts was analyzed by using inductively coupled plasma and atomic absorption (ICP–AAS). BET surface area and porosity measurements were carried out by N₂ adsorption at 77 K using a Micromeritics 2010 instrument. UV-visible diffuse reflectance spectroscopy experiments were performed with a Shimadzu UV2100 apparatus with a nominal resolution of ca. 1 nm using BaSO₄ as reference. Band gap analysis was carried out following standard procedures by plotting (hνα)^1/2 (hν = excitation energy, α = absorption coefficient) vs. energy.¹ Raman spectra were recorded using a Horiba iH320 spectrometer and He : Ne laser excitation (632.8 nm). Sample labels are: T for pure TiO₂, and TFex for Fe–TiO₂ (where x corresponds to that atomic percentage of Fe). Precursor solids after drying are presented with a P before the sample label. Nominal values of Fe content for calcined samples (600 °C) are correct within an error of 3%.

Time-resolved hard X-ray diffraction (TR-XRD) data were collected at beamline ID15B (86.8 keV, λ = 0.143 Å, ΔE/E = 1.4 × 10⁻³) in the European Synchrotron Radiation Facility (ESRF, Grenoble, France) using a digital flat-panel X-ray detector (Trixel Pixium 4700).⁴⁰ Calibration of the X-ray wavelength was made using a NIST LaB₆ powder. In the TR-XRD experiments dealing with the thermal evolution of titania nanomaterials, the sample (ca. 10 mg) was kept in a 1 mm quartz capillary of 0.1 mm wall thickness and heated from 298 to 1023 K (25–750 °C) with a ramp of 3 °C min⁻¹ under a 20% O₂/He using a modified version of a plug-flow reactor system due to Chupas et al.⁴¹ which ensures a temperature control of ±1 °C. XRD patterns were taken at 10 °C intervals (with a measuring time of ca. 50 s per spectrum). A chromel–alumel thermocouple, inserted directly into the sample bed, was used to measure the temperature of the sample. Two dimensional powder patterns were collected at two sample-detector distances (ca. 0.4 m for PDF and 1.3 for high-resolution XRD) and the powder rings were subsequently radially integrated after applying geometrical and X-ray polarization corrections. Average grain/particle domain sizes (D) were calculated from the most intense diffraction peak (101) using the Scherrer formula.⁴²

XAFS spectroscopy was performed at the bending magnet beamline BM23 in ESRF. The storage ring conditions were 6 GeV and 200–150 mA. The measures were performed using a Si(111) monochomator (2.0 × 10⁻⁴ ΔE/E), and Si mirrors were used to eliminate higher harmonics in the beam. Three ionization chambers are filled with the optimal He/N₂ gas mixture at a total pressure of 2 bars, in order to have an absorption of 30% in I0 and 70% in I1 and I2 at the Fe K-edge (7112 eV). The monochromator was calibrated with a Fe foil and we constantly monitored the spectra of such foil in transmission mode in order to account for small energy shifts (<1 eV) during the measurements. The vertical exit-slit size was fixed at 0.3 mm, and the horizontal slit size was adjusted to 2.5 mm to ensure a proper counting statistics. The pre-edge region was scanned with 0.5 eV steps. Along the edge the step size was reduced to 0.4 eV in order to obtain adequate resolution for the X-ray absorption near edge structure (XANES). The spectra were collected in transmission mode. EXAFS spectra were analyzed using the Artemis program. Phase and amplitude functions were obtained with the FEFF8.2 program using an anatase-type structure having Fe as the central atom in a cation position of the anatase structure. Fits of the Fourier transform (FT; k²-weighted) EXAFS data were performed in R-space between 1.0 and 3.03 Å. The K-range used was 2.5–12.12 Å⁻¹. This gives a total of 13 free parameters according to Nyquist theorem.

Diffuse Reflectance Infrared Fourier Transform Spectra (DRIFTS) were taken in a Bruker Equinox 55 FTIR spectrometer fitted with an MCT detector. The DRIFTS cell (Harrick) was fitted with CaF₂ windows and a heating cartridge that allowed samples to be heated to 600 °C. Samples of ca. 60 mg were ramped at 5 °C min⁻¹ up to 600 °C under synthetic air (20 % O₂ in He). The spectra consisted of 70 accumulations with a total of 1 min acquisition time, at 4 cm⁻¹ resolution.

Activity for the gas-phase photo-oxidation of toluene was tested in a continuous flow annular photoreactor^5,39 containing ca. 40 mg of photocatalyst as a thin layer coating on a pyrex tube. The corresponding amount of catalyst was suspended in 1 ml of water, painted on a pyrex tube (cut-off at ca. 290 nm) and dried at room temperature. The reacting mixture (100 ml min⁻¹) was prepared by injecting toluene (Panreac, spectroscopic grade) into a wet (ca. 75% relative humidity) 20 vol% O₂/N₂ flow before entering at room temperature into the photoreactor, yielding an organic inlet concentration of ca. 800 ppmv. After flowing the mixture for 3–4 h in the dark (control test), the catalyst was irradiated by four lamps symmetrically positioned outside the photoreactor. The photocatalytic tests were performed under a radiation spectrum simulating sunlight (Philips TL 6W/54–765) as well as under pure UV-light irradiation (Philips TL 6W/08) using catalysts calcined at 600 °C. Reaction rates measured as toluene disappearance (C balance above 95%) were evaluated under steady state conditions, typically achieved after 4–5 h from the beginning of irradiation. No change in activity was detected for all samples within 24 h after reaching steady state conditions. The concentration of reactants and products was analyzed using an on-line gas chromatograph (Agilent GC 6890) equipped with HP-PLOT-Q/HP-Innowax columns (0.5/0.32 mm I.D. × 30 m) and TCD/FID detectors for the quantification of CO₂ and organic substances (toluene, photo-catalytic products) respectively.

Results and discussion

As mentioned above, the detailed structural characterization of nanosolids is a must in order to adequately interpret photoactivity. To this end, and due to the uncertain structural scenario reported in the specific case of Fe-doped TiO₂ materials,^{1,2,10,22,35,37} we followed the genesis of the anatase phase from amorphous powders using a tool (total scattering/XRD) which can describe simultaneously the local, mid, and long range order of the materials.

Total scattering PDF-XRD (pair distribution function of X-ray diffraction data) signals are plotted in Fig. 1 for two representative samples. The thermal evolution from the initial amorphous structure to well crystallized materials under an O₂/He atmosphere is clearly evidenced with increasing temperature. The absence of hypothetical cations at interstitial positions is evident as the corresponding Ti–O–Ti distances are only observed (of course within the detection limit of the technique; likely 2–3 at% of cation content) for Ti cations located at substitutional positions.⁴³ A detailed plot is added at the right to analyze the behavior of the samples after nucleation (the onset of this is determined with the independent high-resolution measurement of the anatase (101) reflection –see experimental section for details). This is the most important temperature range in terms of defining the defect distribution of the crystalline anatase nanomaterial. We analyzed the intensity behavior of all peaks present, extracted the PDF functions and found that differences among them are restricted to the ca. 4.2 Å contribution, which has a dominant Ti–O and a weak O–O component.

Fig. 1 Pair distribution function (PDF), G(r), of the undoped (A and B, TiO₂) and the 3 at% Fe doped (C and D, TFe3) samples upon heating in dry air. Right panels contain spectra within ∼100 °C from the onset temperature of each sample.

The normalized (compared to the bare TiO₂ reference) intensity of the 4.2 Å PDF peak for Fe-doped nanomaterials is presented in Fig. 2. As can be seen in the figure, the net intensity of this scattering interaction drops as the Fe content is increased. This indicates that all samples in our series exclusively contain oxygen vacancies as charge neutrality species. The presence of anionic and not cationic charge neutrality species may be driven by the primary particle size which in our Fe-containing systems has already grown to over 10 nm within ca. 75 °C from the onset of nucleation.^28,29 The physical properties of materials calcined at 600 °C are presented in Table 1. In all cases the maximum primary particle size of our materials is about 16–17 nm with only very small variations being observed (e.g. below experimental error of ca. 0.5 nm), indicating a global homogeneity obtained in this parameter within the group of samples studied. Of interest to note, however, is that the charge neutrality vacancies are not localized within the first shell around the Fe ion (corroborated this using Fe K-edge XAS and EXAFS – see below) as the ionic stability favored the presence of Ti⁴⁺ rather than Fe³⁺ in the neighboring of the vacancy.^27,44 The number of anion vacancies increases with the Fe content, as expected.

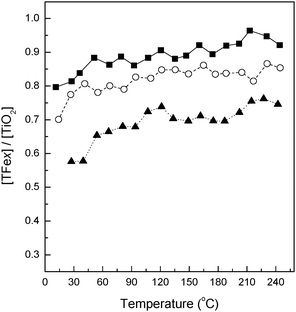Fig. 2 Evolution through relative temperature of the TFex/T intensity ratio of the PDF peak at r = 4.2 Å. T = 0 °C corresponds to the nucleation onset temperature of each sample. Sample characteristics: (■) TFe0.5, (○) TFe1.5, (▲) TFe3.

Table 1 Main physicochemical parameters of the pure and Fe-doped TiO₂ catalysts calcined at T = 600 °C

Sample	BET (m^2 g^−1)	Anatase crystal size^a (nm)	Band gap^b (eV)
a Crystal size of anatase determined by XRD using Scherrer equation. b Considering the oxides indirect band gap semiconductors.
T	31.7	16.0	3.12
TFe0.25	42.0	15.8	3.10
TFe0.5	39.8	16.3	3.09
TFe1	36.9	17.4	2.89
TFe1.5	41.6	17.7	2.87
TFe3	43.9	17.3	—

---

As demonstrated by Fe K-edge XANES and EXAFS, the Fe ion is located at substitutional positions of the anatase structure. A detailed analysis of the Fe 1s/p → 3d pre-edge structure (Fig. 3A) reveals that the electronic transition (centroid of the peak) is located at 7114.1 ± 0.1 eV for all precursor and calcined samples, indicating the Fe³⁺ chemical state in all cases.^45–47 The integrated area of this transition for calcined samples is almost constant (0.104 ± 0.02). The combined analysis of the pre-edge intensity and energetic position provides evidence of a slightly distorted six-fold coordination in all cases^45–47 and consequently establishes the presence of Fe ions at substitutional rather than interstitial positions of the anatase structure.

Fig. 3 Normalized Fe K-edge (A) pre-edge region and (B) XANES region of the calcined at T = 600 °C TFex samples (solid lines) and the precursors P-TFex samples (dashed lines).

Fig. 4 displays the Fourier transform of Fe K-edge EXAFS data for the calcined materials. No significant differences within the series are detected. Fig. 4 also contains the simulated EXAFS signal for the sample containing the highest Fe-content (sample TFe3). The analysis of the EXAFS signal quantifies all of the above-mentioned structural results, pointing out to an iron center having a distorted octahedral geometry (6 coordinated O atoms) with two Fe–O distances (Fe–O₄ = 1.94 Å and Fe–O₂ = 1.97 Å) and interacting in the second shell with 4 Ti atoms with Fe–Ti₄ = 3.02 Å. No Fe–Fe distances are detected indicating the presence of isolated species. These results are in agreement with similar studies performed on Fe implanted TiO₂.⁴⁸ Both Fe–O and Fe–Ti distances are close to the anatase single oxide Ti–O (∼1.95 Å) and Ti–Ti (3.05–3.10 Å) distances. Fe, as other cations, is thus displaying a limited effect on the local structure of neighboring Ti cations and is essentially constant throughout our series.^27,49,50 On the other hand, this fact and the relatively small Fe doping percentages explain that there were no visible effects of Fe doping at the Ti K-edge. This has been previously observed in other anatase doped materials.^27,49 At higher Fe loadings (near and above 5 at%) there may be however another situation where a larger structural modification of anatase local ordering is observed.^7,49–51

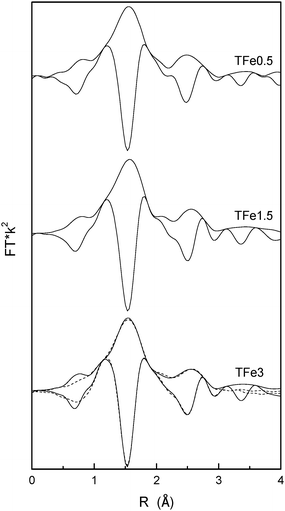Fig. 4 Module and imaginary part Fourier transforms of Fe K-edge EXAFS (solid lines) of the calcined at T = 600 °C TFex samples (where x = 0.5, 1.5 and 3). The simulated signal for the TFe3 sample is also presented (dashed lines).

The same characteristics observed in XANES and EXAFS within the series of samples indicate that Fe surface contribution is roughly equivalent in all samples. Raman spectra of the undoped and the TFex samples calcined at 600 °C (Fig. 5) show the exclusive presence of an anatase phase with peaks at ca. 144, 195, 399, 517 and 639 cm⁻¹, corresponding to the E_g(1), E_g(2), B_1g(1), B_1g(2), A_1g(1) and E_g(3) modes respectively.^5,49 No Raman signals corresponding to iron oxide(s) can be observed in the Fe-doped samples, confirming that Fe does not accumulate significantly at the surface and is present at substitutional positions of the anatase structure, as demonstrated above using XANES and EXAFS. We note, on the other hand, that Fe in the precursor state may have a local order which resembles the anatase structure. This is suggested by the similar pre-edge properties of precursor and calcined samples (Fig. 3), although a more heterogeneous local order is obviously characteristic of the amorphous state and would account for the (modest) broadening of the peak if compared with the corresponding calcined state (Fig. 3A). In any case, the latter clearly shows that the preparation method allows an intimate mixing of the two (Fe, Ti) cations and hetero-cation contact from the initial steps of the preparation of the final solid.

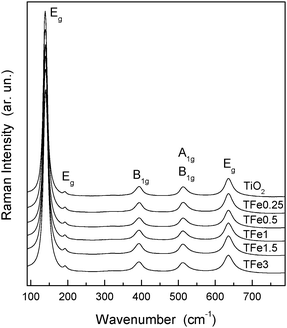Fig. 5 Raman spectra of the indicated undoped (T) and Fe-doped (TFex) samples.

The electronic consequences of the substitutional doping of Ti by Fe, and the concomitant creation of oxygen vacancies in calcined materials, were analyzed using UV-visible spectroscopy. Fig. 6A displays the corresponding diffuse reflectance spectra for calcined materials. Starting with the analysis of the band gap (Fig. 6B), we note firstly that anatase is known to be an indirect band gap semiconductor, although relaxation of energy and moment rules on the nanoscale may induce direct band gap character.^1,10,52 In any case, the band gap behavior throughout the series is similar for both cases (e.g. direct and indirect). Table 1 gives the result of the indirect band gap calculation. This confirms that the presence of Fe in the anatase framework decreases the band gap by a relatively modest amount. The maximum shift obtained is ca. 0.25 eV, for a doping atomic percentage of 1.5%. The trend reported in Table 1 indicates an increasing effect on band gap energy with the increasing content of Fe in the nanomaterial. However the intensity of the additional mid-gap localized electronic states does not allow determination of the corresponding band gap value for samples having larger Fe quantities than 1.5%.

Fig. 6 (A) Diffuse reflectance UV-Vis spectra of the undoped (T) and Fe-doped (TFex) samples. (B) Plot used to estimate band gap considering the oxides indirect gap semiconductors.

Further, two mid (or inter-gap) gap states can also be observed in Fig. 6A at wavelengths above the band gap energy of the materials. The first is located around 425 nm and typically ascribed to Fe 3d excitations into the conduction band.⁴⁴ The second inter-gap state, located at ca. 500 nm, has no unequivocal assignment. While in the past this has generally been ascribed to Fe d–d or “localized charge transfer” (e.g. Fe³⁺ + Fe³⁺ → Fe²⁺ + Fe⁴⁺) transitions,^44,53 new in-depth optical analyses would suggest a potential relationship with anion-defect related states below the Fermi edge.⁵⁴ Although no conclusive assignment regarding this last contribution can be made here, the UV-visible information provides evidence that, from the lower doping quantity tested here, Fe simultaneously induces band gap modification (by altering band structure) and is also responsible for appearance of localized electronic gap states. The two mid-gap contributions already discussed appear more or less in parallel, although the 425 nm is more visible at the lowest loading analyzed (0.25 at%).

To complete the characterization of the materials we followed the calcination treatment using infrared spectroscopy. Using infrared spectroscopy to study the OH and water evolution during the thermal treatment of solid precursors, we can follow the genesis of the oxide-particle surfaces. Importantly we note that, in this case the technique is sensitive to the local structural order. As such, infrared appears as an ideal candidate (in contraposition to microscopy techniques) to analyze situations where amorphous and crystalline phases co-exist or need to be jointly analyzed.^43,55–57 Analysis of OH-containing molecular entities, and their relationship with specific surfaces of the anatase, can be used to establish the primary particle shape of the materials. A similar evolution of the samples is observed for all materials under study and here we will just show illustrative results for the highest temperature, 600 °C.

Fig. 7 presents infrared results and their fitting using Gaussian profiles of the OH contributions.^43,55–57 The derivative of the IR signal throughout the calcination step was used to select the number of contributions. For the fitting procedure the tailing contributions (i.e. below 3600 cm⁻¹ and above 3725 cm⁻¹) were not taken into account. Peaks at low wavenumbers (below 3670 cm⁻¹) are ascribed to OH adspecies present at (101) surface terminations while above this cut-off point bands are ascribed to adspecies at (100) surfaces.^55–57 Anatase nanoparticles typically display a bi-pyramidal structure elongated along the c crystallographic axis that principally exposes (100), (001) and (101) surfaces. The (001) surface is usually detected by IR only for particles with a restricted growth along the c-axis and presenting rather isotropic (along the three spatial axes) particle shapes.^43,55 Thus, the (100)/(101) intensity ratio is typically used as a good indicator of the particle shape and has been consequently utilized to quantitatively measure the elongation of the particle shape along the mentioned crystallographic axis.^55–59 Here this observable is reported in Fig. 8 and clearly indicates that Fe has a continuous effect of the particle shape that is in samples containing Fe at >1% doping levels. The elongation of the particle morphology is thus promoted by iron doping; and this promotion is critically enhanced at ca. 1 at% Fe content.

Fig. 7 DRIFT spectra of the titania catalysts taken at 600 °C under dry air (○) and Gaussian fittings in the region corresponding to isolated OH species (lines). Dashed lines: individual Gaussian function curves; solid lines: simulated total profile; circles: experimental spectra.

Fig. 8 (100)/(101) intensity ratio for OH hydroxyl contributions presented in Fig. 7.

The structural and electronic effects of Fe doping on the anatase can be thus summarized as being related to the formation of a substitutional oxide containing anion vacancies which alter both band gap energy and simultaneously introduce localized mid-gap states. Fe does not appear to substantially modify primary particle size but does have an important effect on primary particle shape for Fe contents around/above 1–1.5 at%. This non-linear shape trend with Fe content appears directly reflected in the surface area behavior of the materials with the Fe content (Table 1). This summary gives a reasonably complete description of the sample series which thus permits interpretation of their photoactivity under light excitation.

Fig. 9 shows steady state reaction rates for the gas-phase photo-oxidation of toluene by the TFex series calcined at 600 °C under artificial sunlight and pure UV irradiation, taking into account the different BET surface area of the samples. We note that expressing the rate per weight unit (mol s⁻¹ g⁻¹) gives the same general behavior presented in Fig. 9, expect for the punctual fact that the TFe0.25 samples present slightly higher activity than the TiO₂ reference. As shown in Fig. 9 such an increment is mostly accounted by surface area differences between the samples and is thus of secondary importance in the context of the present study. For comparison, the photocatalytic results obtained for the commercial reference TiO₂ Degussa P-25 is also included in the figure. Note that a number of catalysts improve the performance of P25 but none of the Fe-containing materials compares favorably with the pure TiO₂ nanomaterial having a similar particle size and obtained using the same preparation procedure. This happens irrespective of the light source nature (UV or sunlight) but the negative effect of Fe presence seems less important while using sunlight; the ratio between UV and sunlight rates for the same sample goes from ca. 8.3 (TiO₂) to 1.4 (TiFe1.5). This is further analyzed below.

Fig. 9 Reaction rates of toluene photo-oxidation of the TiO₂, TFex and reference (Degussa P25 (●)) catalysts under artificial sunlight (left x-axis, cycles) and pure UV-light irradiation (right x-axis, squares) taking into account the BET surface area of the samples (reaction rate, mol s⁻¹ m⁻²).

A similar trend observed under UV and solar lights indicates that surface, or any other morphological rather than electronic property, may be of significance in interpreting photoactivity. In any case, the absence of a positive effect on photoactivity under both UV and solar lights indicates that localized electronic states are most likely present in the bulk of the material and dominate the electron–hole recombination, decreasing the reaction rate compared with the TiO₂ reference system.^5,10,13,18 Such states may affect more dramatically the fate of UV (than visible light) generated charge carriers according to the UV/sunlight rates mentioned above. The potential positive effect of the Fe-induced band gap modification, expected in sunlight experiment, is not observed (Fig. 9).

Comparison of Fig. 8 and 9 do, however, suggest that the activity trend can be understood in relation to the primary shape of the different oxide materials. Both figures indicate a morphological (Fig. 8) and reactive (Fig. 9) transition around 1–1.5 at% Fe loading. This clearly indicates that the dominant structural/electronic effect of Fe is related to shape anisotropy and that this has an opposite trend to shape elongation along the c crystallographic axis. This is in agreement with the current ideas that (100)/(001) faces are intrinsically more active than (101) and is thus consistent with such theory.^10,30,60 However, for the high Fe-loaded samples (i.e. Fe > 1%) the negative effect of the localized electronic states in the bulk (caused by the presence of Fe) seem to be an additional factor affecting photoactivity, since photocatalytic activity further decreases from the TFe1 case (Fig. 8) while elongation remains approximately constant (Fig. 7) with increasing Fe content above 1 at%.^17,37,61 We can therefore suggest that primary particle shape is the key morphological variable to understanding and optimizing the photocatalytic behavior of our Fe-doped titania samples. Any electronic effects, for instance related to mid-gap states, seem to play secondary negative roles in determining overall photoactivity. As noted previously, such electronic states could in turn be related to bulk-located oxygen vacancies, which grow in parallel to the Fe content of the materials and would be the ultimate cause for such a second negative effect.

Conclusions

In this contribution we have synthesized, by microemulsion, and fully characterized the structural and electronic properties of Fe containing titania nanomaterials. After calcination we have obtained a substitutional mixed oxide with anatase structure wherein Fe occupies network cation positions: anion vacancies appear as the exclusive defect to achieve charge neutrality.

The structural modification of the anatase structure produced by Fe doping decreases band gap energy (by at most 0.25 eV) and induces the formation of localized inter-gap states. Both electronic modifications appear monotonically with increasing Fe content of the material, indicating that no differential electronic effects are observed within our series of samples.

The comparison of structural/electronic and morphological properties with photocatalytic behavior evolution within the Fe-doped series indicates that the latter is mostly driven by morphological and, concretely, primary particle shape modification by the doping process. This appears as the dominant variable which determines activity both under UV and visible light excitation. Electronic effects, related to localized mid-gap states, also seem to negatively affect activity but to a significantly lesser degree than morphology.

Acknowledgements

K.C.C. and A.I.-J. would like to acknowledge, respectively, the Marie Curie program (Action FP7-PEOPLE-2009-IEF-253445) and the Ramón y Cajal program (MINEO, Spain) for Post-doctoral Fellowships. Financial support by CICYT project CTQ2010-14872/BQU; the research leading to some of these results has also received funding from the European Union's Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 253445 which is fully appreciated. The ESRF synchrotron and Dr S. Pascarelli are thanked for provision of synchrotron radiation time at lines ID15B and BM23 through, respectively, EU and IHR programs. Olivier Mathon is gratefully acknowledged for help during the XAS data collection.

References

1. M. Fernández-García, A. Martínez-Arias, J. C. Hanson and J. A. Rodriguez, Chem. Rev., 2004, 104, 4063–4104.
2. M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96.
3. A. L. Linsebigler, G. Lu and J. T. Yates Jr., Chem. Rev., 1995, 95, 735–758.
4. G. Palmisano, E. García-López, G. Marci, V. Loddo, S. Yudakal, V. Augugliaro and L. Palmisano, Chem. Commun., 2010, 47, 7074–7089.
5. A. Fuerte, M. D. Hernández-Alonso, A. J. Maira, A. Martínez-Arias, M. Fernández-García, J. C. Conesa, J. Soria and G. Munuera, J. Catal., 2002, 212, 1–9.
6. K. Nagavendi, M. S. Hedge and G. Madras, J. Phys. Chem. B, 2004, 108, 20204–20211.
7. A. Kubacka, M. Fernández-García and G. Colón, J. Catal., 2008, 254, 272–283.
8. A. Y. Choi, Y. Tokurano, S. H. Cho and C.-H. Han, Mater. Sci. Forum, 2011, 695, 129–132.
9. R. I. Bickley, J. S. Lees, R. J. D. Tilley, L. Palmisano and M. Schiavello, J. Chem. Soc., Faraday Trans., 1992, 88, 377–383.
10. A. Kubacka, M. Fernández-García and G. Colón, Chem. Rev., 2012, 112, 1555–1614.
11. W. Wang, B. Gu, L. Liang, W. A. Hamilton and D. J. Weselowsky, J. Phys. Chem. B, 2004, 108, 14789–14792.
12. Z. Zhang, C. Wang, R. Zakaria and J. Y. Ying, J. Phys. Chem. B, 1998, 102, 10871–10878.
13. J. A. Navío, G. Colón, M. C. Macias, C. Real and M. I. Litter, Appl. Catal., A, 1999, 177, 111–120.
14. J. A. Navío, J. J. Testa, P. Djedjeian, J. R. Padrón, D. Rodríguez and M. I. Litter, Appl. Catal., A, 1999, 178, 191–203.
15. M. Kang, S.-J. Ching and J. Y. Park, Catal. Today, 2003, 87, 87–97.
16. E. Piera, M. I. Tejedor, M. E. Zorn and M. A. Anderson, Appl. Catal., B, 2003, 46, 671–685.
17. C. Adan, A. Bahamonde, A. Martínez-Arias, M. Fernández-García, L. A. Pérez-Estrada and S. Malato, Catal. Today, 2007, 129, 79–85.
18. C. Adan, A. Bahamonde, M. Fernández-García and A. Martínez-Arias, Appl. Catal., B, 2007, 72, 11–17.
19. J. Yu, Q. Xiang and M. Zhou, Appl. Catal., B, 2009, 90, 595–602.
20. K. Melghit, O. S. Al-Shukeili and I. Ai-Amri, Ceram. Int., 2009, 35, 433–439.
21. C. Wang, C. Böttcher, D. W. Bahnemann and J. K. Dohrmann, J. Mater. Chem., 2003, 13, 2322–2329.
22. M. I. Litter and J. A. Navío, J. Photochem. Photobiol., A, 1996, 98, 171–181.
23. Q. S. Zhang and Z. K. Zhang, J. Disp. Sci. Technol., 2009, 30, 110–114.
24. K. Qi, B. Fei and J. H. Xin, Thin solid Films, 2011, 519, 2438–2444.
25. S. Sun, J. J. Ding, J. Bao, C. Gao, Z. M. Qi, X. Y. Yang, B. He and C. X. Li, Appl. Surf. Sci., 2012, 258, 5031–5037.
26. J. A. Wang, R. Limas-Ballesteros, T. López, A. Moreno, R. Gómez, O. Novaro and X. Bokhimi, J. Phys. Chem. B, 2001, 105, 6292–6301.
27. C. E. Rodríguez-Torres, A. I. Cabreras, L. A. Errico, C. Adán, F. G. Requejo, M. Weissmann and S. J. Stewart, J. Phys.: Condens. Matter., 2008, 20, 135210–135217.
28. V. Swamy, D. Menzies, B. C. Muddle, A. Zuznetsov, S. Dubrovinsky, Q. Dai and V. Dimitriev, Appl. Phys. Lett., 2006, 88, 243103.
29. I. E. Grey and N. C. Wilson, J. Solid State Chem., 2007, 180, 670–677.
30. W. Q. Fang, X.-Q. Gong and H. G. Yang, J. Phys. Chem.. Lett., 2011, 2, 725–734.
31. G. Liu, J. C. Yu, G. C. Liu and H.-M. Chen, Chem. Commun., 2011, 47, 6763–6783.
32. J. Araña, O. G. Díaz, J. M. D. Rodríguez, J. H. Melían, C. G. I. Cabo, J. P. Peña, M. C. Hidalgo and J. A. Navío, J. Mol. Catal. A: Chem., 2003, 197, 157–165.
33. C. Adan, A. Martínez-Arias, S. Malato and A. Bahamonde, Appl. Catal., B, 2009, 93, 96–102.
34. S. Liu, X. P. Liu, Y. S. Chen and R. Y. Jiang, J. Alloys Compd., 2010, 506, 877–882.
35. J. Yu, Q. Xu and M. Zhou, Appl. Catal., B, 2009, 90, 595–602.
36. J. Z. Zhang, Y. D. Shen, Y. W. Li, Z. G. Hu and J. H. Chu, J. Phys. Chem. C, 2010, 114, 15157–15164.
37. Y. Yalcin, H. Kilic and Z. Cinar, Appl. Catal., B, 2010, 99, 469–477.
38. V. Uskokovic and M. Drofenik, Surf. Rev. Lett., 2005, 12, 239–277.
39. A. Fuerte, M. D. Hernández-Alonso, A. J. Maira, A. Martínez-Arias, M. Fernández-García, J. C. Conesa, J. Soria and G. Munuera, Chem. Commun., 2001, 2718–2719.
40. J. E. Daniels and M. Drakopoulos, J. Synchrotron Radiat., 2009, 16, 463–471.
41. (a) P. J. Chupas, K. W. Chapman, C. Kurtz, J. C. Hanson, P. L. Lee and C. P. Grey, J. Appl. Crystallogr., 2008, 41, 822–827; (b) S. J. A. Figueroa, D. Gibson, T. Mairs, S. Pasternak, M. Newton, M. Di Michiel, J. Andrieux, K. Christoforidis, A. Iglesias-Juez, M. Fernández-García and C. Prestipino, J. Appl. Cryst. (submitted).
42. R. L. Snyder, J. Fiala and H. J. Bunge, “Defects and Microstructure Analysis by Diffraction”, Oxford University Press, New York, 1999.
43. M. Fernández-García, C. Belver, J. C. Hanson, X. Wang and J. A. Rodriguez, J. Am. Chem. Soc., 2007, 129, 13604–13612.
44. T. Umebayashi, T. Yanaki, H. Itoh and K. Asai, J. Phys. Chem. Solids, 2002, 63, 1909–1920.
45. F. Farges, Phys. Chem. Miner., 2001, 28, 619–629.
46. M. Fernández-García, Catal. Rev., 2002, 44, 59–121.
47. T. Yamamoto, X-Ray Spectrom., 2008, 37, 572–584.
48. H. Yamashita, M. Harada, J. Misaka, M. Takeuchi, K. Ikeue and M. Anpo, J. Photochem. Photobiol., A, 2002, 148, 257–261.
49. M. Fernández-García, A. Martínez-Arias, A. Fuerte and J. C. Conesa, J. Phys. Chem. B, 2005, 109, 6075–6083.
50. Z. Ambrus, N. Balázs, T. Alapi, G. Wittmann, P. Sipos, A. Dombi and K. Mogyorósi, Appl. Catal., B, 2008, 81, 27–37.
51. Q. Wu, Q. Zheng and R. van de Krol, J. Phys. Chem. C, 2012, 116, 7219–7226.
52. N. Serpone, D. Lawless and R. Khairutdinov, J. Phys. Chem., 1995, 99, 16555–16565.
53. J. F. Zhu, W. Zhang, H. E. Bin and J. L. Zhang, J. Mol. Catal. A: Chem., 2004, 216, 35–43.
54. J. Z. Zhang, X. Chen, Y. Shen, Y. Li, Z. Hu and J. Chu, Phys. Chem. Chem. Phys., 2011, 13, 13096–13105.
55. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Touthoat, J. Catal., 2004, 226, 54–68.
56. S. Dzwigaj, C. Arrouvel, M. Breysse, C. Geantet, S. Inoue, H. Toulhoat and P. Raybaud, J. Catal., 2005, 236, 245–250.
57. M. Fernández-García, X. Wang, C. Belver, J. C. Hanson and J. A. Rodriguez, J. Phys. Chem. C, 2007, 111, 674–682.
58. C. Delana, E. Fois, S. Coluccia and G. Martra, J. Phys. Chem. C, 2010, 114, 21531–21538.
59. K. C. Christoforidis, A. Iglesias-Juez, S. J. A. Figueroa, M. A. Newton, M. Di Michiel and M. Fernández-García, Phys. Chem. Chem. Phys., 2012, 14, 5628–5634.
60. K. C. Christoforidis, S. J. A. Figueroa and M. Fernández-García, Appl. Catal., B, 2012, 117–118, 310–316.
61. Y. A. Luo, W. S. Tai, H. O. Seo, K. D. Kim, M. J. Kim, N. K. Dey, Y. D. Kim, K.-H. Choi and D. C. Lim, Catal. Lett., 2010, 138, 76–81.

---