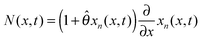Optimal charging profiles for mechanically constrained lithium-ion batteries
Bharatkumar
Suthar
a,
Venkatasailanathan
Ramadesigan
b,
Sumitava
De
a,
Richard D.
Braatz
c and
Venkat R.
Subramanian
*a
aDepartment of Energy, Environmental & Chemical Engineering, Washington University, St. Louis, MO 63130, USA. E-mail: vsubramanian@seas.wustl.edu
bDepartment of Energy Science and Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
cDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 25th October 2013
Abstract
The cost and safety related issues of lithium-ion batteries require intelligent charging profiles that can efficiently utilize the battery. This paper illustrates the application of dynamic optimization in obtaining the optimal current profile for charging a lithium-ion battery using a single-particle model while incorporating intercalation-induced stress generation. In this paper, we focus on the problem of maximizing the charge stored in a given time while restricting the development of stresses inside the particle. Conventional charging profiles for lithium-ion batteries (e.g., constant current followed by constant voltage) were not derived by considering capacity fade mechanisms. These charging profiles are not only inefficient in terms of lifetime usage of the batteries but are also slower since they do not exploit the changing dynamics of the system. Dynamic optimization based approaches have been used to derive optimal charging and discharging profiles with different objective functions. The progress made in understanding the capacity fade mechanisms has paved the way for inclusion of that knowledge in deriving optimal controls. While past efforts included thermal constraints, this paper for the first time presents strategies for optimally charging batteries by guaranteeing minimal mechanical damage to the electrode particles during intercalation. In addition, an executable form of the code has been developed and provided. This code can be used to identify optimal charging profiles for any material and design parameters.
1 Introduction
Lithium-ion chemistries are more attractive for many applications due to high cell voltage, high volumetric and gravimetric energy density (100 Wh kg−1), high power density (300 W kg−1), a good temperature range, a low memory effect, and a relatively long battery life.1–3 Capacity fade, underutilization, and thermal runaway are the main issues that need to be addressed in order to use a lithium-ion battery efficiently and safely for a long time.In order to address the above mentioned issues and utilize the battery efficiently to avoid overdesigning, smarter battery management systems are required that can exploit the dynamics of the battery and derive better operational strategies. In this direction, use of physically meaningful models in deriving these strategies has become a recent trend. Recognizing the potential of reducing the weight and volume of these batteries by 20–25% for vehicular applications, the Department of Energy has recently initiated a $30 M program through ARPA-E named Advanced Management and Protection of Energy Storage Devices (AMPED).4 Several researchers have made significant contributions in this area in the past. Methekar et al.5 looked at the problem of energy maximization within a given time with constraints on voltage and charging time using Control Vector Parameterization (CVP). Klein et al.6 considered the minimum-time charging problem while including constraints on temperature rise and side reactions. Rahimian et al.7 calculated optimal charging current as a function of cycle number during cycling for a lithium-ion battery under the effect of capacity fade using a single-particle model (SPM). Hoke et al.8 used a lithium-ion battery lifetime model to reduce battery degradation in a variable electricity cost environment using the SPM. Suthar et al.9 used a reformulated pseudo 2-dimensional thermal model10 to derive an open loop optimal charging profile to restrict temperature rise in a battery. This paper focuses on the problem of deriving optimal charging profiles for lithium-ion batteries.
Intercalation induced stress generation in electrode particles is one of the main reasons for capacity fade, which affects the capacity in two ways; fracture due to stress (electrical isolation) that reduces the capacity and the effect of loss in the connectivity of the particles.11 To the best of our knowledge, none of the optimal charging profiles reported in the literature includes the intercalation-induced stresses in their derivation. The progress made in understanding the capacity fade mechanisms12–17 has paved the way for inclusion of that knowledge in deriving optimal controls. In this paper, we have incorporated the particle-level stress–strain effect with a single-particle model to derive an optimal charging profile that restricts the peak stresses inside a particle. This paper illustrates that almost the maximum possible amount of charge can be stored within a given time (one hour), if the current profile is optimally derived, with significantly lower stress being developed within the particle. Section 2 reviews various stress models reported in the literature for battery models. Section 3 provides a brief description of the model used to perform the optimization. Section 4 defines the optimal control problem. Section 5 discusses the details of the code provided online. Section 6 presents results and discussion, which are followed by conclusions and future directions.
2 Review of stress models
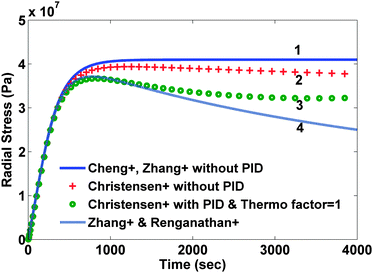
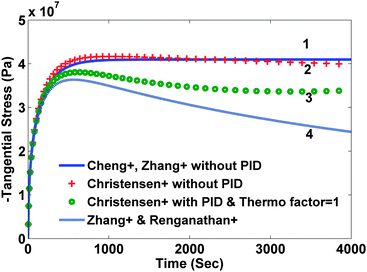
During intercalation of lithium into a graphite particle, significant stress is developed inside the particle. In particular, higher rates of charging yield higher stress. If the stress exceeds the yield stress of a given material, the particle can break and lose contact with the matrix resulting in reduced capacity of the battery. Different models have been developed to quantify the stress developed in a particle with varying degree of sophistications. These modeling efforts can be divided into two categories: strain splitting18–20 and stress splitting.11,14 The theory of the strain splitting approach has been developed by Timoshenko21 where thermal stresses have been modeled using strain splitting, with these models being called thermal analogy models. Here, the intercalation-induced stresses are treated in a similar way to the temperature-induced stresses. A very detailed and rigorous model that used stress splitting was developed by Christensen et al.,11,14 which was shown to be equivalent to the former approach (strain splitting) proposed by Timoshenko.21 In both categories, different models can be obtained depending upon the inclusion of pressure-induced diffusion. The effect of pressure-induced diffusion (PID) becomes prominent once the concentration profile starts to develop. The inclusion of pressure-induced diffusion in the model may not have a large effect on the concentration profiles, but since the stress development depends upon the difference in concentration at different points inside the particle, the inclusion of PID does significantly affect the stress profiles. During intercalation (charging/uptake of lithium by the graphite electrode), PID acts in parallel to concentration gradient-induced diffusion to make the concentration profile flatter, which relaxes the particle.In the first modeling category of strain splitting where intercalation-induced stresses are treated analogous to temperature-induced stresses (thermal analogy models), Zhang et al.19 presented a model that incorporated pressure-induced diffusion. In this model, the partial molar volume and diffusion coefficient were assumed to be independent of the lithium concentration. Additionally, hydrostatic stress was assumed to be the same as the thermodynamic pressure to simplify the pressure-induced diffusion term in the Stefan–Maxwell diffusion equation. These aforementioned assumptions enable decoupling of stress and concentration variables, resulting in a single partial differential equation for concentration. Stress profiles can then be calculated during post-processing from the lithium concentration profile. This approach makes the model very simple while capturing the basics of volume expansion in the particle within a lithium-ion battery. In this model, if pressure-induced diffusion is ignored then analytical results can be obtained for constant-current charging.18 The same model formulation was implemented in a pseudo-2D model of a dual porous insertion electrode cell sandwich comprising lithium cobalt oxide and carbon electrodes, where a moving boundary formulation was used to address two phases involved inside the lithium cobalt oxide electrode by Renganathan et al.20
In the second modeling category, the stress is divided into two components: elastic and thermodynamic. A very detailed and rigorous model has been developed by Christensen et al.14 to model volume expansion and contraction of a lithium insertion compound that calculates stresses due to intercalation and de-intercalation of lithium. This model incorporates dependence of partial molar volume on the state of charge (SOC) as well as an experimentally measured thermodynamic factor that is again a function of the state of charge. Also, the model includes a moving boundary with non-ideal binary diffusion. Fig. 1 and 2 compare stress profiles predicted by the different models available in the literature. The thermodynamic factor is assumed to be 1 in the model developed by Christensen et al.14 (that is, the open-circuit potential is purely Nernstian).
Comparison of different stress values obtained from different modeling approaches
For the current study, we have focused our attention on single particle representation of the electrode.22 In this modeling approach, the behavior of the entire porous electrode is simplified by replacing it with a solid spherical particle. The current density that goes inside this particle is determined by the total surface area of the electrode. The radius of this hypothetical particle is representative of the particle size distribution of the electrode material. This representation of a lithium-ion battery simulates the behavior of a real battery with reasonable accuracy at lower rates of charge and discharge. For the present case, we have not incorporated the state of charge dependent diffusivity and thermodynamic factor. Including these will make the following analysis material specific. Moreover, in order to handle such a large variation in diffusion coefficient with SOC (2 orders of magnitude), different numerical discretization schemes may be needed for efficient simulation and optimization.23–25 Numerical simulation was done for intercalation of lithium into a carbon electrode (charging) for the parameter values presented in Table 1. Both radial and tangential stresses developed in the particle reach maxima and minima respectively and then stay at that value when no pressure-induced diffusion is assumed in the first category of models (see solid curves in Fig. 1 and 2). If pressure-induced diffusion is included in the model, magnitudes of both stresses decrease (dashed curves in Fig. 1 and 2).| Parameter | Symbol and dimensions | Value |
|---|---|---|
| a Values obtained from Christensen et al.17 b Values obtained from Renganathan et al.20 c Values obtained from Northrop et al.10 | ||
| Radius of particle | R n | 12.5 × 10−6 m |
| Stoichiometric maximum concentration | C max n | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 833 mol m−3 833 mol m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| Total surface area of the anode | S n | 0.7824 m2 |
| Diffusion coefficient | D n | 3.9 × 10−14 m2 sec−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
| Faraday's constant | F | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 C mol−1 487 C mol−1 |
| Young's modulus | E n | 15 × 109 Paa |
| Poison's ratio | ν n | 0.3a |
| Molecular weight | Mwn | 78.64 g mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| Density | ρ n | 2.1 g cc−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| Partial molar volume | Ω n | 4.08154 × 10−6 m3 mol−1 |
| Applied current | i app | 1.656 A (1 C) |
| Time scaling | τ | 3600 s |
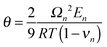
|
3.201754 × 10−5 m3 mol−1 | |
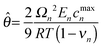
|
1.019214 | |
This decrease is due to the fact that during intercalation PID works in parallel to the Fickian diffusion and hence tries to make the concentration profile flatter, which in turn relaxes the particle. It is important to note that the peak stress occurs when the concentration at the center of the particle starts to change (that is, the concentration profile develops fully). Hence the location of the peak will be mainly affected by the diffusion coefficient and the radius of the particle. The model developed by Christensen et al.14 also shows similar results but the difference becomes prominent with time. In the case of PID, the magnitude of both the stresses becomes extreme and then decreases but in the end the stress profiles flattens out (marked by circles in Fig. 1 and 2) due to the incorporation of variable partial molar volume. In the case when PID is ignored, stress values decrease slightly after attaining maxima (marked by crosses in Fig. 1 and 2).
While the difference between the predicted stress values becomes prominent with time, the initial development of stress profiles is similar in all the cases. Also, the time at which peak stress occurs does not vary too much between all the models. In the following optimization study, we have used two variants of the model developed by Zhang et al.19 to derive at the optimal charging profile. The first variant includes pressure-induced diffusion and the second version does not. In our opinion, this captures both the worst case and the best case. In addition, the moving boundary model involves index-2 Differential Algebraic Equations (DAE) and is computationally challenging to use for optimization. An efficient reformulation was recently published by De et al.26
3 Model description
The detailed description and derivation of the model equations were given by Zhang et al.19 The final equations are summarized here. The mole fraction is governed by a single partial differential equation that is decoupled from the stress equations,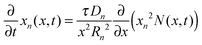 | (1) |
is the dimensionless flux. The description of parameters, their values and units are given in Table 1. The boundary conditions are
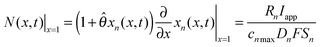 | (2) |
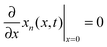 | (3) |
| xn(x, 0) = 0.0078 | (4) |
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) to 0. Radial stress (σr(x, t)), tangential stresses (σt(x, t)), and hydrostatic stress (σh(x, t)) are given by
to 0. Radial stress (σr(x, t)), tangential stresses (σt(x, t)), and hydrostatic stress (σh(x, t)) are given by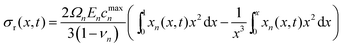 | (5) |
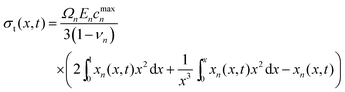 | (6) |
| σh(x, t) = ⅓(σr(x, t) + 2σt(x, t)) | (7) |
Radial stress at the surface of the particle is equal to the external pressure, which is assumed to be zero. From eqn (5) it is clear that maximum radial stress will occur at the center while charging, so a bound on the stress at the center can ensure the bounds hold at all the points in the particle. A similar logic can be extended to eqn (6) so that stress at the surface of the particle will be considered for bounds on the tangential stress. From Fig. 1 and 2 it is clear that stress development occurs at very short times, which poses a very interesting challenge since most of the reformulation and global polynomial approximations performed to make the simulation faster are not accurate at very short times.24,27 Initially while the battery is at rest, the concentration profile in the particle is flat. This kind of behavior is difficult to capture with lower order polynomials. Hence in this work, no solid-phase reformulation is performed to carry out the optimization. The finite difference method is applied to discretize the governing partial differential equation along the radius of the particle x. A fourth-order accurate O(h4) finite difference scheme was implemented at the internal node points with second-order finite difference schemes at the boundaries. Maximum percentage relative error for 40 and 60 node points compared to 100 node points in spatial dimension was found to be 1.4% and 0.6% at t = 0, this error goes to the order of 0.001 very fast (before the stress hits the maxima). 40 internal node points were used to discretize in the spatial dimension. In the finite difference form, the index i goes from 1 to N + 2:
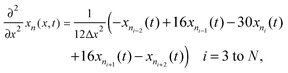 | (8) |
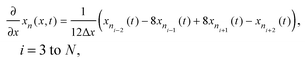 | (9) |
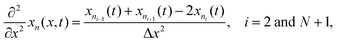 | (10) |
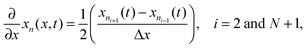 | (11) |
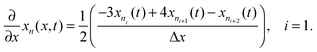 | (12) |
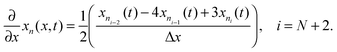 | (13) |
After discretization in x, the resultant set of equations was discretized using the third-order Euler backward difference formula (BDF) in time. A total of 100 node points in time were used with a fixed final time of 1 hour. The complete discretization resulted in a system of [(2 boundary conditions + 40 equations for internal node points) + (1 equation for average mole fraction + 1 equation for radial stress at the center + 1 equation for tangential stress at the surface)] × 100 (node points in time) = 4500 algebraic equations.
4 Problem formulation
The maximization of charge transferred is equivalent to maximization of the average mole fraction (Q) in a limited time with voltage, surface mole fraction, and stress constraints considered with a single-particle model. Numerous methods are available for solving constrained dynamic optimization problems, including (i) variational calculus, (ii) Pontryagin's maximum principle, (iii) control vector iteration, (iv) control vector parameterization, and (v) simultaneous nonlinear programming.28–30 Control vector parameterization (CVP) and simultaneous nonlinear programming are commonly used strategies that employ nonlinear programming (NLP) solvers. This paper uses the simultaneous nonlinear programming approach. The optimal control problem under consideration is: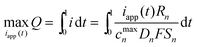 | (14) |
Constraints:
| 0 ≤ iapp (t) ≤ 2 C | (15) |
| 0 ≤ xn (1, t) ≤ 0.6 | (16) |
| σr (x, t) ≤ σmaxr | (17) |
| σt (x, t) ≤ σmaxt | (18) |
The discretized form of this problem statement takes the form
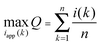 | (19) |
| Fk(z(k +1), z(k), y(k), iapp(k)) = 0 | (20) |
| Gk(z(k), y(k), iapp(k)) = 0 | (21) |
and bounds:
| imin ≤ iapp(k) ≤ imax, |
| ymin ≤ y(k) ≤ ymax, |
| zmin ≤ z(k) ≤ zmax | (22) |
In simultaneous nonlinear programming,28–30 both the control variables and state variables are discretized, which results in a large set of nonlinear equations to be solved simultaneously for obtaining the optimum profile. The resultant system had 4600 variables (4500 states variables with 100 control variables) and hence 100 degrees of freedom. The nonlinear system of 4500 equations was solved using the nonlinear programming (NLP) solver IPOPT31 with constraints on the control variables (2 C rate), mole fraction (0.6), radial stress at the center, and tangential stress at the surface.
5 Code dissemination
An executable code based on 40 internal node points in r with first order backward difference in time with 100 node points is hosted at the authors' website.32 This code can be downloaded and run in any WINDOWS based computer. The instructions and supplementary files required are provided along with the code. This code takes the parameters in Table 1 as input and provides optimal charging profiles as the output. In particular, the code creates the output of (1) charging profiles, (2) radial stress at the center of the particle, (3) tangential stress at the surface of the particle, (4) surface concentration and (5) average concentration. While this paper presents results for graphite, the same code can be used for any intercalation material (silicon, germanium, lithium cobalt oxide, etc.) by just changing the parameters. In addition, the effect of changing radius, diffusion coefficient, and mechanical properties for the same material can also be visualized by simulating this code. This code also provides an option to change the constraint on the maximum stress allowed. The yield stress varies among different materials. By changing the maximum stress allowed, one can use this code to identify the compromise made in the charge stored for a given material and design parameters.It is important to note that the model does not address volume expansion, thermodynamic effect, state of charge dependent diffusivities, non-uniform current distribution in porous electrodes. This code should be viewed as a first release, and future versions will address the inclusion of more detailed phenomena and optimal profiles based on the same.
6 Results and discussion
Case 1: charging for one hour
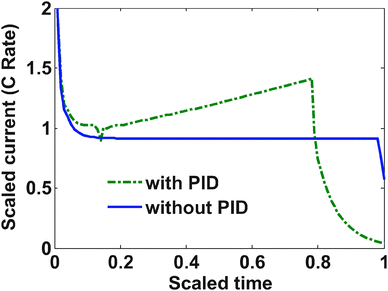
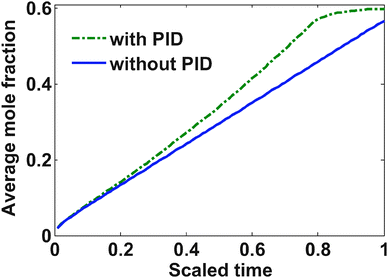
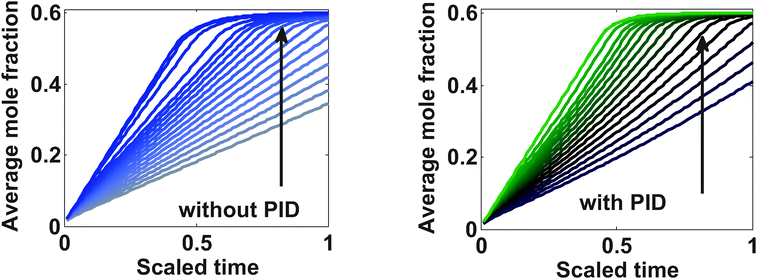
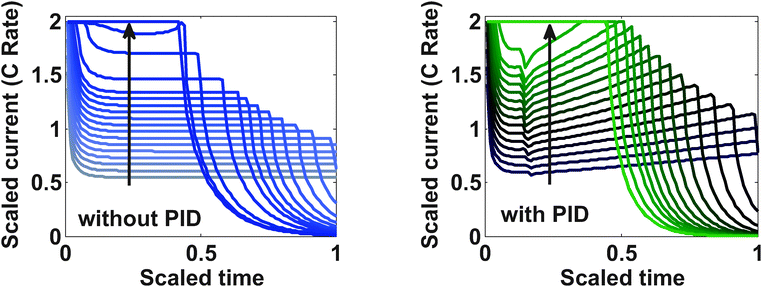
The yield stress for LiC6 is 30 MPa; however, a slightly more relaxed bound on the stress (37.5 MPa) was placed with maximum allowable current of 2 C (3.312 A in this case). Below are the results from the optimization study.The charging profile starts at the maximum allowable C rate. Very soon the tangential stress hits its upper bound, and from that point onwards, the charging current starts to decrease (see Fig. 3). In the case of regular diffusion (with no PID), the current takes a value around 1 C which ensures proper bounds on the stress. In the case of PID, the value of the current ramps up slowly until the surface mole fraction reaches the value of 0.6 (see Fig. 3). This behavior is observed since pressure-induced diffusion helps the particle relax during intercalation and optimized charging profile utilizes this phenomenon to enable an aggressive storage policy. In both the cases, as soon as the surface mole fraction reaches the value of 0.6 (the upper bound of mole fraction at the surface of the particle), the current starts decreasing to make sure this bound is not violated. This part is similar to constant voltage charging.
In the case of pressure-induced diffusion during intercalation, the optimized current profile takes advantage of the relaxation of the profiles inside the particle and can enable more charge to be stored. Fig. 4 shows that the average concentration stored in the particle at the end of charging is more when PID is taken into account in the optimization.
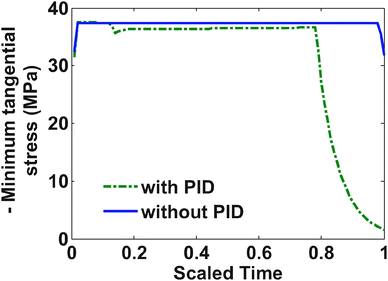
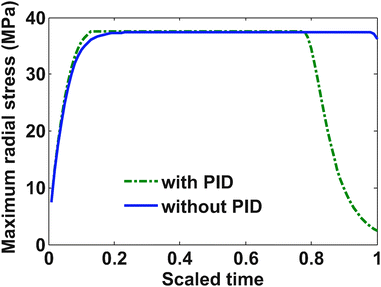
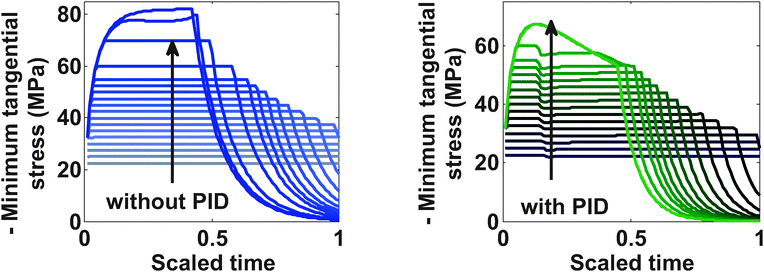
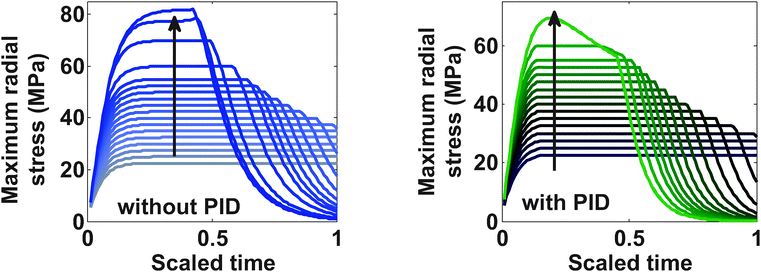
Fig. 5 shows profiles for the tangential stresses. From Fig. 5 it is clear that tangential stress hits its maximum sooner than the radial stress. Hence it will act first as an active constraint. It can be noted that the maximum tangential stress is negative (compressive stress) at the surface of the particle. Fig. 6 shows the radial stress profiles at the center (which in the case of charging is the maximum radial stress). The notch in the current profile in Fig. 3 after which it starts to ramp up is attributed to the radial stress bounds becoming active at that time (see Fig. 6).
Table 2 shows the computational matrix for both cases, with the objective function being the average mole fraction that has the maximum value of 0.6. Since the problem without PID is a linear problem, the time taken to solve that is lesser compared to the case with PID.
| Without PID | With PID | |
|---|---|---|
| Final time (tf) | 1 h | 1 h |
| Objective value (average mole fraction) | 5.65782 | 0.59833 |
| Total CPU sec in IPOPT (w/o function evaluations) | 8.560 | 11.698 |
| Total CPU sec in NLP function evaluations | 0.021 | 0.083 |
| IPOPT tolerance | 1 × 10−7 | 1 × 10−7 |
Case 2: charging for one hour with varying bounds on the maximum stress
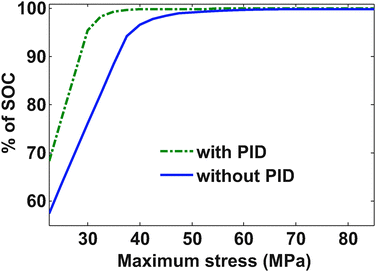
The optimum profile for an unconstrained charge maximization problem mimics the traditionally used constant current followed by constant voltage (CC–CV), (though the value of constant current is optimized and not 1 C). The addition of stress-based constraints will limit the charge stored in a given period of time compared to the CC–CV. The rate of increase of SOC decreases in the later part of the CC–CV profile (while maintaining constant voltage) and that is when the optimized profile can compensate for the charge not stored due to the constraints. In this study, we have enforced the constraints on the radial and tangential stresses while optimizing for charge stored in a given time. Depending on the value of the permitted peak stress the optimal charging profile changes. As the stress constraints are relaxed, the SOC stored gets closer to the SOC stored during the CC–CV protocol. To obtain a Pareto efficiency curve between peak stress and SOC stored, the peak stress allowed was varied from 22.5 MPa to 85 MPa.Fig. 7 shows the Pareto efficiency profile, which indicates that an optimum charging profile can significantly reduce the stress generation with very little or no compromise on the amount of charge stored. For the case in which pressure-induced diffusion is incorporated, the compromise in SOC stored is even smaller. Since the model that we have considered represents the most conservative (without PID) and most aggressive (with PID) cases, all of the Pareto efficiency curves derived by using different models should lie between the two Pareto efficiency curves obtained. Table 3 shows values of the objective function (average mole fraction at the end of one hour) with corresponding values of bounds on the stress in both cases. From the table, it is clear that if we strictly follow the 30 MPa stress limit (which is the yield stress for a carbon-based electrode), the optimized profile can only give up to 0.456 average mole fraction (0.573 for the PID model).
| Sr. no. | Bounds on stress | Without PID | With PID |
|---|---|---|---|
| 1 | 22.5 | 0.344316 | 0.409451 |
| 2 | 25.0 | 0.381707 | 0.462722 |
| 3 | 27.5 | 0.419097 | 0.517975 |
| 4 | 30.0 | 0.456486 | 0.573022 |
| 5 | 32.5 | 0.493878 | 0.590486 |
| 6 | 35.0 | 0.530926 | 0.595931 |
| 7 | 37.5 | 0.565492 | 0.598041 |
| 8 | 40.0 | 0.580106 | 0.598962 |
| 9 | 42.5 | 0.587358 | 0.599406 |
| 10 | 45.0 | 0.591480 | 0.599635 |
| 11 | 47.5 | 0.593965 | 0.599763 |
| 12 | 50.0 | 0.595556 | 0.599839 |
| 13 | 52.5 | 0.596630 | 0.599886 |
| 14 | 55.0 | 0.597362 | 0.599916 |
| 15 | 60.0 | 0.598267 | 0.599947 |
| 16 | 70.0 | 0.599061 | 0.599965 |
| 17 | 80.0 | 0.599310 | 0.599964 |
| 18 | 85.0 | 0.599388 | 0.599964 |
Relaxing this constraint to 40 MPa gives much better results (more that 99% of the maximum possible SOC for PID and more than 96.6% for without PID). If the constraints on the radial and tangential stress are relaxed then the gain in the objective function is marginal whereas the stress values grow significantly.
In this paper, the same constraints on both stresses are used. The bounds on radial and tangential stress need not be the same in general. In addition, limits on the two stresses may not be the same for practical applications. The maximum radial stress at the center of the particle is tensile and the minimum tangential stress at the surface is compressive while charging. If any external compressive stresses are present at the surface of the particle (stress during packing of material), the radial stress profile will shift lower by the same amount.
Fig. 8 shows the average mole fraction at the end of charging with different values of maximum allowable stress. The arrow indicates the direction of the relaxed bounds. Conventionally used experimental charging profiles can be viewed as an optimal profile for the problem with unbounded values for the stress limits, which roughly corresponds to the topmost curve in which the average concentration reaches closest to 0.6 in one hour.
The optimal profile with constraints performed in this simulation suggests that, for more than 99% of the SOC in one hour, the 6th and 12th curves from the bottom in the case of PID and without PID, respectively, are well suited. These curves correspond to 35 MPa (with PID) and 50 MPa (without PID) peak stress development in both cases.
Fig. 9 represents the optimized charging profiles for both cases. As the bounds are relaxed, the optimized charging current takes the shape of constant current followed by a constant voltage profile (CC–CV) for both models. The optimized charging profile for the model with PID shows an interesting trend where the current values drop from the 2 C rate and then again reaches the 2 C rate. As explained earlier, the positive slope of the charging current is proportional to the pressure-induced diffusion effect. Fig. 11 shows the minimum tangential and maximum radial stress profiles for both cases. The dynamics of the minimum tangential stress and maximum radial stress will determine the active stress constraints with time. When PID is included, the tangential stress hits its extremum before the radial stress but the extremum attained by the radial stress has a higher magnitude than for the tangential stress (see Fig. 10). When PID is not modeled, the tangential and radial stresses reach the same maximum magnitude but the tangential stress reaches the extremum faster.
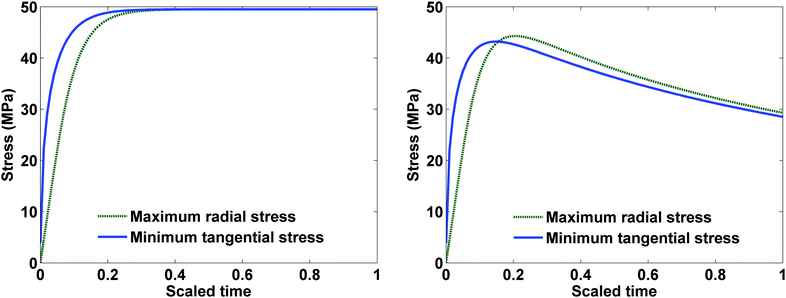 | ||
| Fig. 10 Maximum radial and negative of minimum tangential stress in both cases with a constant charging current of 1 C. | ||
In the case of PID, it is clear from Fig. 10 that tangential stress acts as an active constraint initially (until the dimensionless time goes to about 0.15, perfectly flat tangential stress values are observed in Fig. 11) and later the radial stress governs the maximum possible value of the current (the flat portion of the stress in Fig. 12 after the dimensionless time of about 0.15). In the case without PID, the tangential stress acts as an active constraint for the entire time of charging (Fig. 11).
From the above analysis, it is clear that pressure-induced diffusion helps relax the particle during intercalation. This effect can be exploited to achieve higher SOC during a fixed time.
Most of the existing charging profiles (e.g. CC–CV) depend completely on the experimentally measurable variables (e.g. voltage) which make their implementation simple. The optimal charging profiles derived from dynamic optimization schemes depend on the internal states and other model parameters. Hence implementation of these charging protocols requires state estimation algorithms to be used for predicting these internal states. Future work includes developing semi-empirical laws based on observed states to mimic optimal profiles obtained through offline optimization or developing model predictive control schemes.33–35
7 Conclusion and future directions
The stress–strain effect (mechanical fracture) is a dominant mechanism in capacity fade, in particular for new high capacity materials like germanium and silicon. The need to have safe and smarter use of batteries requires us to incorporate capacity fade mechanisms so that appropriate charging strategies can be devised that can reduce capacity fade. Various models developed to quantify the effect of capacity fade due to mechanical stress–strain effects were reviewed. Two models were chosen that represent the extremes of the stress effect in this particular case. The most conservative (with PID) and most aggressive stress profiles (without PID) lead to different charging protocols and different Pareto efficiency curves. Since the chosen models represent the extremes of the available stress models, the Pareto efficiency curve derived by other models should lie between them. The optimal charging profile was derived for varying the limit of the peak allowable stress generated in the particle. It was found that the optimal charging profiles in both cases were able to reduce the stress developed significantly with very little compromise on the charge stored. The compromise on the charge stored was lesser in the case when PID was modeled. The CPU time reported in this study also suggests that real-time control schemes can be developed that utilize sensors for pressure and strain measurement to arrive at improved charging schemes.The results reported in this paper are based on a single particle model for mechanical-electrochemical behavior without volume expansion. The codes provided herewith solve the specific model discussed. However, the method of deriving optimal profiles based on robust optimization approaches that can handle nonlinear state and path constraints can be used to satisfy any relevant objective (e.g. minimizing capacity fade, efficient utilization of electrode) given a physically meaningful model that can quantify those effects.
For example, possible extensions of the proposed approach include
1. SOC dependent diffusion coefficient: Use of diffusion coefficient varying with SOC has been reported in the literature36 which suggests around 2 orders of magnitude change with change in SOC. The model addressed here solves nonlinear spherical diffusion and hence can adapt to this change very easily. When the diffusion coefficient exhibits strong dependency on SOC, an additional number of node points or more efficient algorithms for spatial discretization may be needed.23
2. Volume expansion: to address significant volume expansion, SPM should be modified to accommodate moving boundaries. Such systems after spatial discretization result in an index-2 DAE system. Special numerical schemes are being studied to simulate these models efficiently.26
3. Porous electrode: SPM needs to be integrated with a pseudo 2D model in order to model the porous electrode and obtain the non-uniform current distribution and reaction rate.37 This will then enable us to accommodate other capacity fade mechanisms (e.g. side reaction).
4. The changing properties (degradation) of the battery material with time make the electrode more vulnerable to mechanical failure. Use of degradation as an internal state which can be propagated in time will help improve the accuracy in predicting the health of a battery.
Inclusion of different physical mechanisms to get close to real systems requires more advances in modeling, simulation and optimization. Many researchers are pursuing dynamic optimization frameworks to derive smart operating protocols.5–9 Continued research in fundamental understanding of underlying physics (e.g. fracture, capacity fade, hot spot formation), with parallel efforts in efficient simulation and reformulation of these detailed models will help define and solve a more realistic optimization problem to guide the way for model based designs for the next generation of energy storage devices.38 Note that providing a robust software framework that can work for detailed nonlinear models is very difficult. This paper should be viewed as a first step towards the same.
Acknowledgements
The authors are thankful for the financial support from the United States Government, Advanced Research Projects Agency – Energy (ARPA-E), U.S. Department of Energy, under award number DE-AR0000275, and McDonnell International Scholar Academy at Washington University in St. Louis.References
- C. Daniel, JOM, 2008, 60, 43–48 CrossRef CAS.
- S. M. Lukic, J. Cao, R. C. Bansal, F. Rodriguez and A. Emadi, IEEE Trans. Ind. Electron. Control Instrum., 2008, 55, 2258–2267 CrossRef.
- V. Pop, H. J. Bergveld, D. Danilov, P. P. L. Regtien and P. H. L. Notten, Battery Management Systems: Accurate State-of-Charge Indication for Battery Powered Applications, Springer, Dordrecht, 2008 Search PubMed.
- Advanced Management and Protection of Energy Storage Devices, http://arpa-e.energy.gov/?q=arpa-e-programs/amped, accessed June 13, 2013.
- R. Methekar, V. Ramadesigan, R. D. Braatz and V. R. Subramanian, ECS Trans., 2010, 25, 139–146 CrossRef CAS PubMed.
- R. Klein, N. A. Chaturvedi, J. Christensen, J. Ahmed, R. Findeisen and A. Kojic, Optimal charging strategies in lithium-ion battery, 2011 Search PubMed.
- S. K. Rahimian, S. C. Rayman and R. E. White, J. Electrochem. Soc., 2010, 157, A1302–A1308 CrossRef CAS PubMed.
- A. Hoke, A. Brissette, D. Maksimovic, A. Pratt and K. Smith, Electric vehicle charge optimization including effects of lithium-ion battery degradation, 2011 Search PubMed.
- B. Suthar, V. Ramadesigan, P. W. C. Northrop, B. Gopaluni, S. Santhanagopalan, R. D. Braatz and V. R. Subramanian, Optimal control and state estimation of lithium-ion batteries using reformulated models, American Control Conference (ACC), 17–19 June, 2013, pp. 5350–5355 Search PubMed.
- P. W. C. Northrop, V. Ramadesigan, S. De and V. R. Subramanian, J. Electrochem. Soc., 2011, 158, A1461–A1477 CrossRef CAS PubMed.
- J. Christensen and J. Newman, J. Electrochem. Soc., 2006, 153, A1019–A1030 CrossRef CAS PubMed.
- C. R. Yang, Y. Y. Wang and C. C. Wan, J. Power Sources, 1998, 72, 66–70 CrossRef CAS.
- P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553 CrossRef CAS PubMed.
- J. Christensen and J. Newman, J. Solid State Electrochem., 2006, 10, 293–319 CrossRef CAS PubMed.
- R. Deshpande, M. Verbrugge, Y.-T. Cheng, J. Wang and P. Liu, J. Electrochem. Soc., 2012, 159, A1730–A1738 CrossRef CAS PubMed.
- P. Arora, R. E. White and M. Doyle, J. Electrochem. Soc., 1998, 145, 3647–3667 CrossRef CAS PubMed.
- J. Christensen, J. Electrochem. Soc., 2010, 157, A366–A380 CrossRef CAS PubMed.
- Y.-T. Cheng and M. W. Verbrugge, J. Power Sources, 2009, 190, 453–460 CrossRef CAS PubMed.
- X. Zhang, W. Shyy and A. Marie Sastry, J. Electrochem. Soc., 2007, 154, A910–A916 CrossRef CAS PubMed.
- S. Renganathan, G. Sikha, S. Santhanagopalan and R. E. White, J. Electrochem. Soc., 2010, 157, A155–A163 CrossRef CAS PubMed.
- S. Timoshenko, Theory of elasticity, section 107, McGraw Hill Book Company, New York, 1934 Search PubMed.
- G. Ning and B. N. Popov, J. Electrochem. Soc., 2004, 151, A1584–A1591 CrossRef CAS PubMed.
- Y. Zeng, P. Albertus, R. Klein, N. Chaturvedi, A. Kojic, M. Z. Bazant and J. Christensen, J. Electrochem. Soc., 2013, 160, A1565–A1571 CrossRef CAS PubMed.
- V. Ramadesigan, V. Boovaragavan, J. C. Pirkle and V. R. Subramanian, J. Electrochem. Soc., 2010, 157, A854–A860 CrossRef CAS PubMed.
- J. C. Forman, S. Bashash, J. L. Stein and H. K. Fathy, J. Electrochem. Soc., 2011, 158, A93–A101 CrossRef CAS PubMed.
- S. De, B. Suthar, D. Rife, G. Sikha and V. R. Subramanian, J. Electrochem. Soc., 2013, 160, A1675–A1683 CrossRef CAS PubMed.
- K. Smith and C. Y. Wang, J. Power Sources, 2006, 161, 628–639 CrossRef CAS PubMed.
- L. T. Biegler, Chemical Engineering and Processing: Process Intensification, 2007, 46, 1043–1053 CrossRef CAS PubMed.
- S. Kameswaran and L. T. Biegler, Comput. Chem. Eng., 2006, 30, 1560–1575 CrossRef CAS PubMed.
- M. D. Canon, C. D. Cullum, Jr. and E. Polak, Theory of Optimal Control and Mathematical Programming, McGraw-Hill, New York, 1970 Search PubMed.
- A. Wächter and L. T. Biegler, Math. Program., 2006, 106, 25–57 CrossRef.
- M.A.P.L.E. Website, http://www.maple.eece.wustl.edu/, accessed June, 2013.
- V. M. Zavala and L. T. Biegler, Comput. Chem. Eng., 2009, 33, 1735–1746 CrossRef CAS PubMed.
- D. Q. Mayne, J. B. Rawlings, C. V. Rao and P. O. M. Scokaert, Automatica, 2000, 36, 789–814 CrossRef.
- M. Morari and J. H. Lee, Comput. Chem. Eng., 1999, 23, 667–682 CrossRef CAS.
- S.-L. Wu, W. Zhang, X. Song, A. K. Shukla, G. Liu, V. Battaglia and V. Srinivasan, J. Electrochem. Soc., 2012, 159, A438–A444 CrossRef CAS PubMed.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1 CrossRef CAS PubMed.
- V. Ramadesigan, P. W. C. Northrop, S. De, S. Santhanagopalan, R. D. Braatz and V. R. Subramanian, J. Electrochem. Soc., 2012, 159, R31–R45 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2014 |