Reaction selectivity in an ionized water dimer: nonadiabatic ab initio dynamics simulations

Abstract

We study dynamical processes following water dimer ionization. The nonadiabatic dynamical simulations of the water dimer radical cation are performed using a surface hopping technique and a Complete Active Space – Self Consistent Field (CASSCF) method for the description of electronic structure. The main goal of this study is to find out whether a state-dependent reactivity is observed for the water dimer radical cation. We provide a detailed mapping of the potential energy surfaces (PESs) in the relevant coordinates for different electronic states. Dynamical patterns are discussed on the basis of static PES cuts and available experimental data. As a product of the reaction, we observed either proton transferred structure (H₃O⁺⋯OH˙) or various dissociated structures (H₃O⁺ + OH˙, H₂O˙⁺ + H₂O, H˙ + OH˙ + H₂O˙⁺). The relative yields are controlled by the populated electronic state of the radical cation. The proton transfer upon the HOMO electron ionization is an ultrafast process, taking less than 100 fs, in cases of higher energy ionization the dynamical processes occur on longer timescales (200–300 fs). We also discuss the implications of our simulations for the efficiency of the recently identified intermolecular coulomb decay (ICD) process in the water dimer.

---

1. Introduction

Light energy radiation initiates a plethora of chemical processes in water.^1,2 At low photon energies, the dominant process is water photodissociation,³ leading to the formation of OH˙ and hydrogen radicals:

H₂O → OH˙ + H˙.

The OH˙ radical is involved in subsequent oxidizing processes and the hydrogen radical can further react with water:

H˙ + H₂O → H₃O⁺ + (e⁻)_solv

with a hydronium cation and a solvated electron being the reaction products.⁴ Alternatively, molecular hydrogen H₂ can be formed.

Ionization of water

H₂O → H₂O˙⁺ + e⁻

in the bulk appears above ∼10 eV.⁵ The ejected electron can relax in bulk water, forming the solvated electron with a presolvated intermediate.^6–11 The water radical cation created during the ionization is an extremely reactive particle which immediately transfers protons to neighboring water molecules:¹

H₂O˙⁺ + H₂O → H₃O⁺ + OH˙.

The final products of the ionization process are thus the same as for the photodissociation process. At even higher energies, new reaction channels are opened, e.g. ionizing the inner valence electrons in water leads to the subsequent autoionization process identified as Intermolecular Coulomb Decay (ICD).^12,13

The processes described above are important in various fields of science and technology. The generation of H₂ upon water irradiation is important in the context of nuclear safety,^1,14 doubly charged complexes can explain the tissue damage by γ radiation and the products of water ionization are highly relevant in the context of indirect oxidative and reductive damage of nucleic acids.^15–17 Understanding water radiation chemistry is a necessary prerequisite for radiotherapeutic applications and radiation protection.¹⁸

Electronic structure of the gas phase water was investigated via photoelectron spectroscopy already in 1970s. Since then it is known that photoionization of an isolated water molecule starts at ∼12 eV and becomes the predominant channel at ∼20 eV.³ The photoionization spectrum of a water molecule consists of four peaks located approximately at 12.6, 14.8, 18.6 and 32.6 eV.¹⁹ These ionization peaks correspond to the ejection of electrons from 1b₁, 3a₁, 1b₂ and 2a₁ molecular orbitals (MO). Later, ionization of water clusters and liquid water drew much attention of both experimentalists^12,20–28 and theoreticians.^20,29–31 The structure of the photoelectron spectrum remains the same in liquid water but the whole spectrum shifts by more than 1 eV (ref. 5) to lower energies due to the long range polarization and the width of the spectrum increases due to the inhomogeneous broadening.

Much less is known on the dynamics following the water photoionization.¹ Numerous kinetic studies using a pulse radiolysis technique have focused on the reactivity of the primary radiation products. The primary photodynamics is, however, still only partially understood. It is generally accepted that the ionization is followed by ultrafast proton transfer. Gauduel et al. reported a lifetime of H₂O˙⁺ less than 100 fs in the bulk water.³² Yet recently Bradforth et al. have argued that the signal observed in this experiment does not correspond to the H₂O˙⁺ intermediate as the photon energy of the pump pulse (8 eV) is too low to generate the H₂O˙⁺ radical cation. They set the upper limit of the H₂O˙⁺ lifetime to 40 fs.³³ This conclusion is in accord with the ab initio molecular dynamics simulations using self-interaction corrected BLYP³³ or the Hartree–Fock (HF) level of theory to describe the electronic structure.²⁹ Despite this progress, the primary events following the photoionization of bulk water remain to be great challenge for experiment.

Experiments on molecular clusters represent an attractive way how to circumvent some of the problems. The reaction does not have to be investigated directly in time as the energy information on the outgoing fragments bears information about the dynamical processes following the ionization. The proton transfer reaction leading to H₃O⁺ and OH˙ has been demonstrated for water dimers in photoelectron–photoion coincidence experiments (PEPICO);³⁴ the non-protonated (H₂O)₂˙⁺ species was shown to be only a minor product. The structure of the (H₂O)₂˙⁺ species has been directly characterized using IR spectroscopy for argon-tagged (H₂O)₂˙⁺.³⁵ The experimental vibrational spectrum proves only the appearance of the proton transferred structure H₃O⁺⋯OH˙ and rules out the hydrazine-like structure [H₂O⋯OH₂]˙⁺. Likewise proton transfer products have been found using infrared spectroscopy for larger clusters.^36,37 Recently another experiment on argon–water clusters proved the possibility of nonprotonized cation generation within threshold ionization.³⁸ The electron impact ionization of the water dimer leads on the other hand to the formation of protonated water H₃O⁺ and non-protonated water H₂O˙⁺.³⁹

The water dimer radical cation has recently been extensively studied by means of quantum chemical and molecular dynamics methods.^35,40–46 The dynamical picture emerging from these studies suggests that the proton transfer reaction starts with a decrease in the distance between H₂O˙⁺ and H₂O units, followed by the proton transfer.⁴⁴ The reaction could in principle be traced by transient spectroscopy.⁴⁴ The majority of the theoretical studies focus on the ground state potential energy surface (D₀) of the ionized system. The major reason for this choice is technical; inclusion of all the relevant electronic states is prohibitively expensive for larger water clusters. The water dimer, on the other hand, is small enough to enable such a detailed study. Quantum dynamical calculations in reduced space of Kamarchik et al.⁴⁴ and ab initio dynamical calculation of Tachikawa⁴³ both suggest that the dynamics starting from two lowest electronic states of water dimer radical cations substantially differs. Furthermore Tachikawa suggests that different final products (the proton transferred (H₃O⁺⋯OH˙) and the hydrazine-like one (H₂O⋯OH₂)˙⁺) arise depending on the initial electronic state. The non-adiabatic effects are, however, neglected in these studies.

The question whether the dynamics following the photoionization of the water dimer is controlled by the initially populated electronic state is the central issue raised here. Is the ionization photodynamics the same, irrespective of whether the electron is ejected from the hydrogen bond donor or the acceptor, from the water lone pair or from the σ bond MO? How fast is the electronic population transferred to the ground electronic state? Does the photodynamics follow the adiabatic or the diabatic route? The water dimer is ideally suited for addressing these questions because it can be described using high-level multi-reference based electronic structure theory which is needed in order to capture non-adiabatic effects and multi-radical species formed. Still, we have to keep in mind that the two distinct units represent two extremes of hydrogen-bonding.

The processes investigated in this work involve multiple electronic states and highly dimensional systems. It is therefore imperative to use approaches that enable both the description of the nuclear motion upon the sudden ionization and of the transfer of electronic population between different electronic states. This can be achieved via various schemes, such as the surface hopping (SH) algorithm of Tully⁴⁷ or the Full Multiple Spawning method of Martínez and Ben-Nun.^48,49 In the past we have already applied the methods of ab initio non-adiabatic dynamics in the context of aqueous photochemistry and radiation chemistry, using the Full Multiple Spawning scheme.⁵⁰ Here we combine the fewest switches surface hopping method with the Complete Active Space – Self Consistent Field (CASSCF) level of electronic structure description. The surface hopping scheme was used for its simplicity and efficient treatment of a large number of highly coupled electronic states. In our recent paper, we showed that quantum effects significantly influence the absorption and photoelectron spectra of small water clusters.^31,51 Therefore, we use here the path integral molecular dynamics (PIMD) sampling scheme for the simulation of initial conditions of the system. We further perform a detailed mapping of the potential energy surfaces (PES) in the relevant coordinates for different electronic states of the ionized water dimer in the valence electron manifold, and we rationalize the observed dynamical patterns. Quantities which can be accessed experimentally are also discussed.

2. Methods

In the following paragraphs, we shortly review the basics of the surface hopping scheme and describe the details of our simulation setup. Then we discuss the generation of initial conditions and we end by the description of electronic structure methods.

2.1 Dynamical methods

The surface hopping (SH, see reviews in ref. 52 and 53) is a semiclassical trajectory based algorithm. The molecule is considered to exist in several electronic states at the same time with distinct state probabilities, yet the nuclear positions evolve classically on a single PES. The stochastic switching from one electronic state to another guarantees proper distribution among different electronic states. Here, we only briefly summarize the basics of the method and its implementation in this work.

The nuclear wavefunction is expanded into an electronic basis:

where r and R represent the vectors of electronic and nuclear coordinates, respectively. The time-dependent Schrödinger equation is integrated (in the adiabatic representation) along the classical path according to the following equation:where E_k is the potential energy of state k, F_kj(R(t)) = 〈ϕ_k(R)|∂/∂R|ϕ_j(R)〉 is the nonadiabatic coupling vector and v(t) is the vector of nuclear velocities. The stochastic hops in the SH method can be guided by various prescriptions; here we have used the fewest switches approach by Tully⁴⁷ in which the hopping probabilities are calculated as:where Δt is the integration timestep. We also applied the empirical decoherence correction as proposed by Truhlar et al.^54,55 and applied for SH methods according to Granucci and Persico.⁵⁶

All simulations have been performed using in-house molecular dynamics software coupled with the MOLPRO 2010.1 simulation package.⁵⁷ Each simulation has been run for 650 fs and an ensemble of 100 trajectories has been used for the inspection of each initial electronic state. Classical Newton equations have been integrated with 0.15 fs timestep using a velocity Verlet integrator. For numerical stability, eqn (2) has been integrated with a 100 000 times smaller time step. The hopping probability has been evaluated at each such substep. The non-adiabatic coupling vectors have been linearly interpolated between integration points. A simple Euler method has been used for the integration of the time-dependent Schrödinger equation.

2.2 Initial conditions

As we describe the system within the semiclassical framework, the dynamics is controlled by a set of initial conditions specifying initial nuclear wavefunction or more generally initial nuclear density. The mapping of the quantum mechanical density on the phase space is in general difficult. Typically, Wigner transformation within the harmonic approximation is done. However, the water dimer has many soft vibrational modes, for which the harmonic approximation is inadequate. Therefore, we follow a different route, using the nuclear density calculated within the Path Integral Molecular Dynamics (PIMD) method. Earlier we have shown that the PIMD based scheme describes well both the photon absorption and photoionization of systems in both harmonic and anharmonic modes.^31,51,58

Initial geometries were sampled from the PIMD simulation using 30 beads. We used the massive Nosé–Hoover chains thermostatting scheme⁵⁹ to maintain the temperature at 180 K. The simulation details are explained in ref. 31 and 51. Since the particle momenta are completely arbitrary in the PIMD scheme, we chose to set the initial velocities to zero. While this approximation will affect the initial dynamics, the final results should not be affected considering the 650 fs length of our trajectories.

2.3 Electronic structure

The major computational bottleneck of the on the fly dynamics is the evaluation of energies, forces and non-adiabatic couplings at the ab initio level. Since we need to run a sufficient number of trajectories for a relatively long time, the application of highly accurate methods such as multi-reference configuration interaction (MRCI) is impractical. On the other hand, the simulation outcome critically depends on the quality of the PES. Moreover, since the studied processes involve PES crossing and may include bond breaking, the use of single-reference methods is questionable. We decided to use the CASSCF method as a compromise between accuracy and computational efficiency. The quality of the CASSCF wavefunction was justified by benchmarking against the MRCI method with the same active space using PES scans along relevant reaction coordinates. We use the 6-31++g** basis set in all electronic structure calculations.

The active space used was mostly constructed in such a way that the electronic states considered were restricted to single-photon ionizations. Therefore we designed the active space only from the orbitals that are doubly occupied in the ground state of the radical cation and one single occupied molecular orbital (SOMO). Such a choice of active space (7 electrons in 4 orbitals using state averaging over 4 states) is stable and efficient, enabling large scale simulations. This minimalistic approach can be safely used for ionization following ejection of 1b₁ (HOMO and HOMO − 1) and 3a₁ electrons (HOMO − 2 and HOMO − 3) while to account for the dynamics following the 1b₂ (HOMO − 4 and HOMO − 5) electron ejection we have to include larger active space with more virtual orbitals as the “two-photon” states are coupled with the originally populated single-photon states. For these states, we have used an active space consisting of 11 electrons in 7 orbitals, using state averaging over 8 states.

3. Results and discussion

3.1 Stationary points on the neutral and radical cation water dimer PES

All our calculations are done for the simplest water complex, the water dimer. Fig. 1 shows geometrical parameters which were found to be important during the photoionization dynamics, in particular, the OO distance, the hydrogen bonding O–H distance, the rotational angle φ and the HOH angle α. The OO distance in its ground state optimal geometry is 2.94 Å, the HOH angle α is 105.5° (donor) and 105.7° (acceptor), the O–H bonds are in the range of 0.96–0.97 Å (optimized at the CCSD/6-31++g** level, see ESI† for xyz coordinates of all relevant structures). In the ground electronic state, water molecules have doubly occupied 1b₁, 3a₁ and 1b₂ orbitals and there observed only a very small charge transfer between the water units. Upon the ionization the electronic structure radically changes and the above structure does not represent a stationary point any more. We have found two local minima on the water dimer radical cation ground state PES. The global minimum is the proton-transferred (H₃O⁺⋯OH˙, PT structure) structure while the second minimum of a hydrazine-like arrangement (HL structure, (H₂O⋯OH₂)˙⁺, see Fig. 2) is higher in energy. This finding is consistent with previous studies.^40,41,45,60

Fig. 1 Geometry of the water dimer. Geometrical parameters used in further discussion are shown.

Fig. 2 Two ground state minimum structures of the water dimer radical cation. The optimal geometries were obtained using the MRCI(11,6)/6-31++g** method.

The relative stability of the two structures critically depends on the electronic structure level used (see Table 1). The PT structure is clearly more stable for the wave function based single-reference methods. The Hartree–Fock method predicts the PT structure to be more stable by 1.18 eV with respect to the HL structure. The results obtained using single-reference methods should, however, be taken with caution as the proton transfer structure is doubly degenerate (due to the presence of the OH˙ radical). Furthermore we show (see results for BLYP functional) that for some DFT methods the relative stability can be reversed which led in the past to incorrect predictions.^46,61–63 The relative stability of the isomers upon including static correlation within the CASSCF method varies significantly with the active space used.

Table 1 The relative stability of the two ground state structure and the transition state (TS) related to the proton transferred (PT) structure. All three structures were optimized at the MRCI(11,6)/6-31++g** level

Method/6-31++g**	ΔE (HL − PT)/eV	ΔE (TS − PT)/eV
HF	1.18	1.02
MP2	0.30	0.83
CCSD	0.42	0.74
CCSD(T)	0.35	0.70
BLYP	−0.33	−0.05
BHandHLYP	0.40	0.76
SA4-CASSCF(7,4)	0.99	1.32
SA8-CASSCF(11,7)	0.77	1.19
SA4-CASPT2(7,4)	0.16	0.55
SA8-CASPT2(11,7)	0.27	0.57
SA4-MRCI(7,4)	0.46	0.84
SA6-MRCI(11,6)	0.20	0.64
SA8-MRCI(11,7)	0.41	0.81

---

The Complete Active Space Perturbation Theory (CASPT2) method also does not provide unequivocal answer on the relative stability. On average, the CASPT2 results predict the HL structure to be destabilized by ∼0.22 eV, less than the prediction of the MP2 method. The MRCI approach provides a compromise stabilization of ∼0.36 eV. Furthermore we calculated also energies of the transition state between PT and HL structures. The energetic difference between the transition state and PT structure is relatively insensitive with respect to the choice of method (higher by ∼0.6–0.8 eV) with the exception of HF and CASSCF methods where the PT structure is over-stabilized. The quantitative variations between different methods however do not change the overall topography of the potential energy surface. Our results are in reasonable agreement with previous studies on the stability of the two isomers.^41,60

3.2 Photoionization dynamics

The most important information on the photoionization events was obtained within the non-adiabatic molecular dynamics simulations. We consider water dimer photodynamics triggered by ionization from the 1b₁ lone pair, and 3a₁ and 1b₂ bonding orbitals. In each case, the photoionization dynamics is different for the electron hole formed in the donor or the acceptor water unit, i.e. we consider six distinct electronic states. In the following sections we discuss separately photodynamics initiated by electron ejection from each molecular orbital considered, always inspecting the donor and the acceptor sites together. The discussion begins with non-adiabatic dynamics simulations which are subsequently analyzed in terms of low-dimensional scans through the potential energy surfaces. The parameters of the Franck–Condon point for all states considered are summarized in Table 2 showing that while in the neutral ground state minimum the charge is mostly localized on a single molecule, for an ensemble of trajectories the situation gets more complicated. Furthermore for some distorted geometries the donor and acceptor states can be switched, e.g. 3a₁ ionization leading to the HOMO − 2 state does not have to represent a donor ionization.

Table 2 The electron distribution in the water dimer. Ionization energies and Mulliken charges on the donor moiety were calculated in the neutral water dimer minimum optimized at the SA8-MRCI(11,7)/6-31++g** level. Ionization energies are calculated as a difference between energies of neutral (at SA1-MRCI(8,6)/6-31++g**) and ionized states. The quantities in the parentheses are the values averaged over 100 initial geometries

Orbital	Moiety	Ionization energy (eV)	Mulliken charge on the donor
a Delocalization artificially augmented due to the switching of donor and acceptor states.
1b1	Donor	11.1 (11.25 ± 0.34)	0.93 (0.94 ± 0.05)
	Acceptor	12.6 (12.40 ± 0.25)	0.18 (0.22 ± 0.23^a)
3a1	Donor	13.4 (13.47 ± 0.48)	0.72 (0.67 ± 0.24^a)
	Acceptor	15.1 (14.91 ± 0.46)	0.13 (0.18 ± 0.16^a)
1b2	Donor	17.7 (17.57 ± 0.57)	0.86 (0.73 ± 0.17^a)
	Acceptor	19.6 (18.91 ± 0.52)	0.35 (0.36 ± 0.30^a)

---

3.2.1 Photoionization dynamics upon the 1b₁ electron ejection. The removal of an electron from HOMO and HOMO − 1 orbitals corresponds to the ionization from the 1b₁ orbitals of the donor and acceptor water units, respectively. The positive hole in the ground ionized state (D₀) is almost completely localized (average Mulliken charge on the donor unit is 0.94e, as calculated at the SA8-MRCI(11,7)/6-31++g** level for the whole initial set of geometries) while in the second ionized state (D₁) the hole is partially delocalized (average charge on the donor unit is 0.22e). However, the initial charge distribution depends on the actual geometry. Similar conclusions based on the EOM-IP-CCSD methodology are drawn in ref. 64. Fig. 3 shows the results of the dynamical simulations, from perspectives of structural rearrangement, electronic population transfer and electron hole migration. The proton transfer in the D₀ state
occurs almost immediately; it starts at 5 fs, with a sharp build-up of the H₃O⁺⋯OH˙ population and is essentially completed in 100 fs.

Fig. 3 Photodynamics of the water dimer upon electron removal from the 1b₁ orbital in the D₀ and D₁ electronic states (left and right part, respectively). Populations of electronic states are shown in the uppermost box; the central boxes show the fraction of dissociated or proton transferred structures; charge localization is shown in the lower boxes. Calculated at the SA4-CASSCF(7,4) level. The relevant discussion is provided in Section 3.2.1.

Our observation is in agreement with the studies of Kamarchik et al.⁴⁴ and Tachikawa et al.⁶⁵ According to our simulations, the PT structure (H₃O⁺⋯OH˙) is always formed. In more than half of the cases we also observed the subsequent dissociation of the PT complex into OH˙ and H₃O⁺ fragments (we consider structures with OO distance bigger than 5 Å as the dissociated ones). The dissociation starts at ∼100 fs and is finished by the time of 250 fs.

The ionization dynamics in the D₁ state is more complex. Although the proton transfer process also takes place, it is much slower, being completed in 250 fs, and the process is much more gradual. The dissociation into fragments is likely to continue even beyond 600 fs. The fragmentation is larger than for the ionization occurring on the D₀ state as there is higher excess energy available. Our full-dimensional non-adiabatic calculations confirm previous suggestion of Kamarchik et al. on much slower proton transfer dynamics for the D₁ state.⁴⁴ On the other hand our results are different from those of Tachikawa et al. who found two distinct non-proton transferred type complexes.⁶⁵ In the final state with a transferred proton, the first two electronic states are degenerate (corresponding to the two ²Π states of the OH˙ radical). As a result, the final population is split between the two states on average 1 : 1, irrespective of the initially populated state. Fig. 3 shows also the evolution of the charge distribution of the trajectories. In the D₀ state the electron is ejected from the donor moiety. The subsequent repolarization of the system demonstrates that the proton transfer takes place. The situation is more delicate in the D₁ state. The CASSCF method used in our simulations predicts the initial charge on the donor molecule of 0.38e (CASSCF estimate being higher than the MRCI value in Table 2). Nevertheless, we assign the state as a positively charged acceptor unit solvated with a neutral hydrogen bond donor molecule. The subsequent dynamical process could then be described as hydrogen atom transfer.

The dynamical calculations helped us single out the leading reaction coordinates during the photoionization process. In the case of ionization into the D₀ state, we observed a very fast proton transfer process. This indicates a direct barrierless process. The most probable mechanism would be an elongation of the O–H bond until the hydrogen gets trapped by the other oxygen atom. Such a direct process without any adjustment of the oxygen atom positions is, however, accompanied by a small, yet noticeable barrier (0.35 eV, see Fig. 4). Indeed, the dynamical calculations suggest that the process starts with a change in the OO distance. The two-dimensional scan shown in Fig. 4 confirms the suggested mechanism. First the OO distance gets shorter, and only once a heavy atom cage is conveniently arranged the proton is transferred.

Fig. 4 2D potential energy surface scan along O–H and OO distances for D₀ and D₁ states. Calculated at the SA6-MRCI(11,6)/6-31++g** level. The steepest descent path is shown for the D₀ state. For the D₁ state, the potential energy surface is flat in the Franck–Condon region. Energies (in eV) are shown relative to the ionic ground state. The question mark represents another possible pathway on the potential energy surface.

Fig. 4 also shows the difference in the topology of the PES for the electronic states with the positive hole on the donor (D₀) or the acceptor (D₁) unit. The proton transfer reaction is in the Franck–Condon region strongly driven by an intense gradient in the D₀ state while the D₁ state is relatively flat in that area. There is yet another coordinate controlling the dynamics in the D₁ state, the angle α of the donor unit (see Fig. 5). According to our calculations the proton transfer proceeds in three steps. First the angle α grows from 105° to almost 180° i.e. the donor molecule linearizes. One would expect that (according to Walsh's rules) the potential energy surface in water upon the ionization of the 1b₁ electron should be flat. This is indeed the case for geometries near the Franck–Condon point. At larger α angles, however, the avoided crossing between the D₁ state (with the 1b₁ electron of the acceptor unit ionized) and the D₂ state (with the 3a₁ electron of the donor unit ionized) leads to switching of these two states. This is consistent with a steep energy decrease along the α angle of the donor unit. At the same time, the OO distance slightly decreases from 2.9 Å to roughly 2.7 Å. Finally the proton (or in this case more likely the hydrogen atom) jumps to the other molecular unit. This mechanism is markedly different from the mechanism taking place in the D₀ state and leads thus to longer dynamics for the proton transfer. Here the driving force is the actual transfer of the H atom, not the shortening of the OO distance (which changes only little). It ought to be mentioned at this point that the low-dimensional PES cuts can sometimes be misleading. Fig. 5 correctly predicts the linearization of the molecule as a start of the process. Yet rapid shortening of the OO distance, once the donor molecule is linear, is also suggested. And while the decrease of the OO distance seems more probable, the role of the OO coordinate is overestimated in such representation (hydrogen being lighter and more mobile).

Fig. 5 2D potential energy surface scan (D₀ and D₁ states) along the α angle and the OO distance. Calculated at the SA6-MRCI(11,6)/6-31++g** level.

3.2.2 Photoionization dynamics upon the 3a₁ electron ejection. The 3a₁ electron has a binding energy of ∼14 eV. The HOMO − 2 state (D₂) has delocalized character, with average Mulliken charge on the donor moiety of 0.67e while the ionization of the HOMO − 3 electron leads to a charge localization on the acceptor water molecule (0.18e on the donor moiety). From our dynamical simulations (Fig. 6), we observe fast electronic relaxation into the ground state of the ion (degenerated in PT geometry with the first excited state) upon the ejection of HOMO − 2 and HOMO − 3 electrons. For the D₂ state, the lifetime of the excited state before relaxation to either the D₀ or the D₁ state takes ∼10 fs, while for the D₃ state, the electronic relaxation takes ∼18 fs. The ejection of an electron from the 3a₁ orbital does not necessarily lead to the PT structure:

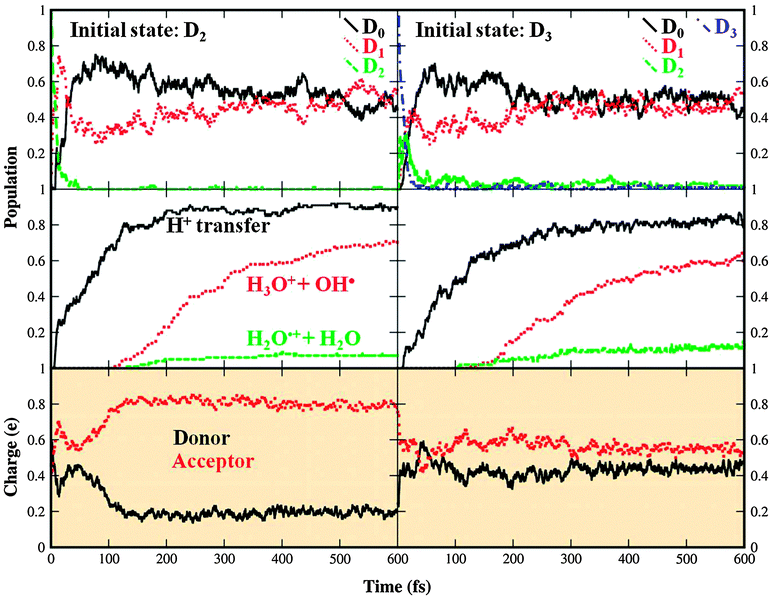Fig. 6 Photodynamics of the water dimer upon electron removal from the 3a₁ orbital in the D₂ and D₃ electronic state (left and right part, respectively). Populations of electronic states are shown in the uppermost box; the central boxes show the fraction of dissociated or proton transferred structures; charge localization is shown in the lower boxes. Calculated at the SA4-CASSCF(7,4) level. The relevant discussion is provided in Section 3.2.2.

The PT structure remains the prevailing reaction product, with the yield of 90 and 80% for the HOMO − 2 and HOMO − 3 states, respectively (see Table 4). Again we could see that in the case of the donor moiety ionization, the proton transfer reaction is faster (completed within 200 fs) than for the acceptor one (completed within 300 fs). The reaction is however in both cases slower than the reaction following 1b₁ electron ionization. The dissociation into the H₃O⁺ and OH˙ fragments starts in both cases after 100 fs and is likely to continue beyond the time of our simulations. The rest of the population is dissociated into H₂O˙⁺ and H₂O units. Again we found that no population stays in the form of undissociated HL structure.

Fig. 6 shows also time evolution of the charge distributions for the D₂ and D₃ states. The initially delocalized charge in the D₂ state quickly localizes on the acceptor moiety. In the D₃ state, the electron is initially ejected from the acceptor molecule. In this case, however, the initial state status completely loses its importance, i.e. we clearly see the charge localization, yet we are unable to state whether the charge is localized on the acceptor or donor unit.

Guided by the dynamical simulations we suggest the following mechanism after the ejection of the electron from the 3a₁ MO of the donor molecule (D₂ state). Direct proton transfer is not possible because of the large energetic barrier in the D₂ state. Geometrically, we observe at the beginning a partial increase in the angle α followed by the rotation of the donor molecule. Within this process, we reach a conical intersection between D₁ and D₂ states. This is a typically almost immediate process completed within 15 fs. The subsequent evolution is schematically shown in Fig. 7. The wave packet can split and different routes (heading either towards the PT structure or to HL structure) can be followed.

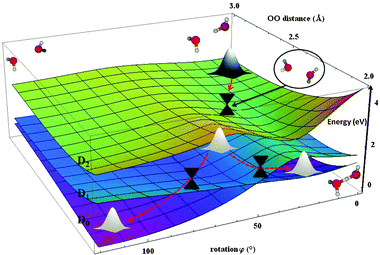Fig. 7 2D PES scan for D₀, D₁ and D₂ electronic states along OO distance and rotation angle φ. Calculated at the SA6-MRCI(11,6)/6-31++g** level. Energies (in eV) are shown relative to the ionic ground state.

The photoionization dynamics in the D₃ state is rather similar. First the hydrogen bond is broken and the HOH angles of both donor and acceptor units grow to reach conical intersections with the lower state. Once the molecule relaxes into the D₁ or D₀ states, the proton or hydrogen transfer may occur. If the proton transfer takes place on the PES of the D₁ state, the process is typically driven by O–H elongation. If, on the other hand, the molecule first relaxes to the ground ionized state, the process is controlled by the decreasing OO distance. Small part of population dissociates into H₂O˙⁺ and H₂O fragments.

3.2.3 Photoionization dynamics upon the 1b₂ electron ejection. The 1b₂ electron can be ionized with more energetic photons above ∼18 eV. The localization/delocalization of the electron hole depends strongly on a particular geometry (see Table 2). In the minimum structure the charge is strongly localized on the donor molecule for the HOMO − 4 (D₄) state and partially delocalized on the acceptor molecule for the HOMO − 5 (D₅) state.

The states formed upon the 1b₂ electron ejection are energetically close to the states of tri-radical character. Therefore we have to extend the active space with an extra virtual orbital to fully account for the description of such states. For the dynamical simulations we are using an active space SA8-CASSCF(11,7). We could observe that the leading coordinates for both electronic states upon the 1b₂ electron ejection are the proton transfer coordinate (O–H⋯O coordinate) and the free (non-hydrogen bonded) O–H coordinate. However, the mechanisms depend on the particular initial geometry. If the tri-radical states are within energetic reach, then we can expect an ultrafast free O–H dissociation (time scale less than 10 fs):

If the tri-radical states are too high in energy, hydrogen transfer or dissociation into H₂O˙⁺ and H₂O can be observed (and takes more than 30 fs).

In our molecular dynamical simulations, we have observed both the proton transfer and the free O–H dissociation. The O–H dissociation is, however, the dominant process. Note that the simulations with the extended active space were rather unstable. Although we could identify the reaction products, we were unable to run the simulations for the entire simulation time of 650 fs (see Table 4 for a tentative quantitative assignment).

To get better idea about interactions with tri-radical electronic states, Fig. 8 shows the potential energy surface along the free O–H bond and the proton transfer coordinate. The 1b₂ (donor) state is the 5th state in the ground state geometry, the 1b₂ (acceptor) state is the 7th state, almost degenerate with a state of tri-radical character. It is clearly seen that the primary process following the electron ejection from the 1b₂ (acceptor) state is the dissociation of the free O–H bond in the acceptor molecule. Such a process is observed already for ionization of isolated water molecules,³⁴ forming OH˙⁺ and H˙ atoms. For the water dimer, however, the situation is different. The population analysis demonstrates that the dissociative products are H˙ + HO˙ + H₂O˙⁺ (see also Table 3 for appearance energies of various dissociative species). Note that if the H₂O˙⁺ radical was formed in larger clusters, the radical would immediately react with a neighboring water molecule forming another OH˙ radical and H₃O⁺ cation. The ionization of the 1b₂ electron thus leads to the formation of three radicals and one electron. Such reactions are therefore highly relevant in the context of water radiation chemistry. Experimentally, the dominant reaction channel for the water dimer photoionization is the proton transfer, forming H₃O⁺ and OH˙ fragments. Even the structures with a nominal formula (H₂O)₂˙⁺ are found to represent proton transfer structures of the H₃O⁺⋯OH˙ type.^35,36

Fig. 8 2D PES scan along free O–H dissociation (OH diss) and proton transfer (OH trans) coordinates for D₀–D₆ electronic states (see text). Calculated at the SA11-MRCI(11,8)/6-31++g** level based on DW-SA20-CASSCF(11,8). The weights for the different states were adapted dynamically⁶⁶ with β parameter set to 3 eV. Energies (in eV) are shown relative to the ionic ground state.

Table 3 Appearance energies of various final states upon (H₂O)₂ ionization. Calculated at the CCSD(T)/aug-cc-pVTZ level

Species	Appearance energy (eV)
(H2O)2	0
H3O^+ + OH˙	11.7
H2O˙^+ + H2O	12.8
OH˙ + H2O˙^+ + H˙	18.2
OH^+ + H2O + H˙	18.5
OH˙ + H2O + H^+	19.2

---

3.2.4 Implications for the efficiency of the ICD process. Our simulations have focused on the ionization from the 1b₁, 3a₁ and 1b₂ orbitals. Upon the ionization from these orbitals, the autoionization (leading to a doubly charged system) is not energetically possible. The nuclear dynamics and non-adiabatic processes thus represent an exclusive mean of energy relaxation. Upon the ionization of the inner valence electron (2a₁), on the other hand, the electron autoionization leading to a doubly charged dimer is energetically open, providing that the two charges reside on different water units. Such a non-local autoionization (Auger) process is called Intermolecular Coulomb Decay (ICD). The process was first proposed theoretically by Cederbaum et al.⁶⁷ and later identified in neon⁶⁸ and water clusters.^12,13 We do not directly investigate this reaction channel in the present work, yet our calculations might provide insight into its efficiency.

Let's concentrate on the primary product of the ICD process, water radical cation H₂O˙⁺. This species is formed via different routes upon the ionization: (i) by a dissociation of hydrazine like structure upon the 3a₁ electron; this channel was shown to be only a minor in our simulation, (ii) within the tri-radical mechanism upon 1b₂ electron ejection; here, the H₂O˙⁺ is a major reaction channel as we have shown above, (iii) within the Intermolecular Coulomb Decay (ICD) process, i.e. via the autoionization process

The electron impact ionization measurements with 70 eV electrons³⁹ have shown that the H₂O˙⁺ radical cation is formed within a yield of 37.5% (the rest is H₃O⁺, note that the experiments were actually performed with the D₂O dimer). With these high energy electrons, the electrons from all valence orbitals are ejected. It follows from the experiment of Jahnke et al.¹² that 100% of the autoionization events result from the ICD process, however, the efficiency of the ICD process in the water dimer is not known. That is, we do not know the fraction of the water dimers with the ionized 2a₁ electron which is deactivated via the internal conversion process without further ionization. Answering this question is important for estimating the yields of a highly damaging H₂O˙⁺ radical.⁶⁹ The results of our simulations together with the electron impact measurements of Buck and Winter³⁹ could provide a hint regarding the efficiency of the ICD process. Unfortunately, we could not find the probabilities of ionization for different electrons in the water dimer by the 70 eV electron. At this point, we can only make a rough estimate based on the assumption that all valence electrons are ionized by the 70 eV electron with equal probability. Since the ionization of the 1b₂ electron leads dominantly to the H₂O˙⁺ cation, the 1b₂ reaction channel should be responsible for 25% yield of the H₂O˙⁺ cation. The ICD process should thus be responsible for remaining 10–20% in the H₂O˙⁺ yield. As two water cations are produced per single ICD step, we can estimate the efficiency of the ICD process to be in the range of 20–40%. Notice again that this is only a tentative conclusion based on the assumption of the equal ionization probabilities.

The ICD process is 100% efficient in the neon dimer (isoelectronic with water).⁶⁸ In water, however, fast nuclear dynamics can take place. The ultrafast proton transfer has been observed upon 1a₁ ionization.^70–73 Our preliminary calculations indicate that this channel is also open upon the 2a₁ electron ionization. The system can then efficiently loose potential energy, closing thus the autoionization channel.

4. Conclusions and outlook

We have simulated photoionization dynamics following the ejection of an electron from outer valence orbitals of the water dimer. Our major goal was to answer the question whether ionization from different molecular orbitals leads to different reaction products, i.e. whether the photoionization reaction takes place diabatically or the reaction proceeds adiabatically upon a fast relaxation into the ground electronic state. The non-adiabatic ab initio dynamical simulation based on the surface hopping method combined with SA4-CASSCF(7,4) (and SA8-CASSCF(11,7)) description of electronic structure has identified reaction paths for the reaction triggered by the ionization of each electron (see Fig. 9 and Table 4). These paths were then investigated using quantum-chemical methods.

Fig. 9 Reaction mechanisms following water dimer ionization. In the case of 3a₁ and 1b₂ ionizations we use the notation donor/acceptor unit ionization. The sum of the branching ratios is not always equal to unity because in some cases the final outcome of the reaction has not been clear by the end of the simulation.

Table 4 Products of water dimer ionization for different initial electronic states. Reaction yields were obtained by averaging of 100 trajectories and calculated using the SA4-CASSCF(7,4) level for 1b₁ and 3a₁ electrons. For the 1b₂ ionization, 50 independent trajectories calculated at the SA8-CASSCF(11,7) level were averaged

Orbital	Moiety	Proton/hydrogen transfer (%)	Dissociation to^a (%):
			H3O^+⋯OH˙	H2O˙^+⋯H2O	H2O˙^+⋯OH˙⋯H˙
a Tentative assignment due to numerical instability of the simulation.
1b1	Donor	100	55	0	0
	Acceptor	100	72	0	0
3a1	Donor	90	70	7	0
	Acceptor	80	62	12	0
1b2	Donor	30	(20)^a	(24)^a	56
	Acceptor	8	(8)^a	(8)^a	84

---

Our findings can be summarized as follows:

1. Fast charge localization and proton transfer complex formation characterize the photoionization dynamics upon the ionization of 1b₁ and 3a₁ electrons both in the donor and in the acceptor molecular units.

2. Hydrazine-like structure represents a minor transient species upon the ejection of the 3a₁ electron, with H₂O˙⁺ and H₂O as the final dissociative products.

3. The ionization of the 1b₂ electron leads to a formation of tri-radical species, corresponding ultimately to OH˙, H˙ and H₂O˙⁺ final products.

4. Ionization from higher electronic states of the ions is characterized by fast (typically 10–50 fs) internal conversion relaxation into the first two ionic states. The dynamics thus takes place primarily adiabatically on the ground state of the water dimer. The reaction outcome is however controlled by the redistribution of the energy among different vibrational modes in the first 100 fs.

5. Based on the analysis of our results and available experimental data, we tentatively conclude that the efficiency of intermolecular coulomb decay in the water dimer is less than unity.

Fig. 9 presents the summary of our simulations showing the fraction of population with proton/hydrogen transfer or dissociative final states. The mechanism for the photoionization dynamics for the different states considered in this study is also sketched in Fig. 9. The results of our calculations are in agreement with existing experiments, demonstrating a dominant role of proton transfer^33,35,36,74 upon low energy ionization and opening new reaction channels when lower-lying electrons are ionized.³⁹ The fact that the proton or hydrogen transfer is a much slower process for the ionization of HOMO − 1 electrons compared to HOMO electrons could also assist the experiment in direct observation of the PT process using femtosecond transient absorption methods. While the 40 fs timescale predicted for the ground ionized state is too short for current laser technologies, the sub-ps dynamics observed in our simulations is well within their reach.

We have demonstrated that the technology of non-adiabatic simulations could be used to model primary events in water radiation chemistry. The current knowledge of the processes initiated by ionizing radiation in water is rather limited.¹ Typically, G-factors for different reactions are provided⁷⁵ and the molecular details are not considered. Even the simulations for a small model dimer system presented in this work suggest significant differences in reactive species formed upon the photo- and radiolysis in water along increasing energy of the ionizing particles. While low energy radiation leads to a formation of a solvated electron and an oxidizing OH˙ radical, an ionizing 1b₂ electron already initiates formation of four radical species (solvated electrons, H, OH˙ and H₂O˙⁺ radicals or radical ions). As it is known that the majority of the biomolecular radiation damage stem from the radiation processes in water, the damage should significantly increase at about 18 eV. To gain more realistic picture of the post-ionization processes in liquid water, one would need to perform simulations for larger water clusters. It would be also interesting to extend present simulations to even higher photon energies. Then processes of the ICD type are open.⁷³

The simulations of the photoionization dynamics in the water dimer could be further augmented, e.g. by accounting for the quantum nature of the atomic nuclei. This might be important considering the role played by the vibrational redistribution events in our simulations. The water dimer represents a special case and is different from structures found in liquid water. Therefore, as a next step, we will investigate larger clusters either in their minimal geometries (cyclic structures up to the pentamer) or for geometries typically found in liquid water, using QM/MM schemes. It would be also desirable to extend our study to inner-valence ionization. In this case, however, the time reserved for the nuclear dynamics would be severely limited by the Auger processes.

Acknowledgements

The authors would like to thank Dr Dana Nachtigallová for stimulating discussions. The work was supported by grant no. 13-34168S by Grant Agency of the Czech Republic. Financial support for OS and DH from specific university research (MSMT No. 21/2013) is acknowledged. MO and OS are students of Max Planck international school “Dynamical Processes in Atoms, Molecules and Solids”.

Notes and references

1. B. C. Garrett, D. A. Dixon, D. M. Camaioni, D. M. Chipman, M. A. Johnson, C. D. Jonah, G. A. Kimmel, J. H. Miller, T. N. Rescigno, P. J. Rossky, S. S. Xantheas, S. D. Colson, A. H. Laufer, D. Ray, P. F. Barbara, D. M. Bartels, K. H. Becker, H. Bowen, S. E. Bradforth, I. Carmichael, J. V. Coe, L. R. Corrales, J. P. Cowin, M. Dupuis, K. B. Eisenthal, J. A. Franz, M. S. Gutowski, K. D. Jordan, B. D. Kay, J. A. LaVerne, S. V. Lymar, T. E. Madey, C. W. McCurdy, D. Meisel, S. Mukamel, A. R. Nilsson, T. M. Orlando, N. G. Petrik, S. M. Pimblott, J. R. Rustad, G. K. Schenter, S. J. Singer, A. Tokmakoff, L. S. Wang, C. Wittig and T. S. Zwier, Chem. Rev., 2005, 105, 355–389.
2. A. Mozumder and Y. Hatano, Charged Particle and Photon Interactions with Matter: Chemical, Physicochemical, and Biological Consequences with Applications, CRC Press, 2003.
3. K. H. Tan, C. E. Brion, P. E. Van der Leeuw and M. J. Van der Wiel, Chem. Phys., 1978, 29, 299–309.
4. M. Ončák, P. Slavíček, V. Poterya, M. Fárník and U. Buck, J. Phys. Chem. A, 2008, 112, 5344–5353.
5. B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. V. Hertel, J. Phys. Chem. A, 2004, 108, 2625–2632.
6. A. Migus, Y. Gauduel, J. L. Martin and A. Antonetti, Phys. Rev. Lett., 1987, 58, 1559–1562.
7. B. Abel, U. Buck, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2012, 14, 22–34.
8. K. R. Siefermann, Y. X. Liu, E. Lugovoy, O. Link, M. Faubel, U. Buck, B. Winter and B. Abel, Nat. Chem., 2010, 2, 274–279.
9. O. Marsalek, F. Uhlig, J. Vandevondele and P. Jungwirth, Acc. Chem. Res., 2012, 45, 23–32.
10. R. M. Forck, I. Dauster, Y. Schieweck, T. Zeuch, U. Buck, M. Ončák and P. Slavíček, J. Chem. Phys., 2010, 132, 221102.
11. E. Alizadeh and L. Sanche, Chem. Rev., 2012, 112, 5578–5602.
12. T. Jahnke, H. Sann, T. Havermeier, K. Kreidi, C. Stuck, M. Meckel, M. Schoffler, N. Neumann, R. Wallauer, S. Voss, A. Czasch, O. Jagutzki, A. Malakzadeh, F. Afaneh, T. Weber, H. Schmidt-Bocking and R. Dorner, Nat. Phys., 2010, 6, 139–142.
13. M. Mucke, M. Braune, S. Barth, M. Forstel, T. Lischke, V. Ulrich, T. Arion, U. Becker, A. Bradshaw and U. Hergenhahn, Nat. Phys., 2010, 6, 143–146.
14. A. Mozumder, J. Phys. Chem. Lett., 2011, 2, 2994–2995.
15. S. G. Swarts, M. D. Sevilla, D. Becker, C. J. Tokar and K. T. Wheeler, Radiat. Res., 1992, 129, 333–344.
16. C. v. Sonntag, Free-Radical-Induced DNA Damage and Its Repair: A Chemical Perspective, Springer, Berlin, 2006.
17. X. Q. Guo, Q. L. Wang, B. M. Swarts and Z. W. Guo, J. Am. Chem. Soc., 2009, 131, 9878–9879.
18. M. G. Stabin, Radiation Protection and Dosimetry: An Introduction to Health Physics, Springer, 2007.
19. M. S. Banna, B. H. Mcquaide, R. Malutzki and V. Schmidt, J. Chem. Phys., 1986, 84, 4739–4744.
20. S. Barth, M. Ončák, V. Ulrich, M. Mucke, T. Lischke, P. Slavíček and U. Hergenhahn, J. Phys. Chem. A, 2009, 113, 13519–13527.
21. L. Belau, K. R. Wilson, S. R. Leone and M. Ahmed, J. Phys. Chem. A, 2007, 111, 10075–10083.
22. H. Shinohara, N. Nishi and N. Washida, J. Chem. Phys., 1986, 84, 5561–5567.
23. H. Shiromaru, H. Shinohara, N. Washida, H. S. Yoo and K. Kimura, Chem. Phys. Lett., 1987, 141, 7–11.
24. S. Tomoda, Y. Achiba and K. Kimurra, Chem. Phys. Lett., 1981, 87, 197–200.
25. O. Bjorneholm, F. Federmann, S. Kakar and T. Moller, J. Chem. Phys., 1999, 111, 546–550.
26. B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211.
27. S. Thürmer, R. Seidel, B. Winter, M. Ončák and P. Slavíček, J. Phys. Chem. A, 2011, 115, 6239–6249.
28. R. Seidel, S. Thürmer and B. Winter, J. Phys. Chem. Lett., 2011, 2, 633–641.
29. A. Furuhama, M. Dupuis and K. Hirao, J. Chem. Phys., 2006, 124, 164310.
30. I. B. Müller and L. S. Cederbaum, J. Chem. Phys., 2006, 125, 204305.
31. O. Svoboda, M. Ončák and P. Slavíček, J. Chem. Phys., 2011, 135, 154302.
32. Y. Gauduel, S. Pommeret, A. Migus and A. Antonetti, Chem. Phys., 1990, 149, 1–10.
33. O. Marsalek, C. G. Elles, P. A. Pieniazek, E. Pluhařová, J. VandeVondele, S. E. Bradforth and P. Jungwirth, J. Chem. Phys., 2011, 135, 224510.
34. K. Norwood, A. Ali and C. Y. Ng, J. Chem. Phys., 1991, 95, 8029–8037.
35. G. H. Gardenier, M. A. Johnson and A. B. McCoy, J. Phys. Chem. A, 2009, 113, 4772–4779.
36. K. Mizuse, J. L. Kuo and A. Fujii, Chem. Sci., 2011, 2, 868–876.
37. K. Mizuse and A. Fujii, J. Phys. Chem. A, 2012, 116, 4868–4877.
38. A. Golan and M. Ahmed, J. Phys. Chem. Lett., 2012, 3, 458–462.
39. U. Buck and M. Winter, ZPhys-e. D: At., Mol. Clusters, 1994, 31, 291–297.
40. P. A. Pieniazek, J. VandeVondele, P. Jungwirth, A. I. Krylov and S. E. Bradforth, J. Phys. Chem. A, 2008, 112, 6159–6170.
41. Q. Y. Cheng, F. A. Evangelista, A. C. Simmonett, Y. Yamaguchi and H. F. Schaefer, J. Phys. Chem. A, 2009, 113, 13779–13789.
42. A. Kumar, M. Kolaski, H. M. Lee and K. S. Kim, J. Phys. Chem. A, 2008, 112, 5502–5508.
43. H. Tachikawa, Phys. Chem. Chem. Phys., 2011, 13, 11206–11212.
44. E. Kamarchik, O. Kostko, J. M. Bowman, M. Ahmed and A. I. Krylov, J. Chem. Phys., 2010, 132, 194311.
45. E. Livshits, R. S. Granot and R. Baer, J. Phys. Chem. A, 2011, 115, 5735–5744.
46. P. R. Pan, Y. S. Lin, M. K. Tsai, J. L. Kuo and J. D. Chai, Phys. Chem. Chem. Phys., 2012, 14, 10705–10712.
47. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
48. M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 1998, 108, 7244–7257.
49. M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175.
50. M. Ončák, P. Slavíček, M. Fárník and U. Buck, J. Phys. Chem. A, 2011, 115, 6155–6168.
51. O. Svoboda, M. Ončák and P. Slavíček, J. Chem. Phys., 2011, 135, 154301.
52. K. Drukker, J. Comput. Phys., 1999, 153, 225–272.
53. M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633.
54. C. Y. Zhu, A. W. Jasper and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 527–540.
55. C. Y. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658–7670.
56. G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114.
57. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, v MOLPRO, a package of ab initio programs, see http://www.molpro.net.
58. M. Ončák, L. Šištík and P. Slavíček, J. Chem. Phys., 2010, 133, 174303.
59. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
60. H. M. Lee and K. S. Kim, J. Chem. Theory Comput., 2009, 5, 976–981.
61. R. N. Barnett and U. Landman, J. Phys. Chem. A, 1997, 101, 164–169.
62. R. N. Barnett and U. Landman, J. Phys. Chem., 1995, 99, 17305–17310.
63. M. Sodupe, J. Bertran, L. Rodriguez-Santiago and E. J. Baerends, J. Phys. Chem. A, 1999, 103, 166–170.
64. P. A. Pieniazek, E. J. Sundstrom, S. E. Bradforth and A. I. Krylov, J. Phys. Chem. A, 2009, 113, 4423–4429.
65. H. Tachikawa, A. Yabushita and M. Kawasaki, Phys. Chem. Chem. Phys., 2011, 13, 20745–20749.
66. M. P. Deskevich, D. J. Nesbitt and H. J. Werner, J. Chem. Phys., 2004, 120, 7281–7289.
67. L. S. Cederbaum, J. Zobeley and F. Tarantelli, Phys. Rev. Lett., 1997, 79, 4778–4781.
68. T. Jahnke, A. Czasch, M. S. Schoffler, S. Schossler, A. Knapp, M. Kasz, J. Titze, C. Wimmer, K. Kreidi, R. E. Grisenti, A. Staudte, O. Jagutzki, U. Hergenhahn, H. Schmidt-Bocking and R. Dorner, Phys. Rev. Lett., 2004, 93, 164301.
69. O. Vendrell, S. D. Stoychev and L. S. Cederbaum, ChemPhysChem, 2010, 11, 1006–1009.
70. M. Odelius, H. Ogasawara, D. Nordlund, O. Fuchs, L. Weinhardt, F. Maier, E. Umbach, C. Heske, Y. Zubavichus, M. Grunze, J. D. Denlinger, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2005, 94, 227401.
71. M. P. Ljungberg, A. Nilsson and L. G. M. Pettersson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 245115.
72. M. P. Ljungberg, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2011, 134, 044513.
73. S. Thürmer, M. Ončák, N. Ottosson, R. Seidel, U. Hergenhahn, S. E. Bradforth, P. Slavíček and B. Winter, Nat. Chem. DOI:10.1038/NCHEM.1680.
74. B. Ruscic, A. F. Wagner, L. B. Harding, R. L. Asher, D. Feller, D. A. Dixon, K. A. Peterson, Y. Song, X. M. Qian, C. Y. Ng, J. B. Liu and W. W. Chen, J. Phys. Chem. A, 2002, 106, 2727–2747.
75. S. M. Pimblott and J. A. LaVerne, Radiat. Res., 1998, 150, 159–169.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp51440d

---