Intramolecular halogen–halogen bonds?

Abstract

By analysing the properties of the electron density in the structurally simple perhalogenated ethanes, X₃C–CY₃ (X, Y = F, Cl), a previously overlooked non-covalent attraction between halogens attached to opposite carbon atoms is found. Quantum chemical calculations extrapolated towards the full solution of the Schrödinger equation reveal the complex nature of the interaction. When at least one of the halogens is a chlorine, the strength of the interaction is comparable to that of hydrogen bonds. Further analysis shows that the bond character is quite different from standard non-covalent halogen bonds and hydrogen bonds; no bond critical points are found between the halogens, and the σ-holes of the halogens are not utilised for bonding. Thus, the nature of the intramolecular halogen⋯halogen bonding studied here appears to be of an unusually strong van der Waals type.

---

Introduction

“The concept of the chemical bond is the most valuable concept in chemistry”, summarised Pauling in 1992.¹ Two decades have not diminished the truism of the conclusion. Our understanding and view of bonds have evolved since the early work by Lewis on two atoms sharing electron pairs.² Ever more exotic bonding situations are being continuously discovered. Via the realisation that two electrons can be shared by three atoms as in the prototypical H₃ cation³ and the boranes,⁴ up to ten-centre two-electron bonds have been proposed.⁵ The opposite of the latter, the two-centre ten-electron bond, that is, the long-sought quintuple bond, was finally tamed in 2005.⁶

The family of bonds involving “simple” carbon atoms has turned out to be much richer than perhaps initially suspected as well. The recently discussed charge-shift carbon–carbon bond found in propellane⁷ is just one of several examples of unorthodox bonding. Despite early theoretical suggestions that standard, four-coordinated carbon could actually prefer planarity,^8,9 it stubbornly remained near tetrahedral to the very end of the last century;¹⁰ the yet-more-curious planar penta-¹¹ and hexa-coordinate¹² carbons still await synthetic reality. Recent years have also witnessed the discovery of new types of weaker bonding interactions. Analogous to the classical hydrogen bonds, the importance of halogen bonds in, for example, crystals and biological systems, has been established.^13–19

Here, we step back from exotic molecules and analyse the bonds between the two CX₃ fragments in perhalogenated ethanes, C₂X₆. Despite their simple appearance, we find a previously overlooked, non-covalent halogen⋯halogen interaction of appreciable strength, when one of the halogens involved is chlorine.

Results and discussion

Homolytic CX₃–CX₃ bond dissociation energies

We begin by examining the homolytic CX₃–CX₃ bond dissociation energy for the different C₂X₆ species studied. The reference electronic energies have been computed by extrapolating the ab initio coupled cluster wave-function energies towards completeness (CC-cf),²⁰ that is, as exact a solution to the Schrödinger equation²¹ as possible. The errors of various other ab initio methods that treat the electron correlation problem in a more approximate manner, as well as density functional theory²² (DFT) methods are assessed, and subsequently used to evaluate the nature of the interaction between the CX₃ fragments.

DFT, while in principle simply a reformulation of wave-function theory and just as exact, suffers from the well-known fact that the form of the true functional is unknown. Thus, approximate functionals of varying degrees of complexity and accuracy are used in real-world applications. Traditional density functionals are known to perform very poorly for the perhalogenated hydrocarbons.^23,24 For this study, we have chosen three functionals, all of which are based on satisfying known properties of the unknown exact density functional. As they have not been parameterised or tuned towards any specific atomic or molecular systems, they can be expected to treat the different C₂X₆ species studied here on equal footing. We also employ the random phase approximation (RPA) in a post Kohn–Sham manner.²⁵ For the wave-function and RPA methods, energies have been computed with the extrapolated aug-cc-pV[T,Z] basis sets, for the DFT methods, the def2-QZVPPD basis set was used; energies have been corrected for basis set superposition error. A detailed description is presented in the Methods section. Table 1 summarises the energies.

Table 1 Reference CX₃–CX₃ bond dissociation electronic energies at the CC-cf level of theory, as well as the errors of more approximate levels of theory (unrelaxed dissociation energies in parentheses); negative relative energies indicate underestimation of the bond strength, energies in kJ mol⁻¹

	C2H6	C2F6	CF3CCl3	C2Cl6
a Using standard enthalpies of formation for CX3 and C2X6 from ref. 26.
CC-cf BDE	403.7 (480.9)	417.9 (425.1)	357.2 (386.1)	301.2 (366.6)
Ab initio
CCSD(T)	−1.9 (−1.9)	−1.1 (−1.0)	+3.8 (+4.2)	−2.0 (−1.3)
CCSD	−13.6 (−12.3)	−8.4 (−6.8)	−7.4 (−3.2)	−20.7 (−13.6)
MP2	+13.3 (+16.0)	+10.1 (+10.5)	+29.5 (+31.8)	+50.2 (+54.4)
DFT
PBE	+0.1 (−5.5)	−45.8 (−48.9)	−49.1 (−52.5)	−71.9 (−75.1)
RevTPSS0-D	−21.2 (−19.2)	−33.8 (−34.0)	−33.0 (−30.5)	−48.9 (−43.7)
LC-revTPSS-D	+5.9 (+11.9)	+0.6 (+2.6)	+4.2 (+19.1)	−11.9 (+17.8)
RPA	−4.0 (−10.0)	−17.3 (−19.3)	−8.9 (−13.7)	−13.2 (−21.1)
ΔH (298 K)
Exp.^a	377.3 ± 0.9	412.9 ± 7.6	—	290.4 ± 10.7
Computed	375.2	407.6	347.9	293.2

---

From Table 1, it is evident that the C₂X₆ species represent quite a challenge for theoretical methods. Of the ab initio wave-function methods, only CCSD(T) provides satisfactory energies. At the CCSD level, the interaction energy is underestimated, especially so for C₂Cl₆. At the MP2 level, the energy is severely overestimated; again, C₂Cl₆ is the most difficult case.

Of the density functionals, the non-empirical, generalised gradient approximation (GGA) functional PBE²⁷ performs well for ethane, but the halogenated ethanes are described poorly. revTPSS0-D is based on the non-empirical revTPSS functional, which belongs to the meta-generalised gradient approximation (meta-GGA) family.²⁸ In addition to the density and its gradient, the meta-GGAs also use information extracted from the orbital-dependent kinetic energy density. This added flexibility in the functional form allows for a more complete satisfaction of properties of the elusive true density functional, compared to GGA functionals. In revTPSS0, we have additionally exchanged 25% of the DFT exchange with “exact” Hartree–Fock exchange, as per physical reasoning.²⁹ Further, the meta-GGAs have been augmented by the dispersion energy correction by Grimme, DFT-D.³⁰ Even at the meta-GGA level, the description of long-range dispersion is inadequate at best. Dispersion is, however, an important part of the interaction between the CX₃ fragments. The DFT-D dispersion contribution to the CX₃–CX₃ unrelaxed interaction energy increases with heavier halogens, being −6.4, −11.9, −14.4, and −17.7 kJ mol⁻¹ for C₂H₆, C₂F₆, CF₃CCl₃, and C₂Cl₆, respectively. Even with the added ingredients, revTPSS0 is not sufficiently accurate for the halogenated ethanes; while the errors decrease, they are still too large for quantitative predictions and analysis.

The LC-revTPSS-D functional performs well. Instead of a constant portion of HF exchange, we apply a long-range correction (LC), which modifies the exchange-interaction between electrons by gradually replacing the pure DFT exchange functional by a Hartree–Fock (HF) description with increasing inter-electronic distance in order to achieve a physically correct asymptotic behaviour of the exchange potential.³¹ The new physics captured by the LC scheme is crucial, as evident by comparing to the still inadequate performance of the revTPSS0-D functional.

Even LC-revTPSS-D has limitations, though. Looking at the unrelaxed dissociation energies, where the atomic arrangements of the CX₃ radical fragments are not allowed to relax from their respective structures in the C₂X₆ molecules, the CCl₃ containing species are seen to be significantly overstabilised at the LC-revTPSS-D level. This overbinding can directly be traced to a poor description of the non-equilibrium structure of the CCl₃ radical: the energy difference between the optimal geometry and that of the C₂Cl₆-derived one is overestimated by 14.8 kJ mol⁻¹.

Long-range dispersion as described by the DFT-D correction is not the only missing ingredient in the DFT description of the interaction; the underbinding is significantly reduced, but not eliminated. This can also be seen from the inadequacy of the wave-function based methods, all of which natively do include dispersion effects. A possible reason for this would be that the intramolecular dispersion interaction in the ethanes is not very long-range, due to the small size of the molecule and the proximity of possibly interacting densities. The random phase approximation (RPA)²⁵ has been shown to capture medium-range non-covalent interactions very successfully in a purely non-empirical manner.³² Also here, RPA works quite well, although an underbinding can be noted for all species in Table 1. Importantly, however, the remaining error in RPA is rather consistent through the series, with the halogenated species treated on equal footing with pristine ethane. This shows that the missing, stabilising interaction between the CX₃ fragments is of complex electron-correlation nature, which is adequately captured only at CCSD(T), LC-revTPSS-D, and RPA levels of theory.

We finish the subsection with some technical notes. The good performance of CCSD(T) validates the use of the CC-cf extrapolation scheme; a large change would indicate that even higher orders of the coupled cluster series would be needed for convergence to the FCI limit.^20,33 Another litmus test for adequacy is the amount of multi-reference (MR) character of the systems studied. This can be evaluated using different diagnostics for the CCSD solution. The T₁ diagnostic proposed by Lee and Taylor³⁴ was for all species found to be below the threshold for trouble, 0.02, with the highest value found for the unrelaxed CCl₃ radical (0.018). The alternative D₁ diagnostic proposed by Janssen and Nielsen³⁵ predicts the CCSD solutions for both the CF₃ and CCl₃ radicals to be somewhat inadequate, with diagnostic values of 0.054 and 0.075, respectively, while all other species are diagnosed well below the threshold of 0.05. For CCSD(T), slight multi-reference is not an issue;³⁶ standard DFT methods are also known to fare well in cases where lower order coupled cluster methods fail due to mild MR.^37–40

For converged interaction energies, basis set superposition error (BSSE), the artificial stabilisation of the molecule compared to its fragments for a given basis set, needs to be accounted for, even with the large basis sets used in this study. For the correlated WF methods, for which the BSSE was estimated at the MP2 level, the largest error is 4.0 kJ mol⁻¹ (C₂F₆). For the DFT methods, the BSSE is always below 0.5 kJ mol⁻¹. The BSSE is largest for RPA, up to 7.5 kJ mol⁻¹ (C₂Cl₆). The high basis set demand of RPA, especially for dispersion type interactions, has been noted before.⁴¹

The analysis that follows is based on the unrelaxed BDEs, as these directly measure the interaction between the CX₃ fragments in the C₂X₆ species, before geometry relaxation effects.

Repulsive halogen⋯halogen interaction?

As seen from Table 1, the (unrelaxed) BDEs consistently decrease upon heavier halogenation, being 481 (C₂H₆), 425 (C₂F₆), 386 (CF₃CCl₃), and 367 (C₂Cl₆) kJ mol⁻¹. In order to establish if this might be due to a repulsive interaction between the halogens, we study the following isodesmic reaction:

C₂H₆ + C₂Cl₆ → 2CH₃CCl₃ (1)

Obviously, in reaction (1), a hypothetical repulsive halogen⋯halogen interaction across CX₃ fragments can only occur in C₂Cl₆. If there would be a significant repulsion between the chlorines, the reaction is expected to be exothermic. Which it turns out to be the reaction energy is −60.2 kJ mol⁻¹ at CC-cf level. This does not necessarily mean that there is repulsion between the chlorines of C₂Cl₆, however; a favourable reaction energy only means that the bonds of the products are, on average, stronger than those of the reactants.

For further insight, we apply the Bickelhaupt–Baerends (BB) energy decomposition analysis⁴² to reaction (1). The BB scheme divides the energy into several components; for our purposes, the least controversial ones suffice: (a) the Pauli repulsion energy, and (b) the total steric interaction. For reaction (1), the two energy components, computed at the revTPSS0-D level between the CX₃ fragments, are, using experimental geometries:

C₂H₆ + C₂Cl₆ → 2CH₃CCl₃

ΔE(Pauli) 677.5 + 851.4 → 2 × 906.1 = +283.3 kJ mol⁻¹

ΔE(steric) 291.9 + 577.3 → 2 × 504.9 = +140.5 kJ mol⁻¹

The slightly varying C–C bond lengths contribute to the steric interactions between fragments. In order to separate this effect from the rest of the interaction, we have also computed the change in repulsion energies using geometries optimised at the MP2 level, with the C–C bond lengths of all three species constrained to that in CH₃CCl₃, 1.5121 Å:⁴³

C₂H₆ + C₂Cl₆ → 2CH₃CCl₃

ΔE(Pauli) 717.5 + 1004.6 → 2 × 906.0 = +89.9 kJ mol⁻¹

ΔE(steric) 305.2 + 674.5 → 2 × 505.0 = +30.4 kJ mol⁻¹

As seen, the steric repulsion increases significantly in the reaction, using both sets of geometries. The BB energy decomposition analysis thus indicates the Cl⋯Cl interaction to actually be attractive. The experimental C–C bond lengths support this notion; the distance between the carbons stays quite similar through the C₂X₆ series, being 1.534,⁴⁴ 1.545,⁴⁵ and 1.564 Å⁴⁶ for X = H, F, and Cl, respectively. With a repulsive interaction, the C–C bond could perhaps be expected to elongate significantly more. Therefore, the decrease in BDE in the C₂X₆ series must arise from another effect. As will be shown later, the culprit is a weakened C–C bond. Before that, let us have a more qualitative look at the nature of non-covalent interactions in the perhalogenated ethanes.

Non-covalent interactions between halogens

Johnson and co-workers recently presented a new method for studying non-covalent interactions (NCIs) in and between molecules.^47,48 The NCI analysis is based on considering three components of the electron density distribution: the density itself (ρ), the reduced gradient of the density (s = |∇ρ|/(2(3π²)^1/3ρ^4/3)), and the Laplacian of the density (∇²ρ). The Laplacian is further decomposed into three eigenvalues, via the Hessian, so that ∇²ρ = λ₁ + λ₂ + λ₃ (λ₁ ≤ λ₂ ≤ λ₃). The second component, λ₂, contains the interesting information; when λ₂ < 0, the interaction is bonding, when λ₂ > 0, the interaction is nonbonding.^47,48 Combining the information from the above three properties of the electron density, the authors identified three main types of NCIs: attractive, moderately strong (e.g., hydrogen bonds), repulsive, moderately strong (e.g., steric interactions), and weak dispersion-type interactions. The beauty of the approach lies in its ability to pinpoint the interactions in real-space, thus enabling a graphical visualisation of the regions where non-covalent interactions occur. In this subsection, we apply the NCI method to the C₂X₆ systems. We begin by noting that the intramolecular halogen⋯halogen distances across CX₃ fragments are just below the sum of the van der Waals radii of the atoms⁴⁹ (r_w(F) = 1.47 Å; r_w(Cl) = 1.75 Å), being 2.74 Å, 2.98 Å, and 3.23 Å for C₂F₆, C₂F₃Cl₃, and C₂Cl₆, respectively; naturally, the distances by themselves cannot be used to infer the nature of any possible bonding between the halogens.

Within the staggered conformation of ethane, no non-covalent interactions are found. For hexafluoroethane, C₂F₆, there is very weak interaction building up between the fluorines on opposite carbon atoms, not substantial enough to trigger the threshold for plotting the interaction. When three of the fluorines are substituted for chlorine in 1,1,1-trifluoro-2,2,2-trichloroethane, CF₃CCl₃, six small regions of weak, dispersion type interactions appear. In hexachloroethane, C₂Cl₆, the interaction becomes even more pronounced. Fig. 1 shows the interacting regions as green disks.

Fig. 1 Non-covalent interaction (NCI) regions (green disks) in (a) CF₃Cl₃ and (b) C₂Cl₆.

The interactions can also be identified in NCI-plots, where the reduced gradient is plotted as a function of the electron density multiplied by the sign of λ₂. Fig. 2 shows these plots for all four C₂X₆ species studied. The plots provide an alternative view to the real-space plot of Fig. 1 and corroborate the findings. The difference between the species appears in the near-zero density region. For ethane, no peaks pointing downwards at the low reduced gradient at low electron density, the hallmark of NCI interactions, are seen. For C₂F₆, small peaks have developed, but as noted above, they are still too weak to be a clear indication of attraction; they are clearly present, however. For CF₃CCl₃ the peaks are deeper still, and finally, for C₂Cl₆, they reach a minimum, a strong indication of interaction. All peaks are also located within the very low electron density region and indicate a dispersion-type interaction.

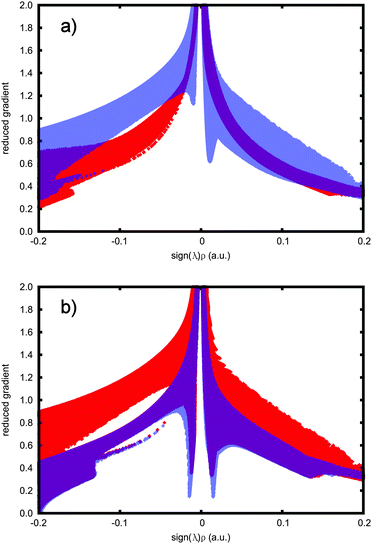Fig. 2 NCI graphs of (a) C₂H₆ (red) and C₂F₆ (translucent blue); (b) CF₃CCl₃ (red) and C₂Cl₆ (translucent blue).

The six interacting regions correspond to the six X⋯X contacts between the halogens attached to opposite carbon atoms of the substituted ethanes. Importantly, they are of dispersion type, that is, attractive. Interestingly, a promolecular NCI analysis, where the electron density is a simple sum of atomic densities, indicates, falsely, that the halogens exert a repulsive steric interaction upon each other. Only when the density is relaxed to the true molecular density is the interaction transformed from being repulsive into being attractive. This is in contrast to all other known cases, where the promolecular-density based interactions have been found to be qualitatively, if not quantitatively, of the same character as those of the relaxed density.^47,48

We note that the relaxed electron density itself does not require a high-level treatment. Already the Hartree–Fock density, which includes no electron correlation (as conventionally defined in quantum chemistry), contains the interacting regions. Describing the energy contribution of these regions, on the other hand, does require a very sophisticated treatment of electron correlation, as discussed in the previous subsection.

Delocalisation indices and energy component analysis

To further elucidate the character of the halogen⋯halogen interaction, we next consider the delocalisation indices (DIs) between atom pairs,⁵⁰ and decompose the total molecular energy into one and two-centre, that is, atomic and bonding contributions with a scaled version of the Salvador–Mayer energy component analysis.^51,52Table 2 summarises the DIs.

Table 2 Delocalisation indices (DI) and the sum of the central C–C bond and the six non-covalent X⋯X interactions computed at the LC-revTPSS-D level

	C2H6	C2F6	CF3CCl3	C2Cl6
DI
C–C	1.014	0.753	0.819	0.889
X⋯X	0.004	0.028	0.046	0.074
∑(C–C; X⋯X)	1.039	0.921	1.093	1.334

---

The DIs, which can be considered as bond orders,^50,53 show an interesting trend. Looking at the central C–C bond, one can see that the bond in methane is of order one, a single bond, as expected. The “bond” between closest-contact hydrogens on opposite carbons is non-existent. For C₂F₆, the situation changes drastically. The C–C bond order decreases to 0.75. The F⋯F non-covalent bond order, while still quite small, is not completely negligible. For CF₃CCl₃, the C–C bond order again increases, along with the F⋯Cl bond order. For C₂Cl₆, the trend continues, and the bond order between the chlorines has increased to 0.074, matching those of intramolecular hydrogen bonds.⁵⁴ Noting that there are six of these weak non-covalent Cl⋯Cl bonds in C₂Cl₆, their contribution to the total bond order between the two CCl₃ fragments becomes substantial. In general, the bond order between the six X⋯X pairs in the molecules follows the trend of interaction strength revealed in the previous subsection. The bond order of the C–C bond is consistent with the polarity of the C–X bond; the more electronegative the X, the more electron density is shifted from the carbon, decreasing the available amount of valence electrons around the carbons for forming a mutual bond.

The energy component analysis, see Table 3, shows yet another variation of the already established theme. The analysis is performed using the PBE functional, which describes the bond dissociation of ethane well, but, as shown, underestimates the CX₃–CX₃ interaction of the halogenated ethanes. The interaction between hydrogens and between fluorines in C₂H₆ and C₂F₆, respectively, is small, and at the PBE level slightly repulsive; a large, attractive contribution suddenly manifests itself between the six F⋯Cl pairs in CF₃CCl₃. In C₂Cl₆, the magnitude of the attraction increases further. At the same time, the carbon bonds weaken significantly upon substitution with heavier halogens. According to the analysis, this occurs for both the individual C–C bond pairs, as well as for the sum of all interactions between a carbon and the atoms in the opposite fragment (which, arguably, is a more robust measure).

Table 3 Energy component analysis of the total bond dissociation energy (BDE) for across-fragment atomic pairs for the C₂X₆ species, computed at the PBE level. The sums of all interactions, that is, the total BDE, are also shown. The last row shows the missing BDE as a difference between the PBE and CC-cf energies. Energies in kJ mol⁻¹

	C2H6	C2F6	CF3CCl3	C2Cl6
E(A,B)
C–C	−363.5	−152.6	−161.2	−132.5
C⋯X	−21.3	−46.4	−13.6/−13.0	−12.5
X⋯X	+2.6	+6.4	−12.8	−14.0
X······X	+0.1	+5.5	−5.3	+0.1
∑(C–C; C⋯X)	−491.4	−431.0	−240.9	−207.7
∑(all) = BDE	−475.4	−376.2	−333.6	−291.5
Missing BDE	−5.5	−48.9	−52.5	−75.1

---

To assess the strength of the interaction, we take the PBE dissociation energies and the scaled Salvador–Mayer component analysis, as a basis for the estimation. Noting that ethane, described well at the PBE level, naturally contains no component of the halogen interaction, the small remaining BDE underestimation of 5.5 kJ mol⁻¹ is taken as a systematic error between the CX₃ fragments of all species, an error, we note, the DFT-D scheme would correct for. Next, we note that a GGA functional like PBE cannot, because of its local nature, describe non-local dispersion interactions at all. Therefore, we first assign the remaining error for the perhalogenated ethanes to be borne purely out of the missing dispersion-type attraction between the halogens, an interaction which the Salvador–Mayer component analysis was not designed to decompose in any case.

By dividing the missing PBE bonding energy equally between the six X⋯X bonds, we get the following halogen⋯halogen interaction strengths: E(F⋯F) in C₂F₆ = −0.8 kJ mol⁻¹; E(F⋯Cl) in CF₃CCl₃ = −20.6 kJ mol⁻¹; E(Cl⋯Cl) in C₂Cl₆ = −25.6 kJ mol⁻¹.

Another way of dividing the missing, dispersion-type energy between CX₃ fragments would be to not assign all of it to the six X⋯X bonds, but rather note that dispersion will occur between all atom pairs across fragments. By distributing the missing BDE according to the relative dispersion interaction strengths as described by the DFT-D correction, the weight of the six X⋯X pairs naturally decreases. Following this partitioning, the halogen⋯halogen interaction strengths become: E(F⋯F) in C₂F₆ = +0.6 kJ mol⁻¹; E(F⋯Cl) in CF₃CCl₃ = −18.8 kJ mol⁻¹; E(Cl⋯Cl) in C₂Cl₆ = −22.2 kJ mol⁻¹. Table 4 lists our final estimates for the interaction between all atomic pairs across fragments.

Table 4 Energy component analysis of the unrelaxed bond dissociation energy (BDE) for cross-fragment atomic pairs for the C₂X₆ species, based on the SM scheme (see Table 3) augmented by dividing the missing BDE according to the relative dispersion interaction strengths of the DFT-D scheme. Energies in kJ mol⁻¹

	C2H6	C2F6	CF3CCl3	C2Cl6
E(A,B)
C–C	−363.5	−152.6	−161.3	−132.6
C⋯X	−21.7	−48.0	−15.0/−15.0	−15.2
X⋯X	+2.2	+0.6	−18.8	−22.2
X······X	−0.1	+3.8	−7.3	−3.2
∑(C–C; C⋯X)	−493.9	−440.3	−251.3	−224.1

---

The interaction between fluorines is very weak, practically zero, in line with the NCI analysis. Both the F⋯Cl and Cl⋯Cl interactions appear to be remarkably strong, on par with normal hydrogen bonds, however. Having six of them assist in increasing the CF₃–CCl₃ and CCl₃–CCl₃ dissociation energies make for substantial contributions. We should again emphasize that the derivation of the halogen interaction strengths here are, out of necessity, based on a set of assumptions. Although reasonable, the assumptions still render the estimates qualitative rather than quantitative.

The estimated interaction energies within the substituted ethanes can be compared to the best estimate total interaction energies of the dihalogens with bond distances elongated to the corresponding values in the C₂X₆ species. For F₂ at 2.740 Å, the interaction energy is −1.4 kJ mol⁻¹,⁵⁵ in line with that in C₂F₆ according to the analysis above. With chlorine, the free dihalogen interaction energies are substantially smaller compared to the perhalogenated ethanes, however. For FCl at 2.979 Å, the interaction energy is ≈−7 kJ mol⁻¹,⁵⁶ and for Cl₂ at 3.234 Å, −15.5 kJ mol⁻¹.⁵⁷

Eclipsed C₂Cl₆

With an attractive Cl⋯Cl interaction in C₂Cl₆ established, it is of interest to investigate why the staggered conformation is preferred⁴⁶ over the eclipsed one. Indeed, rotation is considerably more hindered than in ethane with its barrier of 12.0 ± 0.5 kJ mol⁻¹;⁵⁸ for hexachloroethane, the eclipsed conformation lies higher by 65.1 kJ mol⁻¹ at the CC-cf level, with a computed ΔH^# (298 K) of 62.0 kJ mol⁻¹. In the eclipsed conformation, the C–C bond length, at the MP2 level, elongates from 1.572 Å to 1.660 Å, again in stark contrast to ethane, where the bond length change upon rotation is very small.⁵⁹

We begin by employing the BB scheme,⁴² looking at the changes in Pauli repulsion energy and total steric interaction, when going from the ground state (GS) structure, via a structure obtained by a rotation of 60° (rot), to the fully relaxed transition state (TS):

C₂Cl₆ (GS) → C₂Cl₆ (rot) → C₂Cl₆ (TS) (2)

ΔΔE(Pauli) 0 +102.3 −196.5 kJ mol⁻¹

ΔΔE(steric) 0 +90.3 −113.1 kJ mol⁻¹

We see that upon rotation of the CCl₃ groups into the facing, eclipsed position, the steric repulsion does increase significantly. Upon rotation, the Cl⋯Cl distance is decreased from 3.234 Å to 2.774 Å, which, according to this analysis, is much too close. When the eclipsed conformation is allowed to relax to the true transition state, the repulsion decreases significantly. This is an expected result of the stretching of the central C–C bond followed by a Cl⋯Cl distance increase to 2.956 Å. Indeed, if the CCl₃ groups are rotated back into a staggered conformation from the TS structure, the Pauli and steric repulsions further decrease by 46.9 and 42.7 kJ mol⁻¹, respectively.

Next, we compare the results of the NCI analysis on the three conformations of reaction (2). Fig. 3 shows the regions for the two eclipsed structures considered, and Fig. 4 the corresponding NCI graphs, as well as the graph for the staggered conformation.

Fig. 3 Non-covalent interaction (NCI) regions in (a) rotated C₂Cl₆, (b) fully relaxed transition state of C₂Cl₆, and (c) only repulsive regions of (b).

Fig. 4 NCI graphs of rotated C₂Cl₆ (red), fully relaxed transition state of C₂Cl₆ (translucent blue), and the ground state of C₂Cl₆ (black outline).

We see that the interaction between chlorines in the eclipsed conformations become stronger compared to those in the staggered ground state; both the attractive and repulsive interactions, as defined by the sign of λ₂, increase. The NCI interaction regions in Fig. 3 are divided into two adjacent regions, the region closer to the C–C bond being repulsive, and then abruptly turning attractive further away.

Fig. 4 shows this as well, with the competing types of interactions being strongest for the eclipsed conformation obtained by simple rotation by 60°, gradually decreasing when the eclipsed structure is relaxed to the transition state, ending up in the van der Waals region for the staggered conformation. From Fig. 3 and 4 alone, it is again not possible to directly assess the relative strengths of these interactions. The smooth change in the interaction strength does raise the interesting question of whether the NCI analysis identifies both attractive and repulsive components in the dispersion, van der Waals region close to zero electron density, a topic for future study.

Table 5 shows the intramolecular cross-fragment bond strengths based on the scaled SM scheme augmented by distributing the missing PBE interaction energy to the different pairs according to their relative dispersion strength in the DFT-D scheme. The PBE error is similar in all conformations.

Table 5 Energy component analysis of the total unrelaxed bond dissociation energy (BDE) for cross-fragment atomic pairs in C₂Cl₆ for three conformations: ground state (GS); rotated by 60° to eclipsed (rot); eclipsed transition state (TS). Energies in kJ mol⁻¹

	C2Cl6 (GS)	C2Cl6 (rot)	C2Cl6 (TS)
E(A,B)
C–C	−132.6	−73.0	−105.1
C⋯X	−15.2	−10.3	−16.0
X⋯X	−22.2	−29.2	−29.0
X······X	−3.2	−8.2	−5.9
∑(C–C; C⋯X)	−224.1	−134.6	−201.2
∑(all) = BDE	−366.6	−271.4	−323.4
BDE(PBE) error	75.1	68.7	65.5

---

Upon rotation to the eclipsed conformation, the C–C bond is weakened substantially, recovering when the molecule is allowed to relax to the transition state. The Cl⋯Cl attraction in the eclipsed conformations are actually stronger than in the ground state staggered conformation by 7 kJ mol⁻¹, in line with the NCI results, and as might perhaps be expected by the shorter Cl⋯Cl distance. Now, however, there are only three interacting regions, instead of six.

Thus, a weaker C–C bond and half the number of (short-distance) halogen⋯halogen interactions make hexachloroethane prefer the staggered conformation. As a side note, bond-critical points actually appear between the chlorines in the transition state, along with ring-critical points within the three Cl–C–C–Cl trapezia, features that are missing in the electron density of the ground state.

Comparison to other halogen bonds

Here, we compare the halogen⋯halogen interaction in the CX₃–CX₃ species of this study with established bonding situations involving halogens. Halogen bonds have, as mentioned, established themselves as an important and distinctive class of their own.^13–19 The character of previously discussed bonds involving halogens is elegantly explained by the σ-hole concept advanced by Politzer, Murray, and co-workers.^60–63 The covalent bond between the halogen, involving its partially filled p-type orbital, and another atom gives rise to a positive (or less negative) electrostatic region on the opposite side of the halogen atom, along the R–X bond axis. At the same time a band of negative (or less positive) charge is built up around the positive region. This non-uniformity of the electrostatic potential around the halogen can then lead to non-covalent electrostatic interactions with other molecules, that is, normal halogen bonds. Due to the electrostatic nature of the interaction, these halogen bonds are highly directional, normally forming near linear non-covalent interactions when the site interacting with the halogen is negative, and lateral bonds when the opposite site is positive;⁶³ recently, Hill and Hu have, however, suggested the directionality to be less rigid than perhaps previously supposed.⁶⁴ The close connection between halogen bonds and garden-variety hydrogen bonds has also been discussed.^63,65–68

Fig. 5 shows the electrostatic potential (ESP) for the three perhalogenated ethanes of this study, computed at the revTPSS0-D level. In all of the species, the σ-hole is all but absent on fluorine, but clearly visible around the chlorines. The more strongly positive regions point, as expected, along the C–X axis away from the interacting region between the halogens. For C₂F₆ and C₂Cl₆ symmetry naturally dictates that the electrostatic potential on the facing sides of the halogens has to be equal. The figure shows the facing regions to be close to neutral, thus minimising electrostatic repulsion. It is also evident that in the case of the halogen⋯halogen interaction of the CX₃–CX₃ species, the σ-hole is not utilised, nor responsible for the attraction.

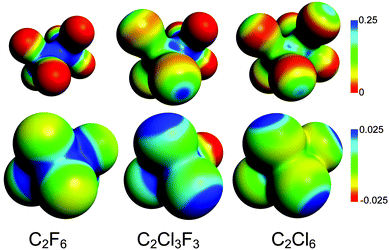Fig. 5 The electrostatic potential (in a.u.) of C₂F₆, C₂Cl₃F₃, and C₂Cl₆, plotted on charge density isosurfaces of 0.03 a.u. (top) and 0.001 a.u. (bottom).

Another difference to known, hydrogen-bond analogues of halogen bonds⁶⁹ is the absence of bond critical points⁷⁰ between the halogens in the present species. The interaction is geometrically quite different as well, with the atomic arrangements by necessity being far from forming optimal angles for conventional hydrogen–halogen-bonds.

Finally, we take a look at the NCI properties of standard, intermolecular halogen bonds via two specific examples: the H₃N⋯ClF and H₃CCl⋯ClCF₃ complexes. Fig. 6 shows the NCI regions and Fig. 7 the NCI plots of the two. The N⋯Cl interaction in H₃N⋯ClF is quite different in character from the halogenated ethanes of this study, with the interacting NCI regions being much more intense. The Cl⋯Cl dihalogen bond in H₃CCl⋯ClCF₃, on the other hand, appears to be quite similar to the intramolecular halogen bonds studied above. The interaction region between the chlorines shows the same features, barring a small additional interaction between one of the hydrogens of H₃CCl and the chlorine of ClCF₃. The typical peaks towards a zero reduced gradient close to zero electron density, see Fig. 7, are there as well. For a more thorough NCI analysis of intermolecular halogen bonds, the reader is directed towards two recent studies.^71,72

Fig. 6 Non-covalent interaction (NCI) regions in (a) H₃N⋯ClF and (b) H₃CCl⋯ClCF₃.

Fig. 7 NCI graphs of H₃N⋯ClF (red) and H₃CCl⋯ClCF₃ (translucent blue).

Summary and conclusions

All the computational and theoretical results presented here strongly suggest that the halogen⋯halogen interaction in the perhalogenated ethanes is real, and furthermore, attractive, provided that at least one of the halogens involved is a chlorine.

Is the interaction a proper bond? The interaction strength, apparently as strong as a hydrogen bond, certainly suggests that, although we emphasise that estimating intramolecular bond strengths is all but trivial. As discussed, there is no bond critical point⁷⁰ between the halogens in the present species, however. During preparation and revision of this paper, it has also become clear that the question is rather controversial, and the case is far from closed.

The NCI analysis points towards a dispersion, van der Waals type interaction. To recover all of the interaction, a rigorous treatment of electron correlation is necessary, suggesting a highly complex type of interaction. It is noteworthy that of the wave-function methods used here, only CCSD(T) treats the long-range interactions beyond a pairwise additive manner,^32,73 and is the only wave-function method to describe the homolytic bond dissociation correctly. Dissecting exactly what kinds of interactions are included in a given density functional is difficult. A possible many-body dispersion interaction being at the heart of the halogen⋯halogen bonds would, however, fit the observation that standard functionals perform exceptionally poorly for the BDE; recently, the DFT description of three-body dispersion was found to be overly repulsive.⁷⁴ Further, RPA also captures the non-pairwise additive nature of dispersion,³² and performs well.

In conclusion, we have explored an overlooked, reasonably strong intramolecular bonding interaction between halogen atoms. The character is rather different from other halogen bonds that arise due to the phenomenon of the σ-hole. The interaction requires that at least one of the halogens is a chlorine, or perhaps a heavier analogue.

In the species studies here, the interaction is partially masked by the fact that the C–C bond is simultaneously weakened upon halogenation, leading to an overall decrease of the total X₃C–CX₃ dissociation energy. Future studies will reveal if this attractive interaction can be found in structurally different arrangements and molecules as well. A similar, if not the same interaction might indeed already have been observed by Schmidbaur et al., who found curiously short intramolecular Br–I contacts in the X-ray structures of halogenated benzenes.⁷⁵

From a practical point of view, we have shown that the LC-revTPSS-D and RPA methods perform quite well, outperformed only by the CCSD(T) level of theory. Thus, promising candidates for studying large halogenated hydrocarbons, a field where density functional theory traditionally has been unsuccessful^23,24 and sufficiently accurate methods computationally much too expensive, have been identified.

On a more general note, it is pleasing to find that the chemistry of seemingly perhaps unremarkable and mundane species still hold surprises in store; we can only echo Coulson in his desire “that the simplest molecules should be carefully investigated”.³

Methods

Reference energies were computed at the ab initio level, by extrapolating the coupled cluster (CC) series, from uncorrelated Hartree–Fock (HF)^76,77 to single and double excitations (CCSD)⁷⁸ and perturbative triples corrections (CCSD(T)),⁷⁹ towards the full configuration-interaction (FCI) limit using Goodson's continued fraction method (CC-cf).²⁰ The open-shell CC calculations were performed on a restricted open-shell reference wave function,^80,81 the other calculations on the radicals have been performed fully unrestricted. The correlation energies of the coupled cluster, second order Møller–Plesset perturbation theory (MP2),^82,83 and random phase approximation (RPA) calculations were extrapolated towards the complete basis set limit (CBS) with the two-point formula by Halkier et al.,⁸⁴ based on calculations using the correlation-consistent polarised basis sets of triple and quadruple-zeta quality, augmented by diffuse functions, aug-cc-pV[T,Q]Z.^85,86 The Hartree–Fock, non-correlated energy was evaluated with the aug-cc-pVQZ basis set. The energies for the density functional theory (DFT) methods were computed using the polarised quadruple-zeta quality basis set augmented by diffuse functions, def2-QZVPPD.^87,88

Basis set superposition error was estimated using the counterpoise correction scheme.⁸⁹ For all correlated WF methods, this was computed at MP2/aug-cc-pV[T,Z] level. For the DFT methods, the BSSE was estimated using the def2-QZVPPD basis set, and for RPA with the extrapolated aug-cc-pV[T,Z] results. In all cases, the correction for the unrelaxed interaction energies was also used for the relaxed fragments.

For the previously unused revTPSS0 and the long-range corrected³¹ LC-revTPSS functionals, the default scaling factor of 1 was used when combined with Grimme's DFT-D correction.³⁰ For the LC-revTPSS functional, the long-range attenuation parameter μ was set to 0.47.⁹⁰ The post-Kohn–Sham RPA calculations were performed using TPSS⁹¹ orbitals.

The electronic energies were computed on experimental structures,^{43–46,92–94} except for CF₃CCl₃ or if otherwise noted, when MP2/aug-cc-pVTZ structures were used. Thermal corrections to room temperature enthalpy, ΔH(298 K), were computed within the harmonic approximation using MP2/aug-cc-pVTZ frequencies (and geometries), employing a scaling factor of 0.953 to account for anharmonicity.⁹⁵ Non-covalent interaction (NCI) and delocalisation indices (DI) were computed at the LC-revTPSS/def2-SVPD level. The DIs were computed with the scheme of Matito et al.,⁵⁰ based on the quantum theory of atoms in molecules (QTAIM).⁷⁰ The Salvador–Mayer energy component analysis^51,52 was performed at the PBE/def2-TZVPPD level, scaled so that the total diatomic contributions across fragments add up to the total BDE, computed at the PBE/def2-QZVPPD level; the atomic radii were defined as follows: r(C) = d(C–C)/2; r(X) = d(C–X)–r(C). The Bickelhaupt–Baerends (BB) energy decomposition analyses⁴² were performed at the revTPSS0-D/QZ4P⁹⁶ level.

The electronic structure calculations were performed using the MOLPRO 2010.1,^97,98 TURBOMOLE 6.4,^99–102 Gaussian09,¹⁰³ and ADF 2012.01^104,105 program packages. The non-covalent interaction plots were produced with NCIplot⁴⁸ and VMD.¹⁰⁶ DIs were computed using the ESI-3D program by E. Matito,¹⁰⁷ and the scaled Salvador–Mayer energy decomposition with a modified version of the ENP-FUZZY program by P. Salvador and I. Mayer. Bond critical points were pursued with ADF and Multiwfn.¹⁰⁸

Acknowledgements

We are grateful to Dr Eduard Matito, Dr Pedro Salvador, and Dr Raphael Berger for enlightening discussions. CSC – the Finnish IT Centre for Science hosted part of the calculations. This work has been supported by the Ministerio de Ciencia e Innovación (MICINN projects JCI-2009-05953, CTQ2011-25086/BQU), the Academy of Finland (project 136079), MICINN and the European Fund for Regional Development (FEDER grant UNGI08-4E-003), and the DIUE of the Generalitat de Catalunya (project 2009SGR528).

Notes and references

1. L. Pauling, J. Chem. Educ., 1992, 69, 519–521.
2. G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785.
3. C. A. Coulson, Math. Proc. Cambridge Philos. Soc., 1935, 31, 244–259.
4. K. S. Pitzer, J. Am. Chem. Soc., 1945, 67, 1126–1132.
5. I. Garcia-Yoldi, J. S. Miller and J. J. Novoa, Phys. Chem. Chem. Phys., 2008, 10, 4106–4109.
6. T. Nguyen, A. D. Sutton, M. Brynda, J. C. Fettinger, G. J. Long and P. P. Power, Science, 2005, 310, 844–847.
7. S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nat. Chem., 2009, 1, 443–449.
8. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
9. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
10. X. Li, L.-S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
11. Z.-X. Wang and P. v. R. Schleyer, Science, 2001, 292, 2465–2469.
12. K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940.
13. M. Fourmigué and P. Batail, Chem. Rev., 2004, 104, 5379–5418.
14. M. Palusiak and S. J. Grabowski, Struct. Chem., 2007, 19, 5–11.
15. E. Parisini, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Chem. Soc. Rev., 2011, 40, 2267–2278.
16. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
17. Y. Lu, T. Shi, Y. Wang, H. Yang, X. Yan, X. Luo, H. Jiang and W. Zhu, J. Med. Chem., 2009, 52, 2854–2862.
18. R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388.
19. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013 10.1039/c3cp00054k.
20. D. Z. Goodson, J. Chem. Phys., 2002, 116, 6948–6956.
21. E. Schrödinger, Ann. Phys., 1926, 79, 361–376.
22. W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266.
23. J. Cioslowski, G. Liu and D. Moncrieff, J. Phys. Chem. A, 1998, 102, 9965–9969.
24. A. C. Olleta and S. I. Lane, Phys. Chem. Chem. Phys., 2001, 3, 811–818.
25. F. Furche, J. Chem. Phys., 2008, 129, 114105.
26. S. P. Sander, J. Abbatt, J. R. Barker, J. B. Burkholder, R. R. Friedl, D. M. Golden, R. E. Huie, C. E. Kolb, M. J. Kurylo, G. K. Moortgat, V. L. Orkin and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 17, JPL Publication 10-6, Jet Propulsion Laboratory, Pasadena, 2011.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. J. Perdew, A. Ruzsinszky, G. Csonka, L. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403.
29. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
30. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
31. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
32. H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084.
33. M. P. Johansson and J. Olsen, J. Chem. Theory Comput., 2008, 4, 1460–1471.
34. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Symp., 1989, 23, 199–207.
35. C. L. Janssen and I. M. B. Nielsen, Chem. Phys. Lett., 1998, 290, 423–430.
36. M. S. Gordon, M. W. Schmidt, G. M. Chaban, K. R. Glaesemann, W. J. Stevens and C. Gonzalez, J. Phys. Chem., 1999, 110, 4199–4207.
37. N. Handy and A. Cohen, Mol. Phys., 2001, 99, 403–412.
38. D. Cremer, M. Filatov, V. Polo, E. Kraka and S. Shaik, Int. J. Mol. Sci., 2002, 3, 604–638.
39. M. P. Johansson and D. Sundholm, J. Chem. Phys., 2004, 120, 3229–3236.
40. J. Gräfenstein and D. Cremer, Theor. Chem. Acc., 2009, 123, 171–182.
41. H. Eshuis and F. Furche, J. Chem. Phys., 2012, 136, 084105.
42. F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2000, vol. 15, pp. 1–86.
43. L. Margulès, M. Carvajal and J. Demaison, J. Mol. Spectrosc., 2008, 247, 160–166.
44. L. S. Bartell and H. K. Higginbotham, J. Chem. Phys., 1965, 42, 851–856.
45. K. L. Gallaher, A. Yokozeki and S. H. Bauer, J. Phys. Chem., 1974, 78, 2389–2395.
46. A. Almenningen, B. Andersen and M. Trætteberg, Acta Chem. Scand., 1964, 18, 603–611.
47. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
48. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
49. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
50. E. Matito, M. Solà, P. Salvador and M. Duran, Faraday Discuss., 2007, 135, 325–345.
51. P. Salvador and I. Mayer, J. Chem. Phys., 2004, 120, 5046–5051.
52. P. Salvador and I. Mayer, J. Chem. Phys., 2007, 126, 234113.
53. X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314.
54. X. Li, Y. Wang, S. Zheng and L. Meng, Struct. Chem., 2012, 23, 1233–1240.
55. L. Bytautas, N. Matsunaga, T. Nagata, M. S. Gordon and K. Ruedenberg, J. Chem. Phys., 2007, 127, 204301.
56. A. B. Alekseyev, H.-P. Liebermann, R. J. Buenker and D. B. Kokh, J. Chem. Phys., 2000, 112, 2274–2284.
57. L. G. M. de Macedo and W. A. de Jong, J. Chem. Phys., 2008, 128, 041101.
58. R. M. Pitzer, Acc. Chem. Res., 1983, 16, 207–210.
59. F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183–4188.
60. T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., Quantum Biol. Symp., 1992, 44, 57–64.
61. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2006, 13, 291–296.
62. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2008, 14, 659–665.
63. P. Politzer, K. E. Riley, F. A. Bulat and J. S. Murray, Comput. Theor. Chem., 2012, 998, 2–8.
64. J. G. Hill and X. Hu, Chem.–Eur. J., 2013, 19, 3620–3628.
65. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395.
66. Z. P. Shields, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 2010, 110, 2823–2832.
67. M. D. Esrafili, J. Mol. Model., 2012, 19, 1417–1427.
68. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294.
69. S. J. Grabowski, J. Phys. Chem. A, 2012, 116, 1838–1845.
70. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon, Oxford, 1990.
71. B. Pinter, N. Nagels, W. A. Herrebout and F. De Proft, Chem.–Eur. J., 2013, 19, 519–530.
72. S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931.
73. B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300.
74. A. Tkatchenko and O. von Lilienfeld, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045116.
75. H. Schmidbaur, O. Minge and S. Nogai, Z. Naturforsch., B: J. Chem. Sci., 2004, 59, 264–268.
76. D. R. Hartree, Proc. Cambridge Philos. Soc., 1928, 25, 89–110.
77. V. Fock, Z. Phys., 1930, 61, 126–148.
78. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
79. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
80. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219–5227.
81. M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326.
82. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
83. J. A. Pople, J. S. Binkley and R. Seeger, Int. J. Quantum Chem., Quantum Chem. Symp., 1976, 10, 1–19.
84. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
85. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
86. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
87. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
88. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
89. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
90. J.-W. Song, T. Hirosawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2007, 126, 154105.
91. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
92. C. Yamada and E. Hirota, J. Chem. Phys., 1983, 78, 1703–1711.
93. J. W. Hudgens, R. D. Johnson, B. P. Tsai and S. A. Kafafi, J. Am. Chem. Soc., 1990, 112, 5763–5772.
94. N. E. Triggs, M. Zahedi, J. W. Nibler, P. DeBarber and J. J. Valentini, J. Chem. Phys., 1992, 96, 1822–1831.
95. NIST Computational Chemistry Comparison and Benchmark Database, ed. R. D. Johnson III, http://cccbdb.nist.gov/, Release 15b, August 2011.
96. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
97. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version, 2010.1, a package of ab initio programs.
98. C. Hampel, K. A. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1–12.
99. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
100. O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354.
101. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
102. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183.
103. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision 01, Gaussian, Inc., Wallingford, CT, 2009.
104. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
105. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
106. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
107. E. Matito, ESI-3D: Electron Sharing Indices Program for 3D Molecular Space Partitioning, IQC-EHU, Girona-Donostia, Spain, 2011.
108. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available: Atomic coordinates and a rotating view of the NCI regions in C₂Cl₆. See DOI: 10.1039/c3cp50962a

---