Modeling catalytic promiscuity in the alkaline phosphatase superfamily

Abstract

In recent years, it has become increasingly clear that promiscuity plays a key role in the evolution of new enzyme function. This finding has helped to elucidate fundamental aspects of molecular evolution. While there has been extensive experimental work on enzyme promiscuity, computational modeling of the chemical details of such promiscuity has traditionally fallen behind the advances in experimental studies, not least due to the nearly prohibitive computational cost involved in examining multiple substrates with multiple potential mechanisms and binding modes in atomic detail with a reasonable degree of accuracy. However, recent advances in both computational methodologies and power have allowed us to reach a stage in the field where we can start to overcome this problem, and molecular simulations can now provide accurate and efficient descriptions of complex biological systems with substantially less computational cost. This has led to significant advances in our understanding of enzyme function and evolution in a broader sense. Here, we will discuss currently available computational approaches that can allow us to probe the underlying molecular basis for enzyme specificity and selectivity, discussing the inherent strengths and weaknesses of each approach. As a case study, we will discuss recent computational work on different members of the alkaline phosphatase superfamily (AP) using a range of different approaches, showing the complementary insights they have provided. We have selected this particular superfamily, as it poses a number of significant challenges for theory, ranging from the complexity of the actual reaction mechanisms involved to the reliable modeling of the catalytic metal centers, as well as the very large system sizes. We will demonstrate that, through current advances in methodologies, computational tools can provide significant insight into the molecular basis for catalytic promiscuity, and, therefore, in turn, the mechanisms of protein functional evolution.

---

1. Introduction

Enzymes are tremendously proficient catalysts, reducing the timescales of biologically relevant chemical reactions from millions of years to fractions of seconds.¹ New enzyme functions are constantly emerging in Nature, as organisms adapt to environmental changes.² The best example of this includes the rapid rate at which bacteria can acquire antibiotic resistance,³ as well as the acquired ability of some enzymes to degrade relatively new synthetic compounds, some of which have evolved in organisms that would have no reason to be exposed to these compounds in their native environments.⁴ From a biological perspective, understanding how enzymes can acquire novel or altered functionality may provide a basis for predicting the emergence of drug resistant mutations in bacteria, understanding the occurrence of oncogenic mutations upon exposure to natural vs. man-made carcinogens,⁵ as well as providing guidance for in vitro and in silico engineering of new enzymes.⁶

In 1976, Jensen⁷ and later O'Brien and Herschlag⁸ posited that enzyme promiscuity, i.e. the ability of many enzymes to catalyze the turnover of multiple substrates, plays a key role in the evolution of new function. The past two and a half decades have seen substantial progress in both experimental and theoretical studies^6,8–26 that aim to rationalize the origin of such promiscuity, as well as illustrate it's applicability in enzyme design. However, addressing the precise origins of enzyme multifunctionality (and therefore by extension it's role in protein evolution) is far from trivial. This is due to the sheer complexity of the problem, which spans from the need to be able to, on the one hand, not just understand the topology of relevant fitness landscapes^27,28 and how this would be perturbed by mutations, but also understand the precise evolutionary role of, for instance, protein–protein interactions²⁹ and protein conformational diversity,^30,31 as well as the fine details of the chemical step in enzyme catalysis (which is a topic of significant debate, as can be seen from the discussion in e.g., ref. 32 and 33 and references cited therein).

The advent of techniques such as error-prone PCR³⁴ has played an important role in laboratory evolution, allowing protein engineers to artificially mimic the process of natural Darwinian evolution in vitro, in order to iteratively refine proteins for desired properties³⁵ such as a specific function or better thermostability. Such approaches also provide valuable insight into how actual proteins evolve.³⁶ That is, through artificially mimicking the process of natural evolution, it is possible to better understand the constraints that determine and limit the evolution of function, as well as constructing putative evolutionary trajectories between modern and ancestral or progenitor-like enzymes (see discussion in ref. 36). Similarly, there have been impressive advances using bioinformatics and machine-learning based approaches in order to predict promiscuous activities,^37,38 reconstruct protein evolutionary trajectories,^28,39 and resurrect ancestral proteins.^40,41 However, computationally addressing this problem at the chemical level poses a significant challenge, due to the tremendous computational cost involved in examining not just native but also promiscuous activities involving multiple substrates with many potential binding modes (that can change upon mutations), as well as the large-scale effect of mutations. As a result of these combined advances in both experimental and theoretical approaches, there has been an explosion of interest in studies of catalytic promiscuity in the literature (Fig. 1).

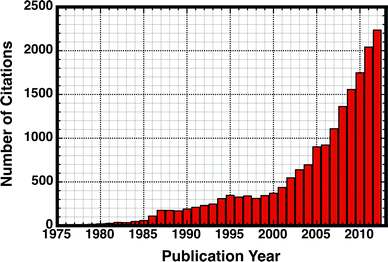Fig. 1 Illustrating the exploding popularity of studies on catalytic promiscuity in the literature. This plot highlights the number of citations to an article with the words “moonlighting” or “promiscuity” in the title, in the period spanning the years 1976–2012. Citation data obtained from Web of Knowledge (http://www.isiknowledge.com).

In the present perspective, we will expand on this idea, and outline the fact that computational power has, in fact, reached a stage where it is finally possible to examine enzymatic catalytic activity for multiple substrates and potential mechanisms, as well as the effect of large numbers of mutations on each of these substrates and mechanisms at the atomic level. This will finally allow us to understand the precise molecular basis for observed multi-functionality in catalytically promiscuous enzymes, and, through the insights this provides, aid us in the artificial engineering of new enzyme functionality. Such computational studies can then also be extended to studying and predicting evolutionary trajectories, as well as rationalizing and guiding laboratory evolution studies. If this is done in a systematic way through an enzyme superfamily, it will allow for the creation of a “roadmap” for the structural and electrostatic contributions to functional evolution within that superfamily.

In the present work, we will begin by outlining the role of catalytic promiscuity in protein evolution. Following from this, we will provide a brief overview of recent advances in relevant computational approaches, comparing the inherent strengths and weaknesses of each of them. Specifically, we will demonstrate that, while individual approaches may have their own specific traps and pitfalls, when selected carefully and in combination, computational tools can be extremely powerful in rationalizing chemical effects in complex biological systems. To illustrate this point, we will present as a case study computational work on different members of the alkaline phosphatase (AP) superfamily by both ourselves and other workers in the field, showing the complementary insights theory can provide, which could not be obtained by experiment alone (although experimental data are critical for providing actual physical observables). The AP superfamily has been a topic of significant research interest in recent years, since its members are not only highly promiscuous, but also, selectivity and specificity patterns within this superfamily are particularly well-defined.¹⁴ That is, there is a wealth of both kinetic and structural data available in the literature due to a large body of experimental work on these systems.^14,42–60 Finally, to conclude, we will discuss future perspectives in the field, in line with the increasing role of computational approaches in rationalizing protein evolution.

2. Catalytic promiscuity and enzyme design

2.1. Classifying different types of promiscuity

As discussed in the introduction, the idea that enzymes are capable of “promiscuous” activities, and that this in turn could play an important role in enzyme evolution, dates back over two and a half decades.⁷ However, the classical image of enzymes as highly specific catalysts⁶¹ still remains in many textbooks. To start this section, we would like to note that the term “promiscuity” itself is currently used to describe a wide range of different phenomena, depending on the circumstances (for an overview, see Fig. 2). For example, Hult and Berglund²⁵ have introduced a classification of promiscuity in terms of the form in which it manifests itself. According to this, they defined three types of promiscuity: condition promiscuity (catalysis of different reactions under conditions different to the native one), substrate promiscuity (catalysis of a range of different substrates through the same mechanism and transition state) and catalytic promiscuity (catalysis of chemically distinct reactions with different transition states). A fourth form of promiscuity, namely product promiscuity (generation of alternative products through the same reaction) has also been recently considered.⁶² Additionally, catalytic promiscuity can be further divided into two different subtypes:²⁵ accidental promiscuity and induced promiscuity, where the former term refers to side-reactions catalyzed by the original wild-type enzymes, and the latter term refers to a system with a completely new reaction established by one or several mutations.²⁵ The term “accidental” used in this classification may lead to the idea that this phenomenon was not supposed to happen in the wild-type enzyme, which of course cannot be established. Considering this semantic problem we would prefer to use the term natural and engineered to refer to these two different aspects of the phenomenon. Finally, Thornton and coworkers⁶³ have also analyzed this phenomenon from a biological perspective, and provided a classification of promiscuity according to the “molecular level” where the promiscuity appears. According to this classification, promiscuity can be manifested at either the individual gene or transcript level, at the individual protein level, or within families and superfamilies of proteins, including close or remote homologs.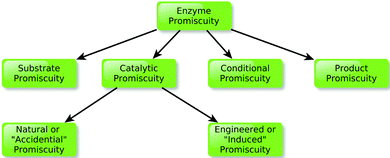

Fig. 2 Schematic overview of the classification of different kinds of promiscuity, as presented in the main text.

Obviously, none of the classifications listed above is absolute, and both the manifestations of promiscuity as well as the level at which it occurs are complementary aspects of the same phenomenon. However, we have raised these examples here in order to introduce the reader to the semantic complexity of the field. During the last few decades, a number of detailed reviews have discussed various aspects of the phenomenon of promiscuity, including mechanistic issues,¹⁵ evolutionary aspects,^11,64 and its role in protein design.^10,63,65 For the purposes of the present work, our focus will specifically be on catalytic promiscuity. Here, we will focus on a slightly different aspect of the field, namely recent advances in computational methodologies that can probe the underlying basis for catalytic promiscuity at the atomic level, as well as the important role they can play in understanding protein functional evolution.

2.2. Harnessing promiscuity in artificial enzyme design

Over the past twenty years, a broad range of approaches have been developed for engineering enzymes, which can be either rational,^26,66–69 based on random evolution,^35,70,71 or even semi-rational approaches that combine the two.^72–77 Computational methods have also emerged as an important tool in protein engineering, even if there is still a lot of room for improvement in this (comparatively) young field.^78,79 In the midst of so many different approaches for enzyme design, one thing that is becoming clear is that one of the most powerful ways forward is to obtain a better understanding of protein evolution in and of itself, and to manipulate the insights this provides for targeted artificial evolution.^36,80

As already discussed, catalytic promiscuity has been suggested to play an important role in the evolution of new enzymes through divergent evolution.⁸ Jensen's original hypothesis⁷ suggested that primitive enzymes displayed low activities and very broad specificities. Over time, evolutionary pressure caused them to divergently evolve in order to acquire higher specificities and activities (Fig. 3). However, and as is clear from ongoing experimental studies today (e.g.ref. 2, 8, 11–16, 22, 23, 58, 62 and 81–83), some of these enzymes appear to have retained varying levels of the promiscuous activities of their generalist progenitors.¹⁵ Therefore, as outlined in Fig. 3, one could use this principle and perform “retroevolution” back towards a generalist progenitor or progenitor-like enzyme, and use this as a trampoline for re-specialization towards new functionality.¹¹ This approach has recently been discussed by Tawfik and coworkers.^2,15 Using in vitro evolution they have demonstrated that the evolution of a new function can be driven by mutations that have little effect on the native function, but large effects on the promiscuous functions.¹⁵

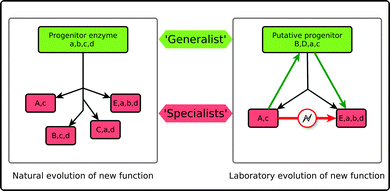Fig. 3 Schematic representation of Jensen's hypothesis for the evolution of enzyme function⁷ (A). According to this hypothesis primitive enzymes, which displayed low activities and broad specificities (denoted by lowercase a, b, c, d), have, once submitted to evolutionary pressure, divergently evolved in order to acquire higher specificities and (sometimes completely new) activities (denoted by upper case letters, e.g. B, D, E). However, they have retained low levels of their original promiscuous activities. This can in turn be exploited in artificial enzyme design (B). That is, direct switches of specificity, e.g., from A to E are rare. However, in the case of a promiscuous enzyme, one could perform “retroevolution” back towards a generalist enzyme, and use this as a trampoline for re-specialization towards new functionality. This figure is adapted from ref. 15.

As we will illustrate in this Perspective, computational approaches provide a unique opportunity for reaching a better understanding of the origins of promiscuity. For example, at the molecular level, structure-based methods, docking approaches and mechanistic analysis can be used in order to reach a greater understanding of the features controlling enzyme catalysis and determining specificity patterns, the possible mechanisms involved, and the prediction of suitable starting points for experimental evolution.^84,85 At the superfamily level, data analysis⁸⁶ and sequence-based methods can be used for the study of evolutionary relationships within large protein families.^37,87

In the present perspective, we will discuss the recent work of both our group and others in the field to model promiscuity in highly multifunctional enzymes. We will demonstrate that computational power has reached a stage where theory can play a substantial role not only in rationalizing experimental observables, but also in playing an active role in predicting evolutionary trajectories. This, by extension, will also ultimately play an important role in artificial enzyme design.

3. Examples of relevant computational approaches

Over the past four decades, molecular modeling has become a well-established discipline, providing essential and unique tools for the study of chemically and biologically relevant systems. The increasing role of this discipline in these areas has been mainly facilitated by the availability of more powerful and efficient hardware/software and the introduction of massively parallelized computer architectures, thus leading to unimaginable advances in terms of the scale and scope of problems that can currently be addressed^88–91 (see Fig. 4 for an overview of how computational power has been increasing since the 1960s). At present, a plethora of techniques are available to study molecular energetics, chemical reactions, and a whole range of chemical and physical properties in molecular and supramolecular systems. Broadly speaking, a twofold classification can be made according to the level of theory used: quantum mechanical (QM) methods (including ab initio approaches, as well as valence bond, and density functional approaches) and molecular mechanics (MM) force field based approaches (including classical molecular dynamics and Monte Carlo simulations). In addition, mixed quantum mechanics/molecular mechanics (QM/MM) approaches have also been developed aiming to combine the strength of both QM (accuracy) and MM (speed) calculations. While presenting a detailed technical overview of different computational approaches is clearly out of the scope of the present perspective, we will present a brief summary of the basic principles associated with the most relevant computational approaches. Specifically, our emphasis in this section will be on QM and QM/MM approaches, as they have been the most extensively used approaches in computational studies of members of the alkaline phosphatase superfamily. For more detailed reviews, we refer the reader to e.g.ref. 92–100.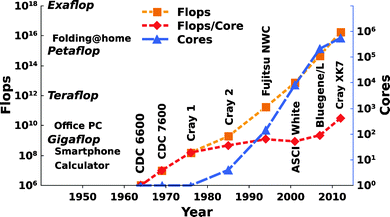

Fig. 4 The increasing performance of (super)computers in Flops (Floating-point operations per second) (orange), Flops per core (red), and number of cores (blue) from the 1960s to the present day. Note, that Flops as performance criteria only help to have a reference between different computers, and also, that the here presented supercomputers are only a representative subset for illustration purposes. The data was collected from ref. 88 and from www.top500.org.

3.1. QM-only approaches

One of the most popular QM-only approaches currently used for the study of enzymatic processes is the cluster model approach (for a more thorough review of the approach we refer to ref. 98, 100–102 and references therein). In this approach, a limited number of atoms are cut out of the enzyme (usually from an X-ray or NMR structure) to represent the most crucial components of the active site region. Other important functional groups in the vicinity of the reacting atoms are represented by small molecules (for instance imidazole can be used to represent histidine, acetate to represent the aspartate side chain, and so forth) and atoms at the periphery of the model are normally fixed to the initial structure in the enzyme. The use of a limited number of atoms (from 20 up to 200)¹⁰² allows the use of quantum mechanical methods, most commonly density functional theory (DFT) based approaches, thus providing a full description of the electronic structure of the system being examined.

Additionally, describing the surrounding environment using implicit solvent (typically) saves substantial computational time. However, although there are many advantages to such models, several limitations are also present in this approach. For example, the assumption that chemical changes involved in the reaction are confined to a relatively small region of the system can in many cases be an oversimplification, particularly as long-range electrostatic interactions play an important role in enzyme catalysis.^103,104 This issue was observed in the (otherwise elegant) study of the catalytic reaction of the Ras-GAP complex¹⁰⁵ (to name one example), where, due to incomplete electrostatic (and thus pK_a) treatments in a limited enzyme model, an incorrect residue was suggested as a general base in the reaction. We would also like to refer the reader to the discussion about the relative advantages and challenges of cluster models (which allow accurate local energy minimization in a small region), and QM/MM studies, which provide an improved description of the coupling to the protein, but only allow for limited sampling, see e.g.ref. 106 and 107. Furthermore, neither conformational sampling (required in order to obtain meaningful convergent results that are not dependent on the precise starting structure used¹⁰⁸) nor entropy effects (which are usually neglected because it is difficult to predict them in the harmonic approximation¹⁰⁹) are currently included in this approach. Finally, the choice of reacting subsystem can substantially affect the outcome of the calculations.^110,111 Despite these challenges, when used with care and with detailed chemical knowledge of the system under study, cluster models can provide useful insights and detailed information of the fundamental chemistry as recently discussed by Ramos and coworkers.¹⁰⁰ Particularly, cluster models provide a fast effective way to perform initial tests of the viability of different mechanistic options.

3.2. QM/MM approaches

If one wants a more complete description of the system under study, one alternative to it is to use QM/MM approaches (for reviews see e.g.ref. 96, 97, 112 and 113). Briefly, the main idea of these approaches is to describe the reactive part of the system under study using a higher-level quantum mechanical approach and the surrounding using a lower level of theory. According to the level of QM theory used, QM/MM approaches can be classified into two types.¹¹³ The first type employs semiempirical approaches such as MNDO, AM1, AM1/d,¹¹⁴ PM3,⁹⁷ empirical valence bond (EVB)¹¹⁵ or self-consistent charge density functional tight binding (SCC-DFTB) methods¹¹⁶ to describe the QM region. The second type relies on the use of ab initio (wave-function based) or more often DFT methods to describe the QM region.

QM/MM approaches (in their different implementations) have become one of the most popular approaches for the study of enzymatic reaction, as they have the advantage of improving the description of the enzyme environment and its contribution to the catalytic process (compared to QM-only approaches using a limited description of the system of interest). However, QM/MM approaches have also been demonstrated to have several limitations. One of the main limitations of these is the large computational cost required for the repeated evaluation of the energies and forces in the QM region, which, by extension, results in limited configurational sampling during the simulation. This is particularly challenging in cases where the system involves a rugged multidimensional landscape,¹¹⁷ as, without proper conformational sampling, one ends up trapped in local minima and different starting conformations can give completely different results (see also discussion in ref. 108). Important advances to resolve this problem have been achieved by means of specialized approaches, such as using a classical potential as a reference for the QM/MM calculations,^118–121 or through other strategies, such as the QM/MM free-energy perturbation (FEP) scheme combined with optimized chain-of-replicas^95,113 or QM/MM interpolated correction methodologies.¹²²

Among the wide variety of approaches available to study enzymes, the one that we choose to use in the majority of our work is the empirical valence bond (EVB) approach of Warshel and coworkers.^115,123 As the name suggests, this is a QM/MM approach based on valence bond (bond description) rather than molecular orbital (atomic description) theory. Its major advantages are that it is, on the one hand, fast enough to perform the extensive conformational sampling required to obtain convergent free energies, while, at the same time, it carries enough chemical information to be able to describe bond making/breaking processes in a physically meaningful way.^115,123 Finally, inherent to the philosophy of the EVB approach is the use of the energy gap reaction coordinate.^123,124 The power of this reaction coordinate comes from the fact that, rather than being a geometric coordinate, it is simply the energy gap between different diabatic (valence bond) states involved in the reaction process, and, as such, allows one to take into account the entire multidimensional nature of the relevant process as well as environmental reorganization without the need to apply external restraints.^125,126 This choice of reaction coordinate also allows for much faster convergence in free energy calculations, compared to other currently popular approaches.¹²⁷

In addition to long established approaches such as the EVB, there have been several interesting developments in this area, which we would like to summarize here. For example, transition path sampling¹²⁸ (which is a Monte-Carlo based rare event sampling approach) has been successfully combined with QM/MM calculations in order to study a range of systems, including human purine nucleotide dephosphorylase¹²⁹ and chorismate mutase.¹³⁰ QM/MM calculations can also be combined with energy minimization across approximate reaction coordinates to obtain the potential energy surface, in an “adiabatic mapping” approach, that has been successfully applied to a range of enzymatic systems.^131–134 Another alternative that has been successfully used to estimate the free energy profiles of enzymatic reactions^19,135–137 is the combination of QM/MM calculations and molecular dynamics simulations, through the application of umbrella sampling and the weighted histogram analysis method (WHAM).^138,139 A final recent development we would like to present in order to conclude this section is the combined quantum mechanical/discrete molecular dynamics (QM/DMD) approach of Alexandrova and coworkers.¹⁴⁰ This approach has been specifically developed for the study of metalloenzymes, and combined the accuracy of QM approaches with extensive sampling of the surroundings using DMD, which has promise to substantially increase the simulation time available to ab inito dynamics of metalloenzymes.

To conclude this section we will refer to the pure use of classical approaches, such as molecular dynamics, in the study of biological systems. These techniques have been one of the most important computational techniques in the study of complex systems, providing important insight into protein mechanics,¹⁴¹ structural-dynamics of proteins,^112,142 and features involved in the binding of substrates,¹⁴³ to name just a few examples. However, as such approaches describe atoms and bonds in a more simplified way,¹⁴⁴ they cannot be used to explore reaction mechanisms, which requires the making and breaking of chemical bonds. As will be seen in the coming sections, thanks to increasing computational power, QM-only and hybrid QM/MM approaches have allowed us to overcome this limitation, investigate the mechanisms of even complex enzyme-catalyzed reactions, and obtain important information about the fundamental chemistry involved in these processes. In addition to this, the use of approaches such as the linear response approximation as well as a novel screening approaches based either on the analysis of electrostatic group contribution or the more rigorous linear response approximation (LRA/β) approach^145,146 allows us to identify and assign the specific contribution of individual residues to the chemical step and transition state stabilization.^147,148 This, in turn, provides a molecular view of enzyme catalysis that can be used for driving artificial protein evolution and artificial enzyme design.

4. The alkaline phosphatase superfamily as a specific case study

As discussed in the Section 2, an increasing number of enzymes have been demonstrated to be capable of the promiscuous turnover of multiple, chemically distinct substrates. Understanding the underlying basis for this phenomenon has been the subject of extensive experimental studies, particularly over the course of the past ∼15 years (e.g.ref. 2, 8, 10, 13–15, 22, 81, 84 and 149–151 to name a few examples). More recently, this topic has also become the focus of increased computational attention,^{16–19,152–157} not least due to the potential of harnessing such promiscuity in artificial enzyme design.¹⁰ In this section, we will use the alkaline phosphatase (AP) superfamily as an example to illustrate both the power of theoretical approaches for rationalizing functional evolution at the atomic level, as well as some of the outlying challenges that still remain to be addressed in the field.

4.1. Overview of the alkaline phosphatase superfamily

The AP superfamily comprises a diverse set of metalloenzymes⁵⁹ with limited sequence homology, but broad similarities in structure and substrate preference.¹⁴ These enzymes preferentially hydrolyze phospho-, sulfo- and (more recently characterized^55,58,158) phosphonocarbohydrate substrates,¹⁴ harnessing a range of metal ions (including Zn²⁺, Ca²⁺, and Mn²⁺) and nucleophiles (serine, threonine and formylglycine), but with otherwise broadly similar active site architectures across the superfamily to achieve this. There are a number of factors that make this superfamily an ideal case study for testing the limits of the ability of computational approaches to address enzyme selectivity. Firstly, as commented in the Introduction, as these systems have been extensively characterized,^{14,42–45,47,48,50–58,60} there is a wealth of kinetic and structural data available for benchmarking and validation of the computational approaches used.

Tying in with this, the specificity and promiscuity of the individual members of this superfamily is well-defined,¹⁴ with members showing not just extensive promiscuity, but also cross-promiscuity, in that the native reaction of one member of this superfamily is often a promiscuous reaction in another (Fig. 5). Therefore, by carefully mapping the structural and electrostatic features linked to selectivity across this superfamily, one can potentially obtain significant insight into the factors dictating differences in functional evolution between superfamily members. The second reason this superfamily is particularly interesting to us as a model system is the inherent challenges in studying the specific reactions involved, which will be discussed in greater detail in Section 4.2.1.

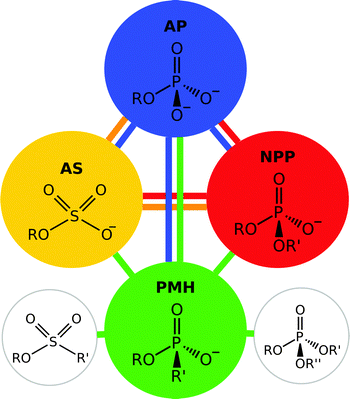Fig. 5 Members of the alkaline phosphatase (AP) superfamily have a tendency towards “cross-promiscuity”, where the native substrate for one enzyme is a promiscuous substrate for another. This figure illustrates the native and promiscuous activities of four different members of the alkaline phosphatase superfamily, specifically alkaline phosphatase (AP), arylsulfatases (PS), nucleotide pyrophosphatase/phosphodiesterase (NPP) and a phosphonate monoester hydrolases (PMH). The substrate shown within each circle represents the native substrate for the enzyme, while the colored lines indicate the relevant promiscuous activities. Additionally, PMHs have been shown to also hydrolyse phosphotriesters and sulfonate monoesters, activities not observed in other members of the superfamily. This figure is adapted from ref. 22.

4.1.1. Alkaline phosphatase and nucleotide pyrophosphate/phosphodiesterase. We will begin our discussion in this section with the name-giving member of the superfamily, alkaline phosphatase (AP), which has been the subject of not just extensive experimental studies (e.g.ref. 42, 45, 49, 50 and 54), but also, an increasing number of computational studies.^16–19,159 As was shown in Fig. 5, AP is primarily a phosphomonoesterase,⁵⁰ but is also capable of promiscuous phosphodiesterase⁴⁴ and sulfatase activities⁵⁰ (although with significantly reduced efficiencies). As the chemical step is not rate-determining in the reaction of AP with p-nitrophenyl phosphate (pNPP),⁴⁵ it has not been possible to measure k_cat for the wild-type enzyme. However, k_cat/K_M for the native phosphomonoesterase⁵⁰ activity has been measured to be 3 × 10⁷ M⁻¹ s⁻¹, in comparison to 5 × 10⁻² M⁻¹ s⁻¹ and 1 × 10⁻² M⁻¹ s⁻¹ for it's promiscuous phosphodiesterase⁴⁴ and sulfatase⁵⁰ activities respectively. Additionally, as can be seen in Fig. 6(A), the active site of AP contains three metal centers:^42,162 two Zn²⁺ that are positioned to interact with the substrate, and with the nucleophile, as well as a third Mg²⁺ coordinated to Asp, Glu, Thr and water molecules, and which has been suggested to indirectly stabilize the charge of the phosphate group in the transition.¹⁶²

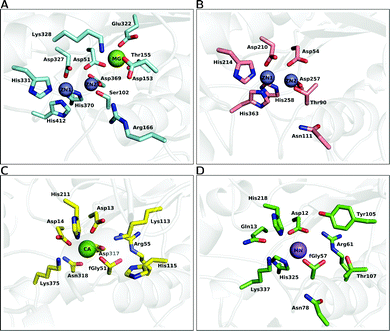Fig. 6 A comparison of the active site architectures of a number of catalytically promiscuous members of the AP superfamily. The upper half illustrates the bimetallic enzymes, (A) alkaline phosphatase (AP) and (B) nucleotide pyrophosphatase/phosphodiesterase (NPP). The lower half illustrates the active sites of (C) Pseudomonas aeruginosa arylsulfatase (AS) and (D) phosphonate monoester hydrolase (PMH). The structures were generated from the PDB files 1ED9⁵⁷ (A), 2GSN¹⁶⁰ (B), 1HDH⁵⁵ (C) and 2VQR¹⁶¹ (D), respectively.

A highly related member of this superfamily is the nucleotide pyrophosphatase/phosphodiesterase (NPP),⁴⁷ which preferentially hydrolyzes phosphate diesters. The enzyme has low sequence identity (8%) with AP,⁴⁷ however it possesses a strongly similar active site. For example, both enzymes contain a bimetallic zinc center, six conserved metal ligands (three aspartic acids and three histidines), and a threonine positioned in a manner analogous to that of a serine residue in AP (see Fig. 6(B)), which makes it difficult to understand the different specificity (primary phosphodiesterase activity and secondary phosphomonoesterase and sulfatase activities) compared to AP (see e.g.ref. 16 as an example of work that aims to address this challenging issue).

4.1.2. Arylsulfatases. Arylsulfatases are highly sequentially, structurally, and mechanistically conserved across eukaryotic and prokaryotic species, which has led to the proposal that they emerged from a common ancestral gene.¹⁶³ Members of this group include N-acetylgalactosamine-4-sulfatase,¹⁶⁴ steryl-sulfatase¹⁶⁵ (ASC), and Pseudomonas aeruginosa arylsulfatase¹⁶¹ (as well as it's human counterparts ASA¹⁶⁶ and ASB,¹⁶⁴ to name a few examples). It has been demonstrated that the arylsulfatase from Pseudomonas aeruginosa (PAS) can catalyze the hydrolysis of both phosphate mono-¹² and diesters¹³ with high efficiency, in addition to its native sulfatase activity.¹⁶¹

An overview of the active site of PAS is presented in Fig. 6(C), for comparison to other members of the superfamily such as AP and NPP. As can be seen from this figure, while there are a number of conserved features in the different active sites, there are also a number of significant differences between them. Most notable of these is the fact that the PAS active site is now mononuclear comprising a single Ca²⁺ cation rather than a dinuclear transition metal center,¹⁶¹ as well as the presence of the unusual formylglycine nucleophile common to all sulfatases.^161,167 That is, a quirk that is common to all sulfatases is the fact that, as a nucleophile, they utilize either a cysteine¹⁶⁸ or serine¹⁶⁹ that is post-translationally modified to give an aldehyde and then hydrated to give a geminal diol (steps I to II of Fig. 7, which shows an overview of the catalytic mechanism of this enzyme). What is particularly remarkable about this enzyme is the comparatively low discrimination it shows for its different substrates,^12,13 which extends to the fact that its promiscuous diesterase activity can almost compete with its native sulfatase activity (for the small model compounds used in the experimental studies).¹³ The proposed mechanism for the native sulfatase activity of PAS involves the attack of a water molecule on an aldehyde to form the corresponding geminal diol, followed by a nucleophilic attack on the sulfate with concomitant leaving group departure, and the subsequent hemiacetal cleavage to regenerate the geminal diol (Fig. 7).^13,161 As illustrated in Fig. 7, an important part of the catalytic mechanism involves the initial deprotonation of the resulting geminal diol (FGly51), two possible candidates have been proposed to act as bases, and on the basis of the crystal structure the nearby metal-coordinated aspartate (Asp317) was proposed.¹⁶¹ More recently, in a revised mechanism, we have proposed that it is one of the histidines that acts as a base in the native reaction (but not in the promiscuous reactions).^20,21

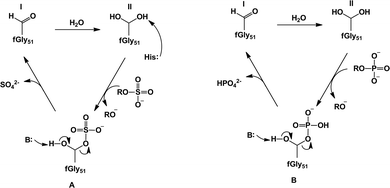Fig. 7 Our proposed revised mechanisms²¹ for (A) sulfate monoester hydrolysis and (B) phosphate ester hydrolysis by Pseudomonas aeruginosa arylsulfatase. In the case of the sulfatase activity, we propose that the sulfuryl group transfer proceeds through a histidine-as-base (His115) mechanism to activate the geminal diol that acts as a nucleophile. In the case of the phosphatase activity, we propose instead that the substrate itself can act as a base to deprotonate the nucleophile. Note that while we have only illustrated the case of a phosphate monoester (B), we also obtained similar results to this for phosphate diesters.²¹ This figure is modified from ref. 21.

4.1.3. Other (related) members of the AP superfamily. The AP superfamily includes a number of different enzymes with substantially different activities (isomerases, hydrolases, and a putative lyase).⁵⁹ Although not the focus of the present perspective, other members of this superfamily include: the cofactor-independent phosphoglycerate mutases (iPGMs),¹⁷⁰ which catalyze the interconversion of 2-phosphoglycerate to 3-phosphoglycerate, phosphonate monoester hydrolases (PMHs), which have been shown to catalyze the hydrolysis of six different substrate classes⁵⁸ (cf.Fig. 6(D)), as well as several related sulfatases.⁵⁹ In addition to the metal-binding motifs, all these enzymes contain a set of conserved amino acid residues,⁵⁹ including a nucleophilic residue sitting on the metal center (e.g. iPGM: Ser, AS and PMH: formylglycine). Remarkably, these members have also shown some degree of promiscuity, and in particular cross-promiscuity. For example, while AP can function as a phosphotransferase, iPGM can also function as a phosphatase.¹⁷¹ Another example is PMH, which possesses four secondary activities previously observed in other members of the AP superfamily (see Fig. 5), as well as, two additional activities: phosphate triester and sulfonate monoesterase (which has never been previously observed for a natural enzyme⁵⁸) activity.

Additionally, other phosphatases from outside the AP superfamily also share many of the active site features found in AP superfamily, suggesting these features may be general for the capacity often observed in enzymes that catalyze phosphoryl transfer.²² Some examples of this include protein phosphatase-1 (PP1),¹⁷² a native phosphate monoesterase which also catalyzes phosphonate monoester hydrolysis; glycerophosphodiesterase (GpdQ),¹⁷³ a diesterase that also catalyzes a series of phosphonate monoesters which are the hydrolysis products of the highly toxic organophosphonate nerve agents, sarin, soman, GF, VX, and rVX;¹⁷⁴ and phosphotriesterase (PTE),¹⁷⁵ which in addition to its native activity also catalyzes phosphodiesters and phosphonates, including organophosphate pesticides and military nerve agents. Note that, similarly to AP/NPP, each of these enzymes contain two metal ions in their active sites, although again the identity of these metal ions is varied depending on the enzyme, and includes: Zn²⁺ and Co²⁺ ions in GpdQ, two Zn²⁺ ions in PTE (although these metal ions can be replaced with Co²⁺, Ni²⁺, Mn²⁺, or Cd²⁺ with full retention of catalytic activity¹⁷⁵), and two Mn²⁺ ions in PP-1 (although these ions could also correspond to Fe²⁺, and/or Co²⁺).¹⁷⁶

4.2. Computational challenges involved in the modeling of alkaline phosphatases

The power of current theoretical approaches has allowed us to not only acquire deeper knowledge of the catalytic features of the AP members, but also to rationalize functional evolution at the atomic level. However, despite the many important contributions to the field, we still face numerous challenges. In this section we will outline some of them, in particular the specific problems associated with the modeling of the AP superfamily members. We hope these points can serve as a guide to both experimentalists and theoreticians when studying these and other related systems.

4.2.1. Modeling metal centers. As discussed in Section 4.1, one of the catalytic features of many promiscuous phosphatases (not just members of the AP superfamily) is the presence of metal ion(s) in their active sites. It has been proposed that the participation of these centers in catalytic reaction may render these enzymes particularly prone to promiscuity.^22,177–179 In fact, several examples^180–183 show that metal substitutions can change catalytic activity or even generate completely novel activities. For example, carbonic anhydrase, which is a promiscuous Zn²⁺-dependent metalloenzyme, demonstrates both novel peroxidase¹⁸⁰ and epoxidase¹⁸¹ activities when the native zinc ion is replaced with manganese. Another example is given by the non-heme Fe²⁺-dependent dioxygenase.¹⁸² Here, the native enzyme shows accidental catalytic promiscuity for hydrolysis of 4-nitrophenyl esters, and replacement of Fe with Zn²⁺ yields an additional esterase activity.

Despite the ubiquitous role of metals in proteins, and in particular their potential for the development of new enzymatic functions, many challenges remain in the modeling of such systems, which include among other aspects the lack of parameters (or even protocols) in the current force fields and technical problems associated with the stability of such systems^184,185 (although this is a non-trivial problem for quantum-chemical approaches to address as well^185,186). Currently, a number of solutions have been suggested to model metal atoms and their interaction with the protein environment. The three most common approaches are the use of a hard sphere model,¹⁸⁷ a covalent bond approach^188,189 and a dummy-model approach.^{185,190–193} The simplest approach is the non-bonded or hard sphere model, in which the metal ligand interactions are simply described through electrostatic and van del Waals parameters. This approach has been highly successful for describing alkali and alkaline-earth ions, but can prove to be challenging for systems having either multinuclear centers with closely located metal ions at the active site¹⁸⁵ or for the correct treatment of transition metals.^187,190 On the other side, covalent or bounded approaches include defined covalent bonds between the metal and ligands, and, while overall useful, such a model will be highly system-dependent and therefore difficult to transfer to other systems.¹⁹⁴ Additionally, the use of explicit (or partial) covalent bonds precludes the study of the effects of ligand exchange around the metal.

An alternative to both these sets of problems is the use of the dummy model approach^185,190 (Fig. 8). In this approach, the metal center is described by a set of cationic dummy atoms placed around the metal nucleus, encouraging a specific coordination geometry on the metal center (note, however, that as this is a non-bonded model, the dummy model retains the flexibility to change ligand coordination, as was seen for e.g.ref. 195). Models for divalent Mn,¹⁹⁰ Mg¹⁸⁵ and Zn^195,196 have been reported, which show a stable coordination sphere without the need of any additional constraint or restrains. A particular advantage of this model is the fact that, by delocalizing charge away from the metal center, this in turn reduces the repulsion between two metal centers, and makes it easier to maintain correct crystallographic geometries without the need for artificial constraints (see e.g.ref. 185, 189). Additionally, these models have been able to reproduce experimental data for catalytic effects of metal substitution with high accuracy.¹⁹⁰ Following from this, Section 5 will discuss recent studies that illustrate the challenges involved in the correct treatment of metal centers.

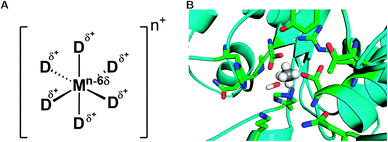Fig. 8 (A) Schematic representation of the dummy model. Shown here is a system with octahedral coordination, however, in principle, the model can be parameterized for any coordination sphere by adjusting the relevant positions and the number of dummy atoms. (B) Representative active site of a phosphonate monoester hydrolase (PDB ID 2VQR⁵⁵), where the active site metal has been replaced by an octahedral dummy model to represent the catalytic Mn²⁺ ion. The central atom and the dummy atoms are shown in grey and white, respectively, and the surrounding ligands have been highlighted to show the metal coordination.

4.2.2. Correct description of S/P centers. As outlined in Fig. 5, the reactions typically catalyzed by members of the AP superfamily involve mono- and dianionic charged substrates, the mechanisms of which are difficult to reliably model with quantitative accuracy using popular DFT approaches. Here, several challenges appear, among them, underestimation of activation barriers,¹⁹⁷ a proper description of these polarizable systems,^198,199 and the correct solvation of charged species²⁰⁰ (which is especially important in the modeling of reactions involving alkaline nucleophiles and large charge transfer). Additionally, a well-known problem with currently available DFT functionals is their tendency to underestimate barrier heights.^{197,201–203} This is not a pitfall of the theory, but rather of the approximated nature of current DFT functionals, which tend to bias toward delocalized electron distributions or fractional charges (referred to as delocalization error).²⁰³ Even though this error, which increase with the size of the system,²⁰² has been corrected for functionals such as CAM-B3LYP²⁰⁴ and LC-BLYP,²⁰⁵ it often cancels out other errors inherent to this approach.¹⁹⁷ Therefore, correcting for it can lead to a worse description of the chemistry involved, making the improvement of current functionals challenging.

An alternative for modeling of phosphorous/sulfur containing molecules is the use of semi-empirical methods such as the AM1/d¹¹⁴ (AM1 formulation with d-orbital extension) method or the empirical valence bond approach of Warshel and coworkers²⁰⁶ (which is a reactive forcefield and therefore not dependent on the orbital description). The AM1/d implementation has been specially parameterized to a combination of high-level DFT calculations and experimental data, with a particular focus on H, O and P atoms. The main advantage of this implementation is that it simultaneously allows for greater conformational sampling along the reaction coordinate than would be viable using a higher level QM approach, while at the same time providing a better description of the solvation effects and of the central phosphorus atom than that currently typically provided by other conventional semi-empirical approaches. Additionally, the empirical valence bond approach, has been rigorously parameterized to reproduce experimental data, and has provided reliable quantitative results when modeling phosphoryl group transfer reactions, as has been seen for numerous systems (see e.g.ref. 20, 21, 190 and 207–209 as well as systems discussed in ref. 103 and references cited therein).

4.2.3. Mechanistic considerations. Finally, one of the most significant challenges when studying the AP superfamily lies in the basic chemistry of the substrates involved, which are typically phosphate, sulfate or phosphonate esters. Fig. 9 outlines potential reaction pathways for the hydrolysis of a simple model phosphate ester. Here, the problems in determining the precise reaction pathways involved lie in the availability of low-lying d-orbitals on the central phosphorus atom, which means that it can readily expand its coordination sphere allowing for pentavalent transition states and intermediates in addition to an elimination–addition (D_N + A_N) dissociative pathway. In addition to this, as has been demonstrated in numerous theoretical studies,^209–212 multiple different pathways on the same surface (including extreme examples in which one pathway proceeds via an intermediate and another does not) can have similar energetics and reproduce relevant experimental observables.^209,213 This makes it difficult to unambiguously distinguish between different mechanisms, and has led to a lot of controversy in the literature as a result.^213,214

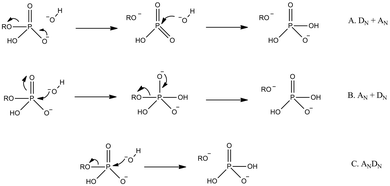Fig. 9 Generalized potential pathways for phosphate monoester hydrolysis, using the illustrative example of hydroxide attack on a phosphate monoester monoanion (we have chosen to show hydroxide rather than water as the nucleophile here to avoid any controversy with regard to proton positions at the transition state). Shown here are stepwise (A) dissociative, (B) associative, and (C) concerted mechanisms. Note that, while we have only shown inline pathways in this figure (nucleophile attacks from the opposite face as the departing leaving group), all pathways can also potentially proceed through corresponding non-inline mechanisms (nucleophile attacks from the same face as the departing leaving group with pseudo-rotation around the phosphorus center). Additionally, the concerted mechanisms can be associative or dissociative in nature, depending on the relative degrees of bond formation and cleavage at the transition state.

5. Examples of recent computational studies

In this section we will highlight some particularly relevant systems that have been extensively studied by means of computational methods. Here, we will both demonstrate the capabilities of current computational methods to provide detailed molecular insight into the action of these enzymes, as well as the current challenges still faced in the field.

5.1. Native phosphomonoesterases and diesterases

The AM1/d approach,¹¹⁴ which is a special adaptation of the semi-empirical AM1 approach to also account for d-orbitals, was introduced in Section 4.2. This approach has been successfully used in a number of studies of different members of the AP superfamily, including the name-giving member alkaline phosphatase,^16,17 and the nucleotide pyrophosphate/phosphodiesterase¹⁸ (NPP), as well as in the study of other phosphatases from outside the AP superfamily.¹⁵⁵ These studies have pioneered this subfield, as they have been the first to rigorously examine these systems computationally, providing a comparison of the nature of the transition state in aqueous solution to that in the enzyme active site, as well as an exploration of key features of the reaction such as charge transfer to the metal centers in the enzymatic reaction, and, more recently, also averaged interaction energies between the substrate and key active site residues.¹⁶

A key feature to come out of these studies pertains to the nature of the transition state of the enzyme catalyzed reaction, which, in all cases, appears to be quite dissociative. Additionally, in the cases where the background reaction was also studied, the enzymatic transition state appears to be substantially more dissociative than its solution counterpart.^16–18 In the case of phosphate monoester hydrolysis,¹⁷ a dissociative transition state would apparently be in line with the traditional interpretation of the experimentally observed linear free energy relationship (LFER) for the hydrolysis of this class of substrate in aqueous solution (see ref. 214 and references cited therein, although note that this interpretation is controversial,²¹³ as discussed below). It would also appear to agree with arguments that electrostatic interactions with positively charged groups in the AP active site do not tighten the transition state compared to the corresponding reaction in aqueous solution,²¹⁵ a conclusion that was again drawn based on the fact that similar Brønsted coefficients are observed when comparing LFER for the hydrolysis of phosphate monoester. The challenge with these empirical conclusions, however, is that not only is the qualitative interpretation of LFER exceedingly complex, particularly in the case of enzyme catalyzed reactions,^209,213 but also both associative and dissociative transition states can give rise to similar LFER.²¹⁰ Additionally, in the case of the spontaneous hydrolysis of phosphate monoesters, we have demonstrated that an associative pathway is as viable as a dissociative one.^212,216 In fact, the preferred pathway appears to rather be dependent on the nature of the leaving group,²⁰⁹ with the system preferring an associative mechanism with basic leaving groups, that becomes gradually more dissociative as the leaving group becomes more acidic.

Now in this particular case, the nucleophiles for the reactions catalyzed by AP and NPP are an ionized serine and threonine, respectively, and therefore one would expect a looser transition state, due to charge–charge repulsion between the incoming nucleophile and the charged substrate (this effect appears to be particularly pronounced in the case of the alkaline hydrolysis of dianionic phosphate monoesters^217,218). However, in the enzymatic reaction, this negative charge repulsion is being shielded by not just the catalytic metal centers, but, in the case of AP, also a nearby positively charged arginine.¹⁶¹ It has been argued that in NPP¹⁸ and AP,^16,17 this is possible because the active site stabilizes the charge distribution of the dissociative transition state. However, one would expect so much positive charge in the presence of a reaction involving charged species to, if anything, tighten the transition state (TS), as it reduces the charge repulsion between the nucleophile and the substrate allowing them to come closer together at the TS. Such a tightening of the transition state has been theoretically observed in similar enzymes,^{20,21,208,209} as well as both experimentally and theoretically in model systems.^219,220 From our work, it appears that a single metal ion is sufficient to render the transition state substantially more associative.^219,221 We would also like to point the readers to another recent computational study of phosphodiester hydrolysis by both APP and NPP,¹⁹ which employed a specialized implementation of density functional theory²²² specially parameterized for phosphate hydrolysis²²³ (SCC-DFTBPR), found significant tightening of the transition state for both enzymes. Specifically, the transition state for the hydrolysis of methyl-p-nitrophenyl phosphate was found to go from P–O distances of 2.43 and 2.23 to the nucleophile and leaving group, respectively, to ∼2.0 and 1.8–1.9 Å for the same two distances in the enzyme active sites.¹⁹ Similarly, another recent QM/MM study of phosphate monoester hydrolysis by the human placental alkaline phosphatase (PLAP) found an associative pathway proceeding through a phosphorane intermediate.²²⁴

To try to understand the discrepancy between these studies, it is useful to examine the structures for the dissociative transition states and intermediates provided in ref. 16–18. That is, a striking feature of these studies is the geometry changes of the Zn²⁺ sites during the process, in one case reaching the unexpectedly long Zn–Zn distance of as high as 7 Å in the transition state,^17,18 as compared to 4.1 Å in the crystal structures.⁵⁶ This is surprising in light of the fact that Zn²⁺ cations are known for having particularly tight coordination.^225,226 This large distance has been commented on other groups than us,¹⁹ and, in particular, a recent study combined EXAFS and X-ray crystallography to demonstrate that the binuclear Zn²⁺ motif remains fairly stable in both AP and NPP during the course of the chemical reaction step.⁵⁴ Our interest in the very large metal separation observed, however, comes from a methodological point of view, as we routinely work with metalloenzymes in our group. That is, correct modeling of metal centers, regardless of the level of theory used, is extremely challenging, and this problem is only aggravated when transition metals are included in the system.¹⁹⁴ Additionally, a known problem when modeling multinuclear metal centers is that excessive repulsion between the metal centers can cause the metal ions to “fly away” from each other,^185,192 as appears to be observed in ref. 16–18. Similarly, particularly in classical models, maintaining correct coordination during the course of the simulation poses it's own challenges.²²⁷

A number of solutions have been used to address this issue, none of which are completely satisfactory, however, all of which mitigate the problem to some extent. For example, in cases where the role of metal ions is purely structural, correct coordination can be maintained by using either full or partial bonds to the surrounding ligands,^189,228 although such a model does not allow for ligand exchange.¹⁸⁹ Alternately, some workers try to address this issue by using a non-bonded model in which medium-to-strong constraints are placed on the metal center and possibly also the surrounding ligands, in order to keep them in place during the simulation.²²⁹ Yet another alternative which sidesteps some of these problems is the dummy model^185,190 presented in Section 4. In our experience of working with metalloenzymes, metal ions moving dramatically during the course of a simulation are usually the result of incorrect electrostatic treatments, which was also commented on in ref. 19.

In any case, the interesting issue here is the fact that this unusual behavior of metal ions appears to be dependent on the size of the QM region used. That is, in an AM1/d study of phosphate monoester hydrolysis by AP, three different QM models were used,¹⁷ which have been highlighted progressively using different colours in Fig. 10. In the first two models, either the Zn²⁺ cations were not included in the QM region at all, or only the Zn²⁺ cations (without the surrounding ligands) were included in the QM region. In both these cases, the binuclear zinc center was stable during the simulation, giving distances that were also in good agreement with higher-level DFT calculations. However, in the third case, the authors used a larger QM region, that included two of the Zn²⁺ metals as well as the surrounding residues, at which point this large repulsion between the metal centers was introduced. What is noteworthy here is that this increase in distance was not caused by the two metal centers being pushed away from each other, but rather, Zn₁ apparently remained relatively stable, whereas Zn₂ was pushed away from Zn₁ (for numbering, see Fig. 10). This is unusual, because if this is the case, then Zn₂ is being pushed directly towards the third metal center (Mg²⁺), which should not happen due to large charge–charge repulsion (the distance between Zn₂ and the third magnesium ion is 4.7 Å in the relevant crystal structure used for this study¹⁷). Additionally, as can be seen from Fig. 6, Zn₂ and the active site Mg are bridged together by the carboxylate sidechain of Asp51. It is possible that, if only the two Zn²⁺ and coordinating residues, but not the Mg²⁺ are included in the QM region, this could create potential problems. However, this discussion is specific to AP, and the authors observed a similar effect in NPP,^16,18 and also in the bacterial phosphotriesterase, PTE.¹⁵⁵

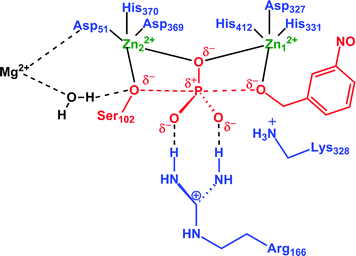Fig. 10 Definition of the three different QM regions used by López-Canut and coworkers¹⁷ in their QM/MM modeling of phosphate monoester hydrolysis by alkaline phosphatase. QM1 includes only the reacting system (in red). QM2 adds the zinc atoms (in green). QM3 incorporates the coordination shells of these two atoms and also Arg166 and Lys328 (in blue). This figure is adapted from ref. 17.

Therefore, this raises a number of key questions: (1) is this inter-metal separation indeed real, or a simulation artifact due to improper treatment of the metal centers by the approach used? This is important to establish, as the dissociative transition states proposed in ref. 16–18 are dependent on this large inter-metal separation, which does not appear to be supported by experimental work.⁵⁴ Tying in with this (2) considering that this large separation only occurs upon increasing the size of the QM region to include the metal centers and surrounding residues,¹⁷ what would happen if the QM region were extended even further to include the third metal center in AP or an even larger QM region for the other systems examined? That is, although it could be tempting to argue that the large internuclear separation is simply a problem with the treatment of the metal centers themselves, this large internuclear separation only seemed to appear once a very large QM region was included. Here, as long as the treatment was limited to just the reacting atoms and the dinuclear metal center, the system appeared to remain reasonably stable. Additionally, while transition metals are in general challenging to model, part of the problems should be mitigated by the d-orbital description included in the AM1/d approach. Therefore, it appears that substantially more validation (either by testing an even larger QM region or comparison to other approaches,¹⁹ or ideally both) is required to provide a definitive answer in either direction, however, we believe that these important works^16–18 simultaneously provide an elegant example of both the power of computational approaches and the insight they can provide, as well as the significant challenges that still remain in the field.

5.2. Sulfatases

As mentioned in Section 4.1.2, sulfatases are unusual, in that they utilize either a serine or cysteine which has been post-translationally modified to give an aldehyde and then hydrated to give a geminal diol (steps I to II of Fig. 7) as the nucleophile. This diol then attacks the relevant sulfate or phosphate ester to give rise to a covalent sulfo(phosphor)-enzyme intermediate (steps II to III) which is broken down by hemiacetal cleavage (steps III to I) to regenerate the aldehyde. This is believed to also involve acid–base catalysis in different steps of the reaction pathway, as will be discussed below. The reason that the formylglycine nucleophile is an unusual choice by the enzyme is the inherent instability of this species, as, for most geminal diols, the equilibrium is strongly in favor of the aldehyde,²³⁰ although this can be dependent on medium, and is apparently mitigated by the presence of the metal center. Additionally, the presence of this geminal diol has been argued to play an important role in the promiscuity for two reasons. Firstly, the ability to break down the product by hemiacetal cleavage sidesteps requires breaking a very thermodynamically unfavorable S–O (or P–O) bond.²³¹ Additionally, an important feature of the mechanism shown in Fig. 7 is that for all transferred groups, regardless of their nature, the covalent intermediate (III of Fig. 7) will be broken down by a common, unifying mechanism.

In order to establish the molecular basis for the observed promiscuity, we started by exploring the fundamental reactions catalyzed by this enzyme in the absence of a catalyst. Specifically, we performed a detailed theoretical comparison of the hydrolyses of the p-nitrophenyl phosphate and sulfate monoesters²¹⁶ (Fig. 11), which are prototype reactions for each class of compound respectively.^232,233 These reactions have been observed to have similar rate constants^234,235 as well as similar experimentally observed isotope effects,^235,236 and have therefore been considered to have virtually identical transition states.²³³ The only anomaly is the large difference in experimentally measured activation entropies, which is +3.5 e.u. for phosphate monoester hydrolysis and −18.5 e.u. for sulfate monoester hydrolysis.²³³ To address this issue,²¹⁶ we performed detailed DFT calculations on both reactions, generating the relevant free energy landscapes for the hydrolysis in each case, and using these to obtain the transition states highlighted in Fig. 11. In doing so, we were able to not only reproduce the virtually identical activation energies and isotope effects (within reasonable deviation from experiment), but also reproduce the large discrepancy observed in the activation entropies. Despite this, there were a number of significant differences in the transition states. That is, while the hydrolysis of the phosphate monoester was found to proceed via a compact, associative transition state, with proton transfer to the substrate²¹⁶ in analogy to a large number of other systems,^{208,209,212,237–239} the hydrolysis of the corresponding sulfate monoester was found to be far more dissociative, with no deprotonation of the nucleophile at the transition state (note that sulfate monoesters are substantially more acidic than their phosphate counterparts). In addition to the difference in the geometries and protonation patterns of the transition states involved, we also found that the hydrolysis of the highly charged p-nitrophenyl phosphate dianion is solvent destabilized, whereas that of the corresponding phosphate monoanion is slightly solvent stabilized.²¹⁶ While these differences are apparently trivial in aqueous solution, giving rise to very similar experimental observables, they are substantial in the fine-tuned environment of an enzyme active site, giving rise to the question of just how such diverse reactions can be catalyzed by the same enzyme in the first place.

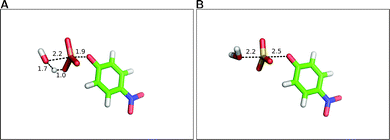Fig. 11 Comparing transition state structures for water attack on (A) p-nitrophenyl phosphate and (B) p-nitrophenyl sulfate. In both cases, the system was examined by generating 2-D energy surfaces. In the case of the phosphate, it was then possible to obtain an unconstrained transition state through direct transition state optimization of the approximate structure from the surface. This was not possible for the corresponding sulfate, so only the approximate transition state is shown here. Note the difference in the proton position, with the hydrolysis of p-nitrophenyl phosphate proceeding with protonation of the phosphate at the transition state, whereas no proton transfer has occurred in the corresponding reaction of p-nitrophenyl sulfate. All distances are in Å. This figure is based on the coordinates provided in the Supporting Information of ref. 216.

To address this issue, we performed detailed EVB studies^20,21 comparing the hydrolysis of p-nitrophenyl sulfate, ethyl-p-nitrophenyl phosphate, bis-p-nitrophenyl phosphate, and p-nitrophenyl phosphate by PAS. As the EVB approach requires the user to define the relevant diabatic states, we explored multiple potential mechanisms, in order to eliminate energetically unfavorable alternatives. As the selectivity is likely to be determined during the group transfer, we focused only on Step II to III of Fig. 7, and did not, at this stage, model the subsequent hemiacetal cleavage. In the case of the phosphate monoester and diesters, we found that the preferred mechanism is a substrate-as-base mechanism, in which the nucleophile is activated by the substrate itself, in analogy to a number of other systems including Ras GTPase^208,209,237 and EF-Tu,^240,241 to name a few examples.

As mentioned above and observed in ref. 216, as sulfate esters are far more acidic, such a mechanism is not available for the native reaction as the sulfate will be a terrible proton acceptor. Here, the preferred mechanism appears instead to be one in which a nearby (more basic) histidine is utilized as a general base to activate the nucleophile.²¹ We also explored the suggestion that a metal-coordinated Asp adjacent to the nucleophile can act as a base,^157,161 but found this mechanism to have very unfavorable energetics, perhaps unsurprisingly in light of the low pK_a of a metal-bound aspartate, as well as the fact that this residue plays a clear structural role and protonating it will be detrimental to the stability of the metal coordination. Additionally, we found no need for acid catalysis to protonate the departing leaving group, however, in this particular case, one is dealing with a very good leaving group (p-nitrophenol) and this may not be the case for more basic leaving groups such as e.g. phenol (to name one example). From the results of this work,^20,21,216 we proposed the revised mechanism shown in Fig. 7(B). Fig. 12 presents a comparison of representative transition states for the different substrates we have studied, and Table 1 presents a comparison of the corresponding distances in enzyme and in aqueous solution, based on data originally presented in ref. 21. We believe that the switch from a substrate-as-base mechanism to needing a general base when moving between the phosphatase and sulfatase activities is significant from an evolutionary perspective, as it puts additional pressure on the enzyme to acquire a general base, which is not necessary for the phosphatase activity. This suggests that the promiscuous activities observed in PAS are merely chemically “simplified” versions of the native sulfatase activity, and also provide one possible reason for the fact that sulfate esters are far less commonly used by Nature than their phosphate counterparts (see also discussion in ref. 213). However, our work^20,21 led to a number of other unexpected observations. The first is with respect to the nature of the transition state for the sulfuryl transfer reaction catalyzed by PAS. That is, as can be seen in Table 1, while the presence of even a single metal ion tightens all transition states with respect to their solution counterparts, this effect is now most pronounced in the case of the sulfate ester which becomes even more associative in the enzyme than any of the phosphate substrates. Additionally, even when we tried to force a more dissociative mechanism for the sulfate ester in aqueous solution by adjusting the relevant forcefield parameters, once moving back to the enzyme (using the same parameter set as for the background reaction), the enzyme tried to substantially tighten the transition state, giving a reaction that was slightly less energetically favorable than the fully associative transition state shown in Fig. 12(A) and Table 1.²¹ In contrast to this, the substrate towards which PAS shows the next most proficient activity is the bis-p-nitrophenyl phosphate diester, which, in the PAS active site, now has the least associative transition state of all substrates studied in our work. When combined with the fact that PAS shows significantly greater proficiency towards monoanionic than dianionic substrates,¹³ this strongly points towards a role for electrostatics in driving the promiscuity. This was verified by overlaying the electrostatic contribution of different active site residues to the calculated activation barrier for the hydrolysis of each substrate (Fig. 13), which shows almost perfect qualitative overlap, with quantitative differences reflecting the differing demands of catalyzing such chemically diverse substrates. This strongly supports our belief that the molecular basis for the promiscuity is purely electrostatic, leading us to argue for chemically-driven protein evolution in this superfamily.²¹

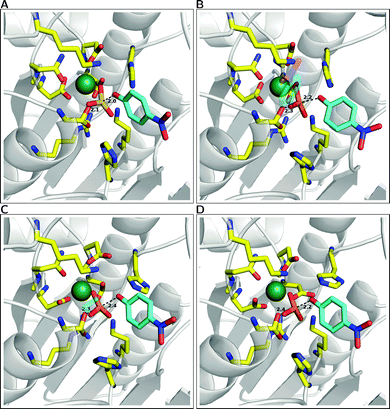Fig. 12 A comparison of the representative transition state structures for the reactions of Pseudomonas aeruginosa arylsulfatase (PAS) complexed with (A) p-nitrophenyl phosphate, (B) ethyl-p-nitrophenyl phosphate, (C) bis-p-nitrophenyl phosphate and (D) p-nitrophenyl sulfate. Labeling for key active site residues can be found in Fig. 6C, and P(S)–O distances to the leaving group and nucleophile oxygens highlighted here are averages over ten trajectories. This figure is based on data presented in Table 1 and ref. 21.

Table 1 A comparison of the changes in transition state geometries for the different substrates shown in Fig. 12, upon moving from aqueous solution to the active site of Pseudomonas auerignosa arylsulfatase. The labels P(S)–O_nuc and P(–S)–O_lg denote Phosphorus(Sulfur)–Oxygen distances^a to the incoming nucleophile and the departing leaving group respectively. The substrates shown here are, in order, (1a) p-nitrophenyl sulfate (associative pathway), (1b) p-nitrophenyl sulfate (dissociative pathway), (2) ethyl-p-nitrophenyl phosphate, (3) bis-p-nitrophenyl phosphate, (4) p-nitrophenyl phosphate. These data were originally presented in ref. 21 (see also ref. 21 and the main text for a discussion of the associative and the dissociative mechanism for the sulfuryl transfer reaction)

Substrate	Water		Enzyme		Difference
	P(S)–Onuc	P(S)–Olg	P(S)–Onuc	P(S)–Olg	P(S)–Onuc	P(S)–Olg
a All distances are in Å and are averages over 10 MD trajectories (500 000 discrete transition state conformations for each substrate).
(1a)	2.257	2.001	2.150	1.979	−0.107	−0.022
(1b)	2.504	2.328	2.348	2.199	−0.156	−0.129
(2)	2.466	2.356	2.320	2.307	−0.146	−0.049
(3)	2.470	2.349	2.401	2.280	−0.069	−0.069
(4)	2.443	2.272	2.350	2.234	−0.093	−0.038

---

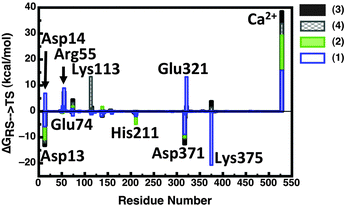Fig. 13 Overlay of the electrostatic group contributions to the calculated activation barrier of Pseudomonas aeruginosa arylsulfatase (PAS) for each substrate calculated using the LRA approach (original data presented in Table S3 of ref. 21). This figure is adapted from ref. 21.

As an aside, we would like to point out that, at a similar time to the publication of our work, an elegant experimental study made a strong case in favor of cooperating active site residues with multiple roles as well as catalytic backups in the case of the promiscuous serum paraoxonase PON1.²⁴² At least qualitatively, this would support our hypothesis, as it reaches similar conclusions on an independent system using different techniques. Therefore, we believe that the examples illustrated here, both in the case of PAS but also in the case of AP and NPP demonstrate that there are a wide variety of computational tools available in order to quantitatively dissect the molecular basis of catalytic promiscuity, and, particularly when different approaches are combined for validation purposes, computational power has reached a stage where we are potentially able to not only rationalize but also guide protein evolution in silico.

6. Overview and future perspectives

In recent years, it has become increasingly clear that enzyme promiscuity plays an important role in protein evolution.^7,8,15 In the present perspective, we have focused on advances in the computational modeling of catalytic promiscuity in the alkaline phosphatase superfamily. We have chosen this system in particular due to the specific challenges these enzymes pose, ranging from the complexity of the actual reaction mechanisms, to the large system size (one of the smaller members of this superfamily, PAS, is a monomer with 536 residues¹⁶¹) to the known problems with reliable treatment of the catalytic metal centers. We demonstrate that, while there are still substantial problems and open questions that need addressing when working with such systems, computational tools can provide significant insight into the chemical processes involved, and computational power has developed to the stage to make large-scale studies finally possible. Following from this, although we have not discussed this topic specifically in this review, there are many groups working on rapid screening approaches in order to predict mutation hotspots and guide laboratory evolution studies.^{145,146,243–245} When combined with fast approaches like the EVB which allow for extensive conformational sampling, and which are known to reliably reproduce and predict the effect of mutations,¹⁰³ this creates a feedback loop by which it is in principle possible to mimic evolution in silico and reproduce evolutionary trajectories obtained from, for instance, laboratory evolution studies. If this is done in a systematic way, comparing the structural and electrostatic features driving specificity and selectivity within an enzyme superfamily will provide a “roadmap” for protein evolution, providing an invaluable tool for subsequent artificial enzyme design.

Acknowledgements

The European Research Council has provided financial support under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 306474. SCLK would also like to thank the Swedish Research Council (Vetenskapsrådet) for a Young Group Leader grant 2010-5026. The authors would like to thank Ulf Ryde, Bert van Loo, and Johan Åqvist for helpful comments on the manuscript. We would also like to thank the Swedish Foundation for Internationalization in Higher Education and Research (STINT) for facilitating valuable discussion with colleagues in the United Kingdom that has substantially helped improve this manuscript. Finally, we would like to thank Joppe van der Spoel, studio de Wilde Muis (http://www.dewildemuis.nl/) for the cover artwork.

References

1. R. Wolfenden and M. J. Snider, Acc. Chem. Res., 2001, 34, 938–945.
2. A. Aharoni, L. Gaidukov, O. Khersonsky, S. McQ Gould, C. Roodveldt and D. S. Tawfik, Nat. Genet., 2005, 37, 73–76.
3. D. I. Andersson and D. Hughes, Drug Resist. Updates, 2012, 15, 162–172.
4. A. N. Bigley and F. M. Raushel, Biochim. Biophys. Acta, 2013, 1834, 443–453.
5. M. Paolini, G. L. Biagi, C. Bauer and G. Cantelli-Forti, Life Sci., 1998, 63, 2141–2146.
6. J. A. Gerlt and P. C. Babbitt, Annu. Rev. Biochem., 2001, 70, 209–246.
7. R. A. Jensen, Annu. Rev. Microbiol., 1976, 30, 409–425.
8. P. J. O'Brien and D. Herschlag, Chem. Biol., 1999, 6, R91–R105.
9. A. Yarnell, Chem. Eng. News, 2003, 81, 33–35.
10. U. T. Bornscheuer and R. J. Kazlauskas, Angew. Chem., Int. Ed., 2004, 43, 6032–6040.
11. O. Khersonsky, C. Roodveldt and D. S. Tawfik, Curr. Opin. Chem. Biol., 2006, 10, 498–508.
12. L. F. Olguin, S. E. Askew, A. C. O'Donoghue and F. Hollfelder, J. Am. Chem. Soc., 2008, 130, 16547–16555.
13. A. C. Babtie, S. Bandyopadhyay, L. F. Olguin and F. Hollfelder, Angew. Chem., Int. Ed., 2009, 48, 3692–3694.
14. S. Jonas and F. Hollfelder, Pure Appl. Chem., 2009, 81, 731–742.
15. O. Khersonsky and D. S. Tawfik, Annu. Rev. Biochem., 2010, 79, 471–505.
16. V. Lopéz-Canut, M. Roca, J. Bertrán, V. Moliner and I. Tuñon, J. Am. Chem. Soc., 2011, 133, 12050–12062.
17. V. Lopéz-Canut, S. Martí, J. Bertrán, V. Moliner and I. Tuñon, J. Phys. Chem. B, 2009, 113, 7816–7824.
18. V. Lopéz-Canut, M. Roca, J. Bertrán, V. Moliner and I. Tuñon, J. Am. Chem. Soc., 2010, 132, 6955–6963.
19. G. Hou and Q. Cui, J. Am. Chem. Soc., 2012, 134, 229–246.
20. J. H. Luo, B. van Loo and S. C. L. Kamerlin, Proteins: Struct., Funct., Bioinf., 2012, 80, 1211–1226.
21. J. Luo, B. van Loo and S. C. L. Kamerlin, FEBS Lett., 2012, 586, 1622–1630.
22. M. F. Mohamed and F. Hollfelder, Biochim. Biophys. Acta, 2013, 1834, 417–424.
23. M. Ben-David, G. Wieczorek, M. Elias, I. Silman, J. L. Sussman and D. S. Tawfik, J. Mol. Biol., 2013, 425, 1028–1038.
24. P. Várnai and A. Warshel, J. Am. Chem. Soc., 2000, 122, 3849–3860.
25. K. Hult and P. Berglund, Trends Biotechnol., 2007, 25, 231–238.
26. M. D. Toscano, K. J. Woycechowsky and D. Hilvert, Angew. Chem., Int. Ed., 2007, 46, 4468–4470.
27. P. A. Romero and F. H. Arnold, Nat. Rev. Mol. Cell Biol., 2009, 10, 866–876.
28. A. E. Lobkovsky, Y. I. Wolf and E. V. Koonin, PLoS Comput. Biol., 2011, 7, e1002302.
29. D. L. Robertson and S. C. Lovell, Biochem. Soc. Trans., 2009, 37, 768–771.
30. L. C. James and D. S. Tawfik, Trends Biochem. Sci., 2003, 28, 361–368.
31. N. Tokuriki and D. S. Tawfik, Science, 2009, 324, 203–207.
32. S. C. L. Kamerlin, J. Mavrí and A. Warshel, FEBS Lett., 2010, 584, 2759–2766.
33. S. C. L. Kamerlin and A. Warshel, Proteins: Struct., Funct., Bioinf., 2010, 78, 1339–1375.
34. E. O. McCullum, B. A. Williams, J. Zhang and J. C. Chaput, Methods Mol. Biol., 2010, 634, 103–109.
35. C. Jäckel, P. Kast and D. Hilvert, Annu. Rev. Biophys., 2008, 37, 153–173.
36. S. G. Peisajovich and D. S. Tawfik, Nat. Methods, 2007, 4, 991–994.
37. P. Carbonell and J.-L. Faulon, Bioinformatics, 2010, 26, 2012–2019.
38. S. Chakraborty and B. J. Rao, PLoS One, 2012, 7, e32011.
39. P. D. Williams, D. D. Pollock, B. P. Blackburne and R. A. Goldstein, PLoS Comput. Biol., 2006, 2, e69.
40. J. M. Thomson, E. A. Gaucher, M. F. Burgan, D. W. De Kee, T. Li, J. P. Aris and S. A. Benner, Nat. Genet., 2005, 37, 630–635.
41. R. Huang, F. Hippauf, D. Rohrbeck, M. Haustein, K. Wenke, J. Feike, N. Sorrelle, B. Piechulla and T. J. Barkman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2966–2971.
42. J. E. Coleman, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 441–483.
43. F. Hollfelder and D. Herschlag, Biochemistry, 1995, 34, 12255–12264.
44. P. J. O'Brien and D. Herschlag, Biochemistry, 2001, 40, 5691–5699.
45. P. J. O'Brien and D. Herschlag, Biochemistry, 2002, 41, 3207–3225.
46. T. T. Simopolous and W. P. Jencks, Biochemistry, 1994, 33, 10375–10380.
47. J. G. Zalatan, T. D. Fenn, T. A. Brunger and D. Herschlag, Biochemistry, 2006, 45, 9788–9803.
48. J. K. Lassila and D. Herschlag, Biochemistry, 2008, 47, 12853–12859.
49. I. Catrina, P. J. O'Brien, J. Purcell, I. Nikolic-Hughes, J. G. Zalatan, A. C. Hengge and D. Herschlag, J. Am. Chem. Soc., 2007, 129, 5760–5765.
50. P. J. O'Brien and D. Herschlag, J. Am. Chem. Soc., 1998, 120, 12369.
51. P. J. O'Brien and D. Herschlag, J. Am. Chem. Soc., 1999, 121, 11022–11023.
52. J. G. Zalatan and D. Herschlag, J. Am. Chem. Soc., 2006, 128, 1293–1303.
53. R. Gijsbers, H. Ceulemans, W. Stalmans and M. Bollen, J. Biol. Chem., 2001, 276, 1361–1368.
54. E. Bobyr, J. K. Lassila, H. I. Wiersma-Koch, T. D. Fenn, J. J. Lee, I. Nikolic-Hughes, K. O. Hodgson, D. C. Rees, B. Hedman and D. Herschlag, J. Mol. Biol., 2012, 415, 102–117.
55. S. Jonas, B. van Loo, M. Hyvönen and F. Hollfelder, J. Mol. Biol., 2008, 384, 120–136.
56. E. E. Kim and H. W. Wyckoff, J. Mol. Biol., 1991, 218, 449.
57. B. Stec, K. M. Holtz and E. R. Kantrowitz, J. Mol. Biol., 2000, 299, 1303–1311.
58. B. van Loo, S. Jonas, A. C. Babtie, A. Benjdia, O. Berteau, M. Hyvönen and F. Hollfelder, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2740–2745.
59. M. Y. Galperin, A. Bairoch and E. V. Koonin, Protein Sci., 1998, 7, 1829–1835.
60. M. Y. Galperin and M. J. Jedrzejas, Proteins, 2001, 45, 318–324.
61. E. Fischer, Ber. Dtsch. Chem. Ges., 1894, 27, 2985–2993.
62. P. Gatti-Lafranconi and F. Hollfelder, ChemBioChem, 2013, 14, 285–292.
63. I. Nobeli, A. D. Favia and J. M. Thornton, Nat. Biotechnol., 2009, 27, 157–167.
64. M. E. Glasner, J. A. Gerlt and P. C. Babbitt, Curr. Opin. Chem. Biol., 2006, 10, 492–497.
65. N. J. Turner, Nat. Chem. Biol., 2009, 5, 567–573.
66. E. D. Getzoff, D. E. Cabelli, C. L. Fisher, H. E. Parge, M. S. Viezzoli, L. Banci and R. A. Hallewell, Nature, 1992, 358, 347–351.
67. R. Chen, A. Greer and A. M. Dean, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 11666–11670.
68. R. Chen, Trends Biotechnol., 2001, 19, 13–14.
69. S. S. Hederos, L. L. Tegler, J. J. Carlsson, B. B. Persson, J. J. Viljanen and K. S. Broo, Org. Biomol. Chem., 2006, 4, 90–97.
70. F. H. Arnold, Acc. Chem. Res., 1998, 31, 125–131.
71. J. Helge and U. T. Bornscheuer, ChemBioChem, 2010, 11, 1861–1866.
72. R. A. Chica, N. Doucet and J. N. Pelletier, Curr. Opin. Biotechnol., 2005, 16, 378–384.
73. M. T. Reetz and J. D. Carballeira, Nat. Protoc., 2007, 2, 891–903.
74. T. S. Chen and A. E. Keating, Protein Sci., 2012, 21, 949–963.
75. D. Roethlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, 164–166.
76. A. N. Alexandrova, D. Röthlisberger, D. Baker and W. L. Jorgensen, J. Am. Chem. Soc., 2008, 130, 15907–15915.
77. O. Khersonsky, D. Röthlisberger, A. M. Wollacott, P. Murphy, O. Dym, S. Albeck, G. Kiss, K. N. Houk, D. Baker and D. S. Tawfik, J. Mol. Biol., 2010, 407, 391–412.
78. D. Baker, Protein Sci., 2010, 19, 1817–1819.
79. A. Barrozo, R. Borstnar, G. Marloie and S. C. L. Kamerlin, Int. J. Mol. Sci., 2012, 13, 12428–12460.
80. M. Goldsmith and D. S. Tawfik, Curr. Opin. Struct. Biol., 2012, 22, 406–412.
81. L. Afriat, C. Roodveldt, G. Manco and D. S. Tawfik, Biochemistry, 2006, 45, 13677–13686.
82. A. Babtie, N. Tokuriki and F. Hollfelder, Curr. Opin. Chem. Biol., 2010, 14, 200–207.
83. H. Garcia-Seisdedos, B. Ibarra-Molero and J. M. Sanchez-Ruiz, PLoS Comput. Biol., 2012, 8, e1002558.
84. M. Elias and D. S. Tawfik, J. Biol. Chem., 2012, 287, 11–20.
85. O. Khersonsky, G. Kiss, D. Röthlisberger, O. Dym, S. Albeck, K. N. Houk, D. Baker and D. S. Tawfik, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10358–10363.
86. R. K. Kuipers, H. J. Jooseten, W. J. van Berkel, N. G. Leferink, E. Rooijen, E. Ittmann, F. van Zimmeren, H. Jochens, U. Bornscheuer, G. Vriend, V. A. dos Santos and P. J. Schaap, Proteins: Struct., Funct., Bioinf., 2010, 78, 2101–2113.
87. I. Sandler, M. Abu-Qarn and A. Aharoni, Mol. BioSyst., 2013, 9, 175–181.
88. W. F. van Gunsteren and H. J. C. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992–1023.
89. W. A. de Jong, E. Bylaska, N. Govind, C. L. Janssen, K. Kowalski, T. Muller, I. M. B. Nielsen, H. J. J. van Dam, V. Veryazov and R. Lindh, Phys. Chem. Chem. Phys., 2010, 12, 6896–6920.
90. D. E. Shaw, M. M. Deneroff, R. O. Dror, J. S. Kuskin, R. H. Larson, J. K. Salmon, C. Young, B. Batson, K. J. Bowers, J. C. Chao, M. P. Eastwood, J. Gagliardo, J. P. Grossman, C. R. Ho, D. J. Ierardi, I. Kolossváry, J. L. Klepeis, T. Layman, C. McLeavey, M. A. Moraes, R. Mueller, E. C. Priest, Y. Shan, J. Spengler, M. Theobald, B. Towles and S. C. Wang, Anton, a special-purpose machine for molecular dynamics simulation, San Diego, California, 2007.
91. L. Dematte and D. Prandi, Briefings Bioinf., 2010, 11, 323–333.
92. W. F. van Gunsteren, D. Bakowies, R. Baron, I. Chandrasekhar, M. Christen, X. Daura, P. Gee, D. P. Geerke, A. Glattli, P. H. Hünenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. van der Vegt and H. B. Yu, Angew. Chem., Int. Ed., 2006, 45, 4064–4092.
93. D. Riccardi, P. Schaefer, Y. Yang, H. Yu, N. Ghosh, X. Prat-Resina, P. König, G. Li, D. Xu, H. Guo, M. Elstner and Q. Cui, J. Phys. Chem. B, 2006, 110, 6458–6469.
94. A. Shurki and A. Warshel, Adv. Protein Chem., 2003, 66, 249–313.
95. H. Hu and W. T. Yang, THEOCHEM, 2009, 898, 17–30.
96. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
97. O. Acevedo and W. L. Jorgensen, Acc. Chem. Res., 2010, 43, 142–151.
98. R. Lonsdale, K. E. Ranaghan and A. J. Mulholland, Chem. Commun., 2010, 46, 2354–2372.
99. S. C. L. Kamerlin, S. Vicatos and A. Warshel, Annu. Rev. Phys. Chem., 2011, 62, 41–64.
100. S. F. Sousa, P. A. Fernandes and M. J. Ramos, Phys. Chem. Chem. Phys., 2012, 14, 12431–12441.
101. P. E. Siegbahn and F. Himo, J. Biol. Inorg. Chem., 2009, 14, 643–651.
102. P. E. M. Siegbahn and F. Himo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336.
103. A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235.
104. M. P. Frushicheva, J. Cao, Z. T. Chu and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16869–16874.
105. A. Cavalli and P. Carloni, J. Am. Chem. Soc., 2002, 124, 3763–3768.
106. R.-Z. Liao, J.-G. Yu and F. Himo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22523–22527.
107. R.-Z. Liao and W. Thiel, J. Chem. Theory Comput., 2012, 8, 3793–3803.
108. S. C. L. Kamerlin, M. Haranczyk and A. Warshel, J. Phys. Chem. B, 2009, 113, 1253–1272.
109. C.-E. Chang, W. Chen and M. K. Gilson, J. Chem. Theory Comput., 2005, 1, 1017–1028.
110. L. H. Hu, J. Eliasson, J. Heimdal and U. Ryde, J. Phys. Chem. A, 2009, 113, 11793–11800.
111. C. V. Sumowski and C. Ochsenfeld, J. Phys. Chem. A, 2009, 113, 11734–11741.
112. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
113. H. Hu and W. Yang, Annu. Rev. Phys. Chem., 2008, 59, 573–601.
114. K. Nam, Q. Cui, J. Gao and D. M. York, J. Chem. Theory Comput., 2007, 3, 486–504.
115. S. C. L. Kamerlin and A. Warshel, Faraday Discuss., 2010, 145, 71–106.
116. G. Hou, X. Zhu, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2012, 8, 4293–4304.
117. M. Klähn, S. Braun-Sand, E. Rosta and A. Warshel, J. Phys. Chem. B, 2005, 109, 15645–15650.
118. M. Štrajbl, G. Hong and A. Warshel, J. Phys. Chem. B, 2002, 106, 13333–13343.
119. E. Rosta, M. Klähn and A. Warshel, J. Phys. Chem. B, 2006, 110, 2934–2941.
120. N. V. Plotnikov, S. C. L. Kamerlin and A. Warshel, J. Phys. Chem. B, 2011, 115, 7950–7962.
121. N. V. Plotnikov and A. Warshel, J. Phys. Chem. B, 2012, 116, 10342–10356.
122. J. J. Ruiz-Pernía, E. Silla, I. Tuñón, S. Martí and V. Moliner, J. Phys. Chem. B, 2004, 108, 8427–8433.
123. A. Warshel, Computer modeling of chemical reactions in enzymes and solutions, Wiley, New York, 1991.
124. A. Warshel, F. Sussman and J.-K. Hwang, J. Mol. Biol., 1988, 201, 139–159.
125. S. C. Kamerlin, S. Vicatos, A. Dryga and A. Warshel, Annu. Rev. Phys. Chem., 2011, 62, 41–64.
126. M. Strajbl, A. Shurki and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14834–14839.
127. L. Mones, P. Kulhánek, I. Simon, A. Laio and M. Fuxreiter, J. Phys. Chem. B, 2009, 113, 7867–7873.
128. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318.
129. S. Saen-Oon, S. Quaytman-Machleder, V. L. Schramm and S. D. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16543–16548.
130. R. Crehuet and M. J. Field, J. Phys. Chem. B, 2007, 111, 5708–5718.
131. A. J. Mulholland, Drug Discovery Today, 2005, 10, 1393–1402.
132. A. Lodola, M. Mor, J. C. Hermann, G. Tarzia, D. Piomelli and A. J. Mulholland, Chem. Commun., 2005, 4399–4401.
133. A. Lodola, M. Mor, J. Zurek, G. Tarzia, D. Piomelli, J. N. Harvey and A. J. Mulholland, Biophys. J., 2007, 92, L20–L22.
134. M. W. Y. Szeto, J. I. Mujika, J. Zurek, A. J. Mulholland and J. N. Harvey, THEOCHEM, 2009, 898, 106–114.
135. G. L. Cui, B. Wang and K. M. Merz, Biochemistry, 2005, 44, 16513–16523.
136. Y. Z. Zhou, S. L. Wang and Y. K. Zhang, J. Phys. Chem. B, 2010, 114, 8817–8825.
137. J. I. Mujika, X. Lopez and A. J. Mulholland, Org. Biomol. Chem., 2012, 10, 1207–1218.
138. A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1989, 63, 1195–1198.
139. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
140. M. Sparta, D. Shirvanyants, F. Ding, N. V. Dokholyan and A. N. Alexandrova, Biophys. J., 2012, 103, 767–776.
141. M. Sotomayor and K. Schulten, Science, 2007, 316, 1144–1148.
142. G. G. Dodson, D. P. Lane and C. S. Verma, EMBO Rep., 2008, 9, 144–150.
143. J. Durrant and J. A. McCammon, BMC Biol., 2011, 9, 71.
144. J. M. Haile, Molecular dynamics simulation: elementary methods, Wiley, New York, 1997.
145. M. Roca, A. Vardi-Kilshtain and A. Warshel, Biochemistry, 2009, 48, 3046–3056.
146. M. P. Frushicheva and A. Warshel, ChemBioChem, 2012, 23, 215–223.
147. I. Muegge, H. Tao and A. Warshel, Protein Eng., 1997, 10, 1363–1372.
148. I. Muegge, T. Schweins and A. Warshel, Proteins: Struct., Funct., Genet., 1998, 30, 407–423.
149. L. Afriat-Jurnou, C. J. Jackson and D. S. Tawfik, Biochemistry, 2012, 51, 6047–6055.
150. U. Alcolombri, M. Elias and D. S. Tawfik, J. Mol. Biol., 2011, 411, 837–853.
151. M. Harel, A. Aharoni, L. Gaidukov, B. Brumshtein, O. Khersonsky, R. Meged, H. Dvir, R. B. G. Ravelli, A. McCarthy, L. Toker, I. Silman, J. L. Sussman and D. S. Tawfik, Nat. Struct. Mol. Biol., 2004, 11, 412–419.
152. S. Martí, J. Andres, V. Moliner, E. Silla, I. Tuñon and J. Bertrán, J. Am. Chem. Soc., 2009, 131, 16156–16161.
153. S. K. Padhi, R. Fujii, G. A. Legatt, S. L. Fossum, R. Berchtold and R. J. Kazlauskas, Chem. Biol., 2010, 17, 863–871.
154. J. Aranda, M. Roca and I. Tuñon, Org. Biomol. Chem., 2012, 10, 5395–5400.
155. V. López-Canut, J. J. Ruiz-Pernía, R. Castillo, V. Moliner and I. Tuñón, Chem.–Eur. J., 2012, 18, 9612–9621.
156. S. Ferrer, S. Martí, V. Moliner, I. Tuñon and J. Bertrán, Phys. Chem. Chem. Phys., 2012, 14, 3482–3489.
157. T. Marino, N. Russo and M. Toscano, Chem.–Eur. J., 2013, 19, 2185–2192.
158. S. B. Dotson, C. E. Smith, C. S. Ling, G. F. Barry and G. M. Kishore, J. Biol. Chem., 1996, 271, 25754–25761.
159. G. L. Borosky and S. Lin, J. Chem. Inf. Model., 2011, 51, 2538–2548.
160. J. G. Zalatan, T. D. Fenn, A. T. Brunger and D. Herschlag, Biochemistry, 2006, 45, 9788–9803.
161. I. Boltes, H. Czapinska, A. Kahnert, R. von Bülow, T. Dierks, B. Schmidt, K. von Figura, M. A. Kertesz and I. Usón, Structure, 2001, 9, 483–491.
162. J. G. Zalatan, T. D. Fenn and D. Herschlag, J. Mol. Biol., 2008, 384, 1174–1189.
163. S. R. Hanson, M. D. Best and C.-H. Wong, Angew. Chem., Int. Ed., 2004, 43, 5736–5763.
164. C. S. Bond, P. R. Clements, S. J. Ashby, C. A. Collyer, S. J. Harrop, J. J. Hopwood and J. M. Guss, Structure, 1997, 5, 277–289.
165. F. G. Hernandez-Guzman, T. Higashiyama, W. Pangborn, Y. Osawa and D. Ghosh, J. Biol. Chem., 2003, 278, 22989–22997.
166. G. Lukatela, N. Krauss, K. Theis, T. Selmer, V. Gieselmann, K. von Figura and W. Saenger, Biochemistry, 1998, 37, 3654–3664.
167. A. Knaust, B. Schmidt, T. Dierks, R. von Bulow and K. von Figura, Biochemistry, 1998, 37, 13941–13946.
168. T. Dierks, M. R. Lecca, P. Schlotterhose, B. Schmidt and K. von Figura, EMBO J., 1999, 18, 2084–2091.
169. T. Dierks, C. Miech, J. Hummerjohann, B. Schmidt, M. A. Kertesz and K. von Figura, J. Biol. Chem., 1998, 273, 25560–25564.
170. M. J. Jedrzejas, M. Chander, P. Setlow and G. Krishnasamy, J. Biol. Chem., 2000, 275, 23146–23153.
171. J. A. Gatehouse and J. R. Knowles, Biochemistry, 1977, 16, 3045–3050.
172. C. McWhirter, E. A. Lund, E. A. Tanifum, G. Feng, Q. I. Sheikh, A. C. Hengge and N. H. Williams, J. Am. Chem. Soc., 2008, 130, 13673–13682.
173. C. J. Jackson, P. D. Carr, J. W. Liu, S. J. Watt, J. L. Beck and D. L. Ollis, J. Mol. Biol., 2007, 367, 1047–1062.
174. E. Ghanem, Y. Li, C. Xu and F. M. Raushel, Biochemistry, 2007, 46, 9032–9040.
175. H. Shim, S. B. Hong and F. M. Raushel, J. Biol. Chem., 1998, 273, 17445–17450.
176. M. Terrak, F. Kerff, K. Langsetmo, T. Tao and R. Dominguez, Nature, 2004, 429, 780–784.
177. M. S. Humble and P. Berglund, Eur. J. Org. Chem., 2011, 3391–3401.
178. J. Steinreiber and T. R. Ward, Coord. Chem. Rev., 2008, 252, 751–766.
179. C. E. Valdez and A. N. Alexandrova, J. Phys. Chem. B, 2012, 116, 10649–10656.
180. K. Okrasa and R. J. Kazlauskas, Chem.–Eur. J., 2006, 12, 1587–1596.
181. A. Fernandez-Gacio, A. Codina, J. Fastrez, O. Riant and P. Soumillion, ChemBioChem, 2006, 7, 1013–1016.
182. S. Leitgeb and B. Nidetzky, ChemBioChem, 2010, 11, 502–505.
183. Q. Jing and R. J. Kazlauskas, ChemCatChem, 2010, 2, 953–957.
184. L. Banci, Curr. Opin. Chem. Biol., 2003, 7, 143–149.
185. P. Oelschlaeger, M. Klahn, W. A. Beard, S. H. Wilson and A. Warshel, J. Mol. Biol., 2007, 366, 687–701.
186. P. E. Siegbahn, J. Biol. Inorg. Chem., 2006, 11, 695–701.
187. J. Åqvist, THEOCHEM, 1992, 256, 135–152.
188. D. Lu and G. A. Voth, Proteins, 1998, 33, 119–134.
189. D. V. Sakharov and C. Lim, J. Am. Chem. Soc., 2005, 127, 4921–4929.
190. J. Åqvist and A. Warshel, J. Am. Chem. Soc., 1990, 112, 2860–2868.
191. Y.-P. Pang, J. Mol. Model., 1999, 5, 196–202.
192. Y.-P. Pang, Proteins: Struct., Funct., Genet., 2001, 45, 183–189.
193. P. Oelschlaeger, R. D. Schmid and J. Pleiss, Biochemistry, 2003, 42, 8945–8956.
194. S. Sousa, P. Fernandes and M. Ramos, in Kinetics and Dynamics, ed. P. Paneth and A. Dybala-Defratyka, Springer, Netherlands, 2010, vol. 12, ch. 11, pp. 299–330.
195. J. Åqvist and A. Warshel, J. Mol. Biol., 1992, 224, 7–14.
196. Y.-P. Pang, K. U. N. Xu, J. E. Yazal and F. G. Prendergast, Protein Sci., 2000, 9, 1857–1865.
197. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
198. P. C. Aeberhard, J. S. Arey, I. C. Lin and U. Rothlisberger, J. Chem. Theory Comput., 2008, 5, 23–28.
199. D. K. Hahn, K. S. RaghuVeer and J. V. Ortiz, J. Phys. Chem. A, 2010, 114, 8142–8155.
200. C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161.
201. R. J. Kassner and W. Yang, J. Am. Chem. Soc., 1977, 99, 4351.
202. A. J. Cohen, P. Mori-Sanchez and W. Yang, Science, 2008, 321, 792–794.
203. E. R. Johnson, P. Mori-Sanchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2008, 129, 204112.
204. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
205. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
206. J.-K. Hwang, G. King, S. Creighton and A. Warshel, J. Am. Chem. Soc., 1988, 110, 5297–5311.
207. T. Schweins, M. Geyer, K. Scheffzek, A. Warshel, H. R. Kalbitzer and A. Wittinghofer, Nat. Struct. Biol., 1995, 2, 36–44.
208. T. M. Glennon, J. Villa and A. Warshel, Biochemistry, 2000, 39, 9641–9651.
209. M. Klähn, E. Rosta and A. Warshel, J. Am. Chem. Soc., 2006, 128, 15310–15323.
210. J. Åqvist, K. Kolmodin, J. Florián and A. Warshel, Chem. Biol., 1999, 6, R71–R80.
211. J. Florián and A. Warshel, J. Phys. Chem. B, 1998, 102, 719–734.
212. S. C. L. Kamerlin, J. Florián and A. Warshel, ChemPhysChem, 2008, 9, 1767–1773.
213. S. C. L. Kamerlin, P. K. Sharma, R. B. Prasad and A. Warshel, Q. Rev. Biophys., 2013, 1–132.
214. J. K. Lassila, J. G. Zalatan and D. Herschlag, Annu. Rev. Biochem., 2011, 80, 8.1–8.34.
215. I. Nikolic-Hughes, D. Rees and D. Herschlag, J. Am. Chem. Soc., 2004, 126, 11814–11819.
216. S. C. L. Kamerlin, J. Org. Chem., 2011, 72, 9228–9238.
217. L. Zhang, D. Xie, D. Xu and H. Guo, Chem. Commun., 2007, 1638–1640.
218. A. Alkherraz, S. C. L. Kamerlin, G. Feng, Q. I. Sheik, A. Warshel and N. H. Williams, Faraday Discuss., 2010, 145, 281–299.
219. S. C. L. Kamerlin and J. Wilkie, Org. Biomol. Chem., 2007, 5, 2098–2108.
220. T. Humphry, M. Forconi, N. H. Williams and A. C. Hengge, J. Am. Chem. Soc., 2004, 126, 11864–11869.
221. F. Duarte, S. R. Vanga, A. Barrozo and S. C. L. Kamerlin, manuscript in preparation.
222. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
223. Y. Yang, H. B. Yu, D. York, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2008, 4, 2067–2084.
224. G. L. Borosky and S. Lin, J. Chem. Inf. Model., 2011, 51, 2538–2548.
225. H. Irving and R. J. P. Williams, Nature, 1948, 162, 746–747.
226. K. J. Waldron, J. C. Rutherford, D. Ford and N. J. Robinson, Nature, 2009, 460, 823–830.
227. Z. R. Wasserman and C. N. Hodge, Proteins, 1996, 24, 227–237.
228. L. Yao, S. Sklenak, H. Yan and R. I. Cukier, J. Phys. Chem. B, 2005, 109, 7500–7510.
229. W. Li, J. Zhang, Y. Su, J. Wang, M. Qin and W. Wang, J. Phys. Chem. B, 2007, 111, 13814–13821.
230. G. Socrates, J. Org. Chem., 1969, 34, 2958–2961.
231. D. R. Edwards, D. C. Lohman and R. V. Wolfenden, J. Am. Chem. Soc., 2012, 134, 525–531.
232. W. W. Cleland and A. C. Hengge, Chem. Rev., 2006, 106, 3252–3278.
233. A. C. Hengge, Acc. Chem. Res., 2002, 35, 105–112.
234. A. J. Kirby and W. P. Jenks, J. Am. Chem. Soc., 1965, 87, 3209.
235. R. H. Hoff, P. Larsen and A. C. Hengge, J. Am. Chem. Soc., 2001, 123, 9338–9344.
236. R. H. Hoff and A. C. Hengge, J. Org. Chem., 1998, 63, 6680–6688.
237. R. Langen, T. Schweins and A. Warshel, Biochemistry, 1992, 31, 8691–8696.
238. S. C. L. Kamerlin, N. H. Williams and A. Warshel, J. Org. Chem., 2008, 73, 6960–6969.
239. E. Rosta, S. C. L. Kamerlin and A. Warshel, Biochemistry, 2008, 47, 3725–3735.
240. A. Liljas, M. Ehrenberg and J. Åqvist, Science, 2011, 333, 37.
241. G. Wallin, S. C. L. Kamerlin and J. Åqvist, Nat. Commun., 2013, 4, 1733.
242. M. Ben-David, M. Elias, J.-J. Filippi, E. Duñach, I. Silman, J. L. Sussman and D. S. Tawfik, J. Mol. Biol., 2012, 418, 181–196.
243. R. Fox, A. Roy, S. Govindarajan, J. Minshull, C. Gustafsson, J. T. Jones and R. Emig, Protein Eng., 2003, 16, 589–597.
244. A. Vardi-Kilshtain, M. Roca and A. Warshel, Biotechnol. J., 2009, 4, 495–500.
245. L. Wickstrom, E. Gallicchio and R. M. Levy, Proteins, 2012, 80, 111–125.

---