 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The water R1(ω) NMRD profiles of a hydrated protein from molecular dynamics simulation†
Yang
Huang
,
Kwangho
Nam
and
Per-Olof
Westlund
*
Department of Chemistry, Umeå University, Umeå, Sweden. E-mail: perolof.westlund@chem.umu.se
First published on 19th June 2013
Abstract
The hydration of a protein, Peroxiredoxin 5, is obtained from a molecular dynamics simulation and compared with the picture of hydration which is obtained by analysing the water proton R1 NMRD profiles using a generally accepted relaxation model [K. Venu, V. P. Denisov and B. Halle, J. Am. Chem. Soc., 1997, 119, 3122]. The discrepancy between the hydration pictures derived from the water R1(ω0)-NMRD profiles and MD is relevant in a discussion of the factors behind the stretched NMRD profile, the distribution of orientational order parameters and residence times of buried water used in the NMRD model.
1 Introduction
In studies of structure and dynamics of biological macromolecules, water plays a crucial role because of the relatively strong and extensive water–biomolecule interactions.1 Both the thermodynamics and kinetics of the biomolecule and water are coupled. It is rather difficult to identify and extract the characteristics of different types of water–biomolecule interactions from experimental results of different spectroscopic techniques. In proton T1 nuclear magnetic resonance dispersion (NMRD) studies, the water proton spin lattice relaxation rates R1(ω0) are measured as a function of proton Larmor frequency (ω0) ranging from 104 to about 108 Hz. Different types of water are characterized by different effective correlation times τc, and show up in the analysis of the R1(ω0)-NMRD profile.For an introduction to the NMRD experiment and the old interpretational controversy concerning the nature of the protein-associated waters that contribute to the relaxation dispersion we recommend the papers by Halle et al.2–4 They have presented a consistent NMRD model describing 1H, 2H and 17O R1-NMRD profiles of several proteins, which is based on the locations, orientational order parameters, and residence times of protein associated water molecules. The model introduces two types of water molecules, namely, α and β waters. The α waters are characterized by an effective correlation time τc short enough compared with the inverse of the maximum Larmor frequency (1 Tesla) of the NMRD experiment (ωmax0τc ≪ 1) and the β waters are characterized by long τc satisfying the non-extreme narrowing regime (ωmax0τc ≥ 0.1), respectively. Consequently, in the NMRD-model reported by Halle et al.,2–4 the α-waters give rise to a field-independent relaxation contribution, whereas β-waters, which are more interesting, give rise to relaxation dispersion profiles. The effective correlation time of a β-water molecule is described by the residence time τW of the water at the protein interface and the protein reorientational correlation time τR
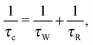 | (1) |
The observed water R1(ω0) dispersion profile may be stretched over a wide frequency range and generally it cannot be described by a single Lorentzian spectral density function. The reasons for the dispersion stretching have been explained in terms of a distribution of water inter-molecular dipole–dipole coupling constants and a distribution of water residence times.5,6 In the present study, we focus on slow tumbling proteins where a distribution of different residence times, which are shorter than or comparable with the protein reorientational correlation time τR, becomes important. The β water molecules are then characterized by different τc values (cf.eqn (1)) and the observed dispersion profile is a sum of many field-dependent dispersion curves. Consequently, the relaxation contribution from β water molecules with τW ≤ τR may explain the common observation of stretching to higher frequencies as well as in the low field region of the NMRD profile. The effect of the quadrupolar dip on the amide proton relaxation rate clearly modifies its NMRD profile. However, based on the explanation of the presence of this dip for immobilized protons,7 the relaxation properties of the amide protons are not transferred to the water protons for slow tumbling proteins and thus do not contribute to the stretching of the water dispersion profile.8
Although the water R1-NMRD profiles can be measured accurately and analyzed using the NMRD-model,2–4 the reliability of the analysis and the corresponding results are difficult to access only from the quality of the fitting of the NMRD model to the experimental NMRD profile. Complementary information can be obtained from crystallographically determined waters. However, it does not provide any information about the time-scales of the dynamics of protein-associated waters, and the resolution of the structure and the model bias in the structure refinement potentially affect the results.
The usefulness of molecular dynamics (MD) simulation for analysing different model assumptions used in spectroscopic studies has previously been demonstrated. Several examples are found, for instance in the study of the pure dephasing vibrational relaxation mechanism in the symmetric vibrational modes of acetonitrile10 and in the ESR lineshape analysis of spin labeled lipid molecules in the lamellar phase of different bilayer membranes.11 MD was also used in a study of the pseudo-rotation model which is often used in nuclear paramagnetic spin relaxation theory.12 In a combined MD and 14N-NMR relaxation study the problem of urea induced protein unfolding was discussed for the urea–lysozyme system.13
Regarding the problem discussed in this paper, Likie and Prendergast14 have used MD simulations to investigate the dynamics of the internal water molecules of fully solvated rat intestinal fatty acid binding protein (I-FABP). They found that the number of long lived intrinsic β-waters could be different from the number of intrinsic waters indicated from the X-ray crystal structure. This is also observed in our study. These results indicate that crystal waters only give an approximative picture of the intrinsic waters present in a soluble protein. However, their MD simulation is relatively short (about 1 ns)14 and consequently, they were unable to determine the distribution function of the residence times of β waters. In the study reported by Garcia and coworkers,15 the hydration of cavities in the interior of staphylococcal nuclease (SN) was characterized in terms of residence times and average location. A 10 ns long MD simulation was performed and 3 internal water molecules were identified for the wild type SN having residence time of 4–10 ns. The water orientational motion is hindered since the mean square deviations were small but the orientational order parameter was not determined. The NMRD study shows two water molecules with residence times larger than 10 ns.16 In exploring the conserved water sites and hydration of a coiled-coil trimerisation motif, a 10 ns MD simulation did not reveal any long residence water and all crystallographic waters had residence times less than 10 ps.17 Henchman and McCammon18 also used MD simulations to characterize the water hydration sites around the protein acetylcholinesterase (AChE). They carried out (10 ns) MD simulation and explored different approaches to identify hydration sites. They found that the number of identified hydration sites is larger than the number of waters identified using X-ray crystallography and that the residence times of those waters vary between several ps and 10 ns. However, these studies do not calculate water T1-NMRD-profiles based on their MD simulations and the stretching property was not discussed.
In this study, we have used MD simulations to evaluate the accuracy and limitations of the water R1-NMRD relaxation model and its analysis in detail. First, we have determined the theoretical NMRD profiles based on the information of the dynamics of protein-associated waters obtained from MD, and analyzed them using the R1-NMRD model. Since the relaxation contributions of different types of water molecules are explicitly known in the present study, they provide reference data to compare the molecular picture of the protein hydration extracted from the R1-NMRD model analysis. Next, the stretching of the NMRD dispersion due to the distribution function of β-water residence times is studied for different reorientation correlation times and compared to the NMRD relaxation model. Last, we have identified a number of buried β water molecules through the analysis and determined their orientational order parameters.
The paper is organized as follows. First, the NMR relaxation theory is reviewed followed by the presentation of the MD simulations of a fully hydrated protein (Peroxiredoxin 5).9 The analysis of the NMRD profiles obtained from the MD simulation is then presented and discussed. Finally, we sum up and some conclusions are given.
2 The water proton R1-NMRD relaxation model
In the strong narrowing regime, the water proton R1-NMRD profile can be expressed in terms of the spectral densities describing the intra- and inter-molecular dipole–dipole relaxation contributions. Here, we review the NMRD model developed by Halle et al.4 The observed relaxation rate is given by an expression describing the population weighted proton spin–lattice relaxation rates of the bulk, Rbulk, and two types of perturbed waters Rα and Rβ, respectively. The relaxation contributions Rbulk and Rα are generally in the extreme narrowing limit and thus field-independent. Therefore we focus on the field-dependent relaxation contributions due to Nβ molecules which are responsible for the relaxation dispersion:4,6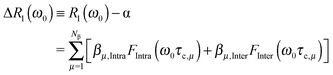 | (2) |
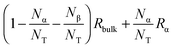 . NT refers to the total number of water molecules per protein, and Rα is determined to be 0.2 s−1 from the MD-simulation data using the averaged correlation time 〈τα〉 = 26 ps. The field-independent relaxation contribution is not further discussed here. The field-dependent intra-molecular relaxation contribution of eqn (2) is expressed as a sum over all β water contributions and is determined by
. NT refers to the total number of water molecules per protein, and Rα is determined to be 0.2 s−1 from the MD-simulation data using the averaged correlation time 〈τα〉 = 26 ps. The field-independent relaxation contribution is not further discussed here. The field-dependent intra-molecular relaxation contribution of eqn (2) is expressed as a sum over all β water contributions and is determined by 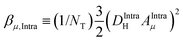 , where the dipole–dipole coupling constant is given as
, where the dipole–dipole coupling constant is given as 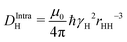 .4 In this expression, μ0, ℏ, γH, and rHH refer vacuum permeability, Planck's constant/2π, the magnetogyric ratio of a proton, and the intra molecular distance between the water protons, respectively. The field-dependent inter-molecular relaxation contribution is determined by
.4 In this expression, μ0, ℏ, γH, and rHH refer vacuum permeability, Planck's constant/2π, the magnetogyric ratio of a proton, and the intra molecular distance between the water protons, respectively. The field-dependent inter-molecular relaxation contribution is determined by 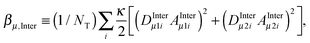 with a dipole–dipole coupling constant for each water proton (denoted 1 and 2, respectively) given by
with a dipole–dipole coupling constant for each water proton (denoted 1 and 2, respectively) given by 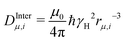 , where rμ,j−3 is the inter molecular distance. AIμ is the generalized orientational order parameter where I refers to intra or inter, and κ = 1 for unlike and
, where rμ,j−3 is the inter molecular distance. AIμ is the generalized orientational order parameter where I refers to intra or inter, and κ = 1 for unlike and 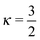 for like proton partners.4 The intra- and the inter-molecular dispersion functions are given by,6
for like proton partners.4 The intra- and the inter-molecular dispersion functions are given by,6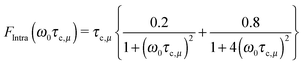 | (3) |
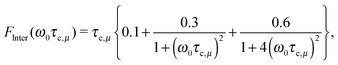 | (4) |
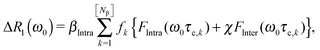 | (5) |
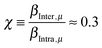 . This ratio is estimated from the MD simulation by calculating the ratio,
. This ratio is estimated from the MD simulation by calculating the ratio, 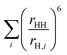 , where rHH is the intra molecular water proton–proton distance and rH,i is the inter proton–proton distances, where the sum is over water proton neighbours.
, where rHH is the intra molecular water proton–proton distance and rH,i is the inter proton–proton distances, where the sum is over water proton neighbours.
3 Molecular dynamics simulations of a fully solvated protein system
To identify different types of waters that influence the water NMRD relaxation, the molecular dynamics (MD) simulations of a fully solvated protein are used. The protein Peroxiredoxin 5 (PrxV) is selected as a model system in the study because it is small and a high resolution crystal structure (below 1.5 Å) is available.19,20 The high resolution structure allows unambiguous identification of water molecules around the protein (see below). In addition, the protein has an important biological function to detoxify highly reactive hydrogen peroxide and alkyl peroxides in the cell.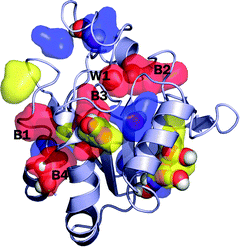 | ||
| Fig. 1 The snapshot structure of the protein Peroxiredoxin 5 (PrxV). The distribution of each long-lived β-water is shown by the color-coded surface representation: the red-colored surface is for the distribution of waters with longer than 10 ns residence time, the yellow-color is for the waters with the residence time between 5 ns and 10 ns, the blue-color is for the residence time between 2 ns and 5 ns, respectively. For clear presentation, we only show several representative long-lived waters. Crystallographic waters that overlap with the long-lived waters are shown by the atom-cleared sphere representation. During the simulation, many crystal waters leave the initial position and bulk waters replace those positions. Not all of the long-lived waters are found at the positions where the crystallographic waters are found. The five most long-lived β-water molecules (with residence time longer than 10 ns) are labeled W1, and B1 to B4, in which W1 is the crystal water and B1 to B4 are bulk waters that are added in the simulation to fully solvate the system. | ||
The system is prepared on the basis of the recent high resolution structure of PrxV (PDB ID: 3MNG).20 It has been suggested that the protein functions by interconverting between the monomeric and the dimeric states,21 and in the present study we use the monomeric form of the protein to simplify the simulation study. The structure of the monomeric PrxV is presented in Fig. 1. In the structure, 288 water molecules are identified as crystal waters and included in the simulation. The system is further solvated with a rhombic dodecahedron (RHDO) box of 3803 water molecules, followed by the removal of any added water molecule that overlaps with the protein and crystal waters. The resulting system contains a total of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393 atoms (2414 protein atoms and 2993 water molecules). Thus, the total number of water molecules in the system is NT = 2993. The CHARMM22 force fields22 and the CMAP correction23 are used to describe the protein. Each water molecule is represented by the three sites TIP3P water model.24 The RHDO periodic boundary conditions with the lattice length 53.8 Å are used, and the electrostatic interactions are evaluated using the particle mesh Ewald summation (PME) method.25
393 atoms (2414 protein atoms and 2993 water molecules). Thus, the total number of water molecules in the system is NT = 2993. The CHARMM22 force fields22 and the CMAP correction23 are used to describe the protein. Each water molecule is represented by the three sites TIP3P water model.24 The RHDO periodic boundary conditions with the lattice length 53.8 Å are used, and the electrostatic interactions are evaluated using the particle mesh Ewald summation (PME) method.25
The system is first energy minimized to relax the coordinates of water molecules and hydrogen atoms of PrxV. After heating up the system to 300 K over 23 ps, the MD simulations are run for 20 ns. The temperature is maintained at 300 K using the Langevin thermostat.26 The simulations are carried out with the 2.0 fs integration time step and the SHAKE algorithm27 is applied to constrain the bonds involving hydrogen atoms. The NAMD program28 is used to perform the MD simulations and the CHARMM program29 in the system preparation, energy minimizations, and trajectory analysis. During the simulation, the coordinates of the protein and water molecules are saved every 1 ps. The saved coordinates are used in the subsequent analysis.
3.1 Identification of generally perturbed water and Nβ long lived intrinsic water molecules
In this study, the perturbed waters denote the water molecules that interact directly with protein atoms and show retarded reorientational correlation times and/or non-zero orientational order parameters. “Perturbed” is also used interchangeably with “protein-associated” water. They comprise both the α and β waters. By following the definition introduced in the NMRD relaxation model (see eqn (2)), the two types of waters (α and β) are determined by their residence times: i.e., the water with long residence time as the β water and the one with short residence time as the α water (at which residence time the two water types can be distinguished is discussed further below). Among β waters, some are residing within the protein structure with few (or no) water neighbors. Here, we note them as the “buried” water. By contrast, α waters interact with the protein but exchange rapidly with the bulk water. They are also called “surface” waters in this study, to distinguish them from the buried waters. In the analysis of the MD trajectory, we identify any water that is within 3.0 Å from any non-hydrogen atom of protein as the perturbed water. Since the 3.0 Å distance criteria corresponds roughly to the hydrogen bonding distance and is in accordance with the rather well corroborated idea that the water perturbation is short ranged.1,3,30 Any water that resides within this distance is expected to show a slower rotational and translational diffusion than bulk water. All NT(=2993) water molecules in the MD-simulation system are followed throughout the 20 ns simulation and the probability of being a bulk water or a perturbed water is determined as the ratio between their residence times and the total time of τT = 20 ns. The average number of such water molecules, 〈NP〉, is 433 ± 13, where the 〈A〉 refers to the average of the observable A over the sampled water configurations. This number is much larger than the number of crystal waters that are included in the simulation. In addition, each crystal water is individually inspected to count the number of internal waters, which is defined in the present work as any water that involves at least two interactions with the protein, and a total of 28 such internal waters are identified. The total number of the perturbed waters Np is given as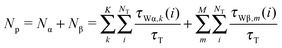 | (6) |
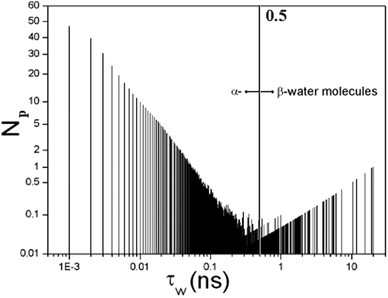 | ||
| Fig. 2 The full distribution function of residence times displaying the number of water molecules N(τW) characterized by a residence time τW. The α water has τW ≤ 0.5 ns and the rest are β water molecules. | ||
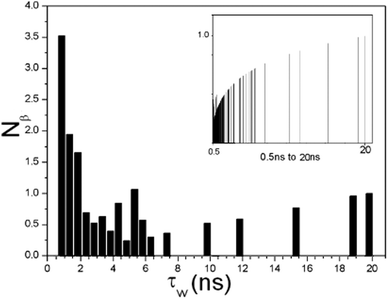 | ||
| Fig. 3 The distribution function of residence time displays the number of β water molecules with residence times in the interval 0.5 < τW ≤ 20 ns. The inset shows the distribution function of residence times displaying the number of water molecules within the selected time range. | ||
We present in ESI,† a Movie S1 showing the dynamic exchange of β-waters (τW > 2.5 ns) around several hydration sites of PrxV. In the movie, the sizes of water molecules are proportional to their τW values and colored according to Fig. 1. The movie suggests that the dynamics of perturbed waters are more complicated than the simple picture based on the analysis of crystallographically determined waters. In particular, it is not possible to determine whether the crystallographically identified waters are either α- or β-waters, exclusively by analyzing their positions and the number of interactions with protein. Many exchanges of waters are observed at each hydration site. Some of them are β-waters with long residence time and some are with relatively short residence time. Sometimes, those sites are occupied by α-waters (thus for much short period of time), before β-waters move in and replace them, making the total number of hydration waters roughly constant.
If the average residence time of water is computed for each hydration site, it may be used to characterize each hydration site, but it may require an MD simulation much longer than 20 ns to achieve a full convergence of the computed (average) residence times. However, this kind of analysis would lose detailed information about the nature of the dynamics of hydration waters, and the Nα and Nβ values determined based on such analysis should be interpreted carefully.
3.2 The water proton orientational order parameter from the MD simulation
The relaxation equation eqn (2) has a generalized orientational order parameter Ak which is proportional to Sk. The S0 is set to be 1.0 in eqn (5). A picture of the orientational order parameters of the β water molecules is obtained from a calculation of the orientational order parameter S0 for each of the NP water molecules.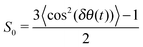 | (7) |
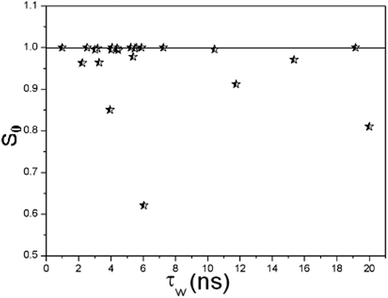 | ||
| Fig. 4 The orientational order parameter S0 for β-waters versus their residence time τW. | ||
4 Results in analysing the R1(ω) NMRD profiles
To access what kind of information can be obtained from the R1-NMRD model analysis and the reliability of the results, we use the water residence time distribution (Fig. 3) determined from MD simulation as an input in the NMRD analysis. We note that the analysis that is performed in this study cannot be performed by using the experimentally determined NMRD profile and X-ray crystallographic structures, because they lack detailed water dynamics information as discussed above. First, we have determined the theoretical proton water R1-NMRD profiles using eqn (2) with three different tumbling rates τR of the whole protein and the entire distribution function of the β-water residence times shown in Fig. 3. Then, the NMRD model of eqn (5) is fitted against the determined NMRD profile for each τR. Since the theoretically determined profiles are used as an input in the analysis, we denote these profiles as the “exact” NMRD profiles. We obtain one, two or three residence times depending on the reorientational correlation time.Fig. 5 displays three (exact) water R1-NMRD profiles obtained from eqn (2) using τR = 50 ns (squares), 10 ns (pyramids), 1 ns (stars), respectively. The τR values are chosen to cover a large range of possible τR values in real experiments. This provides an ideal case to explore the effects of τR on the residence time distribution function, whereas it is not possible to carry out experimentally, because we are unable to manipulate τR independently over a large range. The τR = 1 ns value is a very short and rather unrealistic reorientational correlation time for a global protein, but is included here as an illustrative example of a single τcR1-NMRD dispersion profile. In this case, the NMRD profile is almost uninfluenced by the τW distribution function. The NMRD profile, on the other hand, is influenced by the whole τW distribution function for the slow tumbling protein, such as τR = 50 ns.
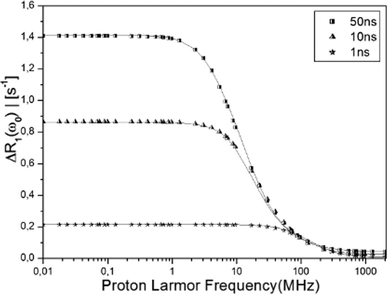 | ||
| Fig. 5 The “exact” NMRD profiles obtained from the MD simulation (eqn (2)) with τR = 50 (squares), 10 (pyramids), 1 (stars) ns are displayed with best fitting NMRD profiles (solid line) calculated using the NMRD model of eqn (5), using one, two and three effective correlation times τc (see Table 1). The model NMRD profile defined by exp-parameters given in Table 1 is not distinguishable from the exact NMRD profile. | ||
The fitting is carried out sequentially. Starting from the shortest τR we first fit eqn (5) against the exact NMRD profile using Nβ1 and one residence time τW,1. We then proceed to τR = 10 ns and add a second dispersion profile with τW,2 and Nβ2. Finally for τR = 50 ns a third residence time τW,3 is introduced with Nβ3 water molecules. This fitting procedure results in three τW distribution functions shown as a–c in Fig. 6. The modeled NMRD profiles are displayed in Fig. 5 as a solid line and the model parameters determined are summarized in Table 1. The analyses indicate that three residence times can be extracted and produce a model NMRD profile conforming well to the exact NMRD displayed in Fig. 5. However, as presented in Fig. 6, the resultant τW-distributions are much simpler than the exact distribution given in Fig. 3. We note that alternative fitting procedures can be applied, possibly producing a different set of τW and Nβ values. This, together with the present fitted results, suggests that the residence time distribution can be interpreted in several ways, and alternative different distribution functions can produce equally good and excellent fitting to the “exact” NMRD profile. One such interpretation is denoted exp in Fig. 6. The exp-distribution is obtained from Fig. 3 by averaging the distribution values from 20 ns to 10 ns, 10 ns to 2 ns and 2 ns to 0.5 ns to give three residence times, τW = 12, 4 and 0.7 ns, respectively, with weight factors that are equal to the natural number of water molecules (Table 1). This model NMRD profile obtained with the exp-distribution fits excellent to the “exact” NMRD profile with τR = 50 ns. The present analysis suggests that detailed information about the intrinsic water dynamics is partly lost in the NRMD model analysis and the residence time distribution differs from the exact distribution of Fig. 3.
| τ R (ns) | τ W1 (ns) | N β1 | τ W2 (ns) | N β2 | τ W3 (ns) | N β3 | χ 2 | Fig. 6 |
|---|---|---|---|---|---|---|---|---|
| 50 | 0.7 | 7 | 4.0 | 6 | 12.0 | 4 | 0.00163 | exp |
| 1 | 0.7 | 17 | — | — | — | — | 0.00039 | a |
| 10 | 0.7 | 9 | 5.1 | 8 | — | — | 0.00634 | b |
| 50 | 0.7 | 7 | 5.1 | 8 | 15.7 | 2 | 0.00275 | c |
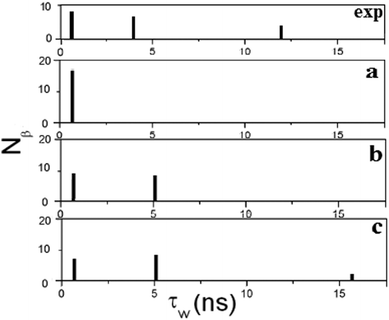 | ||
| Fig. 6 The distribution of residence times obtained from Fig. 5 and listed in Table 1 using the NMRD model. The residence times obtained from the NMRD analysis are displayed in (a) when τR = 1 ns, in (b) when τR = 10 ns and in (c) when τR = 50 ns. The residence times of (c) (see Table 1) can be compared with the averaged distribution function of Fig. 3 displayed in exp. | ||
The results presented in Fig. 5 show that three effective correlation times reproduce well the stretching of the exact NMRD profiles with τR = 50 ns and τR = 10 ns. In Fig. 7, we have analyzed further the stretching of the NMRD profile with τR = 50 ns, by comparing the exact NMRD profile to the model NMRD profiles assuming a single τc value, i.e., 20 ns, 10 ns, and 5 ns. The figure shows that a single Lorentzian function cannot explain the stretching of the NRMD profiles both at low and high fields and therefore, the entire distribution of residence times contributes to the stretching. Nevertheless, the present analysis provides a simple approach to estimate the range of τc by focusing on the low and high field dispersions. In the present case, the range is between τc,min = 5 ns and τc,max = 20 ns. If the reorientational correlation time τR is known, the range of the residence times τW can also be determined straightforwardly. For example, by assuming τR = 50 ns in the present case, τW,min and τW,max are 5.6 ns and 33.3 ns, respectively, which are comparable to the values given in Table 1.
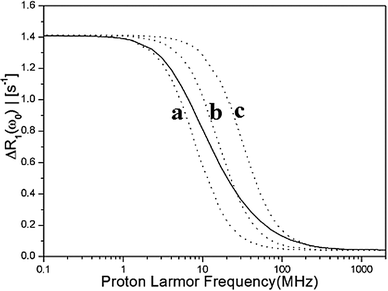 | ||
Fig. 7 The stretched NMRD profile with τR = 50 ns is displayed by a solid line. It is analysed from low fields to high field using a single Lorentzian function 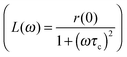 . The low field relaxation rate r(0) = 1.4. The correlation times are: (a) τc = 20 ns, (b) τc = 10 ns, (c) τc = 5 ns. . The low field relaxation rate r(0) = 1.4. The correlation times are: (a) τc = 20 ns, (b) τc = 10 ns, (c) τc = 5 ns. | ||
5 Summary and conclusions
In this study, we have investigated the effects of protein-associated waters on the R1(ω)-NMRD relaxation dispersion. Detailed information about individual β-water dynamics and their residence times is only available using the molecular dynamics (MD) simulation. Using the distribution function of the β-water residence times that are obtained by analyzing waters from all-atom explicit water MD simulation, the R1(ω)-NMRD relaxation profiles are determined theoretically with various protein reorientational correlation times τR (50 ns, 10 ns or 1 ns). These τR tumbling rates are chosen to cover proteins with various sizes (from slowly tumbling proteins (50 ns) to rapidly tumbling small proteins). The theoretically determined (exact) NMRD profiles are then compared to the profiles that are obtained by fitting the NMRD model given in eqn (5) against the theoretical NMRD profiles.We found that the main assumptions made in the formulation of the NMRD relaxation model (eqn (5)) are corroborated by the MD simulation analysis. Compared to the large number of short-lived α waters, a relatively small number of β waters (a total of 17 with τW > 0.5 ns in this study) are identified from the MD simulation, all of them with high orientational order parameters. The order parameters of most of the identified β waters are close to 1.0, and only a few have slightly reduced values. Since the relaxation contribution is proportional to the square of the order parameter (eqn (2)), the waters with reduced order parameters will contribute less to the NMRD profile, and the main relaxation contribution determining the NMRD profile is due to the remaining β waters with large order parameters. Our analysis also suggests that the reduced values are not because of local water motion but because they follow local protein fluctuations. Therefore, they should be interpreted cautiously.
However, the NMRD model yields a much simplified distribution function of water residence times relative to the distribution function obtained by analyzing the MD simulation trajectory (Fig. 6). For slowly tumbling protein, displaying a stretched NMRD profile, an excellent fitting does not reproduce the full distribution of residence times of protein-associated waters (compare Fig. 3 to Fig. 6). This implies that the information content of the (experimentally determined) NMRD profile is not sufficient for a unique determination of the full distribution function of residence times. Furthermore, the NMRD model results in residence time distributions that are rather similar to the distribution function of the block-averaged residence times (Table 1 and Fig. 6). This suggests that the information that is extracted from the NMRD model analysis is more or less averaged over waters with similar residence times.
The analysis of the β waters and their “binding sites” in protein shows that different residence times are sometimes correlated with the same location in the protein. This can be understood as the effect of protein dynamics and local structural fluctuations, which consequently change the residence times of the waters bound in that site. In addition, the crystallographically identified waters are not always β waters. Therefore, the rigid picture from crystallographics, where water residence sites are identified for buried water molecules, is not valid for all β-water molecules. Although it is likely to be true for very long lived waters, for the waters with residence time 1–10 ns their averaged residence times cannot be determined with any high accuracy. This implies that the dynamics of protein-associated waters (both α and β) are rather complex.
Taken together, the present study suggests that we cannot extract information about all β waters and their residence times solely with the information obtained from the analysis of the NMRD model and X-ray structures. The information obtained from the NMRD analysis is rather averaged over waters with similar residence times. Nevertheless, the present analysis clearly demonstrates the influence of the full τW-distribution function on the stretching of the water proton NMRD profiles both in the low field and in the high field region of the dispersion.
Finally, it should be noted that Fig. 3 is obtained from the 20 ns MD simulation and thus may not be fully converged. Since the results of MD simulation are dependent on the length of the simulation, we do not attempt to draw any quantitative conclusion on the water dynamics of the protein Peroxiredoxin V in this study. This is also not the focus of this study. In this study, our focus is on assessing the information content of the NMRD profile and the relaxation model by comparing the water residence times and their distribution determined from the NMRD model analysis to the exact distribution of water residence times, which is used as the input in the NMRD model fitting. Therefore, it is sufficient to have any distribution of residence times which we can consider as a real one and be used to determine the theoretical NMRD profiles. Since the R1(ω0)-NMRD experiments cannot discriminate between all individual β water molecules, we used the MD simulations to generate such information in this study. Therefore, the length of the simulation has no consequences for this study, as far as the length roughly corresponds to the time scale of the protein tumbling rate.
The authors individual contributions
POW: designed and wrote the paper; YH: NMRD simulations and analysis; KN: MD simulation, analysis and wrote the paper.Acknowledgements
This work was supported by the Swedish Research Council to POW, and by the Umeå University to KN. KN acknowledges the High Performance Computer Center North (HPC2N) for providing computational resources.References
- B. Halle, Philos. Trans. R. Soc. London, Ser. B, 2004, 359 Search PubMed.
- V. P. Denisov and B. Halle, J. Am. Chem. Soc., 1994, 116, 10324–10325 CrossRef CAS; V. P. Denisov and B. Halle, J. Mol. Biol., 1995, 245, 682–697 CrossRef; V. P. Denisov and B. Halle, J. Mol. Biol., 1995, 245, 698–709 CrossRef; V. P. Denisov and B. Halle, J. Am. Chem. Soc., 1995, 117, 8456–8465 CrossRef.
- V. P. Denisov, B. Halle, J. Peters and H. D. Hörelin, Biochemistry, 1995, 34, 9046–9051 CrossRef CAS; V. P. Denisov, B. Halle, J. Peters and H. D. Hörelin, Nat. Struct. Biol., 1996, 3, 505–509 CrossRef.
- K. Venu, V. P. Denisov and B. Halle, J. Am. Chem. Soc., 1997, 119, 3122–3134 CrossRef CAS.
- B. Halle, H. Johanneson and K. Venu, J. Magn. Reson., 1998, 135, 1–13 CrossRef CAS.
- B. Halle, V. P. Denisov and K. Venu, Biological Magnetic Reson., in Structure Computation and Dynamics in protein NMR, ed. N. R. Krishna and L. J. Berliner, Kluwer Ac./Pen. Pub., N. Y., 1999, vol. 17 Search PubMed.
- E. P. Sunde and B. Halle, J. Magn. Reson., 2010, 203, 257 CrossRef CAS.
- P.-O. Westlund, Mol. Phys., 2012, 110, 2251 CrossRef CAS; P.-O. Westlund, Mol. Phys., 2009, 107, 2114 CrossRef; P.-O. Westlund, Phys. Chem. Chem. Phys., 2010, 12, 3136 RSC.
- M. S. Seo, S. W. Kang, K. Kim, I. C. Baines, T. H. Lee and S. G. Rhee, J. Biol. Chem., 2000, 275, 20346–20354 CrossRef CAS.
- P.-O. Westlund and R. M. Lynden-Bell, Mol. Phys., 1987, 60, 1189 CrossRef CAS; P.-O. Westlund and R. M. Lynden-Bell, Mol. Phys., 1987, 61, 1541 CrossRef; P.-O. Westlund and R. M. Lynden-Bell, Chem. Phys. Lett., 1989, 154, 67 CrossRef.
- P. Hakansson, P.-O. Westlund, E. Lindahl and O. Edholm, Phys. Chem. Chem. Phys., 2001, 3, 5311 RSC.
- M. Lindberg, A. Laaksonen and P.-O. Westlund, Phys. Chem. Chem. Phys., 2009, 11(44), 10368–10376 RSC.
- M. Lindgren, T. Sparrman and P.-O. Westlund, Spectrochim. Acta, Part A, 2010, 75, 953 CrossRef.
- V. A. Likie and F. G. Prendergast, Proteins: Struct., Funct., Genet., 2001, 43, 65 CrossRef.
- A. Damjanovic, E. B. Garcia-Moreno, E. E. Lattman and A. E. Garcia, Comput. Phys. Commun., 2005, 169, 126 CrossRef CAS.
- V. P. Denisov, J. L. Schlessman, E. B. Garcia-Moreno and B. Halle, Biophys. J., 2004, 87, 3982 CrossRef CAS.
- J. Dolenc, R. Baron, J. J. Missmer, M. O. Steinmetz and W. F. van Gunsteren, ChemBioChem, 2008, 9, 1749 CrossRef CAS.
- R. H. Henchman and J. A. McCammon, J. Comput. Chem., 2001, 23, 861–869 CrossRef.
- C. Evrard, A. Capron, C. Marchand, A. Clippe, R. Wattiez, P. Soumillion, B. Knoops and J.-P. Declercq, J. Mol. Biol., 2004, 337, 1079–1090 CrossRef CAS.
- A. Hall, D. Parsonage, L. B. Poole and P. A. Karplus, J. Mol. Biol., 2010, 402, 194–209 CrossRef CAS.
- B. Knobs, J. Goemaere, V. Van der Eecken and J.-P. Declerce, Antioxid. Redox Signalling, 2011, 15, 817 CrossRef.
- A. D. MacKerell, Jr., D. Bashford, M. Bellot, R. L. Dunbrack, Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef.
- A. D. MacKerell, Jr., M. Feig and C. L. Brooks III, J. Comput. Chem., 2004, 25, 1400–1415 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS.
- J. P. Ryckard, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Shulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS.
- B. R. Brooks, C. L. Brooks III, A. D. MacKerell, Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS.
- B. Halle and H. Wennerström, J. Phys. Chem., 1981, 75, 1939 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp51147b |
| This journal is © the Owner Societies 2013 |
