 Open Access Article
Open Access ArticleMonte Carlo simulation and free energies of mixed oxide nanoparticles
John A.
Purton
*a,
Stephen C.
Parker
b and
Neil L.
Allan
c
aSTFC, Daresbury Laboratory, Warrington, WA4 4AD, UK. E-mail: john.purton@stfc.ac.uk; Fax: +44 (0)1925 603100; Tel: +44 (0)1925 603785
bSchool of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: s.c.parker@bath.ac.uk; Fax: +44 (0)1225 386231; Tel: +44 (0)1225 386505
cSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: n.l.allan@bris.ac.uk; Fax: +44 (0)117 925 1295; Tel: +44 (0)117 928 8308
First published on 20th March 2013
Abstract
A Monte Carlo Exchange technique is used to study the thermodynamic properties of MgO–MnO nanoparticles ranging in size from 1728 to 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ions. The solubility of Mg2+ is much greater in MnO than the reverse, reflecting the difference in size between the two cations. The solubility, for a given temperature, diminishes with nanoparticle size. As the Mn concentration is progressively increased the Mn2+ ions occupy the corners, edges and then surface sites of the nanoparticle before entering subsurface layers. We do not observe any pronounced ordering of the cations within the body of the nanoparticles themselves. The enthalpies of forming ternary nanoparticles from particles of MgO and MnO of the same size vary with the size of the nanoparticle and become more positive for a given concentration as the particle size increases. Free energies of mixing of the two end-member nanoparticles have been determined using the semigrand ensemble. The consolute temperature (the temperature above which there is complete miscibility) increases non-linearly with the size of the nanoparticle by approximately 70% over the size range considered.
952 ions. The solubility of Mg2+ is much greater in MnO than the reverse, reflecting the difference in size between the two cations. The solubility, for a given temperature, diminishes with nanoparticle size. As the Mn concentration is progressively increased the Mn2+ ions occupy the corners, edges and then surface sites of the nanoparticle before entering subsurface layers. We do not observe any pronounced ordering of the cations within the body of the nanoparticles themselves. The enthalpies of forming ternary nanoparticles from particles of MgO and MnO of the same size vary with the size of the nanoparticle and become more positive for a given concentration as the particle size increases. Free energies of mixing of the two end-member nanoparticles have been determined using the semigrand ensemble. The consolute temperature (the temperature above which there is complete miscibility) increases non-linearly with the size of the nanoparticle by approximately 70% over the size range considered.
Introduction
Heterogeneous nanostructures have become increasingly important, since they often exhibit multifunctional capabilities with tuneable or enhanced properties.1 Indeed, the formation of core–shell structures represents one of the most effective experimental approaches for creating heterostructured nanodevices for many technological applications such as high temperature alloys, catalysts and solid oxide fuel cells.2 The fabrication and internal structure (i.e. the distribution of atoms/ions) of these functional nanoparticles is controlled by a variety of parameters such as temperature, chemical environment, rate of growth and diffusion. Ferrando et al.3 have reviewed comprehensively both theoretical and experimental studies of nanoalloy clusters and nanoparticles of metallic elements. Much of the theoretical work has focused on the calculation of the potential energy surface to determine the most stable configuration. Size and surface segregation effects have been considered analytically4 and Monte Carlo methods have been employed to calculate thermodynamic properties of metal nanoparticles, for example the excess enthalpy of mixing5 and segregation of atoms to form core–shell structures.5–10 These papers have concentrated on the properties of nanoalloys, whilst for most ionic nanoparticles computer simulations have largely investigated structure of binary nanoparticles,11e.g. TiO2 clusters12 and nanotubes.13 Nevertheless addition of a third element is frequently used to control fundamental properties such as shape, growth and optical absorption.14 While Pandey and co-workers have worked systematically on compositional distributions in several ternary semiconductor quantum dots,15,16 relatively few papers17,18 have examined the distribution of ions and the associated thermodynamics of oxide nanoparticles despite their evident importance for a wide range of applications.19,20 Just one example is a key positive electrode material in Li-ion batteries, lithium iron phosphate (LiFePO4). Nanoscaling is essential for achieving high rate capability during electrochemical cycling and such olivine nanoparticles show very different phase transition behaviour from that of the bulk olivine phase.21–26 Experimentally, the solubility of lithium in olivines21,24,27) increases with decreasing particle size.Calculation of the thermodynamic properties of ternary nanoparticles is essential to develop our understanding of the distribution of elements within the nanoparticles and how this impacts on the properties of the nanoparticle. Indeed, the thermodynamic properties and chemical composition of a nanoparticle may determine its suitability for technological applications. For example, a miscibility gap may lead to the formation of a core–shell structure to the nanoparticle. In this paper we report results of Monte Carlo simulations to determine the structure and thermodynamic properties of nanoparticles comprised of a mixture of ionic materials, with initial application to small oxide nanoparticles of varying composition and where the cations differ appreciably in size.
For our pilot study MgO–MnO is an appropriate choice of prototype system due to the magnitude of the difference in radius between the larger Mn2+ and the smaller Mg2+ ion (Shannon and Prewitt ionic radii in 6-fold coordination are 0.83 Å and 0.72 Å, respectively).28 This mismatch is neither so small that an essentially ideal solution is formed at all compositions and temperatures nor so large that there is always complete segregation by one cation under all conditions of interest.29 The bulk system has also received considerable attention previously.30 Our calculations explicitly include the effects of temperature and full surface relaxation, are not restricted to the dilute limit and there are no symmetry restraints or mean-field approximations. No assumptions are made as to the positions of the impurity/dopant atoms at the surfaces of the nanoparticles corresponding to a particular total composition; surface segregation and atomic relaxation in the ternary nanoparticle are automatically incorporated and as we shall play crucial roles.
Methodology
The surface of a crystal always provides a different elastic and electrostatic environment from that of the bulk, and so there is a free energy difference between the energy associated with any defect, including an impurity, in the bulk and at the surface of a nanoparticle. Impurities are thus driven to or from the surface. The basis for all our calculations is the well-known Monte Carlo (MC) method modified for nanoparticles of variable composition as described below. All nanoparticles were cubic and constructed from 8-atom units identical to the cubic unit cell of the bulk material. Calculations were undertaken on MnO–MgO mixtures comprising 1728 ions (6 × 6 × 6), 2744 ions (7 × 7 × 7), 4096 ions (8 × 8 × 8), 5832 ions (9 × 9 × 9), 8000 ions (10 × 10 × 10), 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 ions (12 × 12 × 12) and 21
824 ions (12 × 12 × 12) and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ions (14 × 14 × 14). We have considered only the {100} termination of the nanoparticle since the {100} surfaces of both MgO and MnO are considerably more stable than other terminations.31 The rôle of both point defects (vacancies, interstitials) and linear defects (steps, dislocations) on the thermodynamics properties of the nanoparticles are neglected. We do not report results for smaller nanoparticles since the estimated consolute temperature is less than that at which exchange of ions in the simulations is very inefficient (approximately 500 K).
952 ions (14 × 14 × 14). We have considered only the {100} termination of the nanoparticle since the {100} surfaces of both MgO and MnO are considerably more stable than other terminations.31 The rôle of both point defects (vacancies, interstitials) and linear defects (steps, dislocations) on the thermodynamics properties of the nanoparticles are neglected. We do not report results for smaller nanoparticles since the estimated consolute temperature is less than that at which exchange of ions in the simulations is very inefficient (approximately 500 K).
All calculations were performed using the DL_MONTE program32 adapted for use with nanoparticles and were based on an ionic model using two-body potentials to represent short-range forces.33 The total long-range electrostatic energy was evaluated using direct summation (no periodic boundaries were employed). The particular non-Coulombic interaction potentials employed is the very widely used set of Lewis and Catlow first introduced in their study of the parent oxides,34 and implemented here with a cut-off of 12 Å. We have used these previously in studies of bulk MnO–MgO solid solutions and the resulting phase diagram, calculated35 using exchange Monte Carlo and the semigrand canonical ensemble is in good agreement with experiment with a consolute temperature of ≈1150 K. In addition, we have successfully employed this model to calculate segregation energies36 in thin films.
In simulations of non-stoichiometric ionic materials and solid solutions using ‘standard’ MC, kinetic barriers prevent sampling the whole of the configurational space since almost always only one cation arrangement – the initial configuration – is sampled. We have described elsewhere37,38 Monte Carlo Exchange (MCX) simulations in which both the atomic configuration and the atomic coordinates of all the atoms are changed. A single cycle allows for one of three possible moves to be chosen at random with equal probability:
(i) random displacement of an ion. Allowing random moves of randomly selected atoms takes account of relaxation throughout the nanoparticle and vibrational effects. To determine whether the change is accepted or rejected, the usual Metropolis algorithm is applied.39 The maximum change in the atomic displacement for each ionic species has a variable rmax, its magnitude is adjusted automatically during the simulation to maintain an acceptance/rejection ratio of approximately 0.37.
(ii) an exchange of ionic configuration. Changes in ionic configuration are attempted by exchanging the position of a Mn2+ ion and a Mg2+ ion, both chosen at random. Again, the Metropolis algorithm is used to accept or reject any attempted exchange.
(iii) a change in identity of a cation (semigrand ensemble).40 We evaluate the potential energy change ΔUB/A which would result if one species, B were to be converted into another, A. This change in energy is related to the corresponding change in chemical potential ΔμB/A by,
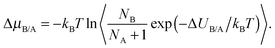 | (1) |
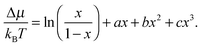 | (2) |
Each calculation consisted of an initial equilibration of 5 × 108 cycles followed subsequently by 5 × 108 production cycles. The larger clusters (>4096 ions) pose a significant computational challenge and for this reason the calculations were performed using a 8 to 128 cores in parallel replicated data strategy.
Results and discussion
We plot quantities of interest as a function of the total mole fraction of Mg2+. We first define, ΔH, the enthalpy of forming ternary nanoparticles from the stoichiometric binary nanoparticles of the same size by the reaction,| xMgnOn + (1 − x)MnnOn = MgxnMn(1−x)nOn, | (3) |
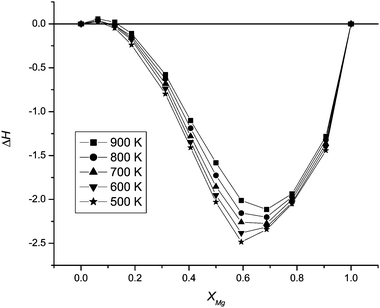 | ||
| Fig. 1 Enthalpies of forming ternary nanoparticles, ΔH (kJ mol−1), for the 1728 ion nanoparticle, defined in eqn (3), as a function of temperature and composition. xMg is the Mg mole fraction, as in eqn (3). The enthalpies in Fig. 1 and 3 are determined per cation to allow comparison with different sized nanoparticles. | ||
The variation of the enthalpy of forming ternary nanoparticles from nanoparticles of MgO and MnO comes from the relative energies of replacing a large cation (Mn2+) with a small cation (Mg2+) or the reverse. Mg–O bonds are stronger (and stiffer) than Mn–O bonds and the {001} surface energy of MgO larger than that of MnO. Thus when a few Mn ions are replaced by Mg in a MnO nanoparticle, the Mg ions are preferentially located within the internal structure of the nanoparticle. They are distributed randomly and do not form a cube-within-cube structure (Fig. 2a–c). The Mg–O bonds are stretched (static lattice simulations of a single Mg substitution indicate a Mg–O bond length of approximately 2.17 Å; while that in the MgO nanoparticles is 2.10 Å). This strain gives rise to a positive enthalpy of forming ternary nanoparticles, and in the bulk material the positive enthalpy of mixing is positive for the same reason.
 | ||
Fig. 2 Snapshots of the structure of nanoparticles. (a) Slice taken through the centre of a 1728 ion nanoparticle at 500 K and xMg ≈ 0.2. (b) Slice taken through the centre of a 4096 ion nanoparticle at 600 K and xMg ≈ 0.2. (c) Slice taken through the centre of a 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticle at 800 K and xMg ≈ 0.3. (d) Complete 21 952 ion nanoparticle at 800 K and xMg ≈ 0.3. (d) Complete 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticle at 800 K and xMg ≈ 0.95. (e) Slice taken through the centre of a 4096 ion nanoparticle at 500 K and xMg ≈ 0.8. In all figures oxide ions are red, magnesium green and manganese purple. 952 ion nanoparticle at 800 K and xMg ≈ 0.95. (e) Slice taken through the centre of a 4096 ion nanoparticle at 500 K and xMg ≈ 0.8. In all figures oxide ions are red, magnesium green and manganese purple. | ||
In contrast, if we start with a MgO nanoparticle and gradually replace the Mg ions by Mn, the enthalpy of forming ternary nanoparticles is negative. This is due to the Mn ions progressively replacing Mg ions at the corners, edges and then in the surface of the nanoparticle (Fig. 2d and e) and the driving force is the lower interface energy. We note in passing that replacement at corners is favoured rather than at edges in contrast to Ca2+ substitution in cubic MgO nanoclusters where the larger size mismatch and pronounced relaxation leads to the reverse behaviour.42
For the 1728 ion nanoparticle, analysis of available sites at corners, edges and surfaces indicates that the nanoparticle is fully covered with Mn at approximately xMg = 0.58. This is very close to the minimum in the 500 K ΔH vs. composition curve in Fig. 1. The enthalpy of forming ternary nanoparticles is relatively insensitive to temperature, although the minimum decreases in magnitude (becomes less negative) and moves to slightly greater values of x (to xMg = 0.7 at 900 K). This trend results from the increase in temperature allowing greater numbers of Mn ions into subsurface layers.
While there is a pronounced preference of Mn2+ in the ternary nanoparticles for the outermost layers, there is no such marked preference for any other sites within the nanoparticles. Thus while there is Mn2+ enrichment at the surface, we do not observe the formation of nanoparticles containing an MgO “core” and an MnO outer “shell” consisting of more than just the surface layer (Fig. 2a–c).
In Fig. 3, we plot the enthalpy of forming ternary nanoparticles as a function of nanoparticle size. The region of positive ΔH becomes progressively greater in both magnitude and extent, while that where ΔH is negative becomes less negative and the position of the minimum moves to a larger value of xMg. These changes arise due to the greater availability of ‘bulklike’ material as the size of the nanoparticle increases and the rôle of the surface becomes less important.
 | ||
| Fig. 3 Calculated values of ΔH (eqn (3)) (kJ mol−1) for different size nanoparticles at 800 K. | ||
A phase diagram showing the stability of the ternary nanoparticles relative to separate binary nanoparticles of the same size (eqn (3)) can be determined using free energy differences from eqn (1) and (2). Fig. 4a–c display the calculated values of ΔμMg/Mn for the 1728, 8000 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion structures respectively and represent typical behaviour (intermediate size nanoparticles display similar behaviour between the extremes). The existence of a minimum and maximum in a Δμ(x) curve indicates a miscibility gap at that temperature. For the 1728 nanoparticle it is clear from the shape of these curves that 500 K and 600 K corresponds to temperatures below the consolute temperature TC (stationary points are evident), and the formation of one-ternary-particle and two-binary-particle regions at different compositions. The Δμ(x) curve for 600 K, is just below the calculated TC, as indicated by the shape of the curve in which the stationary points evident at 500 K have almost disappeared. At 800 K the stationary points are not present and this temperature is above the consolute temperature. In contrast, calculated values of ΔμMg/Mn for the 8000 and 21
952 ion structures respectively and represent typical behaviour (intermediate size nanoparticles display similar behaviour between the extremes). The existence of a minimum and maximum in a Δμ(x) curve indicates a miscibility gap at that temperature. For the 1728 nanoparticle it is clear from the shape of these curves that 500 K and 600 K corresponds to temperatures below the consolute temperature TC (stationary points are evident), and the formation of one-ternary-particle and two-binary-particle regions at different compositions. The Δμ(x) curve for 600 K, is just below the calculated TC, as indicated by the shape of the curve in which the stationary points evident at 500 K have almost disappeared. At 800 K the stationary points are not present and this temperature is above the consolute temperature. In contrast, calculated values of ΔμMg/Mn for the 8000 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticles still exhibit weak stationary points at 800 K and 1000 K respectively and we would still expect the formation of one-ternary particle and two-binary particle regions at different compositions. For these sizes of nanoparticle, the stationary points are not present at 1000 K and 1050 K and the temperature is above TC.
952 ion nanoparticles still exhibit weak stationary points at 800 K and 1000 K respectively and we would still expect the formation of one-ternary particle and two-binary particle regions at different compositions. For these sizes of nanoparticle, the stationary points are not present at 1000 K and 1050 K and the temperature is above TC.
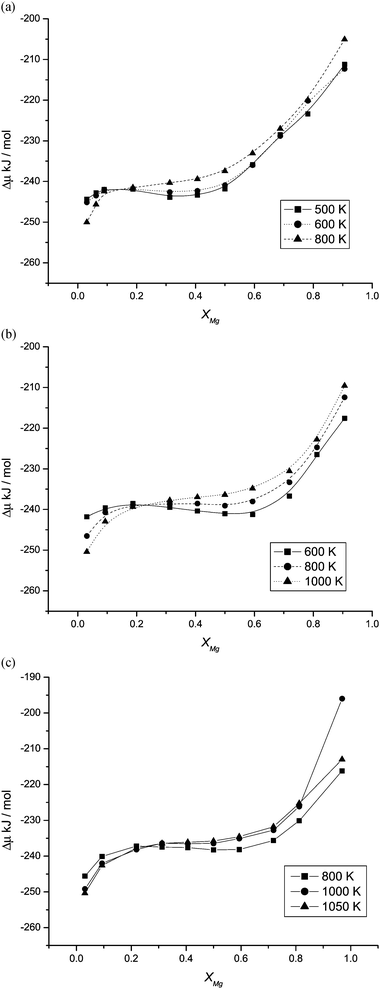 | ||
Fig. 4 Calculated values of ΔμMg/Mn (eqn (2)) for the (a) 1728, (b) 8000 and (c) 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion structures. 952 ion structures. | ||
In Fig. 5a and b we plot calculated values of ΔG for the forming ternary nanoparticles (as defined in eqn (3)) vs. x obtained by integration of eqn (2) at temperatures 500, 600 and 800 K and 600, 800 and 1000 K for the 1728 and 8000 ion nanoparticles respectively. Minima in ΔG at any particular temperature indicate that one-ternary-particle and two-binary-particle regions are formed at different compositions and hence such temperatures lies below TC. For the smaller nanoparticle (Fig. 5a), the two minima in ΔG observed at 500 K and 600 K curve are very weak (especially for 600 K as it is just below TC) and hardly detectable by eye in the figure. At temperatures greater than 640 K, as indicated by the 800 K curve, the dependence of ΔG at all compositions is consistent with complete miscibility. For the larger nanoparticles the minima in the curves are more evident and indicate the one-ternary and two-binary regions of the phase diagram are still present at higher temperatures (e.g., the 600 and 800 K curves for the 8000 ion nanoparticle and 800 and 1000 K curves for the 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticle). The curves at 1000 and 1050 K are, however, consistent with complete miscibility for the 8000 and 21
952 ion nanoparticle). The curves at 1000 and 1050 K are, however, consistent with complete miscibility for the 8000 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticles respectively. Given curves as in Fig. 5, a common tangent construction at each temperature yield the phase diagrams in Fig. 6a and b. The behaviour of the intermediate size nanoparticles exhibit a gradation in their behaviour. For comparison the calculated and experimental phase diagram of bulk MgO–MnO is presented in Fig. 7. Thus by performing calculations at several temperatures for the different size nanoparticles, TC can be determined as a function of the number of ions in the nanoparticle (Fig. 8). The variation with the total number of ions is non-linear. However, limitations in the range of nanoparticle size and sampling of the Monte Carlo method have prevented us from determining whether the curve is sigmoidal as observed in previous studies.30 All the phase diagrams are slightly asymmetric.
952 ion nanoparticles respectively. Given curves as in Fig. 5, a common tangent construction at each temperature yield the phase diagrams in Fig. 6a and b. The behaviour of the intermediate size nanoparticles exhibit a gradation in their behaviour. For comparison the calculated and experimental phase diagram of bulk MgO–MnO is presented in Fig. 7. Thus by performing calculations at several temperatures for the different size nanoparticles, TC can be determined as a function of the number of ions in the nanoparticle (Fig. 8). The variation with the total number of ions is non-linear. However, limitations in the range of nanoparticle size and sampling of the Monte Carlo method have prevented us from determining whether the curve is sigmoidal as observed in previous studies.30 All the phase diagrams are slightly asymmetric.
 | ||
Fig. 5 ΔG (eqn (3)) for the (a) 1728, (b) 8000 and (c) 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion structures. In Fig. 5a the straight line is a guide to the eye. 952 ion structures. In Fig. 5a the straight line is a guide to the eye. | ||
 | ||
Fig. 6 Phase diagrams for the (a) 1728, (b) 8000 and (c) 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ion nanoparticles. Solid squares = binodal, solid diamond = spinodal. 952 ion nanoparticles. Solid squares = binodal, solid diamond = spinodal. | ||
 | ||
| Fig. 7 Calculated (solid lines) and experimental (dashed lines) phase diagrams, and spinodals for bulk MnO–MgO. The experimental results are from ref. 45. | ||
 | ||
| Fig. 8 The consolute temperature TC as a function of particle size (total number of ions). | ||
The calculated phase diagrams for nanoparticles of the same size (eqn (3)) show that at low temperatures (<600 K) the MgO solubility in MnO is low (xMg = 0.05–0.07) and does not vary much between the different nanoparticles and the bulk. In contrast at the same temperatures the solubility of MnO in MgO is much higher in the smaller nanoparticles (as high as xMn = 0.4 at 600 K even for the 8000-ion particle (driven by the interface energies); there is a rapid decrease as the size of the nanoparticle increases. The interface term here enhances the common trend that the compound containing the smaller ion is usually more soluble in the compound with the larger ion than the reverse.
Conclusions
We have employed the Monte Carlo Exchange technique to calculate directly the thermodynamic properties of MnO–MgO clusters as a function of temperature and nanoparticle size (between 1728 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 ions). As the Mn concentration is progressively increased the Mn2+ ions occupy the corners, edges and then surface sites of the nanoparticle. The enthalpy of forming ternary nanoparticles (eqn (3)) depends on the size of the nanoparticle and for given concentration becomes more positive as the particle size increases. Where the enthalpy is negative, the different interface energies of MnO and MgO provide the driving force. Application of the semigrand ensemble has allowed us to determine the mixing free energies of the two end-member nanoparticles. In addition, we find that the consolute temperature initially increases rapidly as a function of nanoparticle size. The rate of increase is reduced for larger nanoparticles. Similar trends were observed for the order parameter in FePt nanoparticles7,43 and the melting properties of PtPd nanoalloys.8 It is important to note that the ternary nanoparticles themselves may well be highly ordered with a shell of MnO around a central MgO core, particularly at xMg ≈ 0.8–0.6 concentrations and low temperatures; the different interface energies of MgO and MnO provide the thermodynamic barrier to forming separate binary nanoparticles. It will be interesting to see to what extent the trends we establish in this paper are more general when size mismatch governs thermodynamic properties of mixing. Our Monte Carlo method is general and we shall apply this in future work to interfaces of technological importance. In particular, we intend to study more complex nanoparticles and explore the influence of changes in surface environment such as hydroxylation.
952 ions). As the Mn concentration is progressively increased the Mn2+ ions occupy the corners, edges and then surface sites of the nanoparticle. The enthalpy of forming ternary nanoparticles (eqn (3)) depends on the size of the nanoparticle and for given concentration becomes more positive as the particle size increases. Where the enthalpy is negative, the different interface energies of MnO and MgO provide the driving force. Application of the semigrand ensemble has allowed us to determine the mixing free energies of the two end-member nanoparticles. In addition, we find that the consolute temperature initially increases rapidly as a function of nanoparticle size. The rate of increase is reduced for larger nanoparticles. Similar trends were observed for the order parameter in FePt nanoparticles7,43 and the melting properties of PtPd nanoalloys.8 It is important to note that the ternary nanoparticles themselves may well be highly ordered with a shell of MnO around a central MgO core, particularly at xMg ≈ 0.8–0.6 concentrations and low temperatures; the different interface energies of MgO and MnO provide the thermodynamic barrier to forming separate binary nanoparticles. It will be interesting to see to what extent the trends we establish in this paper are more general when size mismatch governs thermodynamic properties of mixing. Our Monte Carlo method is general and we shall apply this in future work to interfaces of technological importance. In particular, we intend to study more complex nanoparticles and explore the influence of changes in surface environment such as hydroxylation.
Acknowledgements
Computing resources were provided by STFC's e-science facility. Fig. 2 was prepared using Jmol.44References
- B. Kang and G. Ceder, Nature, 2009, 458, 190 CrossRef CAS.
- B. C. Gates, L. Guczi and H. Knoezinger, Metal Clusters in Catalysis, Elsevier, Amsterdam, 1986 Search PubMed.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845 CrossRef CAS.
- For example, R. Vallée, M. Wautlet, J. P. Dauchot and M. Hecq, Nanotechnology, 2001, 12, 68 Search PubMed.
- T. Van Hoof and M. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115434 CrossRef.
- D. S. Mainardi and P. B. Balbuena, Langmuir, 2001, 17, 2047 CrossRef CAS.
- M. Müller and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 094203 CrossRef.
- G. Wang, M. A. Van Hove, P. N. Ross and M. I. Baskes, J. Chem. Phys., 2004, 121, 5410 CrossRef CAS.
- G. Guisbiers, G. Abudukelimu and D. Hourlier, Nanoscale Res. Lett., 2011, 6, 396 CrossRef.
- H. Y. Kim, D. H. Kim and H. M. Lee, J. Nanosci. Nanotechnol., 2011, 11, 2251 CrossRef CAS.
- For a recent review see C. R. A. Catlow, S. T. Bromley, S. Hamad, M. Mora-Fonz, A. A. Sokol and S. M. Woodley, Phys. Chem. Chem. Phys., 2010, 12, 786 Search PubMed.
- For example, S. M. Woodley, Proc. R. Soc. A, 2011, 467, 2020 Search PubMed.
- For example, J. N. Hart, S. C. Parker and A. A. Lapkin, ACS Nano, 2009, 3, 3401 Search PubMed.
- D. G. Stroppa, L. A. Montoro, A. Beltran, T. G. Conti, R. O. da Silva, J. Andres, E. R. Leite and A. J. Ramirez, Chem.–Eur. J., 2011, 17, 11515 Search PubMed.
- For example, S. C. Pandey and D. Maroudas, J. Chem. Phys., 2011, 135, 23470 Search PubMed and references therein.
- S. C. Pandey and D. Maroudas, J. Appl. Phys., 2011, 110, 123509 Search PubMed and references therein.
- S. M. Woodley, Mater. Manuf. Processes, 2009, 24, 255 Search PubMed.
- X. Wang, J. C. Hanson, J. A. Rodriguez, C. Belver and M. Fernández-García, J. Chem. Phys., 2005, 122, 154711 CrossRef.
- For work on phase segregation in SiO2/TiO2 and SiO2/Fe2O3 nanoparticle aerosols, see S. H. Ehrman, S. K. Friedlander and M. R. Zachariah, J. Mater. Res., 1999, 14, 4553 Search PubMed.
- For work on SnO2/TiO2 composite nanoparticles, K. K. Akurati, A. Vital, R. Hany, B. Bommer, T. Graule and M. Winterer, Int. J. Photoenergy, 2005, 2, 153 Search PubMed.
- N. Meethong, H. Y. S. Huang, W. C. Carter and Y.-M. Chiang, Electrochem. Solid-State Lett., 2007, 10, A134 CrossRef CAS.
- N. Meethong, H. Y. Huang, S. A. Speakman, W. C. Carter and Y.-M. Chiang, Adv. Funct. Mater., 2007, 17, 1115 CrossRef CAS.
- A. Yamada, H. Koizumi, S.-I. Nishimura, N. Sonoyama and R. Kanno, et al. , Nat. Mater., 2006, 5, 357 CrossRef CAS.
- P. Gibot, M. Casas-Cabanas, L. Laffont, S. Levasseur and P. Carlach, et al. , Nat. Mater., 2008, 7, 741 CrossRef CAS.
- N. Meethong, Y.-H. Kao, W. C. Carter and Y.-M. Chiang, Chem. Mater., 2010, 22, 1088 CrossRef CAS.
- M. Tanga, W. C. Carter, J. F. Belak and Y.-M. Chiang, Electrochim. Acta, 2010, 56, 969 Search PubMed.
- B. Burch and M. Z. Bazant, Nano Lett., 2009, 9, 3795 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- J. A. Purton and N. L. Allan, J. Cryst. Growth, 2006, 294, 130 CrossRef CAS.
- N. L. Allan, G. D. Barrera, M. Yu. Lavrentiev, I. T. Todorov and J. A. Purton, J. Mater. Chem., 2001, 11, 63 RSC.
- W. C. Mackrodt, J. Chem. Soc., Faraday Trans., 1989, 2, 541 Search PubMed.
- http://www.ccp5.dl.ac.uk/DLMONTE .
- C. R. A. Catlow and W. C. Mackrodt, in Computer Simulation of Solids, ed. C. R. A Catlow and W. C. Mackrodt, Springer-Verlag, Berlin, 1982, ch. 1, pp. 3–20 Search PubMed.
- G. V. Lewis and C. R. A. Catlow, J. Phys. C: Solid State Phys., 1985, 18, 1149 CrossRef CAS.
- N. L. Allan, G. D. Barrera, R. M. Fracchia, M. Yu. Lavrentiev, M. B. Taylor, I. T. Todorov and J. A. Purton, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094203 CrossRef; I. T. Todorov, N. L. Allan, M. Yu. Lavrentiev, C. L. Freeman, C. E. Mohn and J. A. Purton, J. Phys.: Condens. Matter, 2004, 16, S2751 CrossRef CAS.
- J. A. Purton, M. Y. Lavrentiev and N. L. Allan, Phys. Chem. Chem. Phys., 2005, 7, 3601 RSC.
- J. A. Purton, G. D. Barrera, M. B. Taylor, N. L. Allan and J. D. Blundy, J. Phys. Chem. B, 1998, 102, 5202 CrossRef CAS.
- For an example application to ordering in spinels, see M. Yu. Lavrentiev, J. A. Purton and N. L. Allan, Am. Mineral., 2003, 88, 1522 Search PubMed.
- N. I. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, 2nd edn, Academic Press, San Diego-London, 2002 Search PubMed.
- M. Y. Lavrentiev, N. L. Allan, G. D. Barrera and J. A. Purton, J. Phys. Chem. B, 2001, 105, 3594 CrossRef CAS.
- C. E. Mohn, N. L. Allan and J. H. Harding, Phys. Chem. Chem. Phys., 2009, 11, 3217 RSC; K. McKenna, private communication.
- M. Müller, P. Erhart and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 155412 Search PubMed.
- Jmol: an open-source Java viewer for chemical structures in 3D, http://www.jmol.org/.
- B. J. Wood, R. T. Hackler and D. P. Dobson, Contrib. Mineral. Petrol., 1994, 115, 438 CrossRef CAS.
| This journal is © the Owner Societies 2013 |
