 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long-range Li+ dynamics in the lithium argyrodite Li7PSe6 as probed by rotating-frame spin–lattice relaxation NMR†
V.
Epp
*a,
Ö.
Gün
b,
H.-J.
Deiseroth
b and
M.
Wilkening
*a
aChristian Doppler Laboratory for Lithium-ion Batteries, Graz University of Technology, Institute for Chemistry and Technology of Materials, Stremayrgasse 9, 8010 Graz, Austria. E-mail: viktor.epp@tugraz.at; wilkening@tugraz.at
bUniversity of Siegen, Inorganic Chemistry I, Adolf-Reichwein-Straße 2, 57068 Siegen, Germany
First published on 18th March 2013
Abstract
Lithium-rich argyrodites belong to a relatively new group of fast ion conducting solids. They might serve as powerful electrolytes in all-solid-state lithium-ion batteries being, from a medium-term point of view, the key technology when safe energy storage systems have to be developed. Spin–lattice relaxation (SLR) nuclear magnetic resonance (NMR) measurements carried out in the rotating frame of reference turned out to be the method of choice to study Li dynamics in argyrodites. When plotted as a function of the inverse temperature, the SLR rates log10(R1ρ) reveal an asymmetric diffusion-induced rate peak. The rate peak contains information on the Li jump rate, the activation energy of the hopping process as well as correlation effects. In particular, considering the high-temperature flank of the SLR NMR rate peak recorded in the rotating frame of reference, an activation energy of approximately 0.49 eV is found. This value represents long-range lithium jump diffusion in crystalline Li7PSe6. As an example, at 325 K the Li jump rate determined from SLR NMR is in the order of 1.4 × 105 s−1. The pronounced asymmetry of the rate peak R1ρ(1/T) points to correlated Li motion. It is comparable to that which is typically found for structurally disordered materials showing a broad range of correlation times.
I. Introduction
The development of powerful lithium-ion batteries, which are expected to be the intermediate-term devices to store electrical energy, requires the availability and provision of lithium-ion conductors with a very high Li+ mobility.1–7 In particular, compared to liquid electrolytes, the use of solid ion conductors meets the challenges to design more powerful and highly safe lithium-ion batteries.7,8 These are expected to show a long lifetime which is, in particular, necessary for large-scale, decentralised stationary energy storage. Thus, research on materials for lithium-ion batteries is in line with the imperative goal to reduce our dependence on fossil fuels if we are to store electrical energy from renewable sources and, hence, to combat climate change. Finding suitable solid electrolytes will certainly provide a leap forward towards the development of safe all-solid-state lithium-ion batteries being useful for diverse applications of energy storage systems such as portable electronic devices or even (hybrid) electric vehicles.During the last few years many Li containing solid electrolytes have been screened and also modified for such purposes. However, the number of suitable candidates turns out to be rather rare, see, e.g., ref. 8–14. Essentially, besides chemical inertness, which oxide materials usually show, they have to fulfill the necessary requirement to exhibit an ionic conductivity exceeding, in the ideal case, 10−3 S cm−1 at room temperature.
Quite recently, a new class of Li-rich materials has been investigated, viz. crystalline lithium argyrodites, which exhibit such a sufficiently high Li+ mobility.9,15 So far, Li dynamics of the compounds belonging to the class of Li7PX6 (X = S, Se) and Li6PX5X′ (X′ = Cl, Br, I), which are from a structural point of view closely related to the mineral Ag8GeS6, have mainly been investigated by impedance spectroscopy.9,15–19 Apart from first line shape analyses,9,15 an in-depth Li nuclear magnetic resonance (NMR) spin–lattice relaxation (SLR) study is still missing. It turned out that the highest conductivity was found for the halides rather than for the pure sulfides or selenides.15 Apart from impedance spectroscopy, Li jump rates and thus Li diffusion coefficients can be studied by time-domain Li NMR spectroscopy.20–26 Compared to conductivity measurements, diffusion-induced Li NMR SLR rates solely reflect Li+ diffusivity rather than e− dynamics which might also contribute to the total conductivity probed. In the latter case, contributions arising from other charge carriers have to be carefully eliminated which in some cases might be fraught with great experimental difficulties. By using NMR spectroscopy instead, no special post-preparation of the material to be investigated is necessary and a powdered sample is sufficient to study Li dynamics in detail. Usually the powder is sealed in a small glass ampoule in an inert gas atmosphere to protect it from moisture. Therefore, NMR spectroscopy offers a rather direct and non-destructive access to Li self-diffusion parameters which can easily be converted into (solid-state) Li diffusion coefficients.27–29
In the present case, the low-temperature modification of Li7PSe6, whose structure has been well characterized by both X-ray powder diffraction and high-resolution NMR recently,15 was chosen to study dynamic properties by temperature-variable 7Li NMR spectroscopy. The material served as a first model substance to enlighten Li ion transport properties of lithium-rich argyrodites by NMR SLR methods. Here, NMR SLR rate measurements performed in the so-called rotating frame of reference turned out to be the best choice to study Li self-diffusion processes. The method takes advantage of an oscillating magnetic field B1 (rather than the ordinary external magnetic field B0), which is used to perturb the 7Li spin system in the frame of an SLR NMR experiment.30,31 The associated radio (or locking) frequency ω1 is related to B1via γB1 = ω1 where γ is the magnetogyric ratio of the nucleus under investigation. Since ω1 is in the order of some tens of kHz and ω0 is in the upper MHz range, NMR SLR measurements performed in the rotating frame of reference are sensitive to Li jump rates with values in the order of 104 to 105 s−1, thus, considerable longer correlation times can be probed than it is possible with SLR NMR measurements performed in the laboratory frame of reference being the more common technique to probe ion dynamics by NMR.25,28
In general, monitoring the complete diffusion-induced SLR NMR rate peak, which is obtained when the SLR rate R1ρ is plotted vs. the inverse temperature 1/T, gives access to both the activation energy Ea and the pre-exponential factor τ0−1 determining the underlying Arrhenius relation (see below). Furthermore, it contains information about correlation effects such as structural disorder and Coulomb interactions.32 Therefore, it might be useful to roughly evaluate to what extent short-range Li motions influence the R1ρ rates measured and, thus, ion transport parameters.
II. Experiment
Synthesis and characterization of polycrystalline Li7PSe6 with μm-sized crystallites (as well as the closely related Li7PS6) are described in great detail by Kong et al.15 Both Li7PS6 and Li7PSe6 exhibit two structural modifications with a fully reversible phase transition at 483 K and 437 K, respectively. While the high-temperature modification shows the typical argyrodite-type structure (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m), the crystal structure of the low-temperature modification is closely related to that of the low-temperature form of α-Cu7PSe6 crystallizing with orthorhombic symmetry.15
3m), the crystal structure of the low-temperature modification is closely related to that of the low-temperature form of α-Cu7PSe6 crystallizing with orthorhombic symmetry.15
7Li NMR measurements were conducted on a high performance digital Bruker Avance III spectrometer in connection with a shimmed cryomagnet of a nominal magnetic field of ca. 7 T. This corresponds to a Larmor frequency of ω0/2π = 116 MHz. A commercial high-temperature probe head (Bruker Biospin) was employed allowing π/2 pulse lengths of about 2.9 μs. The measurements were performed at temperatures ranging from 216 K to 416 K, which were monitored using a Eurotherm temperature controller in combination with a type T thermocouple. Measurements at temperatures down to 112 K were carried out using a cryo probe (Bruker) which was operated by evaporating liquid nitrogen. As compared to the standard probe, the π/2 pulse length of the cryo probe was ca. 5.2 μs. Prior to the measurements the sample was vacuum dried and fire sealed in a glass NMR tube of 5 mm in diameter and 3 cm in length.
7Li NMR SLR rates 1/T1 = R1 were acquired by means of the saturation recovery pulse sequence 10 × π/2 − td − π/2 which is depicted in Fig. 1(A).20,33 Here, the initial ten π/2 pulses in rapid succession are used to destroy any longitudinal magnetization Mz before its recovery is recorded as a function of the delay times td. 7Li NMR SLR rates 1/T1ρ = R1ρ were recorded in the rotating frame of reference (SLRρ). To this end the spin-locking technique30–36 was employed (see Fig. 1(B)) where the relaxation of the equilibrium magnetization is probed at rather low magnetic field strengths B1. The corresponding locking frequency was chosen to be ω1/2π ≈ 45 kHz with the duration of the locking pulse tlock varying between 10 μs and 100 ms. The recycle delay for the SLRρ experiments was set to at least 5 × 1/R1. Both R1 and R1ρ were obtained by parameterizing the magnetic transients Mz(td) and Mρ(tlock), respectively, by stretched exponentials. In the case of R1ρ the exponent γ in Mρ(tlock) ∝ exp(−(tlock/T1ρ)γ) ranges from 0.4 to 0.9 (210 K ≤ T ≤ 430 K). For the sake of completeness, temperature-variable 7Li NMR spin–spin relaxation (SSR) rates 1/T2 = R2 were monitored, which were recorded using a solid-echo pulse sequence33 optimized for spin-3/2 nuclei (see Fig. 1(C)). techo denotes the variable interpulse delay. The corresponding NMR spectra were either obtained after irradiation with a single π/2 pulse or using the solid-echo pulse sequence. In the latter case, echoes were recorded at fixed techo of 20 μs; spectra were obtained by Fourier transformation beginning from the echo top.
 | ||
| Fig. 1 (A) The saturation recovery pulse sequence used to probe the SLR NMR rates R1: a comb of closely spaced rf-pulses (π/2)x′ (n ≈ 10) destroys the (initial) longitudinal magnetization (Mz = Meq) so that Mz = 0 at t = 0. The subsequent recovery of Mz(t) is probed with a single π/2-pulse which is sent after a variable relaxation delay t = td. (B) The pulse sequence of the spin-lock technique to record the rotating-frame NMR rates R1ρ: immediately after the π/2-pulse the magnetization M pointing along the (−y′) is locked by the field B1. The decay of Mρ(−y′) is then probed by plotting the height (or area) of the free induction decay (FID) as a function of the locking pulse length tlock. See also ref. 37. In a simplified manner (C) and (D) depict the pulse sequences to record SSR NMR rates and stimulated echo decay curves. See the text for further explanation. | ||
In addition to the SLR and SSR NMR measurements, first 7Li NMR stimulated echoes have been recorded by utilizing the Jeener–Broekaert38 pulse sequence which is in simplified terms shown in Fig. 1(D).21,39–41 Usually, such stimulated echo measurements are sensitive to slow Li dynamics.21,42–48 The technique gives access to single-spin two-time correlation functions21,22,39 and takes advantage of the different electrical environments the Li spins sense during hopping from site to site. Here, so-called 7Li sin–sin hopping correlation functions,21,39i.e., spin-alignment echo (SAE) decay curves,24,25,43 were monitored at a fixed preparation time tp of 12 μs and a variable mixing time tm ranging from 10 μs to 100 s. Appropriate phase cycling is necessary to eliminate unwanted coherences.39
III. Results and discussion
Temperature-variable 7Li NMR spectra of crystalline Li7PSe6 yield first insights into the Li dynamics of the argyrodite. In Fig. 2 various NMR spectra are shown which were recorded at temperatures ranging from 216 to 417 K. They were acquired using a single pulse sequence, thus, quadrupole intensities (see below) are largely suppressed. Typically, at low temperatures, i.e. in the so-called rigid-lattice regime, a dipolar broadened NMR (central) line is observed which can be approximated with a Gaussian. Due to the increasing motion of the Li spins at elevated temperatures dipole–dipole interactions are continuously averaged. Hence, the central NMR line width obeys a motional narrowing (MN) from which the Li jump rate can be roughly estimated. In the present case, even at temperatures as low as 200 K MN has already set in. This can be clearly seen when Fig. 3 is considered where the NMR line width (full width at half maximum), directly read out from the NMR spectra recorded, is plotted vs. T. The dashed line is simply drawn to guide the eye; the rigid-lattice regime is reached at temperatures lower than 150 K.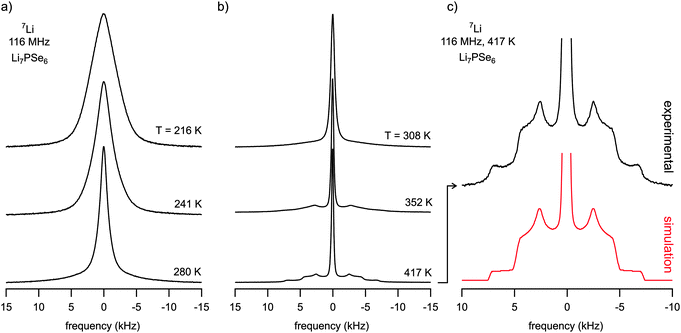 | ||
| Fig. 2 (a) and (b) 7Li NMR spectra of ternary Li7PSe6 recorded at the temperatures indicated. The line width steadily decreases reflecting a pronounced motional narrowing which indicates rapid Li exchange on the NMR time scale defined by the rigid lattice line width of Li7PSe6. Pronounced and well-defined quadrupole powder patterns emerge at temperatures chosen to be higher than 300 K. It is fully developed at 417 K. (c) Magnification of the quadrupole powder pattern of the 7Li NMR recorded at 417 K. The spectrum shown at the bottom displays a simulation of the measured one with the help of WinSolids software49 using a single set of fitting parameters describing the NMR line shape. See the text for further details. | ||
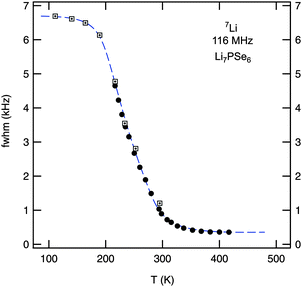 | ||
| Fig. 3 Motional narrowing of the 7Li NMR linewidth of polycrystalline Li7PSe6. While filled symbols (●) represent data points recorded using a standard probe, boxes display the line widths (fwhm) of NMR spectra recorded using a cryo probe. The rigid lattice value, νrl ≈ 6.8 kHz, is reached at temperatures below 150 K. The onset of MN is expected when the Li jump rate reaches values in the order of 103 s−1. See the text for further explanation. | ||
Whereas at the highest temperatures (T > 350 K, that is, the regime of extreme narrowing) the NMR central line, corresponding to the spin-quantum transition I = ±1/2 ⇄ I = ∓1/2, can be well approximated with a Lorentzian, the NMR line in the intermediate temperature range can be represented by the sum of a Lorentzian line and a Gaussian line. However, a strongly heterogeneous narrowing of the NMR central line, which in many cases is reflected by a pronounced difference in line width of the two components,50,51 seems to be absent in the present case. Thus, the lack of clearly recognizable two-phase spectra hampers a quantitative analysis according to that, e.g., presented in ref. 52. Nevertheless, the shape of the central transitions shown in Fig. 2(a) points to a distribution of Li jump rates and, therefore, also to a distribution of Li migration pathways in the Li-argyrodite studied.
Since the MN curve shown in Fig. 3 is obtained by plotting the overall line widths of the spectra recorded, it is only of limited use for the extraction of dynamic jump parameters. Significant MN is expected when the jump rate τ−1 reaches the order of the rigid lattice line width. For example, one might take use of the inflexion point of the curve (Tinfl ≈ 235 K) to estimate τ−1. Using νrl ≈ 6.8 kHz for the NMR line width measured in the rigid lattice regime, the corresponding Li jump rate τ−1 is approximately given by τMN−1 ≈ 2π × νrl ≈ 4 × 104 s−1. Moreover, from the so-called onset temperature (Tonset ≈ 180 K) an activation energy Ea,MN can be roughly estimated according to the expression of Waugh and Fedin,53Ea,MN/meV = 1.62 × Tonset/K. In the present case this yields Ea,MN ≈ 0.3 eV. However, considering the analysis of Faske et al.,51 in the case of a distribution of lithium jump rates, this approach is at risk to underestimate the activation energy obtained and to overestimate the jump rate deduced from MN, respectively. In particular, this is the case when motion-induced line narrowing spans a broad temperature range, here this is more than 100 K, and Tonset is mainly governed by the fraction of fast ions which are presumably subject to, e.g., short-range (or spatially localized) jump processes.52
In the present case, a more precise access to Li jump rates is given by SLR NMR. Before discussing the corresponding results, it is useful to have a closer look on the features of the NMR spectra recorded in the rigid-lattice regime and in the limit of extreme narrowing, i.e., at the highest temperatures where the line width is mainly governed by inhomogeneities of the external magnetic field. Interestingly, in the latter regime a well-defined quadrupole powder pattern shows up. Such electric quadrupole intensities are due to the interaction of the quadrupole moment of the 3/2-spin nucleus, which is a result of the non-spherical charge distribution of the nucleus, being immersed in an electronic environment characterized by a non-vanishing electric field gradient (EFG). The latter is produced by the electric charge distribution in the direct neighbourhood of the nucleus under observation. This additional interaction alters the Zeeman levels and thus the associated (angular) Zeeman frequency ω0 towards ω0 ± ωQ.54 The corresponding quadrupole frequency is given by
| ωQ = ±δπ/2(3cos2Θ − 1 − ηQ sin2Θ cos(2Φ)) | (1) |
In the absence of lithium motions on the kHz scale, quadrupole intensities in the rigid-lattice regime can be made visible by recording NMR solid echoes. Owing to receiver dead-time effects, fast decaying components of an FID are difficult to detect. In Fig. 4 an NMR spectrum recorded in the rigid-lattice regime is shown which has been acquired at 190 K with the help of a two-pulse solid-echo sequence. Besides the Gaussian shaped central line, whose area fraction is about 36% of the total area, a broad quadrupole foot (64%) becomes apparent. The width (fwhm) of the latter component is about 54 kHz and points to a mean rigid-lattice quadrupole coupling constant in the order of 100 kHz. This value is comparable with those of other Li ion conductors studied. With increasing temperature, the rigid-lattice quadrupole interactions are partly averaged due to Li motions with rates as high as 105 s−1. Finally, the well-defined powder pattern, as characterized above, shows up at higher T.
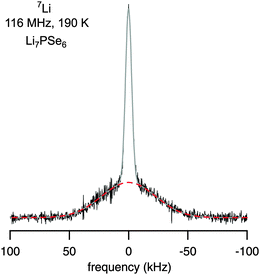 | ||
Fig. 4
7Li solid-echo (first-order quadrupolar) NMR spectrum recorded using a two-pulse sequence at 116 MHz and 190 K. The area fractions of the dipolar broadened central and quadrupole contribution are in agreement with the theoretical ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. Upon increasing temperature, the central line and the broad quadrupole signal narrow due to rapid Li exchange. 6. Upon increasing temperature, the central line and the broad quadrupole signal narrow due to rapid Li exchange. | ||
As mentioned above, straightforward insights into the Li dynamics in the ternary argyrodite are provided by analyzing diffusion-induced 7Li NMR SLR rates.20,21,23–28,37,57,58 In Fig. 5 the R1ρ rates measured in both the laboratory and rotating frames of reference are shown in an Arrhenius plot. The R1 rates reveal a diffusion-induced low-temperature flank pointing to a relatively small activation energy of only 0.28(1) eV. The so-called low-T regime of NMR SLR is sensitive to short-range rather than to long-range lithium diffusion.20 Interestingly, the SLR rates probed in the laboratory frame of reference do not exhibit a R1(1/T) rate peak; above 300 K the rates are independent of temperature and amount to be about 10 s−1. Note that at T < 235 K the rates are increasingly governed by non-diffusive and weakly temperature-dependent background effects which, most likely, can be ascribed to coupling of the Li spins with paramagnetic impurities. However, in the case of NMR SLR measurements in the rotating frame of reference performed at a locking frequency in the order of 45 kHz the R1ρ rates pass through a well-defined maximum showing up at Tmax = 325 K. This allows the direct determination of the Li jump rate τ−1 which can be estimated using the maximum condition ω1τ ≈ 0.5. Note that this estimation is based on an exponential correlation function G(t) leading to symmetric NMR rate peaks (see below). Here, at Tmax the rate τ−1 is in the order of 1.4 × 105 s−1. Compared to the result from NMR motional narrowing it becomes evident that the rate τMN−1 seems to overestimate the jump process because of the reasons discussed above.
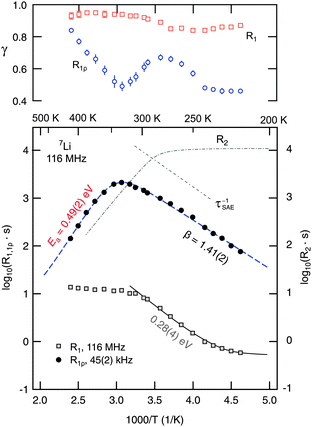 | ||
| Fig. 5 Arrhenius plot of the 7Li NMR SLR rates measured at a Larmor frequency ω0/2π of 116 MHz (R1) and a locking frequency ω1/2π of 45(2) kHz (R1ρ). The dashed line represents a modified BPP fit taking into account a sub-quadratic frequency dependence of the R1ρ rates (R1ρ ∝ ω1−β, β < 2) in the limit ω1τ ≫ 1. The upper figure shows the temperature dependence of γ used to parameterize the corresponding magnetization transients. For comparison, the temperature behaviour of the R2 SSR NMR rates and the decay rates deduced from stimulated echo NMR (see the inset of Fig. 7) are also shown. See the text for further explanation. | ||
A more detailed analysis is achieved by using an appropriate relaxation model20,59 to evaluate the SLR NMR rates R1ρ(1/T) measured. The dashed line shown in Fig. 5 represents a complete relaxation fit according to
| R1ρ(ω1, T) ∝ J3D(ω1, T) ∝ τc/(1 + (2ω1τc)β). | (2) |
Note that the correlation rate τc−1 is in the order of the jump rate τ−1. In general, J3D denotes the spectral density function characterizing electric and magnetic field fluctuations due to three-dimensional ion hopping. Here, the expression of the spectral density function, to which R1ρ(ω1, T) is proportional, is based on the relaxation model of Bloembergen, Purcell and Pound (BPP) introduced for 3D, isotropic diffusion.60 Originally, the exponent β is given by β = 2, which originates from the assumption of an underlying single exponential motional correlation function G(t). J3D is obtained from G(t) by Fourier transformation. In the case of β = 2 this results in a symmetric (Lorentzian shaped) spectral density function J3D.20 Values smaller than two (for β the range 1 < β ≤ 2 is valid) as introduced by Küchler et al.61 lead to asymmetric NMR SLR rate peaks whereby the slope of the low-temperature flank, that is the regime where ω1τ ≫ 1 holds, is smaller than that of the corresponding high-temperature side characterized by the limit ω1τ ≪ 1. In particular, asymmetric NMR SLR rate peaks have been observed for structurally disordered ion conductors. Theoretical investigations show that Coulomb interactions of the moving ions and/or structural disorder seem to be responsible for the asymmetries observed in NMR relaxometry.62–64 A pronounced heterogeneous dynamics, being closely related to structural disorder which can be represented by an irregular formed potential landscape, is expected to include both long-range dynamics as well as localized hopping processes.
In the present case, the R1ρ(ω1,T) data can be best represented by a fit with β = 1.41(2). This result certainly points to a non-exponential motional correlation function. It might directly reflect a heterogeneous potential landscape the Li ions are exposed to. In Li7PSe6 the Li ions occupy multiple, distinctly connected sites as revealed by high-resolution 6Li NMR spectroscopy.15 A relatively low β value, as found here, is comparable to that recently reported for Li ion hopping in Li7La3Zr2O12 (LLZ); LLZ also exhibits a highly complex crystallographic structure where the Li ions are distributed among various inequivalent positions. Let us mention that β < 2 minimally influences the maximum condition used above to estimate the jump rate at the temperature where the rate peak shows up. Taking into account β = 1.41(2), the exact maximum condition is given by
| ω1τ = 0.5(β − 1)−1/β ≈ 0.94 | (3) |
With Ea (0.49(2) eV) and τc,0−1 ≈ τ0−1 (1.6(9) × 1013 s−1) available from the relaxation fit,65 the jump rate following the Arrhenius relation τ−1 = τ0−1exp(−Ea/(kBT)) can be determined. Here, kB denotes Boltzmann's constant. At ambient temperature, this yields τ−1 ≈ 9.5 × 104 s−1. Using the Einstein–Smoluchowski equation, which relates τ−1 with the self-diffusion coefficient Dsdvia
| Dsd = a2/(6τ) | (4) |
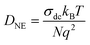 | (5) |
Identifying Ea = 0.49(2) eV (see above) with the activation energy reflecting long-range Li diffusion in Li7PSe6, the slope of the low-T flank of the rate peak of Fig. 5 might be related to Li jump processes taking place on a much shorter length scale. This is expressed by ω1τ ≫ 1 being valid in this temperature range. In the present case, the low-T flank is characterized by Ea,low = 0.21(1) eV, thus, fulfilling the relation Ea,low = (β − 1)Ea. It directly links the frequency dependence of R1ρ ∝ ω1−β to the asymmetry of the diffusion-induced relaxation rate peak R1ρ(1/T). Indeed, the crystallographic structure of Li-containing argyrodites contains structural motifs, viz. Li ions residing in close-by tetrahedral voids, which might help explain the differences between localized, i.e., short-range Li dynamics on the one hand and long-range Li diffusion on the other hand.15 This is also supported by recent theoretical investigations on halide-containing Li-argyrodites.16,17
For comparison with the SLR NMR rates, the γ exponents describing the deviation of the magnetization transients Mρ(tlock), see Fig. 6, from single-exponential time behaviour are also included in Fig. 5. Whereas a straightforward interpretation of γ is generally not available, one might read out two features showing up in the present case. At very low temperatures the exponent is approximately 0.5 which might point to (diffusion-induced) spin–lattice relaxation due to coupling of the 7Li spins primarily to paramagnetic impurities. At even lower temperatures homonuclear spin-diffusion might play an additional role. With increasing diffusivity, γ initially increases before a minimum value is attained at Tmax where the corresponding maximum peak R1ρ(1/T) shows up. Interestingly, when T is further increased and Li diffusion becomes rapid the exponent γ steadily increases towards γ = 1, i.e., single-exponential time behaviour. Note that at very high temperatures the various electrical interactions the Li spins are exposed to are greatly averaged resulting in a quadrupole powder pattern which can be simulated with a single set of (mean) parameters. Thus, when considering the underlying motional correlation function, being at least partly reflected by the exponent γ, it might also change as a function of temperature and seems to tend to become a single exponential in the limit ω1τ ≪ 1. Such an observation is in agreement with the predictions of Ngai and co-workers,66 who have analyzed the shape of motional correlation functions from both NMR and impedance spectroscopy measurements.
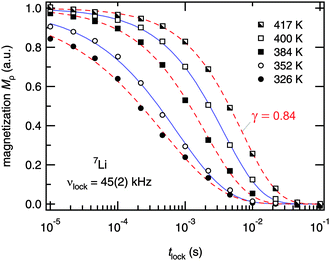 | ||
| Fig. 6 7Li NMR magnetization transients Mρ(tlock) of Li7PSe6 recorded at the temperatures indicated and at ω0/2π = 116 MHz and ω1/2π = ν1 = 45(2) kHz. Dashed and solid lines represent fits according to Mρ(tlock) ∝ exp(−(tlock/T1)γ). At high temperatures, i.e. in the limit ω1τ ≫ 1, the stretching exponent γ increases towards single exponential time behaviour. The decay curves recorded above 360 K represent magnetization transients of the high-temperature flank of the R1ρ(1/T) peak shown in Fig. 5. | ||
For the sake of completeness, R2 SSR NMR rates were recorded at temperatures down to 190 K. In the rigid-lattice regime, T2 is approximately 70 μs. This is in good agreement with the second moment, i.e., the line width of the central transition in this temperature range (6.8 kHz), see above. It is worth mentioning that, as expected, the 7Li NMR solid echoes are composed of a fast and slowly decaying contribution which mirror quadrupolar and dipolar contributions. Irrespective of what is analyzed in detail, i.e., (i) the complete area under the echo, (ii) the amplitude of the quadrupole part or (iii) the area of the slowly decaying dipolar part, at very low T the corresponding transients follow single-exponential time behaviour (see Fig. S1 and S2, ESI†). However, the situation changes upon increasing T. Then, a fast decaying and temperature independent contribution with R2′ = 30 μs shows up (see Fig. S2, ESI†). These rates might reflect a very slow dynamic process. Interestingly, the stimulated echoes, which are presented below, also seem to point to a subset of lithium ions with a very low diffusivity.
For comparison, in Fig. 5 the temperature-dependent R2 rates of the slowly decaying part of the transients are included. The rates start to decrease at T = 260 K. At this temperature the associated jump rate is in the order of 104 s−1, which is in good agreement with the Arrhenius parameters deduced from the R1ρ(1/T) peak. However, the corresponding activation energy, which can be estimated from the linearly decaying part of the R2 curve, turns out to be only 0.4 eV (see also Fig. S2, ESI†). Moreover, the maximum R1ρ rate exceeds R2. Similarly, this has been observed by, e.g., Bertermann et al.56 who recorded R2 rates using a Hahn echo pulse sequence. In doing so, Hahn echo decay seems to be determined by dipolar rather than by quadrupolar interactions as expected.
The present difference between R1ρ and R2 also indicates that the two rates probed are not necessarily influenced by exactly the same relaxation mechanism and/or the same subset of (differently coupled) Li spins. Considering the pre-factor obtained from the R1ρ(1/T) fit (R1ρ = C′ × J3D(2ω1)), which amounts to C′ = 2.95(9) × 109 s−2, thus, being in the order of the square of the rigid-lattice quadrupole coupling constant (see above), we suppose that, besides dipolar ones, fluctuating quadrupolar interactions also play a large role in influencing R1ρ. However, a conclusive answer to what extent dipolar interactions affect the SLR NMR rates probed might only be possible by future 6Li NMR experiments carried out at resonance frequencies comparable to those used for the 7Li NMR measurements.
In addition to NMR SLR measurements in the rotating frame of reference, we have recorded 7Li spin-alignment echo NMR decay curves which are sensitive to slow Li exchange processes between electrically inequivalent Li sites in the argyrodite. Thus, the method takes advantage of the distinct quadrupolar interactions of the jumping Li ions. The decay curves shown in Fig. 7 were obtained by plotting the intensity of the spin-alignment echo (read out at the echo maximum, i.e., at t = tp) as a function of mixing time. The S2 curves reflect the probability to find an Li nuclear spin, which initially (tm = 0) resides on a specific site, on an electrically equivalent site at a later time (t = tm).
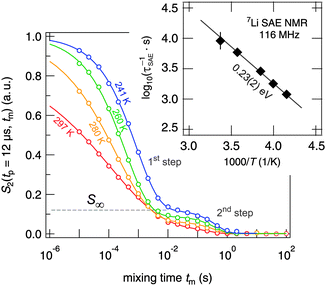 | ||
| Fig. 7 7Li NMR (sin–sin) two-time correlation functions recorded using the Jeener–Broekaert38,39 pulse sequence (116 MHz, tp = 12 μs). While the first decay step of the S2 decay curve reflects Li hopping between electrically inequivalent Li sites in crystalline Li7PSe6, the second one is induced by (quadrupolar) spin–lattice relaxation. Solid lines represent fits with a combination of two stretched exponentials. | ||
Interestingly, echo damping proceeds in two steps.22,26,67 Most likely, the first decay step directly reflects Li hopping; the second step, however, might be induced by (quadrupolar) spin–lattice relaxation and/or spin-diffusion effects. The latter are expected to be characterized by a decay rate τ′′ being in the order of seconds. The full decay curves were parameterized with a combination of two stretched exponentials according to
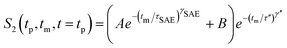 | (6) |
Irrespective of this possible influence on the 7Li NMR S2 curves, even at temperatures as low as 220 K the two-step decay behaviour remains. For example, the (normalized) correlation function recorded at 241 K is characterized by a so-called plateau value S∞ = B/(A + B) (see eqn (6)) which is approximately 0.12. In general, 1/S∞ is related to the number of electrically inequivalent Li sites the ion visits during self diffusion.39 The inverse, 1/S∞, equals the number of available Li sites provided these are equally populated and visited by the spins with the same probability. S∞ = 0.12 leads, at first glance, to approximately eight different Li sites. In fact, there are at least seven electrically inequivalent Li sites occupied in Li7PSe6. It is worth mentioning that, once again, 7Li–7Li dipole–dipole interactions might influence 1/S∞ which usually point to a larger number of sites than actually present in the crystal structure. Such a situation has also been found for SAE NMR measurements on β-eucryptite, LiAlSiO4, single crystals.71 With increasing temperature T, the value S∞ decreases which might be attributed to the increasing averaging of electric quadrupolar as well as magnetic dipolar interactions due to sufficiently fast Li hopping.
Alternatively, the emergence of a distinct plateau might also be interpreted in terms of a small and decoupled sub-ensemble of very slow Li ions that show up at large mixing times and low temperature. However, since the corresponding decay rates associated with the second step (1/τ′′) do not reveal a significant temperature dependence, the above-given explanation, pointing to the averaging of quadrupole interactions, seems to be more suitable to understand the NMR response. Moreover, at higher temperatures the jump process occurring during the evolution period determined by tp might also affect the correlation functions probed. This phenomenon is called motional phase averaging, see ref. 21 for further details.
In contrast to the diffusion process being responsible for the maximum of R1ρ(1/T), the first decay step of the SAE NMR decay curves reflects Li spins diffusing on a rather long time scale. In this context it is worth mentioning once again that, in general, SAE NMR is insensitive to Li+ jumps between electrically inequivalent sites. This also holds for sufficiently fast exchange processes for which echo formation is not possible or for hopping processes leading to elimination of fluctuating EFGs. The latter means fast jump processes involving a small number of preferred but electrically inequivalent sites. Such a process would lead to an averaged but mixing-time independent EFG and is expected to contribute to SLR NMR but it would be invisible for SAE NMR. This view might help understand the difference found between τ−1 from R1ρ(1/T) and τSAE−1. Such a scenario of fast and slowly diffusing spins,16 which allow exchange between each other, is also in agreement with a relatively large final state amplitude for the slow process most likely involving the majority of the Li sites available. As mentioned above, exchange between closely adjacent voids in Li7PSe6, see ref. 15 and 16, might represent such a preferred (spatially localized and fast) hopping process to which SAE NMR is not sensitive, cf. also the illustration of Fig. 7 in ref. 16. The relatively low activation energy deduced from SAE NMR might point to the conclusion that at higher T further hopping processes come into play which are finally detected by R1ρ(1/T) in the high-temperature limit.
For comparison with a recent study on Li4SnS4, let us note that Dehnen and co-workers72 reported on SAE data which reveal low-temperature echo decay damping pointing to an extremely slow Li motional process. This process is reported to be thermally activated by 0.05 eV only. Very recently, by our own group a similar motion process with an activation energy of 0.09 eV was observed for a structurally disordered ion conductor. In contrast to the SAE NMR response probed here, but in analogy to the well-known nearly constant loss (NCL) phenomenon in conductivity spectroscopy, in ref. 73 we interpreted this feature as a result from strictly localized (or caged) motions, see also ref. 74.
Finally, instead of a single (Arrhenius-type) diffusion process we found indications for various motional mechanisms present in Li7PSe6. This also includes the possibility that diffusion mechanisms change as a function of temperature and dominate others in certain ranges. It also helps understand why it is hardly possible to perform a so-called joint fit, see, e.g., ref. 28, of the temperature-variable and frequency-dependent SLR NMR rates R1ρ and R1. Here, the rates R1 might be interpreted as the result of a superposition of different processes leading to 0.28 eV (Fig. 5) in the end. In contrast, long-range Li+ ion dynamics at higher T seem to be determined by an activation energy of 0.49 eV which can be deduced from the R1ρ(1/T) peak in the relaxation limit ω1τc ≪ 1.
IV. Conclusion and outlook
In summary, local electric structures and Li self-diffusion in a polycrystalline sample of Li7PSe6 have been examined by temperature-variable 7Li NMR spectroscopy. Line shape as well as SLR measurements have been used to get insights into translational Li dynamics present. While the first seem to be mainly governed by local exchange processes, with the help of SLR measurements short- as well as long-range diffusion parameters are accessible. In particular, it turned out that SLR measurements performed in the rotating frame of reference are highly suited to characterize Li hopping motions taking place on different length scales in the Li-containing argyrodite. From the diffusion-induced R1ρ SLR rate peak probed, both the activation energy (0.49(2) eV) as well as the pre-exponential factor (1.6(9) × 1013 s−1) of the underlying Arrhenius relation characterizing long-range dynamics (at higher T) could be probed. At ambient temperature, the Li self-diffusion coefficient is approximately 1.3(8) × 10−15 m2 s−1. This points to an Li ion conductivity in the order of 2 × 10−6 S cm−1 at 300 K. In contrast, at lower T Li dynamics seem to be characterized by activation energies ranging from 0.21 eV (R1ρ) to 0.28 eV (R1). Most likely, the relevant diffusion processes being valid in this T range also entail short-range dynamics.The measurements carried out so far build a helpful basis to be used for the comparison with halide containing Li-argyrodites such as Li6PSe5Cl revealing even higher Li conductivities.9,15,17–19,75 Currently, chlorine-containing and bromine-containing argyrodites are investigated in our laboratory. In addition to the first 7Li SAE NMR measurements presented here, the analysis of 6Li NMR hopping correlation functions might be very useful to shed more light on the dynamic processes probed via the generation of stimulated echoes.
Acknowledgements
We thank G. Schmidt (Bruker, Karlsruhe (Germany)) for his help with setting up the NMR spectrometer at the TU Graz and greatly appreciate the valuable comments of an unknown referee. Financial support from the Austrian Federal Ministry of Economy, Family and Youth, and the Austrian National Foundation for Research, Technology and Development as well as by the Deutsche Forschungsgemeinschaft (DFG) is highly appreciated (DFG Research Unit 1277).References
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271 CrossRef CAS.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652 CrossRef CAS.
- J.-M. Tarascon, ChemSusChem, 2008, 1, 777 CrossRef CAS.
- M. Winter and J. O. Besenhard, Electrochim. Acta, 1999, 45, 31 CrossRef CAS.
- A. S. Aricó, P. Bruce, B. Scrosati, J.-M. Tarascon and W. V. Schalkwijc, Nat. Mater., 2005, 4, 366 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- P. Knauth, Solid State Ionics, 2009, 180, 911 CrossRef CAS.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiss and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755 CrossRef CAS.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042 Search PubMed.
- A. Hayashi and M. Tatsumisago, Electron. Mater. Lett., 2012, 8, 199 Search PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, et al. , Nat. Mater., 2011, 10, 682 CrossRef CAS.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg and A. Lotnyk, et al. , Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- S. Narayanan, V. Epp, M. Wilkening and V. Thangadurai, RSC Adv., 2012, 2, 2553 RSC.
- S. T. Kong, O. Gün, B. Koch, H. J. Deiseroth, H. Eckert and C. Reiner, Chem.–Eur. J., 2010, 16, 5138 Search PubMed.
- O. Pecher, S.-T. Kong, T. Goebel, V. Nickel, K. Weichert, C. Reiner, H.-J. Deiseroth, J. Maier, F. Haarmann and D. Zahn, Chem.–Eur. J., 2010, 16, 8347 Search PubMed.
- R. P. Rao and S. Adams, Phys. Status Solidi A, 2011, 208, 1804 CrossRef.
- P. R. Rayavarapu, N. Sharma, V. K. Peterson and S. Adams, J. Solid State Electrochem., 2012, 16, 1807 Search PubMed.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1 Search PubMed.
- P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kräger, Springer, 2005, ch. 9, p. 367 Search PubMed.
- R. Böhmer, K. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87 CrossRef.
- C. Brinkmann, S. Faske, B. Koch and M. Vogel, Z. Phys. Chem., 2010, 224, 1535 CrossRef CAS.
- V. Epp and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 020301 CrossRef.
- M. Wilkening, J. Heine, C. Lyness, A. R. Armstrong and P. G. Bruce, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064302 CrossRef.
- M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53 CrossRef CAS.
- M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024311 CrossRef.
- M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054303 CrossRef.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef.
- A. Kuhn, J.-Y. Choi, L. Robben, F. Tietz, M. Wilkening and P. Heitjans, Z. Phys. Chem., 2012, 226, 525 Search PubMed.
- D. Ailion and C. P. Slichter, Phys. Rev. Lett., 1964, 12, 168 Search PubMed.
- C. P. Slichter and D. Ailion, Phys. Rev. Sect. A, 1964, 135, A1099 Search PubMed.
- E. Fukushima and S. B. W. Roeder, Experimental Pulse NMR: A Nuts and Bolts Approach, Addison-Wesley Pub. Co., Advanced Book Program, Reading, Mass., 1981 Search PubMed.
- D. C. Ailion and C. P. Slichter, Phys. Rev. Sect. A, 1965, 137, A235 Search PubMed.
- D. C. Look and I. J. Lowe, J. Chem. Phys., 1966, 44, 2995 CrossRef CAS.
- T. J. Rowland and F. Y. Fradin, Phys. Rev., 1969, 182, 760 Search PubMed.
- D. Wolf, Phys. Rev. B: Solid State, 1974, 10, 2724 CrossRef CAS.
- A. Kuhn, M. Kunze, P. Sreeraj, H. D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2 Search PubMed.
- J. Jeener and P. Broekaert, Phys. Rev., 1967, 157, 232 CrossRef CAS.
- R. Böhmer, J. Magn. Reson., 2000, 147, 78 CrossRef CAS.
- X.-P. Tang, R. Busch, W. Johnson and Y. Wu, Phys. Rev. Lett., 1998, 81, 5358 CrossRef CAS.
- X.-P. Tang, U. Geyer, R. Busch, W. Johnson and Y. Wu, Nature, 1999, 402, 160 CrossRef CAS.
- R. Böhmer, T. Jörg, F. Qi and A. Titze, Chem. Phys. Lett., 2000, 316, 419 CrossRef CAS.
- F. Qi, T. Jörg and R. Böhmer, Solid State Nucl. Magn. Reson., 2002, 22, 484 CrossRef CAS.
- M. Wilkening and P. Heitjans, J. Phys.: Condens. Matter, 2006, 18, 9849 CrossRef CAS.
- B. Koch and M. Vogel, Solid State Nucl. Magn. Reson., 2008, 34, 37 CrossRef CAS.
- M. Wilkening, W. Küchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901 CrossRef CAS.
- M. Wilkening, D. Gebauer and P. Heitjans, J. Phys.: Condens. Matter, 2008, 20, 022201 CrossRef.
- M. Wilkening, C. Lyness, A. R. Armstrong and P. G. Bruce, J. Phys. Chem. C, 2009, 113, 4741 CrossRef CAS.
- K. Eichele, WSolids 1, Solid-State NMR Spectrum Simulation, Version 1.19.15, University of Tübingen, 2009 Search PubMed.
- M. Wilkening, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2003, 5, 2225 RSC.
- S. Faske, H. Eckert and M. Vogel, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104301 CrossRef.
- M. Storek, R. Böhmer, S. W. Martin, D. Larink and H. Eckert, J. Chem. Phys., 2012, 137, 124507 Search PubMed.
- J. Waugh and I. Fedin, Sov. Phys. Solid State, 1963, 4, 1633.
- A. Abragam, The Principles of Nuclear Magnetism, Clarendon, Oxford, 1961 Search PubMed.
- R. Bertermann and W. Müller-Warmuth, Z. Naturforsch., A: Phys. Sci., 1998, 53, 863 CAS.
- R. Bertermann, W. Müller-Warmuth, C. Jansen, F. Hiltmann and B. Krebs, Solid State Ionics, 1999, 117, 245 Search PubMed.
- D. Brinkmann, Prog. Nucl. Magn. Reson. Spectrosc., 1992, 24, 527 Search PubMed.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018 CrossRef CAS.
- P. M. Richards, in Topics in Current Physics, ed. M. B. Salamon, Springer, Berlin, 1979, vol. 15 Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679 CrossRef CAS.
- W. Küchler, P. Heitjans, A. Payer and R. Schöllhorn, Solid State Ionics, 1994, 70–71, 434 Search PubMed.
- A. Bunde, W. Dieterich, P. Maass and M. Meyer, in Diffusion in Condensed Matter – Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2nd edn, 2005, ch. 20, pp. 813–856 Search PubMed.
- M. Meyer, P. Maass and A. Bunde, Phys. Rev. Lett., 1993, 71, 573 CrossRef CAS.
- K. Funke, Prog. Solid State Chem., 1993, 22, 111 CrossRef CAS.
- Similar values (Ea (0.49(1) eV) and τc,0−1 = 6(3) × 1012 s−1) were obtained by analyzing the rotating-frame SLR NMR data with a Cole–Davidson spectral density function.76 The distribution parameter α of the Cole–Davidson function turned out to be α = 0.42(2).
- C. Leon, J. Habasaki and K. L. Ngai, Z. Phys. Chem., 2009, 223, 1311 Search PubMed.
- M. Vijayakumar, S. Kerisit, Z. Yang, G. L. Graff, J. Liu, J. A. Sears and S. D. Burton, J. Phys. Chem. C, 2009, 113, 20108 CrossRef CAS.
- M. Wilkening, R. Amade, W. Iwaniak and P. Heitjans, Phys. Chem. Chem. Phys., 2006, 9, 1239 Search PubMed.
- M. Wilkening, C. Mühle, M. Jansen and P. Heitjans, J. Phys. Chem. B, 2007, 111, 8691 CrossRef CAS.
- B. Ruprecht, M. Wilkening, R. Uecker and P. Heitjans, Phys. Chem. Chem. Phys., 2012, 14, 11974 RSC.
- F. Qi, G. Diezemann, H. Böhm, J. Lambert and R. Böhmer, J. Magn. Reson., 2004, 169, 225 CrossRef CAS.
- T. Kaib, S. Haddadpour, M. Kapitein, P. Bron, C. Schröder, H. Eckert, B. Roling and S. Dehnen, Chem. Mater., 2013, 24, 2211 Search PubMed.
- V. Epp, C. Brüning, M. Binnewies, P. Heitjans and M. Wilkening, Z. Phys. Chem., 2012, 226, 513 Search PubMed.
- F. Qi, C. Rier, R. Böhmer, W. Franke and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104301 CrossRef.
- R. Prasado Rao, N. Sharma, V. K. Peterson and S. Adams, Solid State Ionics, 2013, 230, 72 Search PubMed.
- P. A. Beckmann, Phys. Rep., 1988, 171, 85 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp44379e |
| This journal is © the Owner Societies 2013 |
