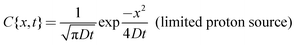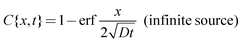Microchannel-induced change of chemical wave propagation dynamics: importance of ratio between the inlet and the channel sizes†
Hideki
Nabika
*,
Mami
Sato
and
Kei
Unoura
Department of Material and Biological Chemistry, Faculty of Science, Yamagata University, 1-4-12 Kojirakawa, Yamagata 990-8560, Japan. E-mail: nabika@sci.kj.yamagata-u.ac.jp; Tel: +81-23-628-4589
First published on 13th November 2012
Abstract
The ability to control chemical wave propagation dynamics could stimulate the science and technology of artificial and biological spatiotemporal oscillating phenomena. In contrast to the conventional chemical approaches to control the wave front dynamics, here we report a physical approach to tune the propagation dynamics under the same chemical conditions. By using well-designed microchannels with different channel widths and depths, the propagation velocity was successfully controlled based on two independent effects: (i) a transition in the proton diffusion mode and (ii) the formation of a slanted wave front. Numerical analysis yielded a simple relationship between the propagation velocity and the microchannel configuration, which offers a simple and general way of controlling chemical wave propagation.
The science of chemical waves offers basic understanding of biological spatiotemporal oscillating phenomena such as signal propagation in neural networks and formation of Turing patterns.1 In biological systems, one important factor that defines each peculiarity and functionality is the propagation velocity or the oscillation rate. In other words, diversity in the propagation velocity brings biodiversity. Exploring the origin of the diversity in the propagation dynamics is a promising way of understanding complicated biological oscillating phenomena. Additionally, chemical wave technology has allowed the development of new functional systems such as information devices,2,3 micropatterning,4 microfreight,5 and image processing.6 In these technological applications, the propagation velocity is a critical parameter that governs performance, and enhancements in controllability can improve their functionality. Thus, from both scientific and technological viewpoints, it is a critical task to understand and control the chemical wave propagation dynamics for further development.
A chemical approach to control chemical wave propagation dynamics has long been explored by many researchers. The simplest approach has been to investigate various chemical species to induce the chemical wave, e.g., systematic research has been reported that compared the proton wave velocity induced by reactions between S2O32−, S4O62−, S2O42−, SO32−, S2O62− and N2H5+ with BrO3−, IO3−, ClO3−, ClO2−, and S2O82−.7 After fixing the species to be used, tuning the concentration of each component is a next step to design the propagation velocity.8–11 To accelerate the propagation velocity, propagation orientation is also an effective parameter, in which either upward9–11 or downward8,10,12–14 propagation can be promoted by convection that can accelerate the chemical reaction at the extended wave front. A recent study reported successful velocity control using water-in-oil microemulsions; the origin of control was explained as an effect of emulsion on the rates and equilibria of chemical reactions.15 Thus, these chemical parameters were capable of controlling the propagation velocity via tuning the chemical reaction kinetics.
However, it is well-known that chemical wave propagation is governed by the reaction–diffusion equation:
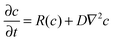 | (1) |
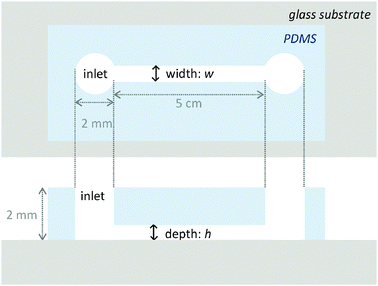 | ||
| Fig. 1 Schematic illustration of a straight-type microchannel with 2 mm-diameter pores at both ends for solution inlet/outlet. | ||
 | ||
| Fig. 2 Snapshots of propagating proton waves in microchannels with (a) 100 μm, (b) 600 μm, and (c) 1000 μm widths. Photos are taken every 2 min. The inlet is positioned at the left side of each microchannel. | ||
Since pH of the original solution before adding H2SO4 is ca. 11, the initial solution in the microchannels exhibited pale yellow colour. On the analogy of iodate–sulfite–thiosulfate system,19 transient formation of bisulfite takes place under initial high pH conditions.
| 2BrO3− + 3S2O32− + 3H2O → 2Br− + 6HSO3− | (1) |
| BrO3− + 3HSO3− + H+ → Br− + 3SO42− + 4H+ | (2) |
The process (2) is autocatalytic and the presence of a small amount of proton increases proton concentration rapidly, which induces a rapid decrease in pH. In the present system, the addition of H2SO4 initiates the autocatalytic reaction (2) and causes a rapid pH decrease at the inlet region. A pH decrease changes the color of solution near the inlet region (left side in Fig. 2) to red, indicating pH of this region becomes less than ca. 4. Autocatalytically produced proton diffuses to the nearby region with low proton concentration by a proton concentration gradient, which leads to the propagation of autocatalytic reaction. As such, the region with high proton concentration, i.e. the low pH region propagates like waves in the microchannel as shown in Fig. 2. After H2SO4 addition, the red region indicating low pH (less than 4) propagates from left to right in any channel with different width. Brightness of red color kept almost constant in the course of propagation. If simple diffusion of proton from the inlet to the microchannel were occurred, the red color should be highest at the inlet and gradually weakens toward the microchannel. Thus, the observed propagation of red color, i.e., propagation of high concentration proton, is a clear indication of the pH wave appearance under the present conditions at any channel width. Snapshot near the inlet clearly demonstrated that the color change corresponding to the pH change actually started in the inlet and propagated to the microchannel (see the ESI,† Fig. S2). The propagation length as a function of time is shown in Fig. 3 for various microchannel widths. As can be clearly seen, propagation velocity (v) increases as the channel width (w) decreases from 2000 μm to 100 μm. In contrast to the w-dependence of v, the width of propagating front that would anti-correlate with the characteristic time τ for chemical reactions in v ≈ (D/τ)0.5 did not show clear w dependence (see the ESI,† Fig. S3). Thus, we can assume that only the diffusion term D would cause w-dependent propagation dynamics.
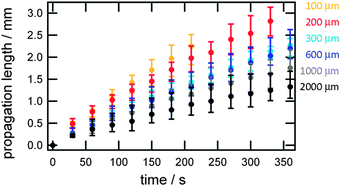 | ||
| Fig. 3 Proton wave propagation length in microchannels with different widths ranging from 100 μm (yellow) to 2000 μm (black). | ||
The classical equation, v ≈ (D/τ)0.5, indicates a dependence of v on D of the reaction species.17 In general, D is expressed as a function of viscosity of medium η
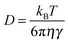 | (3) |
While η and D can be assumed to be invariant over the size scale of our systems, influx of proton from the inlet to the microchannel can induce spatiotemporal dependence of the proton concentration gradient near the inlet, which may alter D∇2c in eqn (1) even if D is constant. We consider two extreme conditions: (i) diffusion from the inlet as a limited proton source and (ii) diffusion from the inlet as an infinite proton source. The former situation can be applied to wider channels, and the latter to narrower channels. The widest microchannel in the present system (w = 2000 μm) has the same width as the inlet (Fig. 4a). In this case, protons at the inlet are continuously depleted by diffusion into the microchannel. Thus, [H+] at the inlet is decreasing continuously with time, which allows us to assume the inlet as a limited proton source. On the other hand, the width of the narrowest microchannel (w = 100 μm) is one-twentieth of the inlet (Fig. 4b). Therefore, proton depletion at the entrance of the microchannel due to diffusion into the channel is rapidly supplemented by the vast proton reservoir in the inlet. Thus, the [H+] change at the inlet is relatively slow and the inlet can be assumed to be an infinite proton source. We calculated changes in the [H+] profile in the microchannels with time using the following equations.
It is clear that the [H+] rapidly decreases and the [H+] gradient vanishes at early stages of diffusion in the wider channel, whereas [H+] near the inlet remains high for long periods in the narrower channel (Fig. 4). This enables the narrower channels to promote and sustain a large proton influx from the inlet to the channel. Since the proton wave is initiated by an influx of protons to the reactive medium,19 the swift proton influx can propagate the proton wave rapidly. This quick onset provides an explanation for faster observed proton wave propagation in the narrower microchannels as shown in Fig. 3. Since the assumption that the proton diffuses from the limited and infinite source at wide and narrow channels, respectively, is an extreme approximation, we need further numerical treatment such as a weighted average of these two extreme equations. These numerical treatments should give physico-chemical insight into the w-dependent D∇2c term, and thus the w-dependent proton wave propagation. We will further investigate from both experimental and numerical approaches, and will report elsewhere.
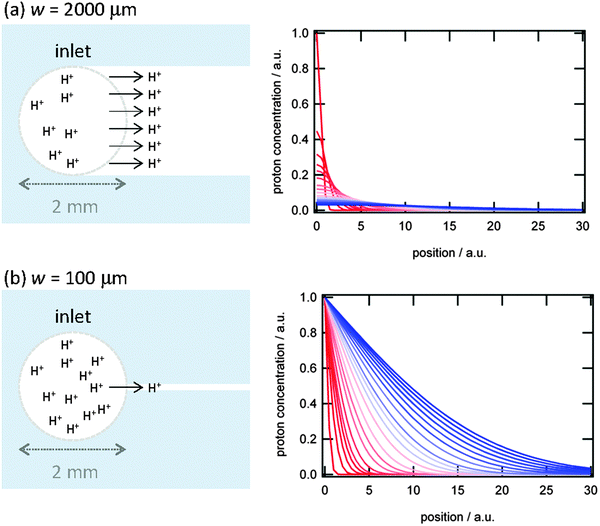 | ||
| Fig. 4 (left) Diffusion of protons from the inlet into the microchannels with different channel width. (right) Change in proton concentration profiles with time from red to blue assuming diffusion from (a) a limited proton source and (b) an infinite proton source. | ||
To quantitatively formularize the channel size dependence, the propagation velocities were evaluated with various channel widths and depths (h) (Fig. 5). As was shown in Fig. 3, the propagation velocity increases with decreasing w. This characteristic feature was observed for both deep (h = 100 μm) and shallow (h = 50 μm) channels. With the same w, the propagation velocity increased in the deeper channel. This behavior is consistent with previous reports revealing that deeper glass capillaries exhibited faster chemical wave propagation because of the formation of slanted wave fronts that can increase the reaction interface area.9 In the present system, we also observed slanted wave fronts (see Fig. S4 in the ESI†). From data for each channel depth, we derived the following relationships between the propagation velocity and the channel width:
| v(μm s−1) = 135 × w−0.5 (h = 100 μm) |
| v(μm s−1) = 59 × w−0.5 (h = 50 μm) |
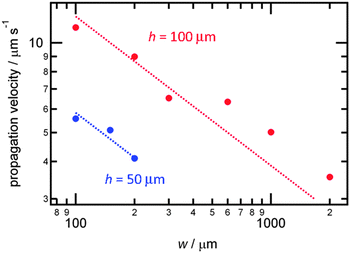 | ||
| Fig. 5 Proton wave propagation velocity as a function of the microchannel width with 100 μm (red) and 50 μm (blue) channel depth. Dotted lines are the least-square fitting results. | ||
In conclusion, we have demonstrated that the width and depth of microchannels can be used as controlling parameters for the propagation of chemical wave velocity. The width dependence comes from a ratio of sizes between the inlet as a proton reservoir and the channel as a proton propagator. Propagation velocity was found to be expressed with a simple equation as a function of the channel width and depth, which offers a simple and general way of controlling chemical wave propagation. The present findings unlock a new frontier of chemical wave science and technology that could also help gain insight into oscillating biological phenomena.
Acknowledgements
This work was partially supported by the Hatakeyama Foundation, The Kao Foundation for Arts and Sciences, and Grants-in-Aid for Scientific Research 22655001 from the Ministry of Education, Culture, Sports, Science, and Technology, Japan.References
- (a) I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics, Oxford University Press, 1998 Search PubMed; (b) A. GoldBeter, Biochemical Oscillations and Cellular Rhythms, Cambridge University Press, 2004 Search PubMed.
- O. Steinbock, P. Kettunen and K. Showalter, J. Phys. Chem., 1996, 100, 18970–18975 CrossRef CAS.
- K. Agladze, R. R. Aliev, T. Yamaguchi and K. Yoshikawa, J. Phys. Chem., 1996, 100, 13895–13897 CrossRef CAS.
- R. Klajn, M. Fialkowski, I. G. Bensemann, A. Bitner, C. J. Campbell, K. Bishop, S. Smoukov and B. A. Grzybowski, Nat. Mater., 2004, 3, 729–735 CrossRef CAS.
- T. Ichino, T. Asahi, H. Kitahata, N. Magome, K. Agladze and K. Yoshikawa, J. Phys. Chem. C, 2008, 112, 3032–3035 CrossRef CAS.
- L. Kuhnert, K. I. Agladze and V. I. Krinsky, Nature, 1989, 337, 244–247 CrossRef CAS.
- L. Szirovicza, I. Nagypál and E. Boga, J. Am. Chem. Soc., 1989, 111, 2842–2845 CrossRef CAS.
- J. A. Pojman, I. P. Nagy and I. R. Epstein, J. Phys. Chem., 1991, 95, 1306–1311 CrossRef CAS.
- J. A. Pojman, I. R. Epstein, T. J. McManus and K. Showalter, J. Phys. Chem., 1991, 95, 1299–1306 CrossRef CAS.
- I. Nagypál, G. Bazsa and I. R. Epstein, J. Am. Chem. Soc., 1986, 108, 3635–3640 CrossRef CAS.
- J. Masere, D. A. Vasquez, B. F. Edwards, J. W. Wilder and K. Showalter, J. Phys. Chem., 1994, 98, 6505–6508 CrossRef CAS.
- C. R. Chinake and R. H. Simoyi, J. Phys. Chem., 1994, 98, 4012–4019 CrossRef CAS.
- A. Komlósi, I. P. Nagy, G. Bazsa and J. A. Pojman, J. Phys. Chem. A, 1998, 102, 9136–9141 CrossRef CAS.
- G. Bazsa and I. R. Epstein, J. Phys. Chem., 1985, 89, 3050–3053 CrossRef CAS.
- R. E. McIlwaine, H. Fenton, S. K. Scott and A. F. Taylor, J. Phys. Chem. C, 2008, 112, 2499 Search PubMed.
- Y. Kuramoto, Chemical Oscillations, Waves, and Turbulence, Dover Publications Inc., 1984 Search PubMed.
- R. Z. Luther, Electrochemistry, 1906, 12, 596–598 Search PubMed.
- N. R. Tas, J. Haneveld, H. V. Jansen, M. Elwenspoek and A. Berg, Appl. Phys. Lett., 2004, 85, 3274–3276 CrossRef CAS.
- G. Rábai, M. Orbán and I. R. Epstein, Acc. Chem. Res., 1990, 23, 258 CrossRef CAS.
- I. B. Levitan and L. K. Kaczmarek, The Neuron: Cell and Molecular Biology, Oxford University Press, New York, 2nd edn, 1996 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp43153j |
| This journal is © the Owner Societies 2013 |