A fluorescent double-network-structured hybrid nanogel as embeddable nanoglucometer for intracellular glucometry†
Jiao Fan‡a, Xiaomei Jiang‡b, Yumei Hua, Yan Sia, Li Dinga and Weitai Wu*ac
aState Key Laboratory for Physical Chemistry of Solid Surfaces, The Key Laboratory for Chemical Biology of Fujian Province, and Department of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China. E-mail: wuwtxmu@xmu.edu.cn
bClinical Laboratory, Huli Center for Maternal and Child Health, Xiamen 361009, China
cCenter for Molecular Imaging and Translational Medicine, School of Public Health, Xiamen University, Xiamen 361005, China
First published on 10th January 2013
Abstract
The development of embeddable and remotely interrogatable nanomaterials that allow dynamic quantification of intracellular glucose levels can contribute to a better understanding of physiology. We develop a fluorescent hybrid nanogel glucometer (FNG) that is applicable for intracellular glucometry. Such a FNG (<200 nm) is comprised of ZnO quantum dots covalently bonded onto a loosely-crosslinked gel network of poly(acrylamide), which is interpenetrated in another relatively highly-crosslinked gel network of poly(N-isopropylacrylamide-co-2-acrylamidomethyl-5-fluorophenylboronic acid). This newly developed double-network-structured FNG can adapt to surrounding media of varying glucose levels, and convert the disruptions in homeostasis of glucose level with high reversibility, sensitivity, and selectivity into fluorescence signals at a fast time response. We demonstrate that the FNG can enter the model B16F10 cells and employ the signal transduction ability for fluorescent intracellular glucometry. Furthermore, we show that intracellular glucose level variations associated with a model biological reaction process can be monitored with a high glucose resolution by using the FNG embedded in cells, whilst the reaction mechanism remains nearly unchanged.
1. Introduction
Knowledge of the intracellular level and flux of glucose, the major transport form of carbon and energy in mammalian organisms, is crucial to our understanding of physiology in both healthy and diseased states.1–7 Traditionally, intracellular glucose levels have predominantly been determined using destructive assays, including enzymatic assays and mass spectrometry.4,7,8 Such assays can only provide dynamic information when carried out with parallel samples and have a limited temporal resolution. Alternatively, isotopes (e.g.13C-glucose) have been used to monitor glucose transport activity,1,5,6 but they cannot measure glucose uptake in a few living cells and have a limited spatial resolution. The challenge of preparing embeddable and remotely interrogatable materials that can provide dynamic information of intracellular glucose levels remains to be solved.Fluorescent materials hold exceptional promise as biosensors.9–11 With the appropriate choice of optical labels, fluorescent biosensors can in theory be excited and the emission interrogated externally. Fluorescent biosensors have been reported for the detection of glucose, but mostly for the macrorealm.12–22 Frommer's group is possibly the first to develop fluorescent biosensors for measuring intracellular glucose levels.2,23–26 In such a typical biosensor, the glucose binding protein (GBP) is coupled terminally with a cyan version of green fluorescent protein (GFP) and a yellow version of GFP. This fluorescent protein based biosensor detected the glucose-induced conformational change in GBP using fluorescence resonance energy transfer (FRET) between the two fluorescent protein variants. An analog fluorescent biosensor was developed by Ye's group by replacing GBP with a glucose indicator protein, which was synthesized by site-directed mutagenesis of GBP at its 16th amino acid residues.27 With those fluorescent protein based biosensors serving as glucometers for intracellular glucometry, image acquisition parameters need to be optimized to obtain the highest possible data quality.25,26 Although even at low signal-to-noise levels (by using little excitation) qualitative data can be obtained, quantitative analysis requires the highest possible signal-to-noise ratio (by using high excitation). However, too-high excitation can lead to photobleaching of the organic fluorophores. As the two fluorophores can have differential photobleaching sensitivity, a change in ratio may be misinterpreted as a FRET change caused by a change in glucose levels. Thus, more stable optical labels, such as quantum dots (QDs), were used in the detection of intracellular glucose.17 This QD based biosensor functioned through the glucose-mediated assembly of 4-((3-boronophenyl)amino)-3-mercapto-4-oxobutanoic acid modified CdTe/ZnTe/ZnS core/shell/shell QDs. The advantages of QDs, including continuous absorption, efficient and tunable emission, and photostability, are significant. Unfortunately, non-glucose induced aggregation (e.g. self aggregation and/or protein induced aggregation) of QDs is inevitable, which often leads to additional changes in fluorescence during glucose monitoring and therefore a rapid decay in sensing abilities.
In this work, we aim to develop a new class of fluorescent QD-polymer hybrid nanogels to demonstrate the concept that a single nanogel particle under a rational design can serve as an embeddable nanoglucometer with high reversibility, as well as negligible interactions with cellular components, for intracellular glucometry. To date, fluorescence sensing of aqueous glucose has been demonstrated on a number of QD-polymer hybrid nanogels, which were prepared by physical immobilization of QDs into the single-network-structured nanogels.18–22 The glucose-induced volume phase transition of the responsive polymer network may change the surface/interface physicochemical environment of the immobilized QDs, leading to changes in fluorescence. Here, we explore this approach in a novel double-network-structured hybrid nanogel. As schematically depicted in Fig. 1a, this newly developed fluorescent hybrid nanogel glucometer (FNG) is comprised of ZnO QDs covalently bonded onto a loosely-crosslinked gel network of poly(acrylamide) [poly(AAm)], which is interpenetrated in another relatively highly-crosslinked gel network of poly(N-isopropylacrylamide-co-2-acrylamidomethyl-5-fluorophenylboronic acid) [poly(NIPAM-co-FPBA)]. It is striking that the single-network-structured hybrid nanogel biosensors reported previously could not be applied in intracellular thermometry because of several remaining issues.18–22 One of the major issues is that they would produce a false response caused by two inevitable problems during repeated swelling–shrinking cycles: (a) gradual shift in the average hydrodynamic radius, 〈Rh〉; (b) slow aggregation or leaching of the physically immobilized QDs from the polymer networks. They would also precipitate in the culture medium. We overcome those problems in the proposed double-network-structured FNG. More importantly, different from previous arts of fluorescent protein based biosensors and QD based biosensors, which were only applied for the measurement of the intracellular glucose level, with the cells being fed with a varying external supply in culture,2,17,23–27 the proposed FNG will be exploited for monitoring the intracellular glucose level variations associated with a biological reaction process.
![(a) Schematic diagram of the FNG and chemical structures of the key components. (b) DLS size distribution of the single-network-structured template nanogel (■, □: [Glucose] = 0 mg dL−1) and the double-network-structured FNG (●, ○: [Glucose] = 0 mg dL−1; ▲, △: [Glucose] = 540 mg dL−1). Closed and open symbols denote the size distribution before and after thirty cycles of adding/removing glucose, respectively. (c) TEM images of the FNG.](/image/article/2013/BM/c2bm00162d/c2bm00162d-f1.gif) | ||
| Fig. 1 (a) Schematic diagram of the FNG and chemical structures of the key components. (b) DLS size distribution of the single-network-structured template nanogel (■, □: [Glucose] = 0 mg dL−1) and the double-network-structured FNG (●, ○: [Glucose] = 0 mg dL−1; ▲, △: [Glucose] = 540 mg dL−1). Closed and open symbols denote the size distribution before and after thirty cycles of adding/removing glucose, respectively. (c) TEM images of the FNG. | ||
2. Results and discussion
2.1. Synthesis of the FNG
In view of the need to function in intracellular environments, three arrangements have been made to the proposed FNG. Firstly, our strategy to prepare the FNG involves first the synthesis of a monodispersed single-network template nanogel of a relative highly-crosslinked (2.4 mol%) copolymer poly(NIPAM-co-FPBA), followed by uploading in an ice bath (rendering a swollen status of the template nanogels, utilizing the fact that this temperature is far below the volume phase transition temperature 32 °C of poly(NIPAM) nanogels),28 and then free-radical polymerization of AAm, zinc methacrylate (Zn(MAA)2) and a crosslinker methylenebisacrylamide (MBAAm) at 80 °C (rendering a collapsed status of the template nanogels) to form a second, ZnO QD-contained, and loosely-crosslinked (0.6 mol%) poly(AAm)-based network inside the single-network template nanogel, so that the glucose-sensitive and fluorescent components can be integrated into a single nano-object. Under such a design, both the FNG and the corresponding poly(NIPAM-co-FPBA) template nanogels were narrowly distributed with a polydispersity index of μ2/〈Γ〉2 ≤ 0.01, as revealed by in situ Dynamic Light Scattering (DLS) measurements carried out in a PBS of pH = 7.4 and 22.1 °C. The FNG had a larger 〈Rh〉 of 48.9 nm than the template nanogels (〈Rh〉 = 30.3 nm) (Fig. 1b). The slightly increased particle size and narrow distribution demonstrated that the second network was successfully incorporated with the first network (i.e. the template nanogel). The formation of new homo-particles other than the FNG during the synthesis is negligible. To further confirm that in a FNG particle the second network was substantially interpenetrated into the first network, rather than simply covering the first network as a shell, a core-shell-structured [poly(NIPAM-co-FPBA)]core-[ZnO@poly(AAm)]shell hybrid nanogel was also synthesized (see SI-1 in ESI†)29,30 for comparison. A double-network-structured gel with the second network interpenetrated into the first network should have a higher apparent crosslinking density than a core-shell-structured gel with the second network simply covering the first network. Of a higher apparent crosslinking density, as expected, the FNG has a significant smaller size, in comparison with the core-shell-structured hybrid nanogels (〈Rh〉 = 96.7 nm). Moreover, it has been documented that the interpenetration of a second polymer with a lower crosslinking density can result in substantial enhancement of the mechanical strength of the gels.31,32 Indeed, while the poly(NIPAM-co-FPBA) template nanogels exhibited a relatively low degree of recovery in 〈Rh〉 (return to ≤76% of the original values), the FNG exhibited a superior reversibility with a high degree of recovery in 〈Rh〉 (return to ≥95% of the original values) even after thirty cycles of swelling–shrinking (Fig. 1b; see below for the details of glucose-responsive volume phase transition). While this result provided additional, though indirect, proof that the FNG indeed had a double-network structure, the highly stable structure and highly reversible swelling–shrinking behavior of the FNG will be an important feature for the following studies.Secondly, in order to suppress the aggregating/leaching of QDs during repeated swelling–shrinking cycles, QDs were tethered to the FNG via covalent bonds using an allylic metallo-organic compound Zn(MAA)2 as a precursor in the synthesis. The covalent bonding of QDs onto gel network chains manifests as the characteristic FTIR absorption at 1600 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and 1441 cm−1 (C–O) (Fig. 2a) for the bridging coordination modes of the acetate group with Zn.33 As the size of the QDs is directly related to the excitonic peak in the UV-vis absorption spectrum, the size of the QDs can be estimated by empirical functions:34
O) and 1441 cm−1 (C–O) (Fig. 2a) for the bridging coordination modes of the acetate group with Zn.33 As the size of the QDs is directly related to the excitonic peak in the UV-vis absorption spectrum, the size of the QDs can be estimated by empirical functions:34
 | (1) |
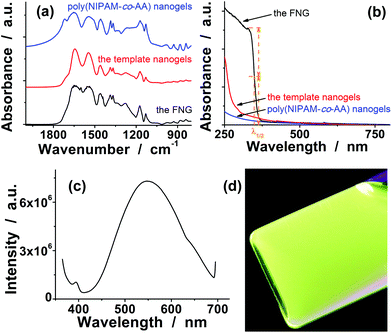 | ||
| Fig. 2 (a) FTIR, (b) UV-vis absorption, and (c) PL spectra of the FNG. FTIR and UV-vis absorption spectra of poly(NIPAM-co-AA) nanogels and poly(NIPAM-co-FPBA) template nanogels were also presented in both (a) and (b) for comparison. (d) The photograph presents the color for the FNG dispersed in PBS of pH 7.4, taken under a UV lamp. | ||
Thirdly, the FNG was uniquely enriched with ionic sulfate groups by using an extraordinary quantity of initiator ammonium persulfate (APS) in the synthesis. The APS/NIPAM molar ratio was 0.39, which was confirmed by elemental analysis of sulfur (the contents of sulfur in the FNG were determined to be 0.986%), while that in common procedures is 0.01–0.046.18–22 Although from a theoretical viewpoint ζ-potential is electric potential in the interfacial double layer at the location of the slipping plane versus a point in the bulk solution away from the interface,35 the ζ-potential measurements (ζ = −42 ± 2 mV, measured in PBS of pH 7.4) indicated a negative surface of the FNG. In recent studies on intercellular thermometry by using temperature-responsive polymer nanogels, Uchiyama's group has demonstrated that the highly hydrophilic surface created by the sulfate groups can protect the nanogels from precipitation at high ionic strength and from localization on the cytoplasmic membrane.36,37
Furthermore, the size of the double-network-structured FNG can be well tuned through varying the synthetic parameters. For example, an increase in the feeding amount of MBAAm in the synthesis of the second network can significantly reduce the 〈Rh〉 of the hybrid nanogels (Fig. 3a). Interestingly, with an increase in the feeding amount of MBAAm in the synthesis of the second network, the typical λ1/2 of the QDs in the nanogels also exhibited a significant blue shift (Fig. 3b), indicating a decrease in the size of the QDs in the nanogels (Fig. 3c). All hybrid nanogels can be reproducible from batch to batch. To focus the topic of this work on glucometry, the FNG made from Zn(MAA)2–AAm–MBAAm (mol ratio) = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133
133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the synthesis of the second network was selected for following studies.
1 in the synthesis of the second network was selected for following studies.
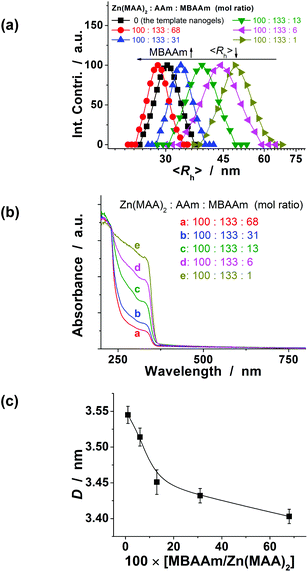 | ||
| Fig. 3 (a) The 〈Rh〉 values, (b) UV-vis absorption spectra, and (c) QD size of the FNG synthesized with different molar ratios of Zn(MAA)2/AAm/MBAAm in the synthesis of the second network. To show the effect of the feeding amount of MBAAm, the feeding amounts of Zn(MAA)2 and AAm were set to 0.100 g and 0.040 g, respectively. | ||
2.2. Glucose-induced volume phase transition
The proposed FNG can adapt to a surrounding medium of varying glucose levels. Fig. 4a shows glucose-dependent 〈Rh〉 values of the FNG, measured in a 5.0 mM PBS of pH = 7.4 at 22.1 °C. The phenylboronic acid (PBA) is known as the best synthetic ligand identified for binding glucose in aqueous media.11,38 The PBA group is in equilibrium between the undissociated (trigonal, uncharged) and the dissociated (tetrahedral, charged) forms in aqueous solution, of which the tetrahedral form prefers binding with glucose to form a boronate ester. The poly(FPBA) units, the glucose recognition element of the FNG, possess not only a lower pKa due to the presence of an electron-withdrawing fluorine group, but also a desirable boron geometry of 2-acrylamidophenylboronate where the tetrahedral form is the dominant species over the wide pH range 2.0–10.0.39,40 The tetrahedral conformation at the boron centre can be further stabilized by electrostatic attraction (Bδ−⋯Nδ+) through the amino groups of poly(AAm) units in the FNG.20,22,41 Consequently, the FNG can be expected to bind glucose sensitively and selectively at a pH of 7.4, which would increase the charge density38 and build up a Donnan potential42 for the nanogel to swell steadily, with an increase in glucose level over the clinically relevant glucose level range of 30–540 mg dL−1 (Fig. 4a; also see ESI-3 in ESI† for the glucose-dependent 〈Rh〉 values of template nanogels). The swelling ratio, 〈Rh,540 mg dL−1〉/〈Rh,0 mg dL−1〉, can reach as high as 1.87, demonstrating the high sensitivity of the FNG to glucose. The reaction of the FNG with glucose is unique, since the formation of the covalent bonds between the PBA group and 1,2-cis-diols of glucose is reversible.38 As glucose is removed from the bathing medium by putting the FNG into a dialysis bag (cutoff 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–14
000–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and dialysis against flowing PBS at ca. 10 cm s−1 (a possible blood flow rate in the circulation system of the human upper limb),43 the dissociation equilibrium shifts back from boronate ester to boronic acid, leading to nearly a superposition of the deswelling curve with the swelling curve. This indicates that in the glucose level range studied there is negligible hysteresis in one cycle of adding and removing glucose; i.e. the glucose-responsive volume phase transition is highly reversible. Moreover, the glucose-responsive volume change of the FNG is independent of the environmental temperature (16–40 °C; Fig. 4b) and pH (5.0–7.8; Fig. 4c). This is also advantageous because the temperature of living cells may slightly increase by thermogenesis of cellular events, and the local pH may be affected by neighbouring/internal structures and decrease by 1–2.5 units.44–46 Besides, the FNG in intracellular glucometry experiments might undergo a temperature change from the culture temperature of 37 °C to room temperature of 25 °C.
000) and dialysis against flowing PBS at ca. 10 cm s−1 (a possible blood flow rate in the circulation system of the human upper limb),43 the dissociation equilibrium shifts back from boronate ester to boronic acid, leading to nearly a superposition of the deswelling curve with the swelling curve. This indicates that in the glucose level range studied there is negligible hysteresis in one cycle of adding and removing glucose; i.e. the glucose-responsive volume phase transition is highly reversible. Moreover, the glucose-responsive volume change of the FNG is independent of the environmental temperature (16–40 °C; Fig. 4b) and pH (5.0–7.8; Fig. 4c). This is also advantageous because the temperature of living cells may slightly increase by thermogenesis of cellular events, and the local pH may be affected by neighbouring/internal structures and decrease by 1–2.5 units.44–46 Besides, the FNG in intracellular glucometry experiments might undergo a temperature change from the culture temperature of 37 °C to room temperature of 25 °C. | ||
| Fig. 4 (a) Glucose-dependent 〈Rh〉 of the FNG. Closed and open symbols denote the increasing and decreasing glucose cycles, respectively. The effect of (b) environmental temperature and (c) pH value on the glucose-responsive volume change of the FNG. | ||
2.3. Glucose-responsive optical properties
The proposed FNG can convert the disruptions in homeostasis of the glucose level into fluorescence signals. Fig. 5a shows typical PL spectra of the FNG (10.0 μg mL−1) dispersed in a PBS of pH = 7.4. With a gradual increase in glucose level, two effects were observed on the yellow-green light emission: (a) a continuous quenching in intensity; and (b) a significant blue shift of the emission position. Both effects are rationalized by an increase in the elastic tension in the expanded polymer network chains (Flory–Huggins theory),47 which could stretch the polymer-QD interface and propagate the strain to the surface of the covalently bonded QDs, and create surface states that can quench the PL.18–22 A similar phenomenon has been reported by our group, namely that short linker molecules (4-((3-boronophenyl)amino)-3-mercapto-4-oxobutanoic acid) can propagate the exogenous strain to the surface of CdTe/ZnTe/ZnS core/shell/shell QDs to create surface quenching states.17 Consequently, when the glucose level was increased to 540.0 mg dL−1, a PL quenching (from 7.32 × 106 a.u. to 1.84 × 105 a.u.) of the FNG as high as 97% and a blue shift of about 53.4 meV (13 nm) were observed. The energy difference is taken as an indication of a change in the cluster–cluster interaction among the QDs in the FNG.17,48 | ||
| Fig. 5 (a) Glucose-dependent PL spectra of the FNG. Scans were taken at 30.0 mg dL−1 intervals from top to bottom, from 0.0 to 540.0 mg dL−1. (b) Evolution of the PL intensity (I) at 549 nm as a function of glucose level. The error bars are within the symbols. (c) PL quenching and recovery cycles upon the repeated adding (540.0 mg dL−1) and removing (0.0 mg dL−1) of glucose in the bathing medium. (d) Linear plot showing the glucose-responsive PL properties in reciprocal space. | ||
Both the PL intensity change (Fig. 5b) and the color change (Fig. 6a) as a function of glucose level mirror that of the glucose-responsive volume change of the FNG (Fig. 4a). This observed relationship serves as further confirmation that the key of the glucose-to-fluorescence signal transduction ability of the FNG is its capability of transducing glucose-responsive volume changes into changes in PL properties. As glucose was removed from the bathing medium of the FNG by dialysis against flowing PBS at ca. 10 cm s−1, the FNG collapsed reversibly from the swelling status back to the original deswelling status (Fig. 1b), leading to a recovery of both the spectral profiles (the emission positions can return to nearly 100% of the original basal values) and intensity (return to ≥90% of the original basal values) upon the removal of glucose even after thirty cycles, thus providing a highly reproducible signal transduction (Fig. 5c and 6b), which is crucial for quantitative detection. The linear plot shown in Fig. 5d gives glucose-dependent PL properties in a more orthogonal fashion. The lowest glucose level reliably detectable with color change was approximately 2.3 mg dL−1; it is reduced to as low as 1.2 mg dL−1 when utilizing the PL intensity change.
 | ||
| Fig. 6 (a) Evolution of the yellow-green light emission position (λ) as a function of glucose level. (b) PL blue-shift and recovery cycles upon the repeated adding (540.0 mg dL−1) and removing (0.0 mg dL−1) of glucose in the bathing medium. | ||
To estimate the time response of glucose-to-fluorescence signal transduction that is potentially achievable, we monitored the response kinetics in terms of changes in PL intensity of the FNG (10.0 μg mL−1) and at 540.0 mg dL−1 glucose (Fig. 7a). The PL intensity can reach approximately 99% of their maximum change in ca. 22 s after adding glucose. The change in PL intensity can be well described by the single-exponential decay function:22,49
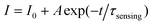 | (2) |
 | ||
| Fig. 7 (a) Characteristic kinetics of the FNG upon addition of glucose (540.0 mg dL−1). Solid line: theoretical fit with eqn (2). (b) The effect of the concentration of the FNG on the characteristic response time τsensing. | ||
The characteristic response time τsensing can thus be determined to be 0.71 ± 0.02 s. This τsensing value should reflect the essential feature of an individual FNG particle, because the engaged concentration of the FNG is below the critical value of ca. 10−2 wt% (the so-called dynamic contact concentration) and the inter-particle interactions can be completely ignored, as predicted by the concept of the screening length.50 This can be further confirmed by the result of additional experiments that the τsensing value is nearly independent of the concentration of the FNG in the range 5–80 μg mL−1 (Fig. 7b). It should be noted that the time response of the double-network-structured FNG is nearly 1.5-fold faster than that of a typical single-network-structured nanogel based biosensor reported very recently (with τsensing ≈ 1.1 s at 540.0 mg dL−1 glucose),22 indicating a great improvement on the response speed of a nanogel based biosensor under the presented design. Considering a general procedure of signal transduction on a nanogel based biosensor, several steps related to the subtle physical chemistry, such as the diffusion of glucose molecules, the adsorption/desorption and partitioning/departitioning of glucose at the solution–nanogel interface, the reaction of glucose with the PBA groups, the structural rearrangements inside the nanogel, and finally a change of the local optical electric field at the QD surface, are known to influence the time response.22,49,51 One or several of these steps in tandem could have led to the faster time response of the FNG over the single-network-structured nanogel based biosensors. Nevertheless, a fast time response is a highly desirable feature of a biosensor for applications towards monitoring dynamic changes.
2.4. Interference tests
A glucometer should have minimal interference from the non-glucose constituents. To examine the potential interference of non-glucose constituents, we conducted a series of experiments to assess the performance of the proposed FNG in complex systems. In the first series of experiments, we investigated the interference from L-lactate and human serum albumin (HSA), the primary interferents if a glucometer was used in bio-systems. The concentration of L-lactate is usually 0.36–0.75 mM in blood at rest,52 but might be significantly high (e.g., 20.0 mM) in both normal and cancer cells because of a low energy supply via the citric cycle and oxidative phosphorylation.53,54 In our design, both the unique molecular structure of FPBA and the formation of intermolecular Bδ−⋯Nδ+ bonds can make the attack of the poly(FPBA) units by lactate become unfavourable. The unique enriched ionic sulfate groups on the surface of the FNG may also block the diffusion of the largely dissociated L-lactate at pH 7.4 (>pKa = 3.5)54 into the nanogel. As a result, a decrease of ≤5.6% in glucose-induced PL change was observed in the presence of 20.0 mM L-lactate (Fig. 8), corresponding to a ≤5.6% lower apparent level of glucose. Clearly, the signal transduction ability of the FNG provides excellent sensitivity and selectivity to glucose over lactate. On the other hand, HSA, the most abundant protein in human serum, is known to undergo a slow non-enzymatic glycation, which eventually can result in the formation of Advanced Glycosylation End Products (AGE). The boronic acids are capable of binding HSA, even in its nonglycosylated state.19,22,55 To examine the impact of HSA on the glucose-to-fluorescence signal transduction ability of the FNG, we have recorded the glucose-induced PL quenching of the FNG in the presence of 44.0 g L−1 HSA (a concentration that is typically found in serum).52Fig. 8 shows that there was barely interference from HSA (a decrease of ≤3.6% in glucose-induced PL change) over the glucose level range 30–540 mg dL−1. HSA has a net negative charge at pH 7.4 (>pI = 4.7). It is possible that the negative surface of the FNG led to a low level of HSA adsorption onto the FNG (the surface density dHSA < 0.05 g m−2, Fig. 8c), resulting in a low level of HSA reacting with the poly(FPBA) units in the FNG. As HSA is a relatively large molecule (∼67 kDa), it is also possible that HSA would only bind those poly(FPBA) units located at the light penetration depth of the FNG, and the initial binding of HSA would subsequently hinder the accessibility of the poly(FPBA) units to more HSA.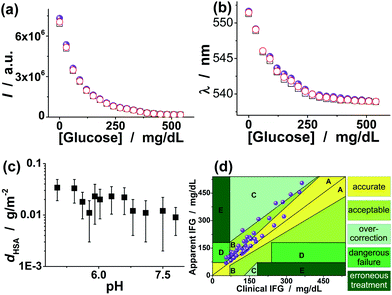 | ||
| Fig. 8 Glucose-responsive (a) PL intensity change and (b) color change in the presence of 20.0 mM L-lactate (□) and 44.0 g L−1 HSA (○), respectively, showing the effect of L-lactate and HSA on the glucose-to-fluorescence signal transduction ability of the FNG dispersed in PBS. The results (spherical symbols) without any L-lactate and HSA were also given for comparison. (c) Isothermal adsorption curve for HSA adsorbed on the FNG. (d) Clarke Error Grid Analysis of glucose sensing in blood serum, showing the glucose-to-fluorescence signal transduction ability of the FNG in a complex bio-system. | ||
In the second series of experiments, various PBS containing D(−)-fructose, D(+)-galactose, D(+)-mannose, pyruvic acid, urea, citric acid, vitamin C, γ-globulins, lysozyme, cholesterol, and common amino acids were investigated, and the relative error of glucose level reading by using the FNG is found to be within ±3.6% (see ESI-4 in ESI† for the data in detail). The FNG clearly shows excellent selectivity for glucose over the non-sugar constituents. As for sugars, while the selectivity of the PBA groups toward glucose is usually inferior to other diols such as fructose,11,38 the concentration of non-glucose sugars in blood (<0.1 mM) is ca. 10 times lower than that of glucose,52 which is thought to also occur in cells (e.g. fructose cannot enter most cells, because they lack glut-5 transporter, which transports fructose into cells),56,57 and hence are not thought to be major interferents. Nonetheless, special design of the boronic acid compounds has been carried out to improve glucose selectivity.39,40,58,59 In recent literature, ortho-substituted aryl boronic acids were demonstrated to be capable of binding fructose with a decreased selectivity relative to glucose under physiological conditions, presumably due to the steric effect of the ortho-positioned methyl substituent, disfavoring the tridentate boronate–fructose complex.60 Besides the local molecular structure of the boronic acids, the synergistic effect derived from the nanogel network structure may also be beneficial to the formation of the bidentate boronate–glucose complex for glucose sensing.20,22,39–41,60 Moreover, the influence of metal ions on the glucose-to-fluorescence signal transduction ability of the FNG was also examined. The relative error of the glucose level reading in the presence of common metal ions (2.0 × 10−3–20.0 mM) found in bio-systems, such as K+, Na+, Ca2+, Mg2+, Ba2+, Al3+, Cu2+, Zn2+, Co2+, and Fe3+, is generally within the range of ±1.0% after taking into account the experimental errors. The slight interference from metal ions is possibly associated with the coordination between the metal ions and the poly(FPBA) units, or simply the enhancement of ionic strength. Both effects would weaken the Donnan potential.
In the third series of experiments, a macro-bio-system, adult blood serum, having an environment similar to the cytoplasm (it is within the cytoplasm that most cellular activities occur)1–3 was adopted as the subject of the FNG. Blood is a specialized connective tissue in fluid form.52 It consists of liquid with cells, proteins, sugars, electrolytes and other substances either dissolved or suspended in the liquid. Plasma and serum are particular liquid components of blood. Plasma is liquid blood with the cells removed, and serum is plasma with the clotting proteins removed. On the basis of the calibration curves in Fig. 5 and 6, the apparent impaired fasting glucose (IFG) of the serums could be obtained, which was compared to the clinical IFG level measured in hospitals by using a standard enzyme-based method. 6% of the data belong to the hypoglycemic range (<70 mg dL−1) versus 56% belonging to the hyperglycemic range (>110 mg dL−1), and 38% were located between them. As shown in Fig. 8d, for the low glucose levels there is a slight overestimation of the readings of the FNG (y axis), and the overestimation increases at the higher levels. According to the definition of the different zones of the Clarke Error Grid Analysis,61 we found that 80% of the points belong to the zones A (accurate zones) and B (acceptable zones), 12% of the total belong to zones C (overcorrection zones) and 8% of the total belong to zones D (dangerous failure). There is no point in zones E (erroneous treatment). Therefore, these results can not only provide further confirmation of the high selectivity of the FNG, but also foreshadow an accurate biosensor for intracellular glucometry.
2.5. Cell internalization of the FNG and intracellular glucometry
Having demonstrated the glucose-to-fluorescence signal transduction ability of the FNG, we tested the ability of the FNG to enter cells and detect intracellular glucose levels using mouse melanoma cell B16F10 as a model. The small sized FNG can attain deeper penetration into poorly permeable tumor cells.62 The cells treated with the FNG were highly luminescent, with fluorescence seen primarily in the cytoplasm (Fig. 9a).63 A cross-sectional Z scan can confirmed the entry of the FNG into the cells (see ESI-5 in ESI†). The use of microinjection or electroporation techniques might help to deliver more FNG into cells. However, for the present purpose it suffices to interrogate remotely and discuss the fluorescence signals. The FNG within the cells can produce a bright color, and the PL intensity can be retained, even after continuous irradiation for 300 min (see ESI-6 in ESI†). This result confirmed the photostability of the FNG embedded in cells. | ||
| Fig. 9 (a) Scanning confocal fluorescence (left), transmission (centre), and overlaid images (right) of B16F10 cells incubated with the FNG (10.0 μg mL−1). (b,c) Response curves in terms of changes in (b) PL intensity and (c) color of the FNG embedded in cells. The total PL properties of a single cell (n = 5, mean ± s.d.) was adopted as a glucose-dependent parameter by the FNG. | ||
Typically, glucose utilization by a cell depends on transport and metabolism. Most mammalian cells transport hexoses into/out of the cytosol (the liquid portion of the cytoplasm), as mediated by a family of monosaccharide facilitators.1–3 B16F10 cells were grown in sugar-free DMEM. When fed different amounts of glucose, the cells labeled with FNG can be optically differentiated using a confocal microscope. Local analysis of the overall PL of the FNG embedded in a cell indicated the difference in intracellular glucose levels. As for the PL intensity change, the fluorescence signal was obtained from fluorescence images by summing the PL intensities of all the pixels within a single cell (n = 5, mean ± s.d.), while for the color change, the fluorescence signal was read from microscope by creating the lambda series and analysing the spectra through a stack dialog window. As Fig. 9b (intensity change) and Fig. 9c (color change) show, the fluorescence signal of the FNG embedded in cells can sharply change when the cells were fed with an external supply of 30–540 mg dL−1 glucose in culture ([Glucose]ex).
Both the PL intensity change (Fig. 9b) and the color change (Fig. 9c) of the FNG embedded in cells as a function of [Glucose]ex mirror that of the FNG dispersed in PBS (Fig. 5b and 6a correspondingly). Meanwhile, two interesting behaviours were observed: (a) without glucose feeding, the emission position appeared at about 548.8 nm, indicating an initial intracellular glucose level of ca. 31.3 mg dL−1, according to the calibration curve shown in Fig. 6a; and (b) when externally supplied with the same [Glucose]ex over 30–540 mg dL−1, neither the glucose-induced PL quenching degree nor blue-shift degree for the FNG embedded in cells is identical to that for the FNG dispersed in PBS, reflecting the fact that the glucose level in cells is different from that in culture. The latter behaviour is possibly due to the fact that the glucose molecule enters most cells by facilitated diffusion, a form of passive transport requiring no energy but requiring transmembrane proteins.1–3 On the basis of the calibration curve shown in Fig. 6a, the intracellular glucose level [Glucose]cell can be readily correct with [Glucose]ex (Fig. 10a). A possible empirical function was also obtained to described the quantitative relationship between [Glucose]cell and [Glucose]ex. It is clear that at a value of [Glucose]ex over 30–540 mg dL−1, the increment of the intracellular glucose level was generally ca. 43–72% of the external supply. This finding is in accordance with the observations on intracellular glucose detection by using fluorescent protein based biosensors23 and QD based biosensors.17 With the color change as a frame of reference, we can further gain the quantificational relationship between the intracellular glucose levels and the PL intensity change of the FNG embedded in cells (Fig. 10b). The calibration curve for intracellular thermometry using the change in the calibrated PL intensity (Ical) can be obtained by approximating the relationship:
 | (3) |
![A comparison of the glucose level in cells [Glucose]cell with that in culture [Glucose]ex, where [Glucose]cell was measured with the FNG using the color change. (b) Calibrated response curve for the PL intensity change, where Ical is the calibrated PL intensity measured with the FNG embedded in cells.](/image/article/2013/BM/c2bm00162d/c2bm00162d-f10.gif) | ||
| Fig. 10 A comparison of the glucose level in cells [Glucose]cell with that in culture [Glucose]ex, where [Glucose]cell was measured with the FNG using the color change. (b) Calibrated response curve for the PL intensity change, where Ical is the calibrated PL intensity measured with the FNG embedded in cells. | ||
Moreover, because the lowest glucose level reliably detectable with the PL intensity change is much lower than that with the color change, the glucose resolution (i.e., the minimum glucose level difference to be significantly discriminated) for the PL intensity change depends on that for the color change. The glucose resolution for the color change was 1.9–2.8 mg dL−1 over the intracellular glucose level range of 30–540 mg dL−1.
For a more practical use of the FNG, intracellular glucose variations induced by biochemical stimuli were considered. Typically, the B16F10 cells labeled with the FNG were fed with lactose (500.0 mg dL−1), a disaccharide sugar that is found most notably in milk and is thought to be associated with cancer,64 and β-galactosidase (4.1 NLU mL−1), which plays an important role in cellular metabolism by breaking down lactose into galactose and glucose (see ESI-7 in ESI†). No noticeable morphological changes were observed on the tested B16F10 cells during the experiment. Fig. 11 indicates the time-domain fluorescence signals (utilizing the PL intensity change) of the FNG embedded in cells exposed to lactose and β-galactosidase, and the corresponding intracellular glucose levels [Glucose]cell,t obtained using the calibration curve shown in Fig. 10b. While a neglectable change in PL properties was observed when fed with an equated amount of lactose, β-galactosidase, or galactose only (see ESI-8 in ESI† for control experiments), it can be seen that the presence of both lactose and β-galactosidase provoked the PL quenching of the FNG embedded in cells. For example, a quenching of ca. 32.5% in Ical occurred after the reaction had proceeded for 5 min, indicating [Glucose]cell,t = 5 min = 36.6 mg dL−1 (Fig. 11a); that is, an intracellular glucose level rising by an increment of 5.3 mg dL−1 was detected. This variation in glucose level greatly exceeded the glucose resolution of the FNG. Moreover, the response kinetics of the FNG (Fig. 7a) is much faster than that of β-galactosidase catalytic hydrolysis of lactose (see ESI-7 in ESI†). Taken together, it allows us to affirm that the FNG can monitor the dynamic changes of intracellular glucose levels.
![(a) Time-domain fluorescence signals of the FNG embedded in cells (■; n = 5, mean ± s.d.) and the corresponding intracellular glucose level [Glucose]cell,t (□), upon the addition of lactose and β-galactosidase to the culture medium. (b) Time-dependent conversion showing the kinetics of β-galactosidase catalytic hydrolysis of lactose, measured with the FNG embedded in cells (□) and the FNG dispersed in PBS (○), respectively. Solid lines: 1st-order kinetic fits.](/image/article/2013/BM/c2bm00162d/c2bm00162d-f11.gif) | ||
| Fig. 11 (a) Time-domain fluorescence signals of the FNG embedded in cells (■; n = 5, mean ± s.d.) and the corresponding intracellular glucose level [Glucose]cell,t (□), upon the addition of lactose and β-galactosidase to the culture medium. (b) Time-dependent conversion showing the kinetics of β-galactosidase catalytic hydrolysis of lactose, measured with the FNG embedded in cells (□) and the FNG dispersed in PBS (○), respectively. Solid lines: 1st-order kinetic fits. | ||
Based on the evolution of glucose level, the apparent rate constant of β-galactosidase (4.1 NLU mL−1) catalytic hydrolysis of lactose can be derived from the fitting of the time-dependent conversion. Here, the conversion was calculated by
 | (4) |
3. Conclusion
We have developed a new class of fluorescent QD-polymer hybrid nanogels that are applicable for intracellular glucometry. The hybrid nanogels were designed to have a double-network structure by incorporation of a glucose-responsive polymer network and a QD-tethered polymer network into a single nanoparticle. Under such a rational design, the hybrid nanogels can serve as a nanoglucometer for glucose-to-fluorescence signal transduction with high reversibility that is not obtainable from single-network-structured nanogel based biosensors. The beauty of this nanoglucometer, which differentiates it from other examples of fluorescent materials and glucose biosensors, is that not only can it be applied for detection of intracellular glucose levels, with the cells being fed with varying external supply in culture, but more importantly, it also can be exploited for monitoring of intracellular glucose level variations associated with a model biological reaction process. A possible function is also proposed to quantitatively correct the glucose level in cells with that of external supply, and continuous work is ongoing to validate and amend this empirical function. This study may serve as a starting point for developing nanoglucometers that can provide valuable scientific information to advance our understanding of the intracellular glucose physiology.4. Experimental section
4.1. Chemicals
D(+)-Glucose, HSA, 2-aminomethyl-5-fluorophenylboronic acid (FPBA), and β-galactosidase from Escherichia coli were purchased from ACROS, Tokyo Chemical Industry, Combi-Blocks Inc., and Sigma-Aldrich, respectively. All other chemicals were purchased from Alfa-Aesar. NIPAM was recrystallized from a hexane–acetone (a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) mixture and dried under vacuum. Acrylic acid (AA) was purified by distillation under reduced pressure. Zn(MAA)2, AAm, MBAAm, sodium dodecyl sulfate (SDS), APS, sodium hydroxide (NaOH), 2,2′-azobis(2-methylpropionamidine) dihydrochloride (AAPH), FPBA, N-(3-dimethylaminopropyl)-N-ethyl-carbodiimide hydrochloride (EDC), potassium dihydrogen phosphate (KH2PO4), dipotassium hydrogenphosphate (K2HPO4), Rhodamine 640, Rhodamine 590, Rhodamine B, D(+)-glucose, β-D-lactose, β-galactosidase, D(−)-fructose, sodium L-lactate, D(+)-galactose, D(+)-mannose, pyruvic acid, urea, citric acid, vitamin C, g-globulins, lysozyme, and amino acids were used as received without further purification. The water used in all experiments was of Millipore Milli-Q grade.
1 volume ratio) mixture and dried under vacuum. Acrylic acid (AA) was purified by distillation under reduced pressure. Zn(MAA)2, AAm, MBAAm, sodium dodecyl sulfate (SDS), APS, sodium hydroxide (NaOH), 2,2′-azobis(2-methylpropionamidine) dihydrochloride (AAPH), FPBA, N-(3-dimethylaminopropyl)-N-ethyl-carbodiimide hydrochloride (EDC), potassium dihydrogen phosphate (KH2PO4), dipotassium hydrogenphosphate (K2HPO4), Rhodamine 640, Rhodamine 590, Rhodamine B, D(+)-glucose, β-D-lactose, β-galactosidase, D(−)-fructose, sodium L-lactate, D(+)-galactose, D(+)-mannose, pyruvic acid, urea, citric acid, vitamin C, g-globulins, lysozyme, and amino acids were used as received without further purification. The water used in all experiments was of Millipore Milli-Q grade.4.2. Synthesis of poly(NIPAM-co-FPBA) template nanogels
A mixture of NIPAM (1.400 g), AA (0.053 g), MBAAm (0.050 g), SDS (0.052 g), and water (95 mL) was poured into a 250 mL three-necked round-bottomed flask equipped with a stirrer, a nitrogen gas inlet, and a condenser. The mixture was heated to 70 °C under a N2 purge. After 30 min, APS (5 mL, 0.965 M) was added to initiate the polymerization. After 5 hours’ reaction, the obtained poly(NIPAM-co-AA) nanogels were purified by centrifugation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, 20 min, 35 °C, Thermo Electron Co. SORVALL® RC-6 PLUS superspeed centrifuge) and 3 days’ dialysis (Spectra/Por® molecular porous membrane tubing, cutoff 12
000 rpm, 20 min, 35 °C, Thermo Electron Co. SORVALL® RC-6 PLUS superspeed centrifuge) and 3 days’ dialysis (Spectra/Por® molecular porous membrane tubing, cutoff 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–14
000–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Dalton MWCO) against water at room temperature. The purified poly(NIPAM-co-AA) nanogels (20 mL) were cooled in an ice bath, and then FPBA (0.235 g) and EDC (0.231 g) were added. The reaction was allowed to proceed for 4 h under stirring in an ice water bath. The resultant poly(NIPAM-co-FPBA) template nanogels were purified by dialysis against water.
000 Dalton MWCO) against water at room temperature. The purified poly(NIPAM-co-AA) nanogels (20 mL) were cooled in an ice bath, and then FPBA (0.235 g) and EDC (0.231 g) were added. The reaction was allowed to proceed for 4 h under stirring in an ice water bath. The resultant poly(NIPAM-co-FPBA) template nanogels were purified by dialysis against water.4.3. Synthesis of the FNG
A mixture of Zn(MAA)2 (0.100 g), AAm (0.040 g), and MBAAm (0.001 g) with poly(NIPAM-co-FPBA) template nanogel dispersion (50 mL) was stirred in an ice bath (∼4 °C) for 24 h in a 150 mL round-bottomed flask under a N2 purge. After that, excess Zn(MAA)2, AAm and MBAAm were removed at room temperature by centrifugation and decantation, and then washed with water for generating no ZnO QDs except in the nanogel. Then the purified mixture was poured into a 250 mL round-bottomed flask equipped with a stirrer, a nitrogen gas inlet, and a condenser. The dispersion was stirred and heated to 80 °C, and then AAPH (1 mL, 0. 103 M) was added. After refluxing for 2 min, NaOH (0.25 mL, 10 M) aqueous solution was added into the reaction system and continuously refluxed for another 1 h. After cooling to room temperature, the produced FNG was purified by centrifugation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, 30 min, 35 °C), redispersed in water, and 3 days’ dialysis against water.
000 rpm, 30 min, 35 °C), redispersed in water, and 3 days’ dialysis against water.4.4. Protein adsorption experiments
Adsorption of HSA on the FNG was carried out by mixing of the protein in phosphate buffer solution (PBS) (5.0 mM) (VHSA = 5.0 mL) at a given concentration (C0 = 44.0 g L−1) to mass (mFNG = 50.0 mg) of the nanogels in tubes at 37.0 °C. After being maintained for 24 h to reach equilibrium, the mixture was centrifuged (37.0 °C, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, and 30 min) and washed by distilled water twice. The protein–FNG complexes were collected and redispersed in PBS (5.0 mL) for analyzing the effect of adsorption of protein on the FNG. Moreover, the protein concentration in the supernatant, CE, was determined using UV-vis absorption at 278 nm, based on the linear calibration curve (R2 > 0.99) measured using the HSA solutions with known concentrations under the same conditions, for the calculation of surface density dHSA of the protein:
000 rpm, and 30 min) and washed by distilled water twice. The protein–FNG complexes were collected and redispersed in PBS (5.0 mL) for analyzing the effect of adsorption of protein on the FNG. Moreover, the protein concentration in the supernatant, CE, was determined using UV-vis absorption at 278 nm, based on the linear calibration curve (R2 > 0.99) measured using the HSA solutions with known concentrations under the same conditions, for the calculation of surface density dHSA of the protein: | (5) |
4.5. Glucose sensing experiments in aqueous media
The FNG was adjusted to an appropriate concentration of 10.0 μg mL−1 for all measurements. To study the glucose-responsive optical properties, photoluminescence (PL) spectra were recorded in 5.0 mM PBS of pH = 7.4 at 22.1 °C and at different glucose levels. For the interference tests, different interferents at appropriate amounts were mixed into the glucose solutions. The experiments were repeated for five times at each glucose level, and the average intensity at 549 nm (I) was used for constructing the model. To simplify the calculation model, the PL intensity of the FNG in PBS of pH = 7.4 without any sugar (I0) were used to calculate the decay of absorption 1/(1 − I/I0) in all experiments.4.6. Optical response kinetics
The PL intensity of the FNG dispersions (10.0 μg mL−1) at 549 nm was measured on a spectrofluorometer equipped with a magnetic stirrer, a temperature controller, and a syringe pump. For kinetic studies, a predetermined amount of glucose solution was quickly injected and mixed with 3 mL FNG dispersion. The change in PL intensity of the dispersion was then recorded as time evolved, with the interval set at 0.01 s. Furthermore, to study the effect of the FNG particle concentration on the characteristic response time τsensing, the measurements were carried out for the FNG of the concentration in the range 5–200 μg mL−1.4.7. Glucose sensing experiments in blood serums
A representative sample of 50 adults, 20 years of age or older, participated in this study. After an overnight fast, participants underwent an oral glucose-tolerance test in the clinical laboratory. Typically, blood samples (7.5–15 mL) were collected from the diabetes patients and from healthy donors, and they were centrifuged and processed within 2 hours of collection. The impaired fasting glucose (IFG) was measured using an enzyme-based method, the POD-GOD method. Principally, glucose is oxidized by glucose oxidase (GOD) to produce gluconate and hydrogen peroxide; the hydrogen peroxide is then oxidatively coupled with 4 amino-antipyrene (4-AAP) and phenol in the presence of peroxidase (POD) to yield a red quinoneimine dye that is measured at 505 nm.11,68 In the chemistry laboratory, the FNG were directly mixed with the blood serum at room temperature, and the PL intensity at 549 nm (I) was recorded and repeated five times at each sample. The apparent IFG levels were read out based on the calibration model constructed in PBS solutions of known glucose levels (also see section 4.5).4.8. Cell internalization of the FNG and intracellular glucometry
Glass base dishes (35 mm) were treated with 0.1% poly-L-lysine in 100 mM PBS for 40 min. The solution was then aspirated and the dishes were washed with PBS three times each. Next, mouse melanoma B16F10 cells (2 × 106 cells per dish) were plated on the glass coverslips at 80% confluence in sugar-free Dulbecco's modified Eagle's medium (DMEM) containing 10% fetal bovine serum (FBS), 1% penicillin-streptomycin. Next day the FNG was diluted in a serum/sugar free medium (200 μL sample plus 1.6 mL serum free medium). The cells were incubated with the FNG in the following two manners: (1) incubated for 2 hours and then sugar-free DMEM (200 μL) was added; (2) incubated for 2 hours and then DMEM (200 μL) containing different concentrations of glucose were added. The final concentration of the FNG for cell culture is ca. 10.0 μg mL−1. After the addition, the sample was incubated for another 4 hours. The control dish contained 2.0 mL of the serum/sugar free medium. After the incubation, the samples were washed with the serum/sugar free medium for cellular imaging.The biochemical stimulus was conducted by quickly replacing the serum/sugar free medium with fresh sugar-free DMEM (1.8 mL), lactose solution (100 μL, in sugar-free DMEM), and β-galactosidase solution (100 μL, in sugar-free DMEM) in a glass base dish containing the FNG-stained B16F10 cells. The temperature of the culture medium was maintained at 37.0 °C during the experiment. Control dishes contained the FNG-stained B16F10 cells plus lactose (plus 100 μL sugar-free DMEM), the FNG-stained B16F10 cells plus β-galactosidase (plus 100 μL sugar-free DMEM), and the FNG-stained B16F10 cells plus galactose (plus 100 μL sugar-free DMEM), respectively.
Live cell imaging was performed on a confocal laser scanning microscope (LEICA TCS SP2 AOBS™) equipped with a HC PL APO CS 20 × 0.7 DRY lens. A UV (405 nm) light was used as the light source. Laser power at the sample plane was 10 mW for all the experiments. A high-resolution Hamamatsu C9100-02 CCD camera was used for acquiring cell images. As for PL intensity change, the fluorescence signal was obtained from fluorescence images by summing the PL intensities of all the pixels within a single cell (n = 5, mean ± s.d.), while for color change, the fluorescence signal was read from the microscope by creating the lambda series and analysing the spectra using the standard LCS software through a stack dialog window.
The glucose resolution (δ[Glucose]cell) was evaluated by:69
 | (6) |
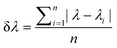 | (7) |
4.9. Other characterizations
The contents of sulfur in the FNG were determined by using a Dionex ICS-1500 ion chromatography system. The crosslink density was estimated by using a Nuclear Magnetic Resonance (NMR) spectroscopy method. The NMR spectra were recorded on a Bruker Avance 400 MHz NMR Spectrometer at 300 ± 0.05 K with pulse width P1 = π/4 and pulse interval D1 = 2.0 s, and the relaxation time and nuclear Overhauser effect were also taken into account for the measurements. The pH values were obtained on a METTLER TOLEDO SevenEasy pH meter. The UV-vis absorption spectra were obtained on a Varian Cary 5000 UV-vis-NIR Spectrometer. The FTIR spectra were recorded with a Nicolet IR200 Fourier transform infrared spectrometer. TEM images were taken on a FEI TECNAI F30 high-resolution transmission electron microscope at an accelerating voltage of 120 kV. Approximately 10 μL of the diluted FNG suspension was air-dried on a carbon-coated copper grid for the TEM measurements. The PL analysis of the FNG dispersions were carried out by using a JOBIN YVON Co. FluoroMax®-4 Spectrofluorometer equipped with a Hamamatsu R2658P photomultiplier tube, calibrated photodiode for excitation reference correction from 185–1010 nm, and a wavelength stepping of 0.02 nm and an integration time of 1 s. The temperature was controlled by a LFI-3751 thermoelectric temperature controller and monitored with a platinum resistance thermometer. The fluorescence quantum yield of ZnO QDs in the FNG was determined by using a Single Photon Counting Controller FluoroHub. The IFG was measured by using a Beckman CX9 Chemistry Analyzer. Experiments of electrophoretic mobility, μE, were carried out on a Malvern Zetasizer Nano S90 particle analyzer on the Zeta-Meter mode and calibrated with standard solutions. The ζ-potential of the nanogel particles was calculated by employing the Smoluchowski relationship:35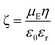 | (8) |
DLS was performed on a 90Plus multi angle particle sizing analyzer equipped with a BI-9000AT digital autocorrelator (Brookhaven Instruments, Inc.) to measure the average hydrodynamic radius 〈Rh〉 and the size distribution. A He-Ne laser (35 mW, 659 nm) was used as the light source. All dispersions were passed through Millipore Millex-HV filters with a pore size of 0.80 μm to remove dust before DLS measurements. In DLS, the Laplace inversion (here the CONTIN method was used) of each measured intensity–intensity time correlation function in a dilute dispersion can lead to a line-width distribution G(Γ). For a purely diffusive relaxation, Γ is related to the translational diffusion coefficient D by (Γ/q2)C→0,q→0 = D, so that G(Γ) can be converted to a transitional diffusion coefficient distribution and 〈Rh〉 distribution by using the Stokes–Einstein equation, 〈Rh〉 = (kBT/6πη)/D, where kB, T, and η are the Boltzmann constant, the absolute temperature, and the solvent viscosity, respectively.70 All DLS measurements were made at scattering angle θ = 90°.
Acknowledgements
We thank the National Natural Science Foundation of China (21274118 and 91227120), the Program for New Century Excellent Talents in Fujian Province University, the Fundamental Research Funds for the Central Universities (2012121016), and the National Found for Fostering Talents of Basic Science (J1030415) for financial support.Notes and references
- H. M. Kalckar and D. B. Ullrey, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 1126 Search PubMed.
- L. Q. Chen, B.-H. Hou, S. Lalonde, H. Takanaga, M. L. Hartung, X.-Q. Qu, W.-J. Guo, J.-G. Kim, W. Underwood, B. Chaudhuri, D. Chermak, G. Antony, F. F. White, S. C. Somerville, M. B. Mudgett and W. B. Frommer, Nature, 2010, 468, 527 Search PubMed.
- L. F. Sun, X. Zeng, C. Y. Yan, X. Y. Sun, X. Q. Gong, Y. Rao and N. Yan, Nature, 2012, 490, 361 Search PubMed.
- A. Y. L. So, T. U. Bernal, M. L. Pillsbury, K. R. Yamamoto and B. J. Feldman, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17582 Search PubMed.
- M. R. Kaadige, R. E. Looper, S. Kamalanaadhan and D. E. Ayer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14878 Search PubMed.
- K. Ohtsubo, M. Z. Chen, J. M. Olefsky and J. D. Marth, Nat. Med., 2011, 17, 1067 Search PubMed.
- L. Ban, N. Pettit, L. Li, A. DStuparu, L. Cai, W. Chen, W. Guan, W. Han, P. G. Wang and M. Mrksich, Nat. Chem. Biol., 2012, 8, 769 Search PubMed.
- S. K. Chacko, A. L. Sunehag, S. Sharma, P. J. J. Sauer and M. W. Haymond, J. Appl. Physiol., 2008, 104, 944 Search PubMed.
- J. C. Pickup, F. Hussain, N. D. Evans, O. J. Rolinski and D. J. S. Birch, Biosens. Bioelectron., 2005, 20, 2555 CrossRef CAS.
- Y. E. Lee and R. Kopelman, Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol., 2009, 1, 98 Search PubMed.
- M. S. Steiner, A. Duerkop and O. S. Wolfbeis, Chem. Soc. Rev., 2011, 40, 4805 RSC.
- J. Yoon and A. W. Czarnik, J. Am. Chem. Soc., 1992, 114, 5874 CrossRef CAS.
- D. B. Cordes, S. Gamsey and B. Singaram, Angew. Chem., Int. Ed., 2006, 45, 3829 CrossRef CAS.
- R. Gill, L. Bahshi, R. Freeman and I. Willner, Angew. Chem., Int. Ed., 2008, 47, 1676 CrossRef CAS.
- B. Tang, L. Cao, K. Xu, L. Zhou, J. Ge and L. Yu, Chem.–Eur. J., 2008, 14, 3637 CrossRef CAS.
- R. Nishiyahu, Y. Kubo, T. D. James and J. S. Fossey, Chem. Commun., 2011, 1106 Search PubMed.
- W. T. Wu, T. Zhou, A. Berliner, P. Banerjee and S. Q. Zhou, Angew. Chem., Int. Ed., 2010, 49, 6554 CrossRef CAS.
- W. T. Wu, T. Zhou, J. Shen and S. Q. Zhou, Chem. Commun., 2009, 4390 RSC.
- W. T. Wu, T. Zhou, M. Aiello and S. Q. Zhou, Biosens. Bioelectron., 2010, 25, 2603 CrossRef CAS.
- W. T. Wu, N. Mitra, E. C. Y. Yan and S. Q. Zhou, ACS Nano, 2010, 4, 4831 CrossRef CAS.
- W. T. Wu, S. M. Chen, Y. M. Hu and S. Q. Zhou, J. Diabetes Sci. Technol., 2012, 6(4), 892 Search PubMed.
- W. T. Wu, J. Shen, Y. X. Li, H. B. Zhu, P. Banerjee and S. Q. Zhou, Biomaterials, 2012, 33, 7115 Search PubMed.
- M. Fehr, S. Lalonde, D. W. Ehrhardt and W. B. Frommer, J. Fluoresc., 2004, 14, 603 Search PubMed.
- C. Bermejo, F. Haerizadeh, H. Takanaga, D. Chermak and W. B. Frommer, Biochem. J., 2010, 432, 399 Search PubMed.
- C. Bermejo, F. Haerizadeh, H. Takanaga, D. Chermak and W. B. Frommer, Nat. Protoc., 2011, 6, 1806 Search PubMed.
- B.-H. Hou, H. Takanaga, G. Grossmann, L.-Q. Chen, X.-Q. Qu, A. M. Jones, S. Lalonde, O. Schweissgut, W. Wiechert and W. B. Frommer, Nat. Protoc., 2011, 6, 1818 Search PubMed.
- S. Jin, J. V. Veetil, J. R. Garrett and K. M. Ye, Biosens. Bioelectron., 2011, 26, 3427 CrossRef CAS.
- C. Wu and S. Q. Zhou, Macromolecules, 1997, 30, 574 CrossRef CAS.
- D. C. Jones and L. A. Lyon, Macromolecules, 2000, 33, 8301 CrossRef CAS.
- C. L. Chi, T. Cai and Z. B. Hu, Langmuir, 2009, 25, 3814 CrossRef CAS.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155 CrossRef CAS.
- S. Liang, Q. M. Yu, H. Yin, Z. L. Wu, T. Kurokawa and J. P. Gong, Chem. Commun., 2009, 7518 RSC.
- H. Xiong, X. Zhao and J. Chen, J. Phys. Chem. B, 2001, 105, 10169 CrossRef CAS.
- E. A. Meulenkamp, J. Phys. Chem. B, 1998, 102, 5566 CrossRef CAS.
- R. J. Hunter, Zeta Potential in Colloid Science, Academic Press, London, 1981 Search PubMed.
- C. Gota, K. Okabe, T. Funatsu, Y. Harada and S. Uchiyama, J. Am. Chem. Soc., 2009, 131, 2766 CrossRef CAS.
- K. Okabe, N. Inada, C. Gota, Y. Harada, T. Funatsu and S. Uchiyama, Nat. Commun., 2012, 3, 705 Search PubMed.
- A. P. Davis and R. S. Wareham, Angew. Chem., Int. Ed., 1999, 38, 2979 CAS.
- M. M. Ward Muscatello, L. E. Stunja and S. A. Asher, Anal. Chem., 2009, 81, 4978 CrossRef CAS.
- X. P. Yang, M. C. Lee, F. Sartain, X. H. Pan and C. R. Lowe, Chem.–Eur. J., 2006, 12, 8491 CrossRef CAS.
- I. Hisamitsu, K. Kataoka, T. Okano and Y. Sakurai, Pharm. Res., 1997, 14, 289 CAS.
- Y. J. Zhang, Y. Guan and S. Q. Zhou, Biomacromolecules, 2006, 7, 3196 CrossRef CAS.
- Y. He, H. Liu and R. Himeno, Int. J. Heat Mass Transfer, 2004, 47, 2735 Search PubMed.
- B. B. Lowell and B. M. Spiegelman, Nature, 2000, 404, 652 CAS.
- C. Stefanadis, C. Chrysochoou, D. Markou, K. Petraki, D. B. Panagiotakos, C. Fasoulakis, A. Kyriakidis, C. Papadimitriou and P. K. Toutouzas, J. Clin. Oncol., 2001, 19, 676 CAS.
- V. P. Torchilin, Pharm. Res., 2006, 24, 1 CrossRef.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, New York, 1975 Search PubMed.
- D. Battaglia, B. Blackman and X. G. Peng, J. Am. Chem. Soc., 2005, 127, 10889 CrossRef CAS.
- J. Yin, D. Dupin, J. F. Li, S. P. Armes and S. Y. Liu, Langmuir, 2008, 24, 9334 CrossRef CAS.
- C. Wu, J. Polym. Sci., Part B: Polym. Phys., 1994, 32, 1503 CrossRef CAS.
- K. E. Shafer-Peltier, C. L. Haynes, M. R. Glucksberg and R. P. Van Duyne, J. Am. Chem. Soc., 2003, 125, 588 CrossRef CAS.
- C. A. Burtis and E. R. Ashwood, Tietz Textbook of Clinical Chemistry, W. B. Saunders, Philadelphia, PA, 3rd edn, 1999 Search PubMed.
- R. Pizzuto, G. Paventi, C. Porcile, D. Sarnataro, A. Daniele and S. Passarella, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 1679 Search PubMed.
- G. S. Posterino and M. W. Fryer, J. Appl. Physiol., 2000, 89, 517 Search PubMed.
- M. M. Muscatello, L. E. Stunja and S. A. Asher, Anal. Chem., 2009, 81, 4978 CrossRef CAS.
- I. I. Concha, F. V. Velasquez, J. M. Martinez, C. Angulo, A. Droppelmann, A. M. Reyes, J. C. Slebe, J. C. Vera and D. W. Golde, Blood, 1997, 89, 4190 Search PubMed.
- G. A. Bray, Am. J. Clin. Nutr., 2007, 86, 895 Search PubMed.
- H. S. Mader and O. S. Wolfbeis, Microchim. Acta, 2008, 162, 1 CrossRef CAS.
- X. C. Yang, Y. F. Cheng, S. Jin and B. H. Wang, Boronic acid-based receptors and chemosensors, in Artificial Receptors for Chemical Sensors, ed. V. M. Mirsky and A. K. Yatsimirsky, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011 Search PubMed.
- J. S. Hansen, J. B. Christensen, T. I. Solling, P. Jakobsen and T. Hoeg-Jensen, Tetrahedron, 2011, 67, 1334 CrossRef CAS.
- W. L. Clarke, D. Cox, L. A. Gonder-Frederick, W. Carter and S. L. Pohl, Diabetes Care, 1987, 10, 622 CrossRef CAS.
- F. Alexis, E. Pridgen, L. K. Molnar and O. C. Farokhzad, Mol. Pharmaceutics, 2008, 5, 505 CrossRef CAS.
- C. Longo, A. Patanarut, T. George, B. Bishop, W. Zhou, C. Fredolini, M. M. Ross, E. Espinia, G. Pellacani, E. F. Petricoin III, L. A. Liotta and A. Luchini, PLoS One, 2009, 4(3), e4763 CrossRef.
- M. T. Faber, A. Jensen, M. Søgaard, E. Høgdall, C. Høgdall, J. Ballkær and S. K. Kjær, Acta Oncol., 2012, 51, 454 Search PubMed.
- J. D. Debord and L. A. Lyon, Langmuir, 2003, 19, 7662 CrossRef CAS.
- Y. Hoshino, T. Kodama, Y. Okahata and K. J. Shea, J. Am. Chem. Soc., 2008, 130, 15242 CrossRef CAS.
- T. Zhou, C. Xiao, J. Fan, S. Chen, J. Shen, W. T. Wu and S. Q. Zhou, Acta Biomater., 2012, 9, 4546 Search PubMed.
- National Committee for Clinical Laboratory Standards. Approved Guideline, NCCLS publication C28-A, Villanova, PA; 1994. http://www.tecodiag.com.
- S. N. Baker, T. M. McCleskey and G. A. Baker, Ionic Liquids IIIB: Fundamentals, Progress, Challenges and Opportunities: Transformations and Processes (ACS Symposium Series, No. 902). American Chemical Society, Washington D.C., 2005 Search PubMed.
- B. Chu, Laser Light Scattering, Academic Press, NY, 2nd edn, 1991 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures and characterization data. See DOI: 10.1039/c2bm00162d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2013 |
