An approach toward quantification of organic compounds in complex environmental samples using high-resolution electrospray ionization mass spectrometry

Abstract

Quantitative analysis of individual compounds in complex mixtures using high-resolution electrospray ionization mass spectrometry (HR-ESI-MS) is complicated by differences in the ionization efficiencies of analyte molecules, mainly resulting in signal suppression during ionization. However, the ability to obtain concentration estimates of compounds in environmental samples is important for data interpretation and comparison. We introduce an approach for estimating mass concentrations of analytes observed in a multicomponent mixture by HR-ESI-MS, without prior separation. The approach relies, in part, on a matrix-matched calibration of the instrument using appropriate standards added to the analyte matrix. An illustration of how the proposed calibration can be applied in practice is provided for aqueous extracts of isoprene photooxidation secondary organic aerosol, with multifunctional organic acid standards. We show that the observed ion sensitivities in ESI are positively correlated with the “adjusted mass,” defined as a product of the molecular mass and the H/C ratio in the molecule (adjusted mass = H/C × molecular mass). The correlation of the observed ESI sensitivity with adjusted mass is associated with the trends of the physical and chemical properties of organic compounds that affect ionization in the positive ion mode, i.e., gas-phase basicity, polarizability, and molecular size.

---

Introduction

High-resolution electrospray ionization mass spectrometry (HR-ESI-MS) is a powerful technique for the identification and characterization of compounds in complex mixtures including aqueous natural organic matter (NOM),^1,2 cloud and fog samples,³ peptide mixtures,⁴ crude oil,⁵ and organic aerosol extracts.^6,7 In these applications, it is desirable to convert raw ion intensities into absolute concentrations, or at the very least, determine the relative abundances of compounds in the mixture. Even modest accuracy provided by the estimation would be invaluable for the interpretation of the experimental results. Obtaining quantitative results from HR-ESI-MS, however, is complicated due to the fact that ionization efficiencies vary with spray conditions (e.g., voltage, solvent, flow rate), analyte chemical properties, and the presence of charge competitors (see ref. 8 and references therein). Consequently, HR-ESI-MS is typically used for detection and identification of compounds in complex mixtures while quantitative measurement studies rely on liquid chromatography separation, stable isotope labelling, and/or intensity calibration using internal standards.⁹

Most studies on the quantification of analyte ions produced by ESI focus on relative ionization efficiency measurements of two standard compounds in pure solvents. This approach is informative, but because the ionization response depends on the concentration and chemical properties of all the solutes in the mixture, two-component mixtures are likely to have different ESI responses compared to multicomponent mixtures.¹⁰ Environmental samples are often a complex mixture of dissolved organics, which simultaneously compete for charge. Nevertheless, quantitative analyses of selected analytes in polymer matrices¹¹ and in secondary organic aerosols (SOA)⁷ have been performed for a few compounds using internal standards. Furthermore, external standards in a realistic matrix, i.e., matrix-matched standards, have been used to overcome matrix effects in the quantification of desired analytes, mostly in physiological samples.^11–14 This matrix-matched calibration can be expanded to assign concentration values to HR-MS peak intensities for all observable compounds in an unknown environmental mixture, if there is a good correlation between the peak intensities and other parameters that can be directly obtained from the mass spectra.

In positive ion mode ESI, analyte molecules are typically converted to protonated [M + H]⁺ or sodiated [M + Na]⁺ species. Therefore, positive mode ionization in ESI enables chemical characterization of molecules that readily form and stabilize a positive charge.^15–18 Many parameters, often interrelated, affect ionization efficiencies within separate compound classes: polarizability, gas-phase basicity (GB, related to proton affinity (PA) by an entropic term − TΔS^o), sodium affinity, and surface activity that may be estimated based on the octanol–water partitioning constant.^15,16,18,19 These properties, and therefore ionization efficiencies, are affected by both the molecular size and the structure of the analyte.

For homologous series of compounds, GB, sodium affinity and average polarizability of compounds are proportional to the molecular size.^20–22 However, GB and sodium affinity are also intrinsically related to structural characteristics like the ionization site or degree of unsaturation.^23–27 Specifically, because the additional π-electrons offer resonance stabilization of the positive charge, GB increases with the degree of unsaturation in molecules when ionization occurs on carbon atoms, such as for aliphatic hydrocarbons,²⁰ carbonyls,²⁷ and cyclic ethers.^25,26 However, when ionization occurs on more basic atoms such as N, S or O, GB decreases with the degree of unsaturation due to the conversion from the sp³ hybridization state to the sp² state of the basic atoms, e.g., going from an amine to an enamine.²⁰ Because the dependence of the ionization efficiency on structural properties, such as the degree of unsaturation, may vary by compound class, the molecular size alone is not directly correlated with the ionization efficiency. Therefore, a combination of factors should be considered when estimating ionization efficiencies, perhaps with one factor describing the size (e.g., mass or volume) and another relating to the structure of the molecule. Calibrations that utilize easily accessible parameters from the mass spectra, as opposed to approaches relying on physico-chemical properties that may not be available in the literature, will facilitate the processing of large HR-ESI-MS datasets from which individual molecular formulas can be determined.

In this work, we introduce a semi-empirical matrix-matched approach to estimate the concentrations of analyte molecules in a complex environmental mixture analyzed by HR-ESI-MS. First, we characterize the positive ion mode ESI response of a few multifunctional organic acid standards in an authentic secondary organic aerosol (SOA) sample matrix without chromatographic separation. Organic acid species are common in SOA^28,29 and other environmental samples,^30,31 which are often highly oxidized and comprise multifunctional polar compounds. We demonstrate that the ESI efficiency of the standards in the SOA matrix is correlated with an “adjusted mass” that explicitly incorporates the contribution of both analyte molecular size and the degree of unsaturation (parameterized by H/C ratios that are conveniently obtained from HR-MS). Subsequently, the apparent relationship between the ESI ionization efficiency and adjusted mass is used to calculate approximate concentrations of analyte compounds in isoprene SOA. This approach provides convenient concentration estimates of organic compounds from raw ion intensities and can be practically applied to environmental samples.

Experimental

SOA from the OH radical initiated photooxidation of isoprene were synthesized and aqueous extracts of SOA were used as a matrix for ESI sensitivity calibrations. SOA were generated and monitored in a 5 m³ photochemical chamber at 70% relative humidity, as described previously.³² The photooxidation time was 5 hours and approximately 500 ppb of isoprene (C₅H₈, Aldrich purity 99%) and 700 ppb of nitrogen oxides (NO + NO₂, added from a mixture of 5000 ppm of NO in N₂) were initially present in the chamber. No additional OH radical precursors were added and no inorganic seed particles were used. The particle size and total SOA mass concentration (in μg m⁻³) were monitored with a scanning mobility particle sizer (TSI, Inc.). SOA samples were collected on PTFE filters (Millipore, 0.2 μm pore), weighed with a microbalance (±1 μg precision, Sartorius ME-5F), and extracted with 10 minute sonication in 1.5–2.0 mL purified water (Aldrich, HPLC grade) to a mass concentration of 200 μg mL⁻¹, comparable to polluted environmental water samples.³³

Ionization sensitivity calibrations were performed by adding an organic acid standard into the aqueous SOA matrix and recording the HR-ESI-MS spectra. Note that we use “HR-ESI-MS” when referring to the high-resolution technique for the determination of analyte masses and only “ESI” when discussing the general aspects of electrospray ionization of organics in a solvent or a sample extract. For each standard compound, the calibration was repeated for four to five different concentrations, which varied over an order of magnitude. Single concentrations of standards were quantitatively transferred to the aqueous SOA matrix from diluted stock solutions (10⁻⁵ to 10⁻³ M) to achieve total organic acid concentrations of 0.1–100 μg mL⁻¹. Four standard compounds were chosen and used individually, with each standard containing two chemical functional groups (e.g., carboxyl and carbonyl or carboxyl and hydroxyl). Standards varied in size and chemical functionality (diacids vs. monoacids, aromatic vs. aliphatic). When selecting the standards, we required that they had different molecular formulas from the compounds already present in SOA to more accurately obtain limits of detection; however this condition need not be imposed under a normal application of the calibration method as background signal can be removed. The addition of standards increased the total volume by less than 10%, and therefore did not significantly dilute the SOA compounds. Table 1 shows the chemical structures and properties of the standards: malic acid (C₄H₆O₅), 3,5-dihydroxybenzoic acid (C₇H₆O₄), pinonic acid (C₁₀H₁₆O₃) and 5-oxoazelaic acid (C₉H₁₄O₄). All standards were used as purchased from Sigma-Aldrich, Inc., with the highest available chemical grade.

Table 1 Positive ion mode ESI calibration using organic mono- and di-acid standards in an aqueous isoprene SOA sample matrix. Effective sensitivity is the slope of the dependence of the signal-to-noise ratio on the mass concentration (μg mL⁻¹) of the added standard. Effective limit-of-detection (LOD) for each ion is the minimum concentration of standard necessary for its detection by HR-ESI-MS within the aqueous SOA matrix

Standard name (formula)	Detected ion	Molecular mass (Da)	Adjusted mass (Da)	Molecular structure	Eff. sensitivity (mL μg^−1)	Eff. LOD (μg mL^−1)
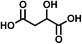
Malic acid (C4H6O5)	Na^+	134.022	201.033		2.68 (±0.02)	8.83 (±2.42)
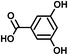
3,5-Dihydroxy benzoic acid (C7H6O4)	Na^+ and H^+	154.027	132.023		Na^+ ion: 0.011 (±0.001)	Na^+ ion: 24.5 (±8.6)
					H^+ ion: 0.09 (±0.02)	H^+ ion: 5.65 (±0.84)
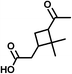
Pinonic acid (C10H16O3)	Na^+ and H^+	184.110	294.576		Na^+ ion: 2.86 (±0.42)	Na^+ ion: 0.30 (±0.10)
					H^+ ion: 2.25 (±0.25)	H^+ ion: 0.74 (±0.14)
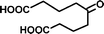
5-Oxoazelaic acid (C9H14O5)	Na^+	202.084	314.353		5.48 (±0.14)	0.02 (±0.01)

---

SOA mixtures in water, spiked with known amounts of the organic acid standards, were electrosprayed into a high-resolution (60 000 m/Δm) linear-ion-trap (LTQ) Orbitrap™ mass spectrometer (Thermo Electron Corporation, Inc.) in the positive ion mode. A mass range of 100–2000 Da was used for experiments, although the observable compounds in the SOA did not exceed 600 Da in size. Samples were introduced with direct infusion using a flow rate of 0.5–1 μL min⁻¹ and ionized with a spray voltage of 4 kV. Analyte compounds were detected as sodiated [M + Na]⁺ and/or protonated [M + H]⁺ species. The instrument was calibrated with a commercial standard mixture of caffeine, MRFA, and Ultramark 1621 (LTQ ESI Positive Ion Calibration Solution, Thermo Scientific, Inc) to maintain high mass accuracy (ca. 0.5 ppm at m/z 500). Accurate mass assignments were performed in the same manner as previously described,^32,34,35 which generated molecular formulas and signal-to-noise (S/N) ratios for all observed ions. Peaks with S/N > 3, as defined by Decon2LS program developed at the Pacific Northwest National Laboratory (PNNL) [http://omics.pnl.gov/software/DeconTools.php], were selected for analysis. Peaks with S/N below 3 threshold were discarded, in effect resetting their intensity to zero. The use of S/N = 3 as the threshold is consistent with the usual definition of the limit of detection. The molecular formulas of the ions were converted to “neutral” molecular formulas (M) by removing a proton or sodium cation. The signals of compounds detected as both protonated and sodiated ions were summed. The individual calibration curves were fit to an appropriate model using least-squares analyses. The degree of deviation from linear or non-linear fits was used as a comparison metric and is reported as the adjusted squared correlation coefficient, [Doublestruck R]², which modifies the centre-of-density R² value (R² = 1 − RSS/TSS) by considering the degrees of freedom (df) of the model ([Doublestruck R]² = 1 − [RSS/df_error]/[TSS/df_total]). [Doublestruck R]² gives a more accurate indication of goodness of fit, especially when a smaller sample size is used. In most cases [Doublestruck R]² ≈ R² and ranges from 0 (poor fit) to 1 (perfect fit), but can be negative if a particularly poor model is used.

Results and discussion

A. Calibration of standards in complex SOA mixtures

A calibration was performed to establish the ESI sensitivity of individual standards of varying size and structure in a complex isoprene SOA mixture. The SOA matrix includes multifunctional organic acids, organic nitrates, carbonyls, and other types of oxygenated compounds present as monomeric and oligomeric structures.^35–37 The isoprene SOA composition is dominated by aliphatic molecules (average H/C ∼ 1.6) that are highly oxidized (average O/C ∼ 0.8) with a molecular weight (MW) range of approximately 100–600 g mol⁻¹. Although the MW of the standard compounds (M_w < 200 g mol⁻¹) are lower, the degree of oxidation (O/C = 0.3–1.2) and chemical functional groups exhibit good overlap with the isoprene SOA and other oxidized complex organic matter in ambient samples. High-MW standards with high O/C and multiple functional groups were not commercially available, which limited the calibration mass range of our study.

Fig. 1 shows that the ion intensities of the standard compounds are proportional to their concentrations in the complex SOA mixture. The dependence is almost linear ([Doublestruck R]² > 0.9) with respect to standard concentration. Positive values of X (concentration) intercepts suggest that analyte compounds are not detected below a certain threshold, and different values of the intercepts suggest that the threshold is dependent on the chemical nature of the analyte. In general, ESI sensitivity is a measure of the ion signal response to concentration. Thus, we define the effective sensitivity (α) as the linear slope of the ion signal (I_i) vs. mass concentration of the analyte ([A]). The effective limit of detection (LOD) is defined as the analyte concentration at which the signal intensity drops below the noise level (I = 0).

I = α[A] + β (1)

LOD = −β/α (2)

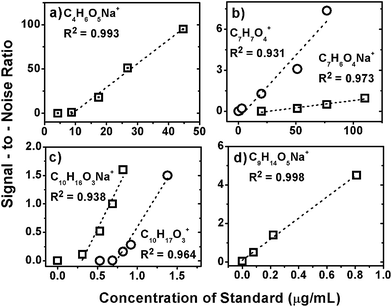Fig. 1 ESI sensitivity response for protonated and/or sodiated peaks from (a) malic acid, (b) 3,5-dihydroxybenzoic acid, (c) pinonic acid and (d) 5-oxoazelaic acid. See Table 1 for additional information about the standards. Only data above the LOD are included in the linear fits.

For the compounds observed in our isoprene photooxidation SOA sample, the LOD corresponds to the concentration at which S/N reaches the value of 3 because peaks with S/N < 3 are rejected by the data processing. Fig. 1 shows that all the standards have negative vertical intercepts, or a positive LOD, due to charge competition by the compounds within the dissolved organic matrix. The α and LOD values for standard compounds are summarized in Table 1. The LOD values can be large; for example, approximately 25 μg mL⁻¹ of 3,5-dihydroxybenzoic acid were needed to be added to the SOA aqueous sample in order to produce a sodiated signal for that compound. Most ions have small to intermediate LOD values, e.g. 0.1–1% by mass in the matrix. However, even these small LOD values may still lead to an underestimation of the concentration of individual compounds in an organic mixture if concentration is calculated assuming that LOD = 0, i.e., [A]_detected = I/α. The true concentration of the analyte has to include a non-zero value of LOD. Therefore, a matrix-dependent correction, like the one presented in this work, should be applied.

In contrast, the ESI detection of standards in a pure solvent does not, and is not expected to, experience such a dramatic offset due to the charge competition. Fig. 2 shows the ESI signal response of sodiated pinonic acid as a representative compound in pure water and in an aqueous SOA matrix as a function of concentration. The LOD of sodiated pinonic acid ion is reduced tenfold in water (LOD ≤ 0.03 μg mL⁻¹) as compared to its value in the SOA matrix (LOD ∼ 0.3 μg mL⁻¹). The variability in the LOD values between different standard compounds (in terms of size and chemical functionality) and different matrices highlight the need for the calibration studies to be performed in a realistic matrix, as opposed to pure solvent.

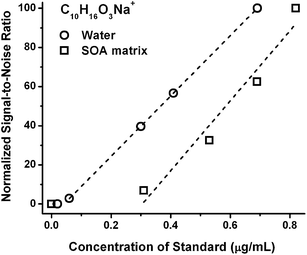Fig. 2 ESI sensitivity response for the sodiated peak of pinonic acid (C₁₀H₁₆O₃) in pure water and in the aqueous isoprene SOA matrix. Only data above the LOD are included in the linear fits.

The effective sensitivity, defined as slope α in eqn (1), measures the ion abundance of the analyte of interest in parallel with other compounds in the matrix. We note that this definition is different from that of other work in the literature,^15,18 which measured the ability of a compound to form gas-phase ions from a single- or two-component solution. Most molecules in our HR-ESI-MS studies were ionized through a single ionization mechanism, but some molecules like pinonic acid were detected as both sodiated and protonated species. Both ionized species were observed for these compounds at concentrations higher than those shown in Fig. 1, although they may not be visible in the graph. The effective sensitivities for such analytes were obtained by summing up the observed intensities of the [M + H]⁺ and [M + Na]⁺ ions as both ions contribute to the ionization potential of the molecule. Likewise, the effective LOD for both ions are summed because using only one LOD value will not accurately correct the ESI signal for the entire concentration of a particular analyte.

Due to the expected dependence of the ionization efficiency on mass and the structure of the standard compounds, the ESI sensitivity for each standard (α_i) and LOD may correlate with the product of neutral molecular mass and the H/C ratio (proxy for degree of unsaturation), which we term “adjusted mass” (AM, units of Da):

AM = (H/C) × (molecular mass) (3)

H/C is commonly used to characterize structure of SOA compounds^6,38 but has not been considered as a factor relevant to the ESI efficiency.

Fig. 3a shows that the ESI sensitivities for the four standards indeed have a strong positive correlation with AM. The sensitivity dependence on AM can be fit well with an exponential rise to a maximum function, y[x] = y₀ + y₁(1 − exp(−R₀·AM)) ([Doublestruck R]² = 0.999) or a linear function ([Doublestruck R]² = 0.985, not shown). The exponential function is more appropriate for high MW compounds because effective sensitivities and LOD (Fig. 3b) exhibit asymptotic behaviour at higher AM. The asymptotic behaviour may arise because higher AM values are correlated with lower unsaturation (π-electron density) but higher average polarizability, which may have opposite effects on ionization in each homologous series. Similar saturation behaviour in properties like GB at higher AM are observed, which is discussed later in the paper.

Fig. 3 Sensitivity and LOD as a function of adjusted mass [AM = (neutral mass) × (H/C ratio)]. Justifications for correlating the effective sensitivity with AM are provided in the text.

In contrast to AM, the ESI sensitivity correlates much more poorly with molecular mass ([Doublestruck R]² = 0.332) and H/C ratio ([Doublestruck R]² = 0.757) individually. The correlation of ESI sensitivity with O/C is also poor ([Doublestruck R]² = −0.353) and furthermore, O/C cannot be used as a calibration parameter for unoxidized molecules. It is remarkable that AM is a better independent variable for our experimental calibration than molecular mass or H/C individually. We propose that the correlation between the effective sensitivity and AM is neither unique to our experiments nor to the specific set of multifunctional standard compounds chosen for this study. The dependence of ESI sensitivity on AM provides the basis for the calibration method reported here.

LOD also appears to be related to AM and increases sharply at low AM (Fig. 3b). This observation highlights the bias of ESI against small molecules when a significant concentration of competing analytes is present. For example, approximately 10 μg mL⁻¹ of malic acid (M + Na⁺ ion m/z 157) in the SOA mixture is needed to overcome the effective LOD, compared to ≤0.03 μg mL⁻¹ needed for 5-oxoazelaic acid (M + Na⁺ ion m/z 225). In addition to the matrix effects, the high value of LOD for small compounds may also be a reflection of specific experimental conditions used in this work, such as relatively high tube lens voltage (150 V) that reduced the transmission of the low-mass ions into the LTQ. The calibration described in this study must be carried out for specific ESI-MS conditions and can then be only applied to experiments performed under those conditions.

B. The adjusted mass axis

The dependence of ESI sensitivity on AM is consistent with other accounts in which both molecular size and degree of unsaturation of organic compounds affect experimental ESI response.^39,40 This association of ESI sensitivity with AM may be rationalized in terms of the effects of the molecular size and structure on the key physico-chemical properties that affect protonation and/or sodiation of organics. These interrelated properties include (a) the ability of the analyte to form cations in the gas phase, which is controlled by GB and sodium affinity and (b) the ability of the analyte ion to stabilize charge, which is controlled by molecular size (mass or volume), degree of unsaturation, and average polarizability.^{16,20,21,41,42} However, any particular parameter may have a different degree of influence on the ionization efficiencies of different homologous series.¹⁵ We focus on GB and polarizability as representative properties as large compilations of data are available in the literature for many compound classes.

Fig. 4 shows that GB correlates well with AM for 13 classes of compounds. Each class of compounds includes 8–23 molecules, depending on the availability of data taken from ref. 43 and references therein. The identities of the compounds used for statistical analysis and their proton affinity (PA), GB, and molecular volume (calculated from atomic radii) values are listed in Table S1 of the ESI.† PA and molecular volume show similar trends with AM as GB (not shown). Linear fits of GB with respect to AM are shown in Fig. 4 for each compound class. There is no particular reason to expect a linear, exponential or any other type of dependence of GB on AM. However, we use correlation coefficients of linear fits as a semi-quantitative comparison for using AM vs. molecular mass or H/C as a calibration parameter. We note that for many types of compounds, there appears to be a saturation effect for GB at higher AM, consistent with the ESI sensitivity behaviours of our calibrant compounds in the SOA matrix.

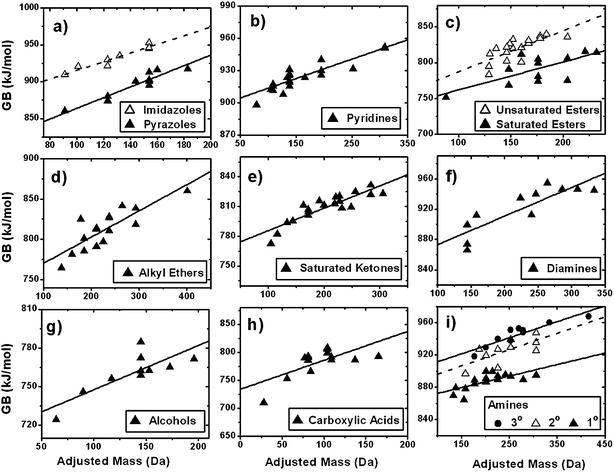Fig. 4 Gas-phase basicity (GB) as a function of adjusted mass for 13 classes of molecules (ref. 43). Linear least-squares fits have been applied and [Doublestruck R]² values are reported in Table 2. Identities of compounds used for analysis are reported in Table S1.†

Table 2 reports the adjusted squared correlation coefficients ([Doublestruck R]²), and the ratios of residual sum of squares (RSS) from correlations of GB to AM compared to correlations of GB to molecular mass or H/C for each compound class. RSS ratios provide a convenient metric for comparing the appropriateness of using these parameters for calibration. As low values for RSS indicate better correlation, values of (RSS_H/C/RSS_AM) or (RSS_mass/RSS_AM) greater than unity imply that AM is a better parameter for the correlation than either molecular mass or H/C. For the linear correlations reported in Table 2, AM is either as good a parameter to use for calibration (RSS ratio ∼ 1) or better (RSS ratio > 1), based on GB, when comparing to molecular mass and H/C ratio. The correlation of GB with AM is good using a linear relationship for the majority of compound classes. However, it is notably poor for the class of carboxylic acids. In contrast, the carboxylic acids used as calibration standards in our work correlated well with AM. The reason for the discrepancy may be due to the absence of additional functional groups for the carboxylic acids in the correlation study. The acid standards chosen for the calibration resembled compounds expected in SOA more closely because they are more oxidized and multifunctional, e.g., they contain additional oxo or hydroxyl groups. The additional alcohol or ketone groups, which in isolated groups correlate well with AM, may provide additional protonation or sodiation sites on the structure of the matrix-matched standards to improve their correlation with AM.

Table 2 [Doublestruck R] ² values for linear least-squares fit for GB (kJ mol⁻¹) as a function of adjusted mass (AM) for 13 classes of molecules. Residual sum of squares (RSS) ratios (please see text for definition) for correlations of AM vs. molecular mass and H/C provide an effective metric for an improvement in fit

Compound class	# Points	Lin. [Doublestruck R]^2 (AM)	RSS Ratios (mass)	RSS Ratios (H/C)
Imidazoles	8	0.921	11	10
Pyrazoles	13	0.886	5.7	8.8
Pyridines	23	0.867	1.9	1.1
Saturated esters	15	0.533	0.7	1.8
Unsaturated esters	15	0.571	1.1	2.0
Alkyl ethers	16	0.687	0.7	2.2
Saturated ketones	20	0.882	1.4	4.1
Diamines	11	0.862	3.9	2.4
Primary amines	16	0.484	1.1	1.5
Secondary amines	11	0.505	0.8	0.9
Tertiary amines	11	0.835	0.8	1.3
Alcohols	10	0.652	1.3	1.1
Carboxylic acids	12	0.465	0.6	0.9
Average values		0.700	2.4	2.9

---

On average, the correlation of GB with AM is better than with molecular mass or H/C by a factor of 2–3. The improvement in fit is ∼2 without the contribution of imidazoles, the class of compounds most well-correlated with AM. Examples of the significant improvements in fit with the AM axis are illustrated in Fig. 5a–c for imidazoles and pyrazoles, for which the GB exhibits poor correlation with molecular mass and H/C ratios. Fig. 5d–f illustrate a difference in the sign of dependence for tertiary amines, the GB of which decreases with H/C but increases with molecular mass and with AM. In all the compound classes used in our study, the GB of alcohols, amines, and alkyl ethers are negatively correlated with H/C for reasons discussed in Section A of Results and discussion. The correlation is positive for nearly all other families of compounds. This observation is consistent with other experimental and theoretical accounts where alcohols, amines and aliphatic ethers deviate in ionization behaviour from other compound classes.²⁰ Despite varying effects of degree of unsaturation on GB, the correlation of GB on AM is always positive for the classes of molecules whose GB values are available in the literature.

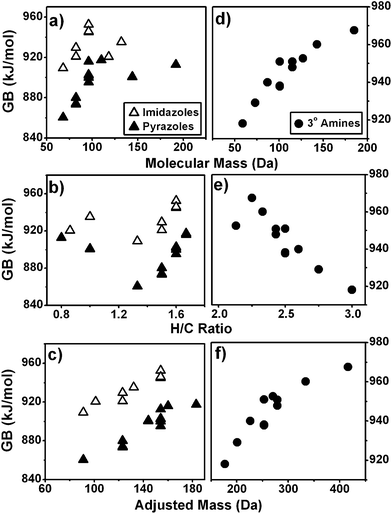Fig. 5 GB as a function of molecular mass, H/C ratios and AM for (a–c) imidazoles and pyrazoles and (d–f) tertiary amines.

Fig. 6 shows that the average polarizability (cm³), which determines the strength of the electrostatic interaction between a positive charge and the analyte, can also have a positive correlation with AM for a large number of hydrocarbons and oxygenated hydrocarbons compounds⁴⁴ listed in Table S2.† This increase in average polarizability with respect to AM is expected because polarizability increases with molecular size and the number of alkyl groups in the molecule,^45,46 which result in higher AM values. Similarly to GB, there is a polarizability saturation effect with size as the change in size becomes increasingly smaller in relation to the total size of the molecule. Polarizability affects sodium affinity and GB to a large extent^47–49 and it is reasonable to assume that both the strength of sodium binding and protonation will increase with AM. It is important to emphasize that even though individual physico-chemical properties considered in this study are correlated with AM, positive ion mode ionization will depend on the combination of many factors. Therefore, experimental calibration of the type performed in this work is essential.

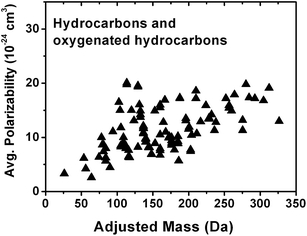Fig. 6 Dependence of average polarizability on adjusted mass for hydrocarbons and oxygenated hydrocarbons listed in Table S2.†

C. Application of sensitivity calibration to a high-resolution mass spectrum

The suggested calibration procedure is applied to an HR-ESI-MS mass spectrum after peak extraction and formula assignment, which makes it possible to calculate AM values for each compound in the mixture from the assigned neutral molecular formulas. Suitable parameterizations of α(AM) (Fig. 3a), and LOD(AM) (Fig. 3b) functions are then used to convert peak intensities into concentrations of individual analyte species:

[A] = I/α(AM) + LOD(AM) (4)

An additional constraint on the total mass concentration of analytes (200 μg mL⁻¹ in this work) in eqn (5) can optionally be used to normalize the [A] values calculated from eqn (4) such that

Because eqn (5) readjusts the predicted [A] values, the calibration is most sensitive to the relative, not absolute, AM-dependent ionization efficiencies of analytes. This effectively reduces errors of the predicted analyte concentrations. Without the normalization viaeqn (5), the sum of predicted [A], i.e. predicted total organic concentration, for several SOA samples of varying composition were higher than the actual total organic concentration by a factor of 2–6. Although quantification of all analytes based on a few standards is fairly approximate, the deviations from the actual total organic concentrations are within the range of other methods. For example, the quantitative analyses of peptides in ESI-MS is achieved within a factor of 3–5 of the true value when calibrating with respect to several observable parameters.⁹

Fig. 7 shows the result of applying the calibration to an experimental mass spectrum of isoprene photooxidation SOA in water. The nonlinear function that extends to higher masses was used to assign approximate analyte concentrations in the isoprene SOA sample. The ratio [A]/I is a measure of change in predicted concentration relative to the experimentally observed ion signals in the spectrum. A constant value of [A]/I throughout the mass spectrum indicates identical sensitivities of analytes in the matrix. The lower mass range has higher [A]/I ratios relative to the higher mass range after applying the calibration because of the lower ionization efficiency of low MW analytes in ESI and bias in ion transmission resulting from potentials used in this study. Higher molecular mass analytes in the range 300–600 Da were generally treated as having similar ionization efficiencies due to the asymptotic behaviour of the calibration curve of both sensitivity and LOD toward higher AM (Fig. 3). This is reflected in the effectively constant [A]/I ratios of analytes with masses >300 Da. The main source of any variance from the [A]/I trend is due to the different H/C of SOA compounds. Because isoprene SOA contains mostly aliphatic molecules, the range over which H/C varies in this work, and hence the variance from the general [A]/I trend, is relatively small (〈H/C〉 = 1.55 ± 0.14). The inset of Fig. 7 shows the calibrated [A] values for each detected compound. The shape of the mass spectrum is generally preserved after applying the calibration but the low masses are enhanced relative to the raw mass spectrum as can be inferred based on the higher [A]/I values at the lower mass range.

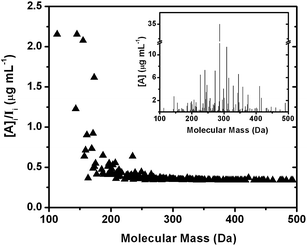Fig. 7 An application of the sensitivity–AM correlation to a mass spectrum of isoprene SOA dissolved in water. The main graph shows the ratio between the estimated mass concentration and the corresponding peak intensity in the raw mass spectrum. The largest variation occurs at a low m/z region where the calibration with standards doped in SOA matrices enhance the signal contribution from low-MW analytes. The inset shows the resulting calibrated mass spectrum.

The approach to assign mass concentrations by application of eqn (4) and (5) in series makes an important simplifying assumption that HR-ESI-MS detects the dominant fraction of organic molecules present in the sample. The accuracy of this assumption depends on the sample. The majority of organic molecules ionize well as either protonated or sodiated species in the positive ion mode ESI, but some samples may contain compounds (e.g., small organosulfates, saturated hydrocarbons, etc.) that are poorly ionizable in the positive ion mode. The appropriate choice of standards becomes increasingly important in these cases.

Although limited data are available, a comparison can be made between the method introduced here and other quantification methods for compounds in isoprene high-NOx photooxidation SOA. For example, 2-methylglyceric acid (C₄H₆O₄, 120.042 Da) is an important component of isoprene high-NOx SOA and has been quantified by Surratt et al. (2006) using ultra-high performance liquid chromatography (UPLC)-ESI-MS. Using this technique, it was determined that 2-methylglyceric acid accounts for 2.7–3.7% of the SOA mass when the SOA is produced under dry (RH < 5%) conditions.³⁶ For consistency in the comparison with Surratt et al. (2006), we applied the calibration procedure to a high-resolution mass spectrum of the isoprene high-NOx SOA sample generated under similar conditions, i.e. low RH (<5%) and using H₂O₂ as a radical precursor, which was reported in an earlier work.³⁵ Using the calibration procedure described in this study, we found 2-methylglyceric acid to be 4 (±2) % of the SOA mass, which is in excellent agreement with the UPLC-ESI-MS technique. As more quantitative information on the composition of SOA becomes available in the future, more extensive validation of the calibration approach proposed in this work will become possible.

Conclusions

In this study, we introduced a new quantification approach for estimating the concentrations of molecules in complex organic mixtures. The approach is based on a calibration of several standards that are structurally similar to molecules in the mixture, from which a relation between their “effective sensitivity” and the novel “adjusted mass” (AM) parameter is obtained and used to estimate concentrations of all the constituents. In isoprene high-NOx SOA, the quantification method predicted a concentration for 2-methylglyceric acid that is comparable to that measured with LC-based techniques. Moreover, concentration values were obtained for all other detected analytes in the isoprene SOA sample, which enhances the utility of this technique. We predict that the proposed intensity-to-concentration conversion will be useful for data interpretation of high-resolution mass spectrometry data. For some studies of environmental samples where the analyte concentrations change due to chemistry, the consistent application of the calibration approach is especially useful for calculating relative concentration values as demonstrated in our recent work.⁵⁰

Furthermore, ESI ionization behaviour in a complex organic matrix was observed to be dramatically different than that in the pure solvents, which are predominantly used to study ionization suppression effects. A surprisingly high initial concentration of the added standard compounds was needed to achieve observable ionization within the sample mixture. Applying the sensitivity and LOD calibration more accurately represents the contribution of ions in the low mass range. As the quantification approach relied on a calibration of standards in an authentic matrix, the results predicted are more representative than those predicted based on physico-chemical properties or from studies of single- or two-component mixtures.

Acknowledgements

The UCI group acknowledges support by the NSF grants AGS-1227579 (SAN) and CHEM-0909227 (TBN). The PNNL group acknowledges support from the Chemical Sciences Division (JL), Office of Basic Energy Sciences of the U.S. DOE, and the intramural research and development program of the W.R. Wiley Environmental Molecular Sciences Laboratory (EMSL). All HR-ESI-MS analyses were performed at EMSL – a national scientific user facility located at PNNL, and sponsored by the Office of Biological and Environmental Research of the U.S. PNNL is operated for US DOE by Battelle Memorial Institute under Contract No. DE-AC06-76RL0 1830.

References

1. T. Reemtsma, J. Chromatogr., A, 2009, 1216, 3687–3701.
2. M. Gonsior, B. M. Peake, W. T. Cooper, D. Podgorski, J. D'Andrilli and W. J. Cooper, Environ. Sci. Technol., 2009, 43, 698–703.
3. L. R. Mazzoleni, B. M. Ehrmann, X. Shen, A. G. Marshall and J. L. Collett, Environ. Sci. Technol., 2010, 44, 3690–3697.
4. J. R. Yates, C. I. Ruse and A. Nakorchevsky, in Annu. Rev. Biomed. Eng., Annual Reviews, Palo Alto, 2009, vol. 11, pp. 49–79.
5. A. G. Marshall and R. P. Rodgers, Acc. Chem. Res., 2004, 37, 53–59.
6. S. A. Nizkorodov, J. Laskin and A. Laskin, Phys. Chem. Chem. Phys., 2011, 13, 3612–3629.
7. W. A. Hall and M. V. Johnston, Aerosol Sci. Technol., 2011, 45, 37–45.
8. P. Kebarle, J. Mass Spectrom., 2000, 35, 804–817.
9. S.-E. Ong and M. Mann, Nat. Chem. Biol., 2005, 1, 252–262.
10. D. S. Selby, M. Guilhaus, J. Murby and R. J. Wells, J. Mass Spectrom., 1998, 33, 1232–1236.
11. M. Stüber and T. Reemtsma, Anal. Bioanal. Chem., 2004, 378, 910–916.
12. A. Fajgelj and A. Ambrus, Principles and Practices of Method Validation, RSC Publishing, London, England, 2000.
13. B. K. Matuszewski, M. L. Constanzer and C. M. Chavez-Eng, Anal. Chem., 1998, 70, 882–889.
14. L. Cuadros-Rodríguez, A. M. García-Campaña, E. Almansa-López, F. J. Egea-González, M. Lourdes Castro Cano, A. Garrido Frenich and J. L. Martínez-Vidal, Anal. Chim. Acta, 2003, 478, 281–301.
15. M. Oss, A. Kruve, K. Herodes and I. Leito, Anal. Chem., 2010, 82, 2865–2872.
16. K. R. Chalcraft, R. Lee, C. Mills and P. Britz-McKibbin, Anal. Chem., 2009, 81, 2506–2515.
17. C. G. Enke, Anal. Chem., 1997, 69, 4885–4893.
18. I. Leito, K. Herodes, M. Huopolainen, K. Virro, A. Künnapas, A. Kruve and R. Tanner, Rapid Commun. Mass Spectrom., 2008, 22, 379–384.
19. G. Bouchoux, F. Djazi, R. Houriet and E. Rolli, J. Org. Chem., 1988, 53, 3498–3501.
20. G. Bouchoux, Mass Spectrom. Rev., 2007, 26, 775–835.
21. G. Bouchoux and J.-Y. Salpin, Mass Spectrom. Rev., 2011, 1–38.
22. M. Mazarin, T. N. T. Phan and L. Charles, Rapid Commun. Mass Spectrom., 2008, 22, 3776–3782.
23. J.-C. Guillemin, M. Decouzon, P.-C. Maria, J.-F. Gal, O. Ma and M. Yaez, J. Phys. Chem. A, 1997, 101, 9525–9530.
24. G. F. Hennion and C. V. DiGiovanna, J. Org. Chem., 1965, 30, 2645–2650.
25. S. Kabli, E. S. E. van Beelen, S. Ingemann, L. Henriksen and S. Hammerum, Int. J. Mass Spectrom., 2006, 249–250, 370–378.
26. G. Bouchoux, D. Leblanc, O. Mo and M. Yanez, J. Org. Chem., 1997, 62, 8439–8448.
27. R. Wolf and H. F. Grutzmacher, New J. Chem., 1990, 14, 379–382.
28. M. Claeys, R. Szmigielski, I. Kourtchev, P. Van der Veken, R. Vermeylen, W. Maenhaut, M. Jaoui, T. E. Kleindienst, M. Lewandowski, J. H. Offenberg and E. O. Edney, Environ. Sci. Technol., 2007, 41, 1628–1634.
29. F. Paulot, J. D. Crounse, H. G. Kjaergaard, J. H. Kroll, J. H. Seinfeld and P. O. Wennberg, Atmos. Chem. Phys., 2009, 9, 1479–1501.
30. J. Collett Jr, B. Daube Jr, J. W. Munger and M. R. Hoffmann, Atmos. Environ., 1989, 23, 999–1007.
31. W. C. Keene and J. N. Galloway, Atmos. Environ., 1984, 18, 2491–2497.
32. T. B. Nguyen, P. J. Roach, J. Laskin, A. Laskin and S. A. Nizkorodov, Atmos. Chem. Phys., 2011, 11, 6931–6944.
33. P. D. Capel, R. Gunde, F. Zuercher and W. Giger, Environ. Sci. Technol., 1990, 24, 722–727.
34. T. B. Nguyen, A. P. Bateman, D. L. Bones, S. A. Nizkorodov, J. Laskin and A. Laskin, Atmos. Environ., 2010, 44, 1032–1042.
35. T. B. Nguyen, J. Laskin, A. Laskin and S. A. Nizkorodov, Environ. Sci. Technol., 2011, 45, 6908–6918.
36. J. D. Surratt, S. M. Murphy, J. H. Kroll, N. L. Ng, L. Hildebrandt, A. Sorooshian, R. Szmigielski, R. Vermeylen, W. Maenhaut, M. Claeys, R. C. Flagan and J. H. Seinfeld, J. Phys. Chem. A, 2006, 110, 9665–9690.
37. A. W. H. Chan, M. N. Chan, J. D. Surratt, P. S. Chhabra, C. L. Loza, J. D. Crounse, L. D. Yee, R. C. Flagan, P. O. Wennberg and J. H. Seinfeld, Atmos. Chem. Phys., 2010, 10, 7169–7188.
38. A. C. Aiken, P. F. Decarlo, J. H. Kroll, D. R. Worsnop, J. A. Huffman, K. S. Docherty, I. M. Ulbrich, C. Mohr, J. R. Kimmel, D. Sueper, Y. Sun, Q. Zhang, A. Trimborn, M. Northway, P. J. Ziemann, M. R. Canagaratna, T. B. Onasch, M. R. Alfarra, A. S. H. Prevot, J. Dommen, J. Duplissy, A. Metzger, U. Baltensperger and J. L. Jimenez, Environ. Sci. Technol., 2008, 42, 4478–4485.
39. K. L. Duffin, J. D. Henion and J. J. Shieh, Anal. Chem., 1991, 63, 1781–1788.
40. M. Koivusalo, P. Haimi, L. Heikinheimo, R. Kostiainen and P. Somerharju, J. Lipid Res., 2001, 42, 663–672.
41. B. M. Ehrmann, T. Henriksen and N. B. Cech, J. Am. Soc. Mass Spectrom., 2008, 19, 719–728.
42. P. Kebarle and M. Peschke, Anal. Chim. Acta, 2000, 406, 11–35.
43. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
44. Atomic and Molecular Polarizabilities, ed. T. M. Miller, 92nd edn, CRC Press, Boca Raton, FL, 2012.
45. K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542.
46. R. W. Taft, M. Taagepera, J. L. M. Abbound, J. F. Wolf, D. J. DeFrees, W. J. Hehre, J. E. Bartmess and R. T. McIver, J. Am. Chem. Soc., 1978, 100, 7765–7767.
47. S. Chinthaka and M. Rodgers, J. Am. Soc. Mass Spectrom., 2012, 1–14.
48. Y. Tsang, F. M. Siu, C. S. Ho, N. L. Ma and C. W. Tsang, Rapid Commun. Mass Spectrom., 2004, 18, 345–355.
49. M. T. Rodgers and P. B. Armentrout, J. Phys. Chem. A, 1999, 103, 4955–4963.
50. T. B. Nguyen, A. Laskin, J. Laskin and S. A. Nizkorodov, Phys. Chem. Chem. Phys., 2012, 14, 9702–9714.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ay25682g

‡ Currently at Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, California, USA 91125.

---