Microrheology of biomaterial hydrogelators
Kelly M.
Schultz
and
Eric M.
Furst
*
Department of Chemical and Biomolecular Engineering and Center for Molecular and Engineering Thermodynamics, University of Delaware, 150 Academy Street, Newark, Delaware 19716, U.S.A. E-mail: furst@udel.edu; Fax: +1 302 831 1048; Tel: +1 302 831 0102
First published on 16th April 2012
Abstract
Microrheology uses the motion of dispersed colloidal probe particles to measure the viscosity or viscoelastic moduli of soft materials. The distinct advantages of microrheology include small sample volume requirements, access to a large range of time scales for the dynamic response and short acquisition times. These advantages make microrheology important for studies of biomaterial hydrogelators. Recent advances have enabled the precise characterization of hydrogelator sol–gel transitions, measurements of rare and scarce materials and high-throughput screening of hydrogel rheology over a large composition space. In this review, we focus on multiple particle tracking microrheology, including the considerations that define its operating regimes and its recent applications. Those interested in biomaterial rheology will find these methods as accessible as bulk rheological measurements and straightforward to implement in their own work.
 Kelly M. Schultz | Kelly M. Schultz is a Howard Hughes Medical Institute postdoctoral research associate at the University of Colorado at Boulder working in the laboratory of Dr Kristi Anseth. Schultz received a BS in Chemical Engineering from Northeastern University. She received her PhD in Chemical Engineering from the University of Delaware as a NSF graduate research fellow under the direction of Eric M. Furst. While at Delaware, she participated in the ACS Excellence in Graduate Polymers Research Symposium. Her current research focuses on the remodeling and degradation of synthetic hydrogel scaffolds during cell migration. |
 Eric M. Furst | Eric M. Furst is an Associate Professor of Chemical and Biomolecular Engineering at the University of Delaware. Furst received his BS with University Honors in Chemical Engineering from Carnegie Mellon University and his PhD from Stanford University. His research groups interests span a wide range of topics in soft matter science and engineering, including microrheology, interfacial phenomena, colloid science, directed self-assembly of colloids and nanoparticles, rheology and colloid electrokinetics. Furst is the recipient of an NSF CAREER award, the 2008 Society of Rheology Publication Award and a 2010 Chaire Joliot at the École Supérieure de Physique et de Chimie Industrielles (ESPCI), Paris. |
1 Introduction
Hydrogels with unprecedented compositional complexity are emerging from research to develop new biomaterials for therapeutic applications, including drug delivery1–6 and artificial cellular scaffolds for use in tissue engineering and wound healing.4,6,7,7–17 In cell culture, this compositional complexity is due in part to the number of biochemical and biophysical cues that must be presented by the material to elicit proper cellular function and cell fate. These include adhesion ligands, proteolytic degradation sites, sequestered soluble proteins, such as growth factors, as well as the supramolecular structure of the hydrogel scaffold itself.4,15,16,18–21 Rheological measurement is often a critical means for characterizing and validating hydrogelation strategies and for gaining insight into their structure and properties. Moreover, the mechanical properties of hydrogels are themselves a key design parameter because the material stiffness provides a critical biophysical cue.22–24 Aside from biological and therapeutic uses, hydrogels are important in engineering and physics applications as well.25–27Despite its importance, rheology can be difficult to perform on many emerging materials, since sufficient material quantities are often hard to synthesize or prohibitively expensive to obtain. Microrheology has emerged as a powerful method that has the potential to aid rheological characterization and advance biomaterials research and engineering. Microrheology has several complementary characteristics: the need for small sample volumes, ranging on the order of 1 to 10 μL, measurement acquisition times on the order of seconds, a large dynamic frequency response (up to megahertz) and the ability to characterize fragile microstructures, such as the incipient structure during a sol–gel transition. These attributes have made microrheology indispensable for understanding scarce materials, specifically those developed for therapeutic applications.
Microrheology is divided into two approaches that are distinguished by the driving force of the probe motion. In active microrheology, the embedded probe particles move in response to an external force, typically generated by optical tweezers or magnetic fields.28,29 Magnetic bead microrheology has a long history in biomaterial rheology, dating to the early twentieth century, when Heilbronn, Seifriz and Freundlich embedded colloidal nickel particles in Echinarachnius parma eggs and gelatin,30–32 and pulled the particles with the magnetic field of an iron core electromagnet. However, the introduction of passive microrheology has stimulated many of the advances in biomaterial microrheology over the past two decades. In passive microrheology, the Brownian or thermal motion of the embedded probe particles is measured and the rheological properties are calculated by the Generalized Stokes–Einstein Relation (GSER).33,34
 | ||
| Fig. 1 Multiple particle tracking microrheology measures random thermal motion of colloidal probe particles embedded in a soft material. Video microscopy images are processed to calculate individual trajectories. The ensemble average of the tracer mean-squared displacements is a measure of the material rheology by the Generalized Stokes–Einstein Relation. In the case shown, the material is gelling with time, leading to a series of curves ranging from a viscous liquid (〈Δr2(t)〉 ∼ t) to an elastic gel (〈Δr2(t)〉 ∼ constant). The mean-squared displacement plot is reprinted with permission from T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001. | ||
In this emerging areas article, we highlight several recent frontiers in which microrheology has advanced the characterization and development of novel hydrogelators. We focus on passive microrheology, and in particular, techniques that require little specialized equipment, with the aim that readers will find these methods at least as straightforward as macrorheological measurements and find them useful for their own work. We begin with a brief overview of passive microrheology, followed by a discussion of the operating regimes of the experiment. After this, we discuss three examples that highlight the strengths of microrheological characterization of biomaterials: measurement of gelation kinetics, high-throughput screening and recent advances combining microrheology and microfluidics.
2 Passive microrheology
2.1 Generalized Stokes–Einstein relation
Beginning in 1995 with the work of Mason and Weitz,33 passive microrheology has become an important characterization method for biomaterial rheology.35–38 In passive microrheology, illustrated in Fig. 1, the Generalized Stokes–Einstein Relation (GSER) is used to relate the mean-squared displacement (MSD) of the particles to the material rheology,28,29,39–41| J(t) = 3πa〈Δr2(t)〉/dkT | (1) |
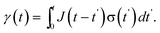 | (2) |
 | ||
| Fig. 2 The material strain γ(t) from an applied step stress σ0 for a viscoelastic liquid and viscoelastic solid. | ||
In eqn (1), d indicates the number of dimensions that the MSD is measured in. For video tracking, it is possible to independently average movement along the Cartesian coordinates that define the imaging plane (in which case, d = 1) or calculate the d = 2 dimensional MSD, 〈Δr2(t)〉 = 〈Δx2(t)〉 + 〈Δy2(t)〉. For light scattering, d = 3. Eqn (1) is valid for all linear viscoelastic fluids and solids in which the material is a continuum, which requires that the probe particle diameter is larger than any characteristic feature size or correlation length. The probe particles must also be sufficiently dilute to avoid particle interactions and potentially changing the intrinsic structure of the material.42
The creep compliance can be converted to other viscoelastic functions, such as the frequency dependent storage and loss moduli, G′(ω) and G′′(ω).43 By noting that the Laplace transforms of the creep compliance and relaxation modulus are related by ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) (s) = 1/s
(s) = 1/s![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (s), the GSER is sometimes written as
(s), the GSER is sometimes written as
 | (3) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) (s)〉 is the Laplace transform of the MSD and s is the Laplace variable. Analytic continuation s = iω can be used to convert this expression to G*(ω) = G′(ω) + iG′′(ω), where
(s)〉 is the Laplace transform of the MSD and s is the Laplace variable. Analytic continuation s = iω can be used to convert this expression to G*(ω) = G′(ω) + iG′′(ω), where  . However, the advantage of eqn (1) is that the MSD can be interpreted without transforming the data collected by multiple particle tracking, as discussed below.
. However, the advantage of eqn (1) is that the MSD can be interpreted without transforming the data collected by multiple particle tracking, as discussed below.
2.2 Multiple particle tracking
Multiple particle tracking is perhaps the most straightforward method for measuring the MSD in a small sample.40 The experiment is quite simple, and requires only a microscope, video camera and a computer for analysis. Bright field or fluorescence illumination can be used. The motion of probe particles dispersed in the material is recorded by video microscopy. These recordings are then analyzed using particle tracking programs, which locate the particles in each video frame and link these locations into trajectories.39 Statistics of the trajectories, such as the MSD, are then calculated. Typically, one tracks ∼100 particles in an image frame, which requires probe volume fractions on the order ϕ ∼ 10−3. Probes are always cleaned prior to use by 3–5 repetitions of light centrifugation, decantation and redispersion in ultra-pure water to remove trace contaminants. The probe particle surface chemistry can also introduce artifacts by changing the local material structure.41,44–46Most particle tracking algorithms track the brightness weighted centroid of each probe throughout the movie.39,40 Measurements of particle trajectories using video microscopy are subject to error from both static and dynamic contributions.47–50 Error is the difference between the observed particle position ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) (t) and the actual position x(t). Dynamic error occurs due to particle motion during the time the camera shutter is open, δ. The static error ε is the inherent error in locating the center of each particle, and is strongly influenced by the signal to noise (S/N) of the imaging system. For a Newtonian fluid, the observed displacement along each Cartesian direction is
(t) and the actual position x(t). Dynamic error occurs due to particle motion during the time the camera shutter is open, δ. The static error ε is the inherent error in locating the center of each particle, and is strongly influenced by the signal to noise (S/N) of the imaging system. For a Newtonian fluid, the observed displacement along each Cartesian direction is
〈Δ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2(t)〉 = 2D(t − δ/3) + 2ε2, 2(t)〉 = 2D(t − δ/3) + 2ε2, | (4) |
2.3 Operating regime of passive microrheology
Because thermal motion is the driving force for passive microrheology, the technique is limited to rather weak moduli and low viscosities (or correspondingly large compliances) compared to macrorheological measurements. As we discuss later, this does not necessarily limit the utility of microrheology; it can still be used to screen whether a hydrogel forms, for instance, even if the compliance is too low to be measured quantitatively. Nonetheless, it is useful to examine the range of material rheology accessible by passive microrheology.We begin by considering the typical limits set by the instrument: the camera acquisition rate and particle tracking error. The reciprocal of the video frame frequency is the minimum time between video frames, τmin = 1/f, and thus, the shortest delay time for the MSD. Assuming that the shutter speed is significantly less than the time between frames, δ ≪ τmin, than we need to only consider the static error contribution to the apparent MSD (cf.eqn (4)). Combining eqns (1) and (4), the minimum compliance is
| Jmin(t) = 6πaε2/kT. | (5) |
Static error becomes more important for viscous fluids. As the MSD approaches ε2, it exhibits an apparent plateau, as shown in Fig. 3, in which we plot the one-dimensional MSD given by eqn (4) as a function of lag time τ for viscosities ranging from 1 mPa s to 10 Pa s. To avoid this plateau, the compliance should be greater than Jmin for all lag times τ > τmin. This is shown by the dashed line in fig. 3, and corresponds to η < kTτmin/6πaε2.
 | ||
| Fig. 3 Calculated mean-squared displacements for 1 μm diameter probe particles in fluids of increasing viscosity from 10−3 to 10 Pa·s. The operating regime for multiple particle tracking microrheology is defined by the shortest and longest lag times and the particle tracking error. Solid curves are the apparent MSD, while the dashed line for η = 0.146 Pa s is the true MSD. | ||
For probe particles with diameter 2a = 1 μm and a typical particle tracking error of ε ≈ 10 nm, the calculated limits above are Gmaxe ≈ 5 Pa (or Jmine ≈ 0.2 Pa−1) and ηmax ≈ 150 mPa s. Eqn (5) also shows the extent to which the range of compliance can be changed by selecting different probe particle sizes. Smaller probes can be used to increase the maximum modulus or viscosity, provided that the continuum approximation of the Stokes drag equation is still satisfied.51
Finally, there is an upper practical limit on the MSD lag times, τmax. This longest lag time is somewhat arbitrary. If it was certain that the fluid was Newtonian, one could wait an indefinite time for the particles to move a sufficient distance to track. But in practice, microscopy is not feasible for materials with such long relaxation times due to instrument errors. Moreover, it is important not to mistake the curvature caused by particle tracking errors for the rheology of the sample. Another concern for more compliant materials is the degradation of the particle tracking statistics due to movement of the particles out of the focal plane, which truncates trajectories.48,50 Finally, there is the overall acquisition time of the measurement to consider; as we discuss in the next section, changes in the material rheology with time, during a hydrogelation reaction, for instance, necessitate shorter acquisition times.
3 Applications to hydrogelators
3.1 Rheology of rare and scarce materials
A distinct advantage of microrheology is the small volume required to make these measurements. Due to this strength, both passive and active microrheological characterization is widely used to characterize scarce materials. Microrheology has been used to measure the rheology of DNA solutions,52,53 protein films54,55 and hydrogelators.19,56–70 Furthermore, measuring the gelation kinetics of materials being used in therapeutic applications is advantageous, giving insight into the final material connectivity and rheology and the time of the gelation reaction, allowing for the engineering of environments that will mimic those found in the human body.3.2 Identification of the sol–gel transition
Passive microrheology can be used to characterize gelation reactions without interfering in the dynamics and assembly of the network structure. Both multiple particle tracking microrheology and light scattering have been used on numerous soft materials that gel, including foods,71–73 hydrogelators,62,63,67,74,75 protein and colloidal solutions76–81 and carbon nanotubes.82In biomaterial hydrogelators, passive microrheology easily identifies the gel time74,76,77 during the gelation reaction or, for equilibrated gels, the gel compositions,65,66 which will be discussed further in the next section. We recently demonstrated that microrheology is capable of providing the same detailed information of gelation reactions as macrorheology, including the gel time and critical exponents of the percolation transition.63
An example of microrheology data collected during a gelation reaction is shown in Fig. 4a for a peptide hydrogelator. Immediately after the initiation of the gelation reaction, the probe particles exhibit diffusion in a viscous medium, for which the MSD increases as the lag time, 〈Δr2(τ)〉 ∼ τ. As the reaction proceeds, the magnitude of the displacement decreases and is accompanied by an onset of subdiffusive dynamics at early lag times. With time, the subdiffusive dynamics grow to encompass longer and longer lag times. Finally, an elastic plateau, where 〈Δr2(τ)〉 is independent of lag time, indicates the formation of an elastic solid.63,66,76,77 Of particular interest during the gelation reaction is the transition from a viscous liquid to a gel; the sensitivity of passive microrheology can detect this transition without disturbing the delicate incipient gel structure. Time-cure superposition, the superposition of viscoelastic functions at different extents of reaction, is used to characterize this transition.
 | ||
| Fig. 4 Time-cure superposition of a 20-residue peptide hydrogel, MAX-1, consisting of an alternating sequence of valine and lysine residues flanking a central tetrapeptide sequence with a high β -turn propensity (a) measured mean-squared using multiple particle tracking microrheology (b) shifted mean-squared displacement into pre- and postgel master curves. Reprinted with permission from T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001. | ||
Time-cure superposition analysis was first applied to measurements of tracer movement in a gelling sample by Larsen and Furst.63 The MSD curves for the pre- and postgel are shifted to form master curves using shift factors, a the abscissa or time shift factor and b the ordinate or mean-squared displacement shift factor. The shift factor a accounts for changes in the material's longest relaxation time during gelation, τL, by a ∼ τ−1L, which is then related to the critical extent of reaction a ∼ (|p − pc|/pc)y. Here, y is the critical scaling exponent of the longest relaxation time and pc is the critical extent of reaction. Similarly, b is related to the critical scaling of the steady state creep compliance by b ∼ 1/J0e ∼ (|p − pc|/pc)z, where, again, z is a critical scaling exponent. Fig. 4 shows an example of this analysis: the mean-squared displacement of the gelling peptide hydrogel is measured using multiple particle tracking microrheology. Fig. 4a is the measured mean-squared displacement and Fig. 4b is the shifted mean-squared displacement curves, which create pre- and postgel master curves.
The critical relaxation exponent is the ratio of the dynamic scaling exponents, y and z, n = z/y. The work done by Corrigan and Donald using a β-lactogloculin protein gel and the original investigation by Larsen and Furst of a β-sheet peptide gel both exhibit a value of n ≈ 0.6 characteristic of Rouse dynamics of fractal polymers.63,64,76,83 Chemically cross-linked poly(ethylene glycol)-high molecular weight heparin (PEG-HMWH) hydrogels exhibit a critical relaxation value of n ≈ 0.5 indicative of a mean-field percolation reaction.65 These critical values, pc and n, are material properties that are not composition dependent, and therefore enable the engineering of the material with precise knowledge of the gelation kinetics.66 Once n is known for a particular substance, it can be used to screen a composition space for hydrogel formation, as we discuss in the next section.
3.3 High-throughput screening
Microrheology not only permits the characterization of scarce and rare materials, but it also enables researchers to screen the material rheology over a large parameter space, including composition,65,66 84–87 changes in environmental stimuli88–90 and even with respect to variations in thermodynamic control variables, such as pressure and temperature.91,92 Active microrheology has been used to screen the mechanical properties of cells93,94 and tissues that mimic blood vessels.95 In the latter case, microrheology techniques enable the measurement of a population of cells experiencing the same deformation, providing statistical significance to the measurements. This is possible due to the small volume of material required for each measurement, but also because of the short data acquisition times.High-throughput screening using microrheology was first proposed by Breedveld and Pine.86 Their work used passive microrheological techniques, including both diffusing wave spectroscopy (light scattering) and multiple particle tracking. Block copolypeptide libraries were screened to create a rheological water/salt/surfactant phase diagram.86 The experiment employed a multi-well plate in a computer controlled stage, which was automated to move from sample to sample as data was acquired. The data analysis was also automated, resulting in experiments that required little human interaction.86 More recent high-throughput microrheology experiments have focused on integrating microrheology and microfluidic devices, which will be discussed further in the next section.89,92,94
Consider the recent example of microrheology measurements to screen the rheology of covalently cross-linked poly(ethylene glycol)-high molecular weight heparin (PEG-HMWH) hydrogels. The goal is to identify the gel compositions in a four-dimensional composition space consisting of the PEG cross-linker molecular weight, the number of cross-linkable sites on each backbone HMWH molecule, the total polymer weight percent of the hydrogel and molar ratio of the HMWH and PEG.
Each hydrogel sample is prepared and equilibrated in parallel. Fig. 5 is the resulting gelation state diagram for hydrogels made with PEG with a number average Mn = 5000. Each subplot shows a different heparin backbone functionality, ranging from 3.9 to 11.8 cross-linkable maleimide sites per heparin. Each square represents one sample point. The color of each data point corresponds to the logarithmic slope of the mean-squared displacement, α = d log〈Δr2(τ)〉/d logτ. For equilibrated hydrogels, knowledge of the critical relaxation exponent enables samples to be differentiated into gels (α < n) and sols (α > n), thus identifying the material compositions that form gels.
 | ||
| Fig. 5 Gelation state diagram for a PEG (Mn 5 000)-HMWH hydrogel. The logarithmic slope of the MSD is α = d log〈Δr2(τ)〉/d logτ. Reprinted with permission from K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, Macromolecules, 2009, 42, 5310–5316. Copyright 2009 American Chemical Society. | ||
The black lines in Fig. 5 represent the lower and upper gelation limits. The lower gelation limit describes the situation when one PEG cross-linker is attached to each HMWH backbone, nPEG = nhepfhep/(fhep − 1) where nPEG and nhep are the moles of PEG and HMWH, respectively, and fhep is the functionality of the heparin backbone. The upper gelation limit describes the condition when there is one cross-linkable site is available for cross-linking on each backbone, nPEG = (fhep − 1)nhep.65,66,96–98 The upper and lower limits not only define the overall composition space for gelation, but it leads to potential new engineering opportunities, such as forming sub-percolated networks that can be cross-linked by additional physical mechanisms, such as protein-heparin interactions.19
3.4 Making microrheology samples with microfluidics
Small sample generation and processing using microfluidics is a natural combination to further advance the throughput of microrheology experiments. Although still in its relatively early stages of development, there are notable examples in the recent literature that hint at its potential across several disciplines. Krayer et al. have created a multi-functional lab on a chip which sorts and manipulates cells to measure their frequency-dependent viscoelastic response94 and Nordstrom et al. report bulk rheology measurements in microfluidic channels on hydrogel particles.99 Sato and Breedveld developed a dialysis device that rapidly changes solvent compositions in polymer and protein solutions for measurements taken using multiple particle tracking.89 Temperature gradients can also be studied by injecting a complex fluid in a microfluidic channel and measuring the subsequent particle motion.92 Recently, our work has focused on developing a characterization technique, μ2rheology, that forms droplet samples in a microfluidic device and uses multiple particle tracking microrheology to measure the rheology.100,101μ 2 Rheology chips use a T-junction to form sample droplets in an immiscible, continuous phase. An image of a microfluidic device is shown in Fig. 6a. The sample droplets are typically 2–5 μL and span the channel cross-section. A large range of compositions can be spanned by generating a linear gradient using pumping programs, illustrated in Fig. 6b. Alternating the flow rates of two inlet streams creates 50–100 droplet samples, each with a unique composition, that are then characterized in a quiescent (non-flowing) state after sealing the device. Initial studies have focused on validating this approach to high-throughput microrheology by measuring the viscosity of glycerine (Fig. 6c) and polymer solutions.100 An example of the utility of μ2 rheology for hydrogel characterization is the gelation state diagram for a PEG-HMWH hydrogel, shown in Fig. 6d. In this state diagram, the black lines represent the upper and lower gelation limits calculated using Flory-Stockmayer theory.96–98,101,102 Good agreement can again be seen with these boundaries along with a dramatic increase in the sample composition resolution, particularly along the percolation boundaries.
 | ||
| Fig. 6 Experimental setup and results of μ2 rheology. (a) An image of a microfluidics device that generates aqueous sample droplets in a silicone oil continuous phase. The gradient in sample composition is demonstrated using water with food coloring. (b) Linear pumping program used to make sample concentration gradient with QA and QB representing the volumetric flow rates of the material being measured (changing the relative concentration of these compounds) and QC is the volumetric flow rate of the continuous phase. (c) μ2 Rheology measurements of glycerine viscosity. (d) Gelation state diagram of PEG (Mn 5000): HMWH (f = 7.7). The logarithmic slope of the MSD is α = d log〈Δr2(τ)〉/d logτ. (a)–(c) Adapted from K. M. Schultz and E. M. Furst, Lab Chip, 2011, 11, 3802–3809. (d) Reprinted with permission from K. M. Schultz, A. V. Bayles, A. D. Baldwin, K. L. Kiick and E. M. Furst, Biomacromolecules, 2011, 12, 4178–4182. Copyright 2011 American Chemical Society. | ||
4 Conclusions and outlook
Microrheology is emerging as an indispensable characterization tool, especially for scarce materials. Small sample requirements make microrheology ideal for screening hydrogelators, especially across complex, multi-dimensional composition spaces.Passive microrheological measurements are limited to soft materials. Despite these constraints, important hydrogel characterization experiments can be performed using microrheology. Time-cure superposition has been shown to be applicable to mean-squared displacement data obtained from multiple particle tracking microrheology. This enables an accurate determination of the critical extent of reaction (gel point), critical exponents such as the relaxation exponent, and leads naturally to the use of high throughput screening to identify the gelation composition state space.
There is plenty of room for further development. In active microrheology, experiments have studied the non-linear microrheological response, which is beyond the characterization limits of passive microrheology.103,104 Non-linear microrheology performed over a large composition space could lead to new methods of “rheological fingerprinting”.105 In passive microrheological techniques the extension of the sol–gel transition investigations could be applied to a degrading material. Preliminary experiments in our laboratory have shown great promise for using time-cure superposition to characterize the degradation of hydrogels and understand degradation reaction mechanisms and the underlying microstructure that evolves.106 Finally, microrheology will greatly benefit from further development of microfluidic devices. Many sophisticated sample generation and manipulation methods have yet to be adapted for microrheology.107–112
Microrheology has many more applications than those discussed in this brief review, and as more materials are developed, for therapeutic, food or industrial applications, there will be a need to improve on existing characterization techniques. This is where the versatility of microrheology will further serve the materials characterization and development.
Acknowledgements
E.M.F. acknowledges financial support for biomaterial microrheology in his laboratory by the National Institutes of Health (Grant No. 2-P20-RR017716). K.M.S. gratefully acknowledges financial support by the NSF Graduate Research Fellowship Program and the Procter and Gamble company.References
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- L. Serra, J. Domenech and N. A. Peppas, Biomaterials, 2006, 27, 5440–5451 CrossRef CAS.
- P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 23–36 CrossRef CAS.
- T. Nie, A. Baldwin, N. Yamaguchi and K. L. Kiick, J. Controlled Release, 2007, 122, 287–296 CrossRef CAS.
- Y. S. Jo, J. Gantz, J. A. Hubbell and M. P. Lutolf, Soft Matter, 2009, 5, 440–446 RSC.
- G. P. Raeber, M. P. Lutolf and J. A. Hubbell, Biophys. J., 2005, 89, 1374–1388 CrossRef CAS.
- M. P. Lutolf, F. E. Weber, H. G. Schmoekel, J. C. Schense, T. Kohler, R. Muller and J. A. Hubbell, Nat. Biotechnol., 2003, 21, 513–518 CrossRef CAS.
- M. P. Lutolf, J. L. Lauer-Fields, H. G. Schoekel, A. T. Metters, F. E. Weber, G. B. Fields and J. A. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5413–5418 CrossRef CAS.
- A. B. Pratt, F. E. Weber, H. G. Schmoekel, R. Muller and J. A. Hubbell, Biotechnol. Bioeng., 2004, 86, 27–36 CrossRef CAS.
- G. P. Raeber, M. P. Lutolf and J. A. Hubbell, Acta Biomater., 2007, 3, 615–629 CrossRef CAS.
- B. D. Fairbanks, E. A. Sims, K. S. Anseth and C. N. Bowman, Macromolecules, 2010, 43, 4113–4119 CrossRef CAS.
- B. D. Fairbanks, M. P. Schwartz, A. E. Halevi, C. R. Nuttelman, C. N. Bowman and K. S. Anseth, Adv. Mater., 2009, 10, 3114–3121 Search PubMed.
- B. K. Mann, A. S. Gobin, A. T. Tsai, R. H. Schmedlen and J. L. West, Biomaterials, 2001, 22, 2045–3051 Search PubMed.
- C. N. Saliinas and K. S. Anseth, J. Dent. Res., 2009, 88, 681–692 CrossRef.
- B. L. Seal and A. Panitch, Macromolecules, 2006, 39, 2268–2274 CrossRef CAS.
- T. Nie, R. E. Akins Jr. and K. L. Kiick, Acta Biomater., 2009, 5, 865–875 CrossRef CAS.
- J. L. West and J. A. Hubbell, React. Polym., 1995, 25, 139–147 CrossRef CAS.
- K. L. Kiick, Soft Matter, 2008, 4, 29–37 RSC.
- N. Yamaguchi, L. Zhang, B.-S. Chae, C. S. Palla, E. M. Furst and K. L. Kiick, J. Am. Chem. Soc., 2007, 129, 3040–3041 CrossRef CAS.
- L. Zhang, E. M. Furst and K. L. Kiick, J. Controlled Release, 2006, 114, 130–142 CrossRef CAS.
- S. E. Sakiyama-Elbert and J. A. Hubbell, J. Controlled Release, 2000, 65, 389–402 CrossRef CAS.
- A. J. Engler, S. Sen, H. Lee Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS.
- D. E. Discher, P. Jamney and Y.-l. Wang, Science, 2005, 310, 1139–1143 CrossRef CAS.
- M. W. Tibbitt, A. M. Kloxin, K. U. Dyamenahalli and K. S. Anseth, Soft Matter, 2010, 6, 5100–5108 RSC.
- M. Karg and T. Hellweg, Curr. Opin. Colloid Interface Sci., 2009, 14, 438–450 CrossRef CAS.
- Z. Zheng, N. Xu, D. T. N. Chen, P. Yunker, A. M. Alsayad, K. B. Aptowicz, P. Habdas, S. R. Nagel and A. G. Yodh, Nature, 2009, 459, 230–233 CrossRef.
- A. Kozina, P. Diaz-Leyva, F. Christian and E. Bartsch, Soft Matter, 2012, 8, 1033–1046 RSC.
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- M. L. Gardel, M. T. Valentine and D. A. Weitz, Microscale Diagnostic Techniques, Springer, 2005 Search PubMed.
- H. Freundlich and W. Seifriz, Z. Phys. Chem., 1922, 104, 232–261 Search PubMed.
- A. Heilbronn, Jahrb. Wiss. Bot., 1922, 61, 284–338 Search PubMed.
- W. Seifriz, J. Exp. Biol., 1924, 1, 431–443 Search PubMed.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS.
- F. Gittes, B. Schnurr, P. D. Olmsted, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 1997, 79, 3286–3289 CrossRef CAS.
- A. Palmer, J. Xu and D. Wirtz, Rheol. Acta, 1998, 37, 97–106 CrossRef CAS.
- J. Apgar, Y. Tseng, E. Fedorov, M. B. Herwig, S. C. Almo and D. Wirtz, Biophys. J., 2000, 79, 1095–1106 CrossRef CAS.
- T. G. Mason, T. Gisler, K. Kroy, E. Frey and D. A. Weitz, J. Rheol., 2000, 44, 917–928 CrossRef CAS.
- L. Le Goff, F. Amblard and E. M. Furst, Phys. Rev. Lett., 2002, 88, 018101 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285 CrossRef CAS.
- D. T. Chen, E. R. Weeks, J. C. Crocker, M. F. Islam, R. Verma, J. Gruber, A. J. Levine, T. C. Tubensky and A. G. Yodh, Phys. Rev. Lett., 2003, 90, 108301 CrossRef CAS.
- A. J. Levine and T. C. Lubensky, Phys. Rev. Lett., 2000, 85, 1774–1777 CrossRef CAS.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley and Sons, Inc., 3rd edn, 1980 Search PubMed.
- J. L. McGrath, J. H. Hartwig and S. C. Kuo, Biophys. J., 2000, 79, 3258–3266 CrossRef CAS.
- J. Y. Huh and E. M. Furst, Phys. Rev. E, 2006, 74, 031802 CrossRef.
- B.-S. Chae and E. M. Furst, Langmuir, 2005, 21, 3084–3089 CrossRef CAS.
- T. Savin and P. S. Doyle, Phys. Rev. E, 2005, 71, 041106 CrossRef.
- T. Savin and P. S. Doyle, Phys. Rev. E, 2007, 76, 021501 CrossRef.
- T. Savin, P. T. Spicer and P. S. Doyle, Appl. Phys. Lett., 2008, 93, 204102 CrossRef.
- T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623–638 CrossRef CAS.
- D. Weihs, T. G. Mason and M. A. Teitell, Biophys. J., 2006, 91, 4296–4305 CrossRef CAS.
- I. A. Hasnain and A. M. Donald, Phys. Rev. E, 2006, 73, 031901 CrossRef CAS.
- M. Moccia, D. Musumeci, G. N. Roviello, S. Fusco, M. Valente, E. M. Bucci, R. Sapio, C. Pedone and P. A. Netti, J. Pept. Sci., 2009, 15, 647–653 CrossRef CAS.
- M. H. Lee, D. H. Reich, K. J. Stebe and R. L. Leheny, Langmuir, 2010, 26, 2650–2658 CrossRef CAS.
- P. Dhar, Y. Cao, T. M. Fischer and J. A. Zasadzinski, Phys. Rev. Lett., 2010, 104, 016001 CrossRef.
- N. Yamaguchi, B.-S. Chae, L. Zhang, K. L. Kiick and E. M. Furst, Biomacromolecules, 2005, 6, 1931–1940 CrossRef CAS.
- M. A. K. Williams, R. R. Vincent, D. N. Pinder and Y. Hemar, J. Non-Newtonian Fluid Mech., 2008, 149, 63–70 CrossRef CAS.
- W. Shen, R. G. H. Lammertink, J. K. Sakata, J. A. Kornfield and D. A. Tirrell, Macromolecules, 2005, 38, 3909–3916 CrossRef CAS.
- C. T. S. Wong Po Foo, J. S. Lee, W. Mulyasasmita, A. Parisi-Amin and S. C. Heilshorn, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 22067–22072 CrossRef.
- H. Boehm, T. A. Mundinger, C. H. J. Boehm, V. Hagel, U. Rauch, J. P. Spatz and J. E. Curtis, Soft Matter, 2009, 5, 4331–4337 RSC.
- S. Topp, V. Prasad, G. C. Cianci, E. R. Weeks and J. P. Gallivan, J. Am. Chem. Soc., 2006, 128, 13994–13995 CrossRef CAS.
- T. Savin and P. S. Doyle, Soft Matter, 2007, 3, 1194–1202 RSC.
- T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001 CrossRef.
- T. H. Larsen, K. M. Schultz and E. M. Furst, Korea-Aust. Rheol. J., 2008, 20, 165–173 Search PubMed.
- K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, Soft Matter, 2009, 5, 740–742 RSC.
- K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, Macromolecules, 2009, 42, 5310–5316 CrossRef CAS.
- T. H. Larsen, M. C. Branco, K. Rajagopal, J. P. Schneider and E. M. Furst, Macromolecules, 2009, 42, 8443–8450 CrossRef CAS.
- D. Velegol and F. Lanni, Biophys. J., 2001, 81, 1786–1792 CrossRef CAS.
- A. Parekh and D. Velegol, Ann. Biomed. Eng., 2007, 35, 1231–1246 CrossRef.
- O. Latinovic, L. A. Hough and H. D. Ou-Yang, J. Biomech., 2010, 43, 500–505 CrossRef.
- A. S. B. Cucheval, R. R. Vincent, Y. Hemar, D. Otter and M. A. K. Williams, Langmuir, 2009, 25, 11827–11834 CrossRef CAS.
- F. Cardinaux, H. Bissig, P. Schurtenberger and F. Scheffold, Food Colloids: self-assembly and material science, RSC Publishing, 2007 Search PubMed.
- C. Heinemann, F. Cardinaux, F. Scheffold, P. Schurtenberger, F. Escher and B. Conde-Petit, Carbohydr. Polym., 2004, 55, 155–161 CrossRef CAS.
- C. Veerman, K. Rajagopal, C. S. Palla, D. J. Pochan, J. P. Schneider and E. M. Furst, Macromolecules, 2006, 39, 6608–6614 CrossRef CAS.
- R. P. Slopek, H. K. McKinley, C. L. Henderson and V. Breedveld, Polymer, 2006, 47, 2263–2268 CrossRef CAS.
- A. M. Corrigan and A. M. Donald, Langmuir, 2009, 25, 8599–8605 CrossRef CAS.
- A. M. Corrigan and A. M. Donald, Eur. Phys. J. E, 2009, 28, 457–462 CrossRef CAS.
- Y. Gao and M. L. Kilfoil, Phys. Rev. Lett., 2007, 99, 078301 CrossRef CAS.
- S. Romer, F. Scheffold and P. Schurtenberger, Phys. Rev. Lett., 2000, 85, 4980–4983 CrossRef CAS.
- Y. Tseng, K. M. An and D. Wirtz, J. Biol. Chem., 2002, 277, 18143–18150 CrossRef CAS.
- Y. Tseng and D. Wirtz, Biophys. J., 2001, 81, 1643–1656 CrossRef CAS.
- D. T. N. Chen, K. Chen, L. A. Hough, M. F. Islam and A. G. Yodh, Macromolecules, 2010, 43, 2048–2053 CrossRef CAS.
- D. Stauffer, A. Coniglio and M. Adam, Adv. Polym. Sci., 1982, 44, 103–158 CrossRef CAS.
- R. R. Vincent and M. A. K. Williams, Carbohydr. Res., 2009, 344, 1863–1871 CrossRef CAS.
- A. P. Nowak, V. Breedveld, L. Pakstis, B. Ozbas, D. J. Pine, D. Pochan and T. J. Deming, Nature, 2002, 417, 424–428 CrossRef CAS.
- V. Breedveld and D. J. Pine, J. Mater. Sci., 2003, 38, 4461–4470 CrossRef CAS.
- A. Goodman, Y. Tseng and D. Wirtz, J. Mol. Biol., 2002, 323, 199–215 CrossRef CAS.
- C. Xu, V. Breedveld and J. Kopecek, Biomacromolecules, 2005, 6, 1739–1749 CrossRef CAS.
- J. Sato and V. Breedveld, J. Rheol., 2006, 50, 1–19 CrossRef CAS.
- R. S. Tu and V. Breedveld, Phys. Rev. E, 2005, 72, 041914 CrossRef.
- C. J. Kloxin and J. H. van Zanten, Macromolecules, 2010, 43, 2084–2087 CrossRef CAS.
- K. Chung, J. K. Cho, E. S. Park, V. Breedveld and H. Lu, Anal. Chem., 2009, 81, 991–999 CrossRef CAS.
- R. C. Spero, L. Vicci, J. Cribb, D. Bober, V. Swaminathan, E. T. O'Brien, S. L. Rogers and R. Superfine, Rev. Sci. Instrum., 2008, 79, 083707 CrossRef.
- J. Krayer, S. Tatic-Lucic and S. Neti, Sens. Actuators, B, 2006, 118, 20–27 CrossRef.
- M. S. Amin, Y. Park, N. Lue, R. R. Dasari, K. Badizadegan, M. S. Feld and G. Popescu, Opt. Express, 2007, 15, 17001–17009 CrossRef CAS.
- P. J. Flory, J. Am. Chem. Soc., 1941, 63, 3083–3090 CrossRef CAS.
- P. J. Flory, J. Phys. Chem., 1942, 46, 132–140 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45–55 CrossRef CAS.
- K. N. Nordstrom, J. P. Gollub and D. J. Durian, Phys. Rev. E, 2011, 84, 021403 CrossRef CAS.
- K. M. Schultz and E. M. Furst, Lab Chip, 2011, 11, 3802–3809 RSC.
- K. M. Schultz, A. V. Bayles, A. D. Baldwin, K. L. Kiick and E. M. Furst, Biomacromolecules, 2011, 12, 4178–4182 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 1st edn, 2003 Search PubMed.
- I. Sriram, A. Meyer and E. M. Furst, Phys. Fluids, 2010, 22, 062003 CrossRef.
- I. Sriram and E. M. Furst, Soft Matter, 2012, 8, 3335–3341 RSC.
- R. H. Ewoldt, C. Clase, A. E. Hosoi and G. H. McKinley, Soft Matter, 2007, 3, 634–643 RSC.
- K. M. Schultz, A. D. Baldwin, K. L. Kiick and E. M. Furst, submitted, 2012 Search PubMed.
- S. R. Quake and A. Scherer, Science, 2000, 290, 1536–1540 CrossRef CAS.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163–4166 CrossRef CAS.
- G. M. Whitesides and A. D. Stroock, Phys. Today, 2001, 54, 42–48 CrossRef CAS.
- J. M. Ng, I. Gitlin, A. D. Stroock and G. M. Whitesides, Electrophoresis, 2002, 23, 3461–3473 CrossRef CAS.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–447 RSC.
- Z. T. Cygan, J. T. Cabral, K. T. Beers and E. J. Amis, Langmuir, 2005, 21, 3629–3634 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
