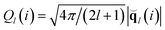Selection mechanism of polymorphs in the crystal nucleation of the Gaussian core model

Abstract

The principle of polymorph selection upon crystal nucleation is one of the fundamental problems in crystallization. Recently we found that for hard spheres the crystal polymorph is already selected by locally favoured packing symmetry in a metastable supercooled state. Here we study whether this scenario is also valid for soft spheres. To do so, we investigate the homogeneous nucleation process of the Gaussian core model (GCM) in supercooled states by means of Monte Carlo computer simulations. We use bond orientational order parameters, which characterize local packing symmetries, to follow the formation of solid nuclei and to distinguish between different polymorphs. We concentrate on two state points, at low and high pressure respectively, for which macroscopic thermodynamics dictates the formation of the different polymorphs (fcc and bcc crystals respectively). We show that the nucleation of the different crystalline structures does not follow Ostwald's step rule of crystallization, and that, despite the underlying phase diagram, the bcc phase is always favoured. In analogy to hard sphere systems, we find a new criterion for polymorph selection: crystallization occurs in precursor regions of high bond orientational order, and the crystal which first nucleates is the one that has the closest symmetry to these ordered regions in the supercooled state.

---

1 Introduction

The freezing transition in particle systems is ultimately promoted by the interparticle repulsion which acts when particles approach each other. Indeed, the diverging repulsive interaction at close separations between the particles, i.e., the resulting excluded volume effect, is often a dominant factor driving crystallization. It is known that the crystal structure into which a system freezes depends on the steepness of the repulsion, with hard repulsions favouring a face-centred cubic (fcc) lattice and soft ones a body-centred cubic (bcc) lattice. However, the underlying mechanism of the kinetic selection of such crystal polymorphs remains elusive.

Nucleation is usually described within classical nucleation theory (CNT) which assumes that, upon cooling, the formation of the stable solid phase is initiated by the nucleation of solid clusters. Such clusters continuously form and dissolve in the supercooled melt, until a nuclei reaches the critical size for which the free energy gain for volume growth overcomes the free energy penalty for surface formation. The phase which is first nucleated is not necessarily the most stable solid phase though. Different criteria have been proposed to explain the complex nucleation pathways which even simple liquids undergo upon crystallization.^1–3 The first and still most credited polymorph selection criterion is Ostwald's step rule⁴ which states that the nucleus formed from the melt is in the phase closest in free energy to the metastable liquid phase. A different criteria was provided by Alexander and McTague⁵ who noted that the Landau-Ginzburg free energy indicated a particular crystalline form independently of the details of the potential (but for monoatomic spherically symmetric fluids only): in two dimensions the crystalline phase would have a triangular or hexagonal structure, while in three dimensions the preferred structure would be the bcc lattice.

Most studies have concentrated on model systems with hard divergent repulsions at short distance. The simplest one is the well known hard sphere (HS) model, where a fluid-to-crystal transition was found more than 50 years ago in pioneering computer simulations by Wood & Jacobson⁶ and Alder & Wainwright,⁷ and experimentally by Pusey & Van Megen.⁸ At odds with the Alexander and McTague prediction, different studies have failed to detect any significant nucleation of the bcc phase,^9,10 while detecting random stacking of fcc and hcp, with a clear preference for the former.^9–16 Another popular model system is the Lennard-Jones (LJ) fluid, where a precursor bcc phase forms for small nuclei which then transforms into the most favourable fcc phase.^17–19

So far the crystallization process has been explained by using a key order parameter, which is the density field ρ(r). For example, the Alexander–McTague theory is based on the expansion of the free energy in terms of density fluctuations. Contrary to this one-order-parameter scenario, we recently proposed that the scalar density field may not be enough to describe crystallization, and we need an additional order parameter, a bond orientational order parameter, which plays a crucial role in the selection of crystal polymorphs.^16,20,21 This scenario is closely linked to development of bond orientational order, whose symmetry is consistent with the equilibrium crystal symmetry, in a supercooled liquid state of glass-forming systems, suggesting an intimate link between glass transition and crystallization, both of which are governed by the same free energy.^21,22 We found that for hard spheres crystal polymorphs are already selected by bond orientational order developed in a metastable state.¹⁶ For the hard-sphere case, bond orientational order is a consequence of the excluded volume effect and the resulting selection of local packing symmetry under the constraint of dense packing. Thus, it is interesting to consider how the softness of the interaction potential affects the selection of local packing symmetry (i.e., the preferred type of bond orientational order) in the metastable supercooled state and eventually the selection of crystal polymorphs.

Soft materials are often characterized by weak effective repulsions which can be tailored through the control of solvent properties, and the existence of a thermodynamically stable solid does not require a singular repulsion for vanishing interatomic separations. An example is offered by the effective interaction between self-avoiding polymers dispersed in an athermal solvent, where the repulsion is finite even when the centers of mass of the polymers overlap.²³ Similar softening of the interaction potential can be seen for many soft particles such as star polymers, polyelectrolyte stars, microgels, hairy particles, and dendrimers.^24–26 While hard divergent potentials favour the nucleation of compact crystals (such as hcp and fcc), soft bounded potentials allow the formation of open crystal structures (like the bcc or simple cubic phases).^24–26 This is because soft particles interacting with the soft bounded potential can explore configurations that are forbidden to hard-sphere systems due to their deformability and interpenetrability.

In the present study we address the homogeneous nucleation in the Gaussian core model (GCM), a soft bounded potential which consists of the pairwise sum of additive Gaussian components, first introduced by Stillinger.²⁷ The GCM is a good model for the effective interaction between the centers of mass of polymers dispersed in a good solvent. The bounded repulsion originates from a loss in configurational entropy due to steric hindrances of the chains as they approach each other. Because the pair potential between GCM particles is bounded, it cannot maintain a crystalline order at high enough pressures, causing a reentrant melting of the solid phase at high densities. As was demonstrated by Stillinger,²⁷ the GCM reduces to the HS model for low enough temperatures and densities, where in fact crystallizes in the fcc phase. At high densities, on the other hand, the model behaves like a weakly correlated “mean field fluid”, due to the large number of neighbours a particle can interact with.^23,28 The GCM can thus be considered as a model which interpolates continuously between the HS fluid, at low pressures and densities, and a mean-field fluid, at high pressures and densities.

It is known that some systems of soft-repulsive potentials such as the penetrable sphere model²⁹ show freezing at any arbitrary temperature to clustered crystals (multiple occupation of lattice sites).^24–26 Thus, the shape of the pair potential determines whether the system exhibits the reentrant melting or cluster crystallization behaviour. Likos et al. showed that the reentrant melting should occur for bounded repulsive potential with a positive definite Fourier transform.³⁰ Since the bounded potential of the GCM has the positive definite Fourier transform, there is only reentrant melting behaviour without clustering. This provides us with an ideal opportunity to study the effect of the softness on crystallization without further complications.

The homogeneous nucleation in the GCM has been recently examined by Lechner et al.^31,32 They showed that the description of the transition is enhanced by taking into account the prestructured particles surrounding the crystalline nucleus. This finding extends to soft potentials what was observed in previous studies of the precursor regions of high bond orientational order in the HS model.²¹ Recently, both experiments^33–35 and simulations^21,31,36 have started to point out deviations from the classical picture of crystallization, suggesting a possible two-step scenario:^21,36,37 crystal nuclei are not formed spontaneously in one step from random fluctuations, but they appear inside preordered precursor regions.

Here we will take advantage of the GCM phase diagram to study the effect of locally favoured packing symmetry on the pathway for crystal nucleation. We will show that Ostwald's step rule cannot account for the observed nucleation pathway observed in our simulations. We will then focus on the precursor regions which trigger the liquid-to-solid transition and show that the selection of the polymorph starts already in the metastable liquid phase.

The organization of this paper is as follows. In Section 2 we describe the simulation methods employed in our study, which comprise free energy calculations and crystal identification through spherical harmonics analysis. Results are presented in Section 3. We discuss our results in Section 4 and we conclude in Section 5.

2 Methods

The Gaussian core model (GCM) is defined by the following pair-wise repulsive potentialwhere r is the pair distance, and ε and σ define respectively the energy and length scales. In the following we adopt natural units, defined such that ε = 1 and σ = 1. We also set the Boltzmann constant to unity, k_B = 1.

The phase diagram of the GCM, reproduced in Fig. 1, has been accurately determined by numerical simulations,^27,38–41 showing the following peculiar properties:

Fig. 1 Phase diagram of the GCM in the P–T plane, reproduced from data in ref. 39. Two solid phases are thermodynamically stable: fcc at low pressures and a reentrant bcc phase at higher pressures. The state points examined in the present work are marked with crosses; in order of increasing P: (P = 0.01,T = 0.00262) in the fcc stability region; and (P = 0.05,T = 0.00520) and (P = 1.00,T = 0.00180) in the bcc stability region.

• Existence of a maximum melting temperature (T^max_m), above which a fluid phase is stable at all densities.

• Reentrant melting, where the solid phase liquefies upon compression.

• A stable bcc crystal, except at low temperatures and densities where fcc becomes favourable.

The presence of a maximum melting temperature is one of the striking features of systems of particles with a bounded repulsive interaction.^24–26 At high temperature and/or pressure the core is unable to give rise to the excluded volume effects responsible for crystallization, and thus the stable phase is the liquid. Furthermore, the GCM shows a solid–solid phase transition from the fcc to the bcc structure, where the fcc phase is stable at low temperature and pressure. In fact, at such conditions the repulsion is strong enough to avoid penetration and the fcc structure is favoured, whereas at high pressure the core is more easily penetrable and the bcc phase becomes the stable one.

Starting from a state point where the fcc phase is favoured, the stability of the bcc can be increased by simply compressing the system. We study different state points: (i) (P = 0.01,T = 0.00262), (ii) (P = 0.05,T = 0.00520), (iii) (P = 1.00,T = 0.00180). The first point is located in the region of stability of the fcc phase, while the others in the region of stability of the bcc phase. In the following we will indicate the different state points just by their pressure. We follow the crystallization process in a system of N = 4000 particles by placing the particles randomly in the simulation box and running NPT Monte Carlo simulations. At state points P = 0.01 and P = 0.05 the liquid is metastable with respect to crystallization, and typical simulation trajectories attain a long metastable state before eventually the nucleation of a crystal exceeding the critical size occurs. The cutoff in the interaction range is set to r_c = 3.7 (as always here, in units of σ), and standard cutoff corrections are accounted for in the calculation of the interaction energy, pressure and chemical potential.

To identify crystal particles we use the local bond-order analysis introduced by Steinhardt et al.,⁴² first applied to study nucleation by Frenkel and co-workers.⁴³ First a (2l + l) dimensional complex vector (q_l) is defined for each particle i as . l is a free integer parameter, and m is an integer that runs from m = −l to m = l. The functions Y_lm are the spherical harmonics and r̂_ij is the vector from particle i to particle j. The sum goes over all neighbouring particles N_b(i) of particle i. Instead of defining the neighbours as all the particles within a cutoff distance (as is usually done in the literature), we instead fix N_b(i) = 12 (the number of nearest neighbours in the perfect hcp and fcc crystals), considering only the 12 closest particles to particle i. The bcc crystal has instead only 8 particles in the first coordination shell, but we have checked that the inclusion of additional 4 particles does not have any quantitative effects on our results. Particle i is then defined as solid if it has at least n_c = 9 connected neighbours (j = 1…9), defined as all neighbouring particles j for which q̂₆(i)·q̂₆(j) > 0.6, where q̂_l = q_l/|q_l|, and . To assert the structural identity of each crystal particle, we improve the averaged bond order parameters introduced by Lechner and Dellago.⁴⁴ We define the quantities q̆_l(i)

where, differently from the definition in ref. 44, the sum from k = 0 to N̆_b(i) runs over all neighbours of the same phase (liquid or solid) of particle i plus the particle i itself. Avoiding the spatial average over particles of different phases allows a more precise study of the particles at the interface between solid and liquid, without biasing the order parameter values of the liquid particles due to the average over solid ones. This choice results in a better separation along the Q₆ axis of liquid and crystal particles (already identified by their number of connected neighbours), as we will show in Fig. 6.

Given the definition of eqn (2), one can construct the rotationally invariant quantities

and
where the term in parentheses is the Wigner 3 − j symbol (which is different from zero only when m₁ + m₂ + m₃ = 0).

To identify the crystal polymorphs, thus, we take advantage of the different symmetries that the crystals have on the W₆ and W₄ axis. The bcc structure is in fact characterized by a positive W₆ distribution while hcp and fcc both have negative W₆ but differ respectively for their positive and negative values of W₄. We adopt the following criterion for crystal classification: first crystal particles are identified as by having at least n_c = 9 connected neighbours. Then, we identify (i) bcc particles as all crystal particles with W₆ > 0; (ii) hcp particles as all crystal particles with W₆ < 0 and W₄ > 0; (iii) fcc particles as all crystal particles with W₆ < 0 and W₄ < 0.

We extract the information on the size of the critical nucleus, the Zeldovich factor and the nucleation rate by means of the mean first-passage time formalism.⁴⁵ The average time it takes the biggest nucleus to reach a given size n for the first time is given by the following expression

where n^* is the critical size of the nucleus, J is the nucleation rate, V the volume and c is linked to the Zeldovich factor Z ().

To compare the relative stability of the different phases we have performed free-energy calculations for the crystal and liquid phases at state points P = 0.01 and P = 0.05. The free energy of the liquid phase is calculated by thermodynamic integration along a path from the ideal gas to the state point of interest. The free energy of the different crystal phases is instead calculated with the Einstein crystal method, which is based on thermodynamic integration from an harmonic crystal (whose free energy can be exactly calculated) to the crystal of interest. The values of the elastic constants for the harmonic crystals were chosen so that the mean square displacement of the Einstein solid approximately matches the mean square displacement of a GCM particle from its reference lattice site. The thermodynamic integrations were conducted with 20 points Gauss–Legendre quadratures. For the details of the calculations we refer to the original literature^46–48 and to ref. 39,40 for a complete account on how to conduct free energy calculations for the Gaussian core model.

3 Results

We first present the results of the free energy calculations in Table 1. In agreement with previous numerical simulations,⁴⁰ we confirm that for low pressures (P = 0.01) the fcc crystal is the phase with the lowest free energy, with the free energy of the hcp phase being very close. At higher pressure (P = 0.05), on the other hand, the bcc crystal becomes the dominant phase, with fcc and hcp having higher free energies. Note that the supersaturation, i.e., the difference between the chemical potentials of the fluid phase and the stable crystal phase (βΔμ = βΔf + βΔP/ρ), is approximately the same for both state points, βΔμ ≅ 0.36. According to these results, Ostwald's step rule predicts a different nucleation pathway for the two state points. In particular we should expect the nucleation of the bcc phase in the fcc stable region for P = 0.01, and vice versa for P = 0.05. In the following we will show that this does not happen and that the two state points show very similar nucleation pathways, with the amount of bcc gradually increasing as the pressure is increased.

Table 1 Excess Helmholtz free energy per particle (β = 1/k_BT), for the bcc, fcc and hcp crystals and for the metastable fluid phase at the state points considered in the text. The simulations of the Einstein crystal were conducted in the NVT ensemble with N = 1372 for the fcc and hcp crystals, and with N = 1458 for the bcc crystal. The error is less than the last reported digit

ρ	T	βf ^ex bcc	βf ^ex fcc	βf ^ex hcp	βf ^ex fluid
0.1050	0.00262	14.825	14.789	14.792	15.149
0.1704	0.00520	26.096	26.148	26.155	26.460

---

We note that the same ordering of the crystals with respect to the free energy is obtained by looking at their equilibrium densities. For P = 0.01 we have ρ_bcc = 0.10654, ρ_hcp = 0.10664 and ρ_fcc = 0.10664. For P = 0.05 we have ρ_bcc = 0.17138, ρ_hcp = 0.17117 and ρ_fcc = 0.17119.

We start by generating many nucleating MC trajectories, as described in the Methods section. The total number of trajectories generated was (i) 340 trajectories for P = 0.01, of which 223 crystallized; (ii) 393 for P = 0.05, of which 204 crystallized. A fit of mean first-passage times to eqn (3) allows us to estimate the size of the critical cluster size in a ≃ 52 particles for both state points. Since the degree of supersaturation, βΔμ, is approximately the same for both state points (Table 1), the equivalence of the critical nucleus size implies also the equivalence of the free energy barrier, βΔf^*, between the fluid and the stable crystal at the two state points. In fact, according to classical nucleation theory, βΔf^* = βΔμa^1/3/2 ≅ 9.4 (in units of k_BT) for both state points. From classical nucleation theory and the knowledge of the critical nucleus size, a, and the thermodynamic driving force, Δμ, it is also possible to extract the value of the interfacial tension, γ = ρ|Δμ|R/2, where R is the critical nucleus radius and is related to a as a = ρ(4πR³/3). For the state points reported in Table 1 we have γ_P = 0.01 = 2.4 × 10⁻⁴ and γ_P = 0.05 = 6.7 × 10⁻⁴. Nucleation rates estimated from mean first-passage analysis are J_P = 0.01 = 2.7 × 10⁻¹¹ and J_P = 0.05 = 3.3 × 10⁻¹¹. Since the thermodynamic driving force is the same for both state points, this difference must come from a difference in the dynamics at the two temperatures, obviously slowing down at the lower temperature.

In Fig. 2 we present the fraction of crystal particles as a function of time during a typical trajectory (at P = 0.05, but the same holds also for P = 0.01). It shows that at the chosen state points the system attains a steady-state metastable stage, in which many subcritical nuclei form and dissolve, followed by a crystallization stage, where eventually one of these nuclei reaches the critical size, growing until the whole system crystallizes (we have checked that, despite the low free energy barrier, the crystallization process originates from one critical nucleus and not by many). During the metastable stage the system is in a steady-state condition, which is due to fluctuations around relative minima of the free-energy surface, and where all thermodynamic control parameters (pressure and temperature) are at equilibrium. The transition to the crystalline state occurs through thermal fluctuations (nucleation events), which are rare enough to allow us to access the metastable state in equilibrium.

Fig. 2 Fraction of crystal particles in a typical MC run for the state point P = 0.05. Trajectory is divided between a metastable stage and a crystallization stage. The inset shows the self intermediate scattering function for both P = 0.05 (circles) and P = 0.01 (squares) state points. The lines are fits to a stretched exponential decay, used to obtain the structural relaxation time in the metastable state. The two snapshots show the evolution of the largest crystal nucleus along the crystallization stage, for sizes just before (left) and after (right) the critical nucleus size. In this example the nucleus is predominantly bcc (blue) and fcc (red), while hcp (green) is almost absent.

To check that indeed the metastable state is in steady-state equilibrium, the inset of Fig. 2 displays the self intermediate scattering function for both state points

where the sum runs over all N = 4000 particles, q is the wave vector, r_i(t) is the position of particle i at time t, and q^max is the modulus of the wave vector which corresponds to the first peak in the structure factor. The lines in the inset of Fig. 2 show that the decay of F_s(q^max,t) is well described by a stretched exponential relation F_s(q^max,t) = exp(−(t/τ)^β) with the following fitting parameters: i) P = 0.01: τ = 332, β = 0.43; ii) P = 0.05: τ = 544, β = 0.48. The parameter τ (which corresponds to the structural relaxation time) is thus, in both cases, several orders of magnitude shorter than the typical length of the metastable trajectories.

A typical nucleation and growth event is shown in Fig. 3 for P = 0.01 (a,b) and P = 0.05 (c,d). Crystal particles are depicted as big spheres, while small spheres denote liquid particles having high bond orientational order (Q > 0.28). The figure shows the development of medium-range bond orientational order in the metastable fluid, and the birth of crystal nuclei occurring inside regions of high Q₆. Typically, within the growing cluster, the different phases are grouped and grow separately. At high pressure, the bcc phase occupies the core of the nucleus (Fig. 3c), with fcc particles forming patches attached to this core (Fig. 3d). At low pressure instead the core of the nucleus can be either fcc (Fig. 3a) or bcc. We speculate that, at pressures lower than the ones considered in this work, the nuclei will predominantly have an fcc core. To study this process in detail, we will now concentrate on the crystallization stage and on the metastable stage separately. From the crystallization stage we extract the average composition of crystallizing nuclei, unveiling the nucleation pathway. We will then try to explain these results based on the liquid properties of the metastable melt. In other words we try to establish a link between the liquid properties and the subsequent nucleation of the solid phase. Such a link is possible since we will show that nucleation most likely occurs in regions of the liquid with high bond orientational order (high Q₆).

Fig. 3 Snapshots of a nucleation and growth event for P = 0.01 (a,b) and P = 0.05 (c,d). Particles are depicted with two different sizes: small spheres are liquid particles with Q₆ > 0.28, while big spheres are crystalline particles in the bcc (blue), hcp (green) or fcc (red) phases. Note that in (a) the nucleation event starts from a fcc core, while in (c) it starts from a bcc core.

3.1 Crystallization stage

Fig. 2 also shows snapshots of the growing critical nucleus for the state point P = 0.05, where it is already evident that nucleation mostly occurs in either the fcc phase (red particles) or, predominantly, in the bcc phase (blue particles). To study in detail the crystallization process we apply the bond orientational analysis described in the Methods section to all crystallizing trajectories. This allows us to study the composition of each solid nucleus as a function of its size. Fig. 4a displays the average number of particles (n̄) for the bcc, hcp and fcc polymorphs, as a function of the total crystal size. For both state points the bcc phase is the dominant phase, at odds with the predictions of Ostwald's step rule. Contrary to Ostawald's step rule, even for small clusters the fraction of bcc particles is higher at P = 0.05 than P = 0.01, while the fraction of fcc and hcp particles is higher at P = 0.01 than P = 0.05. Fig. 4b and 4c report the average fractional composition of nuclei as a function of the nucleus size for the P = 0.01 and P = 0.05 state points respectively. In both cases the fraction of bcc increases as the crystal nucleus gets bigger, but the increase is faster for P = 0.05, where indeed bcc is the thermodynamic stable phase. Particles in the fcc phase account for ∼40% of the solid particles in the small nuclei. But while for P = 0.05 this fraction decreases as the nuclei become bigger, for P = 0.01 the fraction remains constant. The hcp phase plays only a minor role for both state points, accounting for ∼20% of solid particles in small nuclei, with this fraction steadily decreasing as the nuclei become bigger.

Fig. 4 Relation between cluster size and polymorphs. (a) Average number of particles (n̄) for bcc (circles), hcp (diamonds) and fcc (squares) polymorphs as a function of the total crystal size (n). The value of n̄(n) is obtained by averaging the number of particles for each polymorph in a cluster of size n. Full symbols are from simulations at P = 0.05, open symbols from simulations at P = 0.01. (b) Fraction of particles (f̄ = n̄/n) in a given crystalline state as a function of the total crystal size (n) for P = 0.01. (c) Same as (b) but for P = 0.05. In all panels the vertical dashed line denotes the size of the critical nucleus obtained from the mean-passage time analysis.

We also show that the composition of the nuclei changes between the nucleation regime and the growth regime. The vertical dashed line in Fig. 4 indicates the size of the critical nucleus (n_c) obtained from the mean-first passage time analysis (see eqn (3)). For both pressures P = 0.01 (panel b) and P = 0.05 (panel c) the composition of the nucleus for n < n_c is approximately constant, in other words, all polymorphs grow with a constant growth rate. For n > n_c instead the composition of the nuclei depends on the size n. This is most easily seen for pressure P = 0.05 (Fig. 4c) where the fraction of the bcc polymorph steadily increases, at the expenses of both the fcc and hcp phases. This behaviour may partly be understood as follows. In the nucleation regime, crystals repeatedly appear, grow and melt as fluctuations in the multi-dimensional space of density and bond orientational order parameters, and thus the fraction of polymorphs is a reflection of the distribution of the bond order parameters. In particular we will show that the fractional composition of subcritical nuclei can be predicted from the knowledge of the liquid distribution at high Q₆ (see Section 3.2 and Fig. 5, 8 and 9). In the growth regime, on the other hand, the free energy difference between polymorphs and their interfacial tension come into play, promoting the growth of the polymorph most favoured from this respect. A deeper understanding of the growth regime, would need simulations for a bigger number of particles, which are necessary to avoid finite-size effects and artifacts from the periodic boundary conditions.

Fig. 5 Probability distribution in the W₆–Q₆ plane with Q₆ > 0.30 at (a) P = 0.01 and (b) P = 1.00 during the metastable stage. Each panel contains both the surface plot (top) and contour lines (bottom). The liquid and crystal populations are clearly distinguishable at low and high regions of Q₆ respectively. As the pressure is increased, the crystal distribution displays a more pronounced peak at positive values of W₆ which indicates the predominant nucleation of the bcc polymorph.

Fig. 4 has shown that, despite bcc being the dominant phase, the fraction of fcc particles increases with decreasing pressure, possibly becoming the majority phase at low enough pressures. fcc is also favoured over hcp, despite their very small free energy difference (Table 1). We will try to explain these results by examining the metastable trajectories, before the critical nucleus appears.

3.2 Metastable stage

Fig. 5 compares the probability distribution in the W₆–Q₆ plane for particles with high values of Q₆ (Q₆ > 0.30) for the metastable stage at P = 0.01 and P = 1.0 respectively. For both pressures two distinct populations are distinguishable, which correspond to liquid and crystal particles. The use of the order parameters defined in Section 2 is thus very effective in the identification of crystal particles. The main difference between the two pressures is the development at high pressure of a pronounced peak at positive values of W₆ in the crystal population, where the bcc phase is located. This is in agreement with the results obtained during the crystallization stage (Fig. 4), that the tendency towards bcc growth is enhanced at high pressures. It is also clear that the distribution of liquid particles with Q₆ > 0.30 at high pressure (see Fig. 5b) is also shifted to positive values of W₆ with respect to the corresponding liquid distribution at low pressure (see Fig. 5a). In other words, liquid particles of high Q₆ display the same symmetry (positive W₆) of the corresponding crystal phase.

To better analyse the properties of both the liquid and crystal particles, we study the projections of the full probability distribution of the metastable stage onto different axes. Fig. 6 shows the projection on the bond orientational order parameter Q₆ for both solid particles and fluid particles at P = 0.01, P = 0.05 and P = 1.0 in the metastable supercooled state before nucleation takes place. The distributions at all state points display only a minimal overlap, with solid particles having higher Q₆ than liquid particles. By monitoring the trajectories of liquid particles transforming into solids, we see that these come from regions of the liquid with high Q₆. Q₆ is thus a good order parameter to follow the liquid-to-crystal transition.

Fig. 6 Q ₆ probability distribution for particles at P = 0.01, P = 0.05 and P = 1.0 in the metastable supercooled state, with fluid and crystal particles plotted separately. For all the chosen state points, Q₆ is a good order parameter to distinguish between fluid and crystal particles.

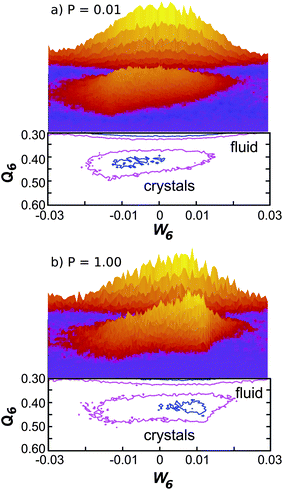
By combining the identification of solid particles, described in Methods, with Voronoi diagrams,⁴⁹ we obtain the local density distribution for each specie in the metastable state, as reported in Fig. 7. The figure shows the density histogram for liquid (dashed line) and solid particles (continuous line). The two distributions have a large overlap, with the average density for the two species differing by less than 0.1%. The extremely small density difference between the liquid and solid phases was already noted by Stillinger,²⁷ who predicted that the density difference goes to zero at the maximum melting temperature, T^max_m. By calculating the average densities of the liquid and solid phase we see that the small precritical nuclei form at the same density as that of the bulk crystals. This is very different from the behaviour in HS simulations,¹⁶ where nucleation is shown to occur at densities much smaller than the bulk crystal densities. This is confirmed in the inset of Fig. 7, which shows the average density of solid particles (continuous line) as a function of the nucleus size. While hard spheres show an increase of crystal density with increasing size,¹⁶ in the GCM the density is constant at all crystal size and equal to the bulk value.

Fig. 7 Density probability distribution for particles in both P = 0.01 and P = 0.05 state points in the metastable supercooled state. The continuous and dashed line are the density histogram for solid and liquid particles respectively. The circles represent the density histogram for liquid particles fulfilling the condition Q₆ > 0.3, proving that liquid particles with high Q₆ have the same density distribution as solid particles. The inset shows the average density of liquid (dashed line) and solid (continuous line) as a function of the size of largest cluster in the system during the nucleation stage. The local density of each particle is determined via Voronoi-diagrams, and the average over solid particles includes the surface particles.

Circles in Fig. 7 display the density histogram for liquid particles having a value of Q₆ higher than 0.3, showing that it coincides with the density histogram of the solid particles. High Q₆ regions are the regions in the fluid phase where crystallization is more likely to occur, so we can conclude that the fluid-to-crystal transition occurs microscopically without any density change. The same conclusion was found to hold for a system of hard spheres.¹⁶ As shown in the inset of Fig. 7, the average density of the system exhibits a small jump at the fluid-to-solid transition, but this is due to the fact that the liquid phase comprises also regions of small Q₆ which on average are less dense. So according to the two-step process scenario of crystal nucleation we can conclude that macroscopically the transition appears to involve a density discontinuity, but microscopically the density is a continuous parameter. The fluid-to-solid transition instead involves a finite jump of the bond orientational order (Q₆) which is a manifestation of the increase of the coherency between neighbours in the solid phase (for a detailed discussion on the behaviour of the density and bond orientational order parameters in the liquid-to-solid transition we refer to ref. 16).

As discussed in the Methods section, we remind that the different crystal environments can be characterized by their different symmetries on the W₄–W₆ plane.¹⁶ bcc is characterized by having a positive W₆, while both fcc and hcp are characterized by a negative value of W₆ and, respectively, by negative and positive values of W₄. We exploit these symmetries in the metastable liquid phase, by considering only particles which are identified as liquid particles.

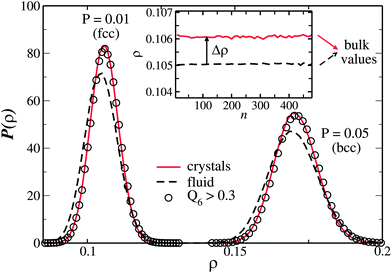
Fig. 8 displays the probability distribution for the order parameter W₄ for liquid particles having negative values of W₆ for P = 0.01 (an analogous result can be obtained for P = 0.05). In this way negative values of W₄ correspond to an fcc-like environment, and positive values of W₄ to an hcp-like environment. The distributions are plotted for different regions in the liquid phase, each characterized by a value of Q₆ higher than a fixed threshold Q^thr₆. Fig. 8 then clearly shows that, while liquid particles with a low value of Q₆ are symmetrically distributed (showing no preference between fcc and hcp-like environments), as the value of Q₆ increases the distribution becomes more and more peaked towards negative values of W₄. This indicates that the regions of the liquid with a high bond orientational order show a clear preference for the fcc-like symmetry over the hcp one. We suggest that this is the reason why, when the solid nucleates from the liquid, it does much more in the fcc crystal than the hcp crystal, despite their very small free energy difference (Table 1). The inset of Fig. 8 shows the W₄ probability distributions at Q^thr₆ = 0.30 for pressures P = 0.01, P = 0.05 and P = 1.0. As the pressure increases the distribution becomes more symmetrical, indicating an increase of the hcp over fcc fraction for higher pressures. Since we did not follow nucleation events for the highest pressure, P = 1.0, it would be interesting verifying this prediction.

Fig. 8 W ₄ probability distribution at P = 0.01 for liquid particles having W₆ < 0 and Q₆ higher than a fixed threshold Q^thr₆. The threshold values plotted are Q₆ > 0.25,0.27,0.29,0.30,0.31,0.32, and the order is given by the arrow. The inset shows the W₄ probability distribution at Q^thr₆ = 0.30 for pressures P = 0.01, P = 0.05 and P = 1.0 (the order is given by the arrow). The P = 1.0 is affected by more noise due to having fewer runs with respect to the low pressure simulations.

By looking at histograms of the order parameter W₆, a similar argument can be used to explain the increase of bcc crystallization as the pressure is increased. Fig. 9 shows the probability histogram for the order parameter W₆ for high Q₆ regions (Q₆ > 0.3) for the state points at P = 0.01, P = 0.05 and P = 1.00. As the pressure is increased the distributions move towards more positive values of W₆ which corresponds to the bcc-symmetry, thus explaining the preference for this phase during the initial stages of nucleation. For P = 0.01 the peak of the distribution has a negative W₆ value, and this is reflected in the fraction of fcc and hcp particles in small nuclei being higher than particles in the bcc phase, as reported in Fig. 4b. As we increase the pressure, the peak goes towards positive values of W₆ and consequently bcc particles become the dominant phase for small nuclei (Fig. 4c and Fig. 5b).

Fig. 9 W ₆ probability distribution for liquid particles having Q₆ > 0.3. Simulations at P = 0.01, 0.05, 1.00 are represented as open squares, circles and diamonds respectively. Lines are guide to the eye. The arrow indicates the direction of increasing pressure.

4 Discussion

Unlike rigid potentials which favour the nucleation of compact phases, in the GCM the liquid phase can coexist with two different crystal structures, the fcc and bcc polymorphs, depending on pressure. The GCM offers thus the possibility to study the effect of the metastable crystal phases on the pathway for crystal nucleation. The role of these metastable pathways was first formulated by Ostwald in 1897, who stated that the crystal phase that is nucleated from the melt is the closest in free energy to the fluid phase.

In our case, if Ostwald's step rule applied strictly we should expect the following pathways based on the free energy calculations reported in Table 1,

P = 0.01: bcc → hcp → fcc

P = 0.05: hcp → fcc → bcc

But, as was shown in Fig. 4, this does not happen. The bcc phase is always the most abundant, especially when we increase the pressure in the system. On the other hand the fraction of fcc particles increases with decreasing pressure. Both these behaviours are the opposite of what is expected from Ostwald's step rule. Furthermore we cannot invoke the bulk phase diagram to explain the results of Fig. 4, as we should expect the fcc phase to be dominant at P = 0.01, where also the hcp phase should be more stable than the bcc phase.

Instead we propose that polymorph selection starts already in the metastable supercooled state. Within the melt, the regions of high bond orientational order (Q₆) display density fluctuations indistinguishable from the solid particles (Fig. 7) while being characterized by a lower bond orientational order (Fig. 6). These regions of high bond orientational order are prestructured, displaying a symmetry which favours the nucleation of the bcc phase at high pressures (Fig. 9), and favours the formation of fcc over hcp (Fig. 8) at low pressures. As we have shown in Section 3, this mechanism accounts for the fractional composition for nuclei smaller than the critical size.

This scenario based on bond orientational ordering in the metastable supercooled liquid well explains the trend that bcc becomes more and more dominant with an increase in pressure, but cannot explain the slightly higher probability of bcc over fcc at P = 0.01 in a simple manner. The relative composition of the nuclei during the growth stage should basically be determined by the difference, with respect to the metastable fluid phase, of both the thermodynamic driving force (chemical potential) and the surface tension of the different polymorphs. From this standpoint, here we consider, besides bond orientational ordering, three other physical factors determining the nucleation barrier: (i) the density difference between the liquid and the crystal nuclei, (ii) the free energy difference between solid and liquid in the nucleation stage, and (iii) the roles of density fluctuations in the supercooled liquid state. On factor (i), we note that in principle the liquid–crystal interface energy is a function of the spatial gradient of not only the bond orientational order but also the density field. The symmetry matching between high Q₆ regions in the supercooled liquid with crystal nuclei certainly reduces the interfacial energy cost. However, we need to consider the density difference across the interface as well. It looks as if the slightly larger liquid–solid density difference for fcc than bcc were responsible for the slight dominance of bcc over fcc at P = 0.01. However, we should note that the local density of liquid regions from which crystal nuclei are formed is higher than the average liquid density. The density of crystal nuclei can be also different from that of bulk crystal. We indeed see that there is essentially little density difference between crystal nuclei and the liquid around them. This suggests that factor (i) may not explain the observed behaviour. On factor (ii), we should note that the free energies of crystal nuclei and liquid are not necessarily the same as those of bulk crystal and liquid, respectively. Furthermore, it is also difficult to distinguish between the interfacial region and the bulk region for the critical crystal nucleus, whose size is so small. Nevertheless, it is expected that the free energy difference is larger for fcc and liquid than for bcc and liquid, and thus it is unlikely that factor (ii) is relevant to the observed behaviour. However, there still remains a possibility that the slightly larger degree of supercooling for bcc than for fcc (see Fig. 1) may increase the nucleation probability of bcc. On factor (iii), there is a possibility that the mechanism proposed by Alexander and McTague⁵ helps the higher probability of the formation of bcc over fcc. This theory shows that the most probable type of density fluctuations has bcc symmetry. For hard spheres, bcc symmetry is not consistent with any of locally favoured packing symmetry, which are fcc, hcp, and icosahedral (ico) structure. Thus, this scenario does not work for HS.¹⁶ For the GCM, on the other hand, bcc is one of the locally favoured packing symmetry and thus this scenario may promote the nucleation of bcc crystals. Although this is a possible scenario, we cannot draw a definite conclusion partly because the differences in the nucleation probability and also in the W₆ between bcc and fcc are rather subtle. This problem will be a subject for future study.

Next we consider how the softness of the interaction potential affects the selection of local packing symmetry, i.e., bond orientational order. For hard spheres, the natural number of nearest neighbours around a particle is 12 under the constraint of dense packing. So the possible candidates of local packing symmetries are fcc, hcp and icosahedral structure (ico). This is the consequence of the characteristics of hard spheres that particles strictly feel only its neighbours: the excluded volume effect. With an increase in softness, particles can feel more distant particles (not only its nearest neighbours, but also the second, third, ⋯ neighbours). For the Gaussian core model, for example, the candidates are not limited to these three symmetries, but include bcc, in which a particle has only 8 nearest neighbours. For the Hertzian model, even more different local symmetries are allowed.⁵⁰ This is the fundamental difference between hard and soft sphere systems. We stress that for hard spheres such local bond orientational ordering is driven purely by entropy that is associated with the degree of freedom of the centers of mass of particles. The system tends to gain the correlational entropy and lower the local free energy. The increase in the softness of the potential weakens the geometrical constraint on the local symmetry selection of the centers of mass configuration under dense packing and increases the significance of elastic (or energetic) contributions. As discussed above, there are three mechanisms which select local configurational symmetry: one is the selection due to the excluded volume effect, which is relevant for HS, the second is the elastic energy, and the third is the selection due to density fluctuations, which is known as the Alexander–McTague scenario. The relative importance of these three factors may be changed by the softness of the interaction potentials. Although we cannot make a definite statement, we have some evidence that the fluctuations of the bond orientational order parameters such as Q₆, W₆, and W₄ are more suppressed with an increase in pressure. This is a consequence of that elastic contributions become more important and the excluded volume effects become less significant with an increase in pressure. This suppression of the fluctuations makes a supercooled liquid more homogeneous and increases the barrier for crystal nucleation. This is consistent with the enhancement of the mean-field nature of a liquid for higher pressures.^23,28 On the tendency that bcc is more favoured than fcc at higher pressure, it is important to recognize that the same free energy dominates crystal and liquid and thus the same bond orientational orders should basically be favoured between crystal and liquid.

Finally, we note that the role of the prestructured regions in the liquid for the crystallization process in the GCM was first proposed in ref. 31. There is a clear link between the prestructured particles of ref. 31 and the high bond orientational order particles of our study. This is already clear from the inspection of Fig. 3, where crystal particles are embedded in regions of high bond orientational order, exactly as prestructured particles wet the crystal nuclei. In ref. 31 these particles are shown to play an important role in determining the correct shape of the free energy barrier for nucleation. In our study the role of these particles is extended to explain the mechanism of polymorph selection. Taken together, these results show that a complete description of the nucleation process needs to take into account the prestructured particles (with high bond orientational order) surrounding crystal nuclei. However, we observe that ref. 31 found that the solid clusters consist of an hcp core, which was not found in our study. The reason for this discrepancy comes from the different protocol used between the two studies for the identification of the crystal phase. In ref. 31, the identity of a crystal particle is assessed by its position in the Q₄–Q₆ map, while in our study we make use of the W₄–W₆ map (as described in the Methods section). We believe the W₄–W₆ map to be more reliable for polymorph identification since it shows far less overlap between the different crystal structures than the Q₄–Q₆ map. We have checked our proposition by visual inspection of the configurations, finding that the W₄–W₆ map gives consistently more accurate results than the Q₄–Q₆ map for the identification of polymorphs.

5 Conclusions

To conclude we have shown that the homogeneous nucleation in the GCM bears many similarities with hard sphere systems,¹⁶ where the role of prestructured regions in the melt has been recently investigated. Unlike hard spheres, the GCM offers the possibility to investigate in depth the nucleation pathway for different target crystals. Another difference is that while nucleation in hard spheres happens at conditions very far from the bulk crystal, in the GCM the fluid immediately crystallizes in a solid with the correct bulk density (even for the smallest precritical nuclei). This might be a consequence of the fact that the crystal density is almost identical to that of the liquid and accordingly there is little interface tension associated with the density gradient.

Here we showed that the basic principle of crystal polymorph selection is common to hard and soft spheres. This suggest the universality of the principle, although further careful studies are necessary to confirm it. Future studies will also concentrate on the role of dynamic heterogeneity, which were shown to be highly suppressed in the high density limit,²⁸ but could still play an important role at low pressures, possibly shedding light on the interplay between crystallization and vitrification.^51,52

Acknowledgements

The authors thank Mathieu Leocmach for fruitful discussions. This work was partially supported by a grant-in-aid from the Ministry of Education, Culture, Sports, Science and Technology, Japan and also by Aihara Project, the FIRST program from JSPS, initiated by CSTP.

References

1. S. Auer and D. Frenkel, Adv. Polym. Sci., 2005, 173, 149–207.
2. R. Sear, J. Phys.: Condens. Matter, 2007, 19, 033101.
3. U. Gasser, J. Phys.: Condens. Matter, 2009, 21, 203101.
4. W. Ostwald, Z. Phys. Chem, 1897, 22, 289–330.
5. S. Alexander and J. McTague, Phys. Rev. Lett., 1978, 41, 702–705.
6. W. W. Wood and J. D. Jacobson, J. Chem. Phys., 1957, 27, 1207–1208.
7. B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208–1209.
8. P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342.
9. U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Science, 2001, 292, 258.
10. B. O'Malley and I. Snook, Phys. Rev. Lett., 2003, 90, 85702.
11. P. N. Pusey, W. Van Megen, P. Bartlett, B. J. Ackerson, J. G. Rarity and S. M. Underwood, Phys. Rev. Lett., 1989, 63, 2753–2756.
12. D. Christian and V. Heiner, Phys. Rev. Lett., 1997, 78, 1811–1814.
13. T. Palberg, Curr. Opin. Colloid Interface Sci., 1997, 2, 607–614.
14. V. Luchnikov, A. Gervois, P. Richard, L. Oger and J. P. Troadec, J. Mol. Liq., 2002, 96–97, 185–194.
15. L. Filion, M. Hermes, R. Ni and M. Dijkstra, J. Chem. Phys., 2010, 133, 244115.
16. J. Russo and H. Tanaka, Arxiv preprint arXiv:1109.0107, 2011.
17. P. R. ten Wolde, M. J. Ruiz-Montero and D. Frenkel, Phys. Rev. Lett., 1995, 75, 2714–2717.
18. H. Wang, H. Gould and W. Klein, Phys. Rev. E, 2007, 76, 031604.
19. C. Desgranges and J. Delhommelle, J. Am. Chem. Soc., 2011, 133, 2872–2874.
20. H. Tanaka, J. Stat. Mech.: Theory Exp., 2010, 2010, P12001.
21. T. Kawasaki and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14036.
22. H. Tanaka, T. Kawasaki, H. Shintani and K. Watanabe, Nat. Mater., 2010, 9, 324–331.
23. A. A. Louis, P. G. Bolhuis and J. P. Hansen, Phys. Rev. E, 2000, 62, 7961–7972.
24. C. N. Likos, Phys. Rep., 2001, 348, 267–439.
25. C. N. Likos, Soft Matter, 2006, 2, 478–498.
26. G. Malescio, J. Phys.: Condens. Matter, 2007, 19, 073101.
27. F. H. Stillinger, J. Chem. Phys., 1976, 65, 3968–3974.
28. A. Ikeda and K. Miyazaki, Phys. Rev. Lett., 2011, 106, 015701.
29. C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453.
30. C. N. Likos, A. Lang, M. Watzlawek and H. Löwen, Phys. Rev. E, 2001, 63, 031206.
31. W. Lechner, C. Dellago and P. G. Bolhuis, Phys. Rev. Lett., 2011, 106, 85701.
32. W. Lechner, C. Dellago and P. G. Bolhuis, J. Chem. Phys., 2011, 135, 154110.
33. H. J. Schöpe, G. Bryant and W. van Megen, Phys. Rev. Lett., 2006, 96, 175701.
34. J. R. Savage and A. D. Dinsmore, Phys. Rev. Lett., 2009, 102, 198302.
35. S. Iacopini, T. Palberg and H. J. Schöpe, J. Chem. Phys., 2009, 130, 084502.
36. T. Schilling, H. J. Schöpe, M. Oettel, G. Opletal and I. Snook, Phys. Rev. Lett., 2010, 105, 25701.
37. J. F. Lutsko and G. Nicolis, Phys. Rev. Lett., 2006, 96, 46102.
38. A. Lang, C. Likos, M. Watzlawek and H. Löwen, J. Phys.: Condens. Matter, 2000, 12, 5087.
39. S. Prestipino, F. Saija and P. V. Giaquinta, Phys. Rev. E, 2005, 71, 050102.
40. S. Prestipino, F. Saija and P. V. Giaquinta, J. Chem. Phys., 2005, 123, 144110.
41. P. Mausbach, A. Ahmed and R. J. Sadus, J. Chem. Phys., 2009, 131, 184507.
42. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B, 1983, 28, 784–805.
43. S. Auer and D. Frenkel, J. Chem. Phys., 2004, 120, 3015–3029.
44. W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707.
45. J. Wedekind, R. Strey and D. Reguera, J. Chem. Phys., 2007, 126, 134103.
46. D. Frenkel and A. J. C. Ladd, J. Chem. Phys., 1984, 81, 3188–3193.
47. J. M. Polson, E. Trizac, S. Pronk and D. Frenkel, J. Chem. Phys., 2000, 112, 5339–5342.
48. C. Vega, E. Sanz, J. L. F. Abascal and E. G. Noya, J. Phys.: Condens. Matter, 2008, 20, 153101.
49. C. H. Rycroft, Chaos, 2009, 19, 041111.
50. J. C. Pàmies, A. Cacciuto and D. Frenkel, J. Chem. Phys., 2009, 131, 044514.
51. E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704.
52. E. Sanz, C. Valeriani, E. Zaccarelli, W. C. K. Poon, P. N. Pusey and M. E. Cates, Phys. Rev. Lett., 2011, 106, 215701.

---