On measuring colloidal volume fractions

Abstract

Hard-sphere colloids are popular as models for testing fundamental theories in condensed matter and statistical physics, from crystal nucleation to the glass transition. A single parameter, the volume fraction (ϕ), characterizes an ideal, monodisperse hard-sphere suspension. In comparing experiments with theories and simulation, researchers to date have paid little attention to likely uncertainties in experimentally-quoted ϕ values. We critically review the experimental measurement of ϕ in hard-sphere colloids, and show that while statistical uncertainties in comparing relative values of ϕ can be as low as 10⁻⁴, systematic errors of ≳3% are probably unavoidable. The consequences of this are illustrated by way of a case study comparing literature data sets on hard-sphere viscosity and diffusion.

---

1 Introduction

Excluded volume effects dominate the behaviour of liquids around the triple point¹ and play a key role in structuring crystalline² and amorphous solids.³ Thus, hard spheres have long functioned as a reference system for theoretical and simulational studies of condensed matter. In 1986, Pusey and van Megen demonstrated⁴ that suspensions of sterically-stabilised polymethylmethacrylate (PMMA) colloids showed nearly-perfect hard-sphere equilibrium phase behaviour, undergoing a first-order phase transition from a fluid to a crystalline state at concentrations around those predicted some time ago by computer simulations for hard spherical particles.^5,6 Soon afterwards, the same authors showed⁷ that PMMA colloids underwent a glass transition at even higher concentrations. Subsequently, in a 1991 review, Pusey enunciated the ‘colloids as atoms’ paradigm⁸—Brownian suspensions can be used as ‘test tube simulations’ of many generic condensed matter phenomena such as crystallization and vitrification. Since then, the use of colloids as models has become very popular, especially since the addition of non-adsorbing polymers can be used to induce an inter-particle attraction ‘tuneable’ separately in its range and depth.^9,10 In such colloid-polymer mixtures, gas-liquid coexistence can be studied,^11,12 including interfaces and criticality,^13,14 as well as novel modes of arrest.¹⁵ Due to their slow intrinsic time scales, colloids are also ideal models for studying phase transition kinetics.¹⁶

While a range of inter-particle interactions are now available in model colloids, hard spheres remain an important reference system for which very direct comparison between experiments and theoretical calculations or computer simulations is in principle possible. The behaviour of a single-sized, or monodisperse, system of hard spheres is controlled by one parameter, the volume fraction ϕ, i.e. the fraction of the total volume V that is filled by N spheres, each of radius a,

Since ϕ is precisely known in theory or simulations, a comparison with experiments is straightforward provided that this quantity is also accurately measurable for real suspensions. Much of the literature has indeed proceeded on this basis, assuming that ϕ is unproblematically known from experiments.

However, as Pusey and van Megen pointed out in a symposium article¹⁷ following their Nature paper,⁴ the experimental determination of ϕ is emphatically not unproblematic, because: (1) no real colloid is truly ‘hard’, since there is always some softness in the interparticle potential; and (2) real colloids always have a finite size distribution, i.e. they are polydisperse. Thus, Pusey and van Megen calculated an experimental ‘effective’ hard-sphere volume fraction ϕ_E, and found that the freezing and melting volume fractions of their system were 0.494 and 0.535 respectively, compared to 0.494 and 0.545 in simulations.^5,6 Their careful conclusion reads: ‘Despite ambiguities …in the experimental determination of the coexistence region this difference is probably significant.’

The same degree of caution has not characterized the literature since. Experimental reports typically do not discuss in any detail the method used for arriving at ϕ. On the other hand, theory or simulations almost always take experimental reports of ϕ at face value and proceed to use the data on this basis. This is unsatisfactory, particularly in situations where theory testing demands a degree of accuracy and certainty in the experimental ϕ that is probably unattainable. In this paper, we critically review a plethora of methods for the experimental determination of ϕ in hard-sphere suspensions, evaluate the degree of accuracy attainable in each case, comment on the potential discrepancies between methods, and give a case study showing how different experiments should be compared taking into account possible difference in ϕ determination.

With the increasing popularity of confocal microscopy, direct counting of particles is becoming a standard method for determining ϕ (see Sec. 5.4). This method depends on knowing the particle size. Thus, after introducing model colloids (Section 2), we review particle sizing (Section 3). The ‘classic’ method for determining ϕ is via the crystallization phase behaviour, which changes with polydispersity.¹⁸ So we review polydispersity measurements (Section 4) before turning to consider the determination of ϕ in detail (Section 5). We finish with a case study (Section 6) and a Conclusion.

2 The particles

We focus on suspensions of nearly-perfect hard spheres. Charge-stabilised colloidal silica particles in water are close to hard-sphere like when the charges are sufficiently screened by salt,^19–21 although any refractive index mismatch leaves van der Waals attraction to be considered. However, a significant drawback of silica as a model system is that these particles have a density ρ ≈ 2.2 g cm⁻³, and it has proved difficult to find solvents that match this density. Sedimentation can be alleviated by using smaller particles, but at the expense of increasing polydispersity. Charged-stabilised polystyrene spheres are also potentially hard-sphere-like, and are easier to density match, though (unlike silica) almost impossible to refractive index match.

A more popular model hard sphere system is PMMA, sterically stabilized by a δ ≲ 10 nm layer of PHSA (poly-12-hydroxystearic acid).²² This layer confers a degree of softness to the interparticle potential on the scale of δ.^23,24 PMMA particles can be dispersed in solvent mixtures that match both the particles' density and index of refraction.^25,26 But particle swelling, particularly by halogenated solvents, is endemic.^27,28 For some solvents used in earlier work, swelling would be complete within a few hours,²⁹ but for the currently popular halogenated solvents this process can take several weeks. Thus the particle size changes over time, though heat shock may speed up the process to taking only a few hours.³⁰ As swelling is poorly characterized, in situ measurement is the only reliable means of ensuring that it is complete before the particles are used in experiments. This is particularly important at high ϕ, where many properties are steep functions of the concentration: an x% increase in the particle radius translates into ≳3x% in ϕ. Thus, e.g., an index-matching mixture of cis-decalin and tetrachloroethylene causes 20% swelling, which has a drastic effect upon ϕ.²⁸ Finally, batch-to-batch variations generate further uncertainties.

Below, we focus on PMMA particles, although much of what we say will also apply to silica and other model systems.

3 Measuring size

The basic parameter characterizing spherical colloidal particles is their radius, a. Some methods of determining ϕ, most obviously by ‘counting’ from confocal microscopy images, depend directly on measuring a. In this section, we critically review the measurement of particle size.

3.1 Definition of particle radius

At first sight, defining ‘the particle radius’ should be simple in a nearly-monodisperse colloid. But this is deceptive, Fig. 1. For sterically-stabilized particles like PMMA, we can usefully define as least four different radii. First, the hydrodynamic radius, a_H, occurs in the relationship between the drag, f, on a particle moving at velocity v in a fluid of viscosity η at low Reynolds numbers, f = ξv, where the friction coefficient

ξ = 6πηa_H. (2)

Fig. 1 Definitions of particle radii. (a) Non-sterically-stabilized particles, e.g.silica, with a core radius a_c. (b) Sterically-stabilized particle, with surface ‘hairs’ (not drawn to scale), where additionally the average hair thickness [small delta, Greek, macron] and the core-shall radius a_CS = a_C + [small delta, Greek, macron] are needed for a full characterisation.

But it is far from clear that a_H is the appropriate radius for determining ϕ, and relating a_H to other, more appropriate, radii (see below) is a non-trivial problem in hydrodynamics. Somewhat more directly related to ϕ is the core radius, a_C, which is the radius of the sterically-stabilized particles minus the stabilizing hairs. Thirdly, if we can determine the average hair thickness [small delta, Greek, macron], then the core–shell radius, a_CS = a_C + [small delta, Greek, macron]. For ‘hairless’ particles, such as charge-stabilized silica, a_CS = a_C. Finally, we may assign an effective hard sphere radius, a_eff, to the particles to obtain the best fit to theory or simulations of hard-sphere behaviour in a certain range of ϕ, so that a_eff is inevitably dependent on the chosen property and ϕ range.

We will not review established sizing methods in any detail, but will reference existing literature and note cautionary points. Then we will introduce a number of newer methods.

3.2 Measuring radius: established methods

Scattering methods have a long history in sizing spherical particles.^31–33 Static and dynamic scattering determine the size of particles by measuring the time-averaged or fluctuating intensity of the scattered light respectively.

Dynamic light scattering (DLS) and its X-ray equivalent, X-ray photon correlation spectroscopy (XPCS), measure the diffusion coefficient of particles, which is related to the friction coefficient via the Stokes–Einstein–Sutherland relation:^34–36D = k_BT/ξ. DLS and XPCS therefore determine a_H (cf.eqn (2)), and are most useful in the case of particles consisting of core only, such as silica, since it is less clear how to relate a_H to a_CS for core–shell particles such as PMMA. Note that the accuracy of this method depends on having an accurate value for η, the solvent viscosity, which is temperature dependent. For example, we have found that for the common solvent mixture cyclohexylbromide and decalin (85%/15% by weight) at 24 °C, η = 2.120 mPa·s and dη/dT = −0.029 mPa·s/K. Thus, a 1 °C uncertainly in T is a 0.3% uncertainty of T but a 1.7% uncertainty in T/η and therefore in a_H.

Static light scattering (SLS), small-angle X-ray scattering (SAXS) or small-angle neutron scattering (SANS) can potentially determine a_C and a_CS. Since the core and shell of (say) a PMMA particle in general have different contrasts to light, X-rays (refractive index, n, in both cases) and neutrons (scattering length, b), the diffraction pattern of a single particle is determined by the interference of radiation scattered from these two parts. Fitting this diffraction pattern (the form factor) therefore can in principle yield a_C and a_CS = a_C + δ. In a solvent with n or b quite different from both the core and the shell, the whole entity scatters more or less as a homogeneous sphere and a radius close to a_CS is returned from form-factor fitting. When solvent mixtures are used to ‘tune’ the relative contrasts of core and shell, even a small amount of a minority component in the solvent mixture can swell the particles by up to 10% or more,^27,28 and the fractional swelling of core and shell is not necessarily identical. In SAXS, where the shell has little contrast, δ cannot be accurately determined; however, the brightness of the beam gives many orders of oscillations in the form factor, allowing very accurate data fitting.

For both static and dynamic scattering, samples must be dilute enough so that the properties of non-interacting particles are measured in the single-scattering limit. The only sure way to know that this has been achieved is to collect data at different ϕ and look for the convergence in the ϕ → 0 limit. Static scattering at finite ϕ gives the static structure factor as a function of scattering vector, S(q). Fitting this to, e.g., the Percus–Yevick form³⁷ or simulations yields simultaneously a_eff and ϕ, although polydispersity is a significant complication.³⁸ Alternatively, the Bragg peaks in S(q) from colloidal crystals at fluid-crystal coexistence can be used to deduce a_eff if the melting point is known (but see Section 4 for caveats).

Electron microscopy (EM) measures a_C of dried particles, because drying collapses the steric-stabilizing ‘hairs’ in core–shell particles such as PMMA, and deswells particles swollen by solvent when dispersed. Various optical microscopies can, in principle, be used in the same way as EM for sizing particles; caveats are pointed out in Section 3.4.

3.3 Measuring radius: newer methods

3.3.1 Differential dynamic microscopy. DLS measures diffusion via determining the intermediate scattering function (ISF), which is the spatial Fourier transform of a time-dependent density-density correlation function;^31–33 it requires a laser and bespoke electronics (a correlator). Recently, a method for measuring the ISF has been demonstrated³⁹ that requires only the use of everyday laboratory equipment, viz., a white-light optical microscope and a CCD camera. This method, differential dynamic microscopy (DDM), exploits the fact that the intensity of a low-resolution microscope image is linearly related to the density of particles in the sample being imaged.⁴⁰ Thus, correlating the Fourier transform of the images gives directly the ISF.

3.3.2 Particle tracking. Being a scattering method, DLS works in reciprocal space. DDM uses microscope images, but also yields the ISF in reciprocal space. In both cases, the measured quantity is the diffusion coefficient, which controls the mean-squared displacement (MSD) of Brownian particles: 〈Δr²(τ)〉 = nDτ, with n = 2, 4 or 6 in 1, 2 or 3 dimensions respectively. Direct real-space methods for measuring the MSD are increasingly popular. The motion of particles in a dilute sample (ϕ ≪ 0.01) can be captured by video microscopy,⁴¹ and the particle motion tracked⁴² using publicly available software.⁴³ Provided the microscope has been properly calibrated, such tracks yield the MSD.

Problems can occur at short and long times. The issue at short times is measurement error due to pixellation. The pixellation error for a particle whose image is N pixels in diameter with individual pixels of width M is roughly M/N; for typical particle sizes, additional ‘dynamical errors’ due to particle movement during finite exposure time are comparable in magnitude.⁴⁴ In 1 dimension, a positional uncertainty of X generates an apparent time-independent MSD of X², giving

〈r²_meas(τ)〉 = 〈r²_true(τ)〉 + X². (3)

If the short-time MSD plateau due to X² is observed, it provides an excellent means of determining the measurement uncertainty X. Fig. 2 shows that it is important to take this term into account for accurate determination of D by tracking. Note that changing the parameters used to identify particle positions can often influence X, for better or worse.⁴²

Fig. 2 Mean square displacement of a_C = 1.5 μm polystyrene spheres in a water-glycerol mixture. (○): raw data; (+): 〈Δx²〉 − X² where the estimated noise level (dashed line) is X = 0.08 μm. Solid line: a linear fit to the raw data in the range 10⁰ < τ < 10¹ s, giving D = 0.0254 μm²/s. With the noise subtracted off, a linear fit to all of the data at τ < 10¹ s gives D = 0.0248 μm² s⁻¹. In this experiment, N = 9 and M = 0.64 μm/pixel, so the estimated noise level M/N = 0.07 μm is comparable to the observed X = 0.08 μm.

At long times, the measured MSD can become non-linear due to particles disappearing from the field of view, either because they leave laterally or because they become defocussed. Since the MSD at any τ is computed based only on particles which have been observed for at least as long as τ, too few particles may contribute at large τ for proper averaging. Moreover, the caveats about temperature control discussed in section 3.2 apply here too. Finally, sample drift can be serious at high ϕ. At low ϕ, however, drift can be neglected if the same MSD is found along the three spatial directions.

3.3.3 Confocal microscopy . By using a pinhole to reject out-of-focus light, laser confocal microscopy is capable of generating images deep inside (∼100 μm) a concentrated suspension of fluorescent colloids. Thus, by processing images taken scanning through a sample, a 3 dimensional image of many thousands of particles can be reconstructed and their coordinates obtained.^43,45 In a sample where particles are touching, the peak of the radial distribution function, g(r), calculated directly from the particle coordinates gives a_CS. Touching particles can be generated in a spun-down sediment,⁴⁶ or by inducing a very short range attraction (e.g. by adding small non-adsorbing polymers). While the first peak of g(r) is typically averaged over ≳ 10⁸ correlations, and so is in principle highly accurate, the particle size in a typical confocal image is ≲10 pixels, which limits the best accuracy to ∼0.1 pixel. Furthermore, microscopy is subject to certain systematic errors^47,48 that affect the determination of g(r). Finally, note that the scanning mechanism drifts, so that calibration on the day of measurement is important.

3.3.4 Holographic microscopy. A collimated laser beam directed through a microscope objective scatters off a particle. The scattered and unscattered beams interfere in the focal plane to form a hologram. At low enough ϕ, the holographic image of a single, optically homogeneous particle can be fitted using Lorenz-Mie theory to determine its position, size, and refractive index.^49–51 This has been demonstrated with ∼100 nm to 10 μm particles. The radius a_C of an individual particle can be measured to ±10–30 nm from a single snapshot.⁵² Multiple measurements further improve on this.⁵¹ The sizing of core–shell particles has not yet been attempted. Note that while this method fails for exactly index-matched particles, a mismatch of as little as 1% is sufficient to render it usable (D. Grier, personal communication). Again, caveats concerning calibration apply.

3.4 Measuring radius: case study

To illustrate the difficulties in pinning down a value for the radius of a batch of particles, we reproduce data for 15 preparations of fluorescent PMMA colloids by Bosma et al.²⁷ ‘Wet’ particles (suspended in hexane) were characterized by SLS (far from index matching, so that a_CS is measured), while dried particles were sized by EM. In some cases, direct measurement of sizes from confocal micrographs was performed. The peak of g(r) from confocal microscopy of a close-packed sample was also reported for one sample. We take the EM radius, always the smallest, to be a_C. In Fig. 3, we plot Δ = a_X − a_C, where a_X is the radius from method X. The likely length of PHSA ‘hairs’ is 6 ± 1 nm,^53,54 although oligomers of up to 15–20 nm may be present.⁵⁴ The hairs therefore account for the lower bound of Δ ≳ 10 nm. Larger Δ values are likely due to particles swelling in hexane, with larger particles swelling more (so that in most cases the swelling is ∼4% of a_CS).

Fig. 3 Radii of different batches of fluorescent PMMA particles determined by various methods:²⁷ ● static light scattering, ▲ confocal microscopy, ■ g(r) peak. For confocal microscopy, the radii were determined by depositing the particles on a surface, finding a region where 15–20 particles were in a line, and determining the distance these aligned particles spanned. As ref. 27 notes, this provides only a ‘rough estimate.’ The g(r) peak datum was determined from other confocal observations as described in Sec. 3.3.3.

The direct confocal measurements are consistently higher than the SLS data by ≳10 nm. This illustrates the difficulty of direct measurements from any optical image: the image of a single particle is far from sharp at the edges, both due to geometric and diffraction effects. The measurement from g(r) is likely more accurate, since it relies on locating particle centres rather than edges. It is not clear why the one example of such measurements shown in Fig. 3 is also significantly higher than the SLS result. Overall, these data illustrates that particles sizes quoted in the experimental literature may be subjected to significant systematic uncertainties that are often not reflected in the (statistical) error bars. This must be taken into account if the particle size is then used in calculating ϕ.

Note that a study using five separate methods to determine the radii of different batches of PMMA particles has been presented before.²³ Such studies are necessary if ϕ is to be determined credibly from a.

4 Measuring polydispersity

Polydispersity in general refers to the existence of a distribution of particle properties, such as size, shape, charge, magnetic moment, etc. Hard sphere colloids have a distribution of radii, P(a), for which we define the polydispersity, σ, as the standard deviation of this distribution divided by the mean:

σ = (〈a²〉 − 〈a²〉)^1/2/〈a〉. (4)

Very monodisperse PMMA has polydispersities approaching 3%, however 5–6% is typical²⁷ for averagely ‘monodisperse’ PMMA. Note that some particles, including PMMA, frequently display a bimodal distribution due to secondary nucleation, so that a full distribution is needed to characterize them.

Polydispersity is relevant here because it affects the equilibrium phase diagram. Monodisperse hard spheres freeze at ϕ_F = 0.494 to form crystals at the melting point ϕ_M = 0.545. These two values are often used as fixed points for determining ϕ in experiments (see Section 5.2). Theory^18,55 and simulations^18,55,56 show that even small σ may shift ϕ_M and ϕ_F significantly, Fig. 4. Indeed, particles with σ higher than some terminal value σ^* will fail to crystallize at all experimentally or in simulations, although theory¹⁸ predicts phase separation into coexisting solid phases. Simulations⁵⁷ predict that σ^* ≈ 7%, consistent with early experiments.⁵⁸ Determining polydispersity is therefore important for measuring ϕ. Note that the whole distribution and not just its variance may matter, e.g. in determination nucleation rates.⁵⁹

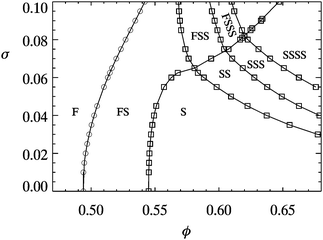Fig. 4 The theoretical phase diagram of hard spheres at different polydispersities, σ. F = fluid, S = (crystalline) solid; thus FSS denotes fluid–solid–solid coexistence. Replotted from ref. 55

Direct imaging, EM or optical microscopy can potentially yield P(a), subject to the same caveats already discussed. But note that larger particles may swell more (Fig. 3; see also ref. 51), giving a correlation between size and shrinkage upon drying, so that wet and dry P(a) may be different. A recent method allows a direct determination of P(a) by using confocal microscopy of a sedimented colloidal suspension.⁶⁰ In this method, the pair-wise separations of particles are used to estimate the sizes of each individual particle. Simulations verify that this works well even in the presence of moderate particle position uncertainty. However, for larger position uncertainty or smaller sample polydispersity, the method can fail.

In DLS or XPCS, the ISF from a hypothetical monodisperse suspension decays exponentially with time. Polydispersity turns the ISF into a sum of exponentials. In static scattering, monodisperse particles give sharp minima in the form factor, which are smeared out by polydispersity. (Note that multiple scattering has the same effect, and so can masquerade as polydispersity.) In principle, these features can be fitted to yield P(a),³¹ subject to all the usual problems and uncertainties associated with solving an inverse problem. For DLS (or XPCS), there are well known algorithms such as CONTIN⁶¹ for backing out P(a)via the distribution of decay times in the ISF. Or, less ambitiously, cumulant analysis⁶² can be used to extract σ. Form factors from static scattering are seldom inverted directly to yield P(a). Instead, one assumes, say, a Gaussian form, and the scattering profile from Mie theory is fitted to obtain 〈a〉 and σ. The effect of small σ (a few %) on the ISF and form factor can be treated analytically,⁶³ and becomes independent of the form of P(a) as σ → 0. The resulting expressions can be used to fit dynamic or static scattering data to yield rather accurate values of σ. Finally, some of the techniques mentioned above can be combined to provide accurate characterization of polydispersity.^64,65

5 Measuring volume fraction

We now turn to describe and evaluate a number of methods for determining the volume fraction of model colloids.

5.1 Measuring mass and density

The method used by Pusey and van Megen to determine ϕ in their classic work on hard-sphere colloid phase behaviour⁷ and described subsequently in detail in a symposium paper¹⁷ remains conceptually the simplest. They dried a suspension of known total (or ‘wet’) mass to determine the mass of dry particles, and converted the resulting mass fraction into ϕ using literature values of the densities of the solvents and of (dry) PMMA. There are multiple assumptions behind this procedure that lead to systematic uncertainties. In particular, this procedure assumes that the properties of dry and wet particles are the same, which, due to solvent absorption and solvation of the ‘hairs’, is unlikely to be true. Thus, many have subsequently proceeded differently. If ϕ has been separately determined for one sample using other methods (e.g. at ϕ_F or ϕ_M, see below), the ratio of mass to volume fractions can be used to calibrate other samples. But the exact relationship between these two quantities is not a direct proportionality, and involves (unknown) ratios of the properties of wet and dry particles.

A more involved procedure is in principle less problematic.⁶⁶ First, one determines the hydrodynamic radius a_H from dynamic light scattering. Then the sedimentation velocity, v_s, of a dilute suspension is determined by analytic centrifugation to obtain the density difference between the (wet) particles and the solvent, Δρ = ρ^wet_p − ρ_s: v_s = 2Δρga_H²/9η₀, where η₀ is the solvent viscosity (separately measured) and g is the gravitational acceleration, although the assumption that the non-slip boundary condition holds at the ‘hairy’ particle surface may not be strictly valid (E. Sloutskin, personal communication). Since liquid densities can be determined very accurately using pycnometry or other densitometric methods if the temperature is controlled, we can measure ρ_s and the density of an arbitrary suspension, ρ, from which its ϕ can be determined using

ρ = ρ_s + ϕΔρ. (5)

5.2 Measuring phase behaviour

A popular method of calibrating ϕ relies on the known phase behaviour of hard spheres. In particular, in the region ϕ_F = 0.494 < ϕ < ϕ_M = 0.545, hard spheres show coexistence of fluid at ϕ_F and crystals at ϕ_M. The fraction of crystals, χ, increases linearly from 0 to 100% over the interval. Measuring χ for a sample within the coexistence region then gives its ϕ. To determine χ accurately, one needs to take into account the compression of the crystalline sediment by its own weight.⁶⁷

The main uncertainty associated with using phase behaviour to calibrate ϕ is the effect of polydispersity. All calculations and simulations to date agree that finite σ increases ϕ_F and ϕ_M. Thus, e.g., in the ‘moment free energy’ calculations shown in Fig. 4, ϕ_F = 0.5074 and ϕ_M = 0.5540 at σ = 5%, the latter being a representative value of a typical preparation of PMMA colloids. To date there has been no independent experimental check on such theoretical predictions, one of the main issues being the measurement of ϕ in polydisperse colloids!

Nevertheless, these results may throw light on one of the puzzles remaining from the original work of Pusey and van Megen,^7,17 who found that if they assumed a freezing point of ϕ_F = 0.494, their measured melting point was ϕ_M = 0.535. The ratio γ of these two values, which characterises the width of the coexistence gap, is γ_PvM = 1.083. For monodisperse colloids, γ_σ = 0 = 1.103, while calculations⁵⁵ for σ = 5% gives γ_σ = 5% = 1.092. It is therefore possible that the narrowing of the coexistence gap observed by Pusey and van Megen is largely due to polydispersity. Note, however, that the phase diagram likely depends on the whole P(a) and not just σ.

An additional source of uncertainty is residual charge^68,69 so that, hard-sphere phase behaviour no longer obtains: crystallization is expected at lower volume fractions (for PMMA, see, e.g.ref. 70). In these cases the phase behaviour cannot be matched to that of hard spheres at all. However, by adding salt, the charges can be screened and hard sphere behaviour recovered to an extent (e.g., for PMMA, see ref. 68).

We mention that confocal microscopy of a sample in the fluid-crystal coexistence region can be used to deduce a value for a_eff by assuming particular values for ϕ_F and ϕ_M,⁷⁰ subject to all the above-mentioned caveats and uncertainties.

5.3 Centrifugation and sedimentation

Perhaps the quickest way to obtain samples with approximately calibrated ϕ is by centrifuging to obtain a sediment that one assumes to be at ‘random close packing’ (RCP), and therefore some known ϕ_RCP, which can then be redispersed with fixed volumes of solvent to give samples at lower concentrations. The method can be applied even with charged particles, since hard centrifugation can reduce even such particles to a mutually-touching amorphous state.⁴⁶

The main problem with this method is that the theoretical status of RCP is still debated, with different simulation algorithms giving different results.^71,72 Experimentally, different regions of the centrifuged sediment have somewhat different concentrations (ϕ = 0.60–0.64 in silica colloids⁷³), and little is known about the almost-certain dependence of sediment structure on centrifugation protocol. Moreover, the spun-down sediment is inevitably compressed, and will expand with time after the cessation of centrifugation, which introduces an extra degree of uncertainty. Finally, the dependence on polydispersity is poorly known.^72,74,75

But centrifugation is convenient, and if the protocol is kept constant, it can be used to produce a series of samples with highly accurate normalized concentrations, viz., ϕ/ϕ_sed, where ϕ_sed is the volume fraction of the sediment.

Under this heading, we may mention that particles with small enough gravitational Péclet number^46,76 (either by virtue of near density matching or by virtue of being small) and low enough polydispersity will sediment slowly under gravity to form sedimentary crystals consisting of more or less randomly-stacked hexagonal close packed (rhcp) layers of particles. If the particles are monodisperse hard spheres, then in this sediment. Again, however, the (largely unknown) effect of polydispersity as well as any changes due to charges need to be taken into account.

5.4 Confocal microscopy and particle counting

Confocal microscopy can be used to locate the position of thousands of particles in a suspension. Thus, if the particle radius, a, is known, then counting N particles in an imaging volume V will yield ϕ directly using eqn (1). Occasional particle mis-identification or missing a particle all together by the software give rise to erroneous ϕ, so that it is important to cross-check particle positions identified against raw images. In particular, particles near the edge of images are often mis-identified, so that in practice a sub-volume only is considered. Finally, uncertainties in a are magnified 3-fold or more in calculating ϕ. This latter uncertainty is compounded by the issue of which of the possible radii (Section 3.1) one should use.

5.5 X-ray transmission

The intensity of X-rays transmitted by a sample is given by I_T = I₀e^−μx, where I₀ is the incident intensity, μ and x are the attenuation coefficient and thickness of the sample. In the case of a colloidal suspension, μ = (1 − ϕ) μ_s + ϕ_Cμ_p, where ϕ_C is the volume fraction of particle cores, and μ_s and μ_p are the attenuation coefficients of the solvent and particles. The negligible amount of electron density represented by sterically-stabilizing ‘hairs’ means that they hardly contribute to the beam attenuation. X-ray transmission can therefore be used to determine ϕ directly for model colloids such as charge-stabilised polystyrene⁷⁷ or silica,⁷⁸ but only the core volume fraction for sterically-stabilised particles.

5.6 Measuring ϕ-dependent properties

The ϕ-dependence of a number of material properties of hard-sphere suspensions are known either from analytic theory or highly accurate simulations. In principle, therefore, measuring these properties can be used to determine ϕ. Here we review three: viscosity, diffusivity and structure factor.

Einstein predicted that in the limit ϕ → 0, the viscosity of a hard-sphere suspension is given by η(ϕ)/η₀ = 1 + (5/2)ϕ, with η₀ being the viscosity of the solvent.³⁶ Thus, in principle, measuring η(ϕ) is a method for determining ϕ (see, e.g., ref. 79). While suspensions in general shear thin, this should not be a problem in the very dilute limit. But temperature control is important, since η₀ is temperature sensitive (cf. Section 3.2).

The problems associated with this method have been detailed before.⁸⁰ In essence, very low ϕ, certainly ≲0.02, must be reached for the Einstein result to be valid; otherwise, second^81,82 and higher order terms in this ‘virial’ expansion need to be taken into account. In the case cited,⁷⁹ using the Einstein relation at ϕ ≈ 0.03 leads to an error in ϕ of ≈7%.⁸⁰ The difficulty, of course, is that in the limit ϕ → 0, very accurate viscometry is needed to distinguish the dilute suspension from pure solvent. Using the Einstein relation to calibrate ϕ in suspensions that are too concentrated for the relation to be valid accounts for some of the spread in literature values of η(ϕ_F), the viscosity of the most concentrated stable fluid state of hard spheres. Interestingly, determining ϕ using the Einstein relation is strictly independent of polydispersity: in the dilute limit, each particle contributes by an additive amount that is proportional to its volume.

Instead of measuring η(ϕ), one could determine the single-particle diffusion coefficient as a function of ϕ. Thus, El Masri et al.⁸³ measured the short-time self diffusion coefficient as a function of volume fraction, D^s_s(ϕ). The difficulty is that there are at least two different predictions for this behaviour^84,85 which leads to a 7% absolute uncertainty in ϕ.

Lastly, we have already mentioned (Section 3.2) that analytical expressions for the static structure factor, S(q), of hard spheres are available. In particular, the closed-form expression from the Percus–Yevick (PY) approximation³⁷ fits simulation data closely, provided that the empirical Verlet-Weis correction to the volume fraction⁸⁶ is applied, i.e. the PY structure factor for volume fraction ϕ′ is used for an experimental sample at ϕ: ϕ′ = ϕ − ϕ²/16. Thus, fitting measured S(q) can yield a measure of ϕ, provided that the particles can be treated as hard spheres. Again, caution about residual charges applies. Alternatively, g(r) determined from confocal microscopy can be fitted to the PY form or to simulation data⁸⁷ to give ϕ.

5.7 Deceptive samples

Finally, we explain how using an accurately calibrated ‘stock colloid’ may still lead to errors in the ϕ of samples.

First, we have already mentioned a number of times the issue of swelling. If particles used for calibrating volume fraction are still in the process of swelling due to solvent absorption, then samples prepared subsequently will have a higher ϕ than the earlier calibration would suggest.

Secondly, preparing samples almost invariably involves transferring suspension from one container (e.g. a bottle of stock) to another (e.g. a capillary for microscopy) using (typically) a pipette or a syringe. Apart from difficulties caused by very high viscosities²¹ and shear thickening,^88,89 there is the problem of jamming of the particles as the suspension enters a constriction,⁹⁰ which leads to a ‘self filtration’ effect. Particles jammed at (say) the entrance to a pipette prevent other particles from entering, but solvent continues to flow, so that the sample inside the pipette has a lower ϕ than the bulk suspension that we hope to transfer. Thus, a sample loaded for confocal microscopy may be more dilute than one expects.

Thirdly, except for very well density-matched samples at a temperature accurately remaining at the temperature at which the density matching was originally achieved, suspension inevitably sediment (or cream) with time at all except ϕ_RCP or ϕ_rhcp. This will lead to concentration gradients. Indeed, such gradients can be deliberately exploited,^{46,70,78,91–93}e.g. to determine equations of state. But in other cases, concentration gradients lead to unintended local deviations from the average ϕ at which the sample as a whole was originally prepared.

Since one of the most important uses of hard-sphere colloids is as a model to study dynamical arrest^15,94,95 and associated properties such as aging,^96,97 any of the above three sources of unintended changes in ϕ will have severe consequences: all suspension properties change very rapidly with ϕ at and above the glass transition (ϕ ≳ 0.58).

5.8 Summary: relative vs. absolute ϕ

The most important message from the preceding critical review is that the statistical errors involved in determining ϕ in the competent use of any of the above methods can almost certainly be brought below the systematic errors involved. Thus, for example, if one uses confocal microscopy to count particles and thus determine ϕ, the major source of uncertainty is likely to be the input radius. Thus, it is perfectly possible to produce a series of samples with relative uncertainty in ϕ of 1 part in 10⁴. However, our collective experience in using many of these methods suggests that the systematic uncertainties are likely to be ≳3%. Thus, for example, the systematic uncertainties in determining the radius of sterically-stablilized particles associated with the combined effects of swelling and hair thickness is unlikely to fall below 1%, which translates into at least 3% uncertainty in ϕ when using methods that depend on knowing the particle size. Turning to the use of phase behaviour, Fig. 4 shows that if we know σ = 0.05 ± 0.01, then ϕ_F ≈ 0.507 ± 0.005, a 1% uncertainty. But a knowledge of the polydispersity at comparable accuracy at σ = 8% translates into some 3–4% uncertainty in ϕ. Importantly none of the calculated phase diagrams for polydisperse hard spheres in the literature has been checked in any detail by experiments or large-scale simulations. Therefore, assuming an overall systematic uncertainty of ≳3% is again cautious.

Over all, then, we believe that, in practice, the uncertainties in estimating ϕ are ≳3%. Far from being a small error, a ≳3% uncertainty in ϕ can have dramatic effects. Thus, e.g., the viscosity of a hard-sphere suspension⁸⁰ grows by a factor of 2 when ϕ increases from 0.47 to 0.49; and the simulated crystal nucleation rate¹⁰⁰ near ϕ_F can change by 10 orders of magnitude for a 1% change in the absolute value of ϕ.

6 A cautionary tale

In this section we give a case study to illustrate how important it is to be critical about experimental ϕ values by analyzing two published data sets. These data sets give as a function of ϕ the long-time self diffusion coefficient, D^L_s(ϕ),⁹⁸ and the low-shear viscosity, η(ϕ),²¹ of PMMA colloids. At the time of publication, the diffusion data was the best and most complete available, and the viscosity data remain one of the most complete to date. The two groups came to quite different conclusions about dynamical divergence at high ϕ. van Megen and his collaborators concluded that D^L_s(ϕ) diverged at ϕ = ϕ_g ≈ 0.58, in a manner consistent with that predicted by mode coupling theory for an ideal glass transition. Chaikin and his collaborators, however, concluded from their η(ϕ) that there was no glass transition at ≈0.58; instead, they suggested that η(ϕ) diverged at RCP, ϕ = 0.64, according to a Vogel–Fulcher law. This controversy is ongoing (see, e.g., ref. 101 and 102). We do not wish to enter into this discussion here; instead, we use older data to illustrate many of the issues concerned with measuring ϕ and using experimental data sets. These issues are, of course, pertinent for the ongoing discussion.

The first thing to notice about these two experiments is that the reported volume fractions cannot be compared directly. Both sets of authors relied on measuring phase behaviour to calibrate ϕ (cf. Section 5.2), but one set of authors took into account polydispersity, and one did not. van Megen and co-workers used ϕ_F = 0.494, the value for monodisperse hard spheres, to determine ϕ, but cautioned that their particles had a polydispersity of σ = 5%. The colloids used by Chaikin and his co-workers also had the same σ, and they used the simulation data of Bolhuis and Kofke⁵⁶ to move freezing to ϕ_F = 0.505 for this polydispersity. Interestingly, the latest analytic calculations agree closely: Wilding and Sollich⁵⁵ give ϕ_F = 0.5074 at σ = 5%, Fig. 4. Thus, we multiply the ϕ value of the van Megen data set by a factor of 0.505/0.494 = 1.022 to make it consistent with the Chaikin ϕ values. The resulting data are shown in Fig. 5. The measurements have been normalised, D^L_s(ϕ) by the single-particle diffusivity, D₀, and η(ϕ) by the solvent viscosity, η₀. The normalized viscosity diverges at higher ϕ than the normalized (inverse) diffusivity.

Fig. 5 (a) Raw data: ■: The normalized long-time self diffusion coefficient of PMMA colloids as a function of ϕ, D₀/D^L_s(ϕ),⁹⁸ with the volume fraction multiplied by 1.022. ▲: The normalized low-shear viscosity of PMMA colloids, η(ϕ)/η₀, as a function of volume fraction.²¹ ◆: the volume fraction of the viscosity data set being multiplied by 0.965. (b) Violation of the SESR, quantified by the factor β (eqn (7)). ◆: Raw data. ■: From theory.⁹⁹ ▲: After the ϕ values of the viscosity data have been multiplied by 0.965.

At ϕ → 0, the solvent viscosity and the single-particle diffusivity are related by the Stokes–Einstein-Sutherland relation (SESR): D₀ = k_BT/6πη₀a. At finite ϕ, there is no a priori reason that a generalized SESR should hold for any of the many diffusion coefficients that can be defined. So we write

where β is a numerical factor that can be restated asWe plot in Fig. 5(b) (diamonds) the β(ϕ) implied by the data sets in Fig. 5(a). In so far as β ≠ 1, the SESR is violated.

Violation of the SESR is widely known for glass-forming systems near the glass transition.¹⁰³ In all experimental cases known (see e.g.ref. 104), β > 1, i.e. the particles diffuse somewhat faster than the viscosity allows according to the SESR. The fact that β drops very substantially below unity at ϕ ≳ 0.4 in Fig. 5(b) is therefore surprising, and merits further analysis.

To proceed, we turn to the work of Banchio et al.,⁹⁹ who have calculated various diffusivities and viscosities of hard sphere suspensions within a mode-coupling framework, and have shown that their results compared well with multiple experimental data sets. Their calculations predict that β as defined in eqn (7) hovers just below unity in the range 0 < ϕ < 0.50. Fig. 5(b) shows that the experimental β(ϕ) from the data plotted in Fig. 5(a) (diamonds) essentially agrees with theory (squares) up to ϕ = 0.35, but start to diverge thereafter.

Since we conclude that absolute values of ϕ are unlikely to be accurate to better than 3–6%, it is interesting to note that multiplying the volume fractions in the viscosity data set by a factor of 0.965 overlaps the two normalized data sets, Fig. 5(a). Not surprisingly, then, this renormalization of ϕ also brings very substantially better agreement in β(ϕ) in the whole range of ϕ covered by theory⁹⁹ (triangles, Fig. 5(b)). Assuming that there is a glass transition at ϕ_g ≈ 0.58, then this renormalization of ϕ also brings the direction of SESR violation in the vicinity of ϕ_g in line with all other known glass formers, viz., β > 1. Quantitatively, the renormalized data agree with the mode-coupling theory prediction that β → 1.06 as ϕ → ϕ_g.^105,106 Thus, we conclude that the supposed disagreement between the two data sets is well within the range of expected uncertainties in ϕ.

7 Conclusion

Hard sphere colloids are now part of the accepted ‘tool kit’ of experimental statistical mechanics. What we aim to do in this critical review is to counsel caution in comparing data from experiments against theory or simulations, because there are substantial, and probably irreducible, systematic errors in determining suspension volume fraction of ≳3%. This situation calls for at least three responses. First, experimentalists need to take the cue from the pioneering work of Pusey and van Megen¹⁷ and always report exactly how they arrive at their quoted ϕ values, and discuss likely sources particularly of systematic errors. Secondly, experimental data sets need to be compared vigilantly against each other to reveal possible discrepancies. Finally, theorists and simulators seeking experimental confirmation of their results should not be too easily satisfied with apparent agreement without in-depth inquiry into the systematic uncertainties in ϕ.

Finally, we note that while perfect hard spheres are indeed characterized by a single thermodynamic variable ϕ, real particles are never truly hard. Some softness in sterically-stabilized particles necessarily comes from compressible ‘hairs’, but this becomes less significant as a increases.²⁴ Moreover, for larger (a ≳ 0.5 μm) PMMA particles, a certain degree of charging seems inevitable,^68,69,87 which cannot be entirely screened by salt (due to limited solubility in organic solvents). Such softness means that accurate measurement of ϕ alone is insufficient, and introduces further substantial uncertainties, which we discuss in a forthcoming publication.

Acknowledgements

We thank P. Bartlett, J. C. Crocker, M. Fuchs, D. J. Pine, P. N. Pusey, H. Tanaka, A. van Blaaderen and D. A. Weitz for helpful discussions over many years, D. Chen for dη/dT data, and P. Sollich for the data in Fig. 4. WCKP was funded by EPSRC grant EP/D071070/1, and performed some of the analysis at the Aspen Center for Theoretical Physics. ERW was supported by a grant from the National Science Foundation (NSF CHE-0910707). CPR was funded by the Royal Society.

References

1. B. Widom, Science, 1967, 157, 375–382.
2. R. C. Evans, Introduction to Crystal Chemistry, Cambridge University Press, 2nd edn, 1964.
3. R. Zallen, The Physics of Amorphous Solids, Wiley-VCH, 1998.
4. P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342.
5. W. G. Hoover and F. H. Ree, J. Chem. Phys., 1967, 47, 4873–4878.
6. W. G. Hoover and F. H. Ree, J. Chem. Phys., 1968, 49, 3609–3617.
7. P. N. Pusey and W. van Megen, Phys. Rev. Lett., 1987, 59, 2083–2086.
8. P. N. Pusey, in Liquids, Freezing and Glass Transition, Pt. 2, ed. J. P. Hansen, D. Levesque and J. Zinn-Justin, Elsevier, 1991, pp. 763–942.
9. W. C. K. Poon, J. Phys.: Condens. Matter, 2002, 14, R859–R880.
10. H. N. W. Lekkerkerker and R. Tuinier, Colloids and the depletion interaction, Springer, 2011.
11. H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564.
12. S. M. Ilett, A. Orrock, W. C. K. Poon and P. N. Pusey, Phys. Rev. E, 1995, 51, 1344–1352.
13. D. G. A. L. Aarts, M. Schmidt and H. N. W. Lekkerkerker, Science, 2004, 304, 847–850.
14. C. P. Royall, D. G. A. L. Aarts and H. Tanaka, Nat. Phys., 2007, 3, 636–640.
15. K. N. Pham, A. M. Puertas, J. Bergenholtz, S. U. Egelhaaf, A. Moussaıd, P. N. Pusey, A. B. Schofield, M. E. Cates, M. Fuchs and W. C. K. Poon, Science, 2002, 296, 104–106.
16. V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815.
17. P. N. Pusey and W. van Megen, in Physics of Complex and Supramolecular Fluids, 1987, ed. S. A. Safran and N. A. Clark, Wiley, 1987, pp. 673–698.
18. M. Fasolo and P. Sollich, Phys. Rev. Lett., 2003, 91, 068301.
19. R. Piazza, T. Bellini and V. Degiorgio, Phys. Rev. Lett., 1993, 71, 4267–4270.
20. T. Shikata and D. S. Pearson, J. Rheol., 1994, 38, 601–616.
21. Z. Cheng, J. Zhu, P. M. Chaikin, S.-E. Phan and W. B. Russel, Phys. Rev. E, 2002, 65, 041405.
22. L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78.
23. G. Bryant, T. Mortensen, S. Henderson, S. Williams and W. van Megen, J. Colloid Interface Sci., 1999, 216, 401–408.
24. G. Bryant, S. R. Williams, L. Qian, I. K. Snook, E. Perez and F. Pincet, Phys. Rev. E, 2002, 66, 060501.
25. P. N. Segrè, F. Liu, P. Umbanhowar and D. A. Weitz, Nature, 2001, 409, 594–597.
26. A. D. Dinsmore, E. R. Weeks, V. Prasad, A. C. Levitt and D. A. Weitz, Appl. Opt., 2001, 40, 4152–4159.
27. G. Bosma, C. Pathmamanoharana, E. H. A. de Hooga, W. K. Kegel, A. van Blaaderen and H. N. W. Lekkerkerker, J. Colloid Interface Sci., 2002, 245, 292–300.
28. T. Ohtsuka, C. P. Royall and H. Tanaka, Europhys. Lett., 2008, 84, 46002.
29. S. M. Underwood, J. R. Taylor and W. van Megen, Langmuir, 1994, 10, 3550–3554.
30. L. J. Kaufman and D. A. Weitz, J. Chem. Phys., 2006, 125, 074716.
31. Neutron, X-rays and Light. Scattering Methods Applied to Soft Condensed Matter, ed. P. Lidner and Th. Zemb, North Holland, 2002.
32. B. J. Berne and R. Pecora, Dynamic Light Scattering, Wiley, New York, 1976.
33. B. Chu, Laser Light Scattering: Basic Principles and Practice. Second Edition, Dover Publications, 2nd edn, 2007.
34. W. Sutherland, Phil. Mag., 1905, 9, 781–785.
35. A. Einstein, Ann. Phys., 1905, 17, 549–560.
36. A. Einstein, Ann. Phys., 1906, 324, 289–306.
37. J. P. Hansen and I. R. Macdonald, Theory of Simple Liquids, Academic Press, 2nd edn, 1986.
38. C. G. de Kruif, W. J. Briels, R. P. May and A. Vrij, Langmuir, 1988, 4, 668–676.
39. R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102.
40. L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Teilleur, G. Bryand, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 2011, 106, 018101.
41. P. Habdas and E. R. Weeks, Curr. Opin. Colloid Interface Sci., 2002, 7, 196–203.
42. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
43. E. R. Weeks and J. C. Crocker, Particle Tracking Using IDL: website, http://www.physics.emory.edu/∼weeks/idl/.
44. T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623–638.
45. V. Prasad, D. Semwogerere and E. R. Weeks, J. Phys.: Condens. Matter, 2007, 19, 113102.
46. R. Kurita and E. R. Weeks, Phys. Rev. E, 2010, 82, 011403.
47. C. P. Royall, A. A. Louis and H. Tanaka, J. Chem. Phys., 2007, 127, 044507.
48. J. Baumgartl and C. Bechinger, Europhys. Lett., 2005, 71, 487–493.
49. J. Sheng, E. Malkiel and J. Katz, Appl. Opt., 2006, 45, 3893–3901.
50. S.-H. Lee and D. G. Grier, Opt. Express, 2007, 15, 1505–1512.
51. F. C. Cheong, B. Sun, R. Dreyfus, J. Amato-Grill, K. Xiao, L. Dixon and D. G. Grier, Opt. Express, 2009, 17, 13071–13079.
52. S.-H. Lee, Y. Roichman, G.-R. Yi, S.-H. Kim, S.-M. Yang, A. van Blaaderen, P. van Oostrum and D. G. Grier, Opt. Express, 2007, 15, 18275–18282.
53. D. J. Cebula, J. W. Goodwin, R. H. Ottewill, G. Jenkin and J. Tabony, Colloid Polym. Sci., 1983, 261, 555–564.
54. S. J. Barsted, L. J. Nowakowska, I. Wagstaff and D. J. Walbridge, Trans. Faraday Soc., 1971, 67, 3598–3603.
55. N. B. Wilding and P. Sollich, Soft Matter, 2011, 7, 4472–4484.
56. P. G. Bolhuis and D. A. Kofke, Phys. Rev. E, 1996, 54, 634–643.
57. E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704.
58. P. N. Pusey, J. Phys., 1987, 48, 709–712.
59. H. J. Schope, G. Bryant and W. van Megen, J. Chem. Phys., 2007, 127, 084505.
60. R. Kurita and E. R. Weeks, Phys. Rev. E, 2011, 84, 030401 (R).
61. W. Brown, Dynamic Light Scattering, Clarendon Press, 1993.
62. B. J. Frisken, Appl. Opt., 2001, 40, 4087–4091.
63. P. N. Pusey and W. van Megen, J. Chem. Phys., 1984, 80, 3513–3520.
64. G. Bryant, S. M., B. Budi and W. van Megen, Langmuir, 2003, 19, 616–621.
65. H. J. Schöpe, O. Marnette, W. van Megen and G. Bryant, Langmuir, 2007, 23, 11534–11539.
66. M. Shutman, A. V. Butenko, A. B. Schofield and E. Sloutskin, Manuscript in preparation.
67. S. E. Paulin and B. J. Ackerson, Phys. Rev. Lett., 1990, 64, 2663–2666.
68. A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517.
69. C. P. Royall, M. E. Leunissen, A. P. Hynninen, M. Dijkstra and A. van Blaaderen, J. Chem. Phys., 2006, 124, 244706.
70. J. Hernández-Guzmán and E. R. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15198–15202.
71. S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067.
72. M. Hermes and M. Dijkstra, Europhys. Lett., 2010, 89, 38005.
73. A. van Blaaderen and P. Wiltzius, Science, 1995, 270, 1177–1179.
74. W. Schaertl and H. Sillescu, J. Stat. Phys., 1994, 77, 1007–1025.
75. R. S. Farr and R. D. Groot, J. Chem. Phys., 2009, 131, 244104.
76. R. P. A. Dullens, D. G. A. L. Aarts and W. K. Kegel, Phys. Rev. Lett., 2006, 97, 228301.
77. K. Davis, W. B. Russel and W. J. Glantschnig, J. Chem. Soc., Faraday Trans., 1991, 87, 411–424.
78. M. A. Rutgers, J. H. Dunsmuir, J. Z. Xue, W. B. Russel and P. M. Chaikin, Phys. Rev. B, 1996, 53, 5043–5046.
79. C. G. de Kruif, E. M. F. van Iersel, A. Vrij and W. B. Russel, J. Chem. Phys., 1985, 83, 4717–4725.
80. W. C. K. Poon, S. P. Meeker, P. N. Pusey and P. N. Segrè, J. Non-Newtonian Fluid Mech., 1996, 67, 179–189.
81. G. K. Batchelor, J. Fluid Mech., 1977, 83, 97–117.
82. J. F. Brady and M. Vicic, J. Rheol., 1995, 39, 545–566.
83. D. El Masri, G. Brambilla, M. Pierno, G. Petekidis, A. B. Schofield, L. Berthier and L. Cipelletti, J. Stat. Mech.: Theory Exp., 2009, P07015.
84. C. W. J. Beenakker and P. Mazur, Phys. A, 1984, 126, 349–370.
85. M. Tokuyama and I. Oppenheim, Phys. Rev. E, 1994, 50, R16–R19.
86. L. Verlet and J.-J. Weis, Phys. Rev. A, 1972, 5, 939–952.
87. M. Schmidt, C. P. Royall, A. Blaaderen and J. Dzubiella, J. Phys.: Condens. Matter, 2008, 20, 494222.
88. H. A. Barnes, J. Rheol., 1989, 33, 329–366.
89. E. Brown and H. M. Jaeger, Phys. Rev. Lett., 2009, 103, 086001.
90. M. D. Haw, Phys. Rev. Lett., 2004, 92, 185506.
91. N. B. Simeonova and W. K. Kegel, Phys. Rev. Lett., 2004, 93, 035701.
92. J. F. Gilchrist, A. T. Chan, E. R. Weeks and J. A. Lewis, Langmuir, 2005, 21, 11040–11047.
93. C. J. Martinez, J. Liu, S. K. Rhodes, E. Luijten, E. R. Weeks and J. A. Lewis, Langmuir, 2005, 21, 9978–9989.
94. W. K. Kegel and A. van Blaaderen, Science, 2000, 287, 290–293.
95. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631.
96. R. E. Courtland and E. R. Weeks, J. Phys.: Condens. Matter, 2003, 15, S359–S365.
97. J. M. Lynch, G. C. Cianci and E. R. Weeks, Phys. Rev. E, 2008, 78, 031410.
98. W. van Megen, T. C. Mortensen, S. R. Williams and J. Müller, Phys. Rev. E, 1998, 58, 6073–6085.
99. A. J. Banchio, G. Nägele and J. Bergenholtz, J. Chem. Phys., 1999, 111, 8721–8740.
100. S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023.
101. G. Brambilla, D. El Masri, M. Pierno, L. Berthier, L. Cipelletti, G. Petekidis and A. B. Schofield, Phys. Rev. Lett., 2009, 102, 085703.
102. W. van Megen and S. R. Williams, Phys. Rev. Lett., 2010, 104, 169601.
103. M. D. Ediger, Annu. Rev. Phys. Chem., 2000, 51, 99–128.
104. I. Chang and H. Sillescu, J. Phys. Chem. B, 1997, 101, 8794–8801.
105. W. Götze and L. Sjogren, Rep. Prog. Phys., 1992, 55, 241–376.
106. M. Fuchs, I. Hofacker and A. Latz, Phys. Rev. A, 1992, 45, 898–912.

---