How do soft particle glasses yield and flow near solid surfaces?

Abstract

We use fluorescence microscopy and particle tracking velocimetry to image the motion of concentrated emulsions and microgel suspensions near solid surfaces. The local deformation involves a combination of slip and bulk flow, which are found to be controlled by surface forces. With smooth surfaces, two slip mechanisms are identified depending on whether particle–wall interactions are repulsive or weakly attractive. In the former case, the materials yield uniformly and the local rheology can be mapped on the macroscopic flow curve. In the latter case, yielding is non-uniform which reveals a continuous distribution of states from the immediate vicinity of the smooth surface to the bulk of the material. The effect of the surface is long-ranged and decays exponentially with the distance, which can be described by a non-local fluidity model. Our results establish a link between surface forces, lubrication and yielding in soft glassy or jammed materials and open new routes to manipulate their flow through the surface chemistry of the confining boundaries.

---

1. Introduction

Soft particle glasses are concentrated suspensions made of soft particles packed at large volume fractions where they interact via soft elastic repulsions. A non-exhaustive list of soft particle glasses includes concentrated emulsions, soft particle suspensions, colloidal pastes and foams. These materials behave like solids at rest but flow like liquids under large stresses. This so-called yielding transition is associated with the specific dense, amorphous structure of the materials. The particles are trapped in the local environment formed by their neighbours (the “cages”) and develop repulsive forces at contact, which restrict and even arrest macroscopic motion. If a stress exceeding the cage elasticity (the yield stress) is applied, they can escape from their cages and move over long distances. In recent years, a significant amount of theoretical and experimental work based on concepts and approaches borrowed from the physics of glassy molecular and polymeric materials has been devoted to understanding bulk properties of soft particle glasses, such as yielding,¹ flow,^2–5aging and slow dynamics.^6–9

In practice, however, macroscopic motion depends not only on the bulk rheology but also on the shearing surfaces. Recent studies have reported various phenomena that point to a strong influence of boundaries on the rheology of yield stress materials. It is well known that concentrated suspensions tend to slip rather than flow near smooth, poorly adhering surfaces.¹⁰ When slip occurs, the deformation is localized to a thin solvent layer adjacent to the wall, resulting in an apparent rheology completely different from the bulk rheology.^11–16 Another intriguing phenomenon is the formation of fluidized shear-bands, which coexist with an unsheared plug flow or a slowly sheared region. Although shear-banding apparently occurs in many different materials—emulsions,^16,17 colloidal crystals,¹⁸ hard sphere glasses,¹⁹ star polymer solutions,^20,21 and Lennard–Jones glasses²²—the underlying physics remains a subject of active research. Recently shear-banding has been described as a mechanical instability associated with thixotropy,^16,17,23aging,²⁴ flow-concentration coupling,²⁵ solid–liquid coexistence,²¹ or start-up flows.²⁶ This picture is probably not universal since parameters like the physical roughness of the shearing surfaces,²⁷ or the confinement of the material^18,19,28,29 play a significant role. These various observations suggest that surface rheology can be distinct from bulk rheology, which raises a number of important questions. How are surface phenomena connected to bulk rheology? Which properties of the shearing surface influence one particular scenario? Is there any underlying universality or does every system exhibit a different behaviour?

In this paper we answer these questions for the case of concentrated emulsions and microgel suspensions with purely repulsive interactions, which constitute two model non-thixotropic yield stress materials. We use high resolution fluorescence microscopy and particle tracking techniques to investigate slip, yielding, and flow of these materials sheared along smooth surfaces with well-controlled surface properties. We identify the existence of two slip mechanisms associated with elastohydrodynamic or simple hydrodynamic lubrication, depending on whether the particle–wall interactions are weakly attractive or repulsive, respectively. Both concentrated emulsions and microgel suspensions start to yield above the yield point. We find a strong influence of the nature of the particle–wall interactions. Flow is homogeneous when the materials are sheared using rough or smooth repulsive surfaces. However, at the same applied stress, the local shear rate is larger near adhering surfaces than near non-adhering and rough surfaces. The velocity profiles near adhering surfaces decay exponentially over a characteristic length, which is unique for a given sheared material. Our study shows that the flow of soft particle glasses is influenced over macroscopic distances by the nature of the surfaces. Rough surfaces, smooth repulsive surfaces and smooth attractive surfaces are all different and yield distinct velocity profiles.

2. Experiments and techniques

2.1. Materials

In this study, we use an emulsion and two microgel suspensions, which are dispersions of soft deformable particles packed into an amorphous structure and interacting through repulsive interactions.⁵Table 1 summarizes the characteristics of the different materials studied.

Table 1 Materials studied in this work and their main rheological properties: microgels in water and glycerol solution (M[w/g]), microgels in water (M[w]), and emulsion in water and glycerol solution (E[w/g]). C: polymer weight concentration; ϕ: volume fraction; R: particle hydrodynamic radius; η₀: solvent viscosity; G₀: low-frequency plateau modulus; σ_y: yield stress; γ_y: yield strain; V* = γ²_yG₀R/η₀: characteristic slip velocity (see Section 4.1)

	C/g g^−1	ϕ	R/μm	η 0/mPa s^−1	G 0/Pa	σ y/Pa	γ y	V*/μm s^−1
M[w/g]	0.016	—	0.22	5.4	110	5.2	0.047	10
M[w]	0.016	—	0.22	1	150	8.1	0.054	96
E[w/g]	—	0.75	1.5	7.9	160	6.2	0.040	50

---

The emulsion is a concentrated dispersion of silicone oil droplets (viscosity: 0.5 Pa s) in a continuous aqueous phase consisting of a water and glycerol mixture with a mass concentration of water of about 60%. The composition of this mixture was finely adjusted so that its refractive index matches that of the oil, resulting in perfectly transparent samples. The emulsion was prepared by adding silicone oil to the water/glycerol mixture containing a large amount of the non-ionic surfactant Triton X (∼30 wt%), under continuous stirring.¹² The final emulsion was carefully washed to eliminate the excess surfactant. The residual surfactant concentration is smaller than 10⁻² g g⁻¹, which guarantees the absence of attractive depletion interactions between the droplets. The size distribution is moderately polydisperse, with a mean droplet radius R ≅ 1.5 μm.

The microgels are colloidal networks prepared by standard emulsion polymerisation techniques using the two monomers ethyl acrylate and methacrylic acid, and a crosslinker.³⁰ The crosslink density can be characterized by the average number of monomer units between two crosslinks, N_x = 140. The products of the synthesis were carefully cleaned by ultrafiltration in order to remove surfactants, unreacted monomers and initiators. The polymer content was accurately determined by drying. Samples were prepared by diluting the stock solutions in de-ionised water (M[w]) or in a mixture of water and glycerol (M[w/g]). As for emulsions, the composition of the water and glycerol mixture was adjusted to have a refractive index matching that of the polymer. The properties of the microgel suspensions reported below do not depend significantly on the nature of the suspending medium. At low pH, the microgels are insoluble in aqueous media and, hence, they are essentially hard particles. Around pH ≅ 9, the methacrylic acidic units become ionized and the microgels swell. In dilute suspensions, the swollen particles have a spherical shape with a hydrodynamic radius R ≈ 220 nm.³¹ At concentrations corresponding to volume fractions of particles above random close-packing (C_m ≅ 0.9 wt%), the microgels pack into concentrated pastes with solid-like properties. In this regime, the particles shrink when the concentration increases, so that the volume fraction ϕ is not a good measure of concentration.³¹ In the following we use the mass concentration as the control parameter.

2.2. Particle tracking microvelocimetry

We have measured the velocity profiles in the concentrated emulsion and the microgel suspensions using Particle Tracking Velocimetry (PTV). The experimental setup is shown in Fig. 1. Experiments were performed in a rotational shear cell (Linkam CSS 450) consisting of a rotating glass plate at the bottom and a fixed microscope coverslip at the top (D = 22 mm). The plate–plate geometry is parallel within ±2 μm over the entire shear zone. The angular velocity of the moving plate (ω) is varied using a micro-step motor between 10⁻³ rad s⁻¹ and 10 rad s⁻¹. The gap between the two plates (h) can be adjusted between 150 μm and 1500 μm; the experiments reported in this work were performed for h = 750 μm. The shear cell was mounted on a direct epifluorescence microscope from Zeiss equipped with a 50× objective (numerical aperture = 0.6; working distance = 3 mm). The samples were seeded at very low concentration (10⁻² wt%) with fluorescent microspheres (radius: 0.5 μm). They were illuminated with light at wavelength λ = 495 nm using a HBO lamp equipped with the appropriate excitation filter (500AF25 from Melles Griot) and a band pass dichroic mirror (FT515 from Zeiss). The light emitted by the fluorescent tracers passes through the dichroic mirror and a detection filter before going to the detector (BP535/30 from Zeiss).

Observations were made at a fixed radius r = 7.5 mm from the axis of rotation. While the observation radius was fixed, its variation would allow for similar variation in applied velocity. In most of the experiments reported here, the flow was scanned vertically by moving the shear cell relative to the objective by increments of about 5 μm. In some instances, we were able to use smaller increments of 1 to 2 μm to explore the vicinity of the surface. The vertical position of the shear cell was controlled independently using a mechanical sensor (Mitutoyo Digimatic). The images were recorded by a progressive scan CCD camera (Pulnix TM6301) connected to a frame grabber (Matrox Meteor II). At each depth we collected up to 200 images of 109 μm × 72 μm each at a rate of 20 frames per second. The local velocity was obtained by tracking the positions of about 100 tracers (in-plane resolution: 0.15 μm) from frame to frame using image processing techniques. We have verified that the local density of tracer particles was constant throughout the gap even after long shearing periods.

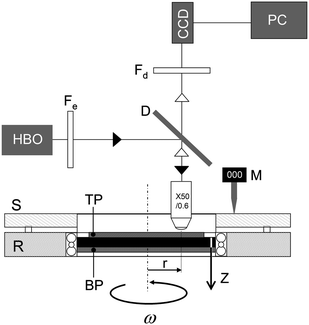Fig. 1 Schematic of the experimental setup. The optical part is composed of a HBO lamp, an emission filter F_e, a dichroic mirror D, a microscope lens 50×, and a detection filter F_d. S and R denote the stator and the rotor of the shearing stage, respectively. The microgel suspensions and the emulsion are sheared between a fixed plate at the top (TP) and a mobile plate at the bottom (BP), which rotates at angular velocity ω. M is a digital mechanical sensor. The origin of the vertical axis (z = 0) is located on the top plate. The observation position is at a distance r = 7.5 mm from the centre of rotation.

2.3. Surface preparation

The mobile plate at the bottom of the rotational cell was coated with waterproof sandpaper to avoid slip (roughness: 20 μm). The fixed plate at the top was a microscope coverslip with negligible residual roughness (<5 nm) but different surface properties. We used three surfaces: (i) glass coverslip surfaces; (ii) polymer surfaces; (iii) glass surfaces grafted with a cationic silane brush. The polymer surfaces were prepared by carefully sticking commercially available scotch tape on glass coverslips (thickness ≅ 0.1 mm). Scotch tape is made from a derivative of cellulose acetate; once correctly applied and cleaned according to the above procedure, it provides a smooth defect free polymer film with negligible roughness. The cationic silane coating was prepared as follows. The glass surface to be coated was first plasma-cleaned for 30 s and carefully dried. It was then immersed into a solution of chloroform containing 1 wt% of (p-chloromethyl)phenyltrichlorosilane (CMPTS). After 60 s of incubation, the surface was carefully rinsed with clean chloroform in order to remove the excess reactant and dried at 90 °C for one hour. Finally, the grafted layer of CMPTS was quaternized by immersing in triethylamine for 24 hours under gentle stirring. After preparation, the glass, polymer and cationic silane surfaces were cleaned with ethanol and deionized water and stored in a dry atmosphere.

These surfaces interact with microgel particles and emulsion droplets through surface forces, which may be attractive or repulsive depending on their nature and the composition of the dispersions. Following the seminal work of Princen, silicone oil droplets dispersed in water do not adhere to hydrophilic glass surfaces wetted by the continuous phase but tend to stick onto hydrophobic polymer surfaces.³² The case of microgel suspensions has been analyzed theoretically in a recent publication, which discussed the influence of particle–wall interactions on the extent of wall-slip.¹⁵ Two mechanisms were shown to govern the magnitude of slip velocity and its variation with shear stress, depending on the nature of the particle–surface interactions. Different sources of attractive interactions were identified and quantified: dispersive, hydrophobic and ionic forces. For instance, microgel particles in water–glycerol solutions over glass are subject to a net attraction due to dispersive forces, while microgels in water over cationic surfaces experience electrostatic attraction with the surface, due to ionic forces between the negatively charged particles and the positive surface. Attractive particle–wall interactions promote adhesion of the microgel particles to the surface. Wall-slip is then governed by a balance between the lift force due to the lubrication flow of solvent between the particles and the wall, and the particle–surface attractive forces. When the refractive indices of the polymer constituting the particles, solvent and surfaces are matched, dispersive forces are negligible, which happens for suspensions of microgels in water–glycerol mixtures over polymer surfaces. This favours the formation of a solvent (water) layer between the particles and the surface, which enhances wall-slip even at very low applied stresses. Both mechanisms were validated through a modified elastohydrodynamic lubrication model that accounts for the effect of short-range interactions for various particle–surface combinations.

2.4. Rheology

Table 1 summarizes the rheological properties of the emulsion and microgel suspensions investigated in this work. They have been measured using shear rheology. The rheometer is a MCR 501 stress-controlled apparatus from Anton-Paar. Conventional characterizations of the viscoelastic properties, yield stress and flow curves were conducted with a cone and plate geometry (diameter: 50 mm; angle: 2°) using rough surfaces to avoid wall slip. The samples were sealed in a water-saturated environment to minimize evaporation. We performed oscillatory dynamic tests and steady-shear measurements using the following methodology that is detailed elsewhere.²¹ Prior to any measurement, the suspensions and the emulsions were presheared by applying a high shear rate (≅10³ s⁻¹ for the microgel suspensions and ≅10² s⁻¹ for the emulsion) for a time interval of 60 s. Preshearing fully fluidizes the solution and brings it to reproducible steady-state flow.⁷

For oscillatory measurements the samples were allowed to relax for 3000 s after preshearing, until which time the increase in storage modulus became very slow and the samples were considered to have reached a quasi-equilibrium state. An oscillatory strain of sufficiently small amplitude (<0.01) and frequency varying between 0.001 Hz and 15 Hz was then applied. The storage modulus exhibits a low frequency plateau while the loss modulus a minimum at frequency ω_m. The low frequency storage modulus G_o is taken as the storage modulus at frequency ω_m.

To connect the flow properties at the microscopic scale to the macroscopic rheology, we also measured the apparent flow curvesσ([small gamma, Greek, dot above]) of the emulsion and microgel suspensions sheared with exactly the same combination of surfaces and protocol as in the PTV experiments. The bottom plate of the rheometer was covered with waterproof sandpaper and the coverslip was mounted on a disposable shaft provided by Anton Paar using a custom-made adaptor. Care was taken during measurements to ensure that the sample had reached steady state at each applied velocity. To that end, after the sample was presheared as described above, the shear rate was decreased to a smaller value and the stress was recorded until it reached a constant value.

3. Experimental results

3.1. Velocity profiles between two rough surfaces

When sheared with rough surfaces at stresses just above the yield stress, microgel suspensions and concentrated emulsions flow homogeneously in the whole range of shear rates accessible by our experimental setup (10⁻⁴ s⁻¹ < [small gamma, Greek, dot above] < 10 s⁻¹). This is illustrated in Fig. 2 which shows typical results obtained for microgel suspensions. Similar results have been obtained for concentrated emulsions. The velocity varies linearly between 0 at the fixed wall and V₀ = ωr at the moving wall (ω: angular velocity; r: radius of observation). There is no evidence of wall slip, confirming that the flow curves measured using rough surfaces are representative of the bulk flow properties. Shear-banding or fracture phenomena sometimes encountered in yield stress materials are also absent.^17,20,33 This establishes that concentrated materials with purely repulsive interactions flow homogeneously when they are sheared between rough surfaces. These results confirm previous results we had obtained at much lower spatial resolution.¹¹

Fig. 2 Velocity profiles in the microgel suspension M[w] sheared between two rough surfaces. For each profile, the angular velocity of the rotating plate is indicated on the top axis (in mrad s⁻¹); the arrows point to the values of the velocity at the wall (V₀ = rω with r = 7.5 mm).

3.2. Velocity profiles near non-adhering smooth surfaces

To investigate how concentrated emulsions and microgels flow near smooth surfaces, we now adopt a shearing configuration where the fixed plate is a smooth coverslip and the movable plate is covered with rough sandpaper. Fig. 3 presents results obtained for the concentrated emulsion E[w/g] against the glass surface and the water–glycerol microgel suspension M[w/g] against the polymer surface, respectively. In Section 2.3, we have referred to this situation as non-adhering as in both cases no net attraction is expected between the particles and the substrate. At low velocities, we observe total slip of the material on the smooth surface resulting in solid body motion. The bulk velocity is equal to the applied velocity down to distances from the surface comparable to the spatial resolution of the setup in the vertical direction (≅2 μm). This indicates that the first layer of droplets in the emulsion (R ≅ 1.5 μm) slips on the substrate. For the microgel suspension (R ≅ 0.2 μm), experiments with better spatial resolution would be required to draw a similar conclusion. At higher applied velocities, the emulsion and the microgel suspension yield and we detect a non-zero velocity gradient in the bulk in addition to wall slip. The shear rate is constant throughout the gap indicating that yielding is uniform throughout the material.

Fig. 3 Velocity profiles of different samples sheared between a rough surface and a smooth repulsive surface. (a) Emulsion E[w/g] with a smooth glass coverslip (at z = 0 μm); (b) microgel suspension M[w/g] sheared with a smooth polymer coated coverslip (at z = 0 μm). The smooth surface is the fixed plate at z = 0 μm and the rough surface is the rotating plate at z = 750 μm. For each profile, the angular velocity of the rotating plate is indicated on the top or right axis (in mrad s⁻¹) and the arrow points to the value of the wall velocity (V₀ = rω with r = 7.5 mm).

3.3. Velocity profiles near weakly adhering smooth surfaces

In Fig. 4 we present velocity profiles in the opposite situation where there exist attractive forces between the particles of the dispersion and the substrate. The velocity profile in Fig. 4(a) is obtained for the emulsion E[w/g] sheared along the polymer surface. The emulsion exhibits total slip resulting in solid-body motion at low applied velocities. It yields at large velocity so that the velocity profiles then involve a combination of wall slip and bulk deformation. Very surprisingly, the velocity profiles are found to be non-linear, the velocity gradient being greater near the smooth surface than near the rough surface. Fig. 4(b) shows the velocity profiles in the microgel suspension M[w/g] sheared along the glass surface. Interestingly, slip is negligible within the experimental accuracy at any velocity suggesting that the particles strongly adhere to the surface. Again, the bulk deformation associated with yielding is non-uniform as for the emulsion E[w/g]. Fig. 4(c) shows the velocity profiles in the microgel suspension M[w] (the solvent is now pure water) sheared along the cationic surface which is attractive for negatively charged microgels. As expected, slip is negligible at any shearing velocity and yielding is non-uniform. Finally, the velocity profile in Fig. 4(d) is obtained for the microgel suspension M[w] sheared along the polymer coated surface. This time the suspension does not adhere totally to the surface resulting in total slip and plug flow at low applied velocities; yielding is non-uniform with a clear curvature in the velocity profiles.

Fig. 4 Velocity profiles of various samples sheared between a rough surface and a smooth attractive surface. (a) Emulsion E[w/g] sheared with a smooth polymer coated coverslip; (b) microgel suspension M[w/g] sheared with a smooth glass coverslip; (c) microgel suspension M[w] with a smooth coverslip covered with a cationic silane coating; (d) microgel suspension M[w] with a smooth polymer coated coverslip. The smooth surface is the fixed plate at z = 0 μm and the rough surface is the rotating plate at z = 750 μm. For each profile, the angular velocity of the rotating plate is indicated on the top axis (in mrad s⁻¹) and the arrow points to the value of the wall velocity (V₀ = rω with r = 7.5 mm).

3.4. Summary of results

The high spatial resolution of the PTV technique developed in the present work has led to unexpected and interesting results concerning the slip and yielding properties of jammed dispersions near smooth surfaces. By comparing Fig. 2, 3 and 4 that illustrate the flow properties of three materials (an emulsion and two microgel suspensions) sheared along surfaces with different surface chemistry, we can draw the following conclusions: (i) although sufficiently attractive surfaces restrain or even suppress slip just like roughened surfaces, they lead to distinctly non-linear velocity profiles at the local scale in the yielding regime (Fig. 4); (ii) for a given material, yielding and flow turn from uniform to non-linear when the surface forces switch from repulsive to attractive [see 3(a)versus4(a) and 3(b)versus4(b)]; (iii) two chemically similar dispersions differing only by the nature of the solvent sheared along the same surface can have drastically distinct flow behaviors [see 3(b)versus4(d)]. To summarize, the nature of the local forces between particles of the dispersion and the shearing surface greatly influences the flow over relatively long distances. While the so-called repulsive or non-adhering case conforms to conventional expectations (total slip and uniform yielding at low and high velocities, respectively), the attractive or adhering situation is characterized by non-uniform yielding with non-constant shear rate throughout the shearing gap. This result could not be anticipated from previous experimental observations, which had insufficient spatial resolution (Δz ≅ 30 μm).¹² In the next section we analyze and interpret these surprising results.

4. Analysis and discussion

4.1. Influence of short range forces on slip properties below the yield stress

Fig. 5 shows the variations of the slip velocity V_S as a function of the applied stress σ for the concentrated emulsion E[w/g] sheared along the glass and polymer coated coverslips. We present two sets of data: (i) direct measurements obtained by extrapolating the velocity profiles to z = 0; (ii) indirect measurements from macroscopic rheology in the plug flow regime where V_S = h[small gamma, Greek, dot above] ([small gamma, Greek, dot above] is the apparent shear rate and h the gap).¹² We identify two regimes of variations separated by a sharp discontinuity at σ = σ_y. In the yielding regime (σ ≥ σ_y), the slip velocity V_S increases linearly with the stress σ, with a slope which is independent of the surface chemistry at the smooth wall. In the plug flow regime (σ < σ_y), the slip velocity measured at a given stress is very sensitive to the nature of the surfaces. It is larger for the glass surface, which is wetted by the continuous phase of the emulsion, than for the polymer surface which is hydrophobic and partially adhering. The slip velocity vanishes at a stress σ_S, the so-called sliding yield stress which we identify as the stress below which the material sticks to the surface therefore suppressing wall slippage. The enlargement shown in the inset of Fig. 5(a) shows that σ_S is negligible for the glass coverslip while it is finite for the polymer coverslip.

Fig. 5 (a) Slip velocity of emulsion E[w/g] at the weakly adhering polymer surface (□, ■) and the non-adhering glass surface (○, ●) versus stress; the inset shows an enlargement of the main graph near the sliding yield stress σ_S (∼1 Pa and 2.5 × 10⁻² Pa, respectively). Data are obtained from PTV (full symbols) and rheology (open symbols). (b) Slip velocity against the excess stress for σ < σ_y.

To characterize the variations in the domain σ < σ_y, the slip velocity is plotted in Fig. 5(b) as a function of the excess stress σ − σ_S. This representation shows that the slip velocity exhibits two different behaviours depending on the nature of the surfaces. For the weakly adhering polymer coverslip, the slip velocity is well represented by the quadratic variation: V_S/V_y ∝ [(σ − σ_y)/(σ_y − σ_S)]², where V_y is the slip velocity for σ = σ_y. For the non-adhering glass coverslip, σ_S is much smaller than σ_y and the slip velocity varies linearly.

These results can be understood in the light of our recent theory of slip in dispersions of soft deformable particles.¹⁵ We model the dispersions as elastic spheres of radius R which are randomly packed in a disordered, jammed configuration. When subjected to shear stresses smaller than the yield stress, the dispersions behave like solid materials with zero bulk deformation and slip at the smooth surface down to the velocity where the adhesion between the particles and the shearing surface is too weak to restrain the slipping motion. The slip motion and the apparent deformation are localized to a thin layer of solvent of thickness δ, which lubricates the contacts between the first layer of particles and the wall. The macroscopic stress is determined by the viscous drag associated with the flow of solvent inside the lubricating film: σ ≈ η₀V_S/δ. The thickness of the lubricating film results from a subtle interplay between surface forces, particle deformation and hydrodynamic effects. At and above the yield stress, we can hypothesize that δ is simply proportional to the distortion of the particles, i.e. δ ∝ γ_yR with the yield strain γ_y being constant, so that the stress–velocity relationship must be linear, in agreement with the results shown in Fig. 5. Moreover, since σ_y = G₀γ_y, we deduce easily that the slip velocity at the yield point is proportional to the characteristic velocity V* = γ²_yG₀R/η₀. Below the yield stress, the situation is more complicated and it is necessary to take into account the nature of the particle–wall interactions.¹⁵

When the wall is preferentially wetted by the continuous phase, adhesion between the particles and the wall is negligible so that the particles or droplets can slip even at very low stresses (σ_S ≅ 0). The thickness of the lubricating film is determined by the amplitude of surface forces and is independent of the slip velocity. Again δ is constant and the stress–velocity relationship is expected to be linear. We have referred to this mechanism as hydrodynamic lubrication (HL). Slip driven by hydrodynamic lubrication explains the results shown in Fig. 5 for the emulsion sheared along the glass surface.

When the particles are attracted to the wall, the particles stick to the surfaces until the stress reaches a value σ_S. However any relative motion between squeezed particles and surface deforms the particles asymmetrically, which results in a lift force opposing the bulk osmotic pressure and maintaining a lubricating film. We have referred to this mechanism as elastohydrodynamic lubrication (EHL). The sliding yield stress σ_S can be estimated as the stress at which the lift force becomes larger than the attractive interactions and EHL becomes effective. For σ_S ≪ σ ≪ σ_y, the thickness of the lubricating film varies with the slip velocity^11,12 as δ ∝ (η₀V_SR/G₀)^1/2, which leads to (V_S/V_y) ∝ (σ/σ_y)² where the characteristic velocity V_y ∝ γ²_y(G₀R/η₀) so that V_y = V* again. These predictions for slip driven by elastohydrodynamic lubrication are in good agreement with the experimental results presented in Fig. 5 for the emulsion sheared along the polymer coated surface.

4.2. Identification of slip regimes

In Fig. 5, the onset of yielding is signalled by a sharp kink, which suggests that the slip properties are completely modified above σ_y. The relation V_S = f(σ) becomes difficult to interpret because the stress is affected by the bulk deformation beyond the slip layer. To circumvent this difficulty, we plot the slip velocity V_S against the applied velocity V₀ at the rough surface. The results are shown in Fig. 6 where both velocities are scaled by the characteristic velocity V*. At low velocities, we have the simple relation V_S = V₀ which characterizes the total slip regime where the materials move in solid body fashion. At higher applied velocities, the materials begin to yield and the slip velocity is considerably affected by the bulk deformation beyond the lubricating film. The slip velocity increases slowly with the applied velocity as V_S ≈ V^0.27₀, independent of the nature of surface chemistry. Presently, we do not have a quantitative theory to explain the variations of the slip velocity in this regime. Our results for slip velocity capture the subtle effect of surface interactions on the point of transition from a total slip to a yielding regime.

Fig. 6 Variations of the slip velocity V_S with the applied velocity V₀ for different materials and particle–surface combinations: ■: M[w/g] against the polymer coated surface; ▲: E[w/g] against the glass surface; △: E[w/g] against the polymer coated surface; ◇: M[w] against the polymer coated surface; ○: M[w]: against the cationic surface. Both V_S and V₀ are scaled by the characteristic velocity V*. Note that full symbols refer to non-adhering situations while open symbols are for weakly adhering cases. The continuous line represents the variations expected for the slip velocity in the total slip regime (no yielding); the dashed lines have a slope equal to 0.27 in double logarithmic coordinates.

4.3. Coexistence of multiple deformation states near smooth attractive surfaces

In Fig. 7 we compare the macroscopic flow curves obtained from conventional shear rheology to the local flow curves, which relate the shear rates at the smooth and rough walls to the shear stress. The latter were obtained by fitting quadratic polynomial equations to the velocity profiles. We use the non-dimensional set of coordinates (, [small sigma, Greek, tilde] = σ/σ_y), where with i = RS and SS represent shear rates at the rough and smooth surfaces, respectively. This set of non-dimensional coordinates is known to collapse the flow curves of different materials onto a master curve.⁴ In the inset, the macroscopic flow curves of emulsions and microgel suspensions measured with rough surfaces do form a master curve that is well described by the phenomenological Herschel-Bulkley equation. The main graph shows that the local flow curves of the emulsion and microgel suspensions sheared between rough and smooth non-adhering surfaces are equal i.e., [small gamma, Greek, dot above]_RS = [small gamma, Greek, dot above]_SS and coincide with the macroscopic flow curve measured with rough surfaces. In the configuration where the smooth surface is adhering, [small gamma, Greek, dot above]_RR and [small gamma, Greek, dot above]_SS are different. The shear rates at the rough surface ([small gamma, Greek, dot above]_RS) still fall on the macroscopic flow curve but the shear rates at the smooth surface ([small gamma, Greek, dot above]_SS) follow a distinct stress–shear rate relationship, which is well described by the power law: . This confirms that yielding near smooth adhering surfaces differs from that near rough surfaces on one hand and smooth repulsive surfaces on the other. The shear rates at the smooth and rough sides quantify two different states of the sheared materials, which coexist at the same stress. The shear rate varies continuously from [small gamma, Greek, dot above]_SS to [small gamma, Greek, dot above]_RS indicating that there exists a continuous distribution of states separating the immediate vicinity of the smooth surface and the bulk of the material. This makes the observed behavior completely different from conventional shear-banding where the two coexisting states of the material are separated by a sharp interface.

Fig. 7 Macroscopic and local rheology of the emulsion E[w/g] and the microgel suspension M[w/g]. The inset shows the collapse of the macroscopic flow curves measured by conventional rheology in the absence of slip (○: E[w/g]; □: M[w/g]). The continuous line is the Herschel–Bulkley equation: with K = 21; n = 0.52 ± 0.02. The main graph represents local rheology data measured in the emulsion E[w/g] (○, ⊗, ●) and the microgel suspension M[w/g] (□, ⊠, ■) for smooth adhering [⊗, ⊠: 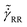; ●, ■: ; from Fig. 4(a) and (b)] and non-adhering surfaces [○, □; from Fig. 3(a) and (b); note that ]. The inset shows that this equation describes the master curve obtained by collapsing the flow curves of the emulsion E[w/g] and the microgel suspension M[w/g].

4.4. Characterization of banded slip profiles and discussion

The results above suggest that the surfaces contribute independently to the deformation so that the velocity profile can be written as the superposition of a contribution arising from the shear deformation at the rough side and a disturbance introduced by the smooth surface. We thus have: V(z) = V_RS(z) − V_e(z), where V_RS(z) = V₀ − (h − z)[small gamma, Greek, dot above]_RS is the linear velocity profile created by the rough surface (V₀ is the applied velocity) and V_e(z) is the extra non-linear term associated with the smooth surface. Since V₀ and [small gamma, Greek, dot above]_RS are known experimentally, V_e(z) can be calculated without any further assumption for each of the experimental velocity profiles shown in Fig. 4(a)–(d). The results are presented in Fig. 8, which shows the reduced velocity Ṽ_e(z) = V_e(z)/V_e(0) against the distance from the smooth surface. V_e(z) has been scaled by V_e(0) = V₀ − h[small gamma, Greek, dot above]_RS − V_S to account for the fact that we are dealing with different surface–particle combinations having different degrees of adhesion. For each studied material, i.e. the emulsion and the two microgel suspensions, the data collapse on a master curve, irrespective of the applied velocity and slip velocity. Both master curves are well described by single exponentials, Ṽ_e(z) = exp (−z/ξ), where ξ = 150 ± 10 μm for both microgels M[w] and M[w/g] and ξ = 70 ± 10 μm for emulsions E[w/g]. This exponential form is robust and cannot be substituted by other analytical functions like power laws.

Fig. 8 Variations of the non-dimensional excess velocity determined from the velocity profiles presented in Fig. 4versus the distance to the smooth surface. The symbols are the same as in Fig. 4 to designate materials and rotation rates. The full lines are best fits to exponentials. The inset shows the variations of the characteristic length ξ with the rotation rate for the concentrated emulsion E[w/g] (○), the microgel suspension M[w/g] sheared along the glass surface (●), and the microgel suspension M[w] sheared along the cationic silane surface (⊕) and the polymer surface (⊗).

In conclusion our analysis provides the following expression for the velocity profiles:

In order to evaluate the accuracy of this expression, each of the velocity profiles in Fig. 4 has been fitted to eqn (1) using ξ as the only free parameter. The fits go through the experimental data with little deviation. The inset of Fig. 8, which shows the variations of the characteristic length ξ with the angular velocity of the shearing stage, exemplifies the result that ξ does not depend on the applied velocity.

4.5. Discussion

The exponential variation of the velocity profiles near the smooth surfaces points to some continuous modification of the sheared microstructure from the smooth surface into the bulk. It is also important to note that the characteristic length ξ is much larger than the particle size indicating that the effect of surfaces is non-local. Although details of the difference between surfaces are uncertain at this time, we speculate that the plasticity of the materials plays a central role. Asperities of the rough surface induce shear-activated rearrangements at different length scales, which, above the yield stress, propagate into the bulk and cause macroscopic flow. Near the yield stress, the dominant contribution to the stress comes from rearrangements and, according to MCT theories³ and recent simulations,³⁴ it is expected to increase as: σ ∝ [small gamma, Greek, dot above]^m_RS, i.e., with m ≈ 0.1. At a smooth adhering surface, the mechanical constraints exerted by the attractive particle–surface interactions affect plastic rearrangements with the surface and, accordingly, the way by which the materials yield. The exponential velocity profiles near smooth adhering surfaces suggest a self-similar distribution of rearrangements so that at a distance z to the wall, only rearrangements smaller than z can exist. This issue has been discussed in a different context for the case of granular materials and foams that also exhibit exponential shear bands near solid boundaries.^35–37 Near the wall, it is likely that clusters of close-packed particles slip relative to each other instead of rearranging. The plane between the first and second layer of particles constitutes the perfect realization of a slip plane but far away there are other weak regions that allow slipping.³⁸ The stress is now dominated by viscous effects arising from internal slip. It can be estimated by considering that internal slip is driven by the EHL mechanism as for simple slip near smooth solid surfaces. For two well-aligned planes slipping parallel to each other with relative velocity V_S = [small gamma, Greek, dot above]R, we then predict: σ/σ_y ∝ (η₀[small gamma, Greek, dot above]/G₀)^1/2, i.e.. The results presented in Fig. 7 support this interpretation. The experimental exponent is smaller than expected as the model does not account for the actual distribution of slip planes.

4.6. Relation with fluidity model

In this section we interpret the shape of the velocity profiles in emulsions and suspensions sheared between a rough and a smooth adhering surface in the light of a simple phenomenological model of glassy dynamics.^8,39 Along the lines of the fluidity model,^28,29 we characterize the rate of plastic rearrangements associated with yielding by a fluidity parameter f, which relates the variation of the shear rate to the local stress above yielding through f = [small gamma, Greek, dot above]/σ. The fluidity depends on the elastic and plastic rearrangements of the packed particles making up the material,³⁹ which may be influenced by the roughness of the surface, its motion and the confinement of the material.^28,29,40 In this description, the flow behavior is non-local because the rearrangements depend on many particles, and their effect on the elastic field is long ranged. Coarse-grain models of these dynamics result in a fluidity that obeys the relationshipwhere f_b = [small gamma, Greek, dot above]_b/σ is the fluidity of the bulk suspension at the applied stress σ and bulk shear rate [small gamma, Greek, dot above]_b, and ξ is the flow cooperativity length. This model has been used to describe the flow of compressed emulsions in microchannels.²⁸

Let us apply this formalism to concentrated emulsions and microgel suspensions sheared between rough and smooth attractive surfaces. The fluidity near the static, smooth surface at z = 0 is f_SS while it is assumed to be f_RS = f_b at the rough surfaces situated at z = h. Note that the fluidity near the smooth surface must be greater than in the bulk resulting in higher shear rates near the smooth surface. Solving eqn (1) with these boundary conditions gives

The velocity field V(z) is determined from dV/dz = σf(z), which may be integrated with the boundary condition V(h) = V₀ to give

where [small gamma, Greek, dot above]_RS and [small gamma, Greek, dot above]_SS are the shear rates at the rough and smooth surface, respectively. This expression can be written in the form:

Interestingly solution (5) can be identified as the experimental form (1). The non-dimensional excess velocity Ṽ_e(z) is given by

which, in the limit of (h − z)/ξ, h/ξ ≫ 1, reduces to the simple exponential form Ṽ_e(z) = exp (−z/ξ) seen in Fig. 8. In fact the decaying exponential closely matches eqn (4) for all values of z, which provides a convenient way to describe the experimental velocity profiles.

5. Conclusions

By directly imaging the flow of two soft glassy or jammed materials sheared between two surfaces, we have been able to measure the velocity profiles with particle scale resolution. Our results point to a strong influence of the roughness and surface chemistry of the boundaries. Smooth surfaces promote wall slip but the microscopic mechanism depends on the nature of particle–surface interactions. Below the yield stress, slip at repulsive surfaces is associated with hydrodynamic lubrication and while it is controlled by elastohydrodynamic lubrication forces at weakly attractive surfaces. Slip can be totally suppressed when the particles strongly adhere to the surfaces. These findings conform to recent theoretical predictions concerning the slip properties of soft particle dispersions.¹⁵

Above the yield stress the lubrication mechanisms are affected by the bulk deformation beyond the slip layer. While non-thixotropic materials are considered to flow homogeneously when sheared in homogeneously stress fields,^16,41 here we show that the mechanism by which purely repulsive concentrated emulsions and microgel suspensions yield and flow near solid surfaces depends on the properties of the surfaces. Near rough and smooth repulsive surfaces, yielding is uniform and the bulk properties are recovered. Near smooth attractive surfaces, yielding is non-uniform revealing a coexistence of dynamical states forming a boundary layer of macroscopic thickness. This scenario is different from shear-banding observed in thixotropic materials where a flowing region coexists with a nearly arrested band.^16,17,23 Experimentally, the velocity profile in the boundary layer is well described by an exponential function with a well-defined characteristic length, which can be derived using the concept of non-local fluidity. In their study of the pressure-driven flow of concentrated emulsions in confined channels, Goyon et al. suggested the existence of a cooperative length that would be intrinsic to the material.²⁸ Here, by contrast, the region adjacent to the smooth surface has the characteristic features of a slip layer related to specific boundary conditions and elastohydrodynamic lubrication.

These results pose several important and fundamental questions. What is the microscopic origin of the length ξ over which yielding is influenced by the smooth surface? Which microscopic parameters and/or material properties determine the value of ξ? How does the interplay between adhesion and plasticity result in internal slip over macroscopic distances? This urges direct determination of the sheared microstructure near different surfaces and for theoretical and numerical investigations of the interplay between adhesion and shear-induced plasticity.

Acknowledgements

We are indebted to Ilias Iliopoulos for assistance in the preparation of cationic charged surfaces. JRS and RTB gratefully acknowledge financial support from the ACS Petroleum Research Fund (grant 41236-AC9) and the National Science Foundation (grant 0854420). The experimental work was performed in part when JRS was visiting ESPCI ParisTech with the support of an Eiffel Excellence scholarship from the French Ministry of Foreign Affairs. MC acknowledges support from the Softcomp European Network of Excellence.

References

1. G. Petekidis, D. Vlassopoulos and P. N. Pusey, J. Phys.: Condens. Matter, 2004, 16, S3955.
2. P. Sollich, F. Lequeux, P. Hébraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020–2024.
3. (a) M. Fuchs and M. E. Cates, Phys. Rev. Lett., 2002, 44, 248304; (b) M. Fuchs, Adv. Polym. Sci., 2010, 236, 55–116.
4. M. Cloitre, R. Borrega, F. Monti and L. Leibler, Phys. Rev. Lett., 2003, 90, 068303.
5. R. T. Bonnecaze and M. Cloitre, Adv. Polym. Sci., 2010, 236, 117–161.
6. S. Fielding, M. E. Cates and P. Sollich, J. Rheol., 2000, 44, 323–369.
7. M. Cloitre, R. Borrega and L. Leibler, Phys. Rev. Lett., 2000, 85, 4819–4822.
8. C. Derec, G. Ducouret, A. Ajdari and F. Lequeux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061403.
9. E. H. Purnomo, D. van den Ende, S. A. Vanapalli and F. Mugele, Phys. Rev. Lett., 2008, 101, 238301.
10. H. A. Barnes, J. Non-Newtonian Fluid Mech., 1999, 81, 133–178.
11. S. P. Meeker, R. T. Bonnecaze and M. Cloitre, Phys. Rev. Lett., 2004, 92, 198302.
12. S. P. Meeker, R. T. Bonnecaze and M. Cloitre, J. Rheol., 2004, 48, 1295–1320.
13. L. Bécu, S. Manneville and A. Colin, Phys. Rev. Lett., 2006, 96, 138302.
14. P. Ballesta, R. Besseling, L. Isa, G. Petekidis and W. C. K. Poon, Phys. Rev. Lett., 2008, 101, 258301.
15. J. Seth, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2008, 52, 1241–1268.
16. J. Paredes, N. Shahidzadeh-Bonn and D. Bonn, J. Phys.: Condens. Matter, 2011, 23, 284116.
17. P. Coussot, J. S. Raynaud, F. Bertrand, P. Moucheront, J. P. Guilbaud, H. T. Huynh, S. Jarny and D. Lesueur, Phys. Rev. Lett., 2002, 88, 218301.
18. I. Cohen, B. Davidovitch, A. B. Schofield, M. P. Brenner and D. A. Weitz, Phys. Rev. Lett., 2006, 97, 215502.
19. L. Isa, R. Besseling and W. C. K. Poon, Phys. Rev. Lett., 2007, 98, 198305.
20. S. A. Rogers, D. Vlassopoulos and P. T. Callaghan, Phys. Rev. Lett., 2008, 100, 128304.
21. B. M. Erwin, D. Vlassopoulos and M. Cloitre, J. Rheol., 2010, 54, 915–939.
22. F. Varnik, L. Bocquet, J.-L. Barrat and L. Berthier, Phys. Rev. Lett., 2003, 90, 095702.
23. P. C. F. Møller, S. Rodts, M. A. J. Michels and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041507.
24. S. Fielding, M. E. Cates and P. Sollich, Soft Matter, 2009, 5, 2378–2382.
25. R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2010, 105, 268301.
26. T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301.
27. T. Gibaud, C. Barentin and S. Manneville, Phys. Rev. Lett., 2008, 101, 258302.
28. J. Goyon, A. Colin, G. Ovarlez, A. Ajdari and L. Bocquet, Nature, 2008, 454, 84–87.
29. J. Goyon, A. Colin and L. Bocquet, Soft Matter, 2010, 6, 2668–2678.
30. M. Cloitre, R. Borrega, F. Monti and L. Leibler, C. R. Phys., 2003, 4, 221–230.
31. R. Borrega, M. Cloitre, I. Betremieux, B. Ernst and L. Leibler, Europhys. Lett., 1999, 47, 729–735.
32. H. M. Princen, J. Colloid Interface Sci., 1985, 105, 150–171.
33. F. Pignon, A. Magnin and J.-M. Piau, J. Rheol., 1996, 40, 573–587.
34. J. R. Seth, PhD thesis, The University of Texas, Austin, 2008.
35. D. M. Mueth, G. F. Debregeas, G. S. Karczmar, P. J. Eng, S. R. Nagel and H. M. Jaeger, Nature, 2000, 406, 385–389.
36. G. Debrégeas and C. Josserand, Europhys. Lett., 2000, 52, 137–143.
37. G. Debrégeas, H. Tabuteau and J.-M. di Meglio, Phys. Rev. Lett., 2001, 87, 178305.
38. A. J. Liu, S. Ramaswamy, T. G. Mason, H. Gang and D. A. Weitz, Phys. Rev. Lett., 1996, 76, 3017–3020.
39. P. Hébraud and F. Lequeux, Phys. Rev. Lett., 1998, 81, 2934–2937.
40. L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001.
41. D. Bonn and M. Denn, Science, 2009, 324, 1401–1402.

---