Polymethine dyes for all-optical switching applications: a quantum-chemical characterization of counter-ion and aggregation effects on the third-order nonlinear optical response†
Sukrit
Mukhopadhyay
,
Chad
Risko
,
Seth R.
Marder
and
Jean-Luc
Brédas‡
*
School of Chemistry and Biochemistry and Center for Organic Materials for All-Optical Switching (COMAS), Georgia Institute of Technology, Atlanta, Georgia 30332-0400. E-mail: jean-luc.bredas@chemistry.gatech.edu
First published on 17th July 2012
Abstract
Polymethine dyes have recently demonstrated promise for all-optical switching applications at telecommunications wavelengths as they can combine large refractive optical nonlinearities with low single-photon and two-photon optical losses. Here, we use density functional theory and symmetry-adapted cluster configuration interaction calculations to characterize model streptocyanine molecules. We first consider the isolated, closed-shell cationic molecules and then complexes formed by the molecules with chloride counter-ions and a series of aggregates. Our goal is to examine the influence of: (i) the presence of counter-ions and (ii) aggregation on the electronic structure and nonlinear optical properties. We find that the counter-ions increase the degree of bond-length alternation along the cyanine backbone, while aggregation significantly reduces the energy window between the lowest one-photon and two-photon excited states. Our results provide insight toward the design of new polymethine derivatives that could maintain large figures-of-merit for all-optical switching applications in the solid state.
I. Introduction
Understanding the relationship between molecular architecture and the resulting electronic, optical and electrostatic properties is key to the design of new chromophores for nonlinear optical (NLO) applications.1–6 Organic molecular materials are of interest for applications such as electro-optic modulation,6 three-dimensional fluorescence microscopy,7,8 optical memory,9,10 nanofabrication,11,12 or optical power limiting.13–15 Recently, interest in all-optical switching (AOS) applications at telecommunications wavelengths (λ = 1300–1550 nm; ħω = 0.95–0.80 eV) has been renewed following the observation that polymethine dyes in dilute solutions can present a large AOS figure-of-merit.16,17 In all-optical switching,18–23 an incoming light beam carrying information is modulated/routed by another light beam without intervention from an electrical signal. The AOS figure-of-merit is given as the ratio between the real part of the third-order nonlinear optical response, Re(γ(−ω; ω,ω,ω)), which modulates the refractive index,24 over the imaginary part, Im(γ(−ω; ω,ω,ω)), which relates to the strength of two-photon absorption and corresponding optical losses. Ideally, the figure-of-merit should be ≫4π.17In most π-conjugated chromophores, the lowest two-photon (2P) excited state appears close to the lowest one-photon (1P) excited state. As a result, for AOS applications, the input frequency ω would need to be kept at less than half the optical gap in order to prevent large 2P optical losses, leading to a large detuning factor Δ, see Fig. 1 (left). However, polymethine dyes have an unusually large gap between the energies of the lowest 1P and 2P excited states,3 in contrast for instance to the situation in polyene-like chromophores; specifically, in polymethine dyes, E(2P) is generally ∼1.7E(1P). The consequence for AOS is that the input frequency ω can now be placed much closer to E(1P), resulting in a small detuning factor Δ, while having 2ω in the energy window between E(1P) and E(2P), see Fig. 1 (right). Another benefit of polymethine dyes is their generally very sharp low-energy absorption bands, which means that a small Δ does not lead to appreciable absorption losses. Thus, the Re(γ) can be significantly increased via pre-resonant enhancement (small Δ) while the Im(γ) can be kept small due to negligible 1P and 2P absorption losses. These features are manifested in selenopyrylium-based cyanine dyes examined by Hales et al. which exhibit AOS figures-of-merit reaching a value as large as 190 in dilute chloroform solutions.17
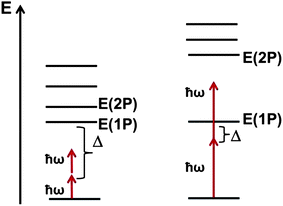 | ||
| Fig. 1 Schematic energy-level diagram for traditional π-conjugated chromophores (left) and polymethine molecules (right). The input photon energy is represented by ħω; the detuning between the input photon energy and the energy of the lowest 1P excited-state is given by Δ. | ||
Practical AOS applications, however, require high number densities of chromophores which are typically not attainable in solution but can be reached in films either of the pure chromophores or of the chromophores dissolved in a polymer at high loadings. Since polymethine dyes are highly polarizable ions well known to be prone to aggregation, it is important to evaluate the impact of the presence of counter-ions and of aggregation effects on their geometric and electronic structure and their nonlinear optical properties. This represents the primary goal of our work. To the best of our knowledge, earlier theoretical studies3,16,17,25–29 of the NLO response of polymethine chromophores have not examined these effects in detail.
We note that investigations of the linear and nonlinear optical properties of molecular aggregates have been reported, based either on the Frenkel-exciton Hamiltonian30 or using a master equation approach.31 These models predict that aggregation can produce strong shifts in absorption maxima and lead to size-enhanced optical nonlinearities, scaling as Nα, where α ≥ 2 and N is the number of molecules in the aggregate.32 Such size enhancement is due to the delocalization of the electronic excitations within the aggregates, leading to concentration of all available oscillator strengths into one or a few excited states, a phenomenon closely related to exciton super-radiance.33 On the other hand, inhomogeneity in the aggregates can lead to localization of the electronic excitations on one or a few molecules and result in the breakdown of the size enhancement effects.34 A drawback of these models, however, is that they do not consider the possible changes in the geometry of the polymethine molecules upon aggregation, which we will show below can be substantial.
To investigate the effect of counter-ions and aggregation on the electronic and optical properties of polymethine dyes, we consider the model streptocyanine molecules shown in Fig. 2. We first examine the five-carbon cyanine ([5-dimethylamino-2,4-pentadienylidene]dimethylammonium), denoted as 5C. This choice is motivated by the fact that the linear and NLO properties of this molecule have been experimentally studied in various solvents, in the solid state, and with different counter-ions.35–37 We then consider the longer cyanines 7C (N,N-dimethyl-N-(7-(dimethylamino)hepta-2,4,6-trienylidene)ammonium) and 9C (N,N-dimethyl-N-(9-(dimethylamino)nona-2,4,6,8-tetraenylidene)ammonium). We take chloride as a representative counter-ion and build aggregates by creating dimeric structures of the molecule–counter-ion complexes.
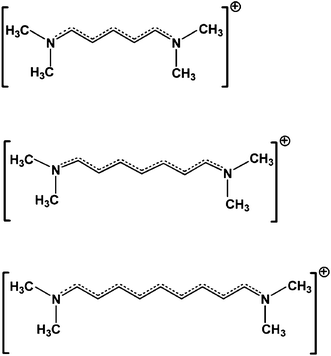 | ||
| Fig. 2 Chemical structures of the 5C, 7C and 9C streptocyanines. | ||
II. Computational methodology
Ground-state geometry optimizations of the model streptocyanines without and with the chloride counter-ion were performed with the ωB97X-D functional and the cc-pVDZ basis set.38 Hereafter, we will refer to the cyanine-chloride complex as a monomer. The long-range corrected ωB97X-D functional was introduced by Chai and Head-Gordon39,40 as a means to take dispersion interactions into account through inclusion of empirical atomic-pair dispersion interactions. Geometry optimizations of the monomer complexes were performed using the counterpoise correction41 in order to avoid basis-set superposition errors (BSSE). Optimizations in the presence of an implicit dielectric medium were carried out with the conductor polarizable continuum model (CPCM);42–45 a dielectric medium representing acetonitrile (ε = 37.5) was used for direct comparison with experiment. At the end of all optimizations, frequency calculations were conducted to assess that the geometries correspond to minima on the ground-state potential energy surface (PES).As the initial starting point of the geometry optimizations of the monomers, the Cl− ion was placed in the molecular (xy) plane of the individual cyanine molecules.46 The optimized geometry of the monomer then served as the starting point for the geometry optimizations of the aggregate dimer. To describe the variety of possible aggregate dimer configurations, we evaluated the binding energy as a function of distance between the two monomer units for four distinct configurations,47 with the intermolecular distance varied along the z-direction. After obtaining the optimal distance between two monomer units, one of the monomer units was displaced individually along the x-axis, or the y-axis, and/or rotated about the z-axis. The initial geometries obtained in this way are then used for further full optimizations of the aggregate dimer configurations at the ωB97X-D/cc-pVDZ level. Here, the 5C cyanine was used as the reference system. Further details on the optimization procedure are presented in the ESI†.
In all instances, an important parameter characterizing the optimized geometries is the degree of bond-length alternation, BLA, along the polymethine backbone. Here, we consider the mean BLA (mBLA), calculated by averaging the absolute differences in the lengths of successive bonds over the entire carbon–carbon backbone.
Symmetry-adapted-cluster/configuration interaction (SAC-CI) calculations48,49 were performed to obtain the vertical excited-state energies, transition dipole moments, and state dipole moments. The SAC-CI method was selected for these evaluations as it incorporates both single and higher-order particle–hole excitations within a chosen active space, a feature that is essential in the description of the 2P states and the third-order NLO properties. In addition, the method is size consistent and therefore allows for a comparison of the electronic and optical properties of the monomers and dimers. A further description of the SAC-CI method is provided in the ESI†. The active space to describe the particle–hole excitations of the monomers included 40 high-lying occupied orbitals and 110 low-lying unoccupied orbitals, while that for the dimers was set to 80 high-lying occupied orbitals and 220 low-lying unoccupied orbitals (i.e., an active space twice as large as that for the monomers); the molecular orbitals used for the SAC-CI calculations were obtained at the Hartree–Fock (HF) – cc-pVDZ level of theory. All geometry optimizations and SAC-CI calculations were performed using the Gaussian09 package.50
The SAC-CI results were then used as input for a sum-over-states (SOS) perturbation approach to evaluate the third-order polarizabilities (γ(ω;ω,−ω,ω)). The magnitudes of γ were computed at the static limit (ħω = 0.0 eV) and with incident photon wavelengths of 1300 nm (ħω = 0.95 eV) and 1550 nm (ħω = 0.80 eV). The general SOS expression for γ is given by eqn. (1):51,52
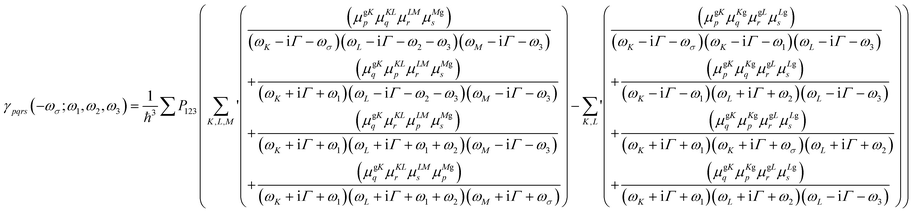 | (1) |
An essential-state model expression can be obtained from the general expression if one makes the reasonable assumption to consider only the few low-lying excited states strongly dipole-coupled to the ground state and the upper-lying states strongly coupled to them. Here, ten excited states are found to be sufficient in the context of essential-state calculations to reproduce the fully converged γ values. Such essential-state models have been shown to work well in predicting the third-order response in both polymethine and polyene-like systems.5,17,54–56
In order to better rationalize the factors affecting the magnitude of γ, it is also very useful to refer to the three-term model (γ3-term), which approximates the full SOS γ expression of eqn (1) by only considering the lowest excited state (e) and a few of the higher-lying excited states (e′) coupled to it (eqn. (2)):54
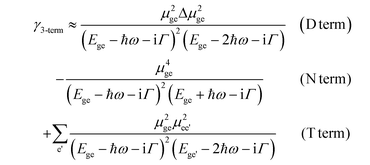 | (2) |
III. Results and discussion
A. Monomer and dimer geometric configurations
We start with 5C as it is the shortest molecule and serves as reference for the series. It is important to note that the crystal structure of the 5C molecule in the presence of a chloride counter-ion is known,57 see Fig. 3, which justifies our choice of this counter-ion for the present work; these crystal data will provide a guide for the assessment of the DFT-optimized monomer and aggregate geometries. The crystal structure is composed of three-dimensional arrays of stacked molecules that, within a stack, form a J-aggregate structure. The unit cell is composed of four cyanine molecules that provide for a number of dimer configurations when considering adjacent molecules within the same stack or on separate stacks. In the crystal structure, the mBLA is 0.049 Å,57 a value that is considerably larger than that expected for isolated, symmetric cyanine molecules. We note that the crystal structures of larger cyanines are usually obtained with bulkier counter-ions58–62 and present packing motifs that are dependent on the nature of counter-ions.60–62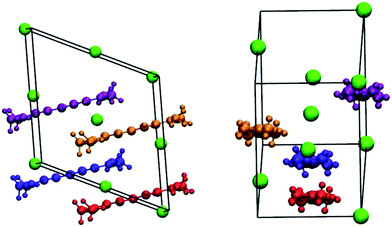 | ||
| Fig. 3 Sketch of the unit cell of 5C with chloride counter-ions, adapted from ref. 57 (the chloride ions are given in green, while the cyanines are noted in orange and blue for molecules within the same stack and in gold and magenta for molecules in neighboring stacks). | ||
The cyanine-counter-ion monomer complexes were evaluated both with and without an imposed C2 symmetry axis (represented by the red line in Fig. 4). Imposition of C2 symmetry leads to geometric configurations that are energetically destabilized relative to the symmetry-relaxed structures. While the energetic difference between the symmetry-imposed and relaxed structures is merely 0.3 kcal mol−1 in 5C, it increases substantially with increasing chain length: 2.9 kcal mol−1 for 7C and 6.1 kcal mol−1 for 9C. The symmetry-relaxed geometries, therefore, were used to construct the aggregate dimer configurations. At this stage, it is important to keep in mind that a symmetric configuration of the chloride counter-ion would modify considerably the structural parameters (in particular, by reducing the degree of bond-length alternation along the cyanine backbone) and, as a consequence, the electronic properties; this in turn would have a substantial influence on the linear and nonlinear optical properties of the cyanine molecules.
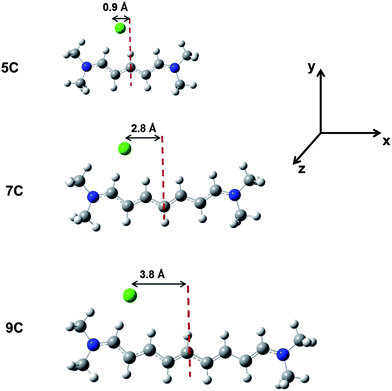 | ||
| Fig. 4 Optimized ground-state structures of the 5C, 7C and 9C monomers as determined at the ωB97X-D/cc-pVDZ level of theory (carbons are represented in grey; hydrogens, white; nitrogens, blue; and chlorides, green). The distances between the Cl− counter-ion and the axis passing through the central carbon atom of the cyanine chain, are also indicated. The x-axis lies along the long axis of the cyanine molecule, the y-axis is along the short axis and directed towards the chloride counter-ion, and the z-axis is perpendicular to the molecular plane. | ||
Importantly, the unconstrained geometries reveal that the chloride ion prefers to localize towards one of the terminal N-atoms, approximately along the axis of the adjacent C–H bond within the xy-plane, as illustrated in Fig. 4. As a result, most of the positive charge carried by the cyanine is drawn towards that end of the molecule. In the case of 5C, the distance between the chloride counter-ion and the nearest N-atom on the cyanine chain is on the order of 4.20 Å (ε = 1)–4.29 Å (ε = 37.5), which compares well with the 4.20 Å distance in the crystal.57
Fig. 5 depicts the evolution of the mean BLA in the cyanine series: (i) for the isolated molecules; (ii) for the monomer complexes in the ‘gas phase’, ε = 1; and (iii) for the monomer complexes in the presence of a dielectric medium with ε = 37.5, which represents acetonitrile (further structural details are presented in the ESI†). The mBLA for the isolated, symmetric cyanines remains small but slightly increases with molecular size (as a modest degree of BLA starts building away from the center of the molecule).63
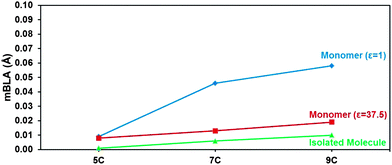 | ||
| Fig. 5 Mean BLA (mBLA) for: (i) the isolated, symmetric cyanine molecules (green triangles); (ii) the cyanine-counter-ion monomer complexes with ε = 1 (blue diamonds); and (iii) the cyanine-counter-ion monomer complexes in a dielectric medium with ε = 37.5 (red squares), at the ωB97X-D/cc-pVDZ level of theory. The solid lines simply serve as a guide to the eye. | ||
In the presence of the counter-ion with no dielectric screening (monomer with ε = 1), the situation becomes very different due to the asymmetric location of the Cl− ion. As seen in Fig. 4, the asymmetry increases especially strongly in going from 5C to 7C. As a result, the mBLA jumps from ∼0.01 Å in 5C to reach ∼0.045 Å in 7C and ∼0.06 Å in 9C. In the presence of a highly polar dielectric medium (ε = 37.5), however, the screening of the electrostatic interactions between counter-ion and cyanine leads to a slight increase in cyanine-counter-ion distance and to a more symmetric geometry; as a result, the mBLA reduces to a level close to that of the isolated molecule. Thus, the environmental parameters are found to exert a very significant influence on the geometric structure of the cyanine molecules.
A large number of configurations were evaluated at the outset of the aggregate dimer examination, with four configurations carried forward for further study; the basis for the selections is described in the ESI†. A first structure, hereafter denoted as the perpendicular configuration, has the x-axes (long axes) of the two cyanine molecules (nearly) perpendicular to each other. The other three configurations represent possible H- or J-type aggregates and have their respective x- and y-axes aligned. Two structures (cofacial-x and cofacial-z) are derived by starting with a perfectly cofacial arrangement of the cyanine-counter-ion dimer and then rotating one of the cyanine molecules about either the x-axis (so that the counter-ions are on the same side of the dimer) or the z-axis (so that the counter-ions are on opposite ends of the dimer); in both cases, one counter-ion lies in the +y-direction while the other lies in the −y-direction. The fourth structure corresponds to a parallel-displaced configuration, which is derived from the cofacial-z configuration by displacing one monomer with respect to the other along the x-axis. Side-view illustrations of these configurations are depicted for 5C in Fig. 6 (those for 7C and 9C can be found in the ESI†).
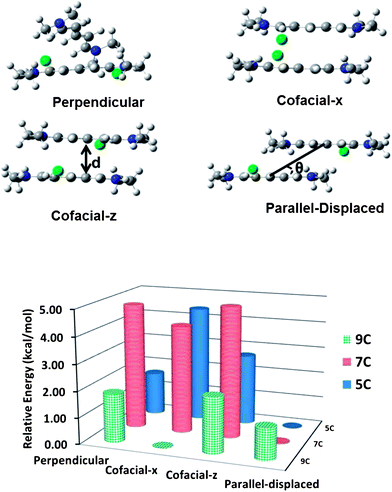 | ||
| Fig. 6 Top: representations of the 5C aggregate dimers in the perpendicular, cofacial-x, cofacial-z, and parallel-displaced configurations, as determined at the ωB97X-D/cc-pVDZ level of theory (carbons in grey, hydrogens in white, nitrogens in blue, and chlorides in green); d represents the plane-to-plane distance and θ is the slip angle between the cyanine monomers (the slip angle is defined as the angle between the axis joining the centers of mass of the cyanine molecules and the molecular planes). Bottom: relative total energies of the dimer configurations with respect to the lowest energy configuration (i.e., the parallel-displaced configuration in 5C and 7C and the cofacial-x configuration in 9C). | ||
For 5C, the relative total energies of the dimer configurations (Table 1) follow the order: parallel-displaced < perpendicular < cofacial-z < cofacial-x. In the parallel-displaced configurations, one of the cyanine monomers is displaced along the long-axis (x-axis), resulting in minimal steric interactions between the terminal methyl groups. The cofacial structures present high-energy configurations, of which the cofacial-x configuration is the highest due to the larger steric interactions between the individual monomers and the closer proximity of the like charges. The total energy of the perpendicular configuration is intermediate between the parallel and cofacial configurations.
| Cyanine | Structural parameter | Optimized geometry | |||
|---|---|---|---|---|---|
| Perpendicular | Cofacial-x | Cofacial-z | Parallel-displaced | ||
| a If the slip angle is 90°, the centers of mass of the individual monomers are exactly on top of one another; values smaller than ∼20° indicate a J-aggregate configuration.64 b The plane–plane distance for 5C in the perpendicular configuration is omitted because the planes of the two chains are not parallel to each other. c The slip angle is the mean of each slip angle measured with respect to each of the monomers. | |||||
| 5C | p–p | —b | 3.46 | 3.48 | 3.10 |
| Slip anglea | 79.27c | 76.31 | 71.33 | 39.18 | |
| RTE | 1.65 | 4.41 | 2.69 | — | |
| 7C | p–p | 3.28 | 3.58 | 3.53 | 2.94 |
| Slip anglea | 82.87 | 89.50 | 76.58 | 36.98 | |
| RTE | 4.77 | 4.10 | 4.94 | — | |
| 9C | p–p | 3.28 | 3.54 | 3.56 | 3.26 |
| Slip anglea | 87.91 | 70.08c | 77.48 | 20.74 | |
| RTE | 1.84 | — | 2.11 | 1.20 | |
The main structural parameters of the aggregates are provided also in Table 1. The plane-to-plane distances in the perpendicular and cofacial configurations are similar to the center-to-center distances, indicating that the centers of the individual monomers in the dimer configurations are (nearly) aligned. These distances vary significantly (as expected) for the parallel-displaced configuration, as evident from the large slip angle; in this configuration, the center-to-center distance is 6.31 Å and the slip angle is ∼39°, which is very similar to the corresponding values in the crystal structure of 5C where two adjacent cyanine molecules in the same stack have a center-to-center distance of 6.25 Å and a slip angle of 35°.57
Trends with regard to the structural parameters and energies are similar in 7C. Interestingly, the perpendicular, cofacial-x and cofacial-z configurations are all higher in energy compared to the parallel-displaced configuration by over 4.0 kcal mol−1. For 9C, however, the picture changes markedly. The cofacial-x configuration now becomes slightly energetically stabilized relative to the parallel-displaced configuration as one of the monomers in the cofacial-x configuration rotates to avoid interactions between neighboring methyl groups. This compares well with experimental data65 that indicate that an increase in chain length leads to an H-aggregate configuration becoming favored over a J-aggregate structure. In addition, the slip angle for the parallel-displaced configuration for 9C is the smallest across the series and is a result of the large displacement (by more than half the length of the cyanine) between the monomers. It is useful to note that, with respect to the 5C and 7C aggregate dimers, the energetic variation among the different 9C aggregation configurations is smallest.
In general, these results underline that the energies of the different configurations are a strong function of the counter-ion position. Furthermore, the smaller differences in the total energy values for the 9C aggregate dimers (and some of the 5C dimers) suggest a larger probability towards the appearance of multiple configurations in an amorphous thin film. On the other hand, the parallel-displaced configuration for 7C is the most stable configuration by a larger margin, pointing to a potentially more homogeneous aggregate morphology in 7C, provided thermodynamic control is possible.
The mBLAs for the four optimized dimer configurations are presented in Fig. 7 (selected bond lengths are tabulated in the ESI†). For 5C, the mBLA is largest (0.047 Å) in the cofacial-x configuration, which is mainly a result of the localization of the chloride counter-ions at the same end of the dimer. Interestingly, the mBLA of this configuration closely matches the experimental value for the 5C molecule in the crystal (0.049 Å). Although the cyanine molecules along the stacks found in the crystal are packed in a parallel-displaced configuration, the positions of the counter-ions from the neighboring stacks provides an asymmetric environment around the cyanine molecules, similar to the cofacial-x configuration.
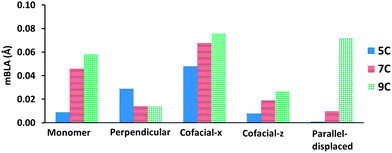 | ||
| Fig. 7 Values of mBLA (Å) for the optimized dimer configurations of 5C, 7C and 9C (ε = 1) at the ωB97X-D/cc-pVDZ level of theory. | ||
The trends in mBLA for 7C are equivalent to those of 5C with the exception of the perpendicular configuration (in 5C, the mBLA is larger as one of the monomer units is displaced towards a terminal nitrogen of the other subunit, resulting in a more symmetry-broken structure). In 9C, it is noteworthy that the mBLA of the parallel-displaced configuration is significantly larger than in the other two cyanine systems. This is due to a large displacement between the monomers that leads to a sharing of the chloride counter-ions by two nitrogen atoms on separate monomers. The mBLA for 9C in the parallel-displaced configuration ends up similar to that of the cofacial-x configuration.
Overall, the results point to the strong influence of the positions of the chloride counter-ions relative to the cyanine molecules on the mBLA in the solid state. If the chloride ions are able to maintain a symmetrical location with respect to the cyanine chains (symmetric dimers), the mBLA remains small; the mBLA of a symmetric dimer (in the cofacial-z configuration) can even be smaller than that of the corresponding monomer. On the other hand, the mBLA can increase considerably with aggregation if the chloride counter-ions are placed on the same ends of the dimer (as in the cofacial-x configuration). Such differences in mBLA can result in large differences in the magnitude of γ, vide infra.
B. One- and two-photon excited-state properties
The vertical excitation energies, oscillator strengths, differences in state dipole moments, and two-photon absorption cross-sections of the cyanine monomers (with ε = 1) are provided in Table 2. As is typical of polymethines, the energies of the lowest two-photon states are calculated to be somewhat lower than twice the energy of the first excited state.| E ge (μge) | μ ee′ | Δμ | δ 2P | |
|---|---|---|---|---|
| 5C | 3.30 (3.68) | — | 0.68 | 0.3 |
| 6.27 (0.10) | 1.29 | 0.42 | 1.18 × 103 | |
| 6.41 (0.46) | 3.35 | 0.55 | 2.70 × 104 | |
| 7C | 2.70 (4.07) | — | 6.71 | 1.0 × 102 |
| 5.22 (0.56) | 4.36 | 1.53 | 4.09 × 104 | |
| 5.52 (0.51) | 3.24 | 2.34 | 4.37 × 104 | |
| 9C | 2.57 (5.13) | — | 12.18 | 5.2 × 102 |
| 4.57 (0.96) | 7.27 | 3.09 | 1.21 × 104 | |
| 4.94 (0.71) | 3.47 | 4.34 | 2.67 × 104 |
As a result of the quasi-symmetric location of the counter-ion in 5C and the small mBLA, the 2P absorption cross-section for the first excited state (1P) is negligible. (We recall that in centrosymmetric molecules, the selection rules are such that any excited state is either 1P-allowed and 2P-forbidden, or the opposite). On the other hand, when we consider the broken-symmetry structure of 5C corresponding to the crystal geometry (mBLA = 0.049 Å), the first excited state gains a significant two-photon absorption cross-section (1.7 × 102 GM).
For the longer cyanines, as expected, the transition energies decrease with increased conjugation length. Due to the broken symmetry, the electronic states have significant state dipole moments; as a result, there can appear large differences in state dipole moments between the 1P excited state and the ground state (large Δμ in eqn (2)); such a situation enhances the D term of eqn (2) and leads to a large 2P absorption cross-section into the first excited state. The consequence is substantial Im(γ) values at telecommunications wavelengths (even if the transition is somewhat off-resonant), thus lowering the AOS figure-of-merit.
The higher excited states for the longer cyanines have large 2P absorption cross-sections that reach 104 GM. This is in particular related to the presence of large transition dipole moments μee′ between the lowest and higher-lying excited states, inducing a large T term in eqn (2).
Table 3 provides the vertical excitation energies, oscillator strengths, and 2P cross-sections for the aggregate dimers. We first turn our attention to the 5C and 7C dimers. The lowest two excited states result from the coupling between the 1P states of the two monomers.66 Because of the orientations of the molecules, in the perpendicular configuration, the two lowest excited states are both optically allowed. In the other configurations, the first excited state is optically weak, while the second is strong. This result is consistent with an H-type aggregation66 even in the case of the parallel-displaced configuration; in the latter instance, we recall that the slip angle is ∼40°, while a slip angle <∼20° is generally required to switch to a J-aggregate structure64 (we discuss this issue in more detail in the ESI†). Overall, the 2P absorption cross-sections for the lowest two excited states (arising from the D and T terms in eqn (2), respectively) are seen to increase with the magnitude of mBLA.
| Perpendicular Ege (μge) [δ2P] | Cofacial-x Ege (μge) [δ2P] | Cofacial-z Ege (μge) [δ2P] | Parallel-displaced Ege (μge) [δ2P] | |
|---|---|---|---|---|
| 5C | 3.15 (3.20) [4.5] | 3.48 (0.80) [7.3] | 2.94 (0.01) [9.1] | 3.30 (0.00) [1.4] |
| 3.52 (3.53) [37.4] | 3.54 (3.99) [24.0] | 3.46 (4.92) [0.0] | 3.38 (5.27) [0.0] | |
| 4.95 (0.47) [40.0] | 4.24 (1.08) [68.7] | 4.55 (0.02) [18.8] | 4.43 (0.48) [125] | |
| 7C | 2.36 (3.87) [4.8] | 2.42 (0.19) [7.4] | 2.04 (0.00) [5.2] | 2.45 (0.14) [15.6] |
| 2.58 (4.77) [30.9] | 3.26 (3.91) [114] | 2.75 (5.82) [0.0] | 2.63 (6.59) [0.0] | |
| 2.99 (1.14) [86.8] | 3.68 (0.29) [30.2] | 2.89 (0.00) [143] | 3.42 (0.30) [71.2] | |
| 9C | 2.10 (4.93) [92.7] | 2.79 (2.25) [49.0] | 1.63 (0.00) [67.1] | 2.88 (6.67) [0.0] |
| 2.17 (5.72) [18.2] | 3.20 (6.04) [547] | 2.48 (7.42) [0.0] | 3.05 (0.00) [1.2 × 103] | |
| 4.11 (0.18) [2.3 × 104] | 3.45 (0.67) [22.0] | 2.48 (0.00) [58.7] | 3.82 (0.00) [310] |
It is also useful to note that the variations in lowest excited-state energies among the different dimer configurations point to a broadening of the optical absorption spectrum upon (uncontrolled) aggregation. Such a broadening is in agreement with the typical evolution observed in going from dilute solutions to thin films.67
Table 3 also collects the characteristics of the third excited state, which is derived from the 2P excited states of the monomers. Very importantly, we observe that the energy gap between the 2P-like third excited state and the 1P-like first two excited states markedly reduces in each of the dimer configurations compared to the monomers. In addition, there appear a number of excited states with appreciable 2P absorption cross-sections, whose energies are lower than twice the energy of the lowest excited state. Thus, the energy window available between the 1P and 2P excited states of individual cyanines closes down in the aggregates, as sketched in Fig. 8 for the 7C species.
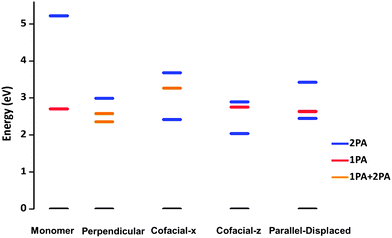 | ||
| Fig. 8 Evolution of the 1P and 2P excited states in 7C from the monomer to the dimer configurations. | ||
In the 9C analogs, similar trends are found. However, we note that the lowest two excited states of the parallel-displaced configuration now present the characteristics of a J-type aggregate, with the first excited state strongly optically allowed and the second one presenting a large 2P cross-section. This is consistent with the small slip angle, ∼20°, optimized for that configuration.
C. Third-order polarizabilities (γ(ω;ω,−ω,ω))
We now turn to a discussion of the static (γstat; ħω = 0.0 eV) and dynamic (γdyn; ħω = 0.80 and 0.95 eV) third-order polarizabilities Re(γ(ω;ω,−ω,ω)) in the cyanine monomers (ε = 1) and dimers, see Table 4. In the case of the monomers, for 5C, the γstat and γdyn values are negative and comparable to those of the isolated, symmetric molecule as the mBLA remains small. The magnitude of γ increases only slightly with the frequency of the incident photon through pre-resonant enhancement, as the detuning factor is large due to the high energy of the first excited state. The magnitudes of γstat and γdyn for the 7C monomer are similar to those of 5C, mainly because of the cancellation of two opposite effects, the positive effect due to the increase in conjugation length being compensated by the appearance of a larger mBLA (in other words, referring to eqn (2), the increase in the magnitude of the N term is compensated by a similar increase in the D term); for 7C, the magnitudes of γstat and γdyn are roughly four times smaller compared to those for the symmetric structure (see the ESI†). Even more pronounced differences are observed in case of 9C. Given the large mBLA imposed by the strongly asymmetric position of the counter-ion, the values of γstat/dyn even become positive in the optimized monomer geometry, due to the large state dipole moment of the first excited state resulting in a dominant D term in eqn (2); we note that the γstat/dyn values are strongly negative in the symmetric structure of the isolated molecule (see the ESI†).| Cyanine | Monomer | Perpendicular | Cofacial-x | Cofacial-z | Parallel-displaced |
|---|---|---|---|---|---|
| Re(γstat) | |||||
| 5C | −220 | −410 | −170 | −640 | −920 |
| 7C | −290 | −2800 | −530 | −3190 | −4870 |
| 9C | +170 | −9760 | −1220 | −7800 | −950 |
| Re(γ1550dyn) | |||||
| 5C | −270 | −490 | −190 | −760 | −1110 |
| 7C | −300 | −3940 | −570 | −4050 | −6670 |
| 9C | +920 | −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
−1300 | −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
−700 |
| Re(γ1300dyn) | |||||
| 5C | −300 | −520 | −200 | −820 | −1200 |
| 7C | −250 | −4540 | −570 | −4330 | −7610 |
| 9C | +1810 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
−1250 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
−370 |
In the case of the dimers, again, the overall finding is that the magnitude of γ closely follows mBLA, with a larger mBLA leading to a smaller (absolute) value of Re(γ). We underline that the perpendicular and cofacial-z configurations of the 9C dimers can reach very large Re(γ) static and dynamic values, on the order of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 × 10−36 esu; however, the significant two-photon absorption cross-sections of the low-lying excited states in these configurations, see Table 3, are expected to lead to substantial optical losses and thus to a small AOS figure-of-merit.
670 × 10−36 esu; however, the significant two-photon absorption cross-sections of the low-lying excited states in these configurations, see Table 3, are expected to lead to substantial optical losses and thus to a small AOS figure-of-merit.
IV. Conclusion
In this work, we have examined the effects of counter-ions and aggregation on the geometric structure and (linear and nonlinear) optical properties of model cyanine dyes containing from 5 to 9 carbons in the backbone. In the isolated cyanine molecules, the geometric structure remains symmetric and the mBLA is small (<0.01 Å).When the counter-ion is present, it tends to localize towards one of the terminal nitrogen atoms. This results in a symmetry-broken geometry of the cyanine backbone (with the extent of symmetry breaking increasing with chain length) and a significant enhancement of the mBLA values. In terms of optical properties, large mBLA values induce substantial 2P cross-sections into the lowest-lying excited states, which is a source of extensive optical losses detrimental to all-optical switching applications. These adverse counter-ion effects strongly reduce upon consideration of a highly polar dielectric medium that screens the electrostatic interactions between counter-ion and cyanine.
Aggregation of the cyanines is also observed to result in adverse effects with regard to AOS applications. First, aggregation can lead to an increased mBLA compared to the cyanine-counter-ion complex; the more so, the more the counter-ions tend to localize towards one end of the aggregates. When considering an amorphous thin film, the variations in aggregate configurations and backbone geometries will trigger broader absorption bands and larger mBLA values. Importantly, we have found that aggregation introduces a large number of 2P-active states close to the lowest 1P state, thereby closing the energy window between the 1P and 2P states that has been demonstrated to be critical to sustain a large AOS figure-of-merit.
These results point to a number of design strategies to develop thin-film structures of polymethine dyes for successful AOS applications.
(i) In order to prevent symmetry-breaking effects and the appearance of large mBLA values, a first strategy would be to limit the extent of the electrostatic interactions between the counter-ions and the polymethine backbones; this can be done by using bulky, chemically soft counter-ions. A second strategy would be to chemically link the counter-ion to the central part of the polymethine backbone, thereby preserving a symmetric structure.
(ii) In order to prevent aggregation, the addition of bulky substituents around the terminal and/or central positions of the polymethine backbone appears to be a desirable strategy.
Efforts along those lines are currently carried out in our Center.
Acknowledgements
This work was supported by the AFOSR MURI program (FA9550-10-1-0558). We would like to thank Drs Yesudas Kada and Gjergji Sini for stimulating discussions.References
- J. L. Bredas, C. Adant, P. Tackx, A. Persoons and B. M. Pierce, Chem. Rev., 1994, 94, 243–278 CrossRef CAS.
- S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J. L. Bredas and B. M. Pierce, Science, 1994, 265, 632–635 CAS.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- C. B. Gorman and S. R. Marder, Chem. Mater., 1995, 7, 215–220 CrossRef CAS.
- M. Rumi, J. E. Ehrlich, A. A. Heikal, J. W. Perry, S. Barlow, Z. Y. Hu, D. McCord-Maughon, T. C. Parker, H. Rockel, S. Thayumanavan, S. R. Marder, D. Beljonne and J. L. Bredas, J. Am. Chem. Soc., 2000, 122, 9500–9510 CrossRef CAS.
- T. D. Kim, J. W. Kang, J. D. Luo, S. H. Jang, J. W. Ka, N. Tucker, J. B. Benedict, L. R. Dalton, T. Gray, R. M. Overney, D. H. Park, W. N. Herman and A. K. Y. Jen, J. Am. Chem. Soc., 2007, 129, 488–489 CrossRef CAS.
- W. R. Zipfel, R. M. Williams and W. W. Webb, Nat. Biotechnol., 2003, 21, 1369–1376 CrossRef CAS.
- M. Drobizhev, N. S. Makarov, S. E. Tillo, T. E. Hughes and A. Rebane, Nat. Methods, 2011, 8, 393–399 CrossRef CAS.
- D. A. Parthenopoulos and P. M. Rentzepis, Science, 1989, 245, 843–845 CAS.
- N. S. Makarov, A. Rebane, M. Drobizhev, H. Wolleb and H. Spahni, J. Opt. Soc. Am. B, 2007, 24, 1874–1885 CrossRef CAS.
- B. H. Cumpston, S. P. Ananthavel, S. Barlow, D. L. Dyer, J. E. Ehrlich, L. L. Erskine, A. A. Heikal, S. M. Kuebler, I. Y. S. Lee, D. McCord-Maughon, J. Q. Qin, H. Rockel, M. Rumi, X. L. Wu, S. R. Marder and J. W. Perry, Nature, 1999, 398, 51–54 CrossRef CAS.
- W. Haske, V. W. Chen, J. M. Hales, W. T. Dong, S. Barlow, S. R. Marder and J. W. Perry, Opt. Express, 2007, 15, 3426–3436 CrossRef CAS.
- C. W. Spangler, J. Mater. Chem., 1999, 9, 2013–2020 RSC.
- J. M. Hales, M. Cozzuol, T. E. O. Screen, H. L. Anderson and J. W. Perry, Opt. Express, 2009, 17, 18478–18488 CrossRef CAS.
- J. E. Ehrlich, X. L. Wu, I. Y. S. Lee, Z. Y. Hu, H. Rockel, S. R. Marder and J. W. Perry, Opt. Lett., 1997, 22, 1843–1845 CrossRef CAS.
- J. D. Matichak, J. M. Hales, S. Ohira, S. Barlow, S. H. Jang, A. K. Y. Jen, J. L. Bredas, J. W. Perry and S. R. Marder, ChemPhysChem, 2010, 11, 130–138 CrossRef CAS.
- J. M. Hales, J. Matichak, S. Barlow, S. Ohira, K. Yesudas, J. L. Bredas, J. W. Perry and S. R. Marder, Science, 2010, 327, 1485–1488 CrossRef CAS.
- M. Soljacic, C. Luo, J. D. Joannopoulos and S. H. Fan, Opt. Lett., 2003, 28, 637–639 CrossRef.
- E. Yablonovitch, Sci. Am., 2001, 285, 34–41 CrossRef.
- V. R. Almeida, C. A. Barrios, R. R. Panepucci and M. Lipson, Nature, 2004, 431, 1081–1084 CrossRef CAS.
- M. Lipson, Nanotechnology, 2004, 15, S622–S627 CrossRef CAS.
- E. Mach, The Principles of Physical Optics; An Historical and Philosophical Treatment, Dover Publications, New York, NY, 1953 Search PubMed.
- M. Hochberg, T. Baehr-Jones, G. X. Wang, M. Shearn, K. Harvard, J. D. Luo, B. Q. Chen, Z. W. Shi, R. Lawson, P. Sullivan, A. K. Y. Jen, L. Dalton and A. Scherer, Nat. Mater., 2006, 5, 703–709 CrossRef CAS.
- R. W. Boyd, Nonlinear Optics, Academic Press, San Diego, CA, 2nd edn, 2003 Search PubMed.
- R. Send, O. Valsson and C. Filippi, J. Chem. Theory Comput., 2011, 7, 444–455 CrossRef CAS.
- O. D. Kachkovski, D. A. Yushchenko, G. O. Kachkovski and D. M. Shut, Dyes Pigm., 2005, 66, 211–221 CrossRef CAS.
- D. Jacquemin, A. Femenias, H. Chermette, I. Ciofini, C. Adamo, J. M. Andre and E. A. Perpete, J. Phys. Chem. A, 2006, 110, 5952–5959 CrossRef CAS.
- A. B. Ryabitsky, A. D. Kachkovski and O. V. Przhonska, THEOCHEM, 2007, 802, 75–83 CrossRef CAS.
- J. M. Hales, S. J. Zheng, S. Barlow, S. R. Marder and J. W. Perry, J. Am. Chem. Soc., 2006, 128, 11362–11363 CrossRef CAS.
- J. Knoester, Chem. Phys. Lett., 1993, 203, 371–377 CrossRef CAS.
- F. C. Spano and S. Mukamel, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 5783–5801 CrossRef CAS.
- K. Kemnitz, K. Yoshihara and T. Tani, J. Phys. Chem., 1990, 94, 3099–3104 CrossRef CAS.
- S. Deboer, K. J. Vink and D. A. Wiersma, Chem. Phys. Lett., 1987, 137, 99–106 CrossRef CAS.
- H. Fidder, J. Knoester and D. A. Wiersma, J. Chem. Phys., 1991, 95, 7880–7890 CrossRef CAS.
- T. Johr, W. Werncke, M. Pfeiffer, A. Lau and L. Dahne, Chem. Phys. Lett., 1995, 246, 521–526 CrossRef CAS.
- B. M. Pierce, Phys. D, 1993, 68, 51–58 CrossRef CAS.
- A. Bianco, M. Del Zoppo and G. Zerbi, Synth. Met., 2001, 125, 81–91 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 84106 CrossRef.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef.
- G. Sini, A. Tessier, J. Pytkowicz and T. Brigaud, Chem.–Eur. J., 2008, 14, 3363–3370 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- Y. Kada, G. Sini and J.-L. Bredas, personal communication, Atlanta, 2011.
- R. F. Fink, J. Seibt, V. Engel, M. Renz, M. Kaupp, S. Lochbrunner, H. M. Zhao, J. Pfister, F. Wurthner and B. Engels, J. Am. Chem. Soc., 2008, 130, 12858–12859 CrossRef CAS.
- H. Nakatsuji and K. Hirao, J. Chem. Phys., 1978, 68, 2053–2065 CrossRef CAS.
- H. Nakatsuji, Chem. Phys. Lett., 1978, 59, 362–364 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.2), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- B. J. Orr and J. F. Ward, Mol. Phys., 1971, 20, 513–526 CrossRef CAS.
- D. M. Bishop, J. M. Luis and B. Kirtman, J. Chem. Phys., 2002, 116, 9729–9739 CrossRef CAS.
- M. Albota, D. Beljonne, J. L. Bredas, J. E. Ehrlich, J. Y. Fu, A. A. Heikal, S. E. Hess, T. Kogej, M. D. Levin, S. R. Marder, D. McCord-Maughon, J. W. Perry, H. Rockel, M. Rumi, C. Subramaniam, W. W. Webb, X. L. Wu and C. Xu, Science, 1998, 281, 1653–1656 CrossRef CAS.
- C. W. Dirk, L. T. Cheng and M. G. Kuzyk, Int. J. Quantum Chem., 1992, 43, 27–36 CrossRef CAS.
- B. M. Pierce, in Nonlinear Optical Properties of Organic Materials IV, ed. K. D. Singer, Proc. SPIE 1560, 1991, pp. 148–161 Search PubMed.
- E. Zojer, D. Beljonne, T. Kogej, H. Vogel, S. R. Marder, J. W. Perry and J. L. Bredas, J. Chem. Phys., 2002, 116, 3646–3658 CrossRef CAS.
- M. Honda, C. Katayama and J. Tanaka, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 90–95 CrossRef.
- L. Dahne and G. Reck, Angew. Chem., Int. Ed. Engl., 1995, 34, 690–692 CrossRef.
- L. Dahne and G. Reck, Z. Kristallogr., 1995, 210, 948–951 CrossRef.
- G. Reck and L. Dahne, http://webcsd.ccdc.cam.ac.uk/display_csd_entry.php?identifier =NEQHEX01, 2006.
- G. Reck and L. Dahne, http://webcsd.ccdc.cam.ac.uk/display_csd_entry.php?identifier =NEQHEX01, 2006.
- G. Reck and L. Dahne, http://webcsd.ccdc.cam.ac.uk/display_csd_entry.php?identifier =NEQHUN, 2006.
- L. M. Tolbert and X. D. Zhao, J. Am. Chem. Soc., 1997, 119, 3253–3258 CrossRef CAS.
- A. Mishra, R. K. Behera, P. K. Behera, B. K. Mishra and G. B. Behera, Chem. Rev., 2000, 100, 1973–2011 CrossRef CAS.
- S. Stoyanov, in Near-Infrared Applications in Biotechnology, ed. R. Raghavachari, Marcel Dekker, New York, NY, 2001, pp. 35–93 Search PubMed.
- J. Cornil, D. A. dos Santos, X. Crispin, R. Silbey and J. L. Bredas, J. Am. Chem. Soc., 1998, 120, 1289–1299 CrossRef CAS.
- P. A. Bouit, C. Aronica, L. Toupet, B. Le Guennic, C. Andraud and O. Maury, J. Am. Chem. Soc., 2010, 132, 4328–4335 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the binding energy evaluations, the SAC-CI method, the structural parameters of the cyanine monomers and dimers, the frontier molecular orbitals of the isolated systems and in the presence of a dielectric continuum, and a discussion on the parallel-displaced dimer configurations. See DOI: 10.1039/c2sc20861j |
| ‡ Also affiliated with: Department of Chemistry, King Abdulaziz University, Jeddah 21589, Saudi Arabia. |
| This journal is © The Royal Society of Chemistry 2012 |
