Conformational analysis of supramolecular polymerization processes of disc-like molecules†
Yoko
Nakano
,
Takashi
Hirose
,
Patrick J. M.
Stals
,
E. W.
Meijer
* and
Anja R. A.
Palmans
*
Laboratory of Macromolecular and Organic Chemistry and Institute for Complex Molecular Systems, Eindhoven University of Technology, P.O. Box 513, 5600 MB, Eindhoven, The Netherlands. E-mail: e.w.meijer@tue.nl; a.palmans@tue.nl
First published on 23rd September 2011
Abstract
N,N′,N′′-Trialkylbenzene-1,3,5-tricarboxamides (BTAs) cooperatively self-assemble into one-dimensional, helical supramolecular polymers in apolar alkane solutions. Previous studies revealed that the position and configuration of the methyl group on the aliphatic side-chain gives rise to an ‘odd–even effect’ both in the shape and the sign of the CD-effect. In this study, we elucidate the molecular origin of this odd–even effect by a combination of TD-DFT calculations and spectroscopic experiments. In addition, we observed a pronounced effect of the molecular structure of the alkane solvent on the shape of the Cotton effects and the thermodynamic parameters describing the cooperative supramolecular polymerization. The results revealed a different ability of solvent molecules governed by the shape of their structure to intercalate into the helical stacks, which influences the conformation of the monomer within the supramolecular polymer. The solvent affects the dihedral angle (θ) between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and the benzene central core of the BTA molecule. These findings help to increase a molecular-level understanding of how the solvent controls the conformation of repeating units in a supramolecular system.
O group and the benzene central core of the BTA molecule. These findings help to increase a molecular-level understanding of how the solvent controls the conformation of repeating units in a supramolecular system.
1. Introduction
The understanding of chirality induction in supramolecular1 and polymeric systems2 has attracted a lot of interest in recent years because of its resemblance to chirogenesis in natural systems and potential applications in chirality sensing3 and enantioselective catalysis.4 Detailed mechanistic studies resulted in a better understanding of the factors governing chirality induction and allowed rational control of these phenomena. Because of the noncovalent nature of supramolecular interactions, temperature and concentration play a key role in the association processes that lead to the formation of well-defined supramolecular aggregates. In addition, the solvent is important since it can stabilize or destabilize the noncovalent interactions responsible for the assembly of molecular components.5 The molecular structure of solvents plays a determining role in aggregation processes. This is highlighted by the ability of chiral solvents to induce a preferred helical conformation in achiral conjugated polymers,6 helical polyisocyanates,7bipyridine based discotics8 and tubular structures.9 In addition, small changes in the solvent structure and polarity can have dramatic effects on the gelation properties of small organic molecules,10 or even induce chirality switching.11 Surprisingly, in supramolecular polymerization processes, the exact role of the solvent during the self-assembly process has received little attention to date.12The system that we consider here is based on N,N′,N′′-trialkylbenzene-1,3,5-tricarboxamide derivatives (BTAs). BTAs are disc-like molecules consisting of a central aromatic benzene core and three alkyl chains coupled by amide bonds to the core. The general structure of BTAs can be found in Fig. 1. The supramolecular structure of this molecule was unambiguously determined by X-ray structural analysis, which revealed that the BTAs form a one-dimensional, linear and helical supramolecular polymer as a result of π–π stacking of the aromatic core and three-fold intermolecular hydrogen bond networks between the amide bonds of neighboring discs in the solid state.13 Similar structures are reasonably considered to exist in the liquid crystalline state,14 the gel state15 and in dilute alkane solution16 as well. In dilute alkane solution, the introduction of one stereogenic methyl substituent at the α-, β-, or γ-position in the aliphatic alkyl chain suffices to induce one helical conformation over the other.14c,17
 | ||
| Fig. 1 Chemical structures of solvent and N,N′,N′′-trialkylbenzene-1,3,5-tricarboxamide derivatives (BTAs) 1a–d. All derivatives possess the (S)-configuration. | ||
Interestingly, the configuration of the methyl substituent determines the sign of the CD spectrum, which is related to a preference for a left-handed (M) or right-handed (P) helical conformation of the helical supramolecular polymer.18 In addition, the position of the methyl substituent determines the shape of the CD spectrum. We hypothesized that this ‘odd–even effect’ in shape and sign originated from steric hindrance of the methyl group in the helical aggregate, which is different for an odd than for an even position.14c Although the self-assembly of chiral alkyl substituted BTAs has been analyzed in our group for a decade,19 the effect of the molecular structure of the solvent on the self-assembly process was never taken into consideration.
Herein, we rationalize the origin of the odd–even effect observed in the methyl substituted BTAs and describe a molecular-level understanding of how the solvent controls the details of the helical packing in the supramolecular polymer system. Four enantiopure BTA compounds, 1a–d, with (S)-configuration were chosen for this study (Fig. 1) and the effect of different alkane solvents (linear, cyclic or branched) on the supramolecular polymerization process was investigated using (temperature-dependent) circular dichroism (CD), ultraviolet (UV) spectroscopy and infrared (IR) spectroscopy. In addition, we applied time-dependent density functional theory (TD-DFT) calculations to get more of an insight into the origin of the Cotton effects of BTAs and explain the origin of the differently shaped Cotton effects by comparing the theoretical and experimental CD curves. From this comprehensive study, it becomes clear that a solvent shell surrounds the helical aggregate and that, depending on its structure, the solvent can intercalate into the helical stack, thus affecting the conformation of the monomer within the stack.
2. Results
2.1 CD Spectroscopy
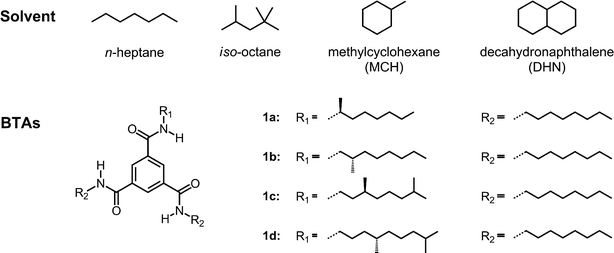
The effect of solvent on the supramolecular polymerization of BTAs 1a–d was investigated by studying their self-assembly in several solvents with different chemical structures; n-heptane, iso-octane, methylcyclohexane (MCH) and decahydronaphthalene (DHN) as linear, branched, monocyclic and bicyclic aliphatic solvents, respectively (Fig. 1). The solvents were selected based on their convenient boiling points (> 90 °C) and their availability as spectroscopic grade solvents. CD measurements were performed on 30 μM solutions of 1a–d at 293 K. The spectra show Cotton effects with a peak at 193 nm in the π–π* transition and at around 223 nm in the n–π* transition region (Fig. 2A–D). The odd–even effect was manifested in a reversal of the sign of the Cotton effect upon the shift of the (S)-stereocenter with respect to the amide group from the α- to the δ-position. In all of the solvents, we found positive Cotton effects for the α- and γ-(S)-methyl substituted BTAs (1a,c) and negative Cotton effects for the β- and δ-(S)-methyl substituted BTAs (1b,d) at 193 nm. At 223 nm, negative Cotton effects for the α- and γ-(S)-methyl substituted BTAs (1a,c) and positive Cotton effects for the β- and δ-(S)-methyl substituted BTAs (1b,d) were observed. This observation is indicative of a reversal of the handedness of the helical supramolecular polymer when the methyl group is changed from an odd to an even position. In addition, as was already reported by our group,14c in MCH, the shape and strength of the Cotton effect of 1a and 1c are nearly identical. However, the Cotton effect of 1a,c differs in shape from that of 1b,d in the n–π* transition region; the CD spectrum in the latter case shows a maximum peak at 216 nm and a shoulder at 242 nm (Fig. 2C). We refer to the CD spectrum comprised of a broad band with one maximum at 223 nm as a type I spectrum and the CD spectrum with two absorption bands, a main band at 216 nm and an accompanying shoulder at 242 nm as a type II spectrum. This suggests that a slight difference in the molecular organization is present depending on the position of the methyl group (i.e. the α- and γ-substitution (odd) or the β- and δ-substitution (even)). The difference could originate from the spatial orientation of the asymmetric methyl group that inflicts small changes on the packing of the aromatic core and/or intermolecular hydrogen bonds, which can affect the shape of the CD spectra. Similar spectra are obtained when iso-octane and DHN are used as the solvent (Fig. 2B,D). Interestingly, in n-heptane, the shape of the CD spectra of 1a–d are always identical, regardless of the position of the methyl group (Fig. 2A), suggesting that n-heptane leads all BTA molecules into the same types of helical packing showing the type I CD spectrum.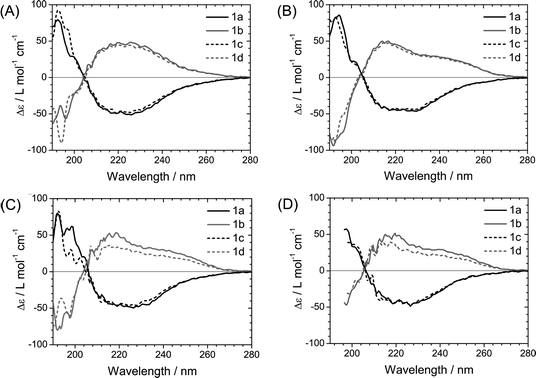 | ||
| Fig. 2 CD spectra of 1a–d recorded at 293 K in n-heptane (A), iso-octane (B), MCH (C) and DHN (D) at a concentration of 30 μM. | ||
2.2 IR measurements
Since the differences in the shape of the Cotton effects were recorded in the n–π* transition region, this observation is likely to result from the different environment of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups within the BTA stack. Previous studies showed that IR spectroscopy is a sensitive tool to assess the nature of the molecular packing of BTAs in the liquid crystalline state and in concentrated solutions,14c,20 and the C
O groups within the BTA stack. Previous studies showed that IR spectroscopy is a sensitive tool to assess the nature of the molecular packing of BTAs in the liquid crystalline state and in concentrated solutions,14c,20 and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration can be evaluated with a high sensitivity.
O stretching vibration can be evaluated with a high sensitivity.
The two different helical packing states were investigated further by IR spectroscopy. IR spectroscopy requires higher concentrations in solution than CD spectroscopy, so we selected DHN in which BTAs 1a–d are easily soluble. In addition, BTAs 1a–d show an odd–even effect in the shape of the CD curves in this solvent. Fig. 3 shows the IR spectra of 1a–d in DHN at 1.8 mM recorded at room temperature (∼20 °C) in the amide I and amide II region and also in the N–H stretching vibration region. The amide I transition consists mainly of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching motion, while amide II consists of a combination of C–N stretching and N–H in-plane bending. For all 1a–d solutions, an N–H stretching vibration at 3240 cm−1 and a C
O stretching motion, while amide II consists of a combination of C–N stretching and N–H in-plane bending. For all 1a–d solutions, an N–H stretching vibration at 3240 cm−1 and a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration at ∼1640 cm−1 were observed, which indicates the presence of hydrogen-bonded species in solution.14c Importantly, a different C
O stretching vibration at ∼1640 cm−1 were observed, which indicates the presence of hydrogen-bonded species in solution.14c Importantly, a different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching pattern between compounds 1a,c and compounds 1b,d was observed that is consistent with the difference in the CD spectral types. The IR spectra in the C
O stretching pattern between compounds 1a,c and compounds 1b,d was observed that is consistent with the difference in the CD spectral types. The IR spectra in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region are always a combination of at least three absorptions with different amplitudes. The amide I peak is a doublet with peaks at 1630 cm−1 and 1645 cm−1, with small shoulders at 1651 cm−1, if the compound shows a type II (1b,d: the methyl group on an even position). In contrast, a singlet peak at 1643 cm−1, with a small shoulder at 1630 cm−1 and 1651 cm−1, is observed for the type I spectrum (1a,c: the methyl at an odd position). This pattern is absent in the N–H stretching region at 3240 cm−1 and the amide II region at 1560 cm−1, where for all compounds the shape of the peaks seems to be the same.
O stretching region are always a combination of at least three absorptions with different amplitudes. The amide I peak is a doublet with peaks at 1630 cm−1 and 1645 cm−1, with small shoulders at 1651 cm−1, if the compound shows a type II (1b,d: the methyl group on an even position). In contrast, a singlet peak at 1643 cm−1, with a small shoulder at 1630 cm−1 and 1651 cm−1, is observed for the type I spectrum (1a,c: the methyl at an odd position). This pattern is absent in the N–H stretching region at 3240 cm−1 and the amide II region at 1560 cm−1, where for all compounds the shape of the peaks seems to be the same.
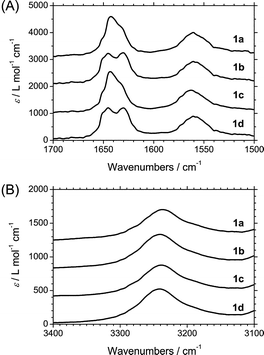 | ||
Fig. 3
IR spectra recorded in amide I (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching) and amide II (coupling of N–H bending and C–N stretching) region (A) and N–H stretching region (B) of solutions of 1a–d in DHN at a concentration of 1.8 mM at RT. The curves are shown with a 1,000 L mol−1 cm−1 offset for (A) and 400 L mol−1 cm−1 offset for (B), respectively. O stretching) and amide II (coupling of N–H bending and C–N stretching) region (A) and N–H stretching region (B) of solutions of 1a–d in DHN at a concentration of 1.8 mM at RT. The curves are shown with a 1,000 L mol−1 cm−1 offset for (A) and 400 L mol−1 cm−1 offset for (B), respectively. | ||
2.3 Thermodynamic parameters
Temperature-dependent CD measurements were performed by monitoring the intensity of the CD signal at 223 nm to derive the thermodynamic parameters of the supramolecular polymerization process of 1a–d. A slow cooling rate of 1 K min−1 was employed to suppress kinetic effects during the polymerization process and the measurements were conducted from 90 °C to −10 °C. For all solutions at a concentration of 30 μM, a cooperative transition could be observed, at which point monomeric BTAs start to self-assemble into a helical polymers (Fig. 4A–D, full spectra in Figs S1–S4†). Fitting the temperature-dependent CD intensity data with the Van der Schoot nucleation–elongation model,12,16b,21 yielded the relevant thermodynamic parameters of the cooperative supramolecular polymerization. This affords an elongation temperature (Te) and enthalpy release upon elongation (he). In addition, a dimensionless equilibrium constant of activation (Ka) that reflects the degree of cooperativity in the polymerization process was derived from fitting the data. | ||
| Fig. 4 The normalized degree of aggregation as a function of temperature for solutions of 1a–d in n-heptane (A), iso-octane (B), MCH (C) and DHN (D) at a concentration of 30 μM. | ||
The relevant thermodynamic parameters for all solutions of 1a–d are reported in Table 1. Shifting the methyl substituent in the aliphatic side chain closer to the amide group, results in a more stable aggregate, as evidenced by an increase in Te (Table 1). This is in line with the results previously reported for a β-(S)-methyl-substituted BTA (1b) and α-, γ-(R)-methyl-substituted BTAs in MCH.14c Moreover, changing the alkane solvent has a noticeable effect on the Te. n-Heptane and iso-octane solutions have a slightly higher Te than the MCH solution, which in turn has a slightly higher Te than the DHN solution. The he values were approximately −56 and −41 kJ mol−1 for 1a–c and 1d, respectively.22 The small Ka value of about 10−4–10−5 indicates that the supramolecular polymerization process is highly cooperative. Remarkably, the Ka values for a solution that shows the type II spectrum are higher than that for the type I spectrum, indicating that the former shows less cooperative growth.
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The iso-octane solutions of 1b,d showed the type II spectrum at lower temperatures (from 50 °C to −10 °C), while they showed the type I spectrum at higher temperatures (from Te to 60 °C) (see the supporting information†). This indicates that, for these solutions, the molecular organization that shows the type I spectrum is more stable than that of the type II spectrum. The iso-octane solutions of 1b,d showed the type II spectrum at lower temperatures (from 50 °C to −10 °C), while they showed the type I spectrum at higher temperatures (from Te to 60 °C) (see the supporting information†). This indicates that, for these solutions, the molecular organization that shows the type I spectrum is more stable than that of the type II spectrum. |
|---|
|
2.4 Calculated CD and UV spectra
The results presented above indicate that both the position of the methyl substituent and the solvent structure play an important role during the self-assembly process. We propose that there is a correlation between the orientation of the side-chains and the molecular structure of solvent for the interaction within the helical packing. The consistent results from both the IR spectroscopy in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region and the CD spectroscopy in n–π* transition region suggest that the small changes in the helical packing are related to a different C
O stretching region and the CD spectroscopy in n–π* transition region suggest that the small changes in the helical packing are related to a different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O environment. One explanation is that the dihedral angle of the C
O environment. One explanation is that the dihedral angle of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group (θ) with respect to the central benzene ring changes depending on the methyl position and/or the solvent applied (Fig. 5A). If the differences in the shape of the Cotton effect are related to the C
O group (θ) with respect to the central benzene ring changes depending on the methyl position and/or the solvent applied (Fig. 5A). If the differences in the shape of the Cotton effect are related to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) with respect to the central benzene core, the dependence of the CD transition on this angle in calculated spectra can provide more evidence for this proposal. For this purpose, we performed TD-DFT calculations in terms of the different C
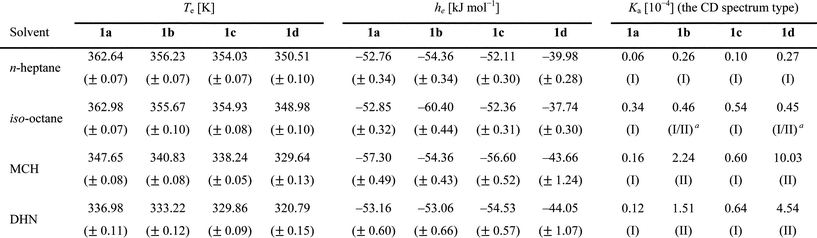
O dihedral angle (θ) with respect to the central benzene core, the dependence of the CD transition on this angle in calculated spectra can provide more evidence for this proposal. For this purpose, we performed TD-DFT calculations in terms of the different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angles (θ) with a RPBE1PBE/6-31++G(2d,p)//B3LYP/6-31G(d) level and compared the calculated CD curves to the measured curves. To reduce the computational costs, the calculations were performed on monomer 1e (Fig. 5A), in which the three long aliphatic side chains were replaced by methyl groups. The three C
O dihedral angles (θ) with a RPBE1PBE/6-31++G(2d,p)//B3LYP/6-31G(d) level and compared the calculated CD curves to the measured curves. To reduce the computational costs, the calculations were performed on monomer 1e (Fig. 5A), in which the three long aliphatic side chains were replaced by methyl groups. The three C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in the molecule were rotated by 10°–60° with respect to the phenyl core plane. In addition, C3 symmetry was applied on the structure during the geometrical optimization. The CD and UV transitions were subsequently calculated with the fully optimized structures.23
O groups in the molecule were rotated by 10°–60° with respect to the phenyl core plane. In addition, C3 symmetry was applied on the structure during the geometrical optimization. The CD and UV transitions were subsequently calculated with the fully optimized structures.23
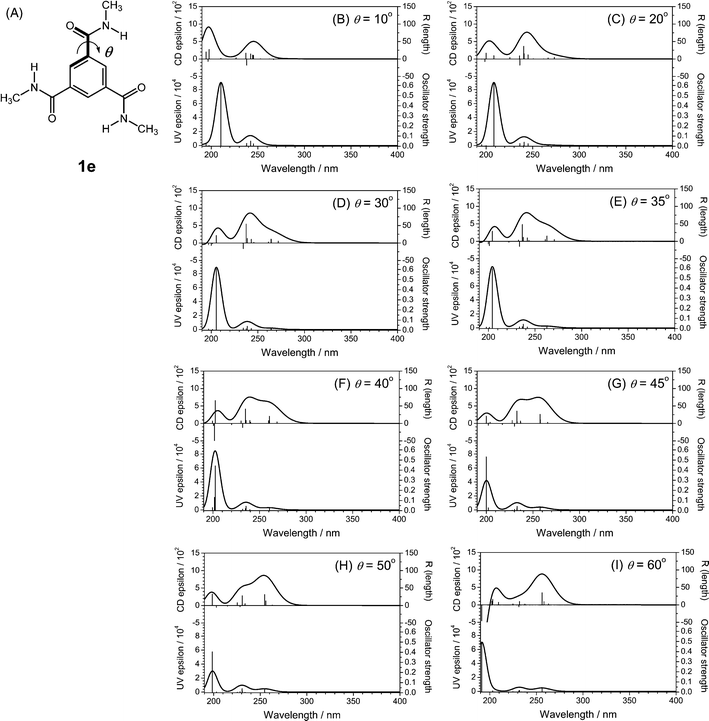 | ||
Fig. 5 The chemical structure of BTA (1e) used in the computational studies (A). The dihedral angle θ used to characterize the DFT geometries is also shown; Calculated CD and UV spectra of the 1e monomer with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angles (θ) with respect to the benzene core of 10° (B), 20° (C), 30° (D), 35° (E), 40° (F), 45° (G), 50° (H) and 60° (I). Calculated spectra were mathematically generated with the sum of gauss distributions of each calculated transition. O dihedral angles (θ) with respect to the benzene core of 10° (B), 20° (C), 30° (D), 35° (E), 40° (F), 45° (G), 50° (H) and 60° (I). Calculated spectra were mathematically generated with the sum of gauss distributions of each calculated transition. | ||
The calculated CD and UV spectra of 1e with different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angles (θ) are presented in Fig. 5B–I. The calculated data reproduce the two different types of Cotton effects measured in the experimental spectra very well, suggesting that the shape of the CD spectra is indeed strongly dependent on the carbonyl dihedral angle (θ). Although the calculations were performed on the monomer, a comparison of the experimental CD spectra of the stacks of 1a–d with the calculated data of the monomer 1e clearly reveals their similarities. The orbital symmetry between phenyl and amide groups closely relates to the forbidden nature of the transitions (see the supporting information†). According to the excited configurations, transitions of the BTA are classified into three general types; (i) the first transition, the lowest energy transition, is assigned to a n–π* electronic transition, which occurs mainly from the lone-pair orbital of the three C
O angles (θ) are presented in Fig. 5B–I. The calculated data reproduce the two different types of Cotton effects measured in the experimental spectra very well, suggesting that the shape of the CD spectra is indeed strongly dependent on the carbonyl dihedral angle (θ). Although the calculations were performed on the monomer, a comparison of the experimental CD spectra of the stacks of 1a–d with the calculated data of the monomer 1e clearly reveals their similarities. The orbital symmetry between phenyl and amide groups closely relates to the forbidden nature of the transitions (see the supporting information†). According to the excited configurations, transitions of the BTA are classified into three general types; (i) the first transition, the lowest energy transition, is assigned to a n–π* electronic transition, which occurs mainly from the lone-pair orbital of the three C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups to the π*-orbital of the phenyl group; (ii) the second transition is a π–π* transition possessing a charge transfer property, in which electron density is donated from the π-orbital of the amide group to the π*-orbital of the phenyl group upon excitation; (iii) the third transition is assigned to a purer π–π* transition on the phenyl group that has a large oscillator strength at higher energy region. As is expected from the orbital theory, the oscillator strength of the first transition tends to increase as the C
O groups to the π*-orbital of the phenyl group; (ii) the second transition is a π–π* transition possessing a charge transfer property, in which electron density is donated from the π-orbital of the amide group to the π*-orbital of the phenyl group upon excitation; (iii) the third transition is assigned to a purer π–π* transition on the phenyl group that has a large oscillator strength at higher energy region. As is expected from the orbital theory, the oscillator strength of the first transition tends to increase as the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) becomes larger because the symmetry of the lone-pair orbital on the amide group and the π-orbital of phenyl group get closer. At high dihedral angles, the n–π* transition becomes more allowed because of symmetry arguments. In addition, the excitation energy of the first transition shifts to higher energy as the conjugation length becomes shorter when increasing the C
O dihedral angle (θ) becomes larger because the symmetry of the lone-pair orbital on the amide group and the π-orbital of phenyl group get closer. At high dihedral angles, the n–π* transition becomes more allowed because of symmetry arguments. In addition, the excitation energy of the first transition shifts to higher energy as the conjugation length becomes shorter when increasing the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) (see the supporting information†).
O dihedral angle (θ) (see the supporting information†).
3. Discussion
Changes in the position of the methyl group on the alkyl chain of BTAs and the solvent molecular structure have a large effect on the molecular organization within the supramolecular polymer, which is reflected by the differently shaped CD spectra. TD-DFT calculations showed that the different types of packing are related to the dihedral angle of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (θ) with the central benzene core. The comparison of the differently shaped CD spectra experimentally observed for BTAs in dilute solutions with the theoretically calculated CD spectra is shown in Fig. 6. It is noteworthy that the rotatory strength of the first and the second transition become compatible when the C
O (θ) with the central benzene core. The comparison of the differently shaped CD spectra experimentally observed for BTAs in dilute solutions with the theoretically calculated CD spectra is shown in Fig. 6. It is noteworthy that the rotatory strength of the first and the second transition become compatible when the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) is around 45°. Thus, the broad band in the type I spectrum is comprised of two transitions having a similar intensity observed with the C
O dihedral angle (θ) is around 45°. Thus, the broad band in the type I spectrum is comprised of two transitions having a similar intensity observed with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle (θ) of 45° (dashed black lines in Fig. 6). The shoulder-like CD band in the type II spectrum is assigned to the lowest n–π* transition with the smaller C
O angle (θ) of 45° (dashed black lines in Fig. 6). The shoulder-like CD band in the type II spectrum is assigned to the lowest n–π* transition with the smaller C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) of 35° (solid gray lines in Fig. 6).
O dihedral angle (θ) of 35° (solid gray lines in Fig. 6).
 | ||
Fig. 6 A comparison of the differently shaped Cotton effects experimentally observed for BTAs in dilute solutions (A; 1b,c in iso-octane) and theoretically calculated CD spectra for 1e with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angles (θ) of 35° and 45° (B). O dihedral angles (θ) of 35° and 45° (B). | ||
To validate the similarities between the experimental and calculated CD spectra, the ratio of the CD intensities at the first and the second transition were determined. The type I spectrum shows a first transition peak at 230 nm and a second transition peak at 216 nm, with an intensity ratio of 1.05. This value corresponds well to the value of 1.14 calculated from the TD-DFT data for a dihedral angle (θ) of 45°. The type II spectrum has a first transition peak at 242 nm and a second transition peak at 215 nm and the intensities show a ratio of 0.65, which concurs very well with the value of 0.65 calculated for the theoretical spectrum with a dihedral angle (θ) of 35° (Table 2). The intensity ratios for the calculated CD spectra with other dihedral angles (θ) of 20°, 30°, 40° and 50° are given in Table S9 in the supporting information†. We conclude that the two positive bands in the n–π* transition calculated for the BTA molecule with the smaller C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ ≈ 35°) are in satisfactory qualitative agreement with the type II CD spectrum and the C
O dihedral angle (θ ≈ 35°) are in satisfactory qualitative agreement with the type II CD spectrum and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle (θ ≈ 45°) with the type I CD spectrum observed in the experimental measurements.
O angle (θ ≈ 45°) with the type I CD spectrum observed in the experimental measurements.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) at each type of molecular organization obtained from experimental measurement and TD-DFT calculation.
O dihedral angle (θ) at each type of molecular organization obtained from experimental measurement and TD-DFT calculation.
| Experimental CD measurement | TD-DFT calculation | |||||||
|---|---|---|---|---|---|---|---|---|
| λ 1st [nm] | λ 2nd [nm] | CD intensity ratio a | K a [10−4] | λ 1st [nm] | λ 2nd [nm] | CD intensity ratio a | θ [°] | |
| a The ratio of CD intensities at the first transition to those at the second transition. | ||||||||
| Type I | 230 | 216 | 1.05 | 0.35 (±0.29) | 258 | 233 | 1.14 | 45 |
| Type II | 242 | 215 | 0.65 | 5.77 (±4.26) | 263 | 236 | 0.65 | 35 |
In addition, the preferred helicity of BTA stacks differs depending on whether the methyl group is placed on an odd or even position when keeping the configuration constant. By means of molecular mechanics calculation methods, we find a preference of α-(S)-methyl substituted BTA (the methyl group on an odd position) for a left-handed helix, while β-(S)-methyl substituted BTA (the methyl group on an even position) forms a right-handed helix by the intermolecular hydrogen bonds between the amide groups (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–H groups) (Fig. 7). Moreover, the spatial orientation of the methyl group at an odd or even position is different. The methyl group on an α (odd) position can be stabilized in a nearly perpendicular arrangement with respect to the aliphatic tail, while the methyl group on a β (even) position is stabilized by a nearly horizontal arrangement (Fig. 7). As a result, the inter-ring distance, dring, is closer in β-methyl substituted BTA than in α-methyl substituted BTA. Indeed, by means of DFT calculation of a trimer, the dring is estimated at 3.63 Å for β-methyl substituted BTA, whereas this distance is longer for α-methyl substituted BTA (estimated at 3.78 Å). This decrease of dring is associated with the decrease of the C
O and N–H groups) (Fig. 7). Moreover, the spatial orientation of the methyl group at an odd or even position is different. The methyl group on an α (odd) position can be stabilized in a nearly perpendicular arrangement with respect to the aliphatic tail, while the methyl group on a β (even) position is stabilized by a nearly horizontal arrangement (Fig. 7). As a result, the inter-ring distance, dring, is closer in β-methyl substituted BTA than in α-methyl substituted BTA. Indeed, by means of DFT calculation of a trimer, the dring is estimated at 3.63 Å for β-methyl substituted BTA, whereas this distance is longer for α-methyl substituted BTA (estimated at 3.78 Å). This decrease of dring is associated with the decrease of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle (θ) and the increase of the O–H distance of the hydrogen bond.18
O angle (θ) and the increase of the O–H distance of the hydrogen bond.18
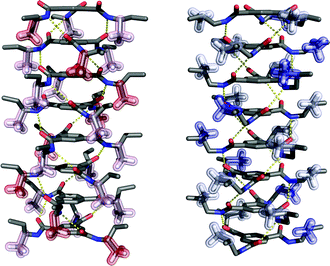 | ||
| Fig. 7 The structures of BTA 8-mers with a methyl substituent at the α-position (left) and β-position (right) with (S)-configuration. | ||
Interestingly, there is no odd–even effect in the shape of the CD spectra when n-heptane is used as the solvent; all spectra are of type I (θ ≈ 45°). We assume that this is because n-heptane can intercalate between horizontal alkyl tails within the stacks of 1b and 1d and increases the dring between consecutive BTA monomers. Consequently, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ) is raised with respect to the central benzene core due to the presence of n-heptane, which results in the type I CD spectrum (θ ≈ 45°). On the other hand, 1b and 1d show type II CD spectra in MCH and DHN, which is indicative of a smaller angle (θ ≈ 35°). While 1b and 1d aggregate in cyclic solvents, the solvent is not able to intercalate between BTA molecules within the stacks. Thus, the C
O dihedral angle (θ) is raised with respect to the central benzene core due to the presence of n-heptane, which results in the type I CD spectrum (θ ≈ 45°). On the other hand, 1b and 1d show type II CD spectra in MCH and DHN, which is indicative of a smaller angle (θ ≈ 35°). While 1b and 1d aggregate in cyclic solvents, the solvent is not able to intercalate between BTA molecules within the stacks. Thus, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moieties can be tilted to different angles with respect to the central core depending on the spatial structure of the aliphatic chains and their interaction with the solvent molecules, and consequently thus results in a change of the shape of the CD spectra.
O moieties can be tilted to different angles with respect to the central core depending on the spatial structure of the aliphatic chains and their interaction with the solvent molecules, and consequently thus results in a change of the shape of the CD spectra.
The thermodynamic parameters describing the cooperative polymerization reveal that the molecular structure of the alkane solvent has an effect on Te. A small decrease in Te is observed going from n-heptane/iso-octane to MCH and DHN. We plotted the Te values as a function of the dielectric constant of the solvent (εsol) (Fig. S5†). n-Heptane, iso-octane, MCH and DHN have εsol values of 1.92, 1.94, 2.02 and 2.15 at 20 °C, respectively.24 The formation of helical stacks linearly depends on the εsol values of the solvent, and the less polar solvent exhibits a higher Te. In contrast, there is no correlation between the Te and the shape or volume of the alkane solvent (Table S1–S4, Figs S6–S8†). The trend in the solvent polarity is, however, not correlated to the shape or sign of the CD effect. Importantly, the Ka value for BTA solutions that show the type II spectrum is higher than that of the type I spectrum, suggesting that the former shows less cooperative growth (Table 2). Since the TD-DFT studies show that the type II spectrum arises from the n–π* transition for which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are tilted around 35° with respect to the central aromatic core, we can assume that the overall dipole moment of one BTA is lower compared to a BTA in which the C
O groups are tilted around 35° with respect to the central aromatic core, we can assume that the overall dipole moment of one BTA is lower compared to a BTA in which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are tilted around 45°. The lower cooperativity for the type II spectrum is in accordance with our previous findings, which showed that the degree of cooperativity is related to polarization effects and to the orientation of the amide dipoles.25 The polarization changes during aggregation and thereby influences the intermolecular hydrogen bonding strength; larger dipole moments are expected to result in a higher degree of cooperativity.
O groups are tilted around 45°. The lower cooperativity for the type II spectrum is in accordance with our previous findings, which showed that the degree of cooperativity is related to polarization effects and to the orientation of the amide dipoles.25 The polarization changes during aggregation and thereby influences the intermolecular hydrogen bonding strength; larger dipole moments are expected to result in a higher degree of cooperativity.
4. Conclusions
Asymmetrically substituted, chiral benzene-1,3,5-tricarboxamides (BTAs) were studied in a combined theoretical and experimental approach. The results gathered from CD and IR spectroscopy in combination with TD-DFT calculations demonstrate that two types of helical packing can be formed by the supramolecular polymer, which can be differentiated by the shape of their CD spectrum. While a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle with respect to the central benzene core of θ ≈ 45° gives rise to a type I CD spectrum, θ ≈ 35° gives rise to a type II CD spectrum. An odd–even effect is present for BTAs, in which the inter-ring distance (dring) of the stacks is determined by the spatial position of the methyl group in the aliphatic tail whether it positioned on an odd or even site. A larger dring corresponds to θ ≈ 45°, while a smaller dring is indicative of θ ≈ 35°.
O dihedral angle with respect to the central benzene core of θ ≈ 45° gives rise to a type I CD spectrum, θ ≈ 35° gives rise to a type II CD spectrum. An odd–even effect is present for BTAs, in which the inter-ring distance (dring) of the stacks is determined by the spatial position of the methyl group in the aliphatic tail whether it positioned on an odd or even site. A larger dring corresponds to θ ≈ 45°, while a smaller dring is indicative of θ ≈ 35°.
The solvent plays an important role in the self-assembly process, as is shown by the change in shape of the Cotton effect depending on the molecular structure of the solvent. In n-heptane, only type I CD spectra are found, indicative of θ ≈ 45°, while in bulky solvents, like MCH and DHN, the type of CD spectrum is determined by the position of the methyl group at an odd or even position. This observation indicates that the dring increases when flexible solvent molecules, such as n-heptane, have the ability to intercalate between the BTA molecules within a stack. As a result of the intercalation, dring increases, as does the dihedral angle θ. Thus, binding of solvent molecules to the aggregate alters the helical packing of the stacks by adjusting the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle (θ). Interestingly, the differences in the dihedral angle (θ) affect the cooperativity of the supramolecular polymerization process. The equilibrium constant of activation (Ka) was estimated by fitting the temperature-dependent CD intensity data to a nucleation-growth model. The results show that Ka values are larger when θ ≈ 35°, which indicates a lower cooperativity.
O dihedral angle (θ). Interestingly, the differences in the dihedral angle (θ) affect the cooperativity of the supramolecular polymerization process. The equilibrium constant of activation (Ka) was estimated by fitting the temperature-dependent CD intensity data to a nucleation-growth model. The results show that Ka values are larger when θ ≈ 35°, which indicates a lower cooperativity.
This work motivates us to propose that the solvent molecules are critically important during the supramolecular polymerization process. We infer from the results discussed here that the solvent molecules take part in the formation of the helical stacks. This selective binding would imply that the molecular structure of solvent molecules is a determining factor in the helical packing of BTA molecules. These findings can help to increase a molecular-level understanding of how the solvent controls the conformation of repeating units in a supramolecular system. This is important in view of a mechanistic understanding of the gelation properties of small organic molecules in organic solvents (organogelators) and the role of solvents in asymmetric catalysis.
Acknowledgements
Tim Paffen, Daniël Haveman and Marly Hummelink are acknowledged for assisting with the synthesis and Jeffrey Everts is acknowledged for performing preliminary measurements. This work was supported by the European Research Council (ERC Advanced Grant No. 246829), the Dutch National Research School Combination Catalysis Controlled by Chemical Design (NRSC-Catalysis) and the Netherlands Organization for Scientific Research (Spinoza-NWO) foundations. T. H. would like to acknowledge the JSPS for a young scientist fellowship.Notes and references
- (a) H. Engelkamp, S. Middelbeek and R. J. M. Nolte, Science, 1999, 284, 785–788 CrossRef CAS; (b) J. M. Fox, T. J. Katz, S. Van Elshocht, T. Verbiest, M. Kauranen, A. Persoons, T. Thongpanchang, T. Krauss and L. Brus, J. Am. Chem. Soc., 1999, 121, 3453–3459 CrossRef CAS; (c) J. P. Hill, W. Jin, A. Kosaka, T. Fukushima, H. Ichihara, T. Shimomura, K. Ito, T. Hashizume, N. Ishii and T. Aida, Science, 2004, 304, 1481–1483 CrossRef CAS; (d) J. P. Gallivan and G. B. Schuster, J. Org. Chem., 1995, 60, 2423–2429 CrossRef CAS; (e) C. Nuckolls, T. J. Katz and L. Castellanos, J. Am. Chem. Soc., 1996, 118, 3767–3768 CrossRef CAS; (f) G. Gottarelli and G. P. Spada, Chem. Rec., 2004, 4, 39–49 CrossRef CAS; (g) C. R. L. P. N Jeukens, P. Jonkheijm, F. J. P. Wijnen, J. C. Gielen, P. C. M. Christianen, A. P. H. J. Schenning, E. W. Meijer and J. C. Maan, J. Am. Chem. Soc., 2005, 127, 8280–8281 CrossRef CAS; (h) F. Würthner, Z. Chen, F. J. M. Hoeben, P. Osswald, C.-C. You, P. Jonkheijm, J.v. Herrikhuyzen, A. P. H. J. Schenning, P. P. A. M. van der Schoot, E. W. Meijer, E. H. A. Beckers, S. C. J. Meskers and R. A. J. Janssen, J. Am. Chem. Soc., 2004, 126, 10611–10618 CrossRef; (i) F. Garcia, P. M. Viruela, E. Matesanz, E. Orti and L. Sanchez, Chem.–Eur. J., 2011, 17, 775–7759 CrossRef.
- (a) E. Yashima, H. Goto and Y. Okamoto, Polym. J., 1998, 30, 69–71 CrossRef CAS; (b) K. Maeda, H. Goto and E. Yashima, Macromolecules, 2001, 34, 1160–1164 CrossRef CAS; (c) J. Tabei, R. Nomura, F. Sanda and T. Masuda, Macromolecules, 2003, 36, 8603–8608 CrossRef CAS; (d) M. Ishikawa, K. Maeda and E. Yashima, J. Am. Chem. Soc., 2002, 124, 7448–7458 CrossRef CAS; (e) E. Yashima, K. Maeda and T. Yamanaka, J. Am. Chem. Soc., 2000, 122, 7813–7814 CrossRef CAS; (f) D. S. Schlitzer and B. M. Novak, J. Am. Chem. Soc., 1998, 120, 2196–2197 CrossRef CAS; (g) K. Maeda, N. Yamamoto and Y. Okamoto, Macromolecules, 1998, 31, 5924–5926 CrossRef CAS; (h) R. Sakai, T. Satoh, R. Kakuchi, H. Kaga and T. Kakuchi, Macromolecules, 2003, 36, 3709–3713 CrossRef CAS; (i) R. Sakai, T. Satoh, R. Kakuchi, H. Kaga and T. Kakuchi, Macromolecules, 2004, 37, 3996–4003 CrossRef CAS; (j) M. M. Green, C. Khatri and N. C. Peterson, J. Am. Chem. Soc., 1993, 115, 4941–4942 CrossRef CAS; (k) P. Dellaportas, S. J. Holder and R. G. Jones, Macromol. Rapid Commun., 2002, 23, 99–103 CrossRef CAS; (l) M. R. Majidi, L. A. P. Kane-Maguire and G. G. Wallace, Polymer, 1995, 36, 3597–3599 CrossRef CAS; (m) L. Arnt and G. N. Tew, Macromolecules, 2004, 37, 1283–1288 CrossRef CAS.
- (a) E. Yashima, Y. Maeda and Y. Okamoto, J. Am. Chem. Soc., 1998, 120, 8895–8896 CrossRef CAS; (b) E. Yashima, Y. Maeda and O. Sato, J. Am. Chem. Soc., 2001, 123, 8159–8160 CrossRef CAS; (c) K. Morino, K. Maeda and E. Yashima, Macromolecules, 2003, 36, 1480–1486 CrossRef CAS; (d) H. Fenniri, B.-L. Deng and A. E. Ribbe, J. Am. Chem. Soc., 2002, 124, 11064–11072 CrossRef CAS.
- (a) G. Roelfes and B. L. Feringa, Angew. Chem., Int. Ed., 2005, 44, 3230–3232 CrossRef CAS; (b) A. J. Boersma, D. Coquière, D. Geerdink, F. Rosati, B. L. Feringa and G. Roelfes, Nat. Chem., 2010, 2, 991–995 CrossRef CAS; (c) J. Wang and B. L. Feringa, Science, 2011, 331, 1429–1432 CrossRef CAS.
- (a) H.-J. Schneider, R. Kramer, S. Simova and U. Schneider, J. Am. Chem. Soc., 1988, 110, 6442–6448 CrossRef CAS; (b) S. B. Ferguson, A. M. Sanford, E. M. Seward and F. Diederich, J. Am. Chem. Soc., 1991, 113, 5410–5419 CrossRef CAS; (c) G. A. Breault, C. A. Hunter and P. C. Mayers, J. Am. Chem. Soc., 1998, 120, 3402–3410 CrossRef CAS; (d) N. J. Buurma, J. L. Cook, C. A. Hunter, C. M. R. Low and J. G. Vinter, Chem. Sci., 2010, 1, 242–246 RSC.
- (a) Y. Nakano, Y. Liu and M. Fujiki, Polym. Chem., 2010, 1, 460–469 RSC; (b) Y. Kawagoe, M. Fujiki and Y. Nakano, New J. Chem., 2010, 34, 637–647 RSC; (c) H. Nakashima, J. R. Koe, K. Torimitsu and M. Fujiki, J. Am. Chem. Soc., 2001, 123, 4847–4848 CrossRef CAS.
- M. M. Green, C. Khatri and N. C. Peterson, J. Am. Chem. Soc., 1993, 115, 4941–4942 CrossRef CAS.
- A. R. A. Palmans, J. A. J. M. Vekemans, E. E. Havinga and E. W. Meijer, Angew. Chem., Int. Ed. Engl., 1997, 36, 2648–2651 CrossRef CAS.
- B. Isare, M. Linares, L. Zargarian, S. Fermandjian, M. Miura, S. Motohashi, N. Vanthuyne, R. Lazzaroni and L. Bouteiller, Chem.–Eur. J., 2010, 16, 173–177 CrossRef CAS.
- (a) T. Pinault, B. Isare and L. Bouteiller, ChemPhysChem, 2006, 7, 816–819 CrossRef CAS; (b) W. Edwards, C. A. Lagadec and D. K. Smith, Soft Matter, 2011, 7, 110–117 RSC; (c) J. van Esch, F. Schoonbeek, M. de Loos, H. Kooijman, A. L. Spek, R. M. Kellogg and B. L. Feringa, Chem.–Eur. J., 1999, 5, 937–950 CrossRef CAS; (d) M. George, G. Tan, V. T. John and R. G. Weiss, Chem.–Eur. J., 2005, 11, 3243–3254 CrossRef CAS; (e) Y. Jeong, K. Hanabusa, H. Masunaga, I. Akiba, K. Miyoshi, S. Sakurai and K. Sakurai, Langmuir, 2005, 21, 586–594 CrossRef CAS; (f) V. Čaplar, L. Frkanec, N. Šijaković and M. Žinić, Chem.–Eur. J., 2010, 16, 3066–3082 CrossRef CAS.
- (a) V. V. Borovkov, G. A. Hembury and Y. Inoue, Angew. Chem., Int. Ed., 2003, 42, 5310–5314 CrossRef CAS; (b) O. Mamula, M. Lama, H. Stoeckli-Evans and S. Shova, Angew. Chem., Int. Ed., 2006, 45, 4940–4944 CrossRef CAS; (c) K. Sakajiri, T. Sugisaki, K. Moriya and S. Kutsumizu, Org. Biomol. Chem., 2009, 7, 3757–3762 RSC; (d) M. Hutin and J. Nitschke, Chem. Commun., 2006, 1724–1726 RSC; (e) A. L. Hofacker and J. R. Parquette, Angew. Chem., Int. Ed., 2005, 44, 1053–1057 CrossRef CAS.
- P. Jonkheijm, P. van der Schoot, A. P. J. H. Schenning and E. W. Meijer, Science, 2006, 313, 80–83 CrossRef CAS.
- (a) M. P. Lightfoot, F. S. Mair, R. G. Pritchard and J. E. Warren, Chem. Commun., 1999, 1945–1946 RSC; (b) P. P. Bose, M. G. B. Drew, A. K. Das and A. Banerjee, Chem. Commun., 2006, 3196–3198 RSC.
- (a) Y. Matsunaga, N. Miyajima, Y. Nakayasu, S. Sakai and M. Yonenaga, Bull. Chem. Soc. Jpn., 1988, 61, 207–210; (b) K. P. van den Hout, R. Martín-Rapún, J. A. J. M. Vekemans and E. W. Meijer, Chem.–Eur. J., 2007, 13, 8111–8124 CrossRef CAS; (c) P. J. M. Stals, M. M. J. Smulders, R. Martín-Rapún, A. R. A. Palmans and E. W. Meijer, Chem.–Eur. J., 2009, 15, 2071–2080 CrossRef CAS.
- (a) K. Hanabusa, C. Koto, M. Kimura, H. Shirai and A. Kakehi, Chem. Lett., 1997, 5, 429–430 CrossRef; (b) Y. Yasuda, E. Iishi, H. Inada and Y. Shirota, Chem. Lett., 1996, 7, 575–576; (c) S. J. Lee, C. R. Park and J. Y. Chang, Langmuir, 2004, 20, 9513–9519 CrossRef CAS; (d) A. Sakamoto, D. Ogata, T. Shikata and K. Hanabusa, Macromolecules, 2005, 38, 8983–8986 CrossRef CAS; (e) T. Shikata, D. Ogata and K. Hanabusa, J. Phys. Chem. B, 2004, 108, 508–514 CrossRef CAS; (f) A. Sakamoto, D. Ogata, T. Shikata, O. Urakawa and K. Hanabusa, Polymer, 2006, 47, 956–960 CrossRef CAS; (g) D. Ogata, T. Shikata and K. Hanabusa, J. Phys. Chem. B, 2004, 108, 15503–15510 CrossRef CAS; (h) M. de Loos, J. H. van Esch, R. M. Kellogg and B. L. Feringa, Tetrahedron, 2007, 63, 7285–7301 CrossRef CAS.
- (a) L. Brunsveld, A. P. H. J. Schenning, M. A. C. Broeren, H. M. Janssen, J. A. J. M. Vekemans and E. W. Meijer, Chem. Lett., 2000, 3, 292–293 CrossRef; (b) M. M. J. Smulders, A. P. H. J. Schenning and Meijer, J. Am. Chem. Soc., 2008, 130, 606–611 CrossRef CAS.
- M. M. J. Smulders, P. J. M. Stals, T. Mes, T. F. E. Paffen, A. J. P. H. Schenning, A. R. A. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2010, 132, 620–626 CrossRef CAS.
- M. M. J. Smulders, T. Buffeteau, D. Cavagnat, M. Wolffs, A. P. H. J. Schenning and E. W. Meijer, Chirality, 2008, 20, 1016–1022 CrossRef CAS.
- A. R. A. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2007, 46, 8948–8968 CrossRef CAS.
- T. F. A. de Greef, M. M. L. Nieuwenhuizen, P. J. M. Stals, C. F. C. Fitie, A. R. A. Palmans, R. P. Sijbesma and E. W. Meijer, Chem. Commun., 2008, 4306–4308 RSC.
- P. van der Schoot, in Supramolecular Polymers, ed. A. Cifferi, Taylor & Francis, London, 2005 Search PubMed.
- The lower he value of 1d than the other BTAs (1a–c) may originate from a different normalization of the CD data, since at room temperature the CD curves are not fully saturated.
- Potential contributions of intermolecular electronic interactions to the Cotton effect were ignored.
- A. Weissberger, Organic Solvents: Physical Properties and Methods of Purification: Vol. 2, 4th edn, Wiley–Interscience Search PubMed.
- I. A. W. Filot, A. R. A. Palmans, P. A. J. Hilbers, R. A. van Santen, E. A. Pidko and T. F. A. de Greef, J. Phys. Chem. B, 2010, 114, 13667–13674 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/c1sc00547b |
| This journal is © The Royal Society of Chemistry 2012 |
