High CO2 solubility, permeability and selectivity in ionic liquids with the tetracyanoborate anion†
Shannon M.
Mahurin
*a,
Patrick C.
Hillesheim
a,
Joshua S.
Yeary
a,
De-en
Jiang
a and
Sheng
Dai
*ab
aChemical Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831. E-mail: mahurinsm@ornl.gov; dais@ornl.gov; Fax: 865-576-5235; Tel: 865-241-3417
bDepartment of Chemistry, University of Tennessee, Knoxville, TN 37996. Fax: 865-576-5235; Tel: 865-576-7307
First published on 2nd October 2012
Abstract
Five different ionic liquids containing the tetracyanoborate anion were synthesized and evaluated for CO2 separation performance. Measured CO2 solubility values were exceptionally high compared to analogous ionic liquids with different anions and ranged from 0.128 mol L−1 atm−1 to 0.148 mol L−1 atm−1. In addition, CO2 permeability and CO2/N2 selectivity values were measured using a supported ionic liquid membrane architecture and the separations performance of the ionic liquid membranes exceeded the Robeson upper bound. These results establish the distinct potential of ionic liquids with the tetracyanoborate, [B(CN)4], anion for the separation of CO2.
Introduction
The selective separation of specific gases from a complex mixture has long been a critical component of many industrial and energy generation processes. Though found in a wide range of applications, the evolution of separations technology has largely been driven by needs and advances in the petroleum and petrochemical industries, such as in the removal of acid gases including CO2 and H2S from natural gas streams. More recently, the elimination of CO2 from postcombustion flue gas emitted by large scale energy generating power plants represents a significant separations challenge with significant potential consequences.Traditionally, liquid absorbents such as aqueous amines have been used to eliminate CO2 from gas streams, either through chemical or physical absorption. However, issues such as solvent loss, degradation and high regeneration energy have led to increased interest in advanced materials and alternative separations methods to enhance or replace these traditional processes. Membranes are part of this growing segment of research because they are reliable, require a smaller footprint, and use less energy for the separation. Room-temperature ionic liquids (RTILs), which are popularly defined as a class of materials that are liquid at or below room temperature and exist completely as ions, have received attention recently as both a liquid absorbent and as a membrane material for gas separations.1–3
Driven by several key properties such as high thermal and chemical stability, a wide electrochemical potential, high ionic conductivity, and negligible vapor pressure, hundreds of ionic liquids have been synthesized and reported, along with associated benefits and potential application.4 Perhaps one of the most important properties of ionic liquids is the ability to tailor many of their physical and chemical properties by combining different cation/anion pairs or by adding functional groups to either the cation or anion. This synthetic variability opens up considerable opportunities to create customized solvents for a particular application or task. For gas separations applications, the negligible vapour pressure and the ability to tailor the interaction of CO2 with the ionic liquid are the most significant properties.
Supported ionic liquid membranes (SILMs) offer a unique separations platform because they combine the advantages of membranes with the ability to tailor the ionic liquid for optimum performance. In principle, a SILM is based on the selective absorption of CO2 into the ionic liquid followed by CO2 transport and desorption.5 Based on the solution-diffusion mechanism, improvements in the performance of a SILM are dependent on balancing the CO2 solubility in the ionic liquid with fast diffusion and desorption. While significant improvements in the chemical sorption of CO2 in ionic liquids have been reported,6,7 it is critical to select ionic liquids that have high physisorption of CO2 rather than high chemisorption as well as fast diffusion.
Though much of the work reported for ionic liquids in CO2 separation has focused on the imidazolium-based ionic liquids, a number of cations including pyrrolidinium, pyridinium, and phosphonium have been explored in an effort to enhance CO2 solubility and CO2/N2 selectivity.8 In addition to the cation, a variety of anions such as [PF6], [BF4], [N(CN)2], and [Tf2N] have been considered as a means to improve performance and advance our understanding of gas transport in ionic liquids.9–11 Ionic liquids that contain the [B(CN)4] anion are a set of liquids that have been somewhat underexplored despite their unique physicochemical properties. Interest in these [B(CN)4] RTILs has generally been limited to use as electrolytes and in dye-sensitized solar cells.12,13 Recently, however, we reported a high CO2 solubility and CO2/N2 selectivity in an imidazolium-based ionic liquid with a [B(CN)4] anion.14
Since this first report of the high CO2 solubility, permeability and CO2/N2 selectivity of the [B(CN)4] anion, interest in this RTIL for gas separations has grown; quantum mechanical calculations and molecular dynamics simulations revealed a weak interaction between the cation and the [B(CN)4] anion responsible for the high CO2 solubility supporting the potential of this RTIL for CO2 separations.15 In this work, we build on these prior results and explore the separations properties of a series of [B(CN)4]-containing RTILs coupled to a variety of cations including imidazolium, pyrrolidinium, and piperidinium. Effects of alkyl chain length and methyl substitution as well as ring structure on the CO2 solubility, permeability and CO2/N2 selectivity were examined. As a class, these RTILs show high CO2 solubility as well as excellent permeability and selectivity values that exceed the Robeson upper bound. Finally, the high CO2 solubility exhibited by these RTILs is examined within the current mechanistic views of gas solubility in ionic liquids.
Results and discussion
Physical properties
The structures of the imidazolium, pyrrolidinium, and piperidinium cations and the [B(CN)4] anion used in this work are shown in Fig. 1. For the imidazolium RTILs, two different alkyl chain lengths were studied and the addition of a methyl group on the C2 hydrogen of the ring was also investigated. The structure of the ionic liquids was verified using NMR spectroscopy (see Supplementary Information). Decomposition temperatures, which were measured by thermogravimetric analysis (TGA), are given in Table 1 and ranged from 361 °C for [C4MPyrr] to 396 °C for [emmim]. These decomposition temperatures are slightly lower than but comparable to those observed in fluorinated anions such as [Tf2N].16–18 In contrast to [Tf2N]-based ionic liquids, both of the cyclical cations, [C4MPyrr] and [C4mpip], with the [B(CN)4] anion displayed lower thermal stabilities than the imidazolium-based RTILs.![The structures of the five cations and the [B(CN)4] anion. The abbreviations are as follows: a) [emim], b) [bmim], c) [emmim], d) [C4MPyrr], e) [C4mpip], f) [B(CN)4].](/image/article/2012/RA/c2ra22342b/c2ra22342b-f1.gif) | ||
| Fig. 1 The structures of the five cations and the [B(CN)4] anion. The abbreviations are as follows: a) [emim], b) [bmim], c) [emmim], d) [C4MPyrr], e) [C4mpip], f) [B(CN)4]. | ||
| Ionic Liquid | Molar Volumea (cm3 mol−1) | Molecular Weight (g mol−1) | Viscosityb (cP) | Ea (kJ mol−1) | Tdec (°C) |
|---|---|---|---|---|---|
| a Obtained for 25 °C. b Acquired at 20 °C | |||||
| [emim][B(CN)4] | 219.46 | 226.04 | 19.5 | 23.3 | 396 |
| [bmim][B(CN)4] | 245.04 | 254.11 | 44.9 | 32.6 | 393 |
| [emmim][B(CN)4] | 226.91 | 240.07 | 36.0 | 29.0 | 396 |
| [C4MPyrr][B(CN)4] | 262.66 | 257.14 | 58.9 | 30.1 | 361 |
| [C4mpip][B(CN)4] | 248.72 | 266.13 | 111 | 36.5 | 373 |
The viscosity of RTILs, which are generally high compared to typical organic solvents, is a critical parameter from a practical sense because a high viscosity will tend to reduce the diffusion of gas through the ionic liquid which can ultimately reduce the performance of the membrane. Many of the models reported to rationalize the diffusivity of gases through RTILs show an inverse relationship between viscosity and diffusivity.19,20 Clearly, for high permeability it is important to use ionic liquids with low viscosity.
The temperature dependent viscosities are shown in Supplementary Information (Table S1†). As expected, the viscosity decreased nonlinearly as the temperature increased. Table 1 shows that the [emim][B(CN)4] exhibited the lowest viscosity of all the RTILs tested while [C4mpip][B(CN)4] showed the highest viscosity. Similar to previously reported results, lengthening the alkyl chain on the cation, e.g., going from ethyl to n-butyl, increased the viscosity.21 The addition of a methyl group on the C2 position of the imidazolium ring also resulted in an increased viscosity in agreement with results previously reported by Noack et al.22 In addition, Crosthwaite et al. measured the viscosities and saw nearly a factor of two increase when the methyl group was added to the C2 position for [hmmim][Tf2N] compared to [hmim][Tf2N].21 In general, use of the [B(CN)4] anion drastically reduced the viscosity compared to [Tf2N] congeners. For example, [bmim][B(CN)4] has a viscosity of 44.4 cP which is nearly 12% lower than the reported [Tf2N] congener23 while [emmim][B(CN)4] has a viscosity of 36.0 cP which is 244% lower than the [Tf2N]-based RTIL.24
Fig. 2 presents the Arrhenius plot for the five ionic liquids. The curves are highly linear confirming that these RTILs follow Arrhenius behaviour. The activation energies for viscous flow given in Table 1 are comparable to literature values.19 These values are included because of applicability in calculating solubility parameters.
![Arrhenius plot of the [B(CN)4]-containing ionic liquids. Solid lines are the best fit lines used to calculate the activation energies.](/image/article/2012/RA/c2ra22342b/c2ra22342b-f2.gif) | ||
| Fig. 2 Arrhenius plot of the [B(CN)4]-containing ionic liquids. Solid lines are the best fit lines used to calculate the activation energies. | ||
CO2 permeability and CO2/N2 selectivity
Gas transport in a SILM follows the typical solution/diffusion mechanism where permeability is related to solubility and diffusivity via the following equation:| P = S D | (1) |
To maximize gas permeability, or membrane productivity, it is important to use materials with both high solubility as well as high diffusivity. The ideal selectivity is then given by ratio of the pure gas permeabilities:
| αij = Pi/Pj = (Si/Sj)·(Di/Dj) | (2) |
Given the comparatively low viscosities of the [B(CN)4] RTILs, the permeabilities were generally expected to be high. Table 2 shows the CO2 permeability values and the CO2/N2 selectivity values for the [B(CN)4] ionic liquids. Note that the [emim][B(CN)4] has been previously reported.14 Traditionally, [emim][Tf2N], which has a permeability of 1702 barrer, has been used as a benchmark for high permeability ionic liquids since it exhibits one of the highest CO2 permeability values.8 With the exception of [C4mpip], all of the [B(CN)4] RTILs investigated show permeability values that are comparable to or exceed [emim][Tf2N]. The lowest viscosity RTIL, [emim][B(CN)4], showed the highest permeability at 2040 barrer while the highest viscosity RTIL showed the lowest permeability. In general, the permeability shows an inverse relationship with the viscosity which is in agreement with previously reported trends in permeability and viscosity.8 The CO2/N2 selectivity values for the [B(CN)4]-based RTILs are also shown in Table 2 along with permeability and selectivity values for [emim][BF4] and [emim][TfO] for additional comparison. In general, the selectivity values of the [B(CN)4] RTILs are quite high, with values ranging from 38 to 53. Interestingly, the N2 permeability in [emim][B(CN)4] is lower than in [emim][Tf2N] and this is at least partially responsible for the high selectivity. A similar effect has been reported by Carlisle for the addition of a nitrile group to an imidazolium cation with the [Tf2N] anion. In that case, the N2 solubility was reduced compared to the unfunctionalized analog leading to higher CO2/N2 selectivity.25
| Ionic Liquid | Permeability (barrer) | CO2/N2 Selectivity | |
|---|---|---|---|
| CO2 | N2 | ||
| a Taken from [Ref. 8]. | |||
| [emim][B(CN)4] | 2040 ± 60 | 38 ± 4 | 53 ± 6 |
| [bmim] [B(CN)4] | 1755 ± 50 | 44 ± 3 | 40 ± 2 |
| [emmim] [B(CN)4] | 1721 ± 80 | 38 ± 4 | 46 ± 5 |
| [C4MPyrr] [B(CN)4] | 1633 ± 60 | 44 ± 3 | 38 ± 2 |
| [C4mpip][B(CN)4] | 961 ± 25 | 26 ± 4 | 37 ± 5 |
| [emim][Tf2N]a | 1702 | 73.6 | 23 |
| [emim][BF4]a | 968.5 | 21.8 | 44.5 |
| [emim] [TfO]a | 1171.4 | 28.9 | 40.5 |
As previously stated, a number of reports have been published describing the relationship between gas diffusion through ionic liquids and viscosity of the liquid. Though the details of the different empirical models as well as the properties included vary, there is general agreement that diffusivity decreases as viscosity increases. As will be discussed in more detail in the next section, the CO2 solubility values for the [B(CN)4] RTILs are high but fairly similar. Differences in gas diffusivity are likely responsible for the relatively large variations in the CO2 permeabilities measured for these RTILs, particularly as the viscosities of the RTILs vary from 19.5 cP to 111 cP.
The use of the selectivity vs. permeability curve, generally referred to as the Robeson plot, has become prevalent in gas separations literature as a method to evaluate membrane materials. This plot, which was first reported as an empirical upper bound for polymeric membranes but was subsequently placed on a firmer theoretical foundation,26,27 demonstrates the compromise that typically exists between high permeability and high selectivity. Most membranes fall below the upper bound line for gas pairs such as CO2/N2, which has provided significant motivation to discover membrane materials that exceed this limit. Fig. 3 shows the Robeson plot with the most recent upper bound line.28 The [B(CN)4] RTILs all exceed the Robeson upper bound line which illustrates the remarkable potential of these ionic liquids for CO2 separation.
![Robeson plot showing the [B(CN)4] anion RTILs in comparison to the upper bound line. The open circles are polymers, filled squares correspond to ionic liquids, and the open triangles are the [B(CN)4] anions in this work. The line is the upper bound.](/image/article/2012/RA/c2ra22342b/c2ra22342b-f3.gif) | ||
| Fig. 3 Robeson plot showing the [B(CN)4] anion RTILs in comparison to the upper bound line. The open circles are polymers, filled squares correspond to ionic liquids, and the open triangles are the [B(CN)4] anions in this work. The line is the upper bound. | ||
Fig. 4 shows the permeability as a function of driving pressure for the [B(CN)4] RTILs. Clearly, there is no dependence of the permeability on the driving pressure which indicates that there is no facilitated transport within the ionic liquids. This confirms that the CO2 is physically absorbed into the ionic liquid and there is no chemisorption of the CO2 molecule to either the cation or the [B(CN)4] anion.
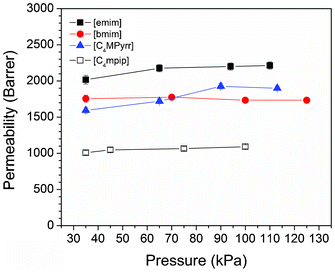 | ||
| Fig. 4 The effect of pressure difference across the membrane on the measured permeability. The lack of pressure dependence suggests non-facilitated gas transport through the ionic liquids. | ||
CO2 solubility
Given the impact of CO2 solubility on gas separations performance, we measured solubility isotherms for the [B(CN)4] RTILS (see Fig. 5) where the ordinate is given in terms of volumetric solubility. The absorption isotherms are highly linear and the slopes appear to be fairly comparable. Quantitatively, the slope of each isotherm was obtained using a linear least squares fit and these values are presented in Table 3. We use volume-based solubility because practical applications of gas capture technologies require knowledge of the amount of CO2 that can be absorbed by a fixed volume of ionic liquid. However CO2 solubility values are often reported on a mole fraction basis in the form of Henry's Law constants according to the following: | (3) |
where x is the mole fraction of CO2 absorbed in the ionic liquid and p is the pressure. To facilitate comparison with literature values, Henry's Law constants are also included in Table 3.
![CO2 absorption isotherms for the [B(CN)4]-containing ionic liquids acquired at 25 °C.](/image/article/2012/RA/c2ra22342b/c2ra22342b-f5.gif) | ||
| Fig. 5 CO2 absorption isotherms for the [B(CN)4]-containing ionic liquids acquired at 25 °C. | ||
| Ionic Liquid | CO2 Solubilitya (mol L−1 atm−1) | HCO2 (atm) | COSMO-RS Prediction | FFV | |
|---|---|---|---|---|---|
| CO2 Soubility | HCO2 | ||||
| a Acquired at 25 °C with ±3% uncertainty | |||||
| [emim][B(CN)4] | 0.128 | 38.9 | 0.19 | 25 | 0.1323 |
| [bmim] [B(CN)4] | 0.132 | 32.3 | 0.21 | 20 | 0.1451 |
| [emmim] [B(CN)4] | 0.148 | 31.9 | 0.31 | 17 | 0.1390 |
| [C4MPyrr] [B(CN)4] | 0.130 | 30.4 | 0.26 | 15 | 0.1520 |
| [C4mpip] [B(CN)4] | 0.128 | 30.2 | 0.26 | 15 | 0.1480 |
In general, all of the [B(CN)4] RTILs exhibited exceptional CO2 solubility values that were larger than the prototypical ionic liquid, [emim][Tf2N], which has a CO2 solubility of 0.103 mol L1 atm−1.29 The [emmim][B(CN)4] RTIL had the highest solubility value at 0.148 mol L−1 atm−1. Interestingly, the lowest CO2 solubility was measured for [emim][B(CN)4], which also had the highest CO2 permeability. This is primarily due to a higher CO2 diffusivity in the [emim][B(CN)4]. The Henry's Law constants show a similar trend as the volumetric solubility though there are some differences. For example, [emmim] showed a higher volumetric solubility than [C4MPyrr] but a higher Henry's constant (higher Henry's constants generally equate to lower solubility). These differences are relatively small and can be attributed to the varying molar weights of the different ionic liquids.30 In fact, the volumetric solubilities for the [emim], [C4MPyrr], and [C4mpip] are very similar.
The three imidazolium RTILs are of particular interest because they allow us to explore the impact of alkyl chain length and methyl substitution on CO2 solubility. Increasing the alkyl chain length from [emim] to [bmim] resulted in a slight increase in CO2 solubility. Furthermore, replacing the C2 hydrogen with a methyl group on the imidazolium ring also improved the CO2 solubility, with the value increasing from 0.128 to 0.148 mol L−1 atm−1. This differs from previous results for [emim][PF6] and [emim][Tf2N] where replacing the C2 hydrogen with a methyl group slightly decreased the CO2 solubility.31
To further probe these results, the COSMOtherm package, which has gained popularity as a method to rapidly estimate properties such as density, free volume and CO2 solubility,32 was used to calculate the CO2 solubility values for each of the RTILs and the results are shown in Table 3. Optimized molecular geometries for each RTIL were used to calculate molecular surfaces (or COSMO surfaces) and thermodynamic properties.
CO2 solubility values predicted using the COSMOtherm package are in very good agreement with the measured values. For example, COSMOtherm predicted that substituting the methyl group at the C2 position would increase the CO2 solubility which is consistent with the measured results and validates the effect of the methyl group for the [B(CN)4] anion. Furthermore, though the predicted Henry's constants are not identical to the measured values, the trend is in excellent agreement, [emim] > [bmim] > [emmim] > [C4MPyrr] > [C4mpip]. In terms of volumetric solubility, COSMOtherm predicted the largest CO2 solubility for [emmim][B(CN)4] which is also in agreement with measured results. Increasing the alkyl chain length from [emim] to [bmim] resulted in a slight increase in both the measured and calculated solubility values in contrast to the alkylimidazolium [Tf2N] RTILs which show decreasing solubility with alkyl chain length.33,34
The high CO2 solubilities for the [B(CN)4] illustrate the unique nature of this anion and reaffirm the ongoing debate over the mechanism governing gas solubility in ionic liquids. While there is general agreement that CO2 solubility in ionic liquids is affected by cation-anion, CO2-anion, and CO2–CO2 interactions, there is some disagreement on the relative importance and magnitude of each interaction.11,35,36 In a recent review, Hu et al. suggested that the combination of two effects, i.e., CO2 insertion into void space (or free volume) in ionic domains of the ionic liquid followed by CO2-ion interactions, is responsible for CO2 solubility in ionic liquids.37 Increasing the size, flexibility or asymmetry of the anion can lead to increased free volume in the ionic regions and enhanced CO2 solubility.
Despite the high symmetry of the [B(CN)4] anion which might suggest low free volume in the ionic domain, free volume can be increased if the ionic liquid can rearrange and accommodate the absorption of CO2. One explanation then for the high CO2 solubility in these RTILs could be the ability of the ionic liquid to rearrange due to reduced interaction between the cations and the [B(CN)4] anion compared to other anions such as [PF6] or [Tf2N]. This is supported by a recent report by Babarao et al. who showed that there is a weaker cation-anion interaction for [emim][B(CN)4] than for [emim][BF4], [emim][PF6], or [emim][Tf2N],15 which could lead to an enhanced ability to rearrange and greater CO2-anion interaction and higher solubility.
Bara et al. recently noted the importance of fractional free volume in estimating CO2 solubility in RTILs.38 The fractional free volume (FFV) was calculated using the COSMOtherm program according to the following equation:
 | (4) |
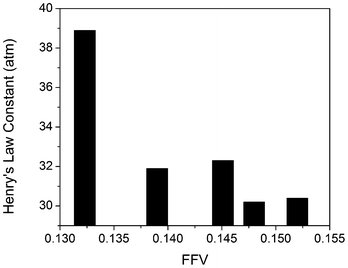 | ||
| Fig. 6 Henry's Law constants as a function of the fractional free volume (FFV). | ||
An interesting comparison is given in Fig. 7 which shows the solubility as a function of molar volume along with the Camper Model for CO2 solubility in RTILs.33 Though the Camper Model was developed to estimate the solubility for imidazolium-based ionic liquids, it is instructive to show as a comparison for the [B(CN)4] ionic liquids. The Camper Model relates the solubility of CO2 in an RTIL to the molar volume only. Here we see that the CO2 solubility in the [B(CN)4] ionic liquids significantly exceed the molar volume dependence, again indicating that additional factors play a role in determining gas solubility.
![Comparison of the solubility of the [B(CN)4]-containing ionic liquids to the Camper Model.](/image/article/2012/RA/c2ra22342b/c2ra22342b-f7.gif) | ||
| Fig. 7 Comparison of the solubility of the [B(CN)4]-containing ionic liquids to the Camper Model. | ||
Conclusions
CO2 permeability, CO2/N2 selectivity and CO2 solubility values were measured for ionic liquids that contain the [B(CN)4] anion and various cations. CO2 permeability and selectivity values exceeded the Robeson upper bound line for all of the [B(CN)4] ionic liquids, suggesting their significant potential as supported ionic liquid membranes. In addition, all of the ionic liquids exhibited high CO2 solubilities ranging from 0.128 mol L−1 atm−1 to 0.148 mol L−1 atm−1. Based on the current views of gas solubility in ionic liquids, we postulate that the high CO2 solubilities result from the combination of reduced cation-anion interactions and enhanced CO2-anion interactions. These results firmly establish [B(CN)4] as a unique anion in offering exceptional separations performance for CO2 when combined with various types of cations to form [B(CN)4]-containing ionic liquids.Experimental
Gas solubility
Gas solubility measurements were obtained using a gravimetric microbalance (Hiden Isochema, IGA). Approximately 60 mg of the RTIL was loaded into the sample container and sealed in the stainless steel chamber. The RTIL was dried and degassed at a temperature of 80 °C and a vacuum pressure of 1 mbar for a minimum of 4 h before recording the dry mass. Mass measurements were then acquired at various CO2 pressures up to 10 atm. The temperature of the sample was maintained using a constant-temperature recirculating water bath.Viscosity
Temperature dependent viscosity measurements were acquired using a cone/plate viscometer (Brookfield, DVII + Pro), which allowed the use of small sample volumes of < 1 mL. The sample was kept at the desired temperature with a recirculating water bath (VWR) for at least 30 min prior to measurement and five separate measurements at each temperature were obtained and averaged.Permeability
The RTIL was loaded into a polyethersulfone membrane with 100 nm pore size by immersing the membrane in the liquid and placing it in a vacuum desiccator overnight. Permeabilites were measured using a constant-volume system consisting of two chambers (permeate and retentate) separated by the membrane. The membrane was positioned on a porous stainless steel support for mechanical stability and loaded into the membrane test chamber where it was evacuated to a pressure of 25 mTorr overnight before measurements were acquired in order to equilibrate the membrane. The retentate side was pressurized with each gas and the pressure rise in the permeate chamber was measured with a Baratron pressure gauge (MKS Instruments) as a function of time to obtain the permeability using the following equation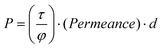 | (5) |
 | (6) |
Calculations
The COSMOtherm program was used to predict gas solubility and Henry's Law constants in the ionic liquids. The COSMOtherm program39 is based on the COSMO-RS (COnductor-like Screening MOdel for Real Solvents)40 theory which links the quantum mechanically calculated, solvated molecular surfaces from the COSMO method to interacting molecular surfaces and macroscopic properties such as solubility via a statistical thermodynamics model. Full COSMO optimization of the molecular structure was obtained with Turbomole V 6.0 at the level of density functional theory (DFT) with the BP86 functional for electron correlation and exchange41 and using the resolution-of-identity (RI) technique and the TZVP basis set.Synthesis of ionic liquids
Sodium and potassium tetracyanoborate were purchased from SelectLab Chemicals. All other chemicals were purchased from Sigma-Aldrich in the highest available purity and used as received. Starting bromide salts, namely 3-ethyl-1,2-dimethyl-1H-imidazol-3-ium bromide,42 3-butyl-1-methyl-1H-imidazol-3-ium bromide,43 1-butyl-1-methylpiperidin-1-ium bromide,44 1-butyl-1-methylpyrrolidin-1-ium bromide,42 were synthesized and purified according to established literature procedures. 1H and 13C NMR spectra were recorded on a Bruker Avance 400, at 400 MHz and 100 MHz respectively. A JEOL (Peabody, MA) JMS-T100LC (AccuTOFTM) orthogonal time-of-flight (TOF) mass spectrometer was used to characterize the compounds. Thermal stabilities were measured using a Thermal Advantage 2950 Analyzer with platinum pans under a nitrogen atmosphere (10 °C min−1 heating to 750 °C). More detailed synthesis procedures are included in the Supplementary Information.†Acknowledgements
S.M.M, J.S.Y., D.J., and S.D. were sponsored by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy. P.C.H. was supported by the Advanced Research Projects Agency – Energy, U.S. Department of Energy.References
- J. E. Brennecke and B. E. Gurkan, J. Phys. Chem. Lett., 2010, 1, 3459–3464 CrossRef CAS.
- C. M. Wang, S. M. Mahurin, H. M. Luo, G. A. Baker, H. R. Li and S. Dai, Green Chem., 2010, 12, 870–874 RSC.
- R. D. Noble and D. L. Gin, J. Membr. Sci., 2011, 369, 1–4 CrossRef CAS.
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS.
- Q. Gan, Y. R. Zou, D. Rooney, P. Nancarrow, J. Thompson, L. Z. Liang and M. Lewis, Adv. Colloid Interface Sci., 2011, 164, 45–55 CrossRef CAS.
- E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, J. Am. Chem. Soc., 2002, 124, 926–927 CrossRef CAS.
- C. M. Wang, X. Y. Luo, H. M. Luo, D. E. Jiang, H. R. Li and S. Dai, Angew. Chem., Int. Ed., 2011, 50, 4918–4922 CrossRef CAS.
- P. Scovazzo, J. Membr. Sci., 2009, 343, 199–211 CrossRef CAS.
- P. Scovazzo, D. Havard, M. McShea, S. Mixon and D. Morgan, J. Membr. Sci., 2009, 327, 41–48 CrossRef CAS.
- M. B. Shiflett, D. W. Drew, R. A. Cantini and A. Yokozeki, Energy Fuels, 2010, 24, 5781–5789 CrossRef CAS.
- J. L. Anthony, J. L. Anderson, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2005, 109, 6366–6374 CrossRef CAS.
- M. Marszalek, Z. F. Fei, D. R. Zhu, R. Scopelliti, P. J. Dyson, S. M. Zakeeruddin and M. Gratzel, Inorg. Chem., 2011, 50, 11561–11567 CrossRef CAS.
- D. B. Kuang, P. Wang, S. Ito, S. M. Zakeeruddin and M. Gratzel, J. Am. Chem. Soc., 2006, 128, 7732–7733 CrossRef CAS.
- S. M. Mahurin, J. S. Lee, G. A. Baker, H. M. Luo and S. Dai, J. Membr. Sci., 2010, 353, 177–183 CrossRef CAS.
- R. Babarao, S. Dai and D. E. Jiang, J. Phys. Chem. B, 2011, 115, 9789–9794 CrossRef CAS.
- C. P. Fredlake, J. M. Crosthwaite, D. G. Hert, S. Aki and J. F. Brennecke, J. Chem. Eng. Data, 2004, 49, 954–964 CrossRef CAS.
- J. G. Huddleston, A. E. Visser, W. M. Reichert, H. D. Willauer, G. A. Broker and R. D. Rogers, Green Chem., 2001, 3, 156–164 RSC.
- H. Tokuda, K. Hayamizu, K. Ishii, M. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110 CrossRef CAS.
- S. S. Moganty and R. E. Baltus, Ind. Eng. Chem. Res., 2010, 49, 5846–5853 CrossRef CAS.
- D. Morgan, L. Ferguson and P. Scovazzo, Ind. Eng. Chem. Res., 2005, 44, 4815–4823 CrossRef CAS.
- J. M. Crosthwaite, M. J. Muldoon, J. K. Dixon, J. L. Anderson and J. F. Brennecke, J. Chem. Thermodyn., 2005, 37, 559–568 CrossRef CAS.
- K. Noack, P. S. Schulz, N. Paape, J. Kiefer, P. Wasserscheid and A. Leipertz, Phys. Chem. Chem. Phys., 2010, 12, 14153–14161 RSC.
- J. N. C. Lopes, M. F. C. Gomes, P. Husson, A. A. H. Padua, L. P. N. Rebelo, S. Sarraute and M. Tariq, J. Phys. Chem. B, 2011, 115, 6088–6099 CrossRef.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef CAS.
- T. K. Carlisle, J. E. Bara, C. J. Gabriel, R. D. Noble and D. L. Gin, Ind. Eng. Chem. Res., 2008, 47, 7005–7012 CrossRef CAS.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- B. D. Freeman, Macromolecules, 1999, 32, 375–380 CrossRef CAS.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- S. M. Mahurin, J. S. Yeary, S. N. Baker, D. E. Jiang, S. Dai and G. A. Baker, J. Membr. Sci., 2012, 401–402, 61–67 CrossRef CAS.
- J. E. Bara, T. K. Carlisle, C. J. Gabriel, D. Camper, A. Finotello, D. L. Gin and R. D. Noble, Ind. Eng. Chem. Res., 2009, 48, 2739–2751 CrossRef CAS.
- C. Cadena, J. L. Anthony, J. K. Shah, T. I. Morrow, J. F. Brennecke and E. J. Maginn, J. Am. Chem. Soc., 2004, 126, 5300–5308 CrossRef CAS.
- J. Palomar, M. Gonzalez-Miquel, A. Polo and F. Rodriguez, Ind. Eng. Chem. Res., 2011, 50, 3452–3463 CrossRef CAS.
- D. Camper, J. Bara, C. Koval and R. Noble, Ind. Eng. Chem. Res., 2006, 45, 6279–6283 CrossRef CAS.
- P. K. Kilaru, P. A. Condemarin and P. Scovazzo, Ind. Eng. Chem. Res., 2008, 47, 900–909 CrossRef CAS.
- P. J. Carvalho and J. A. P. Coutinho, J. Phys. Chem. Lett., 2010, 1, 774–780 CrossRef CAS.
- T. Seki, J. D. Grunwaldt and A. Baiker, J. Phys. Chem. B, 2009, 113, 114–122 CrossRef CAS.
- Y. F. Hu, Z. C. Liu, C. M. Xu and X. M. Zhang, Chem. Soc. Rev., 2011, 40, 3802–3823 RSC.
- M. S. Shannon, J. M. Tedstone, S. P. O. Danielsen, M. S. Hindman, A. C. Irvin and J. E. Bara, Ind. Eng. Chem. Res., 2012, 51, 5565–5576 CrossRef CAS.
- F. Eckert and A. Klamt, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, 2011 Search PubMed.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- R. Ahlrichs, F. Furche and S. Grimme, Chem. Phys. Lett., 2000, 325, 317–321 CrossRef CAS.
- X. W. Chen, X. H. Li, H. B. Song, Y. Qian and F. R. Wang, Tetrahedron Lett., 2011, 52, 3588–3591 CrossRef CAS.
- A. K. Burrell, R. E. Del Sesto, S. N. Baker, T. M. McClesky and G. A. Baker, Green Chem., 2007, 9, 809–809 RSC.
- Z. B. Zhou, H. Matsumoto and K. Tatsumi, Chem.–Eur. J., 2006, 12, 2196–2212 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available: temperature dependent viscosity values, detailed description of synthesis and NMR results are included. See DOI: 10.1039/c2ra22342b |
| This journal is © The Royal Society of Chemistry 2012 |
