Theoretical derivation of ionic current and electronic current and comparison between fitting curves and measured curves
Yang
Ruiquan
,
Jiang
Longfei
,
Zhu
Xufei
*,
Song
Ye
,
Yu
Dongliang
and
Han
Aijun
Key Laboratory of Soft Chemistry and Functional Materials of Education Ministry, Nanjing University of Science & Technology, Nanjing, 210094, People's Republic of China. E-mail: zhuxufei.njust@gmail.com; Fax: +86 25 8427 6082; Tel: +86 25 8431 5949
First published on 16th October 2012
Abstract
The mechanism of metal anodization has been investigated for several decades, however the present models can only partially explain the experimental phenomena. It is known that the total current in the oxide mainly includes ionic current and electronic current. The formation of oxide film is determined by ionic current, and the electronic current gives rise to the evolution of oxygen gas. In this paper, the theoretical expressions for time dependent ionic current and electronic current are derived to deduce the anodizing process. The results indicate that the ionic current decreases exponentially with time, while the electronic current increases with time in a more complicated way. Both types of current will approach infinitely close to a constant value in the steady stage. Consequently, the current evolution under constant anodizing voltage are experimentally investigated for aluminum and titanium anodization. All of the current-transient plots, including that in the formation of both porous and barrier type films, can be well fitted by the proposed expression. The morphology transition between porous and barrier anodic oxide films is determined by the magnitude of electronic current within the oxide.
1. Introduction
Self-ordered porous anodic TiO2 nanotubes (PATNT) and other porous anodic oxides have received considerable attention because of their potential for high technology application in a number of fields.1–3 Porous anodic alumina (PAA) and anodization of valve metals have been widely investigated over six decades.4–6 Many innovative theories have been put forward in different periods. The growth models of PAA and PATNT include the field-assisted dissolution (FAD) model,7–10 the Al3+ or Ti4+ ejection model,11,12 the self-ordering and volume expansion model,13–15 the field-enhanced water dissociation and equifield strength model.16–18 The formation mechanism of PATNT is mainly ascribed to the strongly affects of fluoride anions and the formation of water-soluble [TiF6]2− species.19–24 On one hand, the [TiF6]2− species result from the complexing with Ti4+ ions which are ejected at the oxide-electrolyte interface after migrating through the barrier oxide layer.21 And on the other hand, the [TiF6]2− species result from the chemical attack of the formed TiO2 (eqn (1)).19–24| TiO2 + 6F− + 4H+ → [TiF6]2− + 2H2O | (1) |
However, PATNT has been achieved in an aqueous H2SO4 solution as well as other fluoride free solutions.18,25,26 This fact puts the fluoride effect (eqn (1)) into question.18
Despite the intensive investigation and much deeper interpretation of the PAA and PATNT having been performed extensively, to date, there are still many problems which remain to be solved.18 For example, the exact origin for the gap formation between the nanotubes still requires further investigation.18 The exact description of the interactions between the current oscillations and porous structural features remains unresolved.20 Houser and Hebert pointed out that no model has successfully explained the relationships between PAO morphology and processing parameters.27 It is well known that there are two types of anodic oxide films, nonporous barrier anodic oxide (BAO) and porous anodic oxide (PAO) films. Fig. 1 shows the current–time curves and the different growth manners of BAO and PAO films.6,9–11,19–21 It can be found that the two curves seem to begin to diverge at point c in Fig. 1a. The traditional theories have not given an exact interpretation of the divergence.6,9 It is well known that the growth manners of BAO and PAO are totally different.9–11,19–21 For BAO films, new barrier oxide can be formed both at E/O and O/M interfaces as shown in Fig. 1b.6,9–11 But for PAO films, new oxide of the barrier layer is formed only at the O/M interface during the pore deepening period. Whereas, the field-assisted dissolution or chemical attack of eqn (1) make the pores continuously deepen as shown in Fig. 1c.9–11,19–21 The growth manner of PAO in Fig. 1c has not been demonstrated by experimental findings. For example, the exact content of complex [TiF6]2− or Ti4+ in the electrolyte after the anodizing process has not been analyzed in the correlative literatures. As Patermarakis and coworkers pointed out, the mechanism of PAO formation was hardly derived by direct in situ experimental methods.28,29 Actually, the growing manner of PAO in Fig. 1c is in contrast to the viscous flow model.30–32 Skeldon and coworkers concluded that the generation and development of pores were mainly ascribed to the viscous flow of oxide from the pore base to the pore wall (see Fig. 2b).30–32
 | ||
| Fig. 1 Schematic diagrams of the current-time curves of BAO and PAO (a), the growing manner of BAO (b), and the pore development in PAO (c).6,9–11,19–21 | ||
We have found some absolute closed pores which cannot be explained by the FAD model of PAO.33 Based on the findings and the viscous flow model, we introduced the concept of oxygen bubble mould effect (OBME) and put forward a new growth model of PAA, which emphasized the close relationship between pore generation and oxygen evolution.33,34 The forming processes of the BAO and PAO films were compared in detail. We have concluded that the oxide growing manner of PAO was in accordance with that of BAO as shown in Fig. 1b.34 Diggle and coworkers6 concluded in 1969 that there was no essential difference between PAO and BAO films. We have concluded that the differences between PAO and BAO are the magnitude of the electronic current (ie) or the continuity of oxygen evolution.34 Anodizing total current (i) within the barrier oxide mainly includes ionic current (iion) and ie during the anodizing process. The iion is used to form oxide and the ie gives rise to oxygen gas.34 Formation of nanopores can be ascribed to OBME which results from the sufficient ie. This new model has received considerable attention and citation.35–45 In order to obtain expected PAA or PATNT, great care and attention should be given to the generation of electronic current (or localized dielectric breakdown) and oxygen evolution.41–46
Herein, we focus on the physical nature of the ionic current and electronic current within the anodic oxide and pay more attention to the theoretical expressions of ionic current and electronic current with the anodizing time. The whole derivation was based on ionic current existing as well as electronic current as presented in OBME. A few assumptions and approximations were adopted in this derivate process. As a result, we gave the proximate functional expression of anodizing total current with time. Then we used the results to fit a curve and compared it with the measured curve to show the rationality of the results. The present results may open new possibilities for fast understanding of the kinetics of PAO because the fitted curves show an excellent accordance with the measured curves. Moreover, this combination of theories opens a new way to assemble the PATNT and PAA.
2. Experimental
The commercial titanium foil (100 μm thick, purity 99.5%) was used as a working electrode and another titanium foil served as a counter electrode. The titanium foils were polished using a mixture solution of HF and HNO3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in volume) for 100 s. Subsequently, the samples were rinsed thoroughly with deionized water and dried in the air prior to anodization. Surface-finished titanium foils were anodized in 0.5 wt% NH4F ethylene glycol (EG) solutions under constant voltage (CV = 60 V) at room temperature with vigorous stirring. The commercial aluminum foil (200 μm thick, purity 99.99%) was employed. The aluminum sheets were dipped into 2 wt% sodium hydroxide solution at 70 °C for chemical polishing for 120 s and then electropolished at a constant current density of 120 mAcm−2 for about 90 s in an electrolyte composed of phosphoric acid (80 wt%), chromium trioxide (12 wt%) and deionized water (8 wt%) at 75 °C. The electropolished aluminum sheet was used as the anode, another aluminum sheet with the same purity as a cathode. Surface-finished aluminum sheets were anodized in 0.3 M H2C2O4 aqueous solutions under constant voltage (CV = 45 V) at room temperature with vigorous stirring. In order to compare the difference between the barrier anodic alumina and PAA, the anodizing process of aluminum in 4 wt% (NH4)2C6H8O4 (ammonium adipate) aqueous solution was performed. The current–time curves during anodizing were recorded automatically by a computer measurement system (SY-98).33,34 The morphology of the anodic oxide films was characterized by field-emission scanning electron microscopy (FE-SEM, Zeiss Supra 55 and Hitachi S-4800).
3 in volume) for 100 s. Subsequently, the samples were rinsed thoroughly with deionized water and dried in the air prior to anodization. Surface-finished titanium foils were anodized in 0.5 wt% NH4F ethylene glycol (EG) solutions under constant voltage (CV = 60 V) at room temperature with vigorous stirring. The commercial aluminum foil (200 μm thick, purity 99.99%) was employed. The aluminum sheets were dipped into 2 wt% sodium hydroxide solution at 70 °C for chemical polishing for 120 s and then electropolished at a constant current density of 120 mAcm−2 for about 90 s in an electrolyte composed of phosphoric acid (80 wt%), chromium trioxide (12 wt%) and deionized water (8 wt%) at 75 °C. The electropolished aluminum sheet was used as the anode, another aluminum sheet with the same purity as a cathode. Surface-finished aluminum sheets were anodized in 0.3 M H2C2O4 aqueous solutions under constant voltage (CV = 45 V) at room temperature with vigorous stirring. In order to compare the difference between the barrier anodic alumina and PAA, the anodizing process of aluminum in 4 wt% (NH4)2C6H8O4 (ammonium adipate) aqueous solution was performed. The current–time curves during anodizing were recorded automatically by a computer measurement system (SY-98).33,34 The morphology of the anodic oxide films was characterized by field-emission scanning electron microscopy (FE-SEM, Zeiss Supra 55 and Hitachi S-4800).
3. Results and discussion
3.1 Simple comparison between classic FAD model and OBME model
Many groups have investigated the PAO mechanism, but little literature involved electronic conduction.6,46–48 As Patermarakis and coworkers28,29 pointed out, the ionic current across the barrier layer is practically close to 100% of the imposed current and the electronic current related to oxygen evolution is indeed tiny under all conditions employed. In 2012, however, they also pointed out that electronic current allied with oxygen evolution under high field action most probably occurs via tunnel effect.39 In 2012, Su and coworkers46 proposed the localized dielectric breakdown model. They pointed out that if increasing amounts of water were added to the non-aqueous glycerol solution, enhancing the localized dielectric breakdown effect should lead to roughening of the nanotube walls with ridge formation, more significant electric current generation, more oxygen gas evolution, and lower formation efficiency of the anodic oxides.46 Vrublevsky and coworkers47 indicated that barrier anodic alumina is a good dielectric material, however, electronic current can flow across the anodic alumina during anodizing under the high electric field.47 Albella and coworkers48 have proposed that the anodizing current within the barrier oxide includes iion and ie during the anodizing process. The electronic current ie will grow exponentially and obey the eqn (2):48| ie = ie0eθd | (2) |
Where θ is the impact ionization coefficient, d is the oxide thickness, and ie0 is the primary electronic current which is involved with the anion incorporation and the anion contaminated layer, for example, the anion contaminated alumina called the ACA layer in PAA.8,11,32–34 The generation of electronic current was due to the impurity centers near the ACA interface.
Based on the ie within the barrier oxide and the viscous flow model, we have put forward the OBME model of PAA.33,34 Schematic diagrams of classical FAD model and OBME model are shown in Fig. 2a and Fig. 2b. The foremost distinguish between two models is the growing manner of the new barrier oxide. The OBME model claimed that new barrier oxide was formed both at E/O and O/M interfaces as shown in Fig. 1b. But the FAD model claimed that new barrier oxide was formed only at O/M interface during the pore deepening period as shown in Fig. 1c. In order to found the physical model of theoretical derivation, here we mainly compare their behaviors in pores forming and analyze their localization and rationality.
Fig. 2a shows three development stages (I, II and III) of the pore formation for FAD model.9–11 The barrier oxide grows both at E/O and O/M interfaces, an entire barrier layer is formed quickly at stage I. At stage II, when the embryo pores are formed from the surface to the inside, the barrier oxide changes to form only at O/M interface. It is difficult to explain the great change of the oxide growing manner from stage I to stage II. There are no strict differences between stage II and stage I as shown in Fig. 2a. It is difficult to account for the fall or rise of current at point c and point p of the current–time curve as shown in Fig. 1a. Namely, in FAD model, the columnar pores result from the digging behavior which does not need electronic current. It is just via the chemical corrosion or dissolution aided by the electric field.
 | ||
| Fig. 2 Schematic diagrams of the pore development of the classical FAD model (a)9–11 and oxygen bubbles mould model (b).33,34 | ||
According to the digging manner of the FAD model, it is also concluded easily that only a monolithic porous layer (Fig. 2a) should be obtained and the hexagonal cells (Fig. 2b) are impossible to form, because of the entire barrier layer at stage I. Therefore, many researchers have concluded that the gaps between the neighboring cells or nanotubes cannot be exactly explained.10,18–20,35–37
Fig. 2b also shows three development stages (I, II and III) of the pore formation for OBME model. The pore forming manner of OBME model is contrary to that of FAD model. In stage I, an entire barrier oxide layer is formed quickly at both E/O and O/M interfaces. At the same time, as barrier oxide (BO) film thickens, the outermost layer near the electrolyte will be contaminated by the electrolyte species or anions (F− or C2O42−).8,11,32–34 Three interfaces would appear in the film (Fig. 2b), i.e., electrolyte/ACA interface, ACA/BO interface, BO/M interface. When the barrier oxide grows to the critical thickness dc, the electronic current ie begins to rise and gives rise to evolution of oxygen gas from point c (Fig. 1a). In stage I, the oxygen bubbles are formed under the entire ACA layer. The growth manner of the new barrier oxide does not change and is the same as the initial oxide film. The iion forms barrier oxide and the ie enlarges the oxygen bubbles.34 Garcia-Vergara and coworkers49 in the Manchester group reported oxygen gas formed bubbles within the alumina, with pressures of several hundred MPa, which, in the case of barrier films, grow in size, coalesce and eventually burst.49 In 2012, they found the growth of titanium oxide as well as oxygen-filled cavities.50 It was found that most of the charge passed during growth was consumed in oxygen evolution and the measured current relates to the electronic conduction (ie) properties of the oxide.50 Following the nucleation of crystals, oxygen bubbles were developed within the oxide, the oxygen-filled bubbles within the oxide may rupture, allowing ingress of the electrolyte in proximity to the nanopores.50 Mazzarolo and coworkers50 also concluded ionic conduction leading to oxide growth and electronic conduction leading to oxygen evolution. Generation of oxygen-filled cavities within the film is possible when inward-migrating oxygen ions lose their electrons during migration.50
Before the oxygen bubbles burst, the barrier oxide grows up to the thickest thickness dp (corresponding to the point p in Fig. 1a). Because, the iion = Aexp(BE) = Aexp(BU0/d), where A and B are temperature dependent constants, E is the electric field strength, U0 is the anodizing voltage and d is the thickness of barrier oxide.6,11,35,51 Obviously, the ionic current is inversely proportional to the thickness of barrier oxide. Here, we use the OBME model to analyze the three development stages in Fig. 2b.
When the ACA ruptures and some of the oxygen bubbles burst, the real pores (No.1 in stage II of Fig. 2b) which result from the oxygen bubble mould will be filled by the electrolyte from the point p in Fig. 1a. And then, the barrier oxides decrease to the pore bases for some of the real pores. Therefore, the current begins to rise from point p in Fig. 1a because of the decrease of d. The anodizing process enters into stage II.
In stage II of Fig. 2b, other real pores (No.2) continue to be filled by the electrolyte, the current continue to rise as shown in Fig. 1a. When all the real pores are filled by the electrolyte, the barrier oxides decrease to the pore bases in all of the real pores. The thickness (d) of the barrier oxides decrease to the thinnest and the current increases to the highest corresponding to the point s in Fig. 1a. The anodizing process enters into the stage III.
In order to compare and differentiate the real pores, some FAD holes are shown in Fig. 2b. In fact, two oxygen bubble mould effects are presented.33 One is to exert a high pressure on the barrier oxide, causing a hemispherical indentation at the BO/M interface because of the plasticity of the anodic oxide,49 which is the embryo of the columnar and real pore in PAO as shown in Fig. 2b.33 The other is to change the migration path of O2− and Mn+ (n = 3 or 4) and induce the oxide flow around the bubbles as shown in Fig. 2b.33 The oxide flow manner from pore base to the pore wall accords with the viscous flow model of PAA.27,30–32
In stage III, all the real pores are filled with electrolyte. The bowed barrier oxide layer (BOL) at the bottom may be regarded as a micro-BOL. The growth manner of the bowed micro-BOL is in agreement with that of unbowed barrier anodic oxide (Fig. 1b). Because the electric field distribution across the pore base is illustrated in Fig. 2b (No.2 pore), freshly formed micro-BOL must embrace its own pore. Due to the high pressure of the oxygen bubble at the pore bottom, the freshly formed oxide must migrate from the base to the pore wall as shown in Fig. 2b (No.1 pore). The oxide expansion would induce repulsive forces between neighboring cells. Because the Mn+ at the midpoint Q in Fig. 2b is pulled by two inverse directions electric field (E1 and E2), the migrating direction of Mn+ is determined by the magnitude of the electric field (E1 and E2). For example, the Mn+ ions at the midpoint Q between the pores No.1 and No.2, must migrate to the bottom of pore No.1 or pore No.2, and hardly migrates along the direction of E3 (Fig. 2b). That is, no newly formed oxide will exist along the midpoint line between the pores No.1 and No.2. Consequentially, the gap or boundary is formed between two neighboring cells as shown Fig. 2b. This viewpoint benefits from the equifield strength model.17,18
In summary, based on the OBME model of PAO, a satisfactory explanation for the growth process of columnar pores and the gaps between hexagonal cells is proposed. The bottom thickness of the barrier oxide layer remains constant due to continuous releasing of the oxygen bubbles at the critical thickness dc. The viscous flow of barrier oxide and the oxygen bubbles mould determine the growth of the regular pores in PAO. The gaps between the neighboring cells result from the repulsive forces and the distribution of the electric field at the pore bases. There was no essential difference between PAO and BAO films.6,34 Anodizing current (i) mainly includes iion and ie within the barrier oxide. The iion is used to form oxide and the ie is used to give rise to oxygen gas.
Here, the authors proposed the assumption of electronic current is demonstrated below by the theoretical derivation and the fitting curve.
3.2 Theoretical derivation of ionic current in the anodizing process
As discussed above, in the classical model of PAO, the anodizing process is divided artificially into two steps: the growth of entire barrier layer and the pore formation.9–11 In fact, there is no essential difference between above two steps.6,34 The whole anodizing process can be regarded as a growing process of the barrier oxide throughout.34 Now we give the theoretical derivation in the anodizing process. We will get functional expression of the ionic current and membrane thickness with anodizing time (t). In this process, only ionic current is taken into consideration and the electronic current is ignored temporarily.Make the assumption reaction conditions to be: constant voltage U0 anodization (U0 is less than the sparking voltage or breakdown voltage UB,11,34,51i.e., U0 < UB), constant temperature T0, electrolyte whose concentration keeps c0 is uniform with a vigorous stir.
The following equation should set up throughout the anodizing process:
| U0 = Uox + Uel + UH | (3) |
In eqn (3), Uox is the potential drop between two sides of the membrane, Uel is the potential drop in electrolyte whose resistance can be treated as a constant under vigorous stirring, UH is the overpotential for hydrogen evolution which can be regarded as a constant as this value is small.
And then, the voltage drop across the oxide and electrolyte (U1) can be expressed as:
| U1 = U0 − UH = Uox + Uel = i(RAl + Rel + Rox) ≈ i(Rel + Rox) | (4) |
t = 0, Rox = 0, U1 = i(0)Rel, therefore  .
.
At the very beginning of anodization, only ionic current works while electronic current is a constant small value. This is because oxide membrane is still too thin to provide the condition for initial electrons to be accelerated to high-energy enough as avalanche electrons' appearance needs.48
Electric field strength is a vector E(t). Its modulus |E(t)| = E(t), where E(t) is the electric field in barrier anodic oxide. It is roughly thought to point vertically from metal substrate to electrolyte as Fig. 1b shows. Membrane thickness d(t) is also a function of time.
| U1 = iion(t)Rel + E(t)d(t) | (5) |
 | (6) |
Based on definition of electric current in classical physics, in the membrane, ionic current can be expressed like this:
| iion(t) = qNvS | (7) |
In eqn (7), q (C) refers to electric quantity of Mn+, N (m−3) refers to the number of Mn+ in each unit volume of the membrane, v (m s−1) refers to migration rate of Mn+ in the membrane, S (m2) is the active area. It is well known that the anion O2− also contributes to the ionic current iion. In order to simplify the derivative process, only cationic contribution is considered because there is no influence on the final results. Indeed, the cationic and anionic charges all contribute to the ionic current, e.g., Ti4+ moves in the same direction of electric field, and O2− moves in the opposite direction to the electric field. Two directions movement of Ti4+ and O2− ions can be regarded as an equivalent movement of Mm+ (m > 4). Accordingly, only cationic contribution is considered.
As we all know, in classic physics: v = μE. Here, μ is the charge carrier mobility, E is the electric field strength.
After constant folding, eqn (7) turns into eqn (8):
| iion(t) = αN(t)E(t) | (8) |
 | (9) |
From eqn (8), (6) and (9), we can get:
| d(t) = αβk[U1 − Reliion(t)] | (10) |
Derived from eqn (10) and comparing with eqn (9), we can get eqn (11):
| d′(t) = −αβkReliion′(t) = kiion(t) | (11) |
Where, iion′(t) is the derivative of the ionic current iion(t). Using 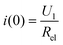 to do a simple integral computation on both sides of eqn (11), we will get eqn (12) and (13):
to do a simple integral computation on both sides of eqn (11), we will get eqn (12) and (13):
 | (12) |
 | (13) |
The physical meaning of eqn (12) and (13): in a constant voltage anodizing process, if only barrier oxide membrane growth (i.e., ionic current) was taken into consideration, then the ionic current attenuates exponentially with a high initial value. This process is short. The membrane thickness has a corresponding limit value, the limit thickness of the barrier oxide membrane. This limit thickness is approximately the breakdown thickness of a barrier oxide membrane.6,11,34,46,51 This shows a considerable accordance with the real situation. Ionic current–time and oxide thickness–time curves can be consequently obtained according to eqn (12) and (13) as shown in Fig. 3. Fig. 3 shows schematic graphs of the theoretical derivation results.
 | ||
| Fig. 3 Schematic graphs of theoretical derivation results (a) ionic current iion–time curve, (b) electronic current ie–time curve, (c) barrier oxide thickness-time curve. | ||
Fig. 3a is a schematic graph of ionic current–time. Curve I (the black one) is the theoretical curve from eqn (12). It can be seen that Fig. 3a is similar to the real BAO curve in Fig. 1a. The real PAO film, curve II (the purple one) represents the real ionic current curve, because the barrier layer of the pore bottom maintains a constant critical thickness and the ionic current cannot depress to zero as curve I. Fig. 3b is the schematic graph of electronic current–time (the derivation processes see below in section 3.3). Fig. 3c is the schematic graph of barrier oxide thickness with time from the theoretical eqn (13).
The above derivative expressions are based on only ionic current which plays an important role in the anodizing process. However, in fact, when the barrier oxide grows to breakdown thickness, the electronic current appears obviously and even sparking phenomenon (galvanoluminescence) can be observed.6,11,34,51 Therefore, in the growth process of barrier oxide, ie must be taken into account just as in our OBME model.
3.3 Theoretical derivation of electronic current in the anodizing process
Here we will present the derivation process of electronic current with oxide thickness or time. Electrolyte anions migrate into membrane under electric field. These anions then play the role of impurity center giving initial electronic current ie0.48 Then, the initial electrons are accelerated with the help of electric field. When high-energy electrons collide with O2−/OH−they give out electrons and O2. The ie0 later changes into avalanche electronic current ie with the oxide thickness increases to a critical value. This critical thickness of barrier oxide corresponds to the point c in Fig. 1a. From the eqn (2) and (13), we can obtain the theoretical expression of electronic current ie with the anodizing time (t): | (14) |
For a stable anodizing process, electronic current cannot rise infinitely, because the anodizing voltage U0 is less than the breakdown voltage UB. We think that appropriate electronic current and oxygen evolution are essential to pore formation. More recently, Patermarakis and other researchers also put forward similar opinions.39,50 So the changes in electronic current with the oxide thickness determine the rate of oxygen evolution. If the reaction has a balanced amount of electronic current, porous membrane is created; if the amount is too small, compact membrane is formed instead. If the magnitude of ie is too high, intense gas evolution and sparking are observed.6,11,34,51 This is the dielectric breakdown of the oxide films. Actually, this prediction is in accordance with the experimental facts.
3.4 Anodizing total current expression as a function of time
According to the theoretical eqn (12) and (14), the anodizing total current-time functional relation can be obtained: | (15) |
We know that ionic current affects membrane growth while electronic current affects oxygen evolution so that pores are formed. As we regard the theoretical eqn (15) as the actual functional relation of total current–time under constant voltage, some revisions are necessary and reasonable, because the above derivative processes are based on the oxide films growth as a compact or entire barrier film. At the beginning, the oxygen bubble stays in the membrane due to high external pressure. As reaction goes on, the oxygen pressure becomes high enough to burst out. Before this, eqn (12)–(14) are acceptable and reasonable. After this, electrolyte enters into the real pores and electric field mainly gathers and redistributes at the pore bottom as shown in Fig. 2b. Reaction enters into the stable period: ionic current and electronic current are both at appropriate values (asymptote) as curve II shows in Fig. 3a and b. The ionic current and electronic current both remain constant due to the barrier layer at the pore bottoms remaining constant, because the two kinds of current are both a function of oxide thickness.34,48 All these make the oxide film growth becomes nearly stable and no longer according to the original growing manner (the barrier or compact oxide growing manner as stage I shown in Fig. 2). All these stabilities come from the oxygen evolution from the critical thickness and the bubbles burst. Therefore, in this stable state, the ionic current no longer decreases according to theoretical eqn (12) and electronic current no longer increases according to theoretical eqn (14). Accordingly, when actual reaction factors are taken into consideration, some constants (Cion and η) should be appended to theoretical eqn (15) and a new eqn (16) can be obtained:
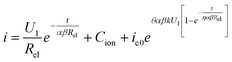 | (16) |
Where, Cion is the correctional parameter of the ionic current to fit the constant ionic current in the oxide film during stable growth stage (corresponding to the critical thickness). The Cion will not make a big difference to the curve shape. We deal with it in this way in order to get a concise and complete conclusion. In theoretical eqn (14), electronic current begins to generate once upon the reaction begins (t = 0 s). But the actual situation is that the electronic current emerges after a certain time lag so that ACA layer formed. So the correctional parameter (η) of time delay is appended to fix this difference. Moreover, from Fig. 3b we can say that η is smaller than 1. In fact, after above correctional process, eqn (16) is in the accordance to the fitting result. If electronic current in eqn (16) is small enough, eqn (16) will give a curve just like BAO curve in Fig. 1a. If electronic current is not so small, eqn (16) will give a curve just like the PAO curve in Fig. 1a.
3.5 Curve fitting according to derivation results and comparison with measured curves
Two measured curves and fitting curves according to eqn (16) as well as their comparison are given below. Fig. 4 shows the comparison between measured curve and fitting curve of current–time. Fig. 4a is measured current–time curve of Ti anodized in 0.5 wt% NH4F-EG solution under constant voltage 60 V. The corresponding SEM image of the PATNT is shown in Fig. 5a. Fig. 4b is fitting current–time curve according to eqn (16) for this anodization. The fitting functional expression is| i = 232e−0.95t + 35.5 + 2.33e2.35(1−e−0.2t) |
 | ||
| Fig. 4 The current–time measured curve (a) for Ti anodized in 0.5 wt% NH4F ethylene glycol solution, the fitted curve (b), and comparison between measured and fitted curve (c). | ||
 | ||
| Fig. 5 SEM images of the PATNT (a), the PAA (b), and the barrier anodic alumina (c). | ||
Fig. 6 shows the comparison of current–time between the fitting curve and the measured curve. The measured current–time curve is obtained for Al anodized in 0.3 M H2C2O4 aqueous solution under a constant voltage of 45 V. The corresponding SEM image of the PAA is shown in Fig. 5b. The fitting current–time curve is obtained according to eqn (16) for this anodization. The fitted functional expression is
| i = 100e−0.3t + 7.41 + 2.11e2.01(1−e−0.02t) |
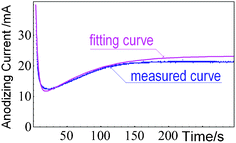 | ||
| Fig. 6 The comparison of current–time between the fitted curve and the measured curve for Al anodized in 0.3 M H2C2O4 aqueous solution. | ||
Fig. 7 shows the comparison of current–time between the fitting curve and the measured curve which is obtained for Al anodized in 4 wt% (NH4)2C6H8O4 aqueous solution under a constant voltage of 160 V. The corresponding SEM image of the barrier anodic alumina is shown in Fig. 5c. This is a classical barrier anodic oxide. The fitting current–time curve is obtained according to eqn (16) for this anodization. The fitted functional expression is
| i = 323e−1.209t + 0.273e1.58(1−e−0.71t) |
 | ||
| Fig. 7 The comparison of current–time between the fitting curve and the measured curve for Al anodized in 4 wt% (NH4)2C6H8O4 aqueous solution. | ||
The above results show that if there is no electronic current, there will not be curves like the measured PAA and PATNT curves. This work is not a pure mathematical derivation. The expression, eqn (16) is obtained by a series of derivations based on specific theoretical models of OBME and oxide viscous flow. In these conditions, the considerable coincidence the fitting curve and measured curve have gives us enough confidence to say that the functional expression is reasonable. Furthermore, the ionic current as well as the electronic current play a significant role in the anodizing process, the OBME proposed and the oxide viscous flow models are correct to a certain degree.
4. Conclusions
In summary, we did some derivations on ionic current and electronic current with time, mainly based on the OBME model. In this process, we used a few approximations and assumptions, but none of them will change the curve trend. Then, we got a proximate function expression for the anodizing total current with time in theory. After that we applied the derivative results to compare to the experimental data. We fit the measured data according to the derivative result (eqn (16)) and found the fitting curve shows an excellent accordance with measured curve. Therefore, we think the opinion that ionic current and electronic current both exist in the anodic oxide is correct and believable. Here, a proximate description is presented in this paper for the first time by the theoretical derivation of ionic current and electronic current. The exact description of the interactions between the current change and porous structural features may be explained in the future. Enough importance should be attached to the present functional expression of two kinds of currents. The present results may open new possibilities for understanding the kinetics of PAO and facilitate to the assembly of PATNT.Acknowledgements
This work was supported financially by the National Natural Science Foundation of China (Grant Nos. 61171043, 51077072).References
- K. S. Napolskii, I. V. Roslyakov, A. Y. Romanchuk, O. O. Kapitanova, A. S. Mankevich, V. A. Lebedev and A. A. Eliseev, J. Mater. Chem., 2012, 22, 11922 RSC.
- F. X. Xiao, J. Mater. Chem., 2012, 22, 7819 RSC.
- B. Platschek, A. Keilbach and T. Bein, Adv. Mater., 2011, 23, 2395 CrossRef CAS.
- S. So, K. Lee and P. Schmuki, J. Am. Chem. Soc., 2012, 134, 11316 CrossRef CAS.
- F. Keller, M. S. Hunter and D. L. Robinson, J. Electrochem. Soc., 1953, 100, 411 CrossRef CAS.
- J. W. Diggle, T. C. Downie and C. W. Goulding, Chem. Rev., 1969, 69, 365 CrossRef CAS.
- J. P. O'Sullivan and G. C. Wood, Proc. R. Soc. London, Ser. A, 1970, 317, 511 CrossRef CAS.
- G. E. Thompson and G. C. Wood, Nature, 1981, 290, 230 CrossRef CAS.
- V. P. Parkhutik and V. I. Shershulsky, J. Phys. D: Appl. Phys., 1992, 25, 1258 CrossRef CAS.
- F. Y. Li, L. Zhang and R. M. Metzger, Chem. Mater., 1998, 10, 2470 CrossRef CAS.
- G. E. Thompson, Thin Solid Films, 1997, 297, 192 CrossRef CAS.
- J. Siejka, C. Ortega and O. An, J. Electrochem. Soc., 1977, 124, 883 CrossRef CAS.
- H. Masuda, F. Hasegwa and S. Ono, J. Electrochem. Soc., 1997, 144, L127 CrossRef CAS.
- O. Iessensky, F. Müller and U. Gösele, Appl. Phys. Lett., 1998, 72, 1173 CrossRef.
- K. Nielsch, J. Choi, K. Schwirn, R. B. Wehrspohn and U. Gösele, Nano Lett., 2002, 2, 677 CrossRef CAS.
- Z. X. Su, M. Bühl and W. Z. Zhou, J. Am. Chem. Soc., 2009, 131, 8697 CrossRef CAS.
- Z. X. Su and W. Z. Zhou, J. Mater. Chem., 2009, 19, 2301 RSC.
- Z. X. Su and W. Z. Zhou, J. Mater. Chem., 2011, 21, 8955 RSC.
- J. M. Macak, H. Tsuchiya, A. Ghicov, K. Yasuda, R. Hahn, S. Bauer and P. Schmuki, Curr. Opin. Solid State Mater. Sci., 2007, 11, 3 CrossRef CAS.
- A. Ghicov and P. Schmuki, Chem. Commun., 2009, 2791 RSC.
- P. Roy, S. Berger and P. Schmuki, Angew. Chem., Int. Ed., 2011, 50, 2904 CrossRef CAS.
- W. Chen, B. Jin, Y. L. Hu, Y. Lu and X. H. Xia, Small, 2012, 7, 1001 CrossRef.
- C. B. Cao, J. L. Li, X. Wang, X. P. Song and Z. Q. Sun, J. Mater. Res., 2011, 26, 437 CrossRef CAS.
- D. Regonini, A. Satka, A. Jaroenworaluck, D. W. E. Allsopp, C. R. Bowen and R. Stevens, Electrochim. Acta, 2012, 74, 244 CrossRef CAS.
- N. F. Fahim and T. Sekino, Chem. Mater., 2009, 21, 1967 CrossRef CAS.
- E. Panaitescu, C. Richter and L. Menon, J. Electrochem. Soc., 2008, 155, E7 CrossRef CAS.
- J. E. Houser and K. R. Hebert, Nat. Mater., 2009, 8, 415 CrossRef CAS.
- G. Patermarakis, J. Electroanal. Chem., 2009, 635, 39 CrossRef CAS.
- G. Patermarakis and K. Moussoutzanis, Electrochim. Acta, 2009, 54, 2434 CrossRef CAS.
- P. Skeldon, G. E. Thompson, S. J. Garcia-Vergara, L. Iglesias-Rubianes and C. E. Blanco-Pinzon, Electrochem. Solid-State Lett., 2006, 9, B47 CrossRef CAS.
- S. J. Garcia-Vergara, P. Skeldon, G. E. Thompson and H. Habazaki, Electrochim. Acta, 2006, 52, 681 CrossRef CAS.
- S. J. Garcia-Vergara, H. Habazaki, P. Skeldon and G. E. Thompson, Electrochim. Acta, 2010, 55, 3175 CrossRef CAS.
- X. F. Zhu, L. Liu, Y. Song, H. B. Jia, H. Yu, X. Xiao and X. L. Yang, Monatsh. Chem., 2008, 139, 999 CrossRef CAS.
- X. F. Zhu, Y. Song, L. Liu, C. Y. Wang, J. Zheng, H. B. Jia and X. Wang, Nanotechnology, 2009, 20, 475303 CrossRef.
- W. Lee, K. Schwirn, M. Steinhart, E. Pippel, R. Scholz and U. Gösele, Nat. Nanotechnol., 2008, 3, 234 CrossRef CAS.
- W. Lee, R. Scholz and U. Gösele, Nano Lett., 2008, 8, 2155 CrossRef CAS.
- D. D. Li, C. H. Jiang, J. H. Jiang and J. G. Lu, Chem. Mater., 2009, 21, 253 CrossRef CAS.
- D. D. Li, L. Zhao, C. H. Jiang and J. G. Lu, Nano Lett., 2010, 10, 2766 CrossRef CAS.
- G. Patermarakis and J. Diakonikolaou, J. Solid State Electrochem., 2012, 16, 2921 CrossRef CAS.
- G. Patermarakis and K. Moussoutzanis, J. Electroanal. Chem., 2011, 659, 176 CrossRef CAS.
- A. Ispas, A. Bund and I. Vrublevsky, J. Solid State Electrochem., 2010, 14, 2121 CrossRef CAS.
- C. K. Chung, R. X. Zhou, T. Y. Liu and W. T. Chang, Nanotechnology, 2009, 20, 055301 CrossRef CAS.
- R. Zhang, K. M. Jiang, Y. Zhu, H. Y. Qi and G.Q. Ding, Appl. Surf. Sci., 2011, 258, 586 CrossRef CAS.
- C. J. Ingham, J. T. Maat and W. M. De. Vos, Biotechnol. Adv., 2012, 30, 1089 CrossRef CAS.
- Y. Li, Z. Y. Ling, X. Hu, Y. S. Liu and Y. Chang, RSC Adv., 2012, 2, 5164 RSC.
- Z. X. Su, W. Z. Zhou, F. L. Jiang and M. C. Hong, J. Mater. Chem., 2012, 22, 535 RSC.
- I. Vrublevsky, A. Jagminas, J. Schreckenbach and W. Goedel, Appl. Surf. Sci., 2007, 253, 4680 CrossRef CAS.
- J. M. Albella, I. Montero and J. M. Martinez-Duart, Electrochim. Acta, 1987, 32, 255 CrossRef CAS.
- S. J. Garcia-Vergara, K. E. Khazmi, P. Skeldon and G. E. Thompson, Corros. Sci., 2006, 48, 2937 CrossRef CAS.
- A. Mazzarolo, M. Curioni, A. Vicenzo, P. Skeldon and G. E. Thompson, Electrochim. Acta, 2012, 75, 288 CrossRef CAS.
- A. Despic and V. P. Parkhutik, Mod. Asp. Electrochem., 1989, 23, 401 Search PubMed.
- Z. T. Y. Al-Abdullah, Y. Y. Shin, R. Kler, C. C. Perry, W. Z. Zhou and Q. Chen, Nanotechnology, 2010, 21, 505601 CrossRef.
| This journal is © The Royal Society of Chemistry 2012 |

