View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C2RA21720A (Paper) RSC Adv., 2012, 2, 12466-12473

The structures and stability of BnNn clusters with octagon(s)†

Li-Hua Gan *, Rui Li and Jie An
School of Chemistry and Chemical Engineering, Southwest University, 400715, China. E-mail: ganlh@swu.edu.cn

Received 7th August 2012 , Accepted 11th October 2012

First published on 12th October 2012

Abstract

The structures and stability of (BN)n clusters with alternate B and N atoms containing squares, hexagons and octagons ((BN)n-F4F6F8) are investigated by using density functional theory. The results demonstrate that the isomers of (BN)n-F4F6F8 clusters generally satisfy the isolated-square rule (ISR) and the square adjacency penalty rule (SAPR). The energetically favorable isomers generally have fewer square–square bonds, larger HOMO–LUMO gaps, lower sphericity and asphericity, as well as lower pyramidalization of B and N atoms than other structures. As a whole, the stability of (BN)n-F4F6F8 clusters decreases with the number of octagons. However, four isomers containing one or two octagons in four isomeric clusters (i.e. (BN)n-F4F6F8 (n = 19, 20, 23, and 24) are more thermodynamically stable than their (BN)n-F4F6 counterparts. Further structural analysis demonstrates that octagon(s) of (BN)n-F4F6F8 clusters can release the strain energy by decreasing the pyramidalization angles of the corresponding vertex. Finally, the entropy effect is examined to evaluate the relative stability of (BN)n-F4F6F8 (n = 19, 20, 23, and 24) clusters at high temperatures.

Introduction

Boron-nitrogen fullerene-like clusters (BN)n have been extensively investigated experimentally1–5 and theoretically6–12 after the discovery of C60 in 1985. As iso-electronic analogues to carbon fullerenes, (BN)n clusters with special properties, such as high-temperature stability, low-dielectric constant, large thermal conductivity and good oxidation resistance are intriguing for both scientific research and device applications. It has been reported that in (BN)n clusters the alternate structures constructed by squares and hexagons (for simplification, hereafter named (BN)n-F4F6) are more stable than the structures constructed by pentagons and hexagons.7–9 Moreover, (BN)n-F4F6 clusters satisfy the isolated-square rule (ISR).13 For ISR-violating isomers with square-square bonds (hereafter named B44 bonds), the isomers with fewer B44 bonds are usually more energetically favorable than those with more B44 bonds, and they satisfy the square adjacency penalty rule (SAPR).12 This is similar to C2n-F5F6 fullerenes obeying the powerful isolated pentagon rule14 and the pentagon adjacency penalty rule.15 Furthermore, it is reported that the most favorable isomers of (BN)n-F4F6 clusters usually have large HOMO–LUMO gaps.12,16,17

However, recently researchers found that some (BN)n-F4F6 isomers with octagon(s) (hereafter named (BN)n-F4F6F8) are more favorable than the ones only constructed with squares and hexagons, such as (BN)13,12 (BN)20,10 and (BN)24.10,17,18 For (BN)13 clusters, it is reported that the isomer with one octagon in C1 symmetry is more thermodynamically stable than the (BN)13-F4F6 isomers. For (BN)20 clusters, the study shows that one isomer of (BN)20 with two octagons in C4h symmetry is more energetically stable than the (BN)20-F4F6 isomers. For (BN)24 clusters, many researchers found that the isomer with zero B44 bonds constructed by two octagons, eight squares and sixteen hexagons in S8 symmetry is more stable than the (BN)24-F4F6 isomers. Moreover, (BN)24 clusters have been synthesized and detected via laser desorption time-of-flight mass spectrometry.4

So far, systematic studies on (BN)n-F4F6F8 are lacking, and their structures and stabilization mechanism are not well understood. Are there more (BN)n-F4F6F8 structures which are more favorable than their (BN)n-F4F6 counterparts? Do (BN)n-F4F6F8 structures satisfy the ISR and SAPR? How does an octagon change the stability of the (BN)n clusters?

In this work, a systematic density functional theory (DFT) study is performed on all possible isomers of (BN)n-F4F6F8 (n = 15–24) clusters to gain insight into their structures and stability. The calculated results demonstrate that (BN)n-F4F6F8 clusters satisfy the ISR and the SAPR. It is found that four isomers with one or two octagons are more thermodynamically stable than their (BN)n-F4F6 counterparts. The influence of B44 bonds, sphericity (SP), asphericity (AS), pyramidalization of atoms (PA), HOMO–LUMO gaps and the enthalpy-entropy interplay on the stability of (BN)n-F4F6F8 clusters are investigated in detail.

Computational details

The coordinates of all considered (BN)n-F4F6F8 clusters are obtained by running the revised version of CaGe software.19 According to the Euler's theorem, (BN)n-F4F6F8 clusters satisfy the following equations:
 
n4 − n8 = 6(1)
 
n4 + n6 + n8 = n + 2(2)
where n, n4, n6 and n8 denote the number of BN, squares, hexagons and octagons. For all (BN)n-F4F6 clusters, n4 is six. The number of all considered isomers is presented in the ESI† (S1). As shown in S1†, the number of isomers with octagon(s) is much larger than that of (BN)n-F4F6. It is known that the stability of (BN)n-F4F6F8 clusters decreases with the number of octagons and it is impossible for those isomers with over two octagons to be energetically more favorable.12,20 Hence, considering the high cost of these calculations, we only investigate the isomers with 0 to 2 octagons. According to the number of octagons, all the considered isomers are classified into three kinds, i.e. non-octagon (hereafter named (BN)n-0F8-i, i refers to the sequence of the isomer), one octagon (BN)n-1F8-i), two octagons (BN)n-2F8-i).

These isomers are first optimized using the PM3 method to produce the primary classifications of energetic and stability. Then the isomers selected from the PM3 optimization with relative energy (RE) within about 150 kcal mol−1 are refined at the HF/3-21G level, and then the B3LYP/6-31G* method is used to determine the lowest energy isomer. In order to test the reliability of B3LYP/6-31G* method, the calculations with BH and HLYP/6-31G*, B3LYP/6-311+G* and MP2/6-31G* methods are also carried out for the three most stable isomers of (BN)15-F4F6F8 clusters, and the results are listed in the ESI† (S2). It shows that the relative energies with different methods are nearly same. Harmonic vibration frequencies are also calculated to confirm that the optimized structures of the lowest energy isomers are minima on the potential energy surface. All the calculations are carried out with GAUSSIAN 03 software package.21

Results and discussion

A. Results

The complete results of all considered isomers calculated at the B3LYP/6-31G* level are given in the ESI† (S3). Frequency calculations at the same level demonstrate that the most stable isomers of (BN)n-F4F6F8 clusters are the minima on the potential energy surface. The optimized structures of the lowest energy isomers of considered clusters are presented in Fig. 1.
The B3LYP/6-31G* optimized structures of the lowest energy isomers of (BN)n-F4F6F8 (n = 15–24) clusters
Fig. 1 The B3LYP/6-31G* optimized structures of the lowest energy isomers of (BN)n-F4F6F8 (n = 15–24) clusters

As shown in S3†, for (BN)15-F4F6F8 clusters, the most stable isomer is (BN)15-0F8-01 with C3h symmetry which has been reported in our previous work,11 followed by (BN)15-1F8-13 in C1 symmetry, which is 55.46 kcal mol−1 higher in energy than the former. For (BN)16 clusters, the most stable isomer is (BN)16-0F8-02 in Td symmetry. The second one is (BN)16-0F8-01 in C1 symmetry, which is 17.10 kcal mol−1 higher in energy than the former. For (BN)17-F4F6F8 clusters, the most stable isomer is (BN)17-0F8-01 in Cs symmetry and the second one is (BN)17-1F8-026 with C1 symmetry, which is 28.88 kcal mol−1 higher in energy than the former; for (BN)18 clusters, the most stable isomer is (BN)18-0F8-02 in S6 symmetry. The second one is (BN)18-1F8-022 in C2 symmetry, and is 9.01 kcal mol−1 higher in energy than the former. For (BN)21-F4F6F8 clusters, the most stable isomer is (BN)21-0F8-01 with C3h symmetry which has been reported,11 followed by (BN)21-1F8-046 in C1 symmetry, which is 7.26 kcal mol−1 higher in energy than the former.

For (BN)19, (BN)20, (BN)23 and (BN)24 clusters, all of their most stable isomers have octagon(s). For (BN)19 polyhedrons, the most stable isomer is (BN)19-1F8-049 with an octagon, which is 15.55 kcal mol−1 lower in energy than the second one (BN)19-0F8-06 without octagon. For (BN)20 polyhedrons, the most stable isomer is (BN)20-2F8-343 with two octagons. The second one is (BN)20-2F8-160, and is 16.14 kcal mol−1 higher in energy than the former. The third one is (BN)20-0F8-06, and its relative energy (RE) is 18.60 kcal mol−1. For (BN)23 clusters, the most stable isomer is (BN)23-1F8-126 with an octagon. The second stable isomer is (BN)23-0F8-03 without an octagon, and it is 11.43 kcal mol−1 higher in energy than the former. The third one is (BN)23-1F8-067 with an octagon, which is 21.78 kcal mol−1 higher in energy than the most stable one. For (BN)24 polyhedrons, the most stable isomer is (BN)24-2F8-1581 with two octagons. The second one is (BN)24-0F8-01, which is 2.08 kcal mol−1 higher in energy than the former. The third one is (BN)24-2F8-3789, and its RE is 18.69 kcal mol−1. Evidently, the isomers containing octagon(s) are energetically competitive with the (BN)n-F4F6 ones.

In order to further investigate the structure of (BN)n-F4F6F8 clusters, we examine the geometrical parameters (bond lengths) of the lowest energy isomers and list them in Table 1. As seen in Table 1, it is evident that the average bond lengths of the lowest energy isomers are all shorter than the B–N (single) bond in H3B–NH3 (1.667 Å), but longer than the B[double bond, length as m-dash]N (double) bond in H2B[double bond, length as m-dash]NH2 (1.391 Å) at the same level of theory. As a whole, the order of the average bond lengths for different kinds of bonds is B48 > B46 > B66 > B68.

Table 1 The B3LYP/6-31G* average bond lengths (Å) and the range of average bond lengths of the lowest energy isomers of (BN)n-F4F6F8 (n = 15–24) clusters
Molecule B46 B48 B66 B68
B15N15-0F8-01 1.478 — 1.456 —
1.469/1.4881 —/— 1.433/1.497 —/—
B16N16-0 F8-02 1.473 — 1.457 —
1.473/1.473 —/— 1.455/1.460 —/—
B17N17-0F8-01 1.473 — 1.462 —
1.457/1.486 —/— 1.396/1.510 —/—
B18N18-0F8-02 1.479 — 1.457 —
1.473/1.487 —/— 1.432/1.482 —/—
B19N19-1F8-049 1.476 1.482 1.458 1.424
1.457/1.499 1.481/1.485 1.417/1.495 1.420/1.434
B20N20-2F8-343 1.477 1.482 1.451 1.422
1.463/1.482 1.482/1.482 1.422/1.481 1.422/1.422
B21N21-0F8-01 1.478 — 1.458 —
1.474/1.487 —/— 1.433/1.476 —/—
B22N22-0F8-09 1.469 — 1.461 —
1.459/1.476 —/— 1.419/1.486 —/—
B23N23-1F8-126 1.473 1.48 1.459 1.42
1.452/1.490 1.477/1.484 1.418/1.490 1.419/1.421
B24N24-2F8-1581 1.474 1.479 1.458 1.419
1.457/1.483 1.479/1.479 1.438/1.480 1.419/1.419
Average 1.475 1.481 1.458 1.421

B. Discussion

1. Binding energies. For comparing the energies of (BN)n-F4F6F8 clusters with each other, the binding energy (BE) of BN unit for (BN)n-F4F6F8 clusters is defined in eqn (3):
 
ugraphic, filename = c2ra21720a-t1.gif(3)
where n is the number of BN, E(BN)n is the energy of an isomer of (BN)n-F4F6F8 clusters, E(B) and E(N) are the energy of an atom of B and N, respectively. According to S3†, the average BE of different (BN)n-F4F6F8 (n = 15–24) clusters are −339.60, −342.24, −343.95, −345.76, −346.84, −347.94, −348.65, −348.44, −351.11, and −351.81 kcal mol−1, respectively. It demonstrates that the stability of (BN)n-F4F6F8 clusters becomes slightly higher as n increases. Moreover, the average BE of all considered isomers with different number of octagons (zero, one and two) are −347.84, −346.90, −346.32 kcal mol−1, respectively. These data indicate that the isomers containing one and two octagons should be considered during searching the lowest energy isomer of (BN)n-F4F6 clusters.
2. B44 bonds. As shown in S3†, the stability of (BN)n-F4F6F8 clusters is influenced by the number of B44 bonds. The lowest energy isomers of (BN)n-F4F6F8 clusters are the structures with zero B44 bonds, in which all the squares are surrounded and separated by hexagons. Thus, the energetically favorable structures of (BN)n-F4F6F8 clusters satisfy the ISR. The isomers with one or more B44 bonds generally have higher energies than ISR-satisfying isomers, demonstrating that they obey the SAPR. To further explain the relation between the energies of (BN)n-F4F6F8 clusters and the number of B44 bonds, the REs and the numbers of B44 bonds are plotted in Fig. 2. Fig. 2 shows that the general trend that the more B44 bonds, the larger the REs. Moreover, the average energy penalty of one B44 bond for different (BN)n-F4F6F8 (n = 15–24) clusters are 44.72, 24.28, 35.75, 15.81, 11.75, 24.30, 17.33, 35.22, 23.72, and 9.44 kcal mol−1, respectively. These facts indicate that the effect of fused squares on the stability of (BN)n-F4F6F8 clusters roughly decreases as n increases. In summary, (BN)n-F4F6F8 clusters satisfy the ISR and the SAPR. This is similar to the case of fullerenes.22
The calculated relative energies (RE) and the numbers of B44 bonds of the considered isomers with different number of octagons at the B3LYP/6-31G* level (“■” “•” “▴” denote the isomers containing none, one and two octagons, respectively).
Fig. 2 The calculated relative energies (RE) and the numbers of B44 bonds of the considered isomers with different number of octagons at the B3LYP/6-31G* level (“■” “•” “▴” denote the isomers containing none, one and two octagons, respectively).
3. HOMO–LUMO gaps. It is known that a large HOMO–LUMO gap could be taken as an indicator of high kinetic stability for carbon fullerenes.23,24 Many researchers have also found that the high stability of the (BN)n-F4F6 clusters is correlated with large HOMO–LUMO gaps.17,25 In order to investigate the relationship between gap and stability of (BN)n-F4F6F8 clusters, the gaps of all considered isomers are calculated and the results are listed in S3†. As a whole, the lowest energy isomers have larger gaps than others. Take (BN)15-F4F6F8 as an example, the lowest energy isomer is (BN)15-0F8-01 with the largest gap of 6.58 eV, and the gaps of the following three isomers are 6.02, 6.14 and 6.08 eV, while the gaps of all the rest isomers are less than 6.00 eV. Moreover, the general trend is that the lower the BE, the larger gaps the isomers have. Furthermore, the orbital energy of the HOMO remains almost constant, while the orbital energy of the LUMO becomes higher as BE decreases, indicating that it is more difficult for the lowest energy isomers to obtain electrons than others.
4. Sphericity (SP) and asphericity (AS). It is reported that the stability of clusters is related to their geometrical shapes which are evaluated by the sphericity parameter (denoted as SP)26 and the asphericity parameter (AS).27 It is found that the carbon fullerenes with approximate sphericity are more stable than others,28 and also the lower the SP (or AS), the more perfect spherical (BN)n the clusters are. Accordingly, the values of SP and AS of all the optimized (BN)n-F4F6F8 isomers at the B3LYP/6-31G* level are obtained by the following eqn (4) and (5), respectively:
 
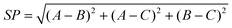ugraphic, filename = c2ra21720a-t2.gif(4)
 
ugraphic, filename = c2ra21720a-t3.gif(5)
where A, B and C are the rotational constants, ri and r0 are the radius distance of atom i from the cage center and the average radius, respectively.

As shown in S3†, for (BN)15-F4F6F8 clusters, the lowest energy isomer is (BN)15-0F8-01 with the lowest values of SP (0.11) and AS (0.30). This is also true for (BN)16-F4F6F8, (BN)20-F4F6F8, and (BN)22-F4F6F8, (BN)23-F4F6F8, and (BN)24-F4F6F8 clusters. For the other considered clusters, the values of SP and AS of the lowest energy isomers are among the lowest values. The general trend is that the lower the BE, the smaller values of SP and AS the isomers have. As a whole, the order of the values of SP and AS among clusters with different numbers of octagons is (BN)n-0F8 < (BN)n-1F8 < (BN)n-2F8. The introduction of one or two octagon(s) for the same-sized clusters will introduce tension squares, and may lead to more B44 bonds. Consequently, their energies increase. However, for (BN)19-F4F6F8 clusters, the lowest energy isomer is (BN)19-1F8-049 with the values of SP (0.07) and AS (0.39), followed by (BN)19-0F8-06 with the values of SP (0.08) and AS (0.65), but neither of them have a B44 bond. This phenomena also occurs in the three isomeric sets ((i.e. (BN)n-F4F6F8 (n = 20, 23, and 24)). In these cases, the number of B44 bonds for (BN)n-F4F6F8 isomers is not increased compared to the (BN)n-F4F6 isomers after the introduction of one or two octagon(s), and these octagon(s) reduce the local curvature of the cages. Therefore, they have lower values of SP and AS and are lower in energy than others. In summary, the shape of the (BN)n-F4F6F8 clusters plays an important role in determining the stability of (BN)n-F4F6F8 structures.

5. Spherical aromaticity. It is well known that spherical aromaticity is an important indicator of chemical stability for a polycyclic π-electron system and aromatic molecules are chemically more stable than those less aromatic or antiaromatic molecules. Maximum spherical aromaticity usually occurs in icosahedral carbon fullerenes when the valence p-shells are completely filled with 2(N + 1)2 electrons.29 Moreover, for carbon fullerenes, the nucleus-independent chemical shift (NICS) has been widely accepted as a reliable parameter of aromaticity.30,31 Accordingly, the NICS value at the cage center of each considered (BN)n-F4F6F8 isomer is calculated by the gauge-independent atomic orbital method to evaluate the chemical stability of the B3LYP/6-31G* optimized structures and the results are presented in S3†. As shown in S3†, the most stable isomers generally have lower SP and AS. Consequently, π orbitals of these isomers are reasonably described by spherical harmonics which should have maximum spherical aromaticity and lower values of NICS than others. However, the trend of NICS values is not in agreement with that of relative energies of different isomers. For example, the values of SP, AS and NICS of the two lowest energy isomers of (BN)15-F4F6F8 clusters are 0.11, 0.30, −3.36; 0.16, 0.50, −3.73, respectively, and the lowest one has lower SP and AS but lager NICS. It suggests that spherical aromaticity measured by the value of NICS may not be used to explain the chemical stability of (BN)n-F4F6F8 clusters.
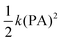6. Pyramidalization angle (PA). It is known that pyramidalization angle (PA) can be used to explain the stability of carbon fullerenes.32 The strain energy resulted from pyramidization can be represented asugraphic, filename = c2ra21720a-t4.gif, where k is the force constant. It is reported that for carbon fullerenes, pentagon-pentagon fusions lead to enhanced strain of a cage surface, hence there should be as little curvature as possible so that the σ-skeleton achieves nearly the ideal sp2 geometry and the adjacent p-like orbitals overlap to the utmost extent.33 The PA can be used to measure the deviation of a sp2-hybridized carbon atom from the plane of three adjacent carbon atoms. It is established that a greater PA leads to lower stability of the carbon in sp2 hybridization, and for those carbon fullerenes containing pentagon-pentagon fusions (B55 bonds), the PA of atoms at the B55 bonds are larger than those of others. As iso-electronic analogue to carbon fullerenes, for (BN)n-F4F6 clusters, B atoms prefer the planar geometry (sp2 hybridization) and N atoms prefer the pyramidalization to accommodate a lone pair of electrons.34 We calculate the PAs of all considered isomers and the PA of each atom of all the optimized (BN)n-F4F6F8 isomers at the B3LYP/6-31G* level are obtained by the following eqn (6):32
 
PA = θσπ − 90°(6)
where θσπ denotes the angle between the p-orbital and its three adjacent B–N bonds.

The average PA of B (denoted as PAB) and N (PAN) atom for each isomer are obtained and also listed in S3†. As shown in S3†, the PAB and PAN of the lowest energy isomer are the lowest of all isomers. For (BN)15-F4F6F8 clusters, the PAB and PAN of the lowest energy isomer (BN)15-0F8-01 are 10.28° and 24.76°, respectively; the values of them for the second isomer (BN)15-1F8-13 are 9.87° and 24.07°, respectively. Evidently, the PAB and PAN of the former are greater than that of the latter, but the former has a larger gap, fewer B44 bond as well as lower SP and AS. This situation also occurs in (BN)21-F4F6F8 clusters. For the other considered clusters, the PAB and PAN of the lowest energy isomer are generally relatively smaller than those of the following ones.

As shown in S3†, the PAB is obviously lower than the PAN for each considered isomer. It demonstrates that the surface of (BN)n-F4F6F8 clusters is crinkly, as also seen from Fig. 1. This is evidently different from the cases in carbon fullerenes, in which the carbon atoms tend to form spherical surfaces and the difference between the PA of adjacent atoms is generally slight. The average PAB and PAN of all considered (BN)n-F4F6F8 (n = 15–24) isomers are 10.45°, 24.69°; 9.98°, 23.65°; 9.62°, 23.00°; 9.30°, 22.27°; 9.01°, 21.80°; 8.73°, 21.21°; 8.53°, 20.73°; 8.70°, 20.78°; 8.16°, 19.81°; 8.04°, 19.54°, respectively, the corresponding differences between PAB and PAN are 14.24°, 13.67°, 13.38°, 12.97°, 12.80°, 12.48°, 12.19°, 12.08°, 11.65°, and 11.50°, respectively. It indicates that the local strain energy decreases as n increases. This is in agreement with the results that (BN)n-F4F6F8 clusters are becoming more favorable than other considered clusters as n increases.

All the PAB and PAN of considered isomers are plotted in the ESI† (S4). As shown in S4†, for each kind of isomer with different numbers of octagons, the lowest energy one has a smaller PAB and PAN than other isomers, and their REs generally increase as the values of PAB and PAN become greater.

7. The effects of octagon(s). To examine the effect of octagons on the structures and stability of (BN)n clusters, the PAs of different kinds of vertices (V446, V448, V466, V468, V666 and V668, the subscripts 4, 6 and 8 denote the square, hexagon and octagon, respectively) of the most stable isomers with different number of octagons are presented in Table 2. It can be seen that the average PAB and PAN satisfy the following order: V446 > V448 > V466 > V468 > V666 > V668. It indicates that a (BN)n-F4F6F8 isomer containing a V446 and V448 vertex is highly energetically unfavorable. Since V446 and V448 vertices certainly involve B44 bonds, it is energetically unfavorable to contain B44 bonds, which is in agreement with the ISR and SAPR. Furthermore, the orders of V466 > V468 and V666 > V668 indicate that the octagon can reduce the steric strain of the cage by decreasing the PA. For small clusters, although the introduction of octagon(s) can reduce the local curvature of the corresponding cages, yet may also increase the number of unfavorable B44 bonds. As the size of a cluster grows, the squares are gradually separated far apart and eventually the B44 subunits fade out from the framework of the cluster. In this case, the inclusion of one or two octagon(s) will not lead to B44 bonds, but can release the local steric strain to stabilize the corresponding cluster. Consequently, some octagon-containing isomers may be more energetically favorable than the (BN)n-F4F6 structures as the cluster size increases.
Table 2 The PA (°) of different kinds of vertices (V446, V448, V466, V468, V666 and V668, the subscripts denote the square, hexagon and octagon, respectively) of the most stable isomers with different octagon(s) and the range of PA of (BN)n-F4F6F8 (n = 15–24) fullerenes
Molecule V446 V448 V466 V468 V666 V668
  PAB PAN PAB PAN PAB PAN PAB PAN PAB PAN PAB PAN
(BN)15-0F8-1 — — — — 10.48 25.07 — — 9.46 23.52 — —
1F8-13 17.29 37.59 — — 10.59 26.64 7.99 20.32 7.01 14.57 — —
2F8-45 15.36 36.99 15.06 33.02 10.95 27.21 7.53 19.26 — — 6.04 12.77
(BN)16-0F8-02 — — — — 10.23 24.59 — — 7.70 16.50 — —
1F8-20 15.57 — — 33.73 10.49 26.27 8.08 — 7.36 12.61 — 11.65
2F8-59 — — — — 10.42 26.88 7.25 19.27 — — — —
(BN)17-0F8-1 — — — — 10.41 25.98 — — 6.95 13.88 — —
1F8-026 15.86 — — 34.09 10.33 26.00 8.05 19.82 7.16 13.56 — 9.04
2F8-050 13.46 32.93 10.59 26.64 9.87 25.76 7.87 19.72 7.44 14.97 4.79 10.06
(BN)18-0F8-02 — — — — 10.30 26.39 — — 6.63 14.03 — —
1F8-022 — — — — 10.07 25.71 7.52 19.76 6.79 13.65 — —
2F8-085 — — 12.74 32.31 9.82 25.48 7.48 18.78 7.89 15.83 5.55 8.82
(BN)19-0F8-06 — — — — 10.54 26.52 — — 6.45 12.88 — —
1F8-049 — — — — 9.96 25.53 7.44 19.58 6.58 13.78 — —
2F8-115 — — 11.28 28.94 9.78 24.66 7.38 19.16 6.93 15.13 5.86 12.06
(BN)20-0F8-06 — — — — 10.44 26.41 — — 6.38 12.83 — —
1F8-029 — — — — 10.17 25.71 7.10 17.66 6.73 14.21 5.16 9.47
2F8-343 — — — — 9.21 23.72 7.32 19.44 6.97 15.02 — —
(BN)21-0F8-1 — — — — 10.37 26.48 — — 6.14 14.06 — —
1F8-046 — — — — 10.33 25.87 7.45 17.87 6.85 13.85 4.45 10.27
2F8-1235 — — — — 9.75 24.49 7.60 17.78 6.82 16.93 5.26 10.22
(BN)22-0F8-09 — — — — 10.22 25.37 — — 6.17 13.46 — —
1F8-056 — — — — 9.80 25.30 7.52 20.09 6.26 12.60 — —
2F8-355 — — — — 9.72 25.60 7.47 19.66 6.16 12.77 3.58 6.93
(BN)23-0F8-03 — — — — 10.31 26.20 — — 5.93 12.70 — —
1F8-126 — — — — 9.69 25.21 7.44 19.88 6.03 12.65 — —
2F8-2469 — — — — 9.58 24.43 7.06 17.72 6.45 13.81 5.36 10.64
(BN)24-0F8-01 — — — — 10.19 25.92 — — 5.90 12.40 — —
1F8-096 — — — — 10.12 25.71 7.03 18.65 6.01 12.17 3.73 10.00
2F8-1581 — — — — 8.80 23.83 7.49 19.78 5.89 12.54 — —
Average 15.51 35.84 12.42 31.46 10.10 25.63 7.51 19.17 6.75 14.18 4.99 10.16

These findings suggest that the isomers with octagon(s) should be considered during the search for the lowest energy isomer of (BN)n clusters. For the (BN)n-F4F6F8 clusters with n larger than 24, it is highly possible for isomers with octagon(s) to be more energetically favorable than the most stable (BN)n-F4F6 clusters.

8. Thermodynamically stabilities. It is known that electronic energetics itself cannot predict relative stabilities in an isomeric system, especially at high temperatures, as stability interchange induced by the enthalpy-entropy interplay is possible. For the four isomeric sets (i.e. (BN)n-F4F6F8 (n = 19, 20, 23, and 24)) in which the most stable structure is found to be (BN)n-F4F6F8 species, we calculated the relative concentrations to clarify their thermodynamically stabilities and to provide hints helpful for experimental synthesis. Entropic effects are included to evaluate the relative concentrations through the Gibbs free energy at the B3LYP/6-31G* level of theory. Considering the high computational cost, only the three most stable isomers are performed equilibrium statistical thermodynamic analyses. Relative concentration (mole fractions) xi of the ith isomer among the m isomers can be expressed through the partition function qi and the ground-state energies ΔHO0,i by a compact formula eqn (7):35
 
ugraphic, filename = c2ra21720a-t5.gif(7)
where R is the gas constant, T is the absolute temperature and ΔHO0,i is the relative ground-state energy.

Fig. 3 shows the temperature evolution of the equilibrium concentrations of (BN)n-F4F6F8 (n = 19, 20, 23, and 24) clusters. Evidently, for three isomeric sets (i.e. (BN)n-F4F6F8 (n = 19, 23, and 24)), the lowest energy isomers are prevalent at certain temperatures while the other isomers have a very small proportion, indicating that the lowest energy isomers should be more thermodynamically stable than the other two isomers over a wide range of temperatures. However, in the case of (BN)20-F4F6F8, the second lowest energy isomer eventually surpasses the lowest energy one around 4600 K and becomes the most populated isomer. This situation also occurs in (BN)24-F4F6F8 clusters, in which the third lowest energy isomer exceeds the second lowest energy one at about 2700 K. These results demonstrate that the lowest energy structure is not necessarily the most abundant one at high temperatures.


B3LYP/6-31G* relative concentrations of the three lowest energy isomers of (BN)n-F4F6F8 clusters (n = 19, 20, 23, and 24, respectively).
Fig. 3 B3LYP/6-31G* relative concentrations of the three lowest energy isomers of (BN)n-F4F6F8 clusters (n = 19, 20, 23, and 24, respectively).

4. Conclusions

DFT calculations demonstrate that the isomers of (BN)n-F4F6F8 clusters (n = 15–24) generally satisfy the ISR and the SAPR. The stability of (BN)n-F4F6F8 clusters usually decreases with the number of octagons. The most energetically stable isomers generally have fewer B44 bonds, larger gaps; lower SP and AS, as well as lower PAB and PAN. Four isomers containing octagon(s) in four isomeric clusters (i.e. (BN)n-F4F6F8 (n = 19, 20, 23, and 24)) are predicted to be more thermodynamically stable than their (BN)n-F4F6 counterparts. Further structural analysis demonstrates that introducing an octagon can release strain energy of the cage. It is thought that many more isomers with octagon(s) may exist which are more energetically favorable for (BN)n-F4F6 clusters as n increases.

Acknowledgements

This work was supported by the Fundamental Research Funds for the Central Universities (XDJK2010C002), and the National Natural Science Foundation of China (51272216).

References

  1. N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966 CAS .
  2. T. Oku, T. Hirano, M. Kuno, T. Kusunose, K. Niihare and K. Suganuma, Mater. Sci. Eng., B, 2000, 74, 206 CrossRef .
  3. T. Oku, M. Kuno, H. Kitahara and I. Nartia, Int. J. Inorg. Mater., 2001, 3, 597 CrossRef CAS .
  4. T. Oku, A. Nishiwaki, I. Narita and M. Gonda, Chem. Phys. Lett., 2003, 380, 620 CrossRef CAS .
  5. R. T. Paine and C. K. Narula, Chem. Rev., 1990, 90, 73 CrossRef CAS .
  6. D. L. Strout, J. Phys. Chem. A, 2001, 105, 261 CrossRef CAS .
  7. H. S. Wu, X. H. Xu, F. Q. Zhang and H. J. Jiao, J. Phys. Chem. A, 2003, 107, 6609 CrossRef CAS .
  8. D. L. Strout, Chem. Phys. Lett., 2004, 383, 95 CrossRef CAS .
  9. H. S. Wu, X. H. Xu and D. L. Strout, J. Mol. Model., 2005, 2, 1 CrossRef .
  10. H. S. Wu and H. J. Jiao, J. Mol. Model., 2006, 12, 537 CrossRef CAS .
  11. R. Li, L. H. Gan, L. Lin, J. Q. Liu and J. Zhao, THEOCHEM, 2009, 911, 75 CrossRef CAS .
  12. R. Li, L. H. Gan, Q. Li and J. An, Chem. Phys. Lett., 2009, 482, 121 CrossRef CAS .
  13. P. W. Fowler, T. Heine, D. Mitchell, R. Schmidtb and G. J. Seifertb, J. Chem. Soc., Faraday Trans., 1996, 92, 2197 RSC .
  14. H. W. Kroto, Nature, 1987, 329, 529 CrossRef CAS .
  15. E. Albertazzi, C. Domene, P. W. Fowler, T. Heine, G. Seifert, C. V. Alsenoy and F. Zerbetto, Phys. Chem. Chem. Phys., 1999, 1, 2913 RSC .
  16. M. L. Sun, Z. Slanina and S. L. Lee, Chem. Phys. Lett., 1995, 233, 279 CrossRef CAS .
  17. R. R. Zope, T. Baruah, M. R. Pederson and B. I. Dunlap, Chem. Phys. Lett., 2004, 393, 300 CrossRef CAS .
  18. H. S. Wu and H. J. Jiao, Chem. Phys. Lett., 2004, 386, 369 CrossRef CAS .
  19. http://www.mathematik.uni-bielefeld.de/~CaGe/  .
  20. L. H. Gan, R. Li and L. X. Gao, THEOCHEM, 2010, 945, 8 CrossRef CAS .
  21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN03, Revision B. 03, Gaussian, Inc. , Pittsburgh, PA, 2003 Search PubMed .
  22. L. H. Gan, J. Q. Zhao and Q. Hui, J. Comp. Chem., 2010, 31, 1715 CAS .
  23. D. E. Manolopoulos, J. C. May and S. E. Down, Chem. Phys. Lett., 1991, 181, 105 CrossRef CAS .
  24. M. D. Diener and J. M. Alford, Nature, 1998, 393, 668 CrossRef CAS .
  25. G. Seifert, P. W. Fowler, D. Mitchell, D. Porezag and T. Frauenheim, Chem. Phys. Lett., 1997, 268, 352 CrossRef CAS .
  26. S. D. Tendero, F. Martin and M. Alcami, ChemPhysChem, 2005, 6, 92 CrossRef .
  27. P. W. Fowler, T. Heine and F. Zerbetto, J. Phys. Chem. A, 2000, 104, 9625 CrossRef CAS .
  28. M. Reiher and A. Hirsch, Chem.–Eur. J., 2003, 9, 5442 CrossRef CAS .
  29. A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2000, 39, 3915 CrossRef CAS .
  30. X. Lu, Z. Chen, W. Thiel, P. V. R. Schleyer, R. Huang and L. Zheng, J. Am. Chem. Soc., 2004, 126, 14871 CrossRef CAS .
  31. Z. Chen and R. B. King, Chem. Rev., 2005, 105, 3613 CrossRef CAS .
  32. R. C. Haddon, Science, 1993, 261, 1545 CAS .
  33. T. G. Schmalz, W. A. Seitz, D. J. Klein and G. E. Hite, J. Am. Chem. Soc., 1988, 110, 1113 CrossRef CAS .
  34. H. Y. Zhu, T. G. Schmalz and D. J. Klein, Int. J. Quantum Chem., 1997, 63, 393 CrossRef CAS .
  35. Z. Slanina, Int. Rev. Phys. Chem., 1987, 6, 251 CrossRef CAS .

Footnote

† Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra21720a
This journal is © The Royal Society of Chemistry 2012
Click here to see how this site uses Cookies. View our privacy policy here.