Microporous metal–organic framework containing cages with adjustable portal dimensions for adsorptive CO₂ separation

Abstract

The excellent breakthrough separation performance of a new microporous MOF for CO₂/N₂ and CO₂/CH₄ gas mixtures results from the combination of different equilibrium uptake amounts depending on the adsorption enthalpies of the adsorbates and different uptake kinetics depending on their kinetic diameters.

---

Introduction

Microporous metal–organic frameworks (MOFs) are considered to be very promising materials for selective gas adsorption and separation applications because of their large uptake capacities and tunable pore properties.¹ For efficient separation of gas mixtures, the uptake capacity of the porous materials is of primary concern, and this capacity is strongly correlated to the specific surface area of the materials and the chemical nature of the pore surface.² More importantly, the porous materials should show selectivity for adsorbates based on adsorption thermodynamics or adsorption kinetics or both. Microporous MOFs could be ideal platforms for gas separation applications, especially for adsorptive CO₂ capture and sequestration.³

On the other hand, the uptake capacity and pore properties of a microporous MOF can be relatively easily controlled by modulating the building components, metal ions and organic linkers. The selectivity of the MOF for adsorbates has so far been investigated by analyzing its sorption behaviors. Thermodynamic selectivity for adsorbates could be obtained by controlling pore surface properties with different adsorption enthalpies,⁴ and kinetic selectivity can also be achieved by adjusting portal dimensions for size-exclusive molecular sieving.⁵ Laboratory demonstrations of the real gas separation capabilities of microporous MOFs have been relatively easily evaluated by performing breakthrough experiments.⁶

Here, we report a new MOF with interlinked cages and narrow portal dimensions and demonstrate its sorption behaviors. The separation capabilities of the MOF for CO₂/N₂ and CO₂/CH₄ gas mixtures were evaluated using breakthrough experiments.

Experimental

General procedures

All reagents were purchased from commercial sources and were used without further purification. Elemental analysis (EA) (C, H, and N) was performed using a Thermo Scientific FLASH 2000 elemental analyzer at the Ulsan National Institute of Science & Technology, Korea. FT-IR spectra were recorded in the range 4000–400 cm⁻¹ using a Varian 670 FT-IR spectrophotometer.

Preparation of H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2DMA·4H₂O, 1

19.0 mg (0.080 mmol) CoCl₂·6H₂O and 17.5 mg (0.040 mmol) 4′,4′′-benzene-1,3,5-triyl-tribenzoic acid (H₃BTB) were dissolved in a mixed solvent of anhydrous N,N′-dimethylacetamide (DMA) and H₂O (DMA : H₂O = 10 : 2–3, v/v). The solution was sealed in a glass tube and heated to 120 °C for 1 d. Block-shaped purple crystals were collected and washed with DMA. Yield = 12.4 mg, 46.7%. EA for H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2DMA·4H₂O (C₁₂₈H_115.67N₅O_34.3Co_6.5, fw = 2655.84 g mol⁻¹), 1. Calc.: C, 57.89; H, 4.39; N, 2.64%. Found: C, 58.13; H, 4.35; N, 2.80%. IR (KBr, cm⁻¹): 3606 (vw), 3436 (s, b), 3068 (vw), 3031 (vw), 2937 (vw), 1606 (s), 1587 (s), 1547 (s), 1508 (w), 1402 (s), 1311 (vw), 1263 (vw), 1244 (vw), 1187 (w), 1145 (vw), 1108 (vw), 1015 (m), 965 (vw), 891 (vw), 855 (s), 805 (m), 779 (s), 700 (m), 670 (m), 599 (vw), 591 (w), 572 (w), 493 (m). The activated sample, 1a, was prepared by soaking as-synthesized 1 in methylene chloride for 3 d, and then vacuum drying at 250 °C for 5 h. EA was done in air for H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3]·H₂O (C₁₀₈H_63.67O_26.3Co_6.5, fw = 2165.71 g mol⁻¹), 1a. Calc.: C, 59.90; H, 2.96; N, 0.00%. Found: C, 59.79; H, 3.25; N, 0.31%. IR (KBr, cm⁻¹): 3445 (s, b), 3066 (vw), 3034 (vw), 2938 (vw), 2927 (vw), 1934 (vw), 1807 (vw), 1609 (s), 1582 (s), 1529 (s), 1508 (w), 1402 (s), 1305 (vw), 1247 (vw), 1179 (w), 1144 (vw), 1104 (vw), 1014 (m), 892 (vw), 851 (s), 808 (m), 775 (s), 703 (m), 667 (m), 565 (vw), 478 (m).

Crystallographic data collection and refinement of the structure H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2DMA·4H₂O, 1

A crystal was coated with Paratone oil and the diffraction data were measured at 173 K with Mo-Kα radiation on an X-ray diffraction camera system using an imaging plate equipped with a graphite-crystal incident-beam monochromator. The RAPID-AUTO software⁷ was used for data collection and processing. The structure was solved by direct methods and refined by full-matrix least-squares calculations using the XS and XL programs of the SHELXTL PLUS software package,⁸ respectively. Seven cobalt sites with one on a crystallographic inversion center, four ligands, two μ³-hydroxo groups with one on a crystallographic threefold rotation axis, three DMA molecules ligated to a cobalt atom, and three lattice water molecule sites with a total of two-thirds site occupancy were observed as an asymmetric unit (Fig. S1, ESI†). The μ³-OH group on a crystallographic threefold rotation axis (O2M atom) is involved in a hydrogen-bonding interaction with a lattice water molecule. The carboxylate groups of the ligands, except for three carboxylates ligated to a terminal 6-coordinate cobalt center and one of the ligated DMA molecules, were statistically disordered. All nonhydrogen atoms, except the minor sites of the disordered carboxylate residues, were refined anisotropically; the hydrogen atoms were assigned isotropic displacement coefficients U(H) = 1.2 U (C and μ³-OH) and 1.5 U (C_methyl), and their coordinates were allowed to ride on their respective atoms. The hydrogen atoms attached to the lattice water molecules were not included in the least-squares refinement. The least-squares refinement was performed with the modification of the structure factors for the electron densities of the completely disordered solvent region (8836 ų, 16.7% of the crystal volume, 1700 solvent electrons [∼35 DMA molecules] per unit cell) using the SQUEEZE option of PLATON.⁹ The final refinement of the structural model was performed under geometry and displacement parameter restraints, DFIX, DANG, DELU and ISOR, for the statistically disordered DMA molecule and under displacement parameter restraint, ISOR, for the lattice water molecules. Crystal data for 1: H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2/3H₂O (C₁₂₀H₉₀N₃O₂₉Co_6.5), fw = 2421.00 g mol⁻¹, rhombohedral, space group R3̄, a = b = 36.820(5) Å, c = 45.036(9) Å, V = 52876(15) ų, Z = 18, μ (Mo-Kα, λ = 0.71073 Å) = 0.970 mm⁻¹, d_calc = 1.369 mg cm⁻³, F(000) = 22293, 125 964 reflections were collected, 26 172 were unique [R_int = 0.0709]. R₁ (wR₂) = 0.0645 (0.1482) for 20,381 reflections [I > 2σ(I)], R₁ (wR₂) = 0.0807 (0.1542) for all reflections. The largest difference peak and hole were 1.315 and −0.749 e Å⁻³, respectively, see ESI.†

TGA measurements

Thermal gravimetric analysis (TGA) was performed using a Q600 system of TA Instruments under flowing N₂ gas with a heating rate of 5 °C min⁻¹ between ambient temperature and 700 °C.

PXRD measurements

Powder X-ray diffraction (PXRD) data were recorded using a Rigaku D/M 2500T automated diffractometer at room temperature with a step size of 0.02° in 2θ angle. The variable-temperature PXRD (VT-PXRD) measurements were carried out in air, and the sample was heated gradually from room temperature to the designated temperature with a holding time of at least 30 min at each temperature. Simulated PXRD patterns were calculated with the Material Studio program using the single-crystal data.¹⁰

Gas sorption measurements

All gas sorption isotherms were measured using a BELSORP-max (BEL Japan, Inc.) with a standard volumetric technique using N₂ (with purity of 99.999%), H₂ (99.9999%), CO₂ (99.999%), CO (99.998%), and CH₄ (99.95%) as adsorbates.

Breakthrough experiments

The breakthrough experiments were conducted on 1a for CO₂/N₂ (50 : 50 v/v) and CO₂/CH₄ (50 : 50 v/v) mixtures with a total gas flow rate of 20 cm³ min⁻¹ at 195 and 298 K, by using a setup that was slightly modified from that reported previously (Fig. S2, ESI†).^6a Approximately 1 g of the activated sample, 1a, was loaded in a vertical sample cell (0.64 cm inner diameter). The sample was further activated under flowing He at a flow rate of 50 cm³ min⁻¹ at 523 K for 6 h, and then the reactor was slowly cooled to ambient temperature. The mass intensities of the mixture gases passing through the reactor were monitored on a Pfeiffer Prisma QMS 200 mass spectrometer detecting ion peaks at m/z⁺ = 4 (He⁺), 15 (CH₃⁺), 28 (N₂⁺), and 44 (CO₂⁺). The 17.1% reduced relative intensity of CO₂ coming from the fragmentation of CO₂⁺ to CO⁺ was corrected based on preliminary mass measurements for a pure CO₂ gas stream. The relative intensity of N₂ in the breakthrough experiment for CO₂/N₂ mixture gases was also corrected for the additional CO⁺ fragment that has the same m/z⁺ = 28 as N₂⁺. To avoid interference by the O⁺ (m/z⁺ = 16) fragment from CO₂ in the intensity for CH₄⁺ peak (m/z⁺ = 16), the m/z⁺ = 15-peak measurement was used for the intensity of CH₄⁺. The amount of CH₄ was estimated from the intensity of the CH₃⁺ peak based on preliminary mass measurements of the CH₄⁺ peak (52.8%) and its fragmented CH₃⁺ peak (47.2%).

Result and discussion

It was reported that the solvothermal reaction of CoCl₂·6H₂O with 4′,4′′-benzene-1,3,5-triyl-tribenzoic acid (H₃BTB) in N,N′-dimethylacetamide (DMA) resulted in either a two-dimensional (2-D) MOF of a 3,6-connected kgd net topology or a three-dimensional (3-D) MOF with an unprecedented 3,6-connected net topology, depending on the reaction temperature and the reactant concentrations.¹¹ In the MOFs, a linear trinuclear Co₃(COO)₆ secondary building unit (SBU) served as a 6-connected node. However, a similar but hydrosolvothermal reaction in a mixed solvent of DMA and H₂O generated a completely different 3-D MOF, H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2DMA·4H₂O (1).

Structural description of 1

1 contains three different cobalt carboxylate clusters as secondary building units (SBUs). Two of them are 8-connected SBUs (8c-SBU) of the same 4-6-4 coordinate linear trinuclear cobalt cluster, Co₃(COO)₆ (Fig. 1a and b), and the remaining SBU is a 4-connected SBU (4c-SBU) of the 4–6 coordinate dinuclear cobalt cluster, Co₂(COO)₃ (Fig. 1c).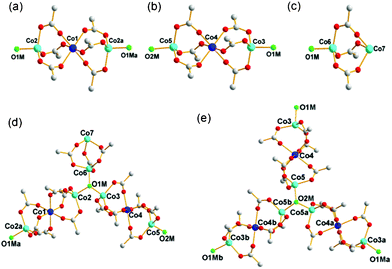

Fig. 1 The SBUs in the network of 1. (a) and (b) The two 8-connected SBUs of the 4-6-4 coordinate linear trinuclear cobalt cluster, Co₃(COO)₆. (c) The 4-connected SBU of the 4-6 coordinate dinuclear cobalt cluster, Co₂(COO)₃. (d) and (e) The two 3-connected μ³-OH groups linked to three different cobalt clusters. Color code: cobalt in the center of the linear trinuclear cobalt clusters, blue; the remaining cobalt, cyan; μ³-OH, green; oxygen, red; carbon, gray. Symmetry code: a = −y, 1 + x − y, z; b = −1 − x + y, −x, z.

Examination of the network connectivity shows that these cobalt clusters are interconnected via four 3-connected BTB nodes and two 3-connected μ³-OH groups (Fig. 1d and e) to form a 3-D network with a complicated net topology. The assignment of the two μ³-O atoms as the OH residues was based on the geometry around the bridging oxygen atoms, such as the Co–O bond distances and the Co–O–Co bond angles. The one-third cationic charge per asymmetric unit needed for the charge balance of 1 was assumed to be from an unidentified proton attached to a lattice water molecule with one-third site occupancy. First, the two 8-connected SBUs and a 4-connected SBU are interconnected via two 3-connected μ³-OH nodes to form a corrugated two-dimensional (2-D) layer of a uninodal 3-connected hcb net topology (Fig. 2), where the 8c-SBUs could be considered as a ditopic linker and the 4c-SBU as a terminal residue with no further connectivity. The corrugated 2-D layers are stacked along the crystallographic c-axis in a staggered manner (Fig. 3a–d), and the stacked 2-D layers are further interconnected via four different 3-connected BTB ligands to form a three-dimensional (3-D) network with an unprecedented 3,3,3,3,3,3,4,8,8-connected net topology (Fig. 3e).¹²

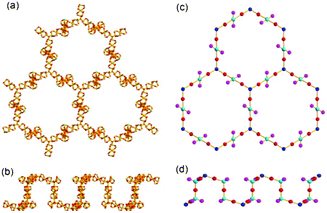Fig. 2 Ball-and-stick diagrams of a corrugated 2-D sheet consisting of the cobalt clusters, Co₂(COO)₃ and Co₃(COO)₆, connected via 3-connected μ³-OH groups in (a) top view and (b) side view. Schematic drawings of the 2-D network of an hcb net topology in (c) top view and (d) side view, where the SBUs were represented using the balls and the connectivity between the SBUs using the sticks.

Fig. 3 Schematic drawings of two layers stacked in a staggered manner in (a) side and (b) top views, and of three stacked layers in (c) side and (d) top views. (e) The three stacked 2-D layers are connected via four different 3-connected BTB ligands, where the yellow balls represent the 3-connected BTBs.

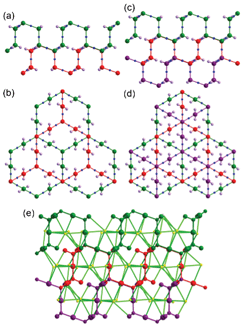
The complicated network of 1 contains three different cages: Cage A with (8c-SBU)₆(BTB)₆(μ³-OH)₂; Cage B with (8c-SBU)₇(4c-SBU)₂(BTB)₄(μ³-OH)₄; and Cage C with ((8c-SBU)₆(4c-SBU)₂(BTB)₃(μ³-OH)₄(DMF)₃)₂ as structural components. Cage A, with a local S₆ point symmetry, consists of six BTB ligands as edge components of the cage and the ligands are connected via six 8c-Co₃ SBUs and two μ³-OH residues to form a cage with a pore diameter of ∼9 Å with six oval-shaped portals (Fig. 4).

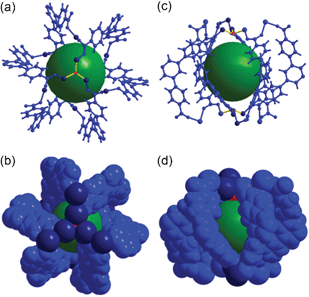Fig. 4 Ball-and-stick and space-filling models of Cage A with a local S₆ point symmetry. Top view of (a) the ball-and-stick and (b) space-filling models. Side view of (c) the ball-and-stick and (d) space-filling models. Color code: BTB, blue; cobalt, dark blue; μ³-O, red; dummy ball representing the cavity of Cage A, green.

Cage B, with a pseudo-C₃ point symmetry, consists of four BTB ligands as triangular facial components of the tetrahedral cage and the three corners of the ligands are connected via seven 8c-SBUs, two 4c-SBUs, and four μ³-OH residues to form a cage with a pore diameter of ∼5.6 Å (Fig. 5).

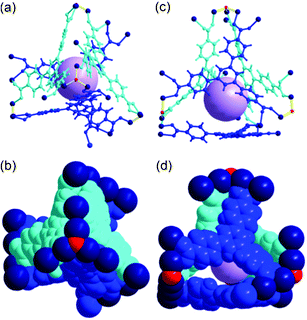Fig. 5 Ball-and-stick and space-filling models of Cage B with a pseudo-C₃ point symmetry. Top view of (a) the ball-and-stick and (b) space-filling models. Side view of (c) the ball-and-stick and (d) space-filling models. Color code: BTB, blue and cyan; cobalt, dark blue; μ³-O, red; dummy ball representing the cavity of Cage B, violet.

Cage A is surrounded by six Cage Bs to form an AB₆ cage cluster (Fig. 6). All six portals of Cage A are shared with the six Cage B portals and the pore of Cage A is only accessible via the pores of the Cage Bs. Three edges of the tetrahedral cage are open as portals and the remaining three edges are closed. Cage C has the same local S₆ point symmetry as Cage A, but is a dimeric cage of two one-face-open tetrahedra (Fig. 7). The one-face-open tetrahedron consists of three BTB ligands connected via six 8c-Co₃ SBUs, two 4c-Co₂ SBUs, and four μ³-OH residues. The pore diameter of cage C is ∼8.4 Å.

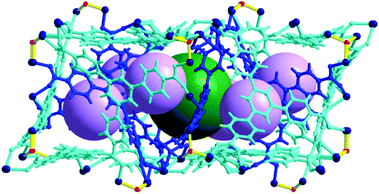Fig. 6 Ball-and-stick model of the AB₆ cage cluster, where Cage A is surrounded by six Cage Bs. Color code: BTB, blue and cyan; cobalt, dark blue; μ³-O, red; dummy balls representing the cavities of Cage A and Cage B, green and violet, respectively.

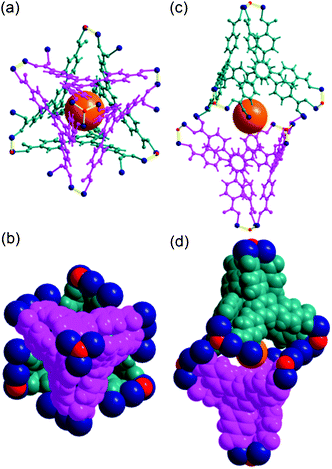Fig. 7 Ball-and-stick and space-filling models of Cage C with a pseudo-S₆ point symmetry. Top view of (a) the ball-and-stick and (b) space-filling models of Cage C. Side view of (c) the ball-and-stick and (d) space-filling models. Color code: BTB, pink and dark cyan; cobalt, dark blue; μ³-O, red; dummy ball representing the cavity of Cage C, orange.

In the packing of the cages, the AB₆ cage clusters are arranged at the eight vertices of a hypothetical primitive unit cell and Cage C is at the body center of this unit cell (Fig. S3, ESI†). The cages, with their total pore volume (9383 ų) corresponding to ∼18% of the total unit cell volume, are arranged as shown in Fig. 8. However, the portals of Cage C between the dimeric one-face-open tetrahedra are blocked by one ligated DMA molecule at the terminal dinuclear cobalt ions (Fig. S4, ESI†). In addition, the potential passages between the pores of Cage B and Cage C are also blocked via the other ligated DMA molecules at the terminal dinuclear cobalt ions (Fig. S5, ESI†).

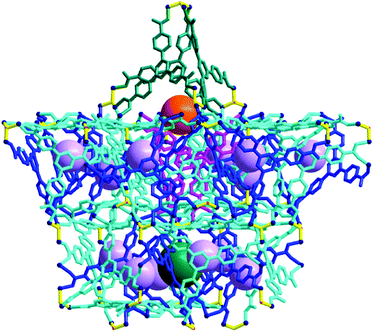Fig. 8 Packing diagram of 1 as a ball-and-stick model with three different types of cages, where the pores of the cages are represented using the green, violet, and orange dummy balls.

TGA of 1

TGA data of as-synthesized sample 1 in flowing N₂ conditions are shown in Fig. S6. The first 2.5% weight loss of 1 up to 150 °C corresponds to the loss of four lattice water molecules in the pores and the second 16.4% weight loss up to 340 °C corresponds to the loss of two lattice DMA molecules in the pores and three DMA molecules ligated to the terminal cobalt ion of the 4c-SBU. The subsequent two-step weight loss up to 700 °C leads to the complete decomposition of the whole structure.

PXRD analysis of 1

The PXRD pattern of as-synthesized 1 is similar to the simulated PXRD pattern from the structural model of single-crystal 1 (Fig. S7, ESI†), which confirms that the single crystal is representative of the bulk sample.

The variable-temperature powder X-ray diffraction (VT-PXRD) patterns of 1 indicate that the framework structure is stable up to 150 °C (Fig. 9). The peak broadening starts at 175 °C, especially for the peaks at higher diffraction angles, while preserving the major diffraction peaks at lower diffraction angles. The sample finally loses its crystallinity completely at 350 °C. The removal of the water molecules in the pores up to 150 °C does not affect the structural integrity of 1 (Fig. S6, ESI†). The removal of the DMA molecules, especially the DMA molecules ligated to the cobalt center, up to 300 °C, inevitably alters the coordination geometry of the cobalt center. The alteration reduces the short-range ordering around the altered cobalt center in the crystal, while preserving the overall long-range ordering of the whole framework structure of 1.

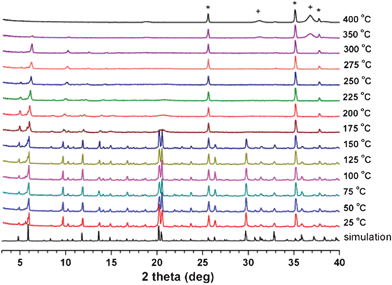Fig. 9 VT-PXRD patterns of as-synthesized 1. Peaks with crosses and stars represent Co₃O₄ and the α-Al₂O₃ of the high-temperature sample holder, respectively.

To access the pores in the framework, the ligated DMA molecules blocking the portals of the pores must be removed from the framework. Activated sample 1a was prepared by soaking 1 in methylene chloride for 3 d, and then vacuum drying at 250 °C for 5 h. The thermal gravimetric analysis (TGA) data of activated 1a briefly exposed to air showed a 0.7% weight loss up to 160 °C, then no further weight loss before the decomposition of the framework structure at around 350 °C (Fig. S8, ESI†),‡ showing that all the DMA molecules, including the ligated ones, could be completely removed from the framework by vacuum drying at 250 °C. The elemental analysis result of 1a also supports the complete removal of the ligated DMA molecules.

PXRD analysis of 1a

The disappearance of the high-angle diffraction peaks in the PXRD pattern of 1a, while preserving the low-angle diffraction pattern intact, suggests that even though the overall packing structure of the activated sample is very similar to that of the as-synthesized sample, the local environment around the cages is no longer the same as that of the as-synthesized sample. The PXRD pattern of 1a is different from that of the as-synthesized sample, but similar to that of as-synthesized 1 taken at 250 °C in air (Fig. S7, S9, ESI†). The disappearance of the high-angle diffraction peaks, while preserving the low-angle diffraction pattern intact, suggests that even though the overall packing structure of the activated sample is very similar to that of the as-synthesized sample, the local environment around the cages is no longer the same as that of the as-synthesized sample.

Sorption behaviours of 1a

At 77 K, the N₂ and H₂ sorption isotherms on 1a show that 1a does not have any accessible pore surface for N₂ and H₂ (Fig. S10, ESI†). The H₂ sorption isotherms on 1a indicate that the portal dimensions of the pores at 77 K are smaller than the kinetic diameter (KD) of H₂ (2.89 Å).

However, at 195 K, the type I isotherms of the CO₂ sorption on 1a with the adsorbed CO₂ amount of ∼81 cm³ g⁻¹ at 1 bar show that the portal dimensions of the cages are larger than the KD of CO₂ (3.3 Å) and the accessible pores are microporous (Fig. 10). Unlike the N₂ sorption at 77 K, the sorption isotherms at 195 K indicate a small amount of N₂ sorption (∼14 cm³ g⁻¹ at 1 bar) with hysteresis. The sorption kinetics of N₂ on 1a at 195 K is extremely slow compared with that of CO₂ sorption. The sorption behavior of CH₄ and CO is also somewhat similar to that of N₂. Both adsorbates show small adsorbed amounts with hysteresis and slow sorption kinetics. These results strongly suggest that the portal dimensions of the pores at 195 K are in the KD range of adsorbates (N₂, 3.64; CO, 3.76; CH₄, 3.8 Å). The smaller H₂ may also access the pores at 195 K. However, it appears that the interaction of H₂ with the pore surface is not strong enough to cause adsorption.

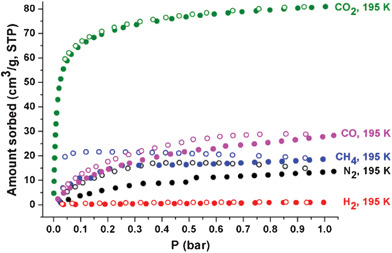Fig. 10 Sorption isotherms of CO₂ (green), CO (pink), CH₄ (blue), N₂ (black), and H₂ (red) on 1a at 195 K. Solid and open shapes represent adsorption and desorption, respectively.

The gas sorption isotherms on 1a at 273 and 293 K are basically similar to those at 195 K, except for the overall reduction of sorption amounts with no significant hysteresis during the adsorption and desorption processes (Fig. S11, S12, ESI†). The average adsorption enthalpy of CO₂, −25.6 kJ mol⁻¹, and the adsorption enthalpy at zero coverage, −27.2 kJ mol⁻¹, calculated from the adsorption isotherms at 273 and 293 K, are within the expected range for MOFs with no specific interacting sites, where the adsorption enthalpy was calculated using a virial equation (Fig. 11).¹³ The average adsorption enthalpies of CH₄ and CO, −21.9 and −18.5 kJ mol⁻¹, and the corresponding adsorption enthalpies at zero coverage, 22.6 and −19.1 kJ mol⁻¹, respectively, were also calculated from the adsorption isotherms at 273 and 293 K using the same method. It is noticeable that the adsorbed amount of CH₄ at 195 K and 1 bar (19 cm³ g⁻¹) is smaller than that of CO (28 cm³ g⁻¹), even though the adsorption enthalpy of CH₄ is slightly larger than that of CO (Fig. 10, 11d and 11f). The adsorption enthalpies of CO₂ and CO calculated from the adsorption isotherms for three different temperatures, 195, 273, and 293 K, are similar to those from the adsorption isotherms for 273 and 293 K (Fig. 11b and f). However, the adsorption enthalpy of CH₄ calculated from the adsorption isotherms for three different temperatures, 195, 273, and 293 K, (−13.0 kJ mol⁻¹) is much smaller than that calculated from the adsorption isotherms for 273 and 293 K (−21.9 kJ mol⁻¹) (Fig. 11d). CO₂ and CO can access the pores of 1a over the whole temperature range. However, CH₄ can access most pores of 1a at 273 and 293 K, but has only limited access to those pores at 195 K. The portal dimensions of the pores of 1a are temperature-dependent and CH₄ can access only part of the pores, because the portal dimensions of some pores at 195 K are smaller than the KD of CH₄.

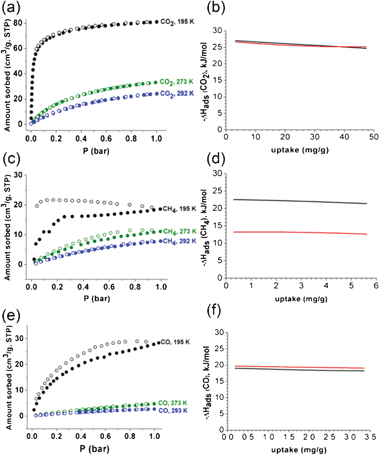Fig. 11 Sorption isotherms of (a) CO₂, (c) CH₄, and (e) CO on 1a at 195, 273, and 293 K, respectively, and the corresponding adsorption enthalpies of (b) CO₂, (d) CH₄, and (f) CO. Solid and open shapes in the sorption isotherms represent adsorption and desorption isotherms, respectively. The adsorption enthalpies calculated by using the two adsorption isotherms at 273 and 293 K are represented in black, and those calculated by using the three adsorption isotherms at 195, 273 and 293 K are marked in red.

The ability of a material to separate gases by adsorption is dependent on the selectivity for gas mixtures. In addition to the equilibrium uptake amount, the uptake kinetics of adsorbates is also an important factor in gas separation applications. Breakthrough experiments were carried out to test the gas separation capabilities of activated 1a. Approximately 1 g of 1a was exposed to gas streams containing binary mixtures of CO₂/N₂ (50 : 50 v/v) and CO₂/CH₄ (50 : 50 v/v) at a flow rate of 20 cm³ min⁻¹ at 195 and 298 K. The breakthrough profile for the CO₂/N₂ mixture on 1a at 195 K is like an idealized profile (Fig. 12a). The outlet gas composition consists of pure N₂ for ∼200 s before the breakthrough of CO₂. The plateau observed in the N₂ breakthrough curve suggests that 1a does not adsorb N₂ at all, probably because of the extremely slow adsorption kinetics at 195 K, as observed in the N₂ sorption measurement. After the saturation of 1a by CO₂, the composition of the outlet gases slowly approaches that of the feed gas. It is worth noting that the adsorbed CO₂ on 1a could be removed easily by flowing He at a flow rate of 50 cm³ min⁻¹ for 30 min at ambient temperature for the next cycle of the breakthrough experiment. The breakthrough profile for the CO₂/CH₄ mixture on 1a at 195 K is similar to that for the CO₂/N₂ mixture (Fig. 12a and b). The outlet gas composition consists of pure N₂ for ∼150 s before the breakthrough of CO₂. The simultaneous adsorption of CH₄ on 1a with the adsorption of CO₂ results in the reduced breakthrough time for CO₂ in the profile for the CO₂/CH₄ mixture.

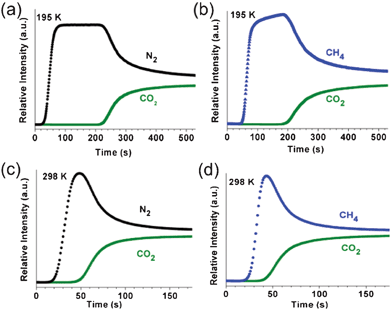Fig. 12 Breakthrough curves on 1a using (a, c) CO₂/N₂ (50 : 50 v/v) and (b, d) CO₂/CH₄ (50 : 50 v/v) mixture gases with a total gas flow rate of 20 cm³ min⁻¹ at 195 and 298 K, respectively.

The breakthrough profiles for the CO₂/N₂ and CO₂/CH₄ mixture on 1a at 298 K showed significantly reduced breakthrough times (Fig. 12c and d), mainly due to the reduced adsorption capacity of 1a for CO₂ at this temperature (Fig. S14, ESI†).

Conclusions

We have successfully synthesized a new, microporous MOF, H_1/3[(Co^II_13/2(BTB)₄(OH)_4/3(DMA)₃]·2DMA·4H₂O, consisting of three different interlinked cages. This MOF, when activated at 250 °C, was found to selectively adsorb CO₂ over N₂ or CH₄ at 195 K. In the activated sample 1a, the portals are being opened and most of the pores are accessible for CO₂ with its relatively small KD at 195 K. However, the portals are partially open to other adsorbates such as N₂, CO, and CH₄, which have larger KDs. It is noticeable that the sorption kinetics of N₂, CO, and CH₄ at 195 K are much slower than that of CO₂. As expected, at 273 and 293 K, there were significant reductions in the uptake of all the adsorbates compared with those at 195 K; however, the sorption kinetics were significantly increased.

The excellent breakthrough separation performance of 1a for CO₂/N₂ and CO₂/CH₄ gas mixtures is the result of the combined selectivity coming from both the different equilibrium uptake amounts depending on the adsorption enthalpies of the adsorbates and the different uptake kinetics depending on the KDs of the adsorbates. In addition, 1a could easily be regenerated for the next cycle of the breakthrough experiment by simply flowing He at ambient temperature. We believe that our work has important implications in the search for crystalline microporous materials that are more efficient in adsorptive CO₂ separation.

Acknowledgements

This work was supported by 2012-0008827, 2012-003077, 2012R1A3A2048833 and WCU programs (R31-2011-000-20012-0) through the National Research Foundation of Korea.

References

1. (a) H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674; (b) J.-R. Li, J. Scully and H.-C. Zhou, Chem. Rev., 2012, 112, 869–932; (c) J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
2. (a) O. K. Farha, A. Ö. Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948; (b) H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428; (c) D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357–5361; (d) A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998–17999.
3. (a) K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781; (b) D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082; (c) S. Keskin, T. M. van Heest and D. S. Sholl, Chem. Sus. Chem., 2010, 3, 879–891; (d) J.-R. Li, Y. Ma, M. C. McCarthy, J. Sculley, J. Yu, H.-K. Jeong, P. B. Balbuena and H. C. Zhou, Coord. Chem. Rev., 2011, 255, 1791–1823; (e) B. Wang, A. P. Côté, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Nature, 2008, 453, 207–211; (f) R. Eguchi, S. Uchida and N. Mizuno, Angew. Chem., Int. Ed., 2012, 51, 1635–1639; (g) K. L. Kauffman, J. T. Culp, A. J. Allen, L. Espinal, W. Wong-Ng, T. D. Brown, A. Goodman, M. P. Bernardo, R. J. Pancoast, D. Chirdon and C. Matranga, Angew. Chem., Int. Ed., 2011, 50, 10888–10892; (h) W. Zhuang, D. Yuan, D. Liu, C. Zhong, J.-G. Li and H.-C. Zhou, Chem. Mater., 2012, 24, 18–25.
4. (a) R. Vaidhyanathan, S. S. Iremonger, G. K. H. Shimizu, P. G. Boyd, S. Alavi and T. K. Woo, Science, 2010, 330, 650–653; (b) B. Zheng, J. Bai, J. Duan, L. Wojtas and M. J. J. Zaworotko, J. Am. Chem. Soc., 2011, 133, 748–751; (c) S. Couck, J. F. M. Denayer, G. V. Baron, T. Rémy, J. Gascon and F. Kapteijn, J. Am. Chem. Soc., 2009, 131, 6326–6327; (d) A. Demessence, D. M. D'Alessandro, M. L. Foo and J. R. Long, J. Am. Chem. Soc., 2009, 131, 8784–8786; (e) J. An, S. J. Geib and N. L. Rosi, J. Am. Chem. Soc., 2010, 132, 38–39; (f) J.-B. Lin, J.-P. Zhang and X.-M. Chen, J. Am. Chem. Soc., 2010, 132, 6654–6656; (g) J. An and N. L. Rosi, J. Am. Chem. Soc., 2010, 132, 5578–5579; (h) A. Torrisi, R. G. Bell and C. Mellot-Draznieks, Cryst. Growth Des., 2010, 10, 2839–2841; (i) R. Vaidhyanathan, S. S. Iremonger, K. W. Dawson and G. K. H. Shimizu, Chem. Commun., 2009, 5230–5232.
5. (a) D. N. Dybtsev, H. Chun, S. H. Yoon, D. Kim and K. Kim, J. Am. Chem. Soc., 2004, 126, 32–33; (b) K. Li, D. H. Olson, J. Seidel, T. J. Emge, H. Gong, H. Zeng and J. Li, J. Am. Chem. Soc., 2009, 131, 10368–10369; (c) C. Y. Lee, Y.-S. Bae, N. C. Jeong, O. K. Farha, A. A. Sarjeant, C. L. Stern, P. Nickias, R. Q. Snurr, J. T. Hupp and S. T. Nguyen, J. Am. Chem. Soc., 2011, 133, 5228–5231; (d) E. Haldoupis, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2010, 132, 7528–7539; (e) S. Horike, Y. Inubushi, T. Hori, T. Fukushima and S. Kitagawa, Chem. Sci., 2012, 3, 116–120.
6. (a) H. Hayashi, A. P. Côté, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Nat. Mater., 2007, 6, 501–506; (b) R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Science, 2008, 319, 939–943; (c) L. Bastin, P. S. Bárcia, E. J. Hurtado, J. A. C. Silva, A. E. Rodrigues and B. Chen, J. Phys. Chem. C, 2008, 112, 1575–1581; (d) L. Hamon, P. L. Llewellyn, T. Devic, A. Ghoufi, G. Clet, V. Guillerm, G. D. Pirngruber, G. Maurin, C. Serre, G. Driver, W. van Beek, E. Jolimaître, A. Vimont, M. Daturi and G. Férey, J. Am. Chem. Soc., 2009, 131, 17490–17499; (e) V. Finsy, L. Ma, L. Alaerts, D. E. De Vos, G. V. Baron and J. F. M. Denayer, Microporous Mesoporous Mater., 2009, 120, 221–227; (f) E. Q. Procopio, F. Linares, C. Montoro, V. Colombo, A. Maspero, E. Barea and J. A. R. Navarro, Angew. Chem., Int. Ed., 2010, 49, 7308–7311; (g) D. Britt, H. Furukawa, B. Wang, T. G. Glovor and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 49, 20637–20640; (h) B. Li, Z. Zhang, Y. Li, K. Yao, Y. Zhu, Z. Deng, F. Yang, X. Zhou, G. Li, H. Wu, N. Nijem, Y. J. Chabal, Z. Lai, Y. Han, Z. Shi, S. Feng and J. Li, Angew. Chem., Int. Ed., 2012, 51, 1412–1415; (i) E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822; (j) A. C. Kizzie, A. G. Wong-Foy and A. J. Matzger, Langmuir, 2011, 27, 6368–6373; (k) V. Colombo, C. Montoro, A. Maspero, G. Palmisano, N. Masciocchi, S. Galli, E. Barea and A. R. Navarro, J. Am. Chem. Soc., 2012, 134, 12830–12843.
7. Rapid Auto software, R-Axis series, Cat. No. 9220B101, Rigaku Corporation.
8. SHELX program: G. M. SheldrickActa Crystallogr. Sect. A 2008, 64, 112–122.
9. A. L. Spek, PLATON program: Acta Crystallogr. Sect. A 1990, 46, 194–201.
10. Materials Studio program, version 4.3, Accelrys, San Diego, CA, 2008.
11. D. Kim, X. Song, J. H. Yoon and M. S. Lah, Cryst. Growth Des., 2012, 12, 4186–4193.
12. A. Blatov, IUCr CompComm Newsletter, 2006, 7, 4 , TOPOS is available at http://www.topos.ssu.samara.ru/..
13. (a) J. L. C. Rowsell and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 1304–1315; (b) M. Dincă, A. Dailly, Y. Lie, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876–16883.

---

Footnotes

† Electronic supplementary information (ESI) available: Structural drawings, TGA, PXRD, gas sorption data, and breakthrough experimental setup. CCDC reference number 894096. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2ra22118g

‡ The 0.7% weight loss corresponds to water molecules that were readsorbed from the air when 1a was exposed to air during the sample preparation for the TGA experiment.

---