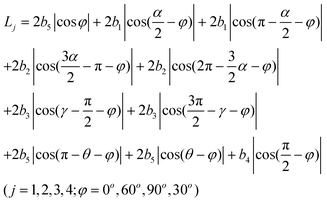DOI:
10.1039/C2RA21581K
(Paper)
RSC Adv., 2012,
2, 12182-12189
Radial collapse of carbon nanotubes without and with Stone–Wales defects under hydrostatic pressure
Received
26th July 2012
, Accepted 5th October 2012
First published on 5th October 2012
Abstract
The effects of carbon nanotube (CNT) chirality, Stone–Wales (SW) defects and defect orientation on the radial collapse and elasticity of single-walled CNTs (SWNTs) were investigated using molecular mechanics and molecular dynamics (MD) simulations. It is found that the collapse pressure (Pc) of the armchair SWNT is 13.75 times higher than that of the zigzag SWNT. Moreover, the armchair SWNT with SW defects is easier to collapse compared to the intrinsic armchair SWNT, while the zigzag SWNT with SW defects is more difficult to collapse compared to the intrinsic zigzag SWNT; the SW2 defect makes Pc of SWNT (10, 10) decrease by 11.0%, while the SW4 defect makes Pc of SWNT (17, 0) increase by 100.0%. We introduce a model for SWNTs deformed in the radial direction according to the projection of the C–C bond along the bending direction. The model is validated for defect-free SWNTs and is then used to study the radial collapse of SWNTs with SW defects. The effect of chirality and SW defect on the radial collapse of SWNTs can be understood by the model. The strong sensitivity of radial collapse of SWNTs to chirality and SW defect can provide some guidance for high load structural applications of SWNTs.
I Introduction
Since carbon nanotubes (CNTs) were discovered,1 extensive experimental and theoretical studies have been made to reveal CNTs' unique physical and mechanical properties. It is well-known that the CNTs possess high axial Young's moduli (∼1 TPa),2–4 high axial tensile strength (∼63 GPa)5 and high axial strain at break (∼40%).6 It shows that the stiffness and strength of CNTs are in the range of TPa and GPa, respectively. The fact that CNTs are extremely lightweight compared to other materials makes them potential candidates as reinforcing fibers in superstrong composites.7–9
The mechanical properties of CNTs and CNT–polymer composites have been studied through theoretical, experimental and computational analysis.10–12 Results reported in the recent studies have indicated that the mechanical properties obtained from experiments tend to be lower than those obtained from computational analysis.12 Several reasons have been assigned for this disparity. On the one hand, CNTs disperse in various orientations experimentally, while CNTs in the constructed composites model usually directionally align. On the other hand, experimental processes could introduce defects into the CNTs, while computational models are based on a perfect CNT molecular material structure.13 Experimental observations have revealed that topological defects, such as the 5-7-7-5 Stone–Wales (SW) defects, are commonly present in CNTs.14 These local defects can alter not only the inelastic properties, but also the elastic properties of CNTs, such as Young's modulus and Poisson's ratio. Consequently, these defects may alter the longitudinal, lateral stiffness, and flexural rigidity in response to tension, torsion and bending, respectively. Because of the unique planar hexagonal structure of CNTs, topological defects can alter the deformation response and hence the elastic properties. In addition, defects can also be potential sites where an irreversible mechanical response is initiated.15
As noted above, defects in CNTs have an impact on their mechanical properties, and hence its mechanism is needed to be understood thoroughly. Recently, the degradation of mechanical properties, including axial tension and compression, of CNTs induced by defects has been well studied theoretically.16–22 In the present paper, molecular mechanics (MM) and molecular dynamics (MD) simulations are used to investigate the effects of single-walled CNTs (SWNTs) chirality, SW defects and defect orientation on the radial collapse and elasticity of SWNTs without and with SW defects under hydrostatic pressure. The collapse pressure (Pc) of SWNTs affected by SWNT chirality, SW defect and defect orientation is specifically evaluated. What's more, we introduce a model for SWNTs with different chiralities deformed in the radial direction and apply this model to investigate their deformation characteristics and stability under hydrostatic pressure. The model is validated for defect-free SWNTs and is then used to study the collapse of SWNTs with SW defects. The model enables us to detect the chemical bonding topology unit of the chiral graphene and define the projection of C–C bond along the bending direction to evaluate the collapse of SWNTs in the radial direction. The projection is expressed in terms of bond lengths and bond angles in hexagons, pentagons or heptagons functions. The variation trend of Pc predicted for SWNTs with and without SW defects using the model is in accordance with the results of MD simulations. The effect of chirality and SW defects on the radial collapse of SWNTs can be understood by the model. The influence of SWNTs chirality and SW defects on the radial collapse of SWNTs can provide some guidance for high load structural application of SWNTs.
II Simulation methods
The simulations were carried out using a commercial software package called Materials Studio (MS) developed by Accelrys Software, Inc. MD and MM simulations were carried out on a supercell containing a SWNT using the condensed-phase optimized molecular potential for atomistic simulation studies (COMPASS) force-field method. The COMPASS force-field is a parametrized, tested and validated first ab initio force-field, which enables an accurate prediction of various gas-phase and condensed-phase properties of most of the common organic and inorganic materials.23–26 Moreover, it has been proven to be applicable in describing the mechanical properties of CNTs.27,28 In simulations, periodic boundary conditions were employed. MM simulations were performed to find the thermal stable morphology and achieve a conformation with minimum potential energy for all SWNTs. All MD simulations were performed in the NPT ensemble, and a fixed time step size of 1 fs was used in all cases. The Andersen thermostat method was employed to control the system at the temperature of 1 K and the interactions were determined within a cutoff distance of 9.5 Å. The SWNT was initially equilibrated at atmospheric pressure and subsequently subjected to step-wise monotonically hydrostatic pressure increments, allowing the unit cell volume to equilibrate for at least 30 ps at each step. The reduced volume ratio (V/V0), where V and V0 are the unit cell volumes at an applied pressure and atmospheric pressure, respectively, was measured as a function of applied hydrostatic pressure.
III Results and discussion
III.I The radial collapse of the intrinsic SWNT (10, 10)
Here, we demonstrate the existence of the shape transitions of the intrinsic SWNT under hydrostatic pressure. The simulations show that when a SWNT deforms under pressure, it undergoes two shape transitions: (1) changing from a cycle to an oval; (2) changing from an oval to collapse, as shown in Fig. 1(a). We define two critical pressures, Pm and Pc, where Pm is the pressure to make the SWNT undergo a transition from a collapsed shape to circle shape upon unloading, and Pc is the pressure to collapse the SWNT upon loading. According to the loading curve (black dash dot line) and the unloading curve (red dots line) in Fig. 1(a), we can find that the Pc and Pm of the intrinsic SWNT (10, 10) are 5.5 and 3.2 GPa, respectively. Moreover, the curve shape is a hysteresis loop.
 |
| | Fig. 1 (a) Loading and unloading curves of SWNT (10, 10) as a function of hydrostatic pressure. The insets are the structures for intrinsic SWNT at different pressures. (b) Concentration profiles of the initial, elliptical and collapsed SWNT (10, 10) along the y axis. | |
In order to characterize the geometric deformation of the SWNT (10, 10) clearly, the concentration profiles of the initial, elliptical and collapsed SWNTs (10, 10) at 0.0001 GPa, 5.0 GPa and 5.5 GPa along the y axis are shown in Fig. 1(b), respectively. Herein, we manually placed the initial, elliptical and collapsed SWNT (10, 10) in a box with the same center of mass and orientation for comparison. The concentration profile was calculated for 3D periodic structures by computing the atom-density profile within evenly spaced slices parallel to the bc, ca and ab planes. In practice, this is equivalent to taking a, b and c components of the fractional coordinates of each atom and independently generating a plot for each component. We defined three distances of the opposite walls of the initial, elliptical and collapsed SWNT (10, 10), d1–d3, as shown in Fig. 1(b). As marked in Fig. 1(b), d1 is 12.241 Å, d2 is 10.711 Å and d3 is 3.061 Å. The d3 is less than 3.4 Å, which is the shortest distance of the graphite layer and almost enters the strong-adhesive-binding region of the chemical bond. So we can conclude that the SWNT (10, 10) assumes complete collapse above the critical pressure 5.5 GPa. The results are in agreement with the former experimental and simulation results.29,30 The experimental results demonstrate that the smaller diameter SWNTs (mean diameter ∼0.8 nm) collapse at a higher pressure of 6.6 ± 0.8 GPa compared to the transitions pressure of 2.1 ± 0.2 GPa for the larger diameter SWNT (mean diameter ∼1.4 nm) material.29 Our results are in the range of experimental results29 and this confirms the validity of the simulation method used here.
We tracked some kinds of energies in the system to reveal the physical mechanism of the collapse of SWNT (10, 10), as shown in Table 1, where the total energy consists of the internal energy and the non-bond energy which consists of the van der Waal (vdW) energy and electrostatic energy. Herein, the electrostatic energy of the intrinsic SWNTs is zero. Upon loading, the external pressure makes the total energy of the system increase and the increment of the internal energy is larger than the decrement of the vdW energy. The increment of the internal energy indicates that there exists the stress on the laterals of SWNTs due to the structure deformation of SWNTs. The decrement of the vdW energy indicates that the opposite walls of SWNTs have almost entered the strong-adhesive-binding region of the chemical bonds and the attractive vdW force exists between the opposite walls of the collapsed SWNT. When the system unloads the external pressure, the stress on the laterals of SWNTs must overcome the attractive vdW force primarily and then make the SWNT (10, 10) transition from a collapsed to circle shape. Therefore, the SWNT (10, 10) shows the hysteretic radial elasticity and its loading and unloading curve shapes are hysteresis loops.
Table 1 Energy details of cylindrical and collapsed SWNTs
| Chirality |
Energy (Kcal mol−1) |
Cylindrical SWNT (E1) |
Collapsed SWNT (E2) |
ΔE = E2 − E1 |
| (10, 10) |
Total energy |
1768.819 |
2974.537 |
1205.718 |
| Internal energy |
1256.938 |
2575.833 |
1318.895 |
| vdW energy |
511.881 |
398.704 |
−113.177 |
| Electrostatic energy |
0 |
0 |
0 |
III.II The effect of chirality on radial collapse of SWNTs
We first calculated Pc of the perfect SWNTs with different chiralities. The initial atomic configurations of periodic SWNTs were obtained by creating the planar hexagonal carbon atom network corresponding to a (n, m) SWNT cut open axially. The corresponding chiral angle θ and diameter Dn of a SWNT with (n, m) indices could be determined using the rolling graphene model:31| |  | (1) |
Where B is the C–C bond length. Each C–C bond length was 1.42 Å. The total number of atoms, diameters and lengths for each SWNT are presented in Table 2.
Table 2 Total number of atoms, diameter and length of each chiral nanotube utilized in MD simulations
| Type of SWNTs |
C
|
Nanotube (D) |
Length |
Angle |
| (10,10) |
1200 |
13.56 |
73.800 |
30.00 |
| (12, 8) |
1216 |
13.65 |
74.276 |
23.43 |
| (13, 7) |
1216 |
13.76 |
74.884 |
20.18 |
| (14, 5) |
1164 |
13.36 |
72.670 |
14.71 |
| (15, 4) |
1204 |
13.58 |
73.908 |
11.52 |
| (17, 0) |
1156 |
13.31 |
72.420 |
0.00 |
The chirality dependence of SWNT collapse has been studied, as shown in Fig. 2. The SWNTs with different chiralities and similar sizes were performed in the MD simulations. Fig. 2(a) shows the loading and unloading curves of the SWNTs with different chiralities as a function of applied hydrostatic pressure. We can find that except for the armchair SWNT the loading and unloading curves of SWNTs with other chiralities don't shape the hysteresis loops. This shows that the radial elasticity of the armchair SWNT is superior to that of the other chiral SWNTs. In other words, the collapse state of the SWNT (10, 10) is metastable; the collapse state of other chiral SWNTs is energetically favorable. As shown in Fig. 2(b), we can find that the Pc of SWNTs are as follows: Pc (10, 10) > Pc (12, 8) > Pc (13, 7) > Pc (14, 5) > Pc (15, 4) > Pc (17, 0) (Pc (n, m) denotes Pc of the SWNTs with chirality (n, m)). It shows that the SWNT chirality has much influence on the radial collapse of SWNTs. The Pc of the armchair SWNT is 13.75 times higher than that of the zigzag SWNT and is 2.5 times higher than that of the SWNTs with other chiralities. In addition, we can find that when θ is between 11.52° and 23.43°, the chirality has little influence on the collapse of SWNT, which is in agreement with the results reported before.29
 |
| | Fig. 2 Effect of different chiralities on the collapse of SWNTs. (a) Loading and unloading curves of SWNTs with different chiralities as a function of applied hydrostatic pressure and (b) collapse pressure Pc as a function of the SWNT chirality. | |
The energy difference ΔE of the cylindrical and collapsed SWNTs with different chiralities is shown in Table 3. We can find that the increment of internal energy of the SWNTs is less than the decrement of vdW energy of the SWNTs, except for SWNT (10, 10). In other words, upon unloading, the stress on laterals of collapsed SWNTs isn't strong enough to overcome the attractive vdW force between the opposite walls of the collapsed SWNTs; so the collapsed state of the chiral SWNTs, except for SWNT (10, 10), is energetically favorable. Therefore, the loading and unloading curves of the SWNTs, except for the SWNT (10, 10), don't shape hysteresis loops. For SWNT (10, 10), it has been shown that the loading and unloading curves of SWNT (10, 10) can shape a hysteresis loop in the former section, which indicates that the collapse state of SWNT (10, 10) is metastable. In other words, the radial elasticity of SWNT (10, 10) is superior to that of SWNTs with other chiralities.
Table 3 Energy difference of cylindrical and collapsed SWNTs with different chiralities
| ΔE (Kcal mol−1) |
(10, 10) |
(12, 8) |
(13, 7) |
(14, 5) |
(15, 4) |
(17, 0) |
| ΔE(vdW energy) |
−396.15 |
−738.032 |
−682.589 |
−719.117 |
−756.789 |
−710.265 |
| ΔE(internal energy) |
3888.388 |
657.833 |
682.445 |
683.452 |
750.759 |
689.504 |
III.III The effect of SW defects on the radial collapse of SWNTs
Topological defects, such as SW defects, are commonly present in CNTs, which play an important role in the load transfer in CNTs. In the following section, we study the effect of SW defects on the radial collapse of SWNT (10, 10) and SWNT (17, 0) with nearly equal radius and length. A SW defect can be formed by π/2 bond rotation in a graphene network, which transforms four hexagons into two pentagons and two heptagons, as shown in Fig. 3. Fig. 3 shows illustrations of armchair SWNT (10, 10) and zigzag SWNT (17, 0) with SW defects. The SW defects with different orientations are marked by SW1, SW2, SW3 and SW4 (the red carbon atoms represent the structure of a SW defect). The structural phase transition to a defective phase is eventually arrested by a defect–defect interaction at high defect density. Therefore, in our study the defect density is low enough that this interaction does not significantly disturb the onset of radial collapse. As shown in Fig. 3, in the model of SWNT (10, 10), there exists a SW defect in the length of ten cycles, for SWNT (17, 0) tube there exists a SW defect in the length of six cycles. In other words, the SW defects concentrations of SWNT (10, 10) and SWNT (17, 0) are 0.041 Å−1. MM simulations were performed to find the thermal stable morphology and achieve a conformation with minimum potential energy for SWNTs with SW defects.
 |
| | Fig. 3 Illustrations of armchair SWNT (10, 10) and zigzag SWNT (17, 0) with SW defects; the SW defects with different orientations are marked by SW1, SW2, SW3 and SW4 (the red carbon atoms represent the structure of a SW defect). | |
The radial collapse of SWNT (10, 10) and SWNT (17, 0) with SW defects was investigated using MD simulations. Fig. 4 shows the loading and unloading curves of the SWNTs without and with defects. We can find that the Pc of the intrinsic SWNT (10, 10), SWNT (10, 10) with the SW1 defect and SWNT (10, 10) with the SW2 defect are 5.5, 5.1 and 4.9 GPa, respectively, while the Pc of the intrinsic SWNT (17, 0), SWNT (17, 0) with the SW3 defect and SWNT (17, 0) with the SW4 defect are 0.4, 0.5 and 0.8 GPa, respectively. The results show that the armchair SWNT with SW defects is easy to collapse compared to the intrinsic armchair SWNT, while the zigzag SWNT with SW defects is difficult to collapse compared to the intrinsic zigzag SWNT; the SW2 defect makes Pc of SWNT (10, 10) decrease by 11.0%, while the SW4 defect makes Pc of SWNT (17, 0) increase by 100.0%, which indicates that the SW defect orientation has a large influence on the radial collapse of the SWNTs.
 |
| | Fig. 4 Loading and unloading curves of the SWNTs without and with SW defects. | |
III.IV The mechanism of radial collapse of SWNTs without and with SW defects
The ability of radial bending of SWNTs’ walls under the external force should be determined in order to understand the mechanism of radial collapse of SWNTs without and with SW defects under hydrostatic pressure. Herein, we introduce a model to understand the mechanism of the radial deformation of SWNTs. The model enables us to detect the chemical bonding topology unit of chiral graphene and define the projection of the C–C bond along the bending direction, which can be used to evaluate the collapse of SWNTs with and without SW defects.
It is well-known that the CNTs can be visualized as seamlessly rolled-up graphene sheets (ribbons); the topology units of CNT and graphene are the hexagon ring made up of six C–C bonds. Fig. 5(a) shows the atomic surface area partition of a chiral tube. This atomic surface area partition of a chiral tube can be regarded as the bending of graphene along the bending direction. The bending ability of the graphene sheet along the bending direction should determine the radial collapse character of SWNT. In addition, we find that the orientation of the hexagon ring is different along the bending direction and the z axis of the graphene sheet. As shown in Fig. 5(b), along the bending direction of graphene, we can find the topological unit of zigzag graphene in the armchair SWNT, and the topological unit of armchair graphene in the zigzag SWNT. We can investigate the mechanism of the chirality effect on the collapse of SWNT by studying the bending ability of chiral graphene sheets along the bending direction.
 |
| | Fig. 5 (a) Atomic surface area partition of a chiral tube and (b) six types of SWNTs with different chiralities along the z axis and six graphene chiralities along the bending direction (the red carbon atoms represent the structure of a hexagon ring). | |
Fig. 6(a) shows the structure of the chiral graphene sheet. It can be obtained by rotating armchair graphene degrees (θ) towards the right. Herein, θ is the chiral angle of graphene and the angles α, β and γ depend on the chiral angle. We define L as the projection of six C–C bonds in a hexagon ring along the bending direction.
 |
| | Fig. 6 (a) The structure of the chiral graphene sheet; (b) change of L following the change of the SWNT chirality. | |
| | |
L = 2B(cosα + sinβ + cosγ)
| (2) |
| | |
α = θ + 30°, β = θ, γ = 30° − θ
| (3) |
| |

| (4) |
The magnitude of
L represents the obstacle that needs to be overcome in the bending process of
graphene. In other words, the larger
L is, the more difficult it is for
graphene to bend.
With the chiral angles θ, we can calculate the project vertical to the bending direction of six C–C bonds in graphene sheet as shown in Table 4. Therefore, we can obtain the change of L following the change of the SWNT chirality, as shown in Fig. 6(b). We can find that the values of L are as follows: L(10,10) > L(12,8) > L(13,7) > L(14,5) > L(15,4) > L(17,0) (L (n,m) denotes L of SWNTs with chirality (n,m)). These results show that the zigzag SWNT is the easiest to bend and collapse, while armchair SWNT is the most difficult to bend and collapse. Moreover, a similar phenomenon is also found in other research.32 We can find that the structural transition law of SWNTs with different chiralities predicted by the model is in accordance with the results of MD simulations, which suggests that the effect of chirality on the radial collapse of SWNTs can be understood by the present model.
Table 4 Projection vertical to the bending orientation of six C–C bonds
| SWNT |
(17, 0) |
(15, 4) |
(14, 5) |
(13, 7) |
(12, 8) |
(10, 10) |
| Graphene |
armchair (30) |
11.52 |
14.71 |
20.18 |
23.43 |
zigzag (0) |
|
α (°) |
30 |
41.52 |
44.71 |
50.18 |
53.43 |
60 |
|
β (°) |
0 |
11.52 |
14.71 |
20.18 |
23.43 |
30 |
|
γ (°) |
30 |
18.48 |
15.29 |
9.82 |
6.57 |
0 |
|
L
|
4.9190 |
5.3871 |
5.4789 |
5.5968 |
5.6427 |
5.6800 |
The sp2-hybridized carbon atoms can arrange themselves into a variety of different polygons, not only hexagons, but also different structures, such as pentagons and heptagons.33 Therefore, we can proceed to apply the present model to SWNTs with SW defects. The chemical bonding topology of the graphene with SW defects can be detected and used to reveal the physical mechanisms of radial collapse of the SWNTs with SW defects. The SWNT with SW defects can be visualized as seamlessly rolled-up graphene sheets with SW defects along the bending direction. The collapse process of the SWNT with SW defects can be considered to be the bending process of the graphene nanoribbon with SW defects. Herein, in order to study the influence of SW defects on the radial collapse of SWNTs, we calculate the L of all C–C bonds in a SW defect and compare them to that of all C–C bonds in four hexagons transformed due to the same sp2-hybridization of the hexagons, pentagons and heptagons.
Fig. 7 shows the atomic networks of four hexagons transformed and generated SW defects in SWNTs; we can obtain the structure b, c, d (2, 3, 4) by rotating structure a (1) degrees (ϕ) towards the right. Fig. 8 shows the bond lengths and bond angles in the SW defect structure. We marked five kinds of bond length for b1, b2, b3, b4, b5 and five kinds of bond angle for α, β, γ, φ, θ in the structure of the SW defect. So, the general formulas for L of the four hexagons transformed and the generated SW defects along bending direction can be followed as
| |  | (5) |
| | 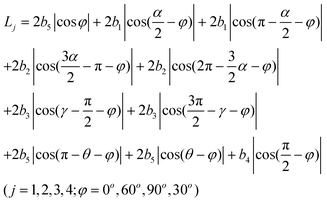 | (6) |
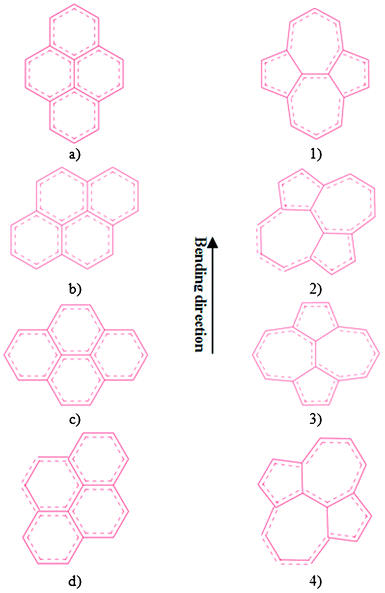 |
| | Fig. 7 Atomic networks of four hexagons transformed and generated SW defects. (a,1) Structures of four hexagonsa and generated a SW1 defect in SWNT (10, 10), (b, 2) structures of four hexagonsb and generated a SW2 defect in SWNT (10, 10), (c, 3) structures of four hexagonsc and generated a SW3 defect in SWNT (17, 0), and (d, 4) structures of four hexagonsd and generated a SW4 defect in SWNT (17, 0). | |
 |
| | Fig. 8 (a) Lengths of C–C bonds (bond lengths) in the SW defect structure and (b) angles between C–C bonds (bond angles) in the SW defect structure. | |
Herein, we marked the L of four hexagonsa and SW1 defects in SWNT (10, 10) for La, L1; marked L of four hexagonsb and SW2 defects in SWNT (10, 10) for Lb, L2; marked L of four hexagonsc and SW3 defect in SWNT (17, 0) for Lc, L3 and marked L of four hexagonsd and SW4 defect in SWNT (17, 0) for Ld, L4. We can calculate the La, L1, Lb, L2, Lc, L3, Ld, L4 for 18.46 Å, 18.25 Å, 17.75 Å, 16.96 Å, 14.76 Å, 15.20 Å, 15.99 Å, 17.44 Å; and it shows La > L1, Lb > L2 and Lc < L3, Ld < L4. It indicates that the SW defects have much influence on the collapse of SWNTs. Moreover, these results show that the SWNT (10, 10) with SW defects is easy to collapse compared to intrinsic SWNT (10, 10), while the SWNT (17, 0) with SW defects is difficult to collapse compared to intrinsic SWNT (17, 0). Fig. 9 shows illustrations of collapsed SWNT (10, 10) with a SW2 defect and collapsed SWNT (17, 0) with a SW4 defect. We can find that the collapse of SWNT (10, 10) easily happens at the local defect, while the collapse of SWNT (17, 0) easily happens at the planar hexagons. It once again proves that the SWNT (10, 10) with SW defects is easier to collapse compared to intrinsic SWNT (10, 10), while the SWNT (17, 0) with SW defects is more difficult to collapse compared to intrinsic SWNT (17, 0). In addition, we can calculate that (L4 − Ld)/Ld (8.6%) > (L3 − Lc)/Lc (2.9%) and (Lb − L2)/Lb (4.5%) > (La − L1)/La (1.1%). It shows that the influence of the SW defect orientation on the collapse of SWNT (17, 0) is larger than that of the SW defect orientation on the collapse of SWNT (10, 10), which is agreement with the third section's results. According to the discussion above, the variation trend of Pc predicted using this model for SWNTs with and without SW defects is in accordance with the results of MD simulations. The effect of chirality and SW defect on the radial collapse of SWNTs can be understood by the model proposed.
 |
| | Fig. 9 Illustrations of the SWNT (10, 10) with a SW2 defect, SWNT(17, 0) with a SW4 defect, collapsed SWNT (10, 10) with a SW2 defect and collapsed SWNT (17, 0) with a SW4 defect (the red carbon atoms represent the structure of a SW defect). | |
Conclusions
In this study, we investigated the effects of CNT chirality, SW defects and defect orientation on the radial collapse and elasticity of SWNTs using MM and MD simulations. It is found that the Pc of the armchair SWNT is 13.75 times higher than that of the zigzag SWNT. Moreover, the armchair SWNT with SW defects is easier to collapse compared to the intrinsic armchair SWNT, while the zigzag SWNT with SW defects is more difficult to collapse compared to the intrinsic zigzag SWNT; the SW2 defect makes Pc of SWNT (10, 10) decrease by 11.0%, while the SW4 makes Pc of SWNT (17, 0) increase by 100.0%. We introduced a model for SWNTs deformed in the radial direction according to the projection of the C–C bond along the bending direction. The model is validated for defect-free SWNTs and is then used to study the radial collapse of SWNTs with SW defects. The effect of chirality and SW defects on the radial collapse of SWNTs can be understood by the model. The strong sensitivity of radial collapse of SWNTs to chirality and SW defects can provide some guidance for high load structural application of SWNTs.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (10974258), the Fundamental Research Funds for the Central Universities (11CX05002A, 11CX0460A) and the Natural Science Foundation of Shandong Province (ZR2010AL009, ZR2011AL023).
References
- S. Lijima, Nature, 1991, 354, 56–58 CrossRef.
- P. Poncharal, Z. L. Wang, D. Ugarte and W. A. De Heer, Science, 1999, 283, 1513–1516 CrossRef CAS.
- C. Y. Li and T. W. Chou, Int. J. Solids Struct., 2005, 40, 2487–2499 CrossRef.
- M. F. Yu, O. Lourie, M. J. Dyer, K. Moloni, T. F. Kelly and R. S. Ruoff, Science, 2000, 287, 637–640 CrossRef CAS.
- B. I. Yakobson, M. P. Campbell, C. J. Brabec and J. Bernholc, Comput. Mater. Sci., 1997, 8, 341–348 CrossRef CAS.
- M. Zhang, K. R. Atkinson and R. H. Baughman, Science, 2004, 306, 1358–1361 CrossRef CAS.
- K. Suggs and X. Q. Wang, Nanoscale, 2010, 2, 385–388 RSC.
- A. Laachachi, A. Vivet, G. Nouet, B. B. Doudou, C. Poilane, J. Chen, J. Bo Bai and M. Ayachi, Mater. Lett., 2008, 62, 394–397 CrossRef CAS.
- A. Vivet, B. B. Doudou, C. Poilane, J. Chen and M. Ayachi, J. Mater. Sci., 2011, 46, 1322–1327 CrossRef CAS.
- R. Zhu, E. Pan and A. K. Roy, Mater. Sci. Eng., A, 2007, 447, 51–57 CrossRef.
- J. Gou, B. Minaie, B. Wang, Z. Liang and C. Zhang, Comput. Mater. Sci., 2004, 31, 225–236 CrossRef CAS.
- H. D. Wagner, Chem. Phys. Lett., 2002, 361, 57–61 CrossRef.
- J. A. Rodríguez-Manzo, A. Tolvanen, A. V. Krasheninnikov, K. Nordlund, A. Demortière and F. Banhart, Nanoscale, 2010, 2, 901–905 RSC.
- T. W. Ebbesen and T. Takada, Carbon, 1995, 33, 973–978 CrossRef CAS.
- B. I. Yakobson, C. J. Brabec and J. Bernholc, Phys. Rev. Lett., 1996, 76, 2511–2514 CrossRef CAS.
- N. Chandra, S. Namilae and C. Shet, Phys. Rev. B, 2004, 69, 094101 CrossRef.
- Y. Miyamoto, A. Rubio, S. Berber, M. Yoon and D. Tomanek, Phys. Rev. B, 2004, 69, 121413(R) CrossRef.
- X. Huang, H. Y. Yuan, K. J. Hsia and S. Zhang, Nano Res., 2010, 3, 32–42 CrossRef CAS.
- S. L. Mielke, D. Troya, S. Zhang, J. L. Li, S. Xiao, R. Car, R. S. Ruoff, G. C. Schatz and T. Belytschko, Chem. Phys. Lett., 2004, 390, 413–420 CrossRef CAS.
- Q. Lu and B. Bhattacharya, Nanotechnology, 2005, 16, 555–566 CrossRef CAS.
- K. Talukdar and A. K. Mitra, Compos. Struct., 2010, 92, 1701–1705 CrossRef.
- J. R. Xiao, J. Staniszewski and J. W. Gillespie Jr, Compos. Struct., 2009, 88, 602–609 CrossRef.
- K. Y. Yan, Q. Z. Xue, D. Xia, H. J. Chen, J. Xie and M. D. Dong, ACS Nano, 2009, 3, 2235–2240 CrossRef CAS.
- J. Xie, Q. Z. Xue, H. J. Chen, D. Xia, C. Lv and M. Ma, J. Phys. Chem. C, 2010, 114, 2100–2107 CAS.
- H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- Q. Wang, W. H. Duan, K. M. Liew and X. Q. He, Appl. Phys. Lett., 2007, 90, 033110 CrossRef.
- Q. Wang, Nano Lett., 2009, 9, 245–249 CrossRef CAS.
- J. A. Elliott, J. K. W. Sandler, A. H. Windle, R. J. Young and M. S. P. Shaffer, Phys. Rev. Lett., 2004, 92, 095501 CrossRef.
- X. P. Yang, G. Wu and J. M. Dong, Appl. Phys. Lett., 2006, 89, 113101 CrossRef.
- M. Al-Haik, M. Y. Hussaini and H. Garmestani, J. Appl. Phys., 2005, 97, 074306 CrossRef.
- L. Y. Chu, Q. Z. Xue, T. Zhang and C. C. Ling, J. Phys. Chem. C, 2011, 115, 15217–15224 CAS.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.