Impact of point defects on electronic structure in Y₂Ti₂O₇

Abstract

With many technologies and applications downscaling to nanometer dimensions, the influence of single point defects on electronic structure has shown an increasingly profound impact on optical and electrical properties, and advancing fundamental understanding is critical to defect engineering and control of materials properties. In the present study, first-principles calculations based on density functional theory (DFT) are carried out to study the effects of Ti point defects on the electronic structure of Y₂Ti₂O₇. In the literature, it has been demonstrated that conventional DFT tends to produce delocalized holes and electrons in defective oxide materials due to insufficient cancellation of the self-interaction energy and underestimation of the band gap, which results in an incorrect description of the electronic structure of the system. In an effort to better understand the accuracy of DFT in describing the behavior of Y₂Ti₂O₇ with point defects, the calculated results obtained from DFT and DFT+U methods are compared, including the geometrical distortion, the localization of the defect states and the position of the defect levels in the band gap. Using DFT, distorted geometries around the Ti vacancy and interstitial are found, along with localized oxygen holes and Ti electrons, both of which compare well with the DFT+U results, suggesting that the conventional DFT can be used to describe the localization of the Ti defects in Y₂Ti₂O₇. One major difference in the DFT and DFT+U calculations is the energy position of the defect levels, for which DFT+U results in the states positioned deep in the band gap. Since the DFT+U method suffers from the dependence of the results on the empirical parameter U and no experimental results on the energy position of the defect states are available to tune this U value, care must be taken in applying DFT+U to electronic structure calculations of Y₂Ti₂O₇ with point defects. Based on the DFT method, the most preferred charge state is determined by the formation energies for charged point defects. Moving the Fermi level across the band gap has slight effects on the charge state, and the Ti vacancy and interstitial are found to be in −4 and +4 charge states, respectively.

---

Introduction

Intrinsic and extrinsic point defects in semiconductors are of crucial importance in determining the optical and electrical properties of materials.¹ As key properties of defects, the formation energies, charge states, donor and acceptor levels, optical transition energies and migration energies for defects in numerous semiconductors have gained significant attention.^2–6 In particular, the electronic states in the valence or conduction bands, which are induced by defects, may trap charge carriers and influence the electronic structure of materials.⁶ Fundamental knowledge of the electronic structure in the presence of point defects is, thus, very important to understanding the properties and performance of materials.

As important host matrix materials for the immobilization of actinides,^7,8 the radiation behavior of pyrochlores has been extensively studied, both experimentally and theoretically.^9–12 It has been reported that all the titanate pyrochlores undergo irradiation-induced amorphization, while zirconate pyrochlores are more resistant to irradiation and transform to the disordered defect-fluorite structure, which is extremely stable under irradiation, with the exception of La₂Zr₂O₇.^12–14 Chartier et al. have demonstrated by molecular dynamics simulations that point defects, such as split interstitials, play a key role in the irradiation response of pyrochlores.⁹ In order to explain the different response behavior of pyrochlores to irradiation, a number of theoretical calculations of defect formation energies and electronic structures of ideal pyrochlores have been carried out;^15–21 however, the effects of the intrinsic and extrinsic point defects on the electronic structures of pyrochlores, a critical step to understanding the underlying mechanisms, are not yet well understood.

Y₂Ti₂O₇ is an important member of the pyrochlore family,^22,23 which has also demonstrated potential applications as a photocatalyst for water splitting, a host material for efficient Er³⁺ luminescence, and an oxygen-ion conductor.^24–26 It has been reported in the literature that doping Y₂Ti₂O₇ with Ca²⁺ improves the oxygen ionic conductivity, and the defect site created by Ca²⁺ plays an important role in oxygen migration.^24,27 Therefore, studies of the electronic structure of Y₂Ti₂O₇ containing point defects not only contribute to better understanding the pyrochlore behavior under irradiation, but also provide a fundamental insight into controlling the ionic and electronic conductivity of pyrochlores. In the present work, we use Y₂Ti₂O₇ as a model system for pyrochlores, because of its technological importance and its simple electronic structure, to investigate the electronic structures associated with point defects in the bulk phase.

In the literature, there has been an intensive debate on the calculational method for the electronic structures of defective titania (TiO₂) in its bulk and surface states. Na-Phattalung et al.²⁸ have studied point defects in anatase titania using the standard DFT method, and the prediction of delocalized defect states was inconsistent with the localized polaronic²⁹ description from experimental data.³⁰ The existence of a rather broad gap state lying about 0.8 eV below the conduction band edge in reduced rutile titania, as revealed by ultraviolet photoelectron spectroscopy and electron energy loss spectroscopy experiments,^31,32 also cannot be described by conventional DFT. Some examples have been reported to illustrate the difficulty of applying DFT to describe defect properties in other insulators.³³ Due to the inability to properly describe localized defect states in oxides, it is generally thought that one needs to go beyond conventional DFT. The two most common schemes to circumvent the deficiency with DFT are the use of hybrid functionals³⁴ and the DFT+U method.³⁵ In recent years, these two methods have been widely employed to investigate defects in titania,^36–40 and the experimental results are well described. The hybrid functionals and DFT+U methods improve the description of electronic structures, but suffer from the use of “empirical” parameters. In the hybrid DFT, a degree of exact exchange is introduced by mixing DFT and Hartree Fock; in DFT+U, a Hubbard U correction, which represents an on-site Coulomb repulsion among selected orbitals,⁴¹ is added. Very recently, by using resonant photoelectron diffraction, Krüger et al.⁴² showed that the defect charge of reduced TiO₂(110) surfaces is delocalized over several surface and subsurface Ti sites, which agrees well with the standard DFT calculations,⁴³ but is at odds with the calculation of Valentin et al.⁴⁴ who used the B3LYP hybrid functional. These extensive debates, thus, suggest that we must be cautious to choose appropriate calculational methods to describe the electronic structure of defective system.

In the present study, both standard DFT and DFT+U methods are employed to study the electronic structure of Y₂Ti₂O₇ with a Ti vacancy, interstitial or Frenkel pair. Our main aims are to investigate the impact of point defects on the electronic structure, and to analyze the response of two different methods in the presence of the same defect. In particular, we will focus on the local distortion around the defect, the spin localization, spin distribution and the position of the defect states in the gap.

Computational details

The density functional calculations are performed with the Vienna Ab Initio Simulation Package (VASP).^45,46 A plane-wave basis set with a cutoff energy of 450 eV is employed to describe the electronic wave function. For both DFT and DFT+U, the ionic potentials are described by projector augmented-wave pseudopotentials, and the exchange–correlation energies are treated using the generalized gradient approximation (GGA) parameterized by Perdew and Wang,⁴⁷ with spin-polarized effects considered. In the DFT+U calculations, the approach of Dudarev et al.⁴⁸ is employed, by which the effective U values of 5.25 eV for O 2p, and 4.2 eV for Ti 3d, as suggested by Morgan and Watson³⁷ for defective titania, are used. Computations are based on a supercell consisting of 88 atoms with a 4 × 4 × 4 k-point sampling in reciprocal space. To verify that the 88-atom supercell is adequate to neglect the interaction between defects due to the periodic boundary condition, simulations with a larger supercell consisting of 176 atoms are performed. The difference in formation energies for a Frenkel pair between the two cells is 0.08 eV, demonstrating that the 88-atom supercell is adequate. Structural optimizations are carried out at variable cell shape and volume, as well as under the condition that the Hellmann–Feynman force on each atom should be smaller than 0.01 eV Å⁻¹.

Results and discussion

In A₂B₂O₆O′ pyrochlore (see Fig. 1 in reference⁴⁹), A, B, O and O′ atoms occupy 16d (1/2, 1/2, 1/2), 16c (0, 0, 0), 48f (x, 1/8, 1/8) and 8b (3/8, 3/8, 3/8), respectively. The site of the missing oxygen that could complete the anion sublattice to form a fluorite structure is 8a (1/8, 1/8, 1/8). The pyrochlore structure can be described by the lattice constant a₀ and the internal parameter x for the O_48f positions. The optimized a₀ and x_O48f for Y₂Ti₂O₇ are 10.11 Å and 0.3301, respectively, which agree well the experimental values of 10.1 Å and 0.330.¹²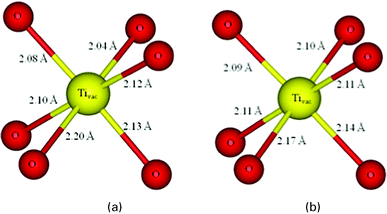

Fig. 1 The local geometrical structure around the Ti vacancy in Y₂Ti₂O₇ obtained from (a) DFT and (b) DFT+U methods.

We first study the electronic structure of Y₂Ti₂O₇ with a Ti vacancy (Ti_vac), which is created by removing one Ti atom from the supercell. In defective TiO₂, it has been demonstrated that the electron delocalization predicted by DFT is connected to the symmetric structure around the defect, and only DFT+U or hybrid DFT can achieve the correct asymmetric structure for the electron localization.³⁹ In the case of Y₂Ti₂O₇, the local geometrical structures around the Ti vacancy obtained by DFT and DFT+U methods are shown in Fig. 1(a) and (b), respectively. In bulk Y₂Ti₂O₇, the Ti atom is six-coordinated to O_48f atoms in a distorted octahedron with a bond length of ∼1.96 Å. When this atom is removed, the nearest neighboring O atoms are displaced outward by ∼0.15 Å from the vacancy site as a result of the effective negative charge state of the vacancy site interacting repulsively with the nearby anions. Different from the case of defective TiO₂,^38,39 both DFT and DFT+U predict the structural distortion around the Ti vacancy in Y₂Ti₂O₇, with an average <Ti_vac–O> bond length difference of 0.008 Å, suggesting that in Y₂Ti₂O₇ with a Ti_vac the structural deformation around the defect is independent of the choice of the functional. Bader charge analysis shows that the electron population of the six O atoms surrounding the Ti vacancy dramatically decreases from the bulk value of ∼1.23 |e| to ∼0.99 |e|, indicating the gain of electrons by the Ti vacancy and the negative character of its charge state. These findings are consistent with theoretical calculations of cation vacancies in other semiconductors such as ZnO, TiO₂ and UO₂,^2,4,50 in which the cation vacancies are suggested to be acceptor-type defects and are negatively charged.

The density of state (DOS) distributions for Y₂Ti₂O₇ containing a Ti_vac are plotted in Fig. 2. Fig. 2(a) presents the total DOS obtained by DFT. Bulk Y₂Ti₂O₇ has a direct band gap with an energy of 2.75 eV, which is smaller than the experimental value of 3.12 eV.⁵¹ It appears that the creation of a Ti vacancy affects the valence band structure of bulk Y₂Ti₂O₇ by shifting the Fermi level from the bulk value of 3.26 eV to a value of 2.86 eV and creating p-type doping characteristics. However, such character cannot be reproduced by the DFT+U method, since the Fermi level shifts to a slightly higher energy level, indicating that the on-site Coulomb interaction is overcorrected. The partial DOS shows that the defect levels are mainly contributed by the O atoms surrounding the Ti vacancy. These states are partially occupied and unoccupied, indicating that the negative charge state at the vacancy site is not strong enough to hold all the electrons locally. Application of Hubbard U correction, on the other hand, leads to splitting of these two states and pushing one state to reside deep in the band gap. Obviously, the energy position of the defect level significantly depends on the method employed. Unfortunately, there are no experimental data available in the literature to exactly determine the energy level of the defect state and to adjust the effective U value in DFT+U.

Fig. 2 Density of state (DOS) distribution for Y₂Ti₂O₇ with the Ti vacancy. (a) Total DOS compared with that for the bulk phase obtained by DFT. (b) Total DOS compared with that for the bulk phase obtained by DFT+U. (c) Site-projected partial DOS for the oxygen atom obtained by DFT. (d) Site-projected partial DOS for the oxygen atom obtained by DFT+U. E_F indicates the Fermi level. Near O: one of the oxygen atoms neighboring the Ti vacancy site; lattice O: one of the oxygen lattice atoms far from the vacancy site.

In order to further shed light on the performance of DFT in describing the electronic structure of Y₂Ti₂O₇ containing a Ti_vac, we analyze the spin density for the Ti vacancy defect state. The spin densities obtained by DFT and DFT+U are shown in Fig. 3(a) and (b), respectively. Interestingly, the DFT method predicts that the hole states induced by the Ti vacancy correspond to polarons at six oxygen atoms surrounding the Ti vacancy and the defect states are mainly localized on these oxygen atoms rather than delocalized over the whole system, different from the case of defective titania.^38,39 This agrees well with the DFT+U results, although DFT+U leads to a stronger localization. These results indicate that conventional DFT describes well the localization of the Ti vacancy defect in Y₂Ti₂O₇.

Fig. 3 Spin density for the Ti vacancy defect state inY₂Ti₂O₇ obtained by (a) DFT and (b) DFT+U. The charge isosurface is shown at 0.006 e Å⁻³.

The Ti interstitial is another important point defect in titanate pyrochlores. Our previous study¹⁰ has shown that the vacant 8a site, the bridge site between two neighboring cations along the <010> direction and the split interstitial along the <111> direction are degenerate in energy, forming stable cation interstitial configurations with low formation energies of 1.2 eV. In the present study, only the Ti interstitial occupying the vacant 8a site is considered (Ti_8a). The total density of states for Y₂Ti₂O₇ with and without the Ti interstitial, as obtained by DFT, is compared in Fig. 4(a). In contrast to the case of the Ti vacancy, the existence of a Ti interstitial induces a defect state near the conduction band rather than the valence band, which is predominantly of Ti 3d character. The Fermi level shifts from the bulk value of 3.26 eV to 5.85 eV and is located just above the conduction band, resulting in n-type doping of Y₂Ti₂O₇. In nonstoichiometric TiO_2−x, the electrons donated by the octahedral Ti interstitial are also found to transfer to conduction bands as free carriers.⁵²Fig. 4(c) presents the site-projected partial density of states for the interstitial Ti and the Ti atoms near and far from the interstitial site. It is shown that both the Ti interstitial and its surrounding Ti atoms contribute to the defect level. The DFT+U results, as shown in Fig. 4(b) and (d), also predict the n-type character of the Ti interstitial, and the contribution of the Ti interstitial and its Ti neighbors to the defect states. The primary difference between DFT and DFT+U calculations is that the defect states are partially occupied and unoccupied by DFT, while DFT+U leads to a complete occupation of the defect states. Also, the defect levels obtained by DFT+U are further away from the bottom of the conduction band.

Fig. 4 Density of state (DOS) distribution for Y₂Ti₂O₇ with the Ti interstitial. (a) Total DOS compared with that for the bulk phase obtained by DFT. (b) Total DOS compared with that for the bulk phase obtained by DFT+U. (c) Site-projected partial DOS for the titanium atom obtained by DFT (different scales are used for the ordinate in the two regions divided by the dash-dot line for clarity). (d) Site-projected partial DOS for the titanium atom obtained by DFT+U. E_F indicates the Fermi level. Near Ti: one of the Ti atoms neighboring the Ti interstitial site; lattice Ti: one of the Ti lattice atoms far from the interstitial site.

In pyrochlores, the 8a site is a vacant anion site, which interacts with four Ti neighbors. Fig. 5 illustrates the local geometrical structure around the Ti_8a obtained from DFT and DFT+U methods. Unexpectedly, DFT+U predicts a relatively more symmetric local structure than DFT, with a difference of 0.008 Å in the average bond length. The difference in the symmetry of the local structure may lead to a different net spin of the defective system. The spin density for Ti_8a defect state inY₂Ti₂O₇ obtained by DFT and DFT+U methods are shown in Fig. 6(a) and (b), respectively. The Ti_8a introduces four excess electrons. Both DFT and DFT+U predict that the excess electrons are mainly localized on the Ti interstitial and their four neighboring Ti atoms, even though the spin distribution is slightly different. The total magnetic moments are predicted to be 1.74 and 1.78 μB by DFT and DFT+U, respectively. Bader charge analysis shows that the electron population of these four Ti neighbors decreases from the bulk value of ∼2.20 |e| to ∼1.95 |e|, and the Bader charge for the interstitial is ∼1.44 |e|, which also suggests that local charge transfer from the Ti interstitial to its Ti neighbors occurs from the introduction of excess electrons by the Ti interstitial. After structural relaxation, the repulsive interaction between the positive Ti interstitial and its neighboring cations push the Ti neighbors outward from the interstitial site by ∼0.27 Å. The Ti interstitial also interacts with six neighboring oxygen atoms with a bond distance of ∼2.06 Å, which is ∼0.1 Å larger than that between the lattice Ti and its oxygen neighbors, even though the Bader charge for the oxygen atoms changes less than ∼0.03 |e|.

Fig. 5 The local geometrical structure around the Ti_8a in Y₂Ti₂O₇ obtained from (a) DFT and (b) DFT+U methods.

Fig. 6 Spin density for the Ti_8a defect state inY₂Ti₂O₇ obtained by (a) DFT and (b) DFT+U. The charge isosurface is shown at 0.006 e Å⁻³.

Under irradiation, Ti occupation at the 8a site is accompanied by the creation of a Ti vacancy,¹⁰ and the effects of the simultaneous presence of both point defects on the electronic structure of Y₂Ti₂O₇ remain unknown. We thus further consider Ti Frenkel pairs consisting of a Ti_8a interstitial and a Ti vacancy that is either the first- or second-neighbor of the Ti_8a. The separation distance for these two types of Frenkel pairs are 4.37 and 5.35 Å, respectively. For Ti_8a with a first-neighbor Ti vacancy, the configuration is unstable and recombination occurs upon structural relaxation. The second Frenkel pair is stable and the following discussions are based on its optimized geometries. A comparison of the total density of states for Y₂Ti₂O₇ with Ti_8a+Ti_vac and bulk Y₂Ti₂O₇ is shown in Fig. 7(a). In the case of the individual Ti vacancy and interstitial, the defect states affect their respective valence and conduction band, which shifts the Fermi level to lower and higher energy values by 0.4 and 2.59 eV, respectively. For the Ti Frenkel pair, the Fermi level shifts to lower energy value by only 0.09 eV, and defect states appear at the bottom of the conduction band, showing a compromise between the influences of individual vacancy and interstitial on valence and conduction bands. This results in a reduction of the energy gap by 0.33 eV between the highest occupied and lowest unoccupied states. The site-projected partial density of states for the oxygen and Ti atoms near and far from the Frenkel pair site are shown in Fig. 7(c) and (e). It can be seen that the oxygen atoms around the Ti vacancy and the Ti interstitial behave somewhat differently from the lattice O and Ti atoms, and both contribute to the defect states. The Bader charge for the nearest neighboring O atoms is about 0.12 |e| larger than that for the lattice O, which is half the value for Y₂Ti₂O₇ containing an individual Ti vacancy. As for the Ti atoms surrounding the Ti interstitial, the Bader charge difference between them and the lattice Ti atom is only 0.09 |e|, indicating weak interactions between the Ti interstitial and its neighboring Ti atoms. The electron population for the Ti interstitial is 1.88 |e|, which leads to strong interaction between it and the neighboring oxygen atoms. DFT+U, on the other hand, shifts the Fermi level to a higher energy value by 0.08 eV, and completely localizes the defect state. When considering the concomitant presence of the Ti vacancy and interstitial, there are no excess electrons. Thus, internal charge transfer from the Ti interstitial to the oxygen holes neighboring the Ti vacancy defect occurs independently of the exchange-functional employed.

Fig. 7 Density of state (DOS) distribution for Y₂Ti₂O₇ with the Ti Frenkel pair. (a) Total DOS compared with that for the bulk phase obtained by DFT. (b) Total DOS compared with that for the bulk phase obtained by DFT+U. (c) Site-projected partial DOS for the oxygen atom obtained by DFT. (d) Site-projected partial DOS for the oxygen atom obtained by DFT+U. (e) Site-projected partial DOS for the titanium atom obtained by DFT (different scales are used for the ordinate in the two regions divided by the dash-dot line for clarity). (f) Site-projected partial DOS for the titanium atom obtained by DFT+U. E_F indicates the Fermi level. Near O: one of the oxygen atoms neighboring the Ti vacancy site; lattice O: one of the oxygen lattice atoms far from the vacancy site; near Ti: one of the Ti atoms neighboring the Ti interstitial site; lattice Ti: one of the Ti lattice atoms far from the interstitial site.

Electrons or holes associated with a given defect can be localized or delocalized depending on the character of the defect, the nature of the host material, and the degree of local polaronic distortion following the formation of the defect.³⁹ For systems like defective titania and Al-doped silica,⁵³ conventional DFT fails to describe the structural deformation around the defect and the localization of the defect state; however, in our case, the local structure and the spin localization around the defect obtained from DFT and DFT+U are very similar to each other. What is most affected by the choice of the functional used is the relative position of the defect states. This raises a question about to what extent the Coulomb interaction should be corrected by DFT+U. Unfortunately, experimental investigations of the point defects in Y₂Ti₂O₇ are scarce in the literature, and no data are available for comparison. Hence, experimental measurements are needed to unravel the position of the defect levels and to tune the U value in DFT+U.

To determine the relative stability of the point defects discussed above, the defect formation energies for the Ti vacancy and interstitial (charge states from −4 to +4) are calculated by a DFT method. The formation energy is defined by E_f = E_def−E_perfect + n_iμ_Ti + q(E_VBM + E_F).⁵ Here, E_def and E_perfect are the total energies of the supercell with and without a defect, respectively, n_i is the number of atoms being removed or added, and μ_Ti is the chemical potential of Ti. The value of μ_Ti is obtained under Ti-rich conditions, i.e., , where is the total energy of the Ti atom in its bulk state. E_F is the Fermi level of the system. 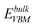E_VBM is the energy at the valence band maximum, which is adjusted by , where is the energy cost in removing one electron from the perfect supercell and ΔV is the averaged difference between the local potentials far from the defects in the defective supercell and the corresponding ones in the perfect supercell. The additional charge q is set by adding or removing electrons from the supercell.

The formation energies for the Ti vacancy and interstitial are plotted as a function of the position of the Fermi level in the band gap in Fig. 8. The Fermi level at the valence band maximum and at the conduction band bottom is set to 0 and 2.8 eV, respectively. It appears that the lowest formation energies for the Ti vacancy and interstitial correspond principally to the −4 and +4 charge states, respectively, except when the Fermi level is very close to the valence or conduction bands, suggesting that the Ti vacancy and interstitial are acceptor- and donor-type defects, respectively. The formation energy for the Frenkel pairs is defined as the sum of the formation energies of a Ti vacancy (q charge state) and a Ti interstitial (−q charge state).⁴ The association of a negatively charged vacancy and a positively charged interstitial is preferred over the association of neutral defects, and the tetravalent vacancy and interstitial have the lowest formation energy. For the neutral vacancy and interstitial, the formation energies compare well with previous theoretical calculations.¹⁰

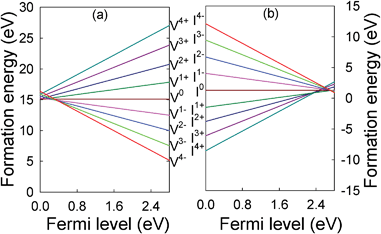Fig. 8 Formation energies for the (a) Ti vacancy and (b) Ti interstitial in different charge states in Y₂Ti₂O₇ as a function of the Fermi level.

Conclusions

In summary, the electronic structure of Y₂Ti₂O₇ with point defects has been studied by DFT and DFT+U methods. The presence of point defects alters the electronic structure of Y₂Ti₂O₇. By conventional DFT, the creation of a Ti vacancy (or interstitial) affects the valence (or conduction) band structure of the bulk Y₂Ti₂O₇, exhibiting characteristics of p-type (or n-type) doping of Y₂Ti₂O₇. However, the p-type character induced by a Ti vacancy cannot be reproduced by DFT+U due to overcorrection of the on-site Coulomb interaction. Both methods give a similar description of stability, local structure and spin localization for Ti defects, while the position of the defect states depends on the method employed. Experimental measurements are needed to determine the precise position of the defect levels. The Ti vacancy and interstitial act as acceptor and donor defects with corresponding negative and positive charge states, respectively. These findings will serve as a basis to advance the understanding of defect-driven phenomena related to irradiation effects, ionic and electronic conductivities, and photocatalytic activities of pyrochlores.

Acknowledgements

This work was supported by the U.S. Department of Energy, Basic Energy Sciences, Materials Science and Engineering Division. The theoretical calculations were performed using the supercomputer resources at the Environmental Molecular Science Laboratory located at Pacific Northwest National Laboratory. Dr Xiao also acknowledges the partial support of the National Natural Science Foundation of China (Grant No. 11004023), and the Scientific Research Foundation for Returned Overseas Chinese Scholars, State Education Ministry during the initial phases of this study.

References

1. M. Nolan, S. D. Elliott, J. S. Mulley, R. A. Bennett, M. Basham and P. Mulheran, Phys. Rev. B, 2008, 77, 235424.
2. F. Oba, M. Choi, A. Togo and I. Tanaka, Sci. Technol. Adv. Mater., 2011, 12, 034302.
3. A. S. Foster, F. L. Gejo, A. L. Shluger and R. M. Nieminen, Phys. Rev. B, 2002, 65, 174117.
4. J.-P. Crocombette, D. Torumba and A. Chartier, Phys. Rev. B, 2011, 83, 184107.
5. J.-C. Wu, J. Zheng, P. Wu and R. Xu, J. Phys. Chem. C, 2011, 115, 5675.
6. M. J. Puska, J. Phys.: Condens. Matter, 1989, 1, 7347.
7. R. C. Ewing, W. J. Weber and J. Lian, J. Appl. Phys., 2004, 95, 5949.
8. X. J. Wang, H. Y. Xiao, X. T. Zu and W. J. Weber, J. Nucl. Mater., 2011, 419, 105.
9. A. Chartier, G. Catillon and J. P. Crocombette, Phys. Rev. Lett., 2009, 102(15), 155503.
10. H. Y. Xiao, F. Gao and W. J. Weber, J. Phys.: Condens. Matter, 2010, 22, 415801.
11. W. J. Weber and R. C. Ewing, Science, 2000, 289, 2051.
12. J. Lian, J. Chen, L. M. Wang, R. C. Ewing, J. M. Farmer, L. A. Boatner and K. B. Helean, Phys. Rev. B, 2003, 68, 134107.
13. A. Chartier, C. Meis, J. P. Crocombette, W. J. Weber and L. R. Corrales, Phys. Rev. Lett., 2005, 94, 025505.
14. H. Y. Xiao, F. X. Zhang, F. Gao, M. Lang, R. C. Ewing and W. J. Weber, Phys. Chem. Chem. Phys., 2010, 12, 12472.
15. A. Chartier, C. Meis, W. J. Weber and L. R. Corrales, Phys. Rev. B, 2002, 65, 134116.
16. J. M. Pruneda and E. Artacho, Phys. Rev. B, 2005, 72, 085107.
17. R. E. Willford, W. J. Weber and R. Devanathan, J. Electroceram., 1999, 3, 409.
18. H. Y. Xiao, X. T. Zu, F. Gao and W. J. Weber, J. Appl. Phys., 2008, 104, 073503.
19. W. R. Panero, L. P. Stixrude and R. C. Ewing, Phys. Rev. B, 2004, 70, 054110.
20. H. Y. Xiao, L. M. Wang, X. T. Zu, J. Lian and R. C. Ewing, J. Phys.: Condens. Matter, 2007, 19, 346203.
21. Z. L. Zhang, H. Y. Xiao, X. T. Zu, F. Gao and W. J. Weber, J. Mater. Res., 2009, 24, 1335–1341.
22. H. Y. Xiao, F. Gao and W. J. Weber, Phys. Rev. B, 2009, 80, 212102.
23. H. Y. Xiao, Y. W. Zhang and W. J. Weber, Phys. Chem. Chem. Phys., 2012, 14, 6556.
24. N. Kim and C. P. Grey, Dalton Trans., 2004, 3048.
25. R. Abe, M. Higashi, K. Sayama, Y. Abe and H. Sugihara, J. Phys. Chem. B, 2006, 110, 2219.
26. M. Langlet, P. Jenouvrier, R. Rimet and J. Fick, Opt. Mater., 2004, 25, 141.
27. S. Kramer, M. Spears and H. L. Tuller, Solid State Ionics, 1994, 72, 59.
28. S. Na-Phattalung, M. F. Smith, K. Kim, M.-H. Du, S.-H. Wei, S. B. Zhang and S. Limpijumnong, Phys. Rev. B, 2006, 73, 125205.
29. O. F. Schirmer, J. Phys.: Condens. Matter, 2006, 18, R667.
30. S. Yang, L. E. Halliburton, A. Manivannan, P. H. Bunton, D. B. Baker, M. Klemm, S. Horn and A. Fujishima, Appl. Phys. Lett., 2009, 94, 162114.
31. M. A. Henderson, W. S. . Epling, C. H. F. Peden and C. L. Perkins, J. Phys. Chem. B, 2003, 107, 534.
32. R. L. Kurtz, R. Stock-Bauer and T. E. Madey, Surf. Sci., 1989, 218, 178.
33. M. V. Ganduglia-Pirovano, A. Hofman and J. Sauer, Surf. Sci. Rep., 2007, 62, 219.
34. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
35. V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Phys. Rev. B, 1993, 48, 16929.
36. B. J. Morgan and G. W. Watson, J. Phys. Chem. C, 2010, 114, 2321.
37. B. J. Morgan and G. W. Watson, Phys. Rev. B, 2009, 80, 233102.
38. A. Iwaszuk and M. Nolan, J. Phys.: Condens. Matter, 2011, 23, 334207.
39. E. Finazzi, C. D. Valentin, G. Pacchioni and A. Selloni, J. Chem. Phys., 2008, 129, 154113.
40. J. Stausholm-Møller, H. H. Kristoffersen, B. Hinnemann, G. K. H. Madsen and B. Hammer, J. Chem. Phys., 2010, 133, 144708.
41. H. Y. Xiao and W. J. Weber, J. Phys. Chem. B, 2011, 115, 6524.
42. P. Krüger, S. Bourgeois, B. Domenichini, H. Magnan, D. Chandesris, P. L. Fèvre, A. M. Flank, J. Jupille, L. Floreano, A. Cossaro, A. Verdini and A. Morgante, Phys. Rev. Lett., 2008, 100, 055501.
43. P. J. D. Lindan, N. M. Harrison, M. J. Gillan and J. A. White, Phys. Rev. B, 1997, 55, 15919.
44. C. D. Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803.
45. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
46. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
47. J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 45, 13244.
48. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505.
49. N. Li, H. Y. Xiao, X. T. Zu, L. M. Wang, R. C. Ewing, J. Lian and F. Gao, J. Appl. Phys., 2007, 102(6), 063704.
50. T. Bak, J. Nowotny, M. Rekas and C. C. Sorrell, J. Phys. Chem. Solids, 2003, 64, 1057.
51. A. K. Pandit, T. H. Ansari, M. Prasad, R. A. Singh and B. M. Wanklyn, Mater. Lett., 1991, 12, 77.
52. E. Cho, S. Han, H.-S. Ahn, K.-R. Lee, S. K. Kim and C. S. Hwang, Phys. Rev. B, 2006, 73, 193202.
53. G. Pacchioni, J. Chem. Phys., 2008, 128, 182505.

---