DOI:
10.1039/C2RA20985C
(Paper)
RSC Adv., 2012,
2, 12384-12391
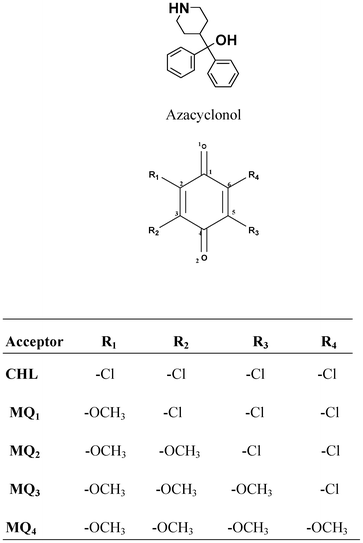
Spectral, electrochemical and theoretical studies on the charge transfer complexes of azacyclonol with novel substituted 1,4-benzoquinones possessing tunable electron acceptor properties†
Received
18th May 2012
, Accepted 6th October 2012
First published on 11th October 2012
Abstract
The charge transfer (CT) complexes of a series of novel electron acceptors, 1,4-benzoquinones possessing a variable number of chloro and methoxy groups, with azacyclonol were investigated using various spectral techniques, such as UV-vis, 1H NMR, FT-IR, LC-MS and fluorescence. The stoichiometry of the CT complexes was determined by Job's continuous variation method and was found to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in all cases. The rate of the CT interaction was observed to decrease from CHL to MQ4 and this variation is well supported by the formation constant and enthalpy of activation values. The half wave potentials, E1/2, for the electro-reduction of these acceptors, evaluated using cyclic voltammetry, were 91, −69, −232, −383 and −556 mV, indicating progressive weakening of the electron accepting properties of the acceptors from CHL to MQ4. Ab initio DFT calculations predicted that the variation in the bond lengths of the carbonyl moieties and the charge densities on the carbonyl oxygen atoms depend largely on the nature of the substituent present in the quinone ring. These variations have been in line with the observed FT-IR spectra of the acceptors. Also the HOMODonor–LUMOAcceptor energy gaps linearly correlate with the association constants evaluated using fluorescence data. The equilibrium, kinetic, electrochemical and theoretical investigations of the CT interaction of these quinones indicated that progressive replacement of an electron withdrawing chlorine atom (−I effect) by an electron releasing methoxy group (+M effect) makes these acceptors progressively weaker.
1 in all cases. The rate of the CT interaction was observed to decrease from CHL to MQ4 and this variation is well supported by the formation constant and enthalpy of activation values. The half wave potentials, E1/2, for the electro-reduction of these acceptors, evaluated using cyclic voltammetry, were 91, −69, −232, −383 and −556 mV, indicating progressive weakening of the electron accepting properties of the acceptors from CHL to MQ4. Ab initio DFT calculations predicted that the variation in the bond lengths of the carbonyl moieties and the charge densities on the carbonyl oxygen atoms depend largely on the nature of the substituent present in the quinone ring. These variations have been in line with the observed FT-IR spectra of the acceptors. Also the HOMODonor–LUMOAcceptor energy gaps linearly correlate with the association constants evaluated using fluorescence data. The equilibrium, kinetic, electrochemical and theoretical investigations of the CT interaction of these quinones indicated that progressive replacement of an electron withdrawing chlorine atom (−I effect) by an electron releasing methoxy group (+M effect) makes these acceptors progressively weaker.
Introduction
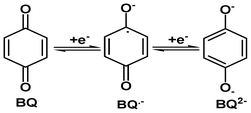
Quinones are one of the most significant classes of organic compounds, as their applications range into various fields, like biology,1,2 pharmaceuticals,3 water management4 and agriculture5etc. Quinones play an integral role in many biological electron transfer processes.6,7 It is reported that the biological activity of these compounds is due to the redox chemistry of the quinone system.1,8 The quinone ring accepts one or two electrons to form the corresponding radical-anion (Q˙−) and hydroquinone dianion (Q2−). These species interact with crucial cellular molecules, such as DNA, proteins and oxygen, tuning their biological activity by accepting the electrons in the correct site.1,8,9
The ability of the quinones to accept one or two electrons depends directly on their chemical structures.10 It is known that the redox chemistry of these substances can be modified either by directly adding a substituent to the quinone ring11 or by attaching a substituted phenyl ring to the quinone system.12 However, for some applications, fine tuning of the electron accepting properties is required. To achieve this, many attempts have been made to synthesize quinone systems with substituted phenyl rings directly attached to it and to study their redox chemistry. The biological activities of such systems have also been documented.13
During the recent past, a great deal of research has been carried out on the charge transfer complexes of quinones because of their wide applications, ranging from chemistry, materials science and medicine to biology.14–17 In biological systems quinones exist in the form of substituted p-benzoquinones, such as plastoquinones,18 Vitamin K,19 ubiquinones2,20etc. Also, these naturally occurring quinones possess a variable number of methoxy groups. Although a good amount of work, on the study of charge transfer (CT) complexes of a number of quinones with variety of donors, has been carried out,21–24 reports related to quinones with systematic variation of substituents are rare in the literature. The main objective, therefore, of the present endeavor is to study the charge transfer complexes and redox chemistry of 1,4-benzoquinones with a variable number of chloro and methoxy groups. Though these chosen quinones are known to synthetic organic chemists as intermediates, to the best of our knowledge this is the first systematic investigation on the charge transfer complexes of these quinones as electron acceptors. In the frame of Density Functional Theory (DFT) we have also performed the complete optimization of the geometry for these quinones.
Experimental
Materials and measurements
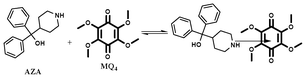
The electron acceptor chloranil (CHL) (Aldrich, India) was used without further purification and other methoxy substituted chloranil derivatives (MQ1–4) were prepared by a reported method.25 Spectroscopy grade solvents (Merck, India) were used as received. The electron donor drug azacyclonol was obtained as a gift sample from a local pharmaceutical company and was used as received. The purity of the donor was ascertained using its m.p. (found 161 °C; lit. 160–163 °C). The structures of the donor and the acceptors are shown below.
Solutions for the spectroscopic measurements were prepared by dissolving accurately weighed amounts of donor (D) and acceptor (A) in an appropriate volume of solvent immediately before running the spectra. The electronic absorption spectra were recorded on a JASCO (V630, Japan) double beam spectrophotometer using 1 cm matched quartz cells. The temperature of the cell holder was controlled with a water flow (±0.1 °C). Fluorescence spectra were recorded in a JASCO (6200, Japan) spectrofluorimeter. The excitation emission slit width (5 nm) and scan rate (250 nm) were kept constant for all of the experiments. FT-IR spectra were recorded in a JASCO (FT-IR 460 Plus, Japan) spectrometer. 1H NMR spectra were recorded at Madurai Kamaraj University, Madurai in a Brucker NMR spectrometer (300 MHz, Switzerland). The electrochemical measurements were carried out with a CHI electrochemical workstation (Model 643B, Austin, TX, USA).
Preparation and characterization of methoxy substituted quinones
1,4-Benzoquinones possessing varying number of chloro and methoxy substituents were prepared and purified as reported elsewhere.25 An excess amount of sodium methoxide was added into a stirred solution of chloroanil in methanol at RT under N2 atm. The reaction mixture was stirred for 12 h at 70 °C and was cooled to room temperature. Then the reaction mixture was added to 200 ml of water and stirred for 1 h at RT. The crude material formed was filtered through a filter paper and the residue was purified using column chromatography (Silica gel 60–120 by using a 5–10% ethyl acetate/pet ether (boiling point 40–60 °C) mixture). The percentage yields of various quinones obtained by this method are shown in Scheme 1. For the preparation of MQ4, 4 equiv. of sodium methoxide was added into MQ1 under the same preparation conditions.
3,5,6-trichloro-2-methoxycyclohexa-2,5-diene-1,4-dione (MQ1).
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 4.19 (s, 3H); FT-IR (KBr, cm−1): 1680 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1668 (C
O), 1668 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1567 (C
O), 1567 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 295 nm (π–π*), log ε 4.24; Anal. calcd. for C7H3Cl3O3: C, 34.82; H, 1.25; N, 0.0; found: C, 36.17; H, 1.74; N, 0.0; m.p. 172 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 295 nm (π–π*), log ε 4.24; Anal. calcd. for C7H3Cl3O3: C, 34.82; H, 1.25; N, 0.0; found: C, 36.17; H, 1.74; N, 0.0; m.p. 172 °C.
5,6-dichloro-2,3-dimethoxycyclohexa-2,5-diene-1,4-dione (MQ2).
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 4.07 (s, 3H), 4.12 (s, 3H); FT-IR (KBr, cm−1): 1668 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 300 nm (π–π*), log ε 4.23; Anal. calcd. for C8H6Cl2O4: C, 40.54; H, 2.55; N, 0.0; found: C, 41.24; H, 2.66; N, 0.0; m.p. 124 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 300 nm (π–π*), log ε 4.23; Anal. calcd. for C8H6Cl2O4: C, 40.54; H, 2.55; N, 0.0; found: C, 41.24; H, 2.66; N, 0.0; m.p. 124 °C.
6-chloro-2,3,5-trimethoxycyclohexa-2,5-diene-1,4-dione (MQ3).
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 3.92 (s, 3H), 4.07 (s, 3H), 4.12 (s, 3H); FT-IR (KBr, cm−1): 1666 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 302 nm (π–π*), log ε 4.24; Anal. calcd. for C9H9ClO5: C, 46.47; H, 3.90; N, 0.0; found: C, 46.17; H, 3.78; N, 0.0; m.p. 83 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 302 nm (π–π*), log ε 4.24; Anal. calcd. for C9H9ClO5: C, 46.47; H, 3.90; N, 0.0; found: C, 46.17; H, 3.78; N, 0.0; m.p. 83 °C.
2,3,5,6-tetramethoxycyclohexa-2,5-diene-1,4-dione (MQ4).
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 3.92 (s, 12H); FT-IR (KBr, cm−1): 1668 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 309 nm (π–π*), log ε 4.25; Anal. calcd. for C10H12O6: C, 52.63; H, 5.30; N, 0.0; found: C, 53.12; H, 5.58; N, 0.0; m.p. 134 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 309 nm (π–π*), log ε 4.25; Anal. calcd. for C10H12O6: C, 52.63; H, 5.30; N, 0.0; found: C, 53.12; H, 5.58; N, 0.0; m.p. 134 °C.
Kinetic procedure
The kinetics of the interaction of azacyclonol with the acceptors (CHL, MQ1–4) were followed at three different temperatures in 1,2-dichloroethane under pseudo-first-order conditions, keeping [D] ≫ [A]. The increase in absorbance of the corresponding new peaks at 442 nm (AZA-CHL), 564 nm (AZA-MQ1, AZA-MQ2, AZA-MQ3) and 260 nm (AZA-MQ4) with elapse of time was recorded. The pseudo-first-order rate constants (k1) were calculated from the gradients of log (A∞–At) against time plots, where A∞ and At represent the absorbance at infinity and time t, respectively. The second order rate constants were calculated by dividing k1 by [D].26,27
Results and discussion
Stoichiometry of the interaction
The stochiometry of the CT complexes formed between AZA and the acceptors was determined by Job's continuous variation method using emission data.28 In all the cases, symmetrical curves with a maximum at 0.5 mole fraction indicated the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (D
1 (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A) CT complex (Fig. 1). The photometric titration measurements were also performed for the determination of the stoichiometry in these interactions. For that, the concentration of the donor in the reaction mixtures was kept constant while the concentrations of the acceptors were varied over a wide range. The results of the photometric curves (Fig. 1S†) also indicated that the stoichiometry of the interaction, in all the cases, was 1
A) CT complex (Fig. 1). The photometric titration measurements were also performed for the determination of the stoichiometry in these interactions. For that, the concentration of the donor in the reaction mixtures was kept constant while the concentrations of the acceptors were varied over a wide range. The results of the photometric curves (Fig. 1S†) also indicated that the stoichiometry of the interaction, in all the cases, was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (D
1 (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A).29,30
A).29,30
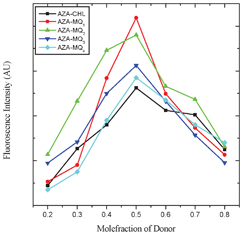 |
| | Fig. 1 Job's continuous variation plots for AZA-CHL, AZA-MQ1, AZA-MQ2, AZA-MQ3 and AZA-MQ4 in 1,2-dichloroethane at 298 K. | |
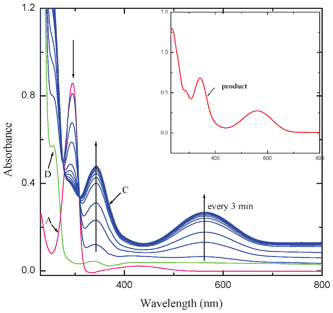
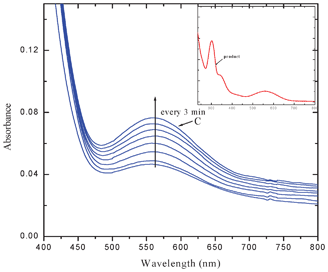
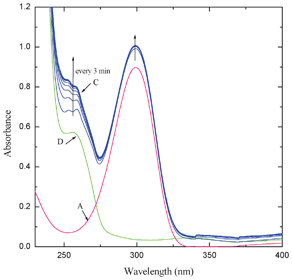
The intensity of the bands at 564 and 342 nm increased with elapse of time while that of the band at 295 nm decreased. Two clear isosbestic points appeared at 308 and 276 nm. The interaction of MQ2 and MQ3 (Fig. 3) and also CHL (Fig. 2S†) with AZA, exhibited similar electronic spectral behavior. These observed new low energy bands cannot be considered as the characteristic absorption bands of an outer complex because: the formation of the outer complex may be an instantaneous process and its concentration may be too low to detect and also this may immediately be converted to the final product. This is well supported by the fact that the final product extracted, in all these cases, exhibited superimposable electronic spectra. In the case of the interaction of MQ4 with AZA, the intensities of the peaks corresponding to the pure D and A increased with elapse of time, indicating the formation of a weak CT complex between them. This may be due to the fact that, as there is no replaceable Cl-atom in MQ4, formation of the final product by the reaction with AZA is ruled out (Fig. 4).
The pseudo-first-order rate constants (k1) for the formation of the products as a function of [D] and [A] are collected in Table 1S†. It is evident from the results that the rate of the interaction is independent of the initial concentration of A, indicating first order dependence on [A]. The rate constant values increased with an increase in [D] and in all the cases, a plot of log k1versus log [D] is linear (r > 0.98) with a slope close to one, indicating first order dependence of rate on [D]. This was further supported by the constancy in k2 values.26,27 These observations indicated that the interaction of AZA with these acceptors, except MQ4, proceed via the following plausible mechanism (Scheme 2).
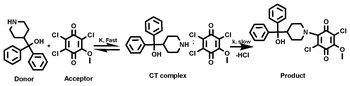 |
| | Scheme 2 The interaction of AZA with MQ1. | |
The above mechanism leads to the following rate law
| Rate = k[CT complex] or Rate = k1[D][A] |
where
k1 =
Kk.
In the case of MQ4 as the acceptor, it is the formation of a weak CT association between the partners, as depicted below.
The rate constants as a function of temperature along with thermodynamic parameters are collected in Table 1. It is evident from the results that the enthalpy of activation, which is a measure of strength of the interaction between the donor and the acceptor in a molecular complex,31 follows the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4.
Table 1 Kinetic and thermodynamic parameters for the interaction of the donor with the acceptors in 1,2-dichloroethane
| Systems |
λ nm |
k
1 (10−4) sec−1 |
ΔH#![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−ΔS#![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔG#![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| 298 |
305 |
313 K |
|
ΔH# kJ mol−1; ΔS# J K−1 mol−1; ΔG# kJ mol−1
|
| AZA-CHL |
441 |
38.5 |
42.3 |
46.8 |
8 |
285 |
92 |
| AZA-MQ1 |
564 |
35.8 |
39.6 |
42.5 |
6 |
289 |
92 |
| AZA-MQ2 |
564 |
29.8 |
34.2 |
37.8 |
10 |
279 |
93 |
| AZA-MQ3 |
564 |
26.5 |
31.2 |
35.9 |
13 |
269 |
93 |
| AZA-MQ4 |
260 |
20.2 |
26.4 |
29.5 |
16 |
258 |
93 |
An attempt was also made to characterize the charge transfer complexes formed in these reactions. For that the absorbance of the new bands were measured using constant acceptor concentration and varying concentrations of the donor, but always [D] ≫ [A].28,32 The formation constants (K) and molar extinction coefficients (ε) of the CT complexes were determined spectrophotometrically using the Scott equation.33 The values of K and ε determined are given in Table 2. The observed high values of K suggested that the formed complexes are of a strong type34 and the linearity of the Scott plots (r > 0.98) further supports this result.
Table 2 Formation constants and extinction coefficients of all the systems, carried out in 1,2-dichloroethane at 298 K
| Systems |
Formation constant |
Extinction coefficient |
Association constant |
|
K (dm3 mol−1) |
log ε (dm3 mol−1 cm−1) |
K
f (mole L−1) |
| AZA-CHL |
1829 |
4.64 |
14 × 104 |
| AZA-MQ1 |
1602 |
4.63 |
9 × 104 |
| AZA-MQ2 |
961 |
4.59 |
7 × 104 |
| AZA-MQ3 |
855 |
4.58 |
6 × 104 |
| AZA-MQ4 |
622 |
4.57 |
3 × 104 |
Characterization of the interaction product
In all the cases (except the AZA-MQ4 system), the final product was obtained by stirring equimolar 1,2-dichloroethane solutions of the donor and the acceptor at room temperature for 24 h. The solid obtained, after evaporation of the solvent, was purified using column chromatography (silica gel 60–120 by using a 5–10% ethyl acetate/pet ether mixture). The products were characterized using analytical (CHN) and spectral (1H NMR, FT-IR, LC-MS) techniques. The results obtained are:
AZA-CHL product: [2,3,5-trichloro-6-(4-(hydroxydiphenylmethyl)piperidin-1-yl) cyclohexa-2,5-diene-1,4-dione].
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 1.38 (t, J = 6 Hz, 2H), 1.58–1.66 (m, 2H), 2.90 (t, J = 9 Hz, 1H), 3.28 (t, J = 9 Hz, 2H), 3.76 (d, J = 9 Hz, 2H), 5.42 (s, 1H), 7.14 (t, J = 6 Hz, 2H), 7.28 (t, J = 6 Hz, 4H), 7.55 (t, J = 3 Hz, 4H); FT-IR (KBr, cm−1): 3522 (O–H), 1685 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1633 (C
O), 1633 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C24H20Cl3NO3: 476.78; found: 477.2; Anal. calcd. for C24H20Cl3NO3: C, 60.46; H, 4.23; N, 2.94: found: C, 60.17; H, 4.40; N, 2.81.
O); LCMS: Calcd. For C24H20Cl3NO3: 476.78; found: 477.2; Anal. calcd. for C24H20Cl3NO3: C, 60.46; H, 4.23; N, 2.94: found: C, 60.17; H, 4.40; N, 2.81.
AZA-MQ1 product: [2,5-dichloro-3-(4-(hydroxydiphenylmethyl)piperidin-1-yl)-6-methoxycyclohexa-2,5-diene-1,4-dione].
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 1.24 (d, J = 3 Hz, 2H), 1.39 (d, J = 6 Hz, 2H), 2.90 (t, J = 9 Hz, 1H), 3.28 (t, J = 12 Hz, 2H), 3.76 (d, J = 12 Hz, 2H), 4.08 (s, 3H), 5.41 (s, 1H), 7.15 (t, J = 6 Hz, 2H), 7.30(t, J = 9 Hz, 4H), 7.56 (d, J = 9 Hz, 4H); FT-IR (KBr, cm−1): 3377(O–H), 1677 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1644 (C
O), 1644 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C25H23Cl2NO4: 472.36; found: 474.1. Anal. calcd. for C25H23Cl2NO4: C, 63.57; H, 4.91; N, 2.97: found: C, 63.38; H, 4.87; N, 2.89.
O); LCMS: Calcd. For C25H23Cl2NO4: 472.36; found: 474.1. Anal. calcd. for C25H23Cl2NO4: C, 63.57; H, 4.91; N, 2.97: found: C, 63.38; H, 4.87; N, 2.89.
AZA-MQ2 product: [2-chloro-3-(4-(hydroxydiphenylmethyl)piperidin-1-yl)-5,6-dimethoxycyclohexa-2,5-diene-1,4-dione].
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 1.32 (t, J = 12 Hz, 2H), 1.52–1.63 (m, 2H), 2.82 (t, J = 12 Hz, 1H), 3.13 (t, J = 12 Hz, 2H), 3.56 (d, J = 12 Hz, 2H), 3.65 (s, 3H), 4.07 (s, 3H), 5.37 (s, 1H), 7.15 (t, J = 6 Hz, 2H), 7.29 (t, J = 6 Hz, 4H), 7.55 (d, J = 6 Hz, 4H); FT-IR (KBr, cm−1): 3383 (O–H), 1670 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C26H26ClNO5: 467.94; found: 467.8. Anal. calcd. for C26H26ClNO5: C, 66.73; H, 5.60; N, 2.99: found: C, 66.64; H, 5.53; N, 2.96.
O); LCMS: Calcd. For C26H26ClNO5: 467.94; found: 467.8. Anal. calcd. for C26H26ClNO5: C, 66.73; H, 5.60; N, 2.99: found: C, 66.64; H, 5.53; N, 2.96.
AZA-MQ3 product: [2-(4-(hydroxydiphenylmethyl)piperidin-1-yl)-3,5,6-trimethoxycyclohexa-2,5-diene-1,4-dione].
1H NMR (DMSO-d6, 300 MHz), δ (ppm) 1.50–1.61 (m, 4H), 2.78 (d, J = 12 Hz, 1H), 3.00–3.14 (m, 2H), 3.49 (d, J = 12 Hz, 2H), 3.63 (s, 3H), 3.76 (s, 3H), 3.87 (s, 3H), 5.35 (s, 1H), 7.15 (t, J = 9 Hz, 2H), 7.29 (t, J = 6 Hz, 4H), 7.55 (d, J = 9 Hz, 4H); FT-IR (KBr, cm−1): 3379 (O–H), 1677 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1648 (C
O), 1648 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C27H29NO6: 463.52; found: 464.3. Anal. calcd. for C27H29NO6: C, 69.96; H, 6.31; N, 3.02: found: C, 69.22; H, 6.40; N, 3.04.
O); LCMS: Calcd. For C27H29NO6: 463.52; found: 464.3. Anal. calcd. for C27H29NO6: C, 69.96; H, 6.31; N, 3.02: found: C, 69.22; H, 6.40; N, 3.04.
Fluorescence study
One of the most important binding forces that produces favorable binding of a drug to its target is the CT interaction. The nature and magnitude of drug interaction significantly influences the biological activity of the drug. In the present study an attempt was made to investigate the mode of CT interaction between AZA with these acceptors using fluorescence spectroscopy. The fluorescence spectra were recorded in 1,2-dichloroethane at room temperature in the range 230–730 nm upon excitation at 254 nm for all the systems. It is observed that these acceptors quenched the fluorescence of AZA through CT complexation. The experimental results indicated that the quenching efficiency increased with an increase in the concentration of the acceptors at a fixed concentration of the drug (Fig. 5 and Fig. 12S–15S†). For all the systems, the CT interaction between the quencher and the fluorophore was observed at 292 nm. The fraction of the acceptor bound to the drug (θ) was determined using the following equation,35where F and F0 denote the fluorescence intensities of the drug in a solution with a given concentration of the acceptor and without the acceptor, respectively. From the values of θ the association constant, Kf, for the drug interaction with the acceptors was computed using the method described by Ward.36 It has been shown that for equivalent and independent binding sites:| | 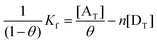 | (2) |
where, n is the number of binding sites, [AT] is the total acceptor concentration and [DT] is the total drug concentration. The plot of 1/(1 − θ) versus [AT]/θ was found to be linear (r > 0.97), for all the systems, indicating that under the experimental conditions all the binding sites are equivalent and independent. The values of Kf obtained from the plots for AZA-CHL, AZA-MQ1, AZA-MQ2, AZA-MQ3 and AZA-MQ4 systems were found to be 14, 9, 7, 6 and 3 × 104 mol L−1, respectively. Parallel to the observation made under the electronic spectral studies, as enumerated earlier, the strength of the complex formation between the partners is in the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4. The standard Gibbs energy change ΔGo was calculated from the Kf using the relation ΔGo = −2.303RTlog10Kf. The ΔGo values for AZA-CHL, AZA-MQ1, AZA-MQ2, AZA-MQ3 and AZA-MQ4 systems were found to be −29, −28, −27.7, −27.4 and −25 kJ, respectively, which indicated that the interactions between the drug and the acceptors are spontaneous.37
![Fluorescence spectra for the AZA-MQ1 system in 1,2-dichloroethane at fixed concentrations of [D] = {8 × 10−4 M (curve D)} and variable concentration of [A](× 10−5) = {1 (curve a), 2 (curve b), 3 (curve c), 4 (curve d), 5 (curve e), 6 (curve f)}M at 298 K.](/image/article/2012/RA/c2ra20985c/c2ra20985c-f5.gif) |
| | Fig. 5 Fluorescence spectra for the AZA-MQ1 system in 1,2-dichloroethane at fixed concentrations of [D] = {8 × 10−4 M (curve D)} and variable concentration of [A](× 10−5) = {1 (curve a), 2 (curve b), 3 (curve c), 4 (curve d), 5 (curve e), 6 (curve f)}M at 298 K. | |
Fluorescence quenching can occur by different mechanisms viz. static or dynamic or both. The Stern–Volmer equation (eqn (3)) is useful in understanding the mechanism of fluorescence quenching,
where
Fo is emission intensity in the absence of quencher (Q),
F is emission intensity at quencher concentration [Q] and
KSV is the Stern–Volmer constant. In the present study, the observed linear Stern–Volmer relationship suggested that either static or dynamic quenching is dominant in all the systems (
Fig. 6).
38,39 The fluorimetric results indicated that the CT interaction between AZA and these acceptors is spontaneous and an increase in the strength of such interaction decreases the fluorescence intensity of AZA.
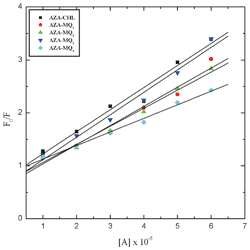 |
| | Fig. 6 Stern–Volmer plots for the fluorescence quenching of AZA with the acceptors in 1,2-dichloroethane at 298 K. | |
Electrochemical studies
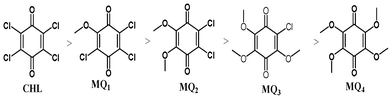
The redox potentials of the acceptors were measured by cyclic voltammetry at room temperature using a conventional two-compartment three electrode cell with a 3 mm Glassy Carbon (GC) disk as the working electrode and 0.1 M tetrabutylammonium perchlorate in acetonitrile as the electrolytic medium. For all the acceptors, the voltammograms, recorded in the potential range from +1.5 V to −0.8 V vs. Ag/AgCl are shown in Fig. 7. To compare the electron accepting properties of these acceptors the electrochemical data of the first wave alone has been considered here. The half wave potential values (E1/2) were evaluated from the voltammograms obtained at a sweep rate of 100 mVs−1, E1/2 = (Epa + Epc)/2, where Epa and Epc correspond to anodic and cathodic peak potentials, respectively. In all the cases, the ratio of ipa/ipc, was found to be nearly unity (Table 3), indicating the reversible nature of the systems.13,40 The results obtained indicated that the E1/2 values become more negative from CHL to MQ4. That is, the electron accepting ability (reduction) of MQ4 is relatively low when compared to CHL, or in other words MQ4 is comparatively a weaker acceptor. This may be due to the fact that progressive replacement of electron withdrawing chlorine atoms (−I effect) by electron releasing methoxy groups (+M effect) rendered the quinone increasingly electron rich and consequently make it as a weak acceptor.13,40 This observation corroborates well with the results obtained in the spectral and kinetic studies enumerated above.
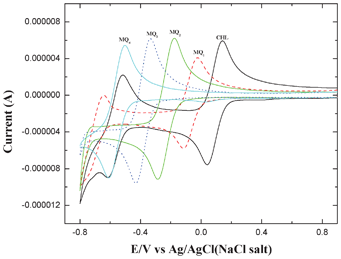 |
| | Fig. 7 Cyclic voltammograms obtained for 1 mM solutions of CHL, MQ1, MQ2, MQ3 and MQ4 in 0.1 M tetrabutylammonium perchlorate at a scan rate of 100 mV s−1. | |
Table 3 Reversible voltammetric parameters for the acceptors
| Acceptor |
E
pc
|
E
pa
|
E
1/2
|
i
pa/ipc |
| CHL |
0.03 |
0.14 |
91 |
0.9 |
| MQ1 |
−0.12 |
−0.02 |
−69 |
1.1 |
| MQ2 |
−0.29 |
−0.18 |
−232 |
0.9 |
| MQ3 |
−0.43 |
−0.33 |
−383 |
1.1 |
| MQ4 |
−0.62 |
−0.50 |
−556 |
1.1 |
Theoretical calculations
To understand the foregoing experimental observations on the CT complex formed between AZA and the acceptors, we have performed the optimization of AZA, CHL, MQ1–4 using Density Functional Theory with the Backle3LYP hybrid functional, by using a basis set of 6-31G. Computations have been performed using the Gaussian 03 Revision D.01 program package.41 The optimized geometry of the donor along with HOMO, and the acceptors along with LUMO, are depicted in Fig. 8.
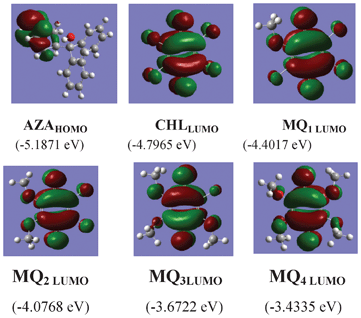 |
| | Fig. 8 The optimized structures for AZA with its HOMO and acceptors with their respective LUMO. | |
As mentioned in the introduction section, the quinone moiety accepts one electron or two electrons to form the corresponding radical-anion (BQ˙−) and hydroquinone radical dianion (BQ2−). The electron accepting capacity and several physicochemical/biological properties of a given quinone depends largely on the substituent present in it.
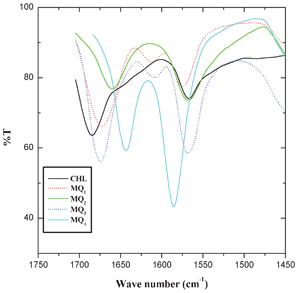
The optimized geometry of the acceptors indicated that the LUMO resides on the carbonyl group of the quinones and in the donor the HOMO resides on the NH moiety of the molecule (Fig. 8). Thus, when the quinone accepts electrons from the piperidine N-atom of the donor, there should be a significant alteration in the bond length and charge density of the carbonyl moiety. Hence, the C1–O1 and C4–O2 bond lengths and the charge density on oxygen atoms (O1 and O2) were carefully analyzed (Table 4 and 5). The results indicate that there is a substantial elongation of both C1–O1 and C4–O2 bonds and also an increase in the charge density on O1 and O2 atoms in the following order: CHL → MQ1 → MQ2 → MQ3 → MQ4. In order to get a better insight into the theoretical results, the FT-IR spectra of these acceptors were also recorded. The symmetrical bond lengths (of C1–O1 and C4–O2) and charge densities (on O1 and O2) observed in CHL, MQ2 and MQ4 systems exhibited a single peak around 1675 cm−1, corresponding to νCO in the FT-IR spectrum of the acceptors (Fig. 9). The unsymmetrical bond lengths (C1–O1 and C4–O2) and charge densities (O1 and O2) observed in MQ1 and MQ3 molecules showed two peaks for νCO (Fig. 9).
Table 4 Geometry of CHL, MQ1−4 with Becke3LYP/6-31G level
| Bond |
CHL |
MQ1 |
MQ2 |
MQ3 |
MQ4 |
| C1–O1 |
1.238 |
1.245 |
1.248 |
1.252 |
1.257 |
| C4–O2 |
1.238 |
1.243 |
1.248 |
1.256 |
1.257 |
| C2–Cl |
1.783 |
— |
— |
— |
— |
| C3–Cl |
1.783 |
1.789 |
— |
— |
— |
| C5–Cl |
1.783 |
1.781 |
1.787 |
— |
— |
| C6–Cl |
1.783 |
1.789 |
1.787 |
1.796 |
— |
| C2–O(R1) |
— |
1.354 |
1.365 |
1.357 |
1.379 |
| C3–O(R2) |
— |
— |
1.365 |
1.380 |
1.363 |
| C5–O(R3) |
— |
— |
— |
1.354 |
1.379 |
| C6–O(R4) |
— |
— |
— |
— |
1.363 |
| C1–C2 |
1.490 |
1.495 |
1.474 |
1.498 |
1.471 |
| C2–C3 |
1.348 |
1.363 |
1.373 |
1.369 |
1.367 |
| C3–C4 |
1.490 |
1.463 |
1.474 |
1.460 |
1.492 |
| C4–C5 |
1.490 |
1.501 |
1.495 |
1.504 |
1.471 |
| C5–C6 |
1.348 |
1.346 |
1.344 |
1.361 |
1.367 |
| C6–C1 |
1.490 |
1.484 |
1.495 |
1.460 |
1.492 |
Table 5 Mulliken charges of CHL, MQ1−4 with Becke3LYP/6-31G level
| Atom |
CHL |
MQ1 |
MQ2 |
MQ3 |
MQ4 |
| C1 |
0.393 |
0.348 |
0.341 |
0.335 |
0.287 |
| C2 |
−0.260 |
0.405 |
0.281 |
0.307 |
0.242 |
| C3 |
−0.260 |
−0.353 |
0.281 |
0.234 |
0.296 |
| C4 |
0.393 |
0.382 |
0.341 |
0.289 |
0.287 |
| C5 |
−0.260 |
−0.264 |
−0.265 |
0.399 |
0.242 |
| C6 |
−0.260 |
−0.265 |
−0.265 |
−0.356 |
0.296 |
| O1 |
−0.332 |
−0.348 |
−0.384 |
−0.403 |
−0.425 |
| O2 |
−0.332 |
−0.354 |
−0.384 |
−0.423 |
−0.425 |
| Cl(R1) |
0.230 |
— |
— |
— |
— |
| Cl(R2) |
0.230 |
0.190 |
— |
— |
— |
| Cl(R3) |
0.230 |
0.225 |
0.206 |
— |
— |
| Cl(R4) |
0.230 |
0.211 |
0.206 |
0.160 |
— |
| O(R1) |
— |
−0.541 |
−0.532 |
−0.538 |
−0.526 |
| O(R2) |
— |
— |
−0.532 |
−0.523 |
−0.540 |
| O(R3) |
— |
— |
— |
−0.544 |
−0.242 |
| O(R4) |
— |
— |
— |
— |
−0.296 |
The energies of the frontier orbitals of the donor and the acceptors, along with the energy corresponding to the CT transition, ΔE (= LUMOacceptor − HOMOAZA),42–44 for all the systems are shown in Fig. 10. It is evident from the figure that the ΔE depends on the nature of the substituent present in the quinone. Also, a good linear correlation obtained between the theoretical energy gap values and the experimentally determined stability constant values (Fig. 11) indicated that the strength of the acceptor decreased in the order:
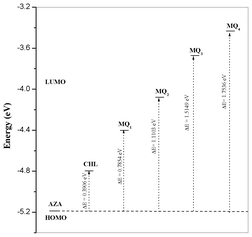 |
| | Fig. 10 Relationship between energies of HOMOAZA and LUMOAcceptor. | |
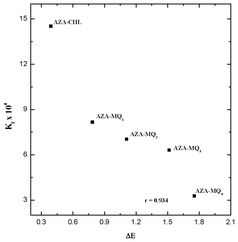 |
| | Fig. 11 Correlation between association constant (Kf) and energy gap (ΔE). | |
Conclusions
The charge transfer properties of 1,4-benzoquinones possessing varying number of chloro and methoxy substituents were, for the first time, investigated. Various spectral techniques have been employed to characterize the final product of these interactions. In all the cases, the stoichiometry of the CT interaction was found to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The trends in the rate constants and formation constants showed that the strength of the complex formation is in the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4. The half wave potential values (E1/2) for the one electron reduction of these acceptors indicated that the electronegativity of the acceptors increased from CHL to MQ4. The observed equilibrium, kinetic and electrochemical properties of these acceptors were found to be well supported by ab initio DFT calculations.
1. The trends in the rate constants and formation constants showed that the strength of the complex formation is in the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4. The half wave potential values (E1/2) for the one electron reduction of these acceptors indicated that the electronegativity of the acceptors increased from CHL to MQ4. The observed equilibrium, kinetic and electrochemical properties of these acceptors were found to be well supported by ab initio DFT calculations.
Acknowledgements
The authors thank the University Grants Commission, New Delhi for its financial assistance to carry out this research work. One of the authors (C.B.) is thankful to the UGC, New Delhi for the award of UGC-BSR Fellowship in Sciences for Meritorious Students.
References
-
Biochemistry of quinones, ed. R. A. Morton, Academic press, New York, 1965 Search PubMed.
- K. Bradley, M. Briman, A. Satr and G. Gruner, Nano Lett., 2004, 4, 253–256 CrossRef CAS.
- B. Prescott, J. Med. Chem., 1969, 12, 181–182 CrossRef CAS.
- E. M. Hodnett, C. Wongwiechintana, W. J. Dunn and P. Marrs, J. Med. Chem., 1983, 26, 570–574 CrossRef CAS.
- J. N. C Lopez, A. W. Johnson, J. F. Grove and M. S. Bulhoes, Cienc. Cult. (Sao Paulo, Braz.), 1977, 29, 1145–1149 Search PubMed.
-
Methods in Enzymology, ed. H. Sies and L. Packer, Elsevier Academic Press, San Diego, London, 2004, vol. 378 and 382 Search PubMed.
- C. A. Wraight, Front. Biosci., 2004, 9, 309–337 CrossRef CAS.
- T. J. Monks, R. P. Hazlik, G. M. Cohen, D. Ross and D. G. Graham, Toxicol. Appl. Pharmacol., 1992, 112, 2–16 CrossRef CAS.
- A. Brunmark and E. Cadenas, Free Radical Biol. Med., 1988, 7, 435–477 CrossRef.
-
P. Zuman, Substituents effects in organic polarography, Plenum Press, New York, 1967 Search PubMed.
- J. L. Huntington and D. G. Davis, J. Electrochem. Soc., 1971, 118, 57–62 CrossRef CAS.
- C. Y. Li, M. L. Caspar and D. W. Dixon, Electrochim. Acta, 1980 Search PubMed.
- M. Aguilar-Martinez, G. Cuevas, M. Jimenes-Estrada, I. Gonzalez, B. Lotina-Hennsen and N. Macias- Ruvalcuba, J. Org. Chem., 1999, 64, 3684–3694 CrossRef CAS.
- S. D. Bella, I. L. Fragala, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 1993, 115, 682 CrossRef.
- F. Kajzar, Y. Okada-Shudo, C. Meritt and Z. Kafafi, Synth. Met., 1998, 94, 91 CrossRef CAS.
- R. Dabestani, K. J. Reszka and M. E. Sigman, J. Photochem. Photobiol., A, 1998, 117, 223 CrossRef CAS.
- G. Burnstock, Curr. Top. Med. Chem., 2004, 4, 793–803 CrossRef CAS.
- D.W. Krogmann, E. Olivero and W. Duane, J. Biol. Chem., 1962, 237, 3292–3295 CAS.
- V. V. Klimov, E. Dolan, E. R. Shaw and B. Ke, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 7227–7231 CrossRef CAS.
-
A. Trebset, H. Eck and S. Wagner, Photosynthetic mechanism of Green Plants, National Academy of Science, Washington DC, 1963, pp 174–194 Search PubMed.
- A. Mostafa and H. S. Bazzi, Spectrochim. Acta, Part A, 2011, 79, 1613–1620 CrossRef CAS.
- S. Y. AlQaradawi, A. Mostafa and H. S. Bazzi, J. Mol. Struct., 2012, 1011, 172–180 CrossRef CAS.
- M. Pandeeswaran and K. P. Elango, Spectrochim. Acta, Part A, 2010, 75, 1462–1469 CrossRef CAS.
- M. S. Refat, S. A. El-Korashy, I. M. El-Deen and S. M. El-Sayed, J. Mol. Struct., 2010, 980, 124–136 CrossRef CAS.
- R. Huot and P. Brassard, Can. J. Chem., 1974, 52, 838–842 CrossRef CAS.
- M. Pandeeswaran, E. H. El-Mossalamy and K. P. Elango, Int. J. Chem. Kinet., 2009, 41, 789–799 CrossRef.
- K. Ganesh, C. Balraj and K. P. Elango, Spectrochim. Acta, Part A, 2011, 79, 1621–1629 CrossRef CAS.
- C. Balraj, K. Ganesh and K. P. Elango, J. Mol. Struct., 2011, 998, 110–118 CrossRef CAS.
- C. A. T. Laia, S. M. B. Costa, D. Phillips and A. W. Parker, Photochem. Photobiol. Sci., 2003, 2, 555–562 CAS.
- M. Gaber and S. S. Al-Shihry, Spectrochim. Acta, Part A, 2005, 62, 526–531 CrossRef CAS.
- M. Pandeeswaran and K. P. Elango, Spectrochim. Acta, Part A, 2009, 72, 789–795 CrossRef CAS.
- M. S. Refat, J. Mol. Struct., 2011, 985, 380–390 CrossRef CAS.
- R. L. Scott, Recl. Trav. Chim. Pays-Bas Belg., 1956, 75, 787–789 CrossRef CAS.
- C. Balraj, K. Ganesh and K. P. Elango, Spectrochim. Acta, Part A, 2011, 79, 1137–1144 CrossRef CAS.
- G. Weber and L. B. Young, J. Biol. Chem., 1964, 239, 1415–1423 CAS.
- L. D. Ward, Methods Enzymol., 1985, 17, 400–415 CrossRef.
- B. P. Kamat and J. Seetharamappa, J. Photosci., 2004, 11, 29–33 CAS.
- J. S. Park, J. N. Wilson, K. I. Hardcastle, U. H. F. Burnz and M. Srinivasarao, J. Am. Chem. Soc., 2006, 128, 7714–7715 CrossRef CAS.
- T. M. Zhou Swager, J. Am. Chem. Soc., 1995, 117, 12593–12602 CrossRef.
- N. Macias-Ruvalcaba, G. Cuevas, I. Gonzalez and A. Aguilar-Martinez, J. Org. Chem., 2002, 67, 3673–3681 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. J. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03W Revision D.01, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- V. A. Nikitina, R. R. Nazmutdinov and G. A. Tsirlina, J. Phys. Chem. B, 2011, 115, 668–677 CrossRef CAS.
- M. S. Liao, Y. Lu, V. D. Parker and S. Scheiner, J. Phys. Chem. A, 2003, 107, 8939–8948 CrossRef CAS.
- D. Sun, S. V. Rosokha and J. K. Kochi, J. Phys. Chem. B, 2007, 111, 6655–6666 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in all cases. The rate of the CT interaction was observed to decrease from CHL to MQ4 and this variation is well supported by the formation constant and enthalpy of activation values. The half wave potentials, E1/2, for the electro-reduction of these acceptors, evaluated using cyclic voltammetry, were 91, −69, −232, −383 and −556 mV, indicating progressive weakening of the electron accepting properties of the acceptors from CHL to MQ4. Ab initio DFT calculations predicted that the variation in the bond lengths of the carbonyl moieties and the charge densities on the carbonyl oxygen atoms depend largely on the nature of the substituent present in the quinone ring. These variations have been in line with the observed FT-IR spectra of the acceptors. Also the HOMODonor–LUMOAcceptor energy gaps linearly correlate with the association constants evaluated using fluorescence data. The equilibrium, kinetic, electrochemical and theoretical investigations of the CT interaction of these quinones indicated that progressive replacement of an electron withdrawing chlorine atom (−I effect) by an electron releasing methoxy group (+M effect) makes these acceptors progressively weaker.
1 in all cases. The rate of the CT interaction was observed to decrease from CHL to MQ4 and this variation is well supported by the formation constant and enthalpy of activation values. The half wave potentials, E1/2, for the electro-reduction of these acceptors, evaluated using cyclic voltammetry, were 91, −69, −232, −383 and −556 mV, indicating progressive weakening of the electron accepting properties of the acceptors from CHL to MQ4. Ab initio DFT calculations predicted that the variation in the bond lengths of the carbonyl moieties and the charge densities on the carbonyl oxygen atoms depend largely on the nature of the substituent present in the quinone ring. These variations have been in line with the observed FT-IR spectra of the acceptors. Also the HOMODonor–LUMOAcceptor energy gaps linearly correlate with the association constants evaluated using fluorescence data. The equilibrium, kinetic, electrochemical and theoretical investigations of the CT interaction of these quinones indicated that progressive replacement of an electron withdrawing chlorine atom (−I effect) by an electron releasing methoxy group (+M effect) makes these acceptors progressively weaker.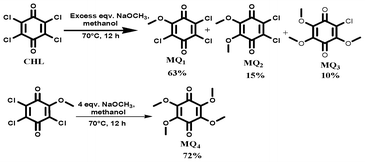
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1668 (C
O), 1668 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1567 (C
O), 1567 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 295 nm (π–π*), log ε 4.24; Anal. calcd. for C7H3Cl3O3: C, 34.82; H, 1.25; N, 0.0; found: C, 36.17; H, 1.74; N, 0.0; m.p. 172 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 295 nm (π–π*), log ε 4.24; Anal. calcd. for C7H3Cl3O3: C, 34.82; H, 1.25; N, 0.0; found: C, 36.17; H, 1.74; N, 0.0; m.p. 172 °C.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 300 nm (π–π*), log ε 4.23; Anal. calcd. for C8H6Cl2O4: C, 40.54; H, 2.55; N, 0.0; found: C, 41.24; H, 2.66; N, 0.0; m.p. 124 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 300 nm (π–π*), log ε 4.23; Anal. calcd. for C8H6Cl2O4: C, 40.54; H, 2.55; N, 0.0; found: C, 41.24; H, 2.66; N, 0.0; m.p. 124 °C.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 302 nm (π–π*), log ε 4.24; Anal. calcd. for C9H9ClO5: C, 46.47; H, 3.90; N, 0.0; found: C, 46.17; H, 3.78; N, 0.0; m.p. 83 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 302 nm (π–π*), log ε 4.24; Anal. calcd. for C9H9ClO5: C, 46.47; H, 3.90; N, 0.0; found: C, 46.17; H, 3.78; N, 0.0; m.p. 83 °C.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1568 (C
O), 1568 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); UV-Vis in 1,2-dichloroethane (λmax): 309 nm (π–π*), log ε 4.25; Anal. calcd. for C10H12O6: C, 52.63; H, 5.30; N, 0.0; found: C, 53.12; H, 5.58; N, 0.0; m.p. 134 °C.
C); UV-Vis in 1,2-dichloroethane (λmax): 309 nm (π–π*), log ε 4.25; Anal. calcd. for C10H12O6: C, 52.63; H, 5.30; N, 0.0; found: C, 53.12; H, 5.58; N, 0.0; m.p. 134 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (D
1 (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A) CT complex (Fig. 1). The photometric titration measurements were also performed for the determination of the stoichiometry in these interactions. For that, the concentration of the donor in the reaction mixtures was kept constant while the concentrations of the acceptors were varied over a wide range. The results of the photometric curves (Fig. 1S†) also indicated that the stoichiometry of the interaction, in all the cases, was 1
A) CT complex (Fig. 1). The photometric titration measurements were also performed for the determination of the stoichiometry in these interactions. For that, the concentration of the donor in the reaction mixtures was kept constant while the concentrations of the acceptors were varied over a wide range. The results of the photometric curves (Fig. 1S†) also indicated that the stoichiometry of the interaction, in all the cases, was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (D
1 (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A).29,30
A).29,30


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1633 (C
O), 1633 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C24H20Cl3NO3: 476.78; found: 477.2; Anal. calcd. for C24H20Cl3NO3: C, 60.46; H, 4.23; N, 2.94: found: C, 60.17; H, 4.40; N, 2.81.
O); LCMS: Calcd. For C24H20Cl3NO3: 476.78; found: 477.2; Anal. calcd. for C24H20Cl3NO3: C, 60.46; H, 4.23; N, 2.94: found: C, 60.17; H, 4.40; N, 2.81.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1644 (C
O), 1644 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C25H23Cl2NO4: 472.36; found: 474.1. Anal. calcd. for C25H23Cl2NO4: C, 63.57; H, 4.91; N, 2.97: found: C, 63.38; H, 4.87; N, 2.89.
O); LCMS: Calcd. For C25H23Cl2NO4: 472.36; found: 474.1. Anal. calcd. for C25H23Cl2NO4: C, 63.57; H, 4.91; N, 2.97: found: C, 63.38; H, 4.87; N, 2.89.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C26H26ClNO5: 467.94; found: 467.8. Anal. calcd. for C26H26ClNO5: C, 66.73; H, 5.60; N, 2.99: found: C, 66.64; H, 5.53; N, 2.96.
O); LCMS: Calcd. For C26H26ClNO5: 467.94; found: 467.8. Anal. calcd. for C26H26ClNO5: C, 66.73; H, 5.60; N, 2.99: found: C, 66.64; H, 5.53; N, 2.96.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1648 (C
O), 1648 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); LCMS: Calcd. For C27H29NO6: 463.52; found: 464.3. Anal. calcd. for C27H29NO6: C, 69.96; H, 6.31; N, 3.02: found: C, 69.22; H, 6.40; N, 3.04.
O); LCMS: Calcd. For C27H29NO6: 463.52; found: 464.3. Anal. calcd. for C27H29NO6: C, 69.96; H, 6.31; N, 3.02: found: C, 69.22; H, 6.40; N, 3.04.
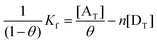
![Fluorescence spectra for the AZA-MQ1 system in 1,2-dichloroethane at fixed concentrations of [D] = {8 × 10−4 M (curve D)} and variable concentration of [A](× 10−5) = {1 (curve a), 2 (curve b), 3 (curve c), 4 (curve d), 5 (curve e), 6 (curve f)}M at 298 K.](/image/article/2012/RA/c2ra20985c/c2ra20985c-f5.gif)





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The trends in the rate constants and formation constants showed that the strength of the complex formation is in the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4. The half wave potential values (E1/2) for the one electron reduction of these acceptors indicated that the electronegativity of the acceptors increased from CHL to MQ4. The observed equilibrium, kinetic and electrochemical properties of these acceptors were found to be well supported by ab initio DFT calculations.
1. The trends in the rate constants and formation constants showed that the strength of the complex formation is in the order AZA-CHL > AZA-MQ1 > AZA-MQ2 > AZA-MQ3 > AZA-MQ4. The half wave potential values (E1/2) for the one electron reduction of these acceptors indicated that the electronegativity of the acceptors increased from CHL to MQ4. The observed equilibrium, kinetic and electrochemical properties of these acceptors were found to be well supported by ab initio DFT calculations.