Determining unknown concentrations of nanoparticles: the particle-impact electrochemistry of nickel and silver
Emma J. E.
Stuart
,
Yi-Ge
Zhou
,
Neil V.
Rees
and
Richard G.
Compton
*
Department of Chemistry, Physical & Theoretical Chemistry Laboratory, Oxford University, South Parks Road, Oxford, OX1 3QZ, United Kingdom. E-mail: Richard.compton@chem.ox.ac.uk; Fax: 44 1865 275410; Tel: 44 1865 275413
First published on 1st June 2012
Abstract
The developing field of particle-impact electrochemistry is rapidly establishing itself as a powerful tool for the interpretation of a wide range of phenomena associated with nanoparticles. In this article we present results showing the characterisation of nickel nanoparticles and, for the first time, a mixture of nanoparticles: in this case nickel and silver. The former are shown not to aggregate in aqueous solution whereas the latter do. We report a novel method for the determination on unknown concentrations of nanoparticles in a sample and demonstrate its use for both aggregating and non-aggregating nanoparticles.
Introduction
Metallic nanoparticles such as nickel are extensively studied in the areas of catalysis, sensing, and electronic applications. However, their interactions with biological systems as well as their environmental and health effects are largely ignored. A number of recent studies report the significant toxicity of metal nanoparticles, such as nickel (NiNPs) and silver (AgNPs) to human lung cells,1,2 and a damaging effect on aquatic organisms.3 Every year, a large amount of engineered metal NPs are released into global water systems raising concerns regarding the environment and public health. Therefore it is highly desirable to urgently develop new techniques to monitor metal NPs in aqueous solution, with a particular need for the characterisation of mixtures of NPs.The electrochemistry of nanoparticles (NPs) during their collisions with electrodes is a rapidly developing field.4 Recent advances include the utilisation of particle impacts to directly characterize and quantify a sample of AgNPs via the anodic particle coulometry (APC) method:5 the extension of APC to characterising AuNPs6 suggests that it may also provide a means for the detection of NiNPs. The electrochemical oxidation of nickel in both alkaline7–9 and acidic solution10,11 has been well studied, as have NiNPs themselves.12,13 In alkaline media, the anodic behavior of nickel results in the production of NiO and Ni(OH)2, while in acidic media, especially in concentrated solutions,11 nickel tends to be dissolved into solution and form Ni2+(aq).
In this paper, we report the sizing and quantification of NiNPs using the APC method in pH 2 solutions of perchloric acid and sodium perchlorate. In addition, we show for the first time the simultaneous detection of mixed metal NP system by monitoring the impact frequency as a function of potential using a model system of a AgNP–NiNP mixture. We also develop a reliable new method to determine the metal NP concentration in aqueous solution by fitting with the integrated flux equation, and demonstrate its use for NiNPs (which are not observed to aggregate over the timescale of the experiment) and AgNPs (which are known to rapidly aggregate5).
Experimental
Nickel nanoparticles (NiNPs) of radii range 15–30 nm were purchased from Nanostructured & Amorphous Materials, Inc. (Houston, Texas, USA). Citrate-capped AgNPs of mean radius 13 ± 2 nm were synthesized according to the method of Pyatenko et al.14,15 NP sizes were confirmed via SEM imaging. Sodium perchlorate (≥98%, NaClO4), sodium dihydrogen citrate (NaC6O7H7 > 99.5%), and potassium chloride (>99.5% Riedel-de-Haan) were supplied by Sigma-Aldrich and used as received. Perchloric acid (70%, HClO4) was purchased from Fisher Chemicals. All solutions were made using ultrapure water of resistivity not less than 18.2 MΩ cm−1 at 298 K (Millipore).The electrochemistry experiments were conducted within a faraday cage using a μAutolab III (Metrohm-Autolab BV, Utrecht, Netherlands) and a three electrode arrangement. Working electrodes used were: a bare glassy carbon (GC, 3 mm in diameter) electrode, or a NiNPs-modified GC electrode, or 6.9 μm radius carbon fibre microelectrode (BASi Inc, Stareton, Warks. UK). A saturated calomel and Ag/AgCl (saturated KCl) were used as reference electrodes (specified in text), and graphite rod as counter electrode. To modify the GC electrode, an aliquot of the suspension of NiNPs was drop-cast on the GC electrode and left to dry under a gentle argon atmosphere. To avoid the aerial oxidation of NiNPs, they were handled in an argon atmosphere at all stages: from transfer out of the sealed sample provided by the supplier, to suspension in deaerated aqueous solution. All experiments were conducted under an argon atmosphere. Spike analysis and fitting was performed using Origin v.8.5 (Microcal Inc).
Results & discussion
1. The particle-impact voltammetry of NiNPs
Voltammograms were recorded for a bare GC electrode and the same GC electrode modified with NiNPs in a solution of 10 mM HClO4 and 100 mM NaClO4, shown in Fig. 1. A distinct anodic stripping peak was observed at the NiNP-modified electrode at ca. + 1.85 V (vs. saturated Ag/AgCl), while there is no oxidation peak but an increase in the anodic current at relatively positive potential on bare GC electrode, corresponding to the oxidation of carbon surface. | ||
| Fig. 1 Voltammograms of a NiNPs modified GC electrode (solid line) and a bare GC electrode (dashed line) recorded in a solution of 10 mM HClO4 and 100 mM NaClO4 at a scan rate of 20 mV s−1. | ||
We next investigated the electro-oxidation of single NiNPs in the same media via the anodic particle coulometry (APC) method through the nanoparticle-electrode collision process.
| Ni(NP) − 2e− → Ni2+(aq) | (1) |
In this experiment, a carbon fibre microelectrode (radius 6.9 μm) was placed in a degassed solution of 10 mM HClO4 and 100 mM NaClO4, and a known concentration of pre-dispersed NiNPs added. The electrode potential was held at +1.7 V (relative to Ag/AgCl) where there is no expected Faradaic processes occurring on the carbon surface, with a data sampling time of 0.5 ms. The oxidative transients were recorded as shown in Fig. 2 (a). Collisions were observed as sharp spikes with durations of 2–10 ms. The procedure was repeated at the potential of 1.0 V and no oxidative spikes were observed, confirming that the Faradaic oxidation is the source of the transients. The collision frequency was found to increase linearly with the concentration of NiNPs shown in Fig. 2 (b), with a rate of 0.22 s−1 pM−1.
 | ||
| Fig. 2 (a) Typical oxidative Faradaic transients of NiNPs in perchlorate solution at the potential of 1.7 V. The inset shows detailed impact spikes. (b) The frequency of spikes as a function of NiNP concentration. | ||
Assuming that the NiNPs are spherical (radius rnp), the maximum charge passed resulting from the complete (2 electrons per atom) oxidation of the NiNPs is given by:
 | (2) |
 | ||
| Fig. 3 (a) Size distributions for NiNPs obtained from APC (○) and SEM (■) data, yielding a most likely radius of 26 nm, and (b) APC data expressed in the no. of Ni atoms oxidised per nanoparticle impact. | ||
2. APC of mixed nanoparticle systems
The APC of AgNPs has been reported previously.5,17,18 A carbon fibre microelectrode (radius 6.9 μm) was placed in a degassed solution of 10 mM HClO4 and 100 mM NaClO4, and a known concentration of pre-dispersed AgNPs added. The average size of the AgNPs had previously been determined to be 13 ± 2 nm (corresponding to ca. 6 × 105 atoms). The electrode potential was held at +0.5 V (relative to saturated Ag/AgCl) beyond the onset potential for impact spikes.5Next, a known concentration of the AgNPs–NiNPs mixture was added into the cell and a range of potentials were applied from +0.2 V to +1.8 V and at each potential the impact frequency recorded. We can see from Fig. 4 that the frequency switches on at the potential of 0.45 V and 1.55 V, corresponding to the direct oxidation of AgNPs and the mixed NPs, respectively. This measurement allows us to simultaneously detect and identify mixed NPs: application of the methodology outlined in section 2 above also enables the determination of the respective concentrations.
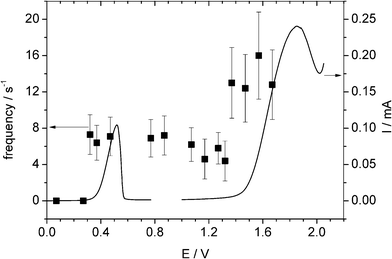 | ||
| Fig. 4 Overlay plot of stripping voltammograms for a AgNP-modified GC electrode and a NiNP-modified GC electrode (right axis) and the impact frequency (left axis). | ||
3. Determination of unknown concentrations of nanoparticles
The steady-state current transient at a microdisk electrode of radius r, assuming a simple n electron oxidation, is given by| I = 4nFCDf(τ) | (3) |
| f(τ) = 0.7854 + 0.8863τ−1/2 + 0.2146exp(0.7823τ−1/2) | (4) |
The experimental observation illustrated in Fig. 2a that impact spikes are more frequent at the start of the chronoamperograms is consistent with this model.
Eqn (4) can also be used to calculate the flux of nanoparticles to the microdisk electrode. For ease of comparison with experimental data, we convert the flux (impacts per second) to the cumulative number of impacts by integrating eqn (4), simplifying the exponential term via a series expansion to 5 terms and introducing electrode area and the Avogadro constant to scale for the number of particle impacts for our electrode area.
| N = NACr3(τ + 1.437τ1/2 + 6.57 × 10−2lnτ − 3.35 × 10−3τ−1 + 3.43 × 10−3τ−1/2 + 3.49 × 10−4τ−3/2) | (5) |
This enables the fitting of experimental data to obtain the nanoparticle concentration, C, by fixing r and D, where r is the radius of the microelectrode (determined by independent electrochemical calibration) and D is calculated from the Stokes–Einstein equation.20
 | (6) |
As a model system for testing this methodology we selected NiNPs due to the absence of aggregation over the experimental timescale as noted above. Fig. 5 shows data of cumulative number of impacts versus time from three separate APC experiments (as described above) using known particle concentrations of 28 ± 4 pM, 54 ± 8 pM and 77 ± 11 pM, with the theoretical lines obtained from optimising eqn (5). The plots give optimised NiNPs concentrations of 30 pM, 60 pM and 80 pM, respectively, in excellent agreement with the known values, demonstrating the usefulness of this method to determine unknown concentrations of nanoparticles. It should be noted that in this methodology, there are no adjustable parameters apart from concentration: the diffusion coefficient of the NP, D is fixed by the NP radius (derived from the APC distribution).
 | ||
| Fig. 5 Integrated Shoup–Szabo fit for the accumulative number of spikes against time at varying NiNPs concentrations of (■) 28, (○) 54, and (▾) 77 pM respectively. The dotted lines show the experimental data and theoretical fit. | ||
Second, as a more challenging nanoparticle system, we selected AgNPs (r = 13 nm) which are known to aggregate in solution, with the average radius observed via APC varying from 13 nm to 29 nm over a period of 2 h.18 A solution of 10 mM citrate and 90 mM KCl was potentiostatted at +0.3 V (vs. SCE) and a known aliquot of AgNPs added so that the concentration of NPs in solution was equal to 56 pM (see Fig. 6). A series of 20 chronoamperometric profiles were recorded over a time period of 8 min with careful timing. Oxidative current spikes were observed in all measurements, however the number of spikes observed per chronoamperograms decreased as the time since dispersion of the sample increased due to aggregation. Fig. 7 demonstrates how the cumulative number of spikes in each profile dwindles from 82 to 36 to 27 spikes per scan at 1, 4 and 8 min time intervals respectively.
 | ||
| Fig. 6 Oxidative Spikes observed in a typical chronoamperometric profile caused by AgNPs colliding with a bare GC electrode (radius 6.9 μm) in 10 mM NaC6O7H7/90 mM KCl at +0.3 V (vs. SCE). The dotted line (....) shows a chronoamperometric profile recorded under the same conditions but with no AgNPs present in solution. | ||
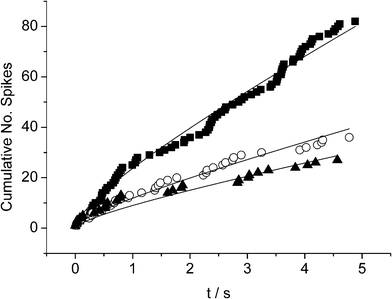 | ||
| Fig. 7 Plots of the accumulative number of spikes vs. time during chronoamperometric measurements at (■) 1, (○) 4 and (▾) 8 mins after AgNP addition respectively, fitted with eqn (6) with fixed D = 1.5 × 10−7 cm2 s−1. | ||
Analysis of impact transients gained at defined times after AgNP addition has shown that as time progresses the average number of NPs in a cluster, χ, increases with χ related to the average radius of the cluster, R, according to:18
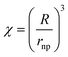 | (7) |
 | (8) |
It is possible to quantify how aggregation progresses with time by applying eqn (5) to the cumulative no. spikes vs. time plots shown in Fig. 7 to determine the particle (single and clusters) concentration, C, with D fixed by the Stokes–Einstein equation as described above. To simplify the automatic fitting of data to simulation, the diffusion coefficient is approximated to be constant and fixed to that of χ = 1 (i.e. R = rnp = 13 nm).† Fitting the experimental data with eqn (5) using the fixed D value (for χ = 1) of 1.5 × 10−7 cm2 s−1, gives average C values of 36 ± 6 pM, 21 ± 5 pM and 17 ± 4 pM for the scans measured at 1, 4 and 8 min time intervals respectively reflecting the aggregation of AgNPs.
Previous work on the aggregation of the same size AgNPs16 determined the variation of mean cluster radius with time. Reinterpretation of that data viaeqn (7), and shown in Fig. 8, enables an empirical expression for χ(t) to be found
| lnχ = 0.42lnt + 0.50 | (9) |
 | ||
| Fig. 8 A plot of ln χ vs. lnt, using data taken from16 according to the text above, with gradient = 0.42 and intercept = 0.50. | ||
Combining eqn (7) and (8), we arrive at an empirical expression of the decrease in concentration of silver nanoparticles (of radius 13 nm) due to aggregation with time
| lnC = −0.42lnt + (lnCD − 0.50) | (10) |
The starting concentration of AgNPs can now be found by plotting the variation in measured concentration (viaeqn (5) and plots such as in Fig. 7) with time and applying eqn (10). Fig. 9 shows a plot of ln C vs. ln t, which shows good agreement with the expression in eqn (10), and yields a value for C0 of 57 ± 10 pM (3.4 × 1010 particles cm−3).
 | ||
| Fig. 9 A plot of ln C vs. ln t. Values for C are calculated from fitting the Shoup and Szabo expression to our experimental data using a fixed D value of 1.5 × 107 cm2 s−1. The C values inferred from multiple scans measured during one minute are averaged to give a single data point at each time interval slope of plot = −0.39 and y-intercept = −31.0. | ||
Separate experiments were conducted to determine the total Ag concentration independently, by first drop-casting a 2μL aliquot of the AgNP suspension onto a glassy carbon macroelectrode and then anodically stripping the silver off to quantify the amount deposited. The charge passed during the stripping stage can then be converted into a number of single AgNPs in the aliquot (by assuming they have the same radius, 13 nm) and thereby C0. An average of five such experiments, gives C0 = 55.7 ± 8.5 pM. This close agreement provides support for this new methodology for determining unknown nanoparticle concentrations.
Conclusions
We have shown that the method of particle-impact voltammetry can be used successfully to characterise nickel nanoparticles, and introduced a new methodology for the determination of unknown concentrations of nanoparticles in the case of aggregating and non-aggregating particles. The use of these methods for mixtures of nickel and silver nanoparticles has been demonstrated, proving the feasibility of particle-impact electrochemistry for real-world applications such as environmental monitoring and chemical analysis.Acknowledgements
The authors thank the Leverhulme Trust (EJS, NVR) and St. John's College Oxford (YGZ) for financial support.References
- M. Ahamed, Toxicol. in Vitro, 2011, 4, 930 CrossRef.
- D. D. Guo, C. H. Wu, X. M. Li, H. Jiang, X. H. Wang and B. A. Chen, J. Nanosci. Nanotechnol., 2008, 5, 2301 CrossRef.
- R. J. Griffitt, J. Luo, J. Gao, J. C. Bonzongo and D. S. Barber, Environ. Toxicol. Chem., 2008, 9, 1972 CrossRef.
- N. V. Rees, Y.-G. Zhou and R. G. Compton, RSC Adv., 2012, 2, 379 RSC.
- Y.-G. Zhou, N. V. Rees and R. G. Compton, Angew. Chem., Int. Ed., 2011, 50, 4219 CrossRef CAS.
- Y.-G. Zhou, N. V. Rees, J. Pillay, R. Tshikhudo, S. Vilakazi and R. G. Compton, Chem. Commun., 2012, 48, 224 RSC.
- A. Seghiouer, J. Chevalet, A. Barhoun and F. Lantelme, J. Electroanal. Chem., 1998, 442, 113 CrossRef CAS.
- J. C. Harfield, K. E. Toghill, C. Batchelor-McAuley, C. Downing and R. G. Compton, Electroanalysis, 2011, 23, 931 CrossRef CAS.
- W. Visscher and E. Barendrecht, Electrochim. Acta, 1980, 25, 651 CrossRef CAS.
- P. Gonzalez, V. A. Cortinez and C. A. Fontan, Talanta, 2002, 58, 679 CrossRef CAS.
- M. Bojinov, J. Electroanal. Chem., 1996, 405, 15 CrossRef.
- A. Ambrosi and M. Pumera, Chem.–Eur. J., 2012, 18, 3338 CrossRef CAS.
- M. Giovanni, A. Ambrosi and M. Pumera, Chem.–Asian J., 2012, 7, 702 CrossRef CAS.
- A. Pyatenko, M. Yamaguchi and M. Suzuki, J. Phys. Chem. C, 2007, 111, 7910 CAS.
- A. Pyatenko, M. Yamaguchi and M. Suzuki, J. Phys. Chem. B, 2005, 109, 2160 CrossRef.
- Y.-G. Zhou, N. V. Rees and R. G. Compton, ChemPhysChem, 2011, 12, 2085 CrossRef CAS.
- Y.-G. Zhou, N. V. Rees and R. G. Compton, Chem. Phys. Lett., 2011, 511, 183 CrossRef CAS.
- N. V. Rees, Y.-G. Zhou and R. G. Compton, ChemPhysChem, 2011, 12, 1645 CrossRef CAS.
- R. G. Compton, C. E. Banks, Understanding voltammetry, Imperial College Press, Singapore, 2nd edn, 2011 Search PubMed.
- K.A. Dill and S. Bromberg, Molecular driving forces, Garland Science, New York, 2002 Search PubMed.
Footnote |
| † Previous studies16 showed R growing from 13 nm to 23 nm in the first 10 min after dispersion. This corresponds to average cluster numbers of 1 to 5.5. From inspection of eqn (6) and (7), it follows that D∝χ−1/2, and so D is approximately constant for the low cluster numbers observed here. |
| This journal is © The Royal Society of Chemistry 2012 |
