DOI:
10.1039/C2RA20495A
(Paper)
RSC Adv., 2012,
2, 5337-5348
Applications of the improved leader-follower cluster analysis (iLFCA) algorithm on large array (LA) and very large array (VLA) hyperspectral mid-infrared imaging datasets†
Received
16th March 2012
, Accepted 19th March 2012
First published on 9th May 2012
Abstract
With the potential and advantages of infrared (IR) spectroscopic applications in biological studies, and the introduction of multi-channel focal plane array (FPA) mid-IR detectors, efficient unsupervised clustering algorithms are required to identify and group similar useful spectra from background or outlier spectra within large hyperspectral datasets. Such classification algorithms are crucial for enabling further multivariate analysis. In this paper, a clustering method coined as the improved leader-follower cluster analysis (iLFCA) algorithm is expounded and demonstrated on two mid-IR imaging datasets of exfoliated oral mucosa cells: a Large Array (LA) 64 × 64 pixels image and a Very Large Array (VLA) simulated 128 × 128 pixels image created as a montage of the original LA data. By concatenating the normalized vector form of each spectrum and its integrated areas of characteristic spectral bands, such as Amide I and II, the specificity and efficacy of the clustering algorithm is enhanced. Human intervention for selecting appropriate user-specified parameters and thresholds is also minimized through the development of an automated bisection search algorithm. This resulted in better computational efficiency for iLFCA compared to its predecessor LFCA algorithm. A comparison of iLFCA and LFCA with a common unsupervised classification method based on Principal Component Analysis (PCA) shows iLFCA achieving better clustering results at shorter computational time. In particular, iLFCA has the capability to process larger datasets, namely VLA datasets, which caused both LFCA and PCA-based methods to fail because of computer memory space limitations. iLFCA can potentially be applied to analyze vibrational microspectroscopic data for diagnosis/screening of biological tissue and cells samples, cell culture growth monitoring, and examination of active pharmaceutical ingredients (APIs) distribution and real-time release of pharmaceutical tablets.
Introduction
The potential of infrared (IR) spectroscopy in biological studies has been demonstrated in numerous research areas, including pathology and microbiology.1–5 As compared to other commonly used analytical techniques, IR spectroscopy has its unique advantages and has thus motivated studies to further explore its applications to provide complementary information or act as a tool for preliminary screenings. For example, tissue biopsy, which is the current “gold standard” of cancer diagnosis, is invasive as it involves the removal of tissues or cells from the patients and requires the examination of these samples by a trained pathologist under a microscope. In contrast, minimally-invasive sampling with IR spectroscopy complemented by computer-aided cancer diagnosis can be applied on bodily fluids, such as blood serum.6 The objectivity and accuracy of such diagnoses are based on training computer algorithms, such as artificial neural networks (ANN).6 Some diagnosis, such as standardized pulsed-field gel electrophoresis (PFGE) DNA-based strain typing is entirely reliable, but it has a long processing time of three days.7 On the other hand, the combination of IR measurements with supervised clustering algorithms is relatively quicker, which potentially provides a preliminary diagnostic screening alternative.7
Different mid-IR measurement techniques can be applied in biological studies, such as reflectance and transmission in both normal and microspectroscopic modes, which can be selected to suit different samples and user requirements.2,5 Through mid-IR spectroscopy, biochemical constituents, such as nucleic acids, glycogen, collagen, various lipids and protein secondary structures, etc., can be identified by different vibrational IR peaks related to their chemical function groups (CH2, CH3, C–C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O, PO2−, etc.) in the wavenumber range of ca. 500–3600 cm−1.8 The introduction of multi-channel mid-IR detectors, such as FPA,9,10 further enhanced the ease of use for IR spectroscopy in biological studies.10,13 In contrast to point mapping IR microspectroscopy, FPA-based global imaging microspectroscopic capability has significantly reduced data collection time for the mid-IR range of ca. 900–4000 cm−1, and increased the number of pixels and the size of microscopic image that can be simultaneously taken in a single measurement or “snapshot”. This global imaging technology, however, has resulted in a new problem—the need for an efficient and systematic procedure to analyze such large arrays of hyperspectral datasets. Hence, it is necessary to develop efficient clustering algorithms that are capable of grouping similar pixels and identifying useful spectra from background or outlier spectra within such large hyperspectral datasets.
O, C–O, PO2−, etc.) in the wavenumber range of ca. 500–3600 cm−1.8 The introduction of multi-channel mid-IR detectors, such as FPA,9,10 further enhanced the ease of use for IR spectroscopy in biological studies.10,13 In contrast to point mapping IR microspectroscopy, FPA-based global imaging microspectroscopic capability has significantly reduced data collection time for the mid-IR range of ca. 900–4000 cm−1, and increased the number of pixels and the size of microscopic image that can be simultaneously taken in a single measurement or “snapshot”. This global imaging technology, however, has resulted in a new problem—the need for an efficient and systematic procedure to analyze such large arrays of hyperspectral datasets. Hence, it is necessary to develop efficient clustering algorithms that are capable of grouping similar pixels and identifying useful spectra from background or outlier spectra within such large hyperspectral datasets.
A number of different classification and clustering methods have been developed and applied on multivariate IR datasets, including hyperspectral FTIR images. A majority of these are supervised methods that employ a set of pre-determined classified data (training set) to establish the relationships between groups and build a classification/clustering model. Soft independent modeling of class analogies (SIMCA), support vector machine (SVM) and artificial neural network analysis (ANN) are typical examples of supervised clustering methods used in pharmaceutical11,12 and biospectroscopic applications13–17. For instance, the utilization of SIMCA on mid-IR images has been employed for the identification of the origin or primary tumor of brain metastases13 and the diagnosis of chronic fatigue syndrome.14 The ability to differentiate between IR spectra of three different tissues types, benign breast, ductal in situ carcinoma (DCIS) and invasive, has been demonstrated using the SVM method.15 Through the use of ANN, it is possible to differentiate between benign and malignant lesions in breast cancer tissue,16 and perform pattern recognition for automated numerical diagnosis in axillary lymph node histology.17
On the other hand, there are unsupervised clustering algorithms, which do not require any a priori information of a training dataset, such as the number of components and the identities or classification of components. Examples of unsupervised algorithms include self-organizing maps (SOM),7 principal component analysis (PCA),16,18 and the leader-follower cluster analysis (LFCA).19,20 The SOM method was used to discriminate between different strains of methicillin-resistant Staphylococcus aureus (MRSA).7 Applications of PCA were employed in the identification of IR spectra from different types of breast tissue, namely fibroadenoma and ductal carcinoma in situ,16 and the classification of NMR spectra of urine from rats subjected to different nephrotoxins (glomerular, papillary and proximal tubular) in an attempt to study drug-induced toxin lesions.18 The algorithm and application of the LFCA method were demonstrated on a LA 64 × 64 pixels image hyperspectral IR dataset of oral mucosa cells.19 By determining the useful spectral vector properties (SVP) of individual spectra, calculating the abstract distances between spectra and utilizing a relative spectral proximity leader-follower linkage method to identify natural groups, the good oral mucosa cells spectra were successfully separated from the background spectra.19 Furthermore, the clustering results from LFCA revealed spectroscopic variation between cellular regions associated with cell perimeter, cell interior and location of the nucleus,19 which is helpful for further multivariate chemometrics analysis.20
In this paper, the computational problem of unsupervised clustering of large hyperspectral IR imaging data is further investigated, in particular, for the LA 64 × 64 pixels and VLA 128 × 128 pixels imaging data. An improved LFCA (iLFCA) algorithm was developed for the automated clustering of LA and VLA imaging data at a faster computational speed compared to its predecessor LFCA that requires comparatively more human intervention. The new iLFCA was successfully tested on the previous 64 × 64 pixels mid-IR imaging data of oral mucosa cells,19 and a simulated montage of 128 × 128 pixels imaging data that was computationally generated from the original 64 × 64 pixels oral mucosa cell data. The improvements in performance and capability of the iLFCA are demonstrated herein alongside a comparison with LFCA and PCA-based unsupervised methods.
Experimental aspects
A Large Array (LA) hyperspectral IR imaging data of exfoliated oral mucosa cells (provided by author W. C.) was used for analysis in this paper. After depositing and air drying the sample on a mid-IR-transparent ZnSe window, a 64 × 64 pixels image was taken using a Varian 7000 FT-IR Stingray Imaging Series spectrometer coupled with a Varian 600 UMA FT-IR microscope and Lancer FPA MCT detector. Each FPA pixel captures an area of approximately 5.5 × 5.5 μm2. Hence the entire 64 × 64 pixels image is equivalent to a sample area of ca. 350 × 350 μm2. The image was acquired with a resolution of 1 cm−1 and co-adds of 16 scans. From the visual image and Amide I absorbance intensity plot of the oral mucosa cells, Fig. 1(a) and (b) respectively, it can be observed that the imaging data consisted of a circular intact cell on the left, and a broken misshapen cell on the right.
 |
| | Fig. 1 Oral mucosa cells IR imaging data, a) visual image of oral mucosa cells, b) colour image of oral mucosa cells at ca. 1665 cm−1 (Amide I) with regions ranging from high (red) to zero (dark blue) intensities observed, c) visual image of simulated oral mucosa cells montage, d) color image of oral mucosa cells montage at ca. 1665 cm−1 (Amide I), e) and f) three ways of splitting the oral mucosa cells montage dataset, horizontal (red), vertical (green) and quadrant (yellow). | |
A simulated montage of 128 × 128 pixels hyperspectral data, formed by combining four of the 64 × 64 pixels original data with different orientations was also created to provide the Very Large Array (VLA) dataset to be tested using the iLFCA, see Fig. 1(c) and (d). It was not possible to acquire this imaging data directly at our laboratory due to the lack of suitable hardware (i.e. no available 128 × 128 pixels FPA detector). Both LA and VLA IR image data (i.e. hyperspectral cube) were transformed into their two-way array data for all cluster analyses herein.
Computation aspects
Based on the validity of the bilinear Lambert–Beer–Bouguer law in eqn (1), the IR absorbance for a mixture Amixsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) with ς number of major components comprising of biomolecular functional group vibrations (e.g. Amide I, II and III, C
) with ς number of major components comprising of biomolecular functional group vibrations (e.g. Amide I, II and III, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, etc.), is the sum of the individual s-th species' conditional molar absorptivities εsk(
O, etc.), is the sum of the individual s-th species' conditional molar absorptivities εsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) at a constant pathlength l multiplied by the respective s-th species' molar concentrations cs for every k-th wavelength
) at a constant pathlength l multiplied by the respective s-th species' molar concentrations cs for every k-th wavelength ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) . The attenuated and source intensities are represented by Isk(
. The attenuated and source intensities are represented by Isk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) and Ioij(
) and Ioij(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) , respectively, and Tsk(
) , respectively, and Tsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) is the transmittance in decimals. Both systematic and random experimental errors, and any spectral absorbance non-linearities are accounted for by the term ϕsk(
) is the transmittance in decimals. Both systematic and random experimental errors, and any spectral absorbance non-linearities are accounted for by the term ϕsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) . A single IR spectrum
) . A single IR spectrum  can thus be represented in a vector form by eqn (2), and a set of n spectra
can thus be represented in a vector form by eqn (2), and a set of n spectra  , consisting of ς major components and v spectroscopic channels, can be written in matrix representation as shown in eqn (3).
, consisting of ς major components and v spectroscopic channels, can be written in matrix representation as shown in eqn (3).| | 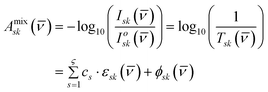 | (1) |
| |  | (2) |
| |  | (3) |
From the mathematical representations in eqn (2) and (3), it is then possible to calculate various spectral vector properties (SVP) of each IR spectrum.19 One frequently used SVP in the iLFCA algorithm is the integrated area between two spectroscopic channels of respective wavelengths/wavenumbers for a particular spectrum, as calculated in eqn (4).
| |  | (4) |
New methodology using iLFCA
Although the LFCA algorithm has shown positive results,19 a significant amount of human intervention, and hence processing time, was required to select appropriate user-defined parameters/thresholds. In our present study, LFCA has also failed to cluster VLA datasets as the abstract Euclidean spectral distance matrix used to determine similarity took up large computer memory space (see Discussion section). Removal of spectra outliers was also necessary prior to LFCA application. In view of these drawbacks, an improved version of the LFCA algorithm, coined as iLFCA, was developed. Four important changes made to the iLFCA algorithm include: (i) use of the concatenated spectra, (ii) use of spectral difference angles from vector inner products as the measure of spectral proximity, (iii) a kernel iLFCA search algorithm for finding leaders amongst a given set of spectral data to be clustered, and (iv) an automated bisection search method for expediting unsupervised clustering so as to reduce computational time. The methodological flow and schematic representation are as follows (see Fig. 2):
i. Form the concatenated matrix from the spectral data
ii. Find the targeted number of clusters using the iLFCA kernel and bisection search algorithms (dotted red box)
iii. Create smaller differentiated clusters through a final round of iLFCA kernel algorithm
 |
| | Fig. 2 New methodology using iLFCA. | |
Improved leader-follower cluster analysis (iLFCA) kernel algorithm
To increase the specificity of the automated iLFCA algorithm, nb number of selected characteristic spectral band integrated areas of the sample IR data,8 such as Amide I and II, can be stringed together as  for each j-th spectrum
for each j-th spectrum  . Eqn (5) shows the nb = 4 bands used in the present study. As the magnitudes of
. Eqn (5) shows the nb = 4 bands used in the present study. As the magnitudes of  and
and  differ, they are normalized (using L∞-norm), in eqn (6) and (7), before being concatenated to form
differ, they are normalized (using L∞-norm), in eqn (6) and (7), before being concatenated to form  or in short
or in short  , of eqn (8). An array of
, of eqn (8). An array of 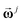 spectral vectors forms the concatenated spectral matrix
spectral vectors forms the concatenated spectral matrix  in eqn (9), which is used in replacement of
in eqn (9), which is used in replacement of  as the abstract coordinates in a relative spectral proximity leader-follower (LF) linkage method to identify natural groups under the iLFCA algorithm. A graphical representation of this concatenation for the present oral mucosa mid-IR imaging data is given in Fig. S1 of the ESI.†
as the abstract coordinates in a relative spectral proximity leader-follower (LF) linkage method to identify natural groups under the iLFCA algorithm. A graphical representation of this concatenation for the present oral mucosa mid-IR imaging data is given in Fig. S1 of the ESI.†| |  | (5) |
| |  | (6) |
| |  | (7) |
| |  | (8) |
| |  | (9) |
In the LFCA algorithm, spectral leaders were selected as the algorithm conducted a brute-force “search and cluster” through the two-way data  in a “top-to-bottom” fashion. This approach resulted in the need for human intervention. Similar to the LFCA algorithm, iLFCA utilizes the abstract proximity of all the other unclustered spectra relative to the chosen leader Li spectrum for clustering. This leader is termed as the interim leader and the measure of proximity is different in the iLFCA. For the original LFCA algorithm, the measure of abstract proximity between spectra was the Euclidean distance, which was found to be suitable as the set of resulting values has a large spread, thus enabling it to represent differences between spectra.19 However, this method generated a distance matrix that required large memory space, and resulted in the failure of the LFCA algorithm when applied to VLA datasets. To handle this problem, the measure of abstract proximity in the iLFCA algorithm is changed to inner products δij or, in practice, spectral difference angles θij in angular degrees based on concatenated spectral vectors, as shown in eqn (10) and (11).19
in a “top-to-bottom” fashion. This approach resulted in the need for human intervention. Similar to the LFCA algorithm, iLFCA utilizes the abstract proximity of all the other unclustered spectra relative to the chosen leader Li spectrum for clustering. This leader is termed as the interim leader and the measure of proximity is different in the iLFCA. For the original LFCA algorithm, the measure of abstract proximity between spectra was the Euclidean distance, which was found to be suitable as the set of resulting values has a large spread, thus enabling it to represent differences between spectra.19 However, this method generated a distance matrix that required large memory space, and resulted in the failure of the LFCA algorithm when applied to VLA datasets. To handle this problem, the measure of abstract proximity in the iLFCA algorithm is changed to inner products δij or, in practice, spectral difference angles θij in angular degrees based on concatenated spectral vectors, as shown in eqn (10) and (11).19
In the new iLFCA clustering, a novel interim leader search algorithm was conceived to automate and quicken the process, and is as follows:
i. Calculate a statistical average spectrum  of the original spectral pool with ntotal number of
of the original spectral pool with ntotal number of  spectra.
spectra.
ii. Rank each j-th spectrum with respect to its proximity to  .
.
iii. Apply the iLFCA algorithm with the first Li interim leader spectrum chosen to be the one closest to the statistical average spectrum  , i.e.
, i.e. for leader index i = 1 or L1.
for leader index i = 1 or L1.
iv. Calculate the statistical mean μi, standard deviation σi and leader-follower linkage criterion γi using eqn (13)–(16) and user-given parameter nLF. Cluster similar spectra within γi alongside Li interim leader's spectrum.
v. Select the next interim leader L2 to be the unclustered spectrum with its  (i = 2) least similar to
(i = 2) least similar to  . Repeat step iv.
. Repeat step iv.
vi. Repeat steps iii to v until all ntotal spectra found their groupings. The Li interim leader spectrum is chosen from the ranking results of ii, such that it is either the next closest from  if i is an odd integer or the next furthest from
if i is an odd integer or the next furthest from  if i is an even integer.
if i is an even integer.
The eventual number of clusters found, nχ, is equal to the number of interim leaders selected from the kernel iLFCA computation. These leader spectra 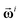 chosen are termed as “interim” because they may not be the eventual (true) leaders of the final set of clusters found (see Results section). The definition of the proximity criteria γi is also different for LFCA and iLFCA, as in eqn (15) and (16).19 Given that the mean μi, standard deviation σi and criteria γi are all positive definite in both eqns, nLF is strictly positive in the original LFCA but it can be negative in iLFCA due to the additional μi. The presence of μi in eqn (15) is introduced to promote greater efficiency.
chosen are termed as “interim” because they may not be the eventual (true) leaders of the final set of clusters found (see Results section). The definition of the proximity criteria γi is also different for LFCA and iLFCA, as in eqn (15) and (16).19 Given that the mean μi, standard deviation σi and criteria γi are all positive definite in both eqns, nLF is strictly positive in the original LFCA but it can be negative in iLFCA due to the additional μi. The presence of μi in eqn (15) is introduced to promote greater efficiency.
| |  | (10) |
| |  | (11) |
| |  | (12) |
| |  | (13) |
| |  | (14) |
| | | γi = μi + nLF × σi, where −2.0 ≤ nLF ≤ 2.0 typically | (15) |
| |  | (16) |
Automated iLFCA search for LA and VLA imaging data
To eliminate the need for human trial and error in finding an appropriate value for nLF and speed up the iLFCA clustering process, an automated search method was devised. This procedure is diagrammatically shown in Fig. 3 for a LA hyperspectral imaging data with 64 or less pixels on either side (i.e. mx and my less than or equal to 64).
The entire LA hyperspectral data was first re-arranged into its corresponding two-way data with (mx × my) spectra and v number of spectroscopic channels (i.e. wavenumber intervals for FTIR imaging data). Next, a set of interim leader spectra was selected from the (mx × my) spectra. In order to avoid arriving at a large number of interim leaders, a novel bisection search algorithm based on the golden ratio was devised to hone in a targeted number of clusters ntargetχ during iLFCA. This bisection search algorithm has two additional features. First, the bisection search maintains the unsupervised nature of iLFCA. Second, this search is applicable to both LA and VLA datasets and potentially deployable on distributed computing platforms (see Discussion section). The automated bisection search algorithm is as follows:
i. Define the integer value of ntargetχ (typically less than or equal to 200) and search range  with upper and lower limits for nLF, where f is the iteration step number.
with upper and lower limits for nLF, where f is the iteration step number.
ii. Perform the kernel iLFCA algorithm for the two extreme ends of  and
and 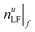 .
.
iii. Calculate  , the difference between the number of clusters,
, the difference between the number of clusters,  , and the user-defined number of clusters, ntargetχ, according to eqn (17) and (18). The
, and the user-defined number of clusters, ntargetχ, according to eqn (17) and (18). The 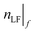 with the lower
with the lower  (either
(either  or
or  ) will be kept as the new
) will be kept as the new  while the other with the higher
while the other with the higher  is to be updated according to step iv.
is to be updated according to step iv.
iv. Using the golden ratio  (or ca. 1.618), calculate the next boundary limit
(or ca. 1.618), calculate the next boundary limit  for the
for the 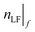 with the higher
with the higher  , according to eqn (19) or (20).
, according to eqn (19) or (20).
v. Repeat steps ii to iv until convergence (i.e. the decrease in the last  or
or  is smaller than the tolerance defined by user, which has a typical value of 1).
is smaller than the tolerance defined by user, which has a typical value of 1).
| |  | (17) |
| |  | (18) |
| |  | (19) |
| |  | (20) |
Once the target number ntargetχ of clustered groups and corresponding ntargetLF parameter value were determined, the resulting interim leader spectra can be further clustered with another application of the kernel iLFCA into different sets of groupings according to the user specified range  at regular intervals. This is to form smaller number of cluster groups of usually ten or less, producing a series of results for the user to qualitatively choose differentiated sets meaningful to the sample context. Clusters which are found to be interesting‡ in this first round can be further sub-classified using a second round of the kernel iLFCA with a different set of
at regular intervals. This is to form smaller number of cluster groups of usually ten or less, producing a series of results for the user to qualitatively choose differentiated sets meaningful to the sample context. Clusters which are found to be interesting‡ in this first round can be further sub-classified using a second round of the kernel iLFCA with a different set of  (see Fig. 3 and Results section) Thus, the interim leaders Li found during the automated iLFCA may not end up as the true leaders after subsequent kernel iLFCA was performed.
(see Fig. 3 and Results section) Thus, the interim leaders Li found during the automated iLFCA may not end up as the true leaders after subsequent kernel iLFCA was performed.
For VLA hyperspectral data with more than 20 million data points, e.g. spatial mx by my dimensions with 128 × 128 pixels FTIR imaging, it is not possible to analyze the entire dataset due to constraints in the largest memory block set in MATLAB® virtual address space on a quad-core CPU workstation. To overcome this computational hurdle, the unfolded two-way VLA data had to be divided into π pieces of two-way LA data as shown in Fig. 4, with each piece separately analyzed using the kernel and automated iLFCA algorithms. For each piece of LA data, ntargetχ number of interim leaders (and thus clusters) was found with the automated and kernel iLFCA procedures. From these (π × ntargetχ) interim leaders of π number of LA data, a smaller set of nχreduced number of interim leaders were selected via another application of the kernel iLFCA algorithm on the set of interim leader spectra with the user-defined  . Any cluster found interesting‡ can be further analyzed with a second application of the kernel iLFCA with
. Any cluster found interesting‡ can be further analyzed with a second application of the kernel iLFCA with  . In this “divide and conquer” manner, not only can the automated iLFCA be applied to VLA data, the application of kernel iLFCA on the interim leader spectra takes into consideration similar spectra that may be found across the different LA datasets and consolidates them in a smaller final number of clusters that is representative of the entire VLA data. Also, all the aforesaid steps for implementing iLFCA on VLA data were performed numerically with minimal human intervention.
. In this “divide and conquer” manner, not only can the automated iLFCA be applied to VLA data, the application of kernel iLFCA on the interim leader spectra takes into consideration similar spectra that may be found across the different LA datasets and consolidates them in a smaller final number of clusters that is representative of the entire VLA data. Also, all the aforesaid steps for implementing iLFCA on VLA data were performed numerically with minimal human intervention.
In this work, all the programming, data preprocessing, LFCA and iLFCA, performed on the IR imaging datasets herein were achieved using in-house programs written with MATLAB version 7.9 (R2009b) on a Hewlett-Packard computer workstation, which operated on Microsoft Windows XP Professional version 2002 and was supported by an IntelCore2 Quad CPU of 2.40 GHz and 2.00 GB RAM. PCA-based hierarchical cluster analyses were computed with MATLAB functions from PLS Toolbox (Eigenvector Research, Inc., Wenatchee, United States) and Statistics Toolbox (MathWorks, Massachusetts, United States), or using in-built functions of the Unscrambler X software (CAMO, Norway).
Results
Oral mucosa cCells 64 × 64 pixels LA dataset
It can be observed in Fig. 1(a) that the mid-IR imaging data consists of a whole cell with its nucleus on the left and an elongated cell on the right, with the latter verified previously as having a broken cell membrane.19 Prior to the application of the iLFCA algorithm, the mid-IR imaging data of the oral mucosa cells 64 × 64 pixels image were preprocessed. First, though the measured spectral range was 900–4000 cm−1, it is not necessary to analyze this entire range since most of the important mid-IR bands assigned to biological components are found in the region between 1050 and 3750 cm−1. In view of this, a truncation of the spectral wavenumber range was done, while maintaining the spectral resolution of 1 cm−1. Next, filtering using the cubic Savitzky–Golay method with 11 frames was performed to improve the signal-to-noise ratio. Offset by the minimum point of each spectrum was then done to ensure that all the values in each spectrum are positive. Last, a L∞-normalisation was done for the concatenation process.
Clustering was performed using the automated iLFCA algorithm on the preprocessed oral mucosa cells 64 × 64 pixels mid-IR imaging data, Ω4096×(2801+4), consisting of 4096 spectra with 2801 spectroscopic (wavenumber) channels and 4 characteristics peak areas (see details in paragraphs below). In contrast to the previous LFCA of the same dataset,19 iLFCA was applied without prior sieving out of outlier spectra. As the amount of computer memory available was sufficient for processing this sizable LA image, iLFCA was applied to the entire dataset without splitting its two-way data array into smaller pieces.
As mentioned above in the Computational Aspects section, the concatenated spectral vector  of eqn (8) was used in replacement of
of eqn (8) was used in replacement of 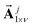 as the abstract spectral coordinates in the iLFCA algorithm. In this case, the characteristic integrated area vector
as the abstract spectral coordinates in the iLFCA algorithm. In this case, the characteristic integrated area vector  included the ranges of ca. 1050–3750 cm−1 (full spectrum), 1546–1556 cm−1 (Amide II), 1646–1656 cm−1 (Amide I), and 2800–3500 cm−1 (broad band centred around 3298 cm−1). The latter 3 regions are highlighted by dotted lines on Fig. 5 right spectral plots.
included the ranges of ca. 1050–3750 cm−1 (full spectrum), 1546–1556 cm−1 (Amide II), 1646–1656 cm−1 (Amide I), and 2800–3500 cm−1 (broad band centred around 3298 cm−1). The latter 3 regions are highlighted by dotted lines on Fig. 5 right spectral plots.
 |
| | Fig. 5 Results of automated iLFCA application to LA oral mucosa cell mid-IR imaging data. | |
In the first step, 200 interim clusters from the LA imaging spectra were found by the aforesaid automated iLFCA golden ratio bisection search algorithm with ntargetχ = 200. After performing one round of kernel iLFCA with n1LF = 1.4 on these 200 clusters, a set of two spectral clusters were found—one with exclusively background spectra and the other is a mixed cluster of cell and background spectra (see Fig. 5 plots). As the background spectra contained a large portion of poor mid-IR transmitted spectra that were caused by the uneven distribution of mid-IR radiation due to optical focusing issues, the segregation of the cells spectra from the poor mid-IR transmitted background spectra was not distinct after one application of iLFCA (see Fig. 5 top left pixel spatial distribution plot). A second round of the kernel iLFCA applied to the 765 spectra cluster with cells and these background spectra using n2LF = 0.0 resulted in the successful separation of cellular FTIR spectra from the background (see Fig. 6). A total of 215 good oral mucosa cells spectra were identified at this stage.
 |
| | Fig. 6 Results of second kernel iLFCA application of LA oral mucosa cell mid-IR imaging data. | |
The spatial distribution of these 215 oral mucosa cell spectra can be further studied by performing a third and final round of iLFCA with n3LF = −0.4. As shown in Fig. 7, the cell spectra distribution matched well with the contour plot of the peak absorbance intensity of Amide I at wavenumber 1665 cm−1. It is observed that clusters 1–4, 6, 8 and 10 made up the perimeters of the two cells while clusters 5, 7, and 9 are located within the interior. The total number and spatial distribution of cell spectra found by iLFCA was comparable to the results obtained through the previous LFCA method.19,20 The time required to perform the automated iLFCA and subsequent kernel iLFCA applications was ca. 1.4 h. In contrast to ca. 20.0 h taken to analyze the same set of data using the predecessor LFCA on the same Hewlett-Packard workstation with IntelCore2 Quad CPU, a huge reduction of ca. 14.3 times in computational time was achieved (see Discussion section for further details).
 |
| | Fig. 7 Results after third round of kernel iLFCA on cells FTIR spectra cluster. | |
Simulated montage oral mucosa cells 128 × 128 pixels VLA dataset
The oral mucosa cells VLA 128 × 128 pixels montage imaging dataset, AVLA16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384×1400, was created by combining four of the original 64 × 64 pixels dataset with different orientations, as seen in Fig. 1(c) and (d). Because the largest memory block allocated in MATLAB virtual address space is insufficient to handle this large number of data points (ca. 23 million data points from AVLA16
384×1400, was created by combining four of the original 64 × 64 pixels dataset with different orientations, as seen in Fig. 1(c) and (d). Because the largest memory block allocated in MATLAB virtual address space is insufficient to handle this large number of data points (ca. 23 million data points from AVLA16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384×1400), it is necessary to split this dataset into π number of smaller pieces of LA data and perform automated iLFCA according to the aforesaid strategy for VLA hyperspectral data (see Fig. 4). To demonstrate the flexibility and robustness of the VLA iLFCA methodology, this large dataset is split in three ways: horizontally, vertically and by quadrants as shown in Fig. 1(e) and (f).
384×1400), it is necessary to split this dataset into π number of smaller pieces of LA data and perform automated iLFCA according to the aforesaid strategy for VLA hyperspectral data (see Fig. 4). To demonstrate the flexibility and robustness of the VLA iLFCA methodology, this large dataset is split in three ways: horizontally, vertically and by quadrants as shown in Fig. 1(e) and (f).
Same as the LA sequence of iLFCA, the concatenated spectral vector 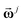 in eqn (8) was used as the abstract spectral coordinates in the VLA iLFCA clustering. The characteristic peaks and integrated areas selected were the same as those for the LA oral mucosa cells dataset.
in eqn (8) was used as the abstract spectral coordinates in the VLA iLFCA clustering. The characteristic peaks and integrated areas selected were the same as those for the LA oral mucosa cells dataset.
The results for applying automated iLFCA and two consecutive rounds of kernel iLFCA to the VLA datasets are shown in Fig. 8 and Fig. 9. An automated iLFCA with ntargetχ = 200 and a subsequent round of kernel iLFCA using n1LF values of 1.8, 1.8 and 3.0 respectively for horizontal, vertical and quadrant split approaches was applied. The cells spectra and the poor mid-IR transmitted background spectra were again separated as a single cluster from the other cluster of background spectra similar to the aforesaid scenario with the original LA data, resulting in 3504 spectra for the horizontal and vertical split approaches and 3436 spectra for the quadrant split (see Fig. 8). The subsequent application of the second kernel iLFCA, with n2LF = 0.2 for the horizontal and vertical split approaches and n2LF = 0.3 for the quadrant split, yielded 954 cells spectra for the first two split approaches and 944 cells spectra for the last. This amounted to 238, 238 and 233 spectra respectively for the horizontal, vertical and quadrant splitting in each stitched original oral mucosa image of the simulated montage. Though these numbers are slightly more than that for iLFCA on the LA data, their mid-IR spectra all belong to oral mucosa cell, and the pixel spatial distribution obtained are comparable to that for the original LA oral mucosa cells imaging dataset (see Fig. 9). Also, the previous LFCA on the LA oral mucosa cell imaging data yielded 236 good quality cell spectra.19
 |
| | Fig. 8 Results of automated iLFCA application to the simulated VLA oral mucosa cell montage data according to piecewise split by a) horizontally, b) vertically and c) quadrants. | |
 |
| | Fig. 9 Results of second application of kernel iLFCA to the simulated VLA oral mucosa cell montage data according to piecewise split by a) horizontally, b) vertically and c) quadrants. | |
Discussion
The basic concept behind the LFCA and iLFCA algorithms is essentially the same. Both attempt to identify natural groups among a set of spectra in a systematic and iterative manner by making use of a relative spectral similarity leader-follower linkage method to distinguish and associate spectra. No a priori assumption of the number or the identities of the groups are required, that is they are strictly unsupervised. However, there are several significant differences between these two methods. First, the iLFCA algorithm performs computer-aided (i.e. automatic) clustering whereas LFCA requires significant amount of human intervention (i.e. non-automatic). iLFCA greatly minimizes any systematic errors arising from human judgments that inevitable vary from person to person. Second, apart from utilizing the spectrum in merely its vector form, as was the case for LFCA, iLFCA also utilizes characteristics spectral band properties, or more specifically, the integrated area of significant bands, to perform calculation and clustering. Third, as shown above, the new iLFCA algorithm is also capable of processing LA imaging datasets in a much shorter time than that taken by the LFCA method. This is an important advantage for the iLFCA in potential fast biomedical diagnosis applications. Furthermore, it was previously reported that the use of Distributed Computing (DC) platform can expedite the multivariate chemometrics analysis of large spectroscopic data with significant reduction in calculation time,21 and the iLFCA strategy for VLA datasets described herein is well-suited to be deployed in such distributed computational platform.
Furthermore, a comparison study of analysis performance and computational time was made for clustering the LA oral mucosa cells 64 × 64 pixels imaging data and its simulated VLA 128 × 128 pixels montage data using LFCA and iLFCA with popular unsupervised clustering methods based on PCA. In essence, PCA reduces the dimensionality of a given dataset by projecting it into a small number of significant orthogonal principal components (PCs). By plotting the scores of two or more PCs against one another, and utilizing a dendrogram or hierarchical clustering methods, the relationships between data points and groups can be identified. For the purpose of this comparison, PCA was carried out using functions available in Unscrambler X and MATLAB R2009b. The PCA algorithms utilized in Unscrambler X were NIPALS and SVD. For MATLAB, PCA calculations were done using the Statistical and Partial Least Squares (PLS) toolboxes (princomp.m and pca.m, respectively), in which the SVD algorithm was employed. Despite the difference in the software and algorithms used, all the 4 sets of PCA results were comparable. Hence the results from MATLAB Statistical toolbox will be used as representative of the PCA results and compared to the LFCA and iLFCA data herein (see Table 1 and also Fig. S2–S4 in the ESI document†).
Table 1 Comparison of performance and computational time between PCA based and leader-follower based unsupervised cluster analysis on LA and VLA mid-IR imaging dataa
| Dataset |
Size of imaging data |
Unscrambler X |
MATLAB |
| PCA (NIPALS algorithm with cross validation) |
PCA (NIPALS algorithm with leverage correction) |
PCA (SVD algorithm with cross validation) |
PCA (Statistics toolbox, SVD algorithm) |
PCA (PLS toolbox, SVD algorithm) |
LFCA |
iLFCA |
|
Notes: F1 (runtime error due to large dataset), F2 (memory error due to large dataset); VLA computation time difference is due to different data splitting approaches (horizontal, vertical and quadrant).
|
| LA |
64 × 64 × 2801 |
3 h |
30 mins |
70 h |
12 mins |
10 mins |
20 h |
1.4 h |
| VLA |
128 × 128 × 1400 |
F1 |
F1 |
F1 |
F2 |
F2 |
F2 |
2.34, 2.40, 2.66 h |
From Table 1, it was observed that all the three unsupervised clustering methods (PCA, LFCA and iLFCA) were capable of analyzing the oral mucosa cells 64 × 64 pixels LA imaging data, but the computational time required ranged from 10 min to 70 h. For PCA, this computational time is highly dependent on its algorithm and whether any data validation method was used. With data validation, the PCA analysis time was greatly protracted. In spite of the fact that the time taken for PCA can be as low as 10 min without data validation, an examination of the clustering results revealed that they are not superior to iLFCA (see Fig. S2–S4 in the ESI document†). All four PCA-based clustering investigated herein were found using the scores based on the first three PCs, which accounted for 96.49% of the total signal (higher PCs were essentially noise related). The abstract Euclidean distance between each and every pair of the scores data points were found and a hierarchical cluster tree was formed from this information. Subsequently, user-defined number of clusters can be specified and determined. However, the discrimination between cells and background mid-IR spectra was extremely poor using the tested PCA-based clustering methods, as shown in Fig. S2–S4.† At the user-specified number of clusters of 30, only spectra in the centre portion of the left cell and outlier spectra were found in distinct clusters, the rest are lost in the background spectra (Fig. S2†). As the number of clusters increased to 50 (Fig. S3†) and 80 (Fig. S4†), increasingly more cell spectra were differentiated from the background. But even at a high number of 80, the pixel locations of cell spectra in the left cell vaguely resemble the visible image Fig. 1(a) and those of the right cell are indistinguishable from background spectra. Therefore, even though some PCA-based methods have faster computational time, their results are not comparable with either LFCA or iLFCA; they are in fact inadmissible for differentiating spectra patterns.
The 20 h taken for LFCA to analyze the oral mucosa cells 64 × 64 pixels LA imaging data includes time for three iterative LFCA rounds and the manual intervention required. With iLFCA, there is an initial bottleneck for the search of interim leaders using the golden ratio bisection method and subsequent rounds of kernel iLFCA proceed relatively fast. There is a significant computational time reduction of 18.6 h (14.3 times improvement) with iLFCA as compared to that achieved by the LFCA method.
Attempts to cluster the oral mucosa cells montage VLA 128 × 128 pixels simulated data failed for all trials using PCA-based methods or the original LFCA, which was due to run time or memory errors. Only iLFCA successfully clustered the VLA dataset. The time taken is acceptable at ca. 2.34, 2.40 and 2.66 h for the three different splitting approaches horizontal, vertical and quadrant respectively. The relatively fast computational time is especially important in view of potential applications, such as clinical pathological diagnosis or real-time release of pharmaceutical tablets during the manufacturing process using near-IR (NIR) imaging.
Conclusion
In this paper, an improved version of the leader-follower cluster analysis (LFCA), coined as iLFCA, is discussed and demonstrated for oral mucosa cells mid-IR imaging datasets with sizes of Large Array (LA) 64 × 64 pixels and Very Large Array (VLA) 128 × 128 pixels. The VLA dataset is a simulated montage data created by combining four of the original LA data with different orientations. With the introduction of several novel computational strategies in the iLFCA approach, the comparisons of its capability, performance and computational time required with the original LFCA and PCA-based unsupervised clustering methods on both LA and VLA datasets demonstrated the greater efficacy of iLFCA. Out of the three methods, only iLFCA was capable of clustering the VLA imaging dataset, and the results from iLFCA (and LFCA) on the LA dataset outshine that of PCA-based methods. It is envisioned that the iLFCA can potentially be applied to other cells and tissue microspectroscopic datasets to differentiate the biomolecular signatures with such samples. Possible applications include analyzing biopsy samples and monitoring cell culture growth (e.g. cancer, microalgae, etc.). iLFCA should also be successful with datasets from other similar optical spectroscopic methods such as NIR and Raman microspectroscopy. As such, it is foreseeable that iLFCA can assess VLA NIR imaging data of pharmaceutical tablets for real-time release applications and examination of active pharmaceutical ingredients (APIs) distribution. For faster computation of VLA and larger hyperspectral datasets, the iLFCA can be potentially deployed under a distributed computing platform.
Symbols used
|
E
| Conditional molar absorptivity matrix |
|
L
i
| The i-th interim leader |
|
f
| Iteration/optimization number |
|
k
| Spectroscopic channel index( ) ) |
|
m
x
| Dimension of pixel image in x direction |
|
m
y
| Dimension of pixel image in y direction |
|
n
target
χ
| Targeted number of clusters |
|
n
LF
| Number of standard deviations, σk, used to calculate the criteria, χ |
|
n
i
| Total number of spectra to be clustered around Li interim leader |
|
s
| Major components index  |
| Δ | Difference between the numbers of clusters from the targeted number of clusters |
| Ω | Concatenated matrix of normalized integrated area and normalized spectra |
|
γ
i
|
Leader-follower linkage criterion of the i-th interim cluster |
|
δ
i
j
| Inner product of the j-th unclustered spectrum w.r.t. interim leader Li |
|
ε
| Conditional molar absorptivity |
|
θ
i
j
| Angular degrees of the j-th unclustered spectrum w.r.t. interim leader Li |
|
μ
i
| Mean of θij of the i-th interim cluster |
|
v
| Number of spectroscopic channels |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
| Wavenumber (cm−1) |
|
π
| Number of LA pieces in VLA |
|
ς
| Number of major components |
|
σ
i
| Standard deviation of θij of the i-th interim cluster |
|
φ
| Golden ratio  or ca. 1.618 or ca. 1.618 |

| Concatenated vector of normalized integrated area and normalized spectra |
Acknowledgements
The authors are grateful to the financial support for the project ICES/09-230B01 that enabled the realization of this work.
References
-
E. Njoroge, S. R. Alty, M. R. Gani and M. Alkatib, Proceedings of the 28th IEEE EMBS Annual International Conference, New York City, USA, 2006 Search PubMed.
- L. Mariey, J. P. Signolle, C. Amiel and J. Travert, Vib. Spectrosc., 2001, 26, 151–159 CrossRef CAS.
- L. Stothers, R. Guevara and A. Macnab, Eur. Urol., 2010, 57, 327–333 CrossRef.
- M. Griebe, M. Daffertshofer, M. Stroick, M. Syren, P. Ahmad-Nejad, M. Neumaier, J. Backhaus, M. G. Hennerici and M. Fatar, Neurosci. Lett., 2007, 420, 29–33 CrossRef CAS.
- C. Krafft, G. Steiner, C. Beleites and R. Salzer, J. Biophotonics, 2009, 2, 13–28 CrossRef CAS.
- J. Backhaus, R. Mueller, N. Formanski, N. Szlama, H. Meerpohl, M. Eidt and P. Bugert, Vib. Spectrosc., 2010, 52, 173–177 CrossRef CAS.
- N. M. Amiali, M. R. Mulvey, J. Sedman, A. E. Simor and A. A. Ismail, J. Microbiol. Methods, 2007, 69, 146–153 CrossRef CAS.
- Z. Movasaghi, S. Rehman and I. ur Rehman, Appl. Spectrosc. Rev., 2008, 43, 134–179 CrossRef CAS.
- J. M. Harnly and R. E. Fields, Appl. Spectrosc., 1997, 51, 334A–351A CrossRef CAS.
- I. W. Levin and R. Bhargava, Annu. Rev. Phys. Chem., 2005, 56, 429–474 CrossRef CAS.
- Y. Roggo, P. Chalus, L. Maurer, C. Lema-Martinez, A. Edmond and N. Jent, J. Pharm. Biomed. Anal., 2007, 44, 683–700 CrossRef CAS.
- C. Gendrin, Y. Roggo and C. Collet, J. Pharm. Biomed. Anal., 2008, 48, 533–553 CrossRef CAS.
- C. Krafft, L. Shapoval, S. B. Sobottka, K. D. Geiger, G. Schackert and R. Salzer, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 883–891 CrossRef CAS.
- A. Sakudo, H. Kuratsune, T. Kobayashi, S. Tajima, Y. Watanabe and K. Ikuta, Biochem. Biophys. Res. Commun., 2006, 345, 1513–1516 CrossRef CAS.
- M. Sattlecker, R. Baker, N. Stone and C. Bessant, Chemom. Intell. Lab. Syst., 2011, 107, 363–370 CrossRef CAS.
- H. Fabian, N. A. N. Thi, M. Eiden, P. Lasch, J. Schmitt and D. Naumann, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 874–882 CrossRef CAS.
- B. Bird, M. Miljkovic, M. J. Romeo, J. Smith, N. Stone, M. W. George and M. Diem, BMC Clin. Pathol., 2008 Search PubMed , 8:8.
- E. Holmes, J. K. Nicholson, A. W. Nicholls, J. C. Lindon, S. C. Connor, S. Polley and J. Connelly, Chemom. Intell. Lab. Syst., 1998, 44, 245–255 CrossRef CAS.
- S. Tan, K. Chen, S. Ong and W. Chew, Analyst, 2008, 133, 1395–1408 RSC.
- W. Xu, K. Chen, D. Liang and W. Chew, Anal. Biochem., 2009, 387, 42–53 CrossRef CAS.
-
W. Chew, S. Ong, M. Garland, Proceedings of AIChE Annual Meeting, San Francisco, CA, 2006 Search PubMed.
Footnotes |
| † Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra20495a/ |
| ‡ Depicted as bold red box within round 1 clustering results in Fig. 3 and Fig. 4 |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O, PO2−, etc.) in the wavenumber range of ca. 500–3600 cm−1.8 The introduction of multi-channel mid-IR detectors, such as FPA,9,10 further enhanced the ease of use for IR spectroscopy in biological studies.10,13 In contrast to point mapping IR microspectroscopy, FPA-based global imaging microspectroscopic capability has significantly reduced data collection time for the mid-IR range of ca. 900–4000 cm−1, and increased the number of pixels and the size of microscopic image that can be simultaneously taken in a single measurement or “snapshot”. This global imaging technology, however, has resulted in a new problem—the need for an efficient and systematic procedure to analyze such large arrays of hyperspectral datasets. Hence, it is necessary to develop efficient clustering algorithms that are capable of grouping similar pixels and identifying useful spectra from background or outlier spectra within such large hyperspectral datasets.
O, C–O, PO2−, etc.) in the wavenumber range of ca. 500–3600 cm−1.8 The introduction of multi-channel mid-IR detectors, such as FPA,9,10 further enhanced the ease of use for IR spectroscopy in biological studies.10,13 In contrast to point mapping IR microspectroscopy, FPA-based global imaging microspectroscopic capability has significantly reduced data collection time for the mid-IR range of ca. 900–4000 cm−1, and increased the number of pixels and the size of microscopic image that can be simultaneously taken in a single measurement or “snapshot”. This global imaging technology, however, has resulted in a new problem—the need for an efficient and systematic procedure to analyze such large arrays of hyperspectral datasets. Hence, it is necessary to develop efficient clustering algorithms that are capable of grouping similar pixels and identifying useful spectra from background or outlier spectra within such large hyperspectral datasets.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) with ς number of major components comprising of biomolecular functional group vibrations (e.g. Amide I, II and III, C
) with ς number of major components comprising of biomolecular functional group vibrations (e.g. Amide I, II and III, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, etc.), is the sum of the individual s-th species' conditional molar absorptivities εsk(
O, etc.), is the sum of the individual s-th species' conditional molar absorptivities εsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) at a constant pathlength l multiplied by the respective s-th species' molar concentrations cs for every k-th wavelength
) at a constant pathlength l multiplied by the respective s-th species' molar concentrations cs for every k-th wavelength ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) . The attenuated and source intensities are represented by Isk(
. The attenuated and source intensities are represented by Isk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) and Ioij(
) and Ioij(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) , respectively, and Tsk(
) , respectively, and Tsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) is the transmittance in decimals. Both systematic and random experimental errors, and any spectral absorbance non-linearities are accounted for by the term ϕsk(
) is the transmittance in decimals. Both systematic and random experimental errors, and any spectral absorbance non-linearities are accounted for by the term ϕsk(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) . A single IR spectrum
) . A single IR spectrum  can thus be represented in a vector form by eqn (2), and a set of n spectra
can thus be represented in a vector form by eqn (2), and a set of n spectra  , consisting of ς major components and v spectroscopic channels, can be written in matrix representation as shown in eqn (3).
, consisting of ς major components and v spectroscopic channels, can be written in matrix representation as shown in eqn (3).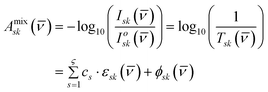




 for each j-th spectrum
for each j-th spectrum  . Eqn (5) shows the nb = 4 bands used in the present study. As the magnitudes of
. Eqn (5) shows the nb = 4 bands used in the present study. As the magnitudes of  and
and  differ, they are normalized (using L∞-norm), in eqn (6) and (7), before being concatenated to form
differ, they are normalized (using L∞-norm), in eqn (6) and (7), before being concatenated to form  or in short
or in short  , of eqn (8). An array of
, of eqn (8). An array of 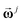 spectral vectors forms the concatenated spectral matrix
spectral vectors forms the concatenated spectral matrix  in eqn (9), which is used in replacement of
in eqn (9), which is used in replacement of  as the abstract coordinates in a relative spectral proximity leader-follower (LF) linkage method to identify natural groups under the iLFCA algorithm. A graphical representation of this concatenation for the present oral mucosa mid-IR imaging data is given in Fig. S1 of the ESI.†
as the abstract coordinates in a relative spectral proximity leader-follower (LF) linkage method to identify natural groups under the iLFCA algorithm. A graphical representation of this concatenation for the present oral mucosa mid-IR imaging data is given in Fig. S1 of the ESI.†




 in a “top-to-bottom” fashion. This approach resulted in the need for human intervention. Similar to the LFCA algorithm, iLFCA utilizes the abstract proximity of all the other unclustered spectra relative to the chosen leader Li spectrum for clustering. This leader is termed as the interim leader and the measure of proximity is different in the iLFCA. For the original LFCA algorithm, the measure of abstract proximity between spectra was the Euclidean distance, which was found to be suitable as the set of resulting values has a large spread, thus enabling it to represent differences between spectra.19 However, this method generated a distance matrix that required large memory space, and resulted in the failure of the LFCA algorithm when applied to VLA datasets. To handle this problem, the measure of abstract proximity in the iLFCA algorithm is changed to inner products δij or, in practice, spectral difference angles θij in angular degrees based on concatenated spectral vectors, as shown in eqn (10) and (11).19
in a “top-to-bottom” fashion. This approach resulted in the need for human intervention. Similar to the LFCA algorithm, iLFCA utilizes the abstract proximity of all the other unclustered spectra relative to the chosen leader Li spectrum for clustering. This leader is termed as the interim leader and the measure of proximity is different in the iLFCA. For the original LFCA algorithm, the measure of abstract proximity between spectra was the Euclidean distance, which was found to be suitable as the set of resulting values has a large spread, thus enabling it to represent differences between spectra.19 However, this method generated a distance matrix that required large memory space, and resulted in the failure of the LFCA algorithm when applied to VLA datasets. To handle this problem, the measure of abstract proximity in the iLFCA algorithm is changed to inner products δij or, in practice, spectral difference angles θij in angular degrees based on concatenated spectral vectors, as shown in eqn (10) and (11).19 of the original spectral pool with ntotal number of
of the original spectral pool with ntotal number of  spectra.
spectra. .
. , i.e.
, i.e. for leader index i = 1 or L1.
for leader index i = 1 or L1. (i = 2) least similar to
(i = 2) least similar to  . Repeat step iv.
. Repeat step iv. if i is an odd integer or the next furthest from
if i is an odd integer or the next furthest from  if i is an even integer.
if i is an even integer.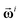 chosen are termed as “interim” because they may not be the eventual (true) leaders of the final set of clusters found (see Results section). The definition of the proximity criteria γi is also different for LFCA and iLFCA, as in eqn (15) and (16).19 Given that the mean μi, standard deviation σi and criteria γi are all positive definite in both eqns, nLF is strictly positive in the original LFCA but it can be negative in iLFCA due to the additional μi. The presence of μi in eqn (15) is introduced to promote greater efficiency.
chosen are termed as “interim” because they may not be the eventual (true) leaders of the final set of clusters found (see Results section). The definition of the proximity criteria γi is also different for LFCA and iLFCA, as in eqn (15) and (16).19 Given that the mean μi, standard deviation σi and criteria γi are all positive definite in both eqns, nLF is strictly positive in the original LFCA but it can be negative in iLFCA due to the additional μi. The presence of μi in eqn (15) is introduced to promote greater efficiency.






 with upper and lower limits for nLF, where f is the iteration step number.
with upper and lower limits for nLF, where f is the iteration step number. and
and 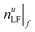 .
. , the difference between the number of clusters,
, the difference between the number of clusters,  , and the user-defined number of clusters, ntargetχ, according to eqn (17) and (18). The
, and the user-defined number of clusters, ntargetχ, according to eqn (17) and (18). The 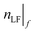 with the lower
with the lower  (either
(either  or
or  ) will be kept as the new
) will be kept as the new  while the other with the higher
while the other with the higher  is to be updated according to step iv.
is to be updated according to step iv. (or ca. 1.618), calculate the next boundary limit
(or ca. 1.618), calculate the next boundary limit  for the
for the 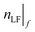 with the higher
with the higher  , according to eqn (19) or (20).
, according to eqn (19) or (20). or
or  is smaller than the tolerance defined by user, which has a typical value of 1).
is smaller than the tolerance defined by user, which has a typical value of 1).



 at regular intervals. This is to form smaller number of cluster groups of usually ten or less, producing a series of results for the user to qualitatively choose differentiated sets meaningful to the sample context. Clusters which are found to be interesting‡ in this first round can be further sub-classified using a second round of the kernel iLFCA with a different set of
at regular intervals. This is to form smaller number of cluster groups of usually ten or less, producing a series of results for the user to qualitatively choose differentiated sets meaningful to the sample context. Clusters which are found to be interesting‡ in this first round can be further sub-classified using a second round of the kernel iLFCA with a different set of  (see Fig. 3 and Results section) Thus, the interim leaders Li found during the automated iLFCA may not end up as the true leaders after subsequent kernel iLFCA was performed.
(see Fig. 3 and Results section) Thus, the interim leaders Li found during the automated iLFCA may not end up as the true leaders after subsequent kernel iLFCA was performed. . Any cluster found interesting‡ can be further analyzed with a second application of the kernel iLFCA with
. Any cluster found interesting‡ can be further analyzed with a second application of the kernel iLFCA with  . In this “divide and conquer” manner, not only can the automated iLFCA be applied to VLA data, the application of kernel iLFCA on the interim leader spectra takes into consideration similar spectra that may be found across the different LA datasets and consolidates them in a smaller final number of clusters that is representative of the entire VLA data. Also, all the aforesaid steps for implementing iLFCA on VLA data were performed numerically with minimal human intervention.
. In this “divide and conquer” manner, not only can the automated iLFCA be applied to VLA data, the application of kernel iLFCA on the interim leader spectra takes into consideration similar spectra that may be found across the different LA datasets and consolidates them in a smaller final number of clusters that is representative of the entire VLA data. Also, all the aforesaid steps for implementing iLFCA on VLA data were performed numerically with minimal human intervention.
 of eqn (8) was used in replacement of
of eqn (8) was used in replacement of 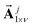 as the abstract spectral coordinates in the iLFCA algorithm. In this case, the characteristic integrated area vector
as the abstract spectral coordinates in the iLFCA algorithm. In this case, the characteristic integrated area vector  included the ranges of ca. 1050–3750 cm−1 (full spectrum), 1546–1556 cm−1 (Amide II), 1646–1656 cm−1 (Amide I), and 2800–3500 cm−1 (broad band centred around 3298 cm−1). The latter 3 regions are highlighted by dotted lines on Fig. 5 right spectral plots.
included the ranges of ca. 1050–3750 cm−1 (full spectrum), 1546–1556 cm−1 (Amide II), 1646–1656 cm−1 (Amide I), and 2800–3500 cm−1 (broad band centred around 3298 cm−1). The latter 3 regions are highlighted by dotted lines on Fig. 5 right spectral plots.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384×1400, was created by combining four of the original 64 × 64 pixels dataset with different orientations, as seen in Fig. 1(c) and (d). Because the largest memory block allocated in MATLAB virtual address space is insufficient to handle this large number of data points (ca. 23 million data points from AVLA16
384×1400, was created by combining four of the original 64 × 64 pixels dataset with different orientations, as seen in Fig. 1(c) and (d). Because the largest memory block allocated in MATLAB virtual address space is insufficient to handle this large number of data points (ca. 23 million data points from AVLA16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384×1400), it is necessary to split this dataset into π number of smaller pieces of LA data and perform automated iLFCA according to the aforesaid strategy for VLA hyperspectral data (see Fig. 4). To demonstrate the flexibility and robustness of the VLA iLFCA methodology, this large dataset is split in three ways: horizontally, vertically and by quadrants as shown in Fig. 1(e) and (f).
384×1400), it is necessary to split this dataset into π number of smaller pieces of LA data and perform automated iLFCA according to the aforesaid strategy for VLA hyperspectral data (see Fig. 4). To demonstrate the flexibility and robustness of the VLA iLFCA methodology, this large dataset is split in three ways: horizontally, vertically and by quadrants as shown in Fig. 1(e) and (f).
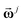 in eqn (8) was used as the abstract spectral coordinates in the VLA iLFCA clustering. The characteristic peaks and integrated areas selected were the same as those for the LA oral mucosa cells dataset.
in eqn (8) was used as the abstract spectral coordinates in the VLA iLFCA clustering. The characteristic peaks and integrated areas selected were the same as those for the LA oral mucosa cells dataset.

 )
) )
)
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
 or ca. 1.618
or ca. 1.618
