High-sensitivity online detection for microfluidics via cavity ringdown spectroscopy
Dean
James
a,
Bobby
Oag
a,
Cathy M.
Rushworth
a,
Jason W. L.
Lee
a,
Joanna
Davies
b,
João T.
Cabral
b and
Claire
Vallance
*a
aDepartment of Chemistry, University of Oxford, Chemistry Research Laboratory, 12 Mansfield Rd, Oxford, OX1 3TA, UK. E-mail: claire.vallance@chem.ox.ac.uk
bDepartment of Chemical Engineering, ACE 311A, Imperial College London, London, SW7 2AZ, UK
First published on 3rd April 2012
Abstract
We report the coupling of cavity ringdown spectroscopy (CRDS) with a microfluidic chip fabricated using a rapid prototyping method, in order to demonstrate high-sensitivity, non-contact online detection in microfluidics. Conventional UV-vis absorption techniques are largely ineffective for microfluidic detection due to the small sample volumes and short path lengths. The multipass absorption achieved in cavity ringdown spectroscopy increases the effective absorption pathlength by several orders of magnitude, and hence enhances the detection sensitivity. A cavity ringdown spectrometer, operating at a single wavelength of 532 nm for the purposes of the proof-of-concept measurements presented here, has been developed for online detection on a polymer/glass microchip fabricated by frontal photopolymerisation. High sensitivity absorption measurements on liquid samples with volumes of tens to hundreds of nanolitres and absorption pathlengths ranging from tens to hundreds of microns are demonstrated. A series of proof-of-concept experiments show that the technique has the ability to monitor both static and time-varying analyte concentrations. Firstly, the detection limit of the system is estimated from a three-standard-deviation error analysis of absorption measurements made on dilute aqueous solutions of potassium permanganate (natural absorption coefficient (4805 ± 10) M−1 cm−1 at 532 nm). The detection limit was found to be ∼210 nM for a 466 μm pathlength, corresponding to an absorption of 1.0 × 10−3 cm−1. Online pH measurements on a 20 nL sample are performed by monitoring the absorption of phenolphthalein indicator present at millimolar concentrations. Finally, CRDS has been applied, for the first time, to monitoring chemical reaction kinetics on a microfluidic chip, tracking the oscillation period of the well-known Belousov–Zhabotinsky reaction.
1 Introduction
Detection and quantification of the tiny volumes of chemical species produced in microfluidic systems remains a major challenge to the full exploitation of microfluidics in biochemical synthesis and analysis. Numerous authors have identified the issue of “efficient extraction and utilisation of the vast amounts of information produced” in microfluidic experiments.1–3 Droplet-based microfluidics have brought a paradigm shift in high-throughput experimentation. Each droplet represents an independent “reactor” volume,4,5 and the ability to produce droplets at up to kHz rates opens up a vast number of applications in biological, chemical and materials synthesis. However, such approaches place additional demands on the detection methods employed, as any detection scheme must be commensurate with these high droplet production rates. At present, chemical analysis is often carried out off-chip6 using conventional laboratory techniques, thus becoming the rate limiting step in what would otherwise be a high-throughput microfluidic reactor.Optical detection provides an appealing approach for online measurements of microfluidic systems. Several optical and spectroscopic on-chip detection methods have thus been integrated with microreactors in recent years to permit the spatio-temporal mapping of reactions and their optimisation, and are the subject of several recent reviews.3,7–10 Laser-induced fluorescence provides a powerful approach for rapid, in situ, detection due to its high sensitivity and small mass requirements, which are well suited to droplet analysis.4,5 Advances in fluorescence lifetime imaging (FLIM) have permitted flow mapping within droplets with 1 μs temporal resolution.11,12 However, such approaches are restricted in scope since they require the presence of fluorophores, and the labelling of reagents is not always possible or is undesirable; for example, in reaction screening and discovery.
UV-vis spectroscopy;13–15 Fourier transform infrared spectrosopy (FT-IR),13,16–18 including multiple-internal reflection (MIR)16 and imaging;18 Raman scattering;13,20–22 microcoil nuclear magnetic resonance (NMR)19,23,24 or stripline detection25 with microcoils; and surface plasmon resonance (SPR), have all been reported as approaches to online detection in microfluidics. In general, these approaches involve a high degree of spatial averaging over large detection areas (for example, in plane optical detection26) or integration over relatively long times17,22 in order to acquire statistically significant spectroscopic data. They are therefore suitable for single phase, continuous reactions with stationary (time-invariant) composition profiles, but are not generally applicable to multiphase flows. Recently, surface-enhanced Resonance Raman spectroscopy (SERRS) has been reported to achieve sub-millisecond time resolution with high sensitivity on droplets containing magnetic nanoparticles,27 and progress in FT-IR imaging has enabled the label-free resolution of segmented flows with ∼100 ms time resolution.18
Advanced UV-vis absorption techniques are particularly attractive for microfluidic detection due to their universal nature and potential for high sensitivity: every analyte absorbs light in some region of the electromagnetic spectrum, and by selecting a wavelength range across which the solvent is transparent and there are no significant overlapping absorption bands from other species, a sufficiently sensitive absorption measurement can allow for label-free analyte detection. However, minute detection volumes (pL–nL) and short path lengths (typically a few hundred microns or less) severely limit the application of traditional single-pass absorption spectroscopy in microdevices. Cavity ringdown spectroscopy (CRDS) is a highly sensitive absorption technique based on the decay of light within a high finesse optical cavity.28 Most CRDS measurements, including ours, employ a simple confocal Fabry–Perot cavity, comprised of two highly reflective concave mirrors (reflectivity > 99.8%). A pulse of laser light is directed into the back face of the first mirror and a small amount couples through the mirror into the cavity. The light is repeatedly reflected back and forth between the mirrors, decaying exponentially with time as a constant fraction couples out from the cavity on each interaction with the mirrors. The decay time constant, or ‘ringdown time’, τ is determined purely by the geometry of the cavity and the round-trip transmission T:

| (1) |
 | (2) |
 | (3) |
CRDS and related techniques are currently amongst the most sensitive spectroscopic absorption techniques available for both the gas-phase30 and the liquid-phase,31,32 although they have been much more widely applied in the gas-phase. The high sensitivity results firstly from the vast increase in optical path length relative to single pass techniques, and secondly from the fact that because the technique relies on a measurement of the rate of decay of light intensity within the cavity rather than on the intensity itself, the signal is decoupled from the initial light intensity and is therefore largely immune to noise arising from shot-to-shot variations in the light source. While the method is relatively insensitive to fluctuations in the incident light intensity, the source intensity is one of the key factors that determine the signal-to-noise ratio of the ringdown signal, and therefore the accuracy to which the ringdown time can be determined.
The high sensitivity of CRDS makes it an attractive option for microfluidics applications, providing a vastly increased optical pathlength without increasing the sample volume probed. To our knowledge, most attempts to couple CRDS with microfluidic systems have so far employed optical fibre loop cavities rather than Fabry–Perot cavities.33 This approach has the advantage that optical fibres are well matched in size to the dimensions of microfluidic channels, with fibre core diameters commonly less than 500 μm. However, fibre-loop CRDS has relatively high intrinsic cavity losses,34 resulting in a reduced sensitivity. Here we describe the application of conventional two-mirror CRDS to the interrogation of microfluidic liquid samples. CRDS measurements on liquid samples are inherently less sensitive than gas-phase measurements due to increased scattering and absorption losses associated with both the sample and its container, but still represent a considerable improvement on single-pass methods. While liquid can be introduced to fill the entire space between the cavity mirrors,35–38 the requirement of probing small liquid sample volumes in microfluidics usually necessitates the introduction of (typically glass) containers (otherwise known as absorption cells) into the cavity. Past work on liquid-phase CRDS has focused on the introduction of cuvettes39,40 or flow cells41,42 into the cavity, with a particular emphasis on the use of CRDS for small volume HPLC. The path lengths and detection sensitivities achieved using these techniques are summarised in Table 1 of ref. 43. The majority of liquid-phase CRDS have probed sample volumes > 1 μL, with notable exceptions being the work of Snyder and coworkers,41 Bechtel and coworkers42 and Alexander.43 The reader is also directed to a recent review of liquid-phase CRDS techniques.44
We report what we believe to be the first example of CRDS measurements on a microfluidic chip inserted into a two-mirror cavity. The chip can be readily fabricated via rapid prototyping and the non-contact nature of the two-mirror approach should allow for the spatio-temporal mapping of the chip, avoiding expensive integrated and less flexible spectroscopic probe arrangements. We have characterised the sensitivity of our microfluidic-CRDS system and also include proof-of-concept demonstrations of pH measurements and real-time tracking of an oscillating reaction.
2 Experimental
2.1 Instrumentation
A schematic of the experimental setup used is shown in Fig. 1(a). The light source is a pulsed Nd/YAG laser: either a Teem Photonics NP-10620-100 (6 μJ per pulse, 900 ps pulse width, 7.4 kHz repetition rate), which was used for the detection limit measurements, or a Teem Photonics SNP-08E-100 (8 μJ per pulse, 900 ps pulse width, 7.4 kHz repetition rate), which was used for the remaining experiments. In each case, the laser output is frequency doubled to produce a beam of 532 nm light. The optical cavity is formed from two concave dielectric mirrors (CVI Melles Griot, reflectivity > 99.8% at 532 nm) with a diameter of 25 mm and a radius of curvature of 1 m. For the majority of experiments presented here, the mirror separation was 875 mm, except for the detection sensitivity measurements described in Section 2.2.1, for which the separation was 585 mm. Light is coupled into the cavity by directing the laser pulse into the rear of one of these mirrors. An iris is placed in front of the cavity such that the beam radius in the centre of the cavity is estimated to be around 300 μm. Light emerging from the cavity is detected by a photomultiplier tube (PMT, Hamamatsu, H6780-20), which is either placed directly behind the second mirror (in which case the PMT is shrouded in blackout material to reduce background signal caused by ambient light), or coupled to the cavity output via a 3 mm diameter liquid light-guide (Edmund Optics, NT53-428). The signal from the PMT is displayed on a digital oscilloscope (Tektronix, TDS 3044B), which is interfaced to a personal computer via a GPIB-USB interface (National Instruments, 778927-01). In all the experiments presented here, the laser pulse duration of 900 ps is less than the round trip time of the cavity, such that the cavity output consists of a train of pulses with exponentially decaying intensities. | ||
| Fig. 1 (a) Schematic of the experimental setup (see text for details); (b) design of the microfluidic chip used for the majority of the work described in this paper. Inlet/outlet ports are labelled A, B, and C. | ||
Data is acquired and analysed in real time using a home-written LabVIEW program. The data acquisition time, corresponding to a full ringdown trace, is typically 1 μs, commensurate with online droplet analysis. However, the data transfer between the oscilloscope and the computer is currently limited to four traces per second. In a typical measurement, the ringdown trace is averaged 512 times on the oscilloscope, and 50 averaged traces are recorded and saved. For each trace, signal intensity and time thresholds are applied if required to limit the data analysis to the exponentially decaying region of the ringdown pulse train. A peak-finding algorithm is employed to determine the baseline-subtracted amplitude S of each peak in the pulse train, and the ringdown time is determined from a linear fit to a log plot of the resulting intensity vs. time data, i.e.
 | (4) |
The microfluidic chip is mounted in the centre of the cavity on a double-rotation (Thorlabs, RP01) and three-axis translation stage (Newport Corporation, 443), with micrometer resolution actuators (Newport Corporation, SM-25), allowing individual microfluidic channels to be precisely located within the laser beam path. Two different designs of microfluidic chip were employed in this work, both fabricated by rapid prototyping of a multifunctional thiol-ene negative resist via frontal photopolymerisation,45–48 and yielding organic solvent resistant polymer matrices sandwiched between two glass faces. The first liquid cell was manufactured by sealing a 100 μm thick glass cover slip against a 1 mm glass microscope slide which had been drilled with inlet and outlet ports. A thiolene-based negative photoresist (Norland Optical Adhesive, NOA 81) was applied around the edges of the cover slip, sealing the system and resulting in a single 5 mm wide, 61 μm deep channel; this cell was employed to make pH measurements, sampling a volume of around 20 nL (assuming in this case a beam radius of around 320 μm). The second type of microdevice was fabricated by sandwiching the thiolene resist between two 141 μm thick glass cover slips, separated by silicon wafer spacers at a distance of 380 μm. A photomask printed on an acetate film with a negative of the chip design (shown in Fig. 1(b)) was then secured over the top layer, and the system was cured via frontal photopolymerisation using a collimated UV source. A calibrated UV light dose was delivered to ensure that the thiolene in the unmasked regions was completely cured. The uncured photoresist was then pushed out of the resulting microfluidic channels (at a temperature of 65 °C, to reduce viscosity) using pressurised air, followed by acetone. The channels were inspected using an inverted microscope (Olympus, IX71) to ensure that no defects or contaminants were present. Nanoports (Upchurch Scientific) were fitted to holes pre-drilled through one of the glass cover slips, forming inlets/outlets capable of connection to a syringe pump. The edge of the completed microfluidic chip was then mounted on a 1 mm thick glass microscope slide, such that the microscope slide did not infringe on the path of the laser, to provide a rigid point at which the chip could be clamped securely in place inside the ringdown cavity. Once mounted within the cavity, one or more syringe pumps (Chemyx Inc, Fusion 400) were used to inject the samples into the microdevice.
Incorporating a microfluidic chip into the cavity introduces four additional surfaces at which scattering and reflection can occur, as illustrated in Fig. 2(a). In order to minimise scattering losses, great care was taken to ensure high quality and cleanliness of all surfaces, including the internal surfaces of the chip. Reflection losses may be reduced either by ensuring that all surfaces are normal to the laser beam, which in practice is extremely difficult to achieve using our current chip fabrication procedure, or by mounting the chip within the cavity at approximately Brewster's angle to the (p-polarised) laser beam. In our setup, the chip is mounted on a rotation stage, allowing the angle of the chip to the cavity axis to be adjusted so as to optimise the ringdown time. Ringdown measurements on an empty cavity indicate that the intrinsic cavity losses resulting from transmission through the mirrors are around 0.2%. An additional loss of typically around 0.5% is incurred by placing a water-filled thiolene-glass microfluidic chip within the cavity at an optimised angle of 59° (see discussion of optimisation procedure below), reducing the measured ringdown time from 952 ns to around 272 ns.
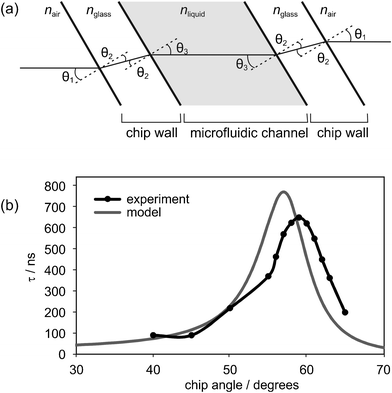 | ||
| Fig. 2 (a) Interfaces experienced by the light beam as it passes through the microfluidic chip; (b) measured dependence of the ringdown time on the incidence angle of the laser to the microfluidic chip within the cavity. The measurements are compared with the results of the simple model described in the text, which is based on quantifying the reflection losses at each interface. | ||
Prior to carrying out any spectroscopic measurements, the dependence of the ringdown signal on the chip angle within the cavity was characterised. Fig. 2(b) shows the experimentally measured ringdown time as a function of the angle between the chip surface normal and the cavity axis. There is a clear maximum in ringdown at an angle of 59°, and this chip angle was used for all further ringdown measurements. We note that at the optimum angle of 59° the optical pathlength through the sample is increased significantly from the optical pathlength at normal incidence.
The dependence of the ringdown time on chip angle may be explained simply by considering the reflection losses at each surface within the cavity. Fig. 2(a) shows the various interfaces encountered by the light beam as it passes through the chip. The angles of refraction at each interface are defined by Snell's law:
| n 1sinθ1 = n2sinθ2 | (5) |
 | (6) |
2.2 Measurements
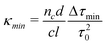 | (7) |
In this work, we define Δτmin as three times the standard deviation (σ) in the baseline ringdown time τ0. It can be seen from eqn (7) that improving the sensitivity of a ringdown measurement relies primarily on minimising the baseline losses to maximise τ0, as well as on increasing the pathlength of light through the sample (l). Short pathlengths are inherent in microfluidic systems, and significant cavity losses are unavoidable when including a microfluidic chip. While this will limit the sensitivity of the system, considerable increases in sensitivity over single pass measurements are still gained by cavity enhancement.
For comparison with the above estimate of our detection sensitivity, the detection limits of the system were also evaluated via absorption measurements on a series of low-concentration aqueous solutions of potassium permanganate, KMnO4, a strongly absorbing species whose visible absorption maximum lies close to the wavelength of our laser (532 nm). Concentrations spanning the range from 10−4 to 10−7 M were prepared by serial dilution, flowed through the microfluidic chip mounted within the cavity at a constant flow rate of 0.2 mL min−1, and probed using CRDS as described above. Between each measurement, the microfluidic chip was flushed with water flowing at 0.2 mL min−1 for five minutes, and a measurement of the baseline ringdown time (τ0) was obtained to ensure that the chip was not contaminated with residual KMnO4 solution. The (natural) absorption coefficient, α, for KMnO4 at 532 nm was determined in a conventional single pass absorption measurement (repeated five times) through a 1 cm cuvette filled with 6.5 × 10−4 M KMnO4 to be (4805 ± 10) M−1 cm−1 (Varian Cary-100 Bio UV-vis spectrometer). Given that the 380 μm pathlength across the chip was found to vary by several tens of microns (measured using a micrometer), as the two chip faces were not perfectly parallel to each other, rather than using a fit of the ringdown data to eqn (3) to determine the α value, instead the pathlength across the chip at the intersection point of the laser beam was determined using α which was precisely known from the UV-vis spectrometer data.
 | ||
| Fig. 3 Structural forms of phenolphthalein. | ||
The process involved in the colour change may be summarised as HInd ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) H+ + Ind−, where HInd and Ind− are the protonated and deprotonated forms of the indicator, respectively, with
H+ + Ind−, where HInd and Ind− are the protonated and deprotonated forms of the indicator, respectively, with
 | (8) |
The concentration of deprotonated phenolphthalein, [Ind−], may be determined from the results of an absorption measurement, using eqn (3). Rearranging eqn (8) then allows the pH to be determined, assuming the initial concentration of indicator is known.
 | (9) |
For these measurements, a stock solution of 0.015 M phenolphthalein solution was prepared in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ethanol and water. For each measurement, 0.1 mL of indicator was added to 5 mL of buffer solution, to give a total indicator concentration of 2.9 × 10−4 M, and the absorption of the resulting solution was determined following a measurement of the ringdown time τ. Two types of buffer solution were used: a sodium tetraborate and hydrochloric acid buffer solution was used for the range of pH 7.6 to 9.4; and a glycine and sodium hydroxide solution was used for the range from pH 9.0 to 11.0. The absorption coefficient of phenolphthalein was determined for each pH used.
1 mixture of ethanol and water. For each measurement, 0.1 mL of indicator was added to 5 mL of buffer solution, to give a total indicator concentration of 2.9 × 10−4 M, and the absorption of the resulting solution was determined following a measurement of the ringdown time τ. Two types of buffer solution were used: a sodium tetraborate and hydrochloric acid buffer solution was used for the range of pH 7.6 to 9.4; and a glycine and sodium hydroxide solution was used for the range from pH 9.0 to 11.0. The absorption coefficient of phenolphthalein was determined for each pH used.
As a reference for comparison, the experiment was repeated in a 1 cm cuvette using a commercial UV/vis spectrometer (Unicam, UV2-100). A concentration of 1.49 × 10−3 M phenolphthalein was used for these measurements, an order of magnitude larger than that used in the microfluidic experiment. To account for this difference, the single-pass data was scaled by the ratio of indicator concentrations.
For simplicity, the reagents (5 mL of 0.23 M NaBrO3 aqueous solution, 5 mL of a 0.31 M malonic acid and 0.059 M NaBr aqueous solution, 5 mL of a 0.019 M Ce(NH4)2(NO3)6 and 2.7 M H2SO4 solution, with 0.1 mL of 0.0125M Ferroin indicator)51 were mixed in bulk prior to being injected into the chip. The reaction mixture was injected into the chip at a flow rate of 0.1 mL min−1, but once the continuous liquid flow had passed the laser beam position, flow was stopped and the oscillations were recorded under static conditions. Ringdown traces were averaged 32 times on the oscilloscope, and data was acquired at a rate of 1 Hz. The oscillations were then followed by monitoring the change in τ over time.
To obtain a reference to compare with, the experiment was repeated at the same concentration in a 1 cm cuvette and monitored as a function of time, via a single-pass 532 nm absorption measurement using the same laser and a silicon photodiode detector (Thorlabs DET 10A).
3 Results and discussion
3.1 Detection limits
As described in Section 2.2.1, ringdown times were recorded for a series of aqueous solutions of KMnO4, with concentrations ranging from 10−4 to 10−7 M. Typical ringdown signals are shown in Fig. 4. When used in combination with the known absorption coefficient α for KMnO4 of (4806 ± 106) M−1 cm−1 (determined in a separate single-pass measurement using a solution housed in a commercial cuvette) these measurements allow us both to determine an accurate value for the pathlength within the microfluidic chip, and to determine the limit of detection for KMnO4. The pathlength is determined from the gradient of a plot of κ against concentration (eqn (3)), shown in Fig. 5, to be 466 ± 10 μm. | ||
| Fig. 4 Typical ringdown traces recorded for a cavity containing a thiolene glass microfluidic chip: reference ringdown recorded when the channels are filled with water (grey trace); ringdown recorded when the channels are filled with 50 μM aqueous KMnO4 solution (black trace). | ||
 | ||
| Fig. 5 Measured absorbance as a function of concentration for a series of aqueous solutions of KMnO4 over the concentration range from 100 nM to 100 μM. | ||
The measured ringdown time for a chip filled with pure water was 271 ns, with a standard deviation of 0.6 ns. Determining the detection limit as described in Section 2.2.1, we have Δτ = 3σ = 1.8 ns, which when substituted into eqn (7) yields an absorbance detection limit of κmin = 1.0 × 10−3 cm−1. This corresponds to a concentration detection limit for KMnO4 of approximately 214 nM in an illuminated volume of 132 ± 3 nL, which is in qualitative agreement with the concentration at which a change in ringdown time can be discerned relative to the reference measurement.
The detection limit can also be estimated from the 3σ uncertainty in the intercept of the plot shown in Fig. 5. The value of 5.2 × 10−3 cm−1 obtained in this way is somewhat higher than that determined above from the baseline noise in our τ0 measurement. This is unsurprising, as the measurement based on τ0 assumes that there are no sources of error other than the intrinsic noise in the ringdown measurement. In reality, factors such as a drift in the cavity alignment and uncertainties in the analyte concentration are likely to contribute to the overall measurement uncertainty.
While we believe our work marks one of the first applications of CRDS to measurements on microfluidic samples, measurements through a similar path length of liquid have been carried out previously. Snyder and coworkers41 used a bespoke high-optical-quality Brewster's angle flow cell with a volume of 10 μL and an optical path length of 300 μm to achieve a detection limit of 6.2 × 10−4 cm−1 at 470 nm. Using the same flow cell, Bechtel and coworkers42 further improved the detection limit to 7.8 × 10−6 cm−1 by replacing the pulsed 470 nm laser source used to excite the cavity with a single-mode continuous wave laser source operating at 488 nm, thus reducing noise on the signal associated with shot-to-shot fluctuations in the laser intensity. Our detection limit is somewhat higher than those reported by Snyder and Bechtel, which can be ascribed primarily to the fact that our simple microfluidic chip is not manufactured from high optical quality components, and almost certainly suffers from small scattering losses at the surfaces. There is scope to improve the optical quality of the microfluidic chip, and therefore to lower our detection limit, but even so, the integrated microfluidic chip CRDS system provides a good general platform for chemical analysis, with the potential for probing smaller sample volumes than the flow cell arrangement.
The detection limit obtained here within a two-mirror cavity can also be compared to that obtained using fibre-loop CRDS techniques. Rushworth et al.34 recently reported a detection limit of 0.11 cm−1 using a cavity comprising a 3.08 m loop of 365 μm core diameter optical fibre. The path length through the sample was 180 μm, corresponding to a total probed sample volume of 19 nL. Using a similar technique,53 Waechter et al. recently reported a detection limit of 4.6 × 10−2 cm−1 in a slightly smaller volume (100 nL compared to 132 nL), but with a significantly longer path length (800 μm compared to 466 μm). In this case, the fibre-loop cavity comprised a 9.25 m loop of 400 μm core diameter optical fibre. While fibre-loop cavities have a number of advantages for measurements on microfluidic samples, being well size-matched to microfluidic channels and inherently able to support a broad range of wavelengths, the detection limits achievable are currently several orders of magnitude poorer than for two-mirror arrangements due to the unavoidably higher cavity losses associated with coupling light into and out of the loop and introducing a sample region.
3.2 pH measurements
As explained in Section 2.2.2, CRDS measurements of the optical absorption by phenolphthalein indicator were used to track the pH of a series of buffer solutions as they flowed through the microfluidic chip. Fig. 6 shows the measured absorbance as a function of pH over this range for the CRDS measurements over the pH range 7.0 to 11.0. The measured absorbance is directly proportional to the concentration of deprotonated indicator, and follows the typical titration curve of a weak acid, and the CRDS measurements are in good agreement with single pass measurements made on a bulk sample contained in a 1 cm cuvette. | ||
| Fig. 6 Absorption measurements as a function of pH for buffered solutions of phenolphthalein indicator. Two different buffers were used to cover the range from pH 7.0 to 11.0. | ||
For a known indicator concentration, the measured absorbance may be converted directly into a pH value using eqn (9). Throughout the steepest part of the titration curve (pH range ∼ 9–10.5), the error on our experimental measurements allows the pH to be measured to ± 0.028 of a pH point. Outside of this range, the titration curve levels off and the absorbance is only weakly dependent on pH, leading to much greater uncertainty. These measurements demonstrate that provided an indicator can be found whose colour change matches the pH region of interest, and a probe wavelength identified that does not overlap with absorption by the sample, introducing a low concentration of an indicator compound to a sample and tracking its absorption provides a general method for pH monitoring on a microfluidic chip.
3.3 Oscillations of the Belousov–Zhabotinsky reaction
To demonstrate the potential use of CRDS for monitoring the progress of chemical reactions occurring on microfluidic chips, the Belousov–Zhabotinsky reaction was performed in the thiolene-glass chip within the cavity, and the ringdown time was monitored as a function of time from reaction initiation. The reaction was carried out with a series of different concentrations of the Ferroin indicator (3.125 × 10−5 M to 5 × 10−4 M) in order to determine the optimum concentration for monitoring the reaction both in CRDS and bulk absorption measurements. Fig. 7 shows example data sets for an indicator concentration of 2.5 × 10−4 M. | ||
| Fig. 7 Absorption signal recorded as a function of time for the oscillating Belousov–Zhabotinsky reaction. The grey trace shows the single-pass absorption recorded at 532 nm when the reaction was carried out in a 1 cm cuvette, while the black trace shows the absorption measured by CRDS when the reaction was carried out on the microfluidic chip shown in Fig. 1(b). | ||
Under our reaction conditions, the oscillation period of the reaction carried out on-chip is similar to that found in bulk solution, around 70 s in both cases. However, the functional forms of the oscillations in the absorption signal are quite different for the two setups, indicating that the detailed kinetics of the reaction are affected considerably by the shape and size of the reaction vessel. After several oscillations, bubbles of CO2 (one of the reaction products) begin to form within the microfluidic channels, degrading the ringdown signal; however the bubbles do not appear to affect the period of oscillation. These results demonstrate that CRDS measurements are easily able to track the kinetics of reactions occurring on a timescale of seconds. In principle, it should be possible to track events occurring on the μs timescale, with even shorter timescales being possible if a time-varying concentration is allowed when fitting the ringdown traces. However, the time resolution of the instrumentation used in this demonstration is limited by the data transfer rate from the oscilloscope to around 250 ms.
3.4 Monitoring droplets in microfluidic systems
In our final demonstration, the CRDS setup was used to follow the flow of droplets or ‘slugs’ of an aqueous phase seeded in a toluene carrier phase, within a microfluidic channel. Fig. 8(a) and 8(b) clearly show the change in ringdown time for two different sets of flow conditions as the slugs of Rhodamine solution pass through the laser beam. To acquire these data, the toluene carrier phase was injected into the chip shown in Fig. 1 through port A at a flow rate of 0.003 mL min−1 (Fig. 8(a)) or 0.05 mL min−1 (Fig. 8(b)), and a 10−6 M aqueous solution of Rhodamine 6G was flowed through port B at 0.005 mL min−1 (Fig. 8(a)) or 0.025 mL min−1 (Fig. 8(b)).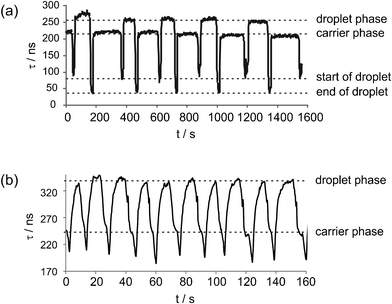 | ||
| Fig. 8 Droplet flow analysis using CRDS on a microfluidic chip. The ringdown time τ is tracked as droplets of 1 × 10−6 M R6G solution in a toluene carrier phase are flowed through a thiolene-glass chip at a total flow rate of (a) 0.008 mL min−1 and (b) 0.075 mL min−1. | ||
The behaviour of τ has several notable features. A clear change in ringdown time is seen as the aqueous (droplet) and toluene (carrier) phases pass through the laser beam. For the data shown in Fig. 8(a), for example, the ringdown time switches from ∼ 220 ns for the toluene phase to ∼ 260 ns for the aqueous phase. As described earlier, the mounting angle of the chip within the cavity has been optimised for measurements on aqueous phases. The refractive indices of water (n = 1.333) and toluene (n = 1.496) differ sufficiently that the ringdown time is longer for the aqueous phase than for the toluene phase, even though Rhodamine absorbs light at the wavelength of the laser. For experiments in which quantitative absorption analysis of droplets is the goal, the chip mounting angle should be optimised to achieve the greatest difference in ringdown time between the droplet and carrier phases. This was the case for the data shown in Fig. 8(b), in which the ringdown times are ∼240 ns for the toluene phase and ∼340 ns for the aqueous phase.
At low flow rates, a sharp reduction in τ is observed as the boundaries of each droplet pass through the laser beam. This is caused by the meniscus at the droplet/carrier phase boundary forming a lens that scatters the incident laser light out of the cavity, dramatically reducing the ringdown time. The consistent form of these scattering signals suggests that the topology of the interface between the two immiscible solutions is identical for each droplet, and a quantitative analysis of the signals could even be used to study droplet morphology. This structure is much less visible in Fig. 8(b), mostly due to the fact that the droplet flow rate in this experiment was close to the limiting time resolution imposed by our current fairly slow data acquisition system.
These results demonstrate the ability of the two-mirror CRDS system to interrogate and distinguish between individual droplets. The acquisition time of the ringdown is of the order of hundreds to thousands of nanoseconds. With an improved data transfer system (currently limited at 4Hz), measurements at kHz or even MHz data rates should become possible, allowing the spatio-temporal resolution of fast moving droplets, commensurate with kHz microfluidic label-free droplet production systems.
4 Conclusions and future work
Thiolene-glass microfluidic chips have been integrated into a two-mirror cavity ringdown spectrometer. By placing a chip at an angle of 59° to minimise reflective and refractive losses, a detection limit of 1.0 × 10−3 cm−1 has been achieved in a sample volume of 132 nL, corresponding to a 214 nM minimum detectable concentration of KMnO4. To illustrate the potential of the system for monitoring a variety of different processes on microfluidic chips, we have presented a number of proof-of-concept demonstrations, including the measurement of pH, reaction monitoring, and droplet flow monitoring. A number of improvements are planned for the future, including minimising the laser ‘footprint’ on the chip to allow smaller microfluidic channels to be probed, expanding the method to probe at multiple wavelengths or across a continuum of wavelengths,54 and upgrading the data acquisition system to allow measurements at rates exceeding the kHz range.Acknowledgements
This work was funded by the United Kingdom Engineering and Physical Sciences Research Council through grant EP/G027838/1.References
- A. deMello, Nature, 2006, 442, 394 CrossRef CAS.
- G. M. Whitesides, Nature, 2006, 442, 368 CrossRef CAS.
- J. P. McMullen and F. Jensen Klavs, Annu. Rev. Anal. Chem., 2010, 3, 19 CrossRef CAS.
- H. Song and R. F. Ismagilov, J. Am. Chem. Soc., 2003, 125(47), 14613 CrossRef CAS.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45(44), 7336 CrossRef CAS.
- F. E. Valera, M. Quaranta, A. Moran, J. Blacker, A. Armstrong, J. T. Cabral and D. G. Blackmond, Angew. Chem., Int. Ed., 2010, 49(14), 2478 CrossRef CAS.
- A. Q. Liu, H. J. Huang, L. K. Chin, Y. F. Yu and X. C. Li, Anal. Bioanal. Chem., 2008, 391(7), 2443 CrossRef CAS.
- P. S. Dittrich and A. Manz, Anal. Bioanal. Chem., 2005, 382(8), 1771 CrossRef CAS.
- K. B. Mogensen, H. Klank and J. P. Kutter, Electrophoresis, 2004, 25(21–22), 3498 CrossRef CAS.
- T. Vilkner, D. Janasek and A. Manz, Anal. Chem., 2004, 76, 3373 CrossRef CAS.
- M. Srisa-Art, A. J. deMello and J. B. Edel, Phys. Rev. Lett., 2008, 101(1), 014502 CrossRef.
- X. C. Solvas, M. Srisa-Art, A. J. deMello and J. B. Edel, Anal. Chem., 2010, 82(9), 3950 CrossRef.
- W. Ferstl, T. Klahn, W. Schweikert, G. Billeb, M. Schwarzer M and S. Lebbecke, Chem. Eng. Technol., 2007, 30, 370 CrossRef CAS.
- F. Benito-Lopez, W. Verboom, M. Kakuta, J. G. E. Gardeniers, R. J. M. Egberink, E. R. Oosterbroek, A. van den Berg and D. N. Reinhoudt, Chem. Commun., 2005, 2857 RSC.
- H. Lu, M. A. Schmidt and K. F. Jensen, Lab Chip, 2001, 1, 22 RSC.
- R. Herzig-Marx, K. T. Queeney, R. J. Jackman, M. A. Schmidt and K. F. Jensen, Anal. Chem., 2004, 76, 6476 CrossRef CAS.
- K. L. A. Chan, S. Gulati, J. B. Edel, A. J. deMello and S. G. Kazarian, Lab Chip, 2009, 9, 2909 RSC.
- K. L. A. Chan, X. Niu, A. J. deMello and S. G. Kazarian, Anal. Chem., 2011, 83(9), 3606 CAS.
- Y. Maguire, I. L. Chuang, S. Zhang and N. Gershenfeld, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(22), 9198 CrossRef CAS.
- P. D. I. Fletcher, S. J. Haswell and X. Zhang, Electrophoresis, 2003, 24, 3239 CrossRef CAS.
- S.-A. Leung, R. F. Winkle, R. C. R. Wootton and A. J. deMello, Analyst, 2005, 130, 46 RSC.
- A. Urakawa, F. Trachsel, P. R. von Rohr and A. Baiker, Analyst, 2008, 133, 1352 RSC.
- H. Wensink, F. Benito-Lopez, D. C. Hermes, W. Verboom, J. G. E. Gardeniers, D. N. Reinhoudt and A. van den Berg, Lab Chip, 2005, 5, 280 RSC.
- A. P. M. Kentgens, J. Bart, P. J. M. van Bentum, A. Brinkmann, E. R. H. van Eck, J. G. E. Gardeniers, J. W. G. Janssen, P. Knijn, S. Vasa and M. H. W. Verkuijlen, J. Chem. Phys., 2008, 128, 052202 CrossRef CAS.
- J. Bart, A. J. Kolkman, A. J. Oosthoek-de Vries, K. Koch, P. J. Nieuwland, J. W. G. Janssen, P. J. M. van Bentum, K. A. M. Ampt, F. P. J. T. Rutjes, S. S. Wijmenga, J. G. E. Gardeniers and A. P. M. Kentgens, J. Am. Chem. Soc., 2009, 131, 5014 CrossRef CAS.
- J.-S. Park, K.-B. Park, K.-S. Shin, H.-D. Park, M.-C. Kim, J.-R. Kim, S.-J. Park and Y.-H. Song, Sens. Actuators, B, 2006, 117(2), 516 CrossRef.
- M. P. Cecchini, J. Hong, C. Lim, J. Choo, T. Albrecht, A. J. deMello and J. B. Edel, Anal. Chem., 2011, 83(8), 3076 CrossRef CAS.
- A. O'Keefe and D. A. G. Deacon, Rev. Sci. Instrum., 1988, 59, 2544 CrossRef CAS.
- Cavity ring-down spectroscopy: techniques and applications, Ed. G. Berden and R. Engeln, John Wiley and Sons Inc, Hoboken, NJ, 2009 Search PubMed.
- G. Berden, R. Peeters and G. Meijer, Int. Rev. Phys. Chem., 2000, 19, 565 CrossRef CAS.
- N. Seetohul, Z. Ali and M. Islam, Analyst, 2009, 134, 1887 RSC.
- F. Li, A. A. Kachanov and R. N. Zare, Anal. Chem., 2007, 79, 5264 CrossRef CAS.
- H.-P. Loock, TrAC, Trends Anal. Chem., 2006, 25(7), 655 CrossRef CAS.
- C. Rushworth, D. James, J. W. L. Lee and C. Vallance, Anal. Chem., 2011, 83, 8492 CrossRef CAS.
- A. J. Hallock, E. S. F. Berman and R. N. Zare, Anal. Chem., 2002, 74(17), 1741 CrossRef CAS.
- B. Bahnev, L. van der Sneppen, A. Wiskerke, F. Ariese, C. Gooijer and W. Ubachs, Anal. Chem., 2005, 77, 1188 CrossRef CAS.
- L. van der Sneppen, A. Wiskerke, F. Ariese, C. Gooijer and W. Ubachs, Anal. Chim. Acta, 2006, 558(1–2), 2 CrossRef CAS.
- L. van der Sneppen, A. E. Wiskerke, F. Ariese, C. Gooijer and W. Ubachs, Appl. Spectrosc., 2006, 60(8), 931 CrossRef CAS.
- S. C. Xu, G. H. Sha and J. C. Xie, Rev. Sci. Instrum., 2002, 73(2), 255 CrossRef CAS.
- L. van der Sneppen, F. Ariese, C. Gooijer and W. Ubachs, J. Chromatogr., A, 2007, 1148(2), 184 CrossRef CAS.
- K. L. Snyder and R. N. Zare, Anal. Chem., 2003, 75(13), 3086 CrossRef CAS.
- K. L. Bechtel, R. N. Zare, A. A. Kachanov, S. S. Sanders and B. A. Paldus, Anal. Chem., 2005, 77(4), 1177 CrossRef CAS.
- A. J. Alexander, Anal. Chem., 2006, 78(15), 5597 CrossRef CAS.
- L. van der Sneppen, F. Ariese, C. Gooijer and W. Ubachs, Annu. Rev. Anal. Chem., 2009, 2, 13 CrossRef CAS.
- J. T. Cabral, S. D. Hudson, C. Harrison and J. F. Douglas, Langmuir, 2004, 20, 10020 CrossRef CAS.
- C. Harrison, J. T. Cabral, C. M. Stafford, A. Karim and E. J. Amis, J. Micromech. Microeng., 2004, 14(1), 153 CrossRef.
- J. T. Cabral and J. F. Douglas, Polymer, 2005, 46, 4230 CrossRef CAS.
- Z. T. Cygan, J. T. Cabral, K. L. Beers and E. J. Amis, Langmuir, 2005, 21, 3629 CrossRef CAS.
- M. Mazurenka, A. J. Orr-Ewing, R. Peverall and G. A. D. Ritchie, Annu. Rep. Prog. Chem., Sect. C, 2005, 101, 100 RSC.
- R. J. Field, E. Koros and R. M. Noyes, J. Am. Chem. Soc., 1972, 94(25), 8649 CrossRef CAS.
- An introduction to nonlinear chemical dynamics: oscillations, waves, patterns, and chaos, ed. I. R. Epstein and J. A. Pojman, Oxford University Press, 1998 Search PubMed.
- A. B. Theberge, F. Courtois, Y. Schaerli, M. Fischlechner, C. Abell, F. Hollfelder and W. T. S. Huck, Angew. Chem. Int. Ed., 2010, 49(34), 5846 CAS.
- H. Waechter, D. Munzke, A. Jang and H.-P. Loock, Anal. Chem., 2011, 83, 2719 CrossRef CAS.
- S. R. T. Neil, C. M. Rushworth, C. Vallance and S. R. Mackenzie, Lab Chip, 2011, 11, 3953 RSC.
| This journal is © The Royal Society of Chemistry 2012 |
